A quantitative assessment of chemical perturbations in thermotropic cyanobiphenyls†
Received
16th February 2016
, Accepted 26th April 2016
First published on 13th May 2016
Abstract
Chemical programming of the temperature domains of existence of liquid crystals is greatly desired by both academic workers and industrial partners. This contribution proposes to combine empirical approaches, which rely on systematic chemical substitutions of mesogenic molecules followed by thermal characterizations, with a rational thermodynamic assessment of the effects induced by chemical perturbations. Taking into account the similarities which exist between temperature-dependent cohesive Gibbs free energy densities (CFEDs) and pressure–temperature phase diagrams modeled with the Clapeyron equation, chemical perturbations are considered as pressure increments along phase boundaries, which control the thermotropic liquid crystalline properties. Taking the familiar calamitic amphiphilic cyanobiphenyl-type mesogens as models, the consequences of (i) methyl substitution of the aromatic polar heads and (ii) connections of bulky silyl groups at the termini of the apolar flexible alkyl chain on the melting and clearing temperatures are quantitatively analyzed. Particular efforts were focused on the translation of the thermodynamic rationalization into a predictive tool accessible to synthetic chemists mainly interested in designing liquid crystals with specific technological applications.
Introduction
Thermotropic liquid crystalline materials are characterized by the formation of fluidic and anisotropic phases, i.e. liquid crystalline phases or mesophases, in a certain temperature range between the ordered crystalline solid and the disordered isotropic liquid states.1 The partial long-range orientational ordering responsible for macroscopic anisotropy in liquid crystalline phases results from the simultaneous optimization of intermolecular interactions (= minimum enthalpic content)2 and excluded volumes (= maximum entropic content).3 Translated at the microscopic level, the design principles of thermotropic mesogenic materials are commonly based on molecules combining rod-like or disk-like rigid anisometric polarizable aromatic cores, providing order, decorated with flexible chains responsible for mobility and fluidity. A micro-segregation between the two different parts of these binary amphiphilic molecules is required for creating two distinct nano-spaces in the mesophase, a process closely related to mixing/demixing procedures observed in AB-type block copolymers. In this context, the Gibbs free energy of mixing4 can be modeled with the help of Huggins–Flory theory (eqn (1)), where ni is the number of moles and ϕi is the volume fraction of the part i in the block copolymer, and χA,B is the so-called interaction parameter.5| | ΔGmix = ΔHmix − TΔSmix = RT(nAϕBχAB) + RT(nA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕA + nB ϕA + nB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕB) ϕB) | (1) |
The last term on the right part of eqn (1) corresponds to the contribution of mixing entropy (−TΔSmix), whereas the first term RT(nAϕBχAB) is of enthalpic origin and measures the adhesion between the two separated phases. The interaction parameter χA,B can be estimated using eqn (2),6 in which Vseg is the reference volume of a unit segment in the polymer and δA and δB are the Hildebrand solubility parameters of each part taken separately.7| |  | (2) |
The square of this parameter, δ2, is related in eqn (3) to the cohesive energy density (CED) of a pure liquid having the same characteristics as those of the selected component of the block copolymer (U < 0 is the cohesive energy in the liquid, Vmol is the molar volume of the liquid and ΔHvap is the molar enthalpy of vaporization).7| |  | (3) |
Since χA,B ≥ 0, the larger the difference (δA − δB)2 between the cohesive energy densities of the two segments of the amphiphilic molecule, the more positive the ΔGmix thus demixing occurs spontaneously, leading to segregation into two separated space domains, each constituted by aggregated A and B segments, respectively. At higher temperature, the contribution of the mixing entropy −TΔSmix = RT(nA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕA + nB
ϕA + nB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕB) (eqn (1)) becomes more negative and it exactly overcomes ΔHmix = nAϕBVseg(δA − δB)2 at T = Ttransition, when ΔGmix = 0. Segregation is then lost at the order–disorder transition temperature, also assigned as the clearing temperature Tclearing in liquid crystals.8 Applied to the formation of nanostructured liquid crystals,6 this thermodynamic approach was successfully used for rationalizing the micro-segregation occurring in mesogenic calamitic cyanobiphenyls,9 cubic-phase-forming liquid crystalline molecules10 and polycatenar pentaerythritol derivatives.11 Whereas the high temperature limit of existence of a mesophase, i.e. its clearing point, can be approached with the help of the CED concept (eqn (3)), the low temperature cutoff, referred to as the melting point, requires the consideration of the closely related cohesion Gibbs free energy density (CFED) given in eqn (4).12,14
ϕB) (eqn (1)) becomes more negative and it exactly overcomes ΔHmix = nAϕBVseg(δA − δB)2 at T = Ttransition, when ΔGmix = 0. Segregation is then lost at the order–disorder transition temperature, also assigned as the clearing temperature Tclearing in liquid crystals.8 Applied to the formation of nanostructured liquid crystals,6 this thermodynamic approach was successfully used for rationalizing the micro-segregation occurring in mesogenic calamitic cyanobiphenyls,9 cubic-phase-forming liquid crystalline molecules10 and polycatenar pentaerythritol derivatives.11 Whereas the high temperature limit of existence of a mesophase, i.e. its clearing point, can be approached with the help of the CED concept (eqn (3)), the low temperature cutoff, referred to as the melting point, requires the consideration of the closely related cohesion Gibbs free energy density (CFED) given in eqn (4).12,14 is the Gibbs energy of cohesion, which estimates the degree of cohesion occurring in a condensed phase at a reference temperature Tref. Let us stress here that Tref is different from the transition temperature Ttr = ΔHtr/ΔStr at which
is the Gibbs energy of cohesion, which estimates the degree of cohesion occurring in a condensed phase at a reference temperature Tref. Let us stress here that Tref is different from the transition temperature Ttr = ΔHtr/ΔStr at which  .12
.12| |  | (4) |
The CFED concept was first exploited for the quantitative analysis of the thermal consequences of methylation reactions of the polar aromatic cores on the liquid crystalline properties of substituted cyanobiphenyls H25C12-LCi′,j (Fig. 1a).15
 |
| | Fig. 1 (a) Chemical structures of substituted cyanobiphenyls H25C12-LCi′,j° and (b) cohesive Gibbs free energy densities CFEDcrystversus melting temperature Tm (blue triangles, Tref = 360.6 K) and CFEDliq-crystversus clearing temperature Tclearing (red disks, Tref = 443.4 K).15 Units: 1.0 J cm−3 = 1.0 MPa. | |
Plots of CFED as a function of Ttr showed two different empirical linear correlations (Fig. 1b).15 The steep slope found for the CFEDcrystversus Tm plot (blue triangles in Fig. 1b) indicated that the cohesive free energy densities in the crystalline phases of H25C12-LCi′,j were not very sensitive to the methylation processes, therefore the melting temperatures were rather constant. In contrast, the flat slope observed for the CFEDliq-crystversus Tc plot (red disks in Fig. 1b) implied that the methylation of the cyanobiphenyl cores induced major changes in the cohesive Gibbs free energies responsible for the stability of the liquid crystalline phase.24 Consequently, the clearing temperatures of the mesogenic compounds H25C12-LCi′,j drastically depended on methylation of the rigid core, while their melting temperatures remained globally unchanged. Such rational and tunable control of the effect of chemical perturbations on the temperature-domain of liquid crystal existence is expected to significantly contribute to technological innovation.16 In this context, the substitution of 4′-cyanobiphenyl derivatives17 is especially appealing because of their worldwide applications as low-molecular weight,6,18 polymeric19 and metal-containing20 liquid crystals exhibiting magnetic and optical responses.
In order to extend the range of accessible transition temperatures for both melting and clearing processes observed in substituted cyanobiphenyls, we report here on the application of the CFED concept (eqn (4)) to the mesogenic R-C10H20-LCi′,j compounds (Scheme 1), in which both flexible alkyl tails and polar aromatic heads undergo physico-chemical stress via the connection of bulky substituents. We argue that the perturbation of the rigid core significantly affects the clearing temperature because the clearing process depends on the decorrelation of the polar heads.21 On the other hand, the melting process, which is associated with the decorrelation of the alkyl chains21 is relatively insensitive to head perturbation (Fig. 1b), but it could be tuned by a significant increase in the molecular polarisabilities of the flexible tails in R-C10H20-LCi′,j compounds along the series R = OH (9 electrons) < R = C2H5 (17 electrons) < R = OTBDMS (87 electrons) < R = OTBDPS (137 electrons).
 |
| | Scheme 1 Chemical structures of liquid crystalline substituted cyanobiphenyls R-C10H20-LCi′,j. | |
Results and discussion
Theoretical thermodynamic background
Since the empirical Trouton's rule fixes a constant value ΔSvap = 85–88 J mol−1 K−1 for the entropy of vaporization of any liquid,22 the associated enthalpy of vaporization of a specific liquid reflects its phase-transition temperature Tvap (eqn (5)) together with the average cohesive energy −U operating in the liquid phase (eqn (6)).23| | | −U = CED·Vmol = ΔHvap − RT = TvapΔSvap − RT | (6) |
In simple words, the estimation of the magnitude of the cohesive energy density (CED) operating in a liquid is sufficient for predicting its vaporization temperature Tvap. Applied to thermotropic liquid crystalline phases, this appealing concept would be of considerable help for programming their domains of existence. However, the lack of analogues of ‘Trouton's rule’ pertinent for the melting (crystal → liquid crystal, Tm) and clearing (liquid crystal → isotropic liquid, Tc) processes limits its pertinence because both enthalpy and entropy variably contribute to the cohesive energy densities operating in crystalline and liquid crystalline phases. The original concept of cohesion energy density (CED), well-suited for rationalizing the vaporization of isotropic liquids, was therefore replaced by that of cohesive Gibbs free energy density (CFED), which is adapted for the melting of crystals (eqn (7)) and the clearing of liquid crystals (eqn (8)). Tref is the reference temperature at which the cohesive Gibbs free energy  is estimated, while
is estimated, while  stand for the enthalpies and entropies of melting (m) and clearing (c) corrected at this temperature.12,13
stand for the enthalpies and entropies of melting (m) and clearing (c) corrected at this temperature.12,13| | 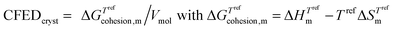 | (7) |
| |  | (8) |
When Tref is reasonably close to the melting or clearing temperatures for a series of compounds as illustrated for the methylation of cyanobiphenyl liquid crystals H25C12-LCi′,j in Fig. 1, the enthalpy and entropy changes recorded at the transition temperatures (Ttr) with the help of differential scanning calorimetry (DSC) are well-suited for estimating the CFED (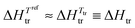 and
and  in eqn (7) and (8)).12,15 Applied to the melting of (i) linear alkanes of increasing length, (ii) organosilanes of increasing volumes and (iii) transition metals or metal oxides of increased polarizabilities,14 the CFEDcryst computed in the solid phases displayed empirical linear correlations with the transition temperatures (eqn (9), Vmol being the molar volume in the crystals).14
in eqn (7) and (8)).12,15 Applied to the melting of (i) linear alkanes of increasing length, (ii) organosilanes of increasing volumes and (iii) transition metals or metal oxides of increased polarizabilities,14 the CFEDcryst computed in the solid phases displayed empirical linear correlations with the transition temperatures (eqn (9), Vmol being the molar volume in the crystals).14| |  | (9) |
Since S = −(∂G/∂T)P,24 the slope of a linear CFED versus Ttr plot (eqn (9)) mirrors the cohesive entropy density α = −ΔStr/Vmol estimated at the reference temperature, a crucial parameter which reflects the sensitivity of the transition temperatures to the applied physico-chemical stress responsible for the emergence of the linear CFED versus Ttr series.15 The introduction of the phase equilibrium condition  into eqn (7) or eqn (8) gives
into eqn (7) or eqn (8) gives| |  | (10) |
Considering the Clapeyron equation adapted to the solid–liquid boundary, ΔStr can be written as| |  | (11) |
where ΔVtr is the change in volume accompanying the phase transition.24
The introduction of eqn (11) into eqn (10) yields
| |  | (12) |
Since
Tref was selected so that
Tref −
Ttr is small, we roughly assume for a non-infinitesimal Δ
T change that (
Ttr −
Tref)/Δ
T → 1,
eqn (12) becomes
| |  | (13) |
To the best of our knowledge, there is no theoretical support for a simple relationship between Δ
Vtr and
Vmol, but chemical intuition suspects a simple positive correlation for some minor perturbations within a series of compounds in the solid state,
24 a trend indeed experimentally found for the melting of linear alkanes with
λ = Δ
Vtr/(
Vmol −
V0) = 0.194(1).
15 Taking into account that the relative molar volume expansion at the transition temperature
λ is a ratio with no physical unit, the computed CFED for a given member of family of compounds reflects the ‘chemical changes’ or ‘chemical efforts’, expressed as a pressure increment Δ
P (
eqn (13) and
Fig. 1b) required for shifting its specific melting temperature toward the reference temperature
Tref of the family.
15
Preparation and mesogenic properties of substituted cyanobiphenyls R-C10H20-LCi′,j
The synthesis of R-C10H20-LCi′,j exploits the esterification of methyl-substituted 4-hydroxy-4′-cyanobiphenyls OCBi′,j with benzoates bearing flexible alkyl chains, a procedure previously optimized for the preparation of H25C12-LCi′,j.15 However, the connection of alkyl/aryl–silyl termini of variable sizes requires specific strategies compatible with their resistances toward acid and basic conditions.25 For the poorly reactive tert-butyldiphenylsilyl derivatives (TBDPS), the adequate silyl chloride was coupled to the liphophilic hydroxybenzaldehyde 1 to give the silylether 2, which was further oxidized into the Si-containing carboxylic acid 3.26 Subsequent esterification with OCBi′,j in the presence of dicyclohexyl-carbodiimide as an activator provided TBDPSO-C10H20-LCi′,j in good yield (Scheme 2, right part). The more sensitive tert-butyldimethyl silyl substituent (TBDMS) did not tolerate the acidic Lindgren conditions (NaClO2/sulfamic acid) used for aldehyde oxidation.27 The decyl chain bearing the TBDMS residue 4 was therefore connected to para-hydroxybenzoic-methylester to give 5, which was hydrolyzed under basic conditions to give the target silylether 6. Esterification with OCBi′,j yielded TBDMSO-C10H20-LCi′,j in fair yields. Finally, acidic deprotection in the presence of fluoride anions quantitatively gave HO-C10H20-LCi′,j (Scheme 2, left part).25
 |
| | Scheme 2 Synthesis of calamitic cyanobiphenyls R-C10H20-LCi′,j (DCC = N,N′-dicyclohexylcarbodiimide, DPTS = 4-[(dimethylamino)pyridinium]-4-toluenesulfonate, 4-ppy = 4-pyrrolidinopyridine, DMAP = 4-(dimethylamino)pyridine). | |
All substituted cyanobiphenyl molecules were isolated as amorphous oils, waxes or solids, the elemental analyses of which indicate the retention of traces of dichloromethane in the silyl-containing compounds TBDPSO-C10H20-LCi′,j and TBDMSO-C10H20-LCi′,j and of water for HO-C10H20-LCi′,j (Table S1 in the ESI†). 1H NMR and 13C NMR spectra confirm the chemical structures shown in Scheme 2, together with the presence of traces of solvents. Thermogravimetric analyses established that (i) solvent contaminants are smoothly removed in the 25–125 °C range (weight loss < 1%), (ii) all compounds remain intact below 190–200 °C and (iii) decompositions with significant weight losses occur only for T > 200 °C (Table S2 and Fig. S1, ESI†). Upon heating the solid samples of TBDPSO-C10H20-LCi′,j, TBDMSO-C10H20-LCi′,j and HO-C10H20-LCi′,j, variable enantiotropic fluidic birefringent textures are observed by polarized optical microscopy (POM), except for the dimethyl compounds RO-C10H20-LC2′,2 which display only monotropic mesophases (Table 1 and Fig. 2; Fig. S2–S4 in the ESI†). This behaviour is characteristic for the implementation of specific arrangements of the molecules in the liquid crystalline phases (Fig. 3 and Table 1), which can be assigned to either smectic A (focal conic fan textures with homeotropic areas illustrated in Fig. 2a) or nematic (schlieren textures illustrated in Fig. 2b) organizations.
Table 1 Transition temperatures, enthalpies and entropies for H25C12-LCi′,j, HO-C10H20-LCi′,j, TBDMSO-C10H20-LCi′,j and TBDPSO-C10H20-LCi′,j (DSC, 10 K min−1)
| Compounds |
Transitionsa |
T
tr
/°C (K) |
ΔHtr/kJ mol−1 |
ΔStr/J mol−1 K−1 |
Ref. |
|
SmA = smectic A phase, SmC = smectic C phase, N = nematic phase, Cr = crystalline state, G = glassy state, I = isotropic liquid.
Transition temperatures (onset point) were obtained during the second heating run. Glass transition temperatures (midpoint) were obtained during the first cooling run.
Monotropic transition.
Transition not detected by DSC, but estimated by POM.
|
|
H25C12-LC0′,0
|
Cr → SmA |
100 (373) |
46.0 |
123.2 |
15
|
| SmA → I |
218 (491) |
3.7 |
7.4 |
|
H25C12-LC3′,0
|
Cr → SmA |
95 (368) |
38.3 |
111.0 |
15
|
| SmA → N |
138 (411) |
— |
— |
| N → I |
153 (426) |
1.6 |
3.7 |
|
H25C12-LC2′,0
|
Cr → N |
81 (354) |
43.7 |
123.2 |
15
|
| N → I |
133 (406) |
1.2 |
2.9 |
|
H25C12-LC0′,3
|
Cr → SmC |
86 (359) |
52.8 |
147.8 |
15
|
| SmC → N |
146 (419) |
— |
— |
| N → I |
149 (422) |
0.7 |
1.7 |
|
H25C12-LC2′,2
|
Cr → I |
91 (364) |
53.9 |
147.7 |
15
|
| (I → N)c |
69 (342) |
— |
— |
|
|
|
HO-C10H20-LC0′,0
|
Cr → N |
121 (394) |
49.0 |
124.4 |
This work |
| N → I |
214 (487) |
1.2 |
2.5 |
|
HO-C10H20-LC3′,0
|
G → N |
115 (388)d |
— |
— |
This work |
| N → I |
161 (434) |
4.7 |
10.8 |
|
HO-C10H20-LC2′,0
|
Cr → N |
106 (379) |
120.0 |
316.7 |
This work |
| N → I |
134 (407) |
5.8 |
14.2 |
|
HO-C10H20-LC0′,3
|
Cr → N |
102 (375) |
129.3 |
344.9 |
This work |
| N → I |
136 (409) |
3.0 |
7.4 |
|
HO-C10H20-LC2′,2
|
Cr → I |
99 (372) |
156.4 |
420.3 |
This work |
| (I → N)c |
68 (341) |
— |
— |
|
|
|
TBDMSO-C10H20-LC0′,0
|
Cr → SmA |
59 (332) |
42.8 |
128.8 |
This work |
| SmA → I |
185 (458) |
17.9 |
39.0 |
|
TBDMSO-C10H20-LC3′,0
|
G → SmA |
−32 (241) |
— |
— |
This work |
| SmA → I |
111 (384) |
3.8 |
9.9 |
|
TBDMSO-C10H20-LC2′,0
|
Cr → SmA |
46 (319) |
18.2 |
57.1 |
This work |
| SmA → I |
90 (363) |
3.5 |
9.6 |
|
TBDMSO-C10H20-LC0′,3
|
Cr → SmA |
60 (333) |
20.6 |
61.8 |
This work |
| SmA → I |
130 (403) |
4.3 |
10.7 |
|
TBDMSO-C10H20-LC2′,2
|
Cr → I |
55 (328) |
32.3 |
98.4 |
This work |
| (I → SmA)c |
16 (289) |
2.4 |
8.1 |
|
|
|
TBDPSO-C10H20-LC0′,0
|
G → SmA |
40 (313)d |
— |
— |
This work |
| SmA → I |
115 (388) |
5.2 |
13.3 |
|
TBDPSO-C10H20-LC3′,0
|
G → SmA |
−17 (256) |
— |
— |
This work |
| SmA → I |
40 (313) |
1.8 |
5.8 |
|
TBDPSO-C10H20-LC2′,0
|
G′ → G |
−98 (175) |
— |
— |
This work |
| G → SmA |
−30 (243) |
— |
— |
| SmA → I |
11 (284) |
1.0 |
3.5 |
|
TBDPSO-C10H20-LC0′,3
|
G → SmA |
−17 (256) |
— |
— |
This work |
| SmA → I |
52 (325) |
2.1 |
6.5 |
|
TBDPSO-C10H20-LC2′,2
|
G′ → G |
−68 (205) |
0.8 |
3.9 |
This work |
| G → I |
−15 (258) |
— |
— |
 |
| | Fig. 2 Selected polarized optical micrographs of (a) TBDMSO-C10H20-LC0′,3 at 373 K (smectic A phase showing focal conic fan textures with homeotropic areas) and (b) HO-C10H20-LC0′,3 at 410 K (nematic phase showing schlieren textures). | |
 |
| | Fig. 3 Mesomorphic ranges and observed thermotropic mesophases for TBDPSO-C10H20-LCi′,j, TBDMSO-C10H20-LCi′,j and HO-C10H20-LCi′,j (scan rate 10 K min−1) compared with those previously reported for H25C12-LCi′,j.15 | |
Variable-temperature small-angle X-ray scatterings confirm these assignments since no low-angle diffraction pattern could be detected for the nematic mesophases obtained upon heating of HO-C10H20-LCi′,j (Fig. S5–S13, ESI†). The observation of one strong sharp peak (d001), sometimes accompanied by a weaker harmonic reflection (d002), is diagnostic for the formation of smectic A mesophases for TBDPSO-C10H20-LCi′,j and TBDMSO-C10H20-LCi′,j (Fig. S14–S32, ESI†), the periodic interlamellar distances of which lie in the 45.64–56.03 Å range, a trend in line with the formation of partial interdigitated bilayers (Appendix 1 in the ESI†).
As previously reported for H25C12-LCi′,j,16 the successive methylation of TBDPSO-C10H20-LCi′,j, TBDMSO-C10H20-LCi′,j or HO-C10H20-LCi′,j decreases the clearing temperatures, while the melting temperatures are much less affected (Fig. 3 and 4). The domain of existence of the liquid crystalline phases is thus reduced from ΔT ≈ 100 K for non-methylated cyanobiphenyls to ΔT ≈ 50 K for monomethylated derivatives and ΔT = 0 K for dimethylated compounds (Fig. 4a and Fig. S33, ESI†). Plots of the transition temperatures for each specific methylated cyanobiphenyl core as a function of increasing size of their flexible chains along the HO-C10H20-LCi′,j < H25C12-LCi′,j < TBDMSO-C10H20-LCi′,j < TBDPSO-C10H20-LCi′,j series show that the tail perturbation decreases both melting and clearing temperatures concomitantly (Fig. 4b and Fig. S34, ESI†). In summary, the methyl substitution of the aromatic cyanobiphenyl core controls the magnitude of the temperature domain over which the mesophase exists, while the tail substitution fixes the temperature of the centroids of the liquid crystalline domain. Consequently, RO-C10H20-LCi′,j scaffolds displaying room temperature liquid crystalline properties together with a significant temperature domain of existence requires a bulky silyl tail (R = TPDPSO) and no methyl substituent.
 |
| | Fig. 4 Melting and clearing temperatures observed for (a) HO-C10H20-LCi′,j upon successive methylation of the cyanobiphenyl heads and (b) R-C10H20-LC0′,3 upon successive connection of bulky groups to the flexible alkyl tails. Vmolecule are the Connolly volumes28 computed for the gas-phase optimized structures (Appendix 1 in the ESI†). The linear dotted traces are guides for the eye. | |
Thermodynamics of phase transitions and cohesive Gibbs free energy densities in substituted cyanobiphenyls RO-C10H20-LCi′,j
Differential scanning calorimetry (DSC) traces recorded for RO-C10H20-LCi′,j (Fig. 5 and Fig. S35–S37, ESI†) confirm the thermal behaviours established by polarized optical microscopy (Fig. 3 and Table 1), which are completed by minor kinetically-delayed reorganization processes for HO-C10H20-LC2′,0 (Fig. 5a), TBDMSO-C10H20-LC2′,0 (Fig. S36b, ESI†) and TBDMSO-C10H20-LC2′,2 (Fig. S36d and Appendix 2 in the ESI†). Transition enthalpies and entropies for the melting (ΔHm, ΔSm) and isotropization processes (ΔHclearing, ΔSclearing) were estimated during the second heating runs by integration of the DSC signals recorded at both 10 K min−1 (standard conditions, Table 2) and 0.5 K min−1 for minimizing deviations from thermodynamic equilibria (Table S4, ESI†). The calculated enthalpy and entropy contributions at the phase transition temperatures are similar at both scan rates (Fig. S35–S37, ESI†) and only the data recorded at standard 10 K min−1 are discussed in the remaining text (those recorded at 0.5 K min−1 are mentioned in the ESI† for comparison).
Table 2 Thermodynamic parameters (ΔHtr and ΔStr) and transition temperatures (Ttr) for the phase transitions H25C12-LCi′,j,16HO-C10H20-LCi′,j, TBDMSO-C10H20-LCi′,j and TBDPSO-C10H20-LCi′,j and associated cohesive Gibbs free energies in the solid (CFEDsolid) and liquid crystalline (CFEDliq-cryst) states (scan rate = 10 K min−1)
| Compounds |
V
mol
/mol cm−3 |
ΔHmeltingb/kJ mol−1 |
ΔSmeltingb/J mol−1 K−1 |
T
melting/K |
CFEDsolidc/J cm−3 |
ΔHclearingb/kJ mol−1 |
ΔSclearingb/J mol−1 K−1 |
T
clearing/K |
CFEDliq-crystd/J cm−3 |
Specific molar volumes Vmol are deduced from the Connolly volume estimated for the optimized gas-phase structures Vmol = NAv·Vmolecule.28
Obtained by DSC at the transition temperatures (10 K min−1).
 with Trefm = 360.3 K (eqn (7)). with Trefm = 360.3 K (eqn (7)).
 with Trefclearing = 393.3 K (eqn (8)).
Glass transition.
Non-mesogenic. with Trefclearing = 393.3 K (eqn (8)).
Glass transition.
Non-mesogenic.
|
|
H25C12-LC0′,0
|
488.5 |
46.0(5) |
123(1) |
373 |
3.2(7) |
3.66(7) |
7.5(1) |
491 |
1.5(2) |
|
H25C12-LC3′,0
|
504.1 |
38.3(4) |
104(1) |
368 |
1.6(5) |
1.57(3) |
3.7(1) |
426 |
0.24(8) |
|
H25C12-LC2′,0
|
503.4 |
43.7(4) |
123(2) |
354 |
−1.5(6) |
1.19(2) |
2.9(1) |
406 |
0.07(7) |
|
H25C12-LC0′,3
|
503.5 |
52.8(5) |
147(2) |
359 |
−0.4(7) |
0.70(2) |
1.7(1) |
422 |
0.10(4) |
|
H25C12-LC2′,2
|
517.7 |
53.9(5) |
148(2) |
364 |
1.1(7) |
|
|
|
|
|
HO-C10H20-LC0′,0
|
472.0 |
49.0(5) |
124(1) |
394 |
8.9(7) |
1.23(2) |
2.5(1) |
487 |
0.50(7) |
|
HO-C10H20-LC3′,0
|
489.2 |
|
|
|
|
0.97(2) |
2.2(1) |
434 |
0.19(5) |
|
HO-C10H20-LC2′,0
|
489.0 |
28.3(3) |
74.6(7) |
379 |
2.9(4) |
1.36(2) |
3.4(1) |
407 |
0.09(8) |
|
HO-C10H20-LC0′,3
|
488.7 |
30.5(3) |
81.3(8) |
375 |
2.5(4) |
0.71(2) |
1.7(1) |
409 |
0.06(4) |
|
HO-C10H20-LC2′,2
|
503.6 |
39.0(4) |
105(1) |
372 |
2.4(5) |
|
|
|
|
|
TBDMSO-C10H20-LC0′,0
|
604.0 |
14.7(2) |
44.2(4) |
332 |
−2.1(2) |
6.1(1) |
13.4(4) |
458 |
1.4(3) |
|
TBDMSO-C10H20-LC3′,0
|
622.6 |
|
|
|
|
3.78(8) |
9.8(2) |
384 |
−0.2(2) |
|
TBDMSO-C10H20-LC2′,0
|
622.1 |
18.2(2) |
57.0(6) |
319 |
−3.8(2) |
3.51(7) |
9.7(2) |
363 |
−0.5(2) |
|
TBDMSO-C10H20-LC0′,3
|
622.2 |
20.6(2) |
61.8(6) |
334 |
−2.6(2) |
4.34(9) |
10.8(2) |
403 |
0.2(2) |
|
TBDMSO-C10H20-LC2′,2
|
637.4 |
|
|
|
|
2.52(5) |
8.8(2) |
286 |
−1.5(1) |
|
TBDPSO-C10H20-LC0′,0
|
716.1 |
|
|
|
|
2.60(5) |
6.7(1) |
388 |
0.0(1) |
|
TBDPSO-C10H20-LC3′,0
|
730.5 |
|
|
|
|
1.82(4) |
5.8(1) |
313 |
−0.64(8) |
|
TBDPSO-C10H20-LC2′,0
|
729.0 |
|
|
|
|
0.97(3) |
3.4(1) |
284 |
−0.52(5) |
|
TBDPSO-C10H20-LC0′,3
|
729.7 |
|
|
|
|
2.09(4) |
6.4(1) |
325 |
−0.60(9) |
|
TBDPSO-C10H20-LC2′,2
|
744.5 |
|
|
|
|
|
|
|
|
 |
| | Fig. 5 DSC thermographs of (a) HOC10H20-LC2′,0, (b) TBDMSOC10H20-LC3′,0 and (c) TBDPSOC10H20-LC2′,0 (scan rate 10 K min−1, heating cycle with red downward peaks, cooling cycle with blue upward peaks). G = glass, Cr = crystal, SmA = smectic A, N = nematic, I = isotropic liquid and * = kinetically-delayed reorganization. | |
Since the minor chemical perturbation induced by the connection of methyl groups to the polar heads, or by the attachment of flexible alkyl chains of increasing polarizabilities (R = OH < TBDMSO < TBDPSO) at the non-polar tails do not drastically alter the average minimum intermolecular contact distances in the condensed phases, both melting and clearing processes exhibit linear enthalpy/entropy compensations for the four series of cyanobiphenyls HO-C10H20-LCi′,j, H25C12-LCi′,j, TBDMSO-C10H20-LCi′,j and TBDPSO-C10H20-LCi′,j (Fig. S38 and S39, ESI†).29 It is therefore acceptable to select only two reference temperatures Tref taken as the average of the observed phase transition temperatures for the melting (Trefm = 360.3 K) and clearing (Trefclearing = 393.3 K) processes. With this in mind, the cohesive Gibbs free energy densities in the solid state at 360.3 K (CFEDsolid collected in Table 2, Fig. 6 and Fig. S40, ESI†) and in the liquid crystalline state at 393.3 K (CFEDliq-cryst collected in Table 2, Fig. 7 and Fig. S41, ESI†) are easily obtained with the help of eqn (7) and (8) and using the transition enthalpies (ΔHmelting and ΔHclearing) and entropies (ΔSmelting and ΔSclearing) estimated at Tmelting, and Tclearing,12 together with the specific molar volumes Vmol taken as the Connolly volumes estimated for the optimized gas-phase structures (Tables S6 and S7, ESI†).28 Each cyanobiphenyl derivative is thus characterized by a 〈Ttr;CFED〉 point in the plots of CFED as a function of the transition temperatures of solids (Fig. 6) or of liquid crystals (Fig. 7). Reminding here that the cohesive free energy densities CFEDs have Pascal units (Fig. 6 and 7) and are proportional to the change in ‘chemical pressure’ produced by the chemical perturbation affecting each compound with respect to a common reference within a family of compounds obeying enthalpy/entropy compensation (eqn (13)), the traces obtained along a given chemical perturbation in Fig. 6 and 7 are reminiscent of, respectively, solid–liquid crystal and liquid crystal–liquid boundaries.15 Consequently, these phase boundaries can be tentatively approached with the help of the Clapeyron equation in its integrated form (eqn (14)),24 in which the enthalpy of phase transition (ΔHtr) and the change in volume accompanying the phase transition (ΔVtr) can be thought as those of the virtual reference compound, which generates the series compounds subjected to successive chemical perturbations.15
| |  | (14) |
when
T is close to the reference temperature
Tref, as it is the case for both melting and clearing temperatures collected for
HO-C10H20-LCi′,j,
H25C12-LCi′,j,
TBDMSO-C10H20-LCi′,j and
TBDPSO-C10H20-LCi′,j, the logarithm can be approximated with ln(
T/
Tref) = ln(1 + (
T −
Tref)/
Tref) ≈ (
T −
Tref)/
Tref and
eqn (14) becomes the equation of a straight line (
eqn (15)), which is well suited for modeling minor perturbations.
24| |  | (15) |
The solid–liquid crystal boundaries (
Fig. 6) and liquid crystal–isotropic liquid boundaries (
Fig. 7) fitted with the Clapeyron
eqn (14) globally reproduce the trend found for the experimental CFED
versus Ttr plots generated by the tail and the head perturbations applied to the
RO-C10H20-LCi′,j family (full black traces in
Fig. 6 and 7).
30 We also note that local linear correlations according to
eqn (15) can be identified (dotted colored traces in
Fig. 6 and 7). Focussing on the melting processes (
Fig. 6), we observe that the successive methylation reactions of the aromatic cyanobiphenyl cores (= head perturbation) have only minor effects on the melting temperatures as long as the flexible alkyl chains are not too polarizable. Large absolute cohesive entropy densities of 0.24(1) ≤ |
SCFED| = (∂CFED/∂
T)
P ≤ 0.31(6) J K
−1 cm
3 are thus measured for the stepwise methylation of
H25C12-LCi′,j (blue dotted line in
Fig. 6a) and
HO-C10H20-LCi′,j (red dotted line in
Fig. 6a). Alternatively, the connection of alkyl tails of increasing size and polarizabilities provides flatter slopes 0.11(3) ≤ |
SCFED| = (∂CFED/∂
T)
P ≤ 0.17(4) J K
−1 cm (
Fig. 6b), which lead to the conclusion that the melting temperatures are amenable to larger tuning upon chemical perturbation of the non-polar flexible tails.
 |
| | Fig. 6 Cohesive free energy densities (CFEDs, scan rate = 10 K min−1) versus transition temperatures for the melting processes highlighting (a) the influence of head substitution and (b) the influence of tail substitution. The full black traces correspond to the solid–liquid crystal boundary fitted with the Clapeyron equation (eqn (14) using an optimized ΔHtr/ΔVtr ratio).30 The dotted colored traces show local linear correlations (eqn (15)) for (a) a given tail substitution and (b) a given head substitution. | |
 |
| | Fig. 7 Cohesive free energy densities (CFEDs, scan rate = 10 K min−1) versus transition temperatures for the clearing processes highlighting (a) the influence of head substitution and (b) the influence of tail substitution. The full black traces correspond to the liquid crystal–liquid boundary fitted with the Clapeyron equation (eqn (14) using an optimized ΔHtr/ΔVtr ratio).30 The dotted colored traces show local linear correlations (eqn (15)) for (a) a given tail substitution and (b) a given head substitution. | |
For the clearing processes, the measured absolute cohesive entropy densities 0.005(2) ≤ |SCFED| = (∂CFED/∂T)P ≤ 0.018(2) J K−1 cm3 (Fig. 7) are one to two orders of magnitude smaller than those found for the melting processes (Fig. 6), which implies that the chemical perturbations applied to both polar head (methylation) and flexible tails (bulky silyl groups) have considerable influence on the clearing temperatures.
Practically speaking, the latter quantitative thermodynamic analysis can be exploited upon plotting the transition temperatures of HO-C10H20-LCi′,j, H25C12-LCi′,j, TBDMSO-C10H20-LCi′,j and TBDPSO-C10H20-LCi′,j as a function of their molecular volumes (Fig. 4 and Fig. S33 and S34, ESI†). Successive methylation reactions of the polar aromatic cyanobiphenyl cores decrease the clearing temperatures much ‘faster’ than the related melting temperatures. Consequently, the considerable ratio of the two pseudo-linear correlations 1.91 ≤ Slopeclearing/Slopemelting ≤ 14.06 drastically limits the liquid crystalline properties of polymethylated cyanobiphenyl derivatives (Fig. 4a and Fig. S33, ESI†). Stepwise connections of substituents of increasing polarizability at the termini of the alkyl chain have roughly the opposite effect leading to a small ratio 0.71 ≤ Slopeclearing/Slopemelting ≤ 1.29 (Fig. 4b and Fig. S34, ESI†). Altogether, polymethylation of the rigid core must be avoided, while large silyl groups should be connected at the termini of the flexible tail for maximizing the temperature domain of existence of the mesophase in these cyanobiphenyl derivatives. Translated in terms of micro-segregation theory,1–3,5–11 one can say that successive methylation of the cyanobiphenyl cores reduces the polarity of the aromatic segment, which favours mixing of the antagonistic part of the amphiphilic molecules. On the other hand, the substitution of the apolar alkyl chain with silyl groups has only minor effects on the polarity of this segment and demixing is maintained under these conditions. The latter thermodynamic approach appears quite general and can be used for quantitatively analyzing various types of chemical perturbations such as the famous polycatenar effect, which drastically shifts the domain of existence of liquid crystals when diverging long alkyl chains are connected, for instance, to mesogenic rod-like 2,2′-bipyridine derivatives (Fig. 8a)31 or 2,6-bis(benzimidazol-2-yl)pyridine derivatives (Fig. 8b).32 When subjected to CFED analysis (Fig. 9), unusually small absolute cohesive entropy densities are computed in the solid state 0.11 ≤ |SCFED| = (∂CFED/∂T)P ≤ 0.13 J K−1 cm3 (Fig. 9a), which can be compared with 0.24 ≤ |SCFED| = (∂CFED/∂T)P ≤ 0.31 J K−1 cm3 found for the cyanobiphenyls HO-C10H20-LCi′,j and H25C12-LCi′,j (Fig. 6a). We suspect that the reduction of the phase cohesion brought by the connection of diverging alkyl chains for polycatenars in the solid state along the two series L1 → L2 → L3 and L4 → L5 → L6 is compensated by a concomitant large increase in molar volumes, which limits the emergence of large cohesive entropy densities. Consequently, some drastic and remarkable decrease of the melting temperatures can be induced upon successive connections of diverging alkoxy chains (black traces in Fig. 8). Alternatively, the absolute cohesive entropy densities measured in the mesophases upon the polycatenar effect (0.013 ≤ SCFED = −(∂CFED/∂T)P ≤ 0.021 J K−1 cm3 (Fig. 9b)) are similar to those reported for cyanobiphenyls (0.005 ≤ SCFED = −(∂CFED/∂T)P ≤ 0.017 J K−1 cm3 in Fig. 7), which ensures clearing temperatures high enough to maintain large domains of existence for the liquid crystalline phases in polycatenars (red traces in Fig. 8).
 |
| | Fig. 8 Melting and clearing temperatures observed in (a) 2,2′-bipyridine polycatenars31 and (b) 2,6-bis(benzimidazol-2-yl)pyridine polycatenars32 upon successive connection of diverging flexible dodecyloxy chains. Vmolecule are the Connolly volumes28 computed for the gas-phase optimized structures. The linear dotted traces are guides for the eye. | |
 |
| | Fig. 9 Plots of cohesive Gibbs free energy densities (CFEDs) versus transition temperatures computed for (a) melting and (b) clearing processes occurring in the polycatenar ligands L1–L3 (red traces)31 and L4–L6 (blue traces).32 The dotted colored traces show the local linear correlations, from which the cohesive entropy densities induced by the polycatenar effect in each series are estimated. | |
Conclusion
The thermodynamic investigation of the phase transitions occurring in the mesogenic substituted cyanobiphenyls HO-C10H20-LCi′,j, H25C12-LCi′,j, TBDMSO-C10H20-LCi′,j and TBDPSO-C10H20-LCi′,j confirms that the cohesion Gibbs free energy density (CFED) estimated at a common reference temperature for a series of compounds obeying H/S compensation can be interpreted as pressure increments produced by a specific ‘chemical perturbation’, which stepwise shifts the phase transition temperatures (Tm or Tclearing). The CFED versus Ttr plots are therefore closely related to P–T diagrams, where the slopes of local linear phase boundaries represent cohesive entropy densities, which can be exploited for programming melting and clearing temperatures in liquid crystals. A steep slope reveals a minor dependence of the transition temperatures upon the considered chemical perturbations, the reverse situation being pertinent for a flat slope. In terms of intermolecular cohesion, a large cohesive entropy density can be understood as the induction, by the selected perturbation, of major modifications in the organization of the phase for a minimal volume increase. It is therefore expected (observed) that chemical perturbations operating in solid phases, where intermolecular interactions are tighter, provide larger cohesive entropy densities than those monitored in less compact liquid-crystalline phases. Applied to calamitic cyanobiphenyl mesogens possessing variable methyl substitutions and tail sizing, the large slopes found for the crystal → liquid crystal melting processes (Fig. 6) point to a limited tuning of the melting temperature (Tm) imposed by these perturbations. We however note that connections of polarizable silyl groups at the end of the flexible apolar alkyl chains (Fig. 6b) produce larger effects on Tm than methylation of the cyanobiphenyl cores (Fig. 6a). In contrast, the flat liquid-crystal → isotropic liquid boundary characterizing the clearing processes (Fig. 7) implies that both perturbations significantly affect the clearing temperatures.
Experimental
Solvents and starting materials
Chemicals were purchased from Sigma-Aldrich and Acros and used without further purification unless otherwise stated. Methylated 4′-hydroxy-4-cyanobiphenyls OCBi′,j,13H25C12-LCi′,j compounds,15 and 10-bromodecan-1-ol33 were prepared according to published procedures. THF and dichloromethane were dried through an alumina cartridge. Silica-gel plates (Merck, 60 F254) were used for thin-layer chromatography, SilicaFlash® silica gel P60 (0.04–0.063 mm) was used for preparative column chromatography.
Synthesis of TBDPSO-C10H20-LCi′,j, TBDMSO-C10H20-LCi′,j and HO-C10H20-LCi′,j
Abbreviations: DCC = N,N′-dicyclohexylcarbodiimide, DPTS = 4-[(dimethylamino)pyridinium]-4-toluenesulfonate, 4-ppy = 4-pyrrolidinopyridine, DMAP = 4-(dimethylamino)pyridine, TBDPS = tert-butyldiphenylsilyl, TBDMS = tert-butylmethylsilyl.
Preparation of [4-(dimethylamino)pyridinium 4-toluenesulfonate] (DPTS).
4-(Dimethylamino)pyridine (DMAP) (20.00 g, 163.71 mmol) and 4-toluenesulfonic acid (28.19 g, 163.71 mmol) were added to toluene (400 mL) in a 1 L flask with a Dean–Stark apparatus was placed on top. The solution was refluxed for 24 h with care taken for water elimination. The mixture was then cooled to room temperature and filtered. The solid was then crystallized in CH2Cl2 to afford pure DPTS (40.51 g, 84%) as white needles. 1H-NMR (400 MHz, DMSO-d6) δ = 8.21 (d, 3J = 7.7 Hz, 2H), 7.48 (d, 3J = 8.1 Hz, 2H), 7.11 (d, 3J = 7.8 Hz, 2H), 6.98 (d, 3J = 7.7 Hz, 2H), 3.17 (s, 6H), 2.28 (s, 3H). 13C NMR (100 MHz, DMSO-d6) δ = 157.48, 145.99, 140.00, 138.47, 128.74, 126.11, 107.56, 40.20, 21.39.
Preparation of compound 1.
A solution of 10-bromodecanol (9.85 g, 41.52 mmol), 4-hydroxybenzaldehyde (4.23 g, 34.60 mmol), K2CO3 (11.48 g, 83.04 mmol) and a catalytic amount of KI in butan-2-one (200 mL) was stirred at reflux for 24 hours. After cooling at room temperature, the solvent was removed under reduced pressure, and the residue was taken up in water and extracted with CH2Cl2. The organic layer was dried over Na2SO4 and evaporated to dryness. The crude product was purified by column chromatography (SiO2, hexane/EtOAc 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25) to give pure 2 (8.26 g, 86%) as a white solid. 1H-NMR (400 MHz, CDCl3) δ = 9.87 (s, 1H), 7.82 (d, 3J = 8.8 Hz, 2H), 6.98 (d, 3J = 8.7 Hz, 2H), 4.03 (t, 3J = 6.5 Hz, 2H), 3.63 (t, 3J = 6.6 Hz, 2H), 1.84–1.77 (m, 2H), 1.60–1.53 (m, 2H), 1.50–1.42 (m, 2H), 1.39–1.31 (m, 10H). 13C-NMR (100 MHz, CDCl3) δ = 190.98, 164.39, 132.12, 129.86, 114.87, 68.54, 63.15, 32.90, 29.62, 29.57, 29.51, 29.43, 29.16, 26.06, 25.85.
25) to give pure 2 (8.26 g, 86%) as a white solid. 1H-NMR (400 MHz, CDCl3) δ = 9.87 (s, 1H), 7.82 (d, 3J = 8.8 Hz, 2H), 6.98 (d, 3J = 8.7 Hz, 2H), 4.03 (t, 3J = 6.5 Hz, 2H), 3.63 (t, 3J = 6.6 Hz, 2H), 1.84–1.77 (m, 2H), 1.60–1.53 (m, 2H), 1.50–1.42 (m, 2H), 1.39–1.31 (m, 10H). 13C-NMR (100 MHz, CDCl3) δ = 190.98, 164.39, 132.12, 129.86, 114.87, 68.54, 63.15, 32.90, 29.62, 29.57, 29.51, 29.43, 29.16, 26.06, 25.85.
Preparation of compound 2.
A solution of 1 (3.00 g, 10.78 mmol), TBDPS-Cl (2.8 mL, 10.78 mmol), imidazole (2.94 g, 43.12 mmol) and a catalytic amount of DMAP in dry CH2Cl2 (20 mL) was stirred at room temperature for 24 hours. The reaction mixture was partitioned between EtOAc (100 mL) and H2O (20 mL). The organic layer was washed with brine (3 × 20 mL), dried over Na2SO4 and evaporated to dryness. The crude product was purified by column chromatography (SiO2, CH2Cl2) to give pure 2 (5.01 g, 90%) as a colorless oil. 1H-NMR (400 MHz, CDCl3) δ = 9.89 (s, 1H), 7.83 (d, 3J = 8.7 Hz, 2H), 7.68 (m, 4H), 7.40 (m, 6H), 7.00 (d, 3J = 8.7 Hz, 2H), 4.05 (t, 3J = 6.6 Hz, 2H), 3.67 (t, 3J = 6.5 Hz, 2H), 1.86–1.79 (m, 2H), 1.61–1.54 (m, 2H), 1.51–1.44 (m, 2H), 1.40–1.29 (m, 10H), 1.06 (s, 9H). 13C-NMR (100 MHz, CDCl3) δ = 190.84, 164.29, 135.59, 134.83, 134.21, 132.01, 129.76, 129.50, 127.73, 127.58, 114.77, 68.44, 64.01, 32.59, 29.53, 29.48, 29.36, 29.34, 29.08, 26.90, 25.98, 25.78, 19.25.
Preparation of compound 3.
A solution of 2 (5.01 g, 9.69 mmol), NaClO2 (4.38 g, 48.45 mmol) and H2NSO3H (5.17 g, 53.30 mmol) in THF (50 mL) and H2O (50 mL) was stirred at room temperature for 2 hours. After evaporation of THF, the aqueous layer was extracted with CH2Cl2 (3 × 50 mL). The organic layer was dried over Na2SO4 and evaporated to dryness. The crude product was purified by recrystallization in hexane to give pure 3 (5.16 g, 100%) as white needles. 1H-NMR (400 MHz, CDCl3) δ = 8.06 (d, 3J = 8.9 Hz, 2H), 7.68 (m, 4H), 7.39 (m, 6H), 6.94 (d, 3J = 8.9 Hz, 2H), 4.03 (t, 3J = 6.6 Hz, 2H), 3.66 (t, 3J = 6.5 Hz, 2H), 1.85–1.78 (m, 2H), 1.60–1.53 (m, 2H), 1.50–1.43 (m, 2H), 1.38–1.28 (m, 10H), 1.05 (s, 9H). 13C-NMR (100 MHz, CDCl3) δ = 171.49, 163.83, 135.73, 134.34, 132.48, 129.62, 127.71, 121.43, 114.35, 68.44, 64.15, 32.72, 29.67, 29.62, 29.49, 29.24, 27.03, 26.13, 25.91, 19.38.
Preparation of compound 4.
A solution of 10-bromodecan-1-ol (17.97 g, 75.76 mmol), TBDMS-Cl (13.70 g, 90.91 mmol), DMAP (850 mg, 7.58 mmol) and imidazole (7.74 g, 113.64 mmol) in dry CH2Cl2 (150 mL) was stirred at room temperature for 12 h. The mixture was washed with H2O (3 × 50 mL) and brine (3 × 50 mL), dried over Na2SO4 and evaporated to dryness. The crude product was purified by column chromatography (SiO2, hexane/EtOAc 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) to provide 4 (18.89 g, 71%) as a colorless oil. 1H-NMR (400 MHz, CDCl3) δ = 3.60 (t, 3J = 6.6 Hz, 2H), 3.41 (t, 3J = 6.9 Hz, 2H), 1.89–1.82 (m, 2H), 1.55–1.47 (m, 2H), 1.46–1.39 (m, 2H), 1.35–1.29 (m, 10H), 0.90 (s, 9H), 0.05 (s, 6H). 13C-NMR (100 MHz, CDCl3) δ = 63.45, 34.17, 33.02, 32.98, 29.65, 29.52, 28.90, 28.32, 26.13, 25.92, −2.3.
2) to provide 4 (18.89 g, 71%) as a colorless oil. 1H-NMR (400 MHz, CDCl3) δ = 3.60 (t, 3J = 6.6 Hz, 2H), 3.41 (t, 3J = 6.9 Hz, 2H), 1.89–1.82 (m, 2H), 1.55–1.47 (m, 2H), 1.46–1.39 (m, 2H), 1.35–1.29 (m, 10H), 0.90 (s, 9H), 0.05 (s, 6H). 13C-NMR (100 MHz, CDCl3) δ = 63.45, 34.17, 33.02, 32.98, 29.65, 29.52, 28.90, 28.32, 26.13, 25.92, −2.3.
Preparation of compound 5.
A solution of methyl-4-hydroxybenzoate (8.18 g, 53.75 mmol), K2CO3 (14.70 g, 106.30 mmol) and a catalytic amount of 18-crown-6 in acetone (200 mL) was stirred at room temperature for 30 minutes. Then, 4 (18.89 g, 53.75 mmol) was added and the mixture was stirred under reflux for 3 days. The mixture was filtered and the precipitate was washed with Et2O (3 × 50 mL). After evaporation to dryness, the residue was dissolved in Et2O and the organic phase was washed with H2O (3 × 100 mL), dried over MgSO4 and evaporated to dryness. The crude product was purified by column chromatography (SiO2, CH2Cl2) to give 5 (17.79 g, 78%) as a white solid. 1H-NMR (400 MHz, CDCl3) δ = 7.98 (d, 3J = 8.7 Hz, 2H), 6.90 (d, 3J = 8.7 Hz, 2H), 4.00 (t, 3J = 6.5 Hz, 2H), 3.88 (s, 3H), 3.60 (t, 3J = 6.6 Hz, 2H), 1.83–1.76 (m, 2H), 1.54–1.42 (m, 4H), 1.38–1.30 (m, 10H), 0.90 (s, 9H), 0.05 (s, 6H). 13C-NMR (100 MHz, CDCl3) δ = 167.03, 163.08, 131.68, 122.43, 114.18, 68.31, 63.43, 51.93, 33.00, 29.67, 29.62, 29.54, 29.47, 29.24, 26.12, 25.92, −5.10.
Preparation of compound 6.
A solution of KOH (2.23 g, 39.74 mmol) in H2O (20 mL) was slowly added to a stirred solution of 5 (14.00 g, 33.11 mmol) in EtOH (60 mL). The mixture was stirred at reflux for 1 h. After evaporation to dryness, the crude product was suspended in H2O and acidified to pH = 1 with 2 M HCl. The precipitate was filtered and dried under vacuum to give a white solid. A small amount of unprotected alcohol was visible by 1H-NMR. Further purification by column chromatography (SiO2, hexane/EtOAc (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1)) was required to obtain pure 6 (3.68 g, 27%) as a white solid. 1H-NMR (400 MHz, CDCl3) δ = 8.05 (d, 3J = 8.9 Hz, 2H), 6.93 (d, 3J = 8.9 Hz, 2H), 4.03 (t, 3J = 6.6 Hz, 2H), 3.60 (t, 3J = 6.6 Hz, 2H), 1.84–1.77 (m, 2H), 1.55–1.43 (m, 4H), 1.39–1.31 (m, 10H), 0.90 (s, 9H), 0.05 (s, 6H). 13C-NMR (100 MHz, CDCl3) δ = 171.31, 163.82, 132.47, 121.42, 114.35, 68.44, 63.48, 33.03, 29.70, 29.64, 29.57, 29.49, 29.24, 26.14, 25.94, 18.54, −5.09.
1)) was required to obtain pure 6 (3.68 g, 27%) as a white solid. 1H-NMR (400 MHz, CDCl3) δ = 8.05 (d, 3J = 8.9 Hz, 2H), 6.93 (d, 3J = 8.9 Hz, 2H), 4.03 (t, 3J = 6.6 Hz, 2H), 3.60 (t, 3J = 6.6 Hz, 2H), 1.84–1.77 (m, 2H), 1.55–1.43 (m, 4H), 1.39–1.31 (m, 10H), 0.90 (s, 9H), 0.05 (s, 6H). 13C-NMR (100 MHz, CDCl3) δ = 171.31, 163.82, 132.47, 121.42, 114.35, 68.44, 63.48, 33.03, 29.70, 29.64, 29.57, 29.49, 29.24, 26.14, 25.94, 18.54, −5.09.
General procedure for the preparation of TBDPSO-C10H20-LCi′,j
To a solution of OCBi′,j (1 eq.), 3 (1.1 eq.) and DPTS (1 eq.) in dry CH2Cl2 (25 mL) stirred at 0 °C were added DCC (1.5 eq.) and 4-ppy (spatula tip). The mixture was allowed to heat slowly to room temperature and stirred for 48 h. After filtration, the solution was evaporated to dryness and the residue was purified by column chromatography (SiO2, CH2Cl2) to afford pure TBDPSO-C10H20-LCi′,j. Yields ranged from 98 to 99%.
TBDPSO-C10H20-LC0′,0
.
Colorless wax (η = 99%). 1H-NMR (400 MHz, CDCl3) δ = 8.17 (d, 3J = 8.9 Hz, 2H), 7.75 (d, 3J = 8.4 Hz, 2H), 7.69 (m, 6H), 7.65 (d, 3J = 8.6 Hz, 2H), 7.45–7.37 (m, 6H), 7.34 (d, 3J = 8.6 Hz, 2H), 7.00 (d, 3J = 8.9 Hz, 2H), 4.06 (t, 3J = 6.5 Hz, 2H), 3.68 (t, 3J = 6.5 Hz, 2H), 1.87–1.80 (m, 2H), 1.61–1.54 (m, 2H), 1.53–1.45 (m, 2H), 1.41–1.30 (m, 10H), 1.07 (s, 9H). 13C-NMR (100 MHz, CDCl3) δ = 164.97, 163.85, 151.73, 145.01, 136.82, 135.71, 134.32, 132.78, 132.49, 129.61, 128.48, 127.82, 127.70, 122.71, 121.33, 119.02, 114.51, 111.12, 68.50, 64.13, 32.71, 29.65, 29.61, 29.84, 29.23, 27.01, 26.12, 25.90, 19.36. Elem. anal. calcd for C46H51NO4Si·0.04CH2Cl2 (713.38 g mol−1): C 77.51, H 7.22, N 1.96; found: C 77.53, H 7.24, N 1.86.
TBDPSO-C10H20-LC3′,0
.
Colorless wax (η = 99%). 1H-NMR (400 MHz, CDCl3) δ = 8.18 (d, 3J = 8.8 Hz, 2H), 7.73 (d, 3J = 8.4 Hz, 2H), 7.68 (m, 6H), 7.50 (d, 4J = 2.3 Hz, 1H), 7.47 (dd, 3J = 8.2 Hz and 4J = 2.4 Hz, 1H), 7.43–7.37 (m, 6H), 7.25 (d, 3J = 8.1 Hz, 1H), 7.00 (d, 3J = 8.9 Hz, 2H), 4.06 (t, 3J = 6.6 Hz, 2H), 3.67 (t, 3J = 6.5 Hz, 2H), 2.31 (s, 3H), 1.87–1.80 (m, 2H), 1.60–1.54 (m, 2H), 1.53–1.45 (m, 2H), 1.40–1.30 (m, 10H), 1.06 (s, 9H). 13C-NMR (100 MHz, CDCl3) δ = 164.72, 163.86, 150.36, 145.25, 137.06, 135.72, 134.34, 132.74, 132.49, 131.48, 130.18, 129.62, 127.86, 127.71, 126.00, 123.07, 121.28, 119.10, 114.55, 111.00, 68.52, 64.14, 32.72, 29.67, 29.63, 29.49, 29.24, 27.02, 26.13, 25.91, 19.38, 16.62. ESI-MS (CH3OH/formic acid 0.01%, soft pos. mode): m/z calcd for C47H55NO5Si [M + H2O]+ 741.4, found 741.5, C47H54NO4Si [M + H]+ 724.4, found 724.5, C41H48NO4Si [M–Ph]+ 646.4, found 646.8. Elem. anal. calcd for C47H53NO4Si·0.2CH2Cl2 (741.00 g mol−1): C 76.51, H 7.26, N 1.89; found: C 76.49, H 7.48, N 1.70.
TBDPSO-C10H20-LC2′,0
.
Colorless wax (η = 99%). 1H-NMR (400 MHz, CDCl3) δ = 8.16 (d, 3J = 8.8 Hz, 2H), 7.73 (d, 3J = 8.2 Hz, 2H), 7.68 (m, 4H), 7.46 (d, 3J = 8.2 Hz, 2H), 7.43–7.36 (m, 6H), 7.25 (d, 3J = 8.3 Hz, 1H), 7.16 (d, 4J = 2.4 Hz, 1H), 7.12 (dd, 3J = 8.2 Hz and 4J = 2.4 Hz, 1H), 6.99 (d, 3J = 8.8 Hz, 2H), 4.06 (t, 3J = 6.5 Hz, 2H), 3.67 (t, 3J = 6.5 Hz, 2H), 2.28 (s, 3H), 1.87–1.80 (m, 2H), 1.61–1.54 (m, 2H), 1.52–1.45 (m, 2H), 1.40–1.30 (m, 10H), 1.06 (s, 9H). 13C-NMR (100 MHz, CDCl3) δ = 165.18, 163.80, 151.04, 146.20, 137.66, 136.90, 135.72, 134.33, 132.46, 132.18, 130.65, 130.23, 129.62, 127.70, 123.95, 121.48, 119.67, 119.04, 114.49, 111.03, 68.50, 64.14, 32.72, 29.67, 29.62, 29.49, 29.24, 27.02, 26.13, 25.91, 20.61, 19.37. ESI-MS (CH3OH/formic acid 0.01%, soft pos. mode): m/z calcd for C47H55NO5Si [M + H2O]+ 741.4, found 741.8, C47H54NO4Si [M + H]+ 724.4, found 724.5, C41H48NO4Si [M–Ph]+ 646.4, found 646.8. Elem. anal. calcd for C47H53NO4Si·0.07CH2Cl2 (729.96 g mol−1): C 77.45, H 7.34, N 1.92; found: C 77.44, H 7.47, N 1.77.
TBDPSO-C10H20-LC0′,3
.
Colorless wax (η = 98%). 1H-NMR (400 MHz, CDCl3) δ = 8.16 (d, 3J = 8.8 Hz, 2H), 7.68 (d, 3J = 7.8 Hz, 4H), 7.63 (d, 3J = 8.6 Hz, 2H), 7.54 (m, 1H), 7.49 (dd, 3J = 8.0 Hz and 4J = 1.7 Hz, 1H), 7.42–7.36 (m, 6H), 7.32 (d, 3J = 8.6 Hz, 2H), 6.99 (d, 3J = 8.8 Hz, 2H), 4.06 (t, 3J = 6.5 Hz, 2H), 3.67 (t, 3J = 6.5 Hz, 2H), 2.63 (s, 3H), 1.87–1.80 (m, 2H), 1.60–1.54 (m, 2H), 1.53–1.45 (m, 2H), 1.40–1.29 (m, 10H), 1.06 (s, 9H). 13C-NMR (100 MHz, CDCl3) δ = 165.01, 163.85, 151.62, 144.89, 142.58, 137.05, 135.73, 134.34, 133.14, 132.50, 129.63, 128.98, 128.48, 127.71, 125.10, 122.62, 121.39, 118.37, 114.51, 111.57, 68.52, 64.14, 32.72, 29.67, 29.63, 29.49, 29.24, 27.02, 26.13, 25.91, 20.82, 19.38. ESI-MS (CH3OH/formic acid 0.01%, soft pos. mode): m/z calcd for C47H55NO5Si [M + H2O]+ 741.4, found 741.7, C47H54NO4Si [M + H]+ 724.4, found 724.5, C41H48NO4Si [M–Ph]+ 646.4, found 646.8. Elem. anal. calcd for C47H53NO4Si·0.05CH2Cl2 (728.26 g mol−1): C 77.60, H 7.35, N 1.92; found: C 77.57, H 7.43, N 1.77.
TBDPSO-C10H20-LC2′,2
.
Colorless oil (η = 98%). 1H-NMR (400 MHz, CDCl3) δ = 8.16 (d, 3J = 8.8 Hz, 2H), 7.68 (m, 4H), 7.59 (m, 1H), 7.54 (dd, 3J = 7.8 Hz and 4J = 1.7 Hz, 1H), 7.45–7.36 (m, 7H), 7.25 (d, 3J = 7.9 Hz, 1H), 7.16 (d, 4J = 2.1 Hz, 1H), 7.11 (m, 1H), 6.99 (d, 3J = 8.9 Hz, 2H), 4.06 (t, 3J = 6.5 Hz, 2H), 3.67 (t, 3J = 6.5 Hz, 2H), 2.13 (s, 3H), 2.06 (s, 3H), 1.87–1.80 (m, 2H), 1.61–1.54 (m, 2H), 1.52–1.45 (m, 2H), 1.41–1.30 (m, 10H), 1.06 (s, 9H). 13C-NMR (100 MHz, CDCl3) δ = 165.13, 163.76, 150.80, 146.02, 137.88, 137.21, 137.04, 135.70, 134.31, 133.57, 132.42, 130.52, 129.74, 129.61, 129.58, 127.69, 123.46, 121.53, 119.41, 119.13, 114.48, 111.41, 68.48, 64.12, 32.70, 29.65, 29.61, 29.47, 29.23, 27.01, 26.12, 25.89, 19.96, 19.86, 19.35. ESI-MS (CH3OH/formic acid 0.01%, soft pos. mode): m/z calcd for C48H57NO5Si [M + H2O]+ 755.4, found 755.7, C48H56NO4Si [M + H]+ 738.4, found 738.9, C42H50NO4Si [M–Ph]+ 660.4, found 660.5. Elem. anal. calcd for C48H55NO4Si·0.01CH2Cl2 (738.89 g mol−1): C 78.01, H 7.55, N 1.90; found: C 78.01, H 7.55, N 1.74.
General procedure for the preparation of TBDMSO-C10H20-LCi′,j
To a solution of OCBi′,j (1 eq.), 6 (1.1 eq.) and DPTS (1 eq.) in dry CH2Cl2 (25 mL) stirred at 0 °C were added DCC (1.5 eq.) and 4-ppy (spatula tip). The mixture was allowed to heat slowly to room temperature and stirred for 48 h. After filtration, the solution was evaporated to dryness and the residue was purified by column chromatography (SiO2, CH2Cl2) to afford pure TBDMSO-C10H20-LCi′,j. Yields ranged from 93 to 99%.
TBDMSO-C10H20-LC0′,0
.
White solid (η = 99%). 1H-NMR (400 MHz, CDCl3) δ = 8.16 (d, 3J = 8.9 Hz, 2H), 7.74 and 7.69 (2d, AB system, 3J = 8.7 Hz, 4H), 7.64 (d, 3J = 8.6 Hz, 2H), 7.33 (d, 3J = 8.6 Hz, 2H), 6.99 (d, 3J = 8.9 Hz, 2H), 4.06 (t, 3J = 6.5 Hz, 2H), 3.61 (t, 3J = 6.6 Hz, 2H), 1.87–1.80 (m, 2H), 1.55–1.45 (m, 4H), 1.41–1.32 (m, 10H), 0.90 (s, 9H), 0.06 (s, 6H). 13C-NMR (100 MHz, CDCl3) δ = 165.00, 163.87, 151.74, 145.04, 136.85, 132.80, 132.50, 128.50, 127.85, 122.72, 121.35, 119.04, 114.52, 111.15, 68.52, 63.47, 33.03, 29.70, 29.64, 29.57, 29.49, 29.24, 26.14, 25.95, 18.54, −5.10. Elem. anal. calcd for C36H47NO4Si·0.01CH2Cl2 (586.70 g mol−1): C 73.74, H 8.19, N 2.39; found: C 73.74, H 8.19, N 2.28.
TBDMSO-C10H20-LC3′,0
.
White solid (η = 93%). 1H-NMR (400 MHz, CDCl3) δ = 8.18 (d, 3J = 8.9 Hz, 2H), 7.73 and 7.68 (2d, AB system, 3J = 8.6, 4H), 7.49 (m, 1H), 7.46 (m, 1H), 7.25 (d, 3J = 8.0 Hz, 1H), 7.00 (d, 3J = 8.9 Hz, 2H), 4.06 (t, 3J = 6.6 Hz, 2H), 3.61 (t, 3J = 6.6 Hz, 2H), 2.31 (s, 3H), 1.87–1.80 (m, 2H), 1.55–1.45 (m, 4H), 1.39–1.32 (m, 10H), 0.90 (s, 9H), 0.06 (s, 6H). 13C-NMR (100 MHz, CDCl3) δ = 164.71, 163.86, 150.36, 145.24, 137.05, 132.72, 132.48, 131.46, 130.17, 127.84, 125.99, 123.06, 121.27, 119.08, 114.54, 111.00, 68.51, 63.46, 33.02, 29.69, 29.63, 29.56, 29.48, 29.23, 26.13, 25.94, 18.53, 16.61, −5.10. Elem. anal. calcd for C37H49NO4Si (599.87 g mol−1): C 74.08, H 8.23, N 2.33; found: C 73.96, H 8.38, N 2.20.
TBDMSO-C10H20-LC2′,0
.
White solid (η = 96%). 1H-NMR (400 MHz, CDCl3) δ = 8.15 (d, 3J = 8.7 Hz, 2H), 7.72 (d, 3J = 8.0 Hz, 2H), 7.45 (d, 3J = 7.9 Hz, 2H), 7.24 (d, 3J = 8.1 Hz, 1H), 7.15 (m, 1H), 7.12 (m, 1H), 6.99 (d, 3J = 8.7 Hz, 2H), 4.05 (t, 3J = 6.5 Hz, 2H), 3.61 (t, 3J = 6.6 Hz, 2H), 2.28 (s, 3H), 1.86–1.80 (m, 2H), 1.56–1.45 (m, 4H), 1.39–1.32 (m, 10H), 0.90 (s, 9H), 0.05 (s, 6H). 13C-NMR (100 MHz, CDCl3) δ = 165.19, 163.81, 151.05, 146.21, 137.67, 136.90, 132.46, 132.18, 130.65, 130.23, 123.95, 121.48, 119.67, 119.04, 114.49, 111.03, 68.50, 63.47, 33.03, 29.70, 29.64, 29.57, 29.50, 29.24, 26.14, 25.95, 20.61, 18.53, −5.10. Elem. anal. calcd for C37H49NO4Si·0.03CH2Cl2 (602.42 g mol−1): C 73.83, H 8.21, N 2.33; found: C 73.88, H 8.34, N 2.20.
TBDMSO-C10H20-LC0′,3
.
White solid (η = 94%). 1H-NMR (400 MHz, CDCl3) δ = 8.16 (d, 3J = 8.9 Hz, 2H), 7.68 (d, 3J = 8.0 Hz, 1H), 7.63 (d, 3J = 8.6 Hz, 2H), 7.54 (m, 1H), 7.49 (m, 1H), 7.32 (d, 3J = 8.6 Hz, 2H), 6.99 (d, 3J = 8.9 Hz, 2H), 4.06 (t, 3J = 6.6 Hz, 2H), 3.61 (t, 3J = 6.6 Hz, 2H), 2.62 (s, 3H), 1.87–1.80 (m, 2H), 1.56–1.45 (m, 4H), 1.39–1.32 (m, 10H), 0.90 (s, 9H), 0.06 (s, 6H). 13C-NMR (100 MHz, CDCl3) δ = 165.01, 163.85, 151.63, 144.89, 142.57, 137.05, 133.14, 132.49, 128.98, 128.47, 125.10, 122.62, 121.38, 118.37, 114.51, 111.57, 68.51, 63.47, 33.03, 29.70, 29.64, 29.57, 29.50, 29.24, 26.14, 25.95, 20.81, 18.54, −5.10. Elem. anal. calcd for C37H49NO4Si·0.04CH2Cl2 (603.27 g mol−1): C 73.74, H 8.20, N 2.32; found: C 73.79, H 8.35, N 2.19.
TBDMSO-C10H20-LC2′,2
.
Pale yellow oil (η = 99%). 1H-NMR (400 MHz, CDCl3) δ = 8.16 (d, 3J = 8.7 Hz, 2H), 7.58 (m, 1H), 7.54 (m, 1H), 7.24 (d, 3J = 7.8 Hz, 1H), 7.16 (m, 1H), 7.10 (m, 2H), 6.99 (d, 3J = 8.5 Hz, 2H), 4.06 (t, 3J = 6.5 Hz, 2H), 3.61 (t, 3J = 6.6 Hz, 2H), 2.13 (s, 3H), 2.06 (s, 3H), 1.87–1.80 (m, 2H), 1.55–1.45 (m, 4H), 1.41–1.32 (m, 10H), 0.90 (s, 9H), 0.06 (s, 6H). 13C-NMR (100 MHz, CDCl3) δ = 165.15, 163.78, 150.82, 146.04, 137.90, 137.23, 137.06, 133.58, 132.43, 130.54, 129.76, 129.60, 123.48, 121.56, 119.43, 119.15, 114.49, 111.44, 68.50, 63.46, 33.02, 29.69, 29.64, 29.57, 29.49, 29.24, 26.14, 25.94, 19.98, 19.87, 18.53, −5.10. Elem. anal. calcd for C38H51NO4Si·0.02CH2Cl2 (615.60 g mol−1): C 74.18, H 8.36, N 2.28; found: C 74.17, H 8.50, N 2.10.
General procedure for the preparation of HO-C10H20-LCi′,j
A solution of Zn(BF4)2·6H2O (10 eq.) in H2O (5 mL) was added to a solution of TBDMSO-C10H20-LCi′,j (1 eq.) in THF (15 mL). The mixture was stirred at 50 °C for 72 h. After evaporation of THF, the precipitate was filtered and washed with H2O to give pure HO-C10H20-LCi′,j. Yields ranged from 93 to 99%.
HO-C10H20-LC0′,0
.
White solid (η = 93%). 1H-NMR (400 MHz, CDCl3) δ = 8.16 (d, 3J = 8.9 Hz, 2H), 7.74 and 7.69 (2d, AB system, 3J = 8.7 Hz, 4H), 7.64 (d, 3J = 8.6 Hz, 2H), 7.33 (d, 3J = 8.6 Hz, 2H), 6.99 (d, 3J = 8.9 Hz, 2H), 4.06 (t, 3J = 6.5 Hz, 2H), 3.61 (t, 3J = 6.6 Hz, 2H), 1.87–1.80 (m, 2H), 1.55–1.45 (m, 4H), 1.41–1.32 (m, 10H), 0.90 (s, 9H), 0.06 (s, 6H). 13C-NMR (100 MHz, CDCl3) δ = 165.00, 163.86, 151.74, 145.04, 136.86, 132.81, 132.51, 128.50, 127.85, 122.72, 121.36, 119.04, 114.52, 111.15, 68.50, 63.20, 32.93, 29.66, 29.61, 29.55, 29.48, 29.23, 26.12, 25.88. Elem. anal. calcd for C30H33NO4·0.16H2O (474.47 g mol−1): C 75.92, H 7.08, N 2.95; found: C 75.93, H 7.15, N 2.74.
HO-C10H20-LC3′,0
.
White solid (η = 99%). 1H-NMR (400 MHz, CDCl3) δ = 8.18 (d, 3J = 8.9 Hz, 2H), 7.73 and 7.68 (2d, AB system, 3J = 8.5, 4H), 7.49 (d, 4J = 2.6 Hz, 1H), 7.46 (dd, 3J = 8.3 Hz and 4J = 2.4 Hz, 1H), 7.25 (d, 3J = 8.4 Hz, 1H), 7.00 (d, 3J = 8.9 Hz, 2H), 4.06 (t, 3J = 6.5 Hz, 2H), 3.65 (t, 3J = 6.6 Hz, 2H), 2.31 (s, 3H), 1.87–1.80 (m, 2H), 1.61–1.54 (m, 3H), 1.52–1.45 (m, 2H), 1.39–1.33 (m, 10H). 13C-NMR (100 MHz, CDCl3) δ = 164.72, 163.85, 150.35, 145.24, 137.06, 132.73, 132.48, 131.46, 130.17, 127.85, 126.00, 123.06, 121.28, 119.08, 114.55, 110.99, 68.50, 63.20, 32.92, 29.65, 29.61, 29.54, 29.46, 29.22, 26.11, 25.87, 16.61. Elem. anal. calcd for C31H35NO4·0.9H2O (501.83 g mol−1): C 74.20, H 7.39, N 2.79; found: C 74.20, H 7.24, N 2.64.
HO-C10H20-LC2′,0
.
White solid (η = 99%). 1H-NMR (400 MHz, CDCl3) δ = 8.15 (d, 3J = 8.9 Hz, 2H), 7.72 (d, 3J = 8.3 Hz, 2H), 7.45 (d, 3J = 8.3 Hz, 2H), 7.24 (d, 3J = 8.2 Hz, 1H), 7.15 (d, 4J = 2.3 Hz, 1H), 7.12 (dd, 3J = 8.2 Hz and 4J = 2.4 Hz, 1H), 6.98 (d, 3J = 8.9 Hz, 2H), 4.06 (t, 3J = 6.5 Hz, 2H), 3.65 (t, 3J = 6.6 Hz, 2H), 2.27 (s, 3H), 1.86–1.79 (m, 2H), 1.61–1.54 (m, 2H), 1.52–1.45 (m, 2H), 1.40–1.33 (m, 10H). 13C-NMR (100 MHz, CDCl3) δ = 165.20, 163.80, 151.04, 146.21, 137.68, 136.91, 132.47, 132.18, 130.65, 130.23, 123.95, 121.49, 119.67, 119.05, 114.49, 111.03, 68.49, 63.22, 32.93, 29.66, 29.61, 29.54, 29.48, 29.23, 26.12, 25.88, 20.61. Elem. anal. calcd for C31H35NO4·0.27H2O (490.48 g mol−1): C 75.91, H 7.30, N 2.86; found: C 75.92, H 7.32, N 2.69.
HO-C10H20-LC0′,3
.
White solid (η = 99%). 1H-NMR (400 MHz, CDCl3) δ = 8.16 (d, 3J = 8.9 Hz, 2H), 7.68 (d, 3J = 8.0 Hz, 1H), 7.63 (d, 3J = 8.6 Hz, 2H), 7.54 (m, 1H), 7.49 (m, 1H), 7.32 (d, 3J = 8.6 Hz, 2H), 6.99 (d, 3J = 8.9 Hz, 2H), 4.06 (t, 3J = 6.5 Hz, 2H), 3.65 (t, 3J = 6.6 Hz, 2H), 2.62 (s, 3H), 1.87–1.80 (m, 2H), 1.61–1.54 (m, 3H), 1.52–1.45 (m, 2H), 1.39–1.33 (m, 10H). 13C-NMR (100 MHz, CDCl3) δ = 165.02, 163.84, 151.62, 144.90, 142.59, 137.07, 133.15, 132.50, 128.98, 128.48, 125.10, 122.63, 121.40, 118.38, 114.52, 111.57, 68.50, 63.22, 32.93, 29.66, 29.62, 29.61, 29.55, 29.48, 29.23, 26.12, 25.88, 20.82. Elem. anal. calcd for C31H35NO4·0.5H2O (494.63 g mol−1): C 75.28, H 7.27, N 2.83; found: C 75.28, H 7.27, N 2.66.
HO-C10H20-LC2′,2
.
White solid (η = 99%). 1H-NMR (400 MHz, CDCl3) δ = 8.15 (d, 3J = 8.9 Hz, 2H), 7.58 (m, 1H), 7.54 (dd, 3J = 7.8 Hz and 4J = 1.7 Hz, 1H), 7.24 (d, 3J = 7.8 Hz, 1H), 7.16 (m, 1H), 7.10 (m, 2H), 6.99 (d, 3J = 8.9 Hz, 2H), 4.06 (t, 3J = 6.5 Hz, 2H), 3.65 (t, 3J = 6.6 Hz, 2H), 2.13 (s, 3H), 2.05 (s, 3H), 1.87–1.80 (m, 2H), 1.61–1.54 (m, 2H), 1.52–1.45 (m, 2H), 1.39–1.34 (m, 10H). 13C-NMR (100 MHz, CDCl3) δ = 165.16, 163.77, 150.81, 146.04, 137.07, 133.59, 132.44, 130.54, 129.76, 129.60, 123.48, 121.57, 119.43, 119.16, 114.49, 111.43, 68.48, 63.21, 32.93, 29.66, 29.61, 29.54, 29.47, 29.23, 26.12, 25.88, 19.98, 19.88. Elem. anal. calcd for C32H37NO4·0.28H2O (504.68 g mol−1): C 76.15, H 7.54, N 2.77; found: C 76.15, H 7.54, N 2.59.
Spectroscopic and analytical measurements
1H and 13C NMR spectra were recorded at 25 °C on a Bruker Avance 400 MHz spectrometer. Chemical shifts are given in ppm with respect to TMS. Pneumatically-assisted electrospray (ESI-MS) mass spectra were recorded in 10−4 M solutions on an Applied Biosystems API 150EX LC/MS System equipped with a Turbo ionspray source®. Elemental analyses were performed by K. L. Buchwalder from the Microchemical Laboratory of the University of Geneva. TGA were performed using a thermogravimetric balance, Mettler Toledo Star Systems (under N2). DSC traces were obtained using Mettler Toledo DSC1 Star Systems differential scanning calorimeters using 3–5 mg samples (10 and 0.5 °C min−1, under N2). Conversion: T (K) = T (°C) + 273.15. Characterisation of the mesophases and the isotropic liquids was performed on a polarizing microscope Leitz Orthoplan-Pol with a Leitz LL 20×/0.40 polarizing objective, and equipped with a Linkam THMS 600 variable-temperature stage. The mathematical analyses were performed by using Igor Pro® (WaveMetrics Inc.) and Excel® (Microsoft) software.
X-Ray crystallography
The crude powder was filled in Lindemann capillaries of 0.8 mm diameter. Low angle powder X-ray diffraction experiments at various temperatures were performed using two different diffractometers:
– An Empyrean (PANalytical) diffractometer in capillary mode, with a focusing X-ray mirror for Cu radiation and a PIXcel3D area detector. Variable temperatures were achieved with a nitrogen cryostreamer (Oxford Cryosystems) (available temperatures: 100–500 K).
– A STOE transmission powder diffractometer system STADI P using a focused monochromatic Cu-Kα1 beam obtained from a curved germanium monochromator (Johann-type) and collected on a curved image plate position-sensitive detector (IP-PSD). Calibration with silicon and copper laurate standards, for high and low angle domains, respectively, was preliminarily performed. Sample capillaries were placed in the high-temperature attachment for measurements in the range of desired temperatures (from −30 up to 240 °C) within 0.05 °C.
Acknowledgements
This work was supported through grants from the Swiss National Science Foundation (grant numbers 200020_140222 and 200020-159881).
References
-
(a) A. Skoulios and D. Guillon, Mol. Cryst. Liq. Cryst., 1988, 165, 317–332 CrossRef CAS;
(b) C. Tschierske, J. Mater. Chem., 2001, 11, 2647–2671 RSC;
(c) C. Tschierske, Chem. Soc. Rev., 2007, 36, 1930–1970 RSC.
-
(a) W. Maier and A. Saupe, Z. Naturforsch., A: Phys. Sci., 1959, 13a, 564–570 Search PubMed;
(b) W. Maier and A. Saupe, Z. Naturforsch., A: Phys. Sci., 1959, 14a, 882–900 CAS;
(c) W. Maier and A. Saupe, Z. Naturforsch., A: Phys. Sci., 1960, 15a, 287–292 CAS;
(d) A. Saupe, Angew. Chem., Int. Ed. Engl., 1968, 7, 97–118 CrossRef CAS;
(e) G. R. Luckhurst and C. Zannoni, Nature, 1977, 267, 412–414 CrossRef CAS.
-
(a) L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659 CrossRef CAS;
(b) G. J. Vroege and H. N. W. Lekkerkerker, Rep. Prog. Phys., 1992, 55, 1241–1309 CrossRef CAS.
- In this contribution, the term free energy systematically refers to Gibbs energy monitored at constant pressure. The related concept of Helmholtz energy, commonly used for condensed phases at constant volume, is not considered here.
-
(a) M. L. Huggins, J. Chem. Phys., 1941, 9, 440 CrossRef CAS;
(b) P. J. Flory, J. Chem. Phys., 1941, 9, 660–661 CrossRef CAS;
(c)
Polymer Blends, ed. D. R. Paul and S. Newman, Academic Press, New York, San Francisco, London, 1978, vol. 2, pp. 25–32 and 116–121 Search PubMed.
- E. Bialecka-Florjanczyk, J. Phys. Chem. B, 2006, 110, 2582–2592 CrossRef CAS PubMed.
-
(a)
J. H. Hildebrand and R. L. Scott, The Solubility of Nonelectrolytes, Reinhold Pub Group, New York, 3rd edn, 1950 Search PubMed;
(b) R. F. Fedors, Polym. Eng. Sci., 1974, 14, 147–154 CrossRef CAS;
(c)
A. F. M. Barton, Handbook of Solubility Parameters and Other Cohesion Parameters, CRC Press, 2nd edn, 1991, p. 127 Search PubMed.
- C. Tschierske, Top. Curr. Chem., 2012, 318, 1–108 CrossRef CAS PubMed.
-
(a) Y. Yamaoka, Y. Tanigushi, S. Yasuzuka, Y. Yamamura and K. Saito, J. Chem. Phys., 2011, 135, 044704 CrossRef PubMed;
(b) T. Miyazawa, Y. Yamamura, M. Hishida, S. Nagatomo, M. Massalska-Arodz and K. Saito, J. Phys. Chem. B, 2013, 117, 8293–8299 CrossRef CAS PubMed.
-
(a) M. Yoneya, K. Araya, E. Nishikawa and H. Yokoyama, J. Phys. Chem. B, 2004, 108, 8099–8101 CrossRef CAS;
(b) M. Yoneya, Chem. Rec., 2011, 11, 66–76 CrossRef CAS PubMed;
(c) Y. Nakazawa, Y. Yamamura, S. Kutsumizu and K. Saito, J. Phys. Soc. Jpn., 2012, 81, 094601 CrossRef.
- A. Pegenau, T. Hegmann, C. Tschierske and S. Diele, Chem. – Eur. J., 1999, 5, 1643–1660 CrossRef CAS.
- T. Dutronc, E. Terazzi, L. Guénée, K.-L. Buchwalder, A. Spoerri, D. Emery, J. Mareda, S. Floquet and C. Piguet, Chem. – Eur. J., 2013, 19, 8447–8456 CrossRef CAS PubMed.
-
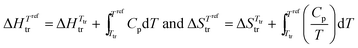 are the enthalpy, respectively entropy of phase transition corrected at the reference temperature. The corrective terms brought by the integration of the heat capacities have been shown in ref. 12 to be negligible for substituted cyanobiphenyls in the |Ttr − Tref| ≤ 150 K range.
are the enthalpy, respectively entropy of phase transition corrected at the reference temperature. The corrective terms brought by the integration of the heat capacities have been shown in ref. 12 to be negligible for substituted cyanobiphenyls in the |Ttr − Tref| ≤ 150 K range.
- T. Dutronc, E. Terazzi and C. Piguet, RSC Adv., 2014, 4, 15740–15748 RSC.
- T. Dutronc, E. Terazzi, L. Guénée, K.-L. Buchwalder, S. Floquet and C. Piguet, Chem. – Eur. J., 2016, 22, 1385–1391 CrossRef CAS PubMed.
-
(a) Y. P. Piryatinskii and O. V. Yaroshchuk, Opt. Spectrosc., 2002, 92, 517–523 CrossRef CAS;
(b) B. Jaishi, P. Mandal and R. Dabowki, Opto-Electron. Rev., 2010, 18, 111–120 CAS;
(c) N. Bielejewska, E. Chrzumnicka, R. Stoarki and D. Bauman, Opto-Electron. Rev., 2010, 18, 197–207 CAS;
(d) Market Research Report on Global and Chinese 4-cyanobiphenyl (CAS 2920-38-9) Industry, 2009–2019, Prof. Research Rep., 2014, PR 601577, 1–150.
- G. W. Gray, K. J. Harrison and J. A. Nash, Electron. Lett., 1973, 9, 130–131 CrossRef CAS.
-
(a)
A. C. Griffin and J. F. Johnson, Liquid Crystals and Ordered Fluids, Plenum Press, New York London, 1984, vol. 4 Search PubMed;
(b)
P. J. Collings and M. Hird, in Introduction to Liquid Crystals: Chemistry and Physics, ed. G. W. Gray and J. W. Goodby, Taylor and Francis Ltd, London Bristol, 1997 Search PubMed;
(c)
Handbook of Liquid Crystals, ed. D. Demus, J. W. Goodby, G. W. Gray, H.-W. Spiess and V. Vill, Wiley-CVH, Weinheim, 1998, vol. 1 and 2A Search PubMed.
-
(a)
Liquid Crystalline and Mesomorphic Polymers, ed. V. P. Shibaev and L. Lam, Springer Verlag, New York, ch. 3, 1994 Search PubMed;
(b) C. T. Imrie and P. A. Henderson, Chem. Soc. Rev., 2007, 36, 2096–2124 RSC.
-
(a) T. Cardinaels, K. Driesen, T. N. Parac-Vogt, B. Heinrich, C. Bourgogne, D. Guillon, B. Donnio and K. Binnemans, Chem. Mater., 2005, 17, 6589–6598 CrossRef CAS;
(b) I. S. Shashikala and D. W. Bruce, Dalton Trans., 2008, 1128–1131 RSC;
(c) E. Terazzi, C. Bourgogne, R. Welter, J.-L. Gallani, D. Guillon, G. Rogez and B. Donnio, Angew. Chem., Int. Ed., 2008, 47, 490–495 CrossRef CAS PubMed;
(d) A. Pana, F. L. Chiriac, M. Secu, I. Pasuk, M. Ferbinteanu, M. Micutz and V. Circu, Dalton Trans., 2015, 44, 14196–14199 RSC.
- E. Terazzi, S. Suarez, S. Torelli, H. Nozary, D. Imbert, O. Mamula, J.-P. Rivera, E. Guillet, J.-M. Bénech, G. Bernardinelli, R. Scopelliti, B. Donnio, D. Guillon, J.-C. G. Bünzli and C. Piguet, Adv. Funct. Mater., 2006, 16, 157–168 CrossRef CAS.
- F. T. Trouton, Philos. Mag., 1884, 18, 54–57 CrossRef.
- Let's stress here that the dependence of ΔHvap with temperature is neglected, which leads to the estimation of an average and unique value of the cohesive energy in the liquid whatever the temperature in its domain of existence.
-
P. W. Atkins and J. de Paula, Physical Chemistry, W. H. Freeman and Company, New York, 9th edn, 2010, pp. 124 and 147 Search PubMed.
-
P. G. M. Wuts and T. W. Greene, Greene’s Protection Groups in Organic Synthesis, Wiley Interscience, Hoboken, New Jersey, 4th edn, 2007, ch. 2 and 10 Search PubMed.
- B. Dardel, D. Guillon, B. Heinrich and R. Deschenaux, J. Mater. Chem., 2001, 11, 2814–2831 RSC.
- B. O. Lindgren and T. Nilsson, Acta Chem. Scand., 1973, 27, 888–890 CrossRef CAS.
- The molecular volumes are taken as the Connolly volumes, which are obtained from the building of the Connolly surface around the molecular structures of complexes observed in their crystal structure and by using a probe radius of 1.4 Å for modelling water solvent molecule ( M. L. Connolly, Science, 1983, 221, 709–713 Search PubMed; M. L. Connolly, J. Appl. Crystallogr., 1983, 16, 548–558) CrossRef CAS.
- C. Piguet, Dalton Trans., 2011, 40, 8059–8071 RSC.
- The full black traces were obtained by non-linear least-square fits of eqn (14) applied to the experimental CFED data and gave
 with, Trefm = 360.3 K, Pref = 1.1(2) MPa, ΔHtr/ΔVtr = 51(7) J cm−3 (Fig. 6) and
with, Trefm = 360.3 K, Pref = 1.1(2) MPa, ΔHtr/ΔVtr = 51(7) J cm−3 (Fig. 6) and  with Trefclearing = 393.3 K, Pref = 0.072(7) MPa, ΔHtr/ΔVtr = 3.7(4) J cm−3 (Fig. 7).
with Trefclearing = 393.3 K, Pref = 0.072(7) MPa, ΔHtr/ΔVtr = 3.7(4) J cm−3 (Fig. 7).
- K. E. Rowe and D. W. Bruce, J. Mater. Chem., 1998, 8, 331–341 RSC.
- A. Escande, L. Guénée, H. Nozary, G. Bernardinelli, F. Gumy, A. Aebischer, J.-C. G. Bünzli, B. Donnio, D. Guillon and C. Piguet, Chem. – Eur. J., 2007, 13, 8696–8713 CrossRef CAS PubMed.
- K. Yonetake, T. Masuko, T. Morishita, K. Suzuki, M. Ueda and R. Nagahata, Macromolecules, 1999, 32, 6578–6586 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp01058j |
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕA + nB
ϕA + nB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕB)
ϕB)

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕA + nB
ϕA + nB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕB) (eqn (1)) becomes more negative and it exactly overcomes ΔHmix = nAϕBVseg(δA − δB)2 at T = Ttransition, when ΔGmix = 0. Segregation is then lost at the order–disorder transition temperature, also assigned as the clearing temperature Tclearing in liquid crystals.8 Applied to the formation of nanostructured liquid crystals,6 this thermodynamic approach was successfully used for rationalizing the micro-segregation occurring in mesogenic calamitic cyanobiphenyls,9 cubic-phase-forming liquid crystalline molecules10 and polycatenar pentaerythritol derivatives.11 Whereas the high temperature limit of existence of a mesophase, i.e. its clearing point, can be approached with the help of the CED concept (eqn (3)), the low temperature cutoff, referred to as the melting point, requires the consideration of the closely related cohesion Gibbs free energy density (CFED) given in eqn (4).12,14
ϕB) (eqn (1)) becomes more negative and it exactly overcomes ΔHmix = nAϕBVseg(δA − δB)2 at T = Ttransition, when ΔGmix = 0. Segregation is then lost at the order–disorder transition temperature, also assigned as the clearing temperature Tclearing in liquid crystals.8 Applied to the formation of nanostructured liquid crystals,6 this thermodynamic approach was successfully used for rationalizing the micro-segregation occurring in mesogenic calamitic cyanobiphenyls,9 cubic-phase-forming liquid crystalline molecules10 and polycatenar pentaerythritol derivatives.11 Whereas the high temperature limit of existence of a mesophase, i.e. its clearing point, can be approached with the help of the CED concept (eqn (3)), the low temperature cutoff, referred to as the melting point, requires the consideration of the closely related cohesion Gibbs free energy density (CFED) given in eqn (4).12,14 is the Gibbs energy of cohesion, which estimates the degree of cohesion occurring in a condensed phase at a reference temperature Tref. Let us stress here that Tref is different from the transition temperature Ttr = ΔHtr/ΔStr at which
is the Gibbs energy of cohesion, which estimates the degree of cohesion occurring in a condensed phase at a reference temperature Tref. Let us stress here that Tref is different from the transition temperature Ttr = ΔHtr/ΔStr at which  .12
.12

 is estimated, while
is estimated, while  stand for the enthalpies and entropies of melting (m) and clearing (c) corrected at this temperature.12,13
stand for the enthalpies and entropies of melting (m) and clearing (c) corrected at this temperature.12,13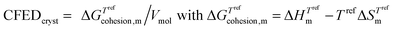

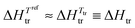 and
and  in eqn (7) and (8)).12,15 Applied to the melting of (i) linear alkanes of increasing length, (ii) organosilanes of increasing volumes and (iii) transition metals or metal oxides of increased polarizabilities,14 the CFEDcryst computed in the solid phases displayed empirical linear correlations with the transition temperatures (eqn (9), Vmol being the molar volume in the crystals).14
in eqn (7) and (8)).12,15 Applied to the melting of (i) linear alkanes of increasing length, (ii) organosilanes of increasing volumes and (iii) transition metals or metal oxides of increased polarizabilities,14 the CFEDcryst computed in the solid phases displayed empirical linear correlations with the transition temperatures (eqn (9), Vmol being the molar volume in the crystals).14
 into eqn (7) or eqn (8) gives
into eqn (7) or eqn (8) gives





 with Trefm = 360.3 K (eqn (7)).
d
with Trefm = 360.3 K (eqn (7)).
d
 with Trefclearing = 393.3 K (eqn (8)).
e Glass transition.
f Non-mesogenic.
with Trefclearing = 393.3 K (eqn (8)).
e Glass transition.
f Non-mesogenic.






![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25) to give pure 2 (8.26 g, 86%) as a white solid. 1H-NMR (400 MHz, CDCl3) δ = 9.87 (s, 1H), 7.82 (d, 3J = 8.8 Hz, 2H), 6.98 (d, 3J = 8.7 Hz, 2H), 4.03 (t, 3J = 6.5 Hz, 2H), 3.63 (t, 3J = 6.6 Hz, 2H), 1.84–1.77 (m, 2H), 1.60–1.53 (m, 2H), 1.50–1.42 (m, 2H), 1.39–1.31 (m, 10H). 13C-NMR (100 MHz, CDCl3) δ = 190.98, 164.39, 132.12, 129.86, 114.87, 68.54, 63.15, 32.90, 29.62, 29.57, 29.51, 29.43, 29.16, 26.06, 25.85.
25) to give pure 2 (8.26 g, 86%) as a white solid. 1H-NMR (400 MHz, CDCl3) δ = 9.87 (s, 1H), 7.82 (d, 3J = 8.8 Hz, 2H), 6.98 (d, 3J = 8.7 Hz, 2H), 4.03 (t, 3J = 6.5 Hz, 2H), 3.63 (t, 3J = 6.6 Hz, 2H), 1.84–1.77 (m, 2H), 1.60–1.53 (m, 2H), 1.50–1.42 (m, 2H), 1.39–1.31 (m, 10H). 13C-NMR (100 MHz, CDCl3) δ = 190.98, 164.39, 132.12, 129.86, 114.87, 68.54, 63.15, 32.90, 29.62, 29.57, 29.51, 29.43, 29.16, 26.06, 25.85.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) to provide 4 (18.89 g, 71%) as a colorless oil. 1H-NMR (400 MHz, CDCl3) δ = 3.60 (t, 3J = 6.6 Hz, 2H), 3.41 (t, 3J = 6.9 Hz, 2H), 1.89–1.82 (m, 2H), 1.55–1.47 (m, 2H), 1.46–1.39 (m, 2H), 1.35–1.29 (m, 10H), 0.90 (s, 9H), 0.05 (s, 6H). 13C-NMR (100 MHz, CDCl3) δ = 63.45, 34.17, 33.02, 32.98, 29.65, 29.52, 28.90, 28.32, 26.13, 25.92, −2.3.
2) to provide 4 (18.89 g, 71%) as a colorless oil. 1H-NMR (400 MHz, CDCl3) δ = 3.60 (t, 3J = 6.6 Hz, 2H), 3.41 (t, 3J = 6.9 Hz, 2H), 1.89–1.82 (m, 2H), 1.55–1.47 (m, 2H), 1.46–1.39 (m, 2H), 1.35–1.29 (m, 10H), 0.90 (s, 9H), 0.05 (s, 6H). 13C-NMR (100 MHz, CDCl3) δ = 63.45, 34.17, 33.02, 32.98, 29.65, 29.52, 28.90, 28.32, 26.13, 25.92, −2.3.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1)) was required to obtain pure 6 (3.68 g, 27%) as a white solid. 1H-NMR (400 MHz, CDCl3) δ = 8.05 (d, 3J = 8.9 Hz, 2H), 6.93 (d, 3J = 8.9 Hz, 2H), 4.03 (t, 3J = 6.6 Hz, 2H), 3.60 (t, 3J = 6.6 Hz, 2H), 1.84–1.77 (m, 2H), 1.55–1.43 (m, 4H), 1.39–1.31 (m, 10H), 0.90 (s, 9H), 0.05 (s, 6H). 13C-NMR (100 MHz, CDCl3) δ = 171.31, 163.82, 132.47, 121.42, 114.35, 68.44, 63.48, 33.03, 29.70, 29.64, 29.57, 29.49, 29.24, 26.14, 25.94, 18.54, −5.09.
1)) was required to obtain pure 6 (3.68 g, 27%) as a white solid. 1H-NMR (400 MHz, CDCl3) δ = 8.05 (d, 3J = 8.9 Hz, 2H), 6.93 (d, 3J = 8.9 Hz, 2H), 4.03 (t, 3J = 6.6 Hz, 2H), 3.60 (t, 3J = 6.6 Hz, 2H), 1.84–1.77 (m, 2H), 1.55–1.43 (m, 4H), 1.39–1.31 (m, 10H), 0.90 (s, 9H), 0.05 (s, 6H). 13C-NMR (100 MHz, CDCl3) δ = 171.31, 163.82, 132.47, 121.42, 114.35, 68.44, 63.48, 33.03, 29.70, 29.64, 29.57, 29.49, 29.24, 26.14, 25.94, 18.54, −5.09.
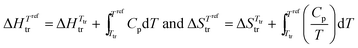 are the enthalpy, respectively entropy of phase transition corrected at the reference temperature. The corrective terms brought by the integration of the heat capacities have been shown in ref. 12 to be negligible for substituted cyanobiphenyls in the |Ttr − Tref| ≤ 150 K range.
are the enthalpy, respectively entropy of phase transition corrected at the reference temperature. The corrective terms brought by the integration of the heat capacities have been shown in ref. 12 to be negligible for substituted cyanobiphenyls in the |Ttr − Tref| ≤ 150 K range. with, Trefm = 360.3 K, Pref = 1.1(2) MPa, ΔHtr/ΔVtr = 51(7) J cm−3 (Fig. 6) and
with, Trefm = 360.3 K, Pref = 1.1(2) MPa, ΔHtr/ΔVtr = 51(7) J cm−3 (Fig. 6) and  with Trefclearing = 393.3 K, Pref = 0.072(7) MPa, ΔHtr/ΔVtr = 3.7(4) J cm−3 (Fig. 7).
with Trefclearing = 393.3 K, Pref = 0.072(7) MPa, ΔHtr/ΔVtr = 3.7(4) J cm−3 (Fig. 7).



