Open Access Article
Open Access ArticleTransient binding accounts for apparent violation of the generalized Stokes–Einstein relation in crowded protein solutions
M.
Rothe†
,
T.
Gruber
,
S.
Gröger
,
J.
Balbach
,
K.
Saalwächter
* and
M.
Roos
*
Martin-Luther-Universität Halle-Wittenberg, Institut für Physik, 06120 Halle (Saale), Germany. E-mail: matthias.roos@physik.uni-halle.de; kay.saalwaechter@physik.uni-halle.de; Tel: +49-345-55-28564 Tel: +49-345-55-28560
First published on 7th June 2016
Abstract
The effect of high concentration, also referred to as crowding conditions, on Brownian motion is of central relevance for the understanding of the physical, chemical and biological properties of proteins in their native environment. Specifically, the simple inverse relationship between the translational diffusion coefficient and the macroscopic solution viscosity as predicted by the generalized Stokes–Einstein (GSE) relation has been the subject of many studies, yet a consensus on its applicability has not been reached. Here, we use isotope-filtered pulsed-field gradient NMR to separately assess the μm-scale diffusivity of two proteins, BSA and an SH3 domain, in mixtures as well as single-protein solutions, and demonstrate that transient binding can account for an apparent violation of the GSE relation. Whereas GSE behavior applies for the single-protein solutions, it does not hold for the protein mixtures. Transient binding behavior in the concentrated mixtures is evidenced by calorimetric experiments and by a significantly increased apparent activation energy of diffusion. In contrast, the temperature dependence of the viscosity, as well as of the diffusivity in single-component solutions, is always dominated by the flow activation energy of pure water. As a practically relevant second result, we further show that, for high protein concentrations, the diffusion of small molecules such as dioxane or water is not generally a suitable probe for the viscosity experienced by the diffusing proteins.
Introduction
The evaluation of experimental and simulation results on translational diffusion usually relies on the Stokes–Einstein (SE) relationship. Its applicability is in principle limited to a relatively large solute, effectively a colloidal particle, experiencing Stokes friction within a continuous effective medium – a condition that is safely fulfilled in dilute protein solutions. In vivo, however, organic matter is as highly concentrated as several 100 grams of biomolecules per liter,1–3 rendering macromolecular crowding an important aspect of molecular processes in the living cell.4–8 Given such a high concentration of dispersed particles, each protein is surrounded by several others of similar size, leading to phenomena well known from colloid science, such as cage effects9,10 and restricted motion.11–13 Such crowding effects dominate in vivo protein diffusivity12 and cause considerably reduced diffusion rates.5,14 Given the altered protein diffusivity in biological systems, the motion of globular proteins has been studied in the cyto-15–19 and nucleoplasm20 as well as in the mitochondrial matrix.21 Along these lines, in shrunken cells with reduced cellular volume, going along with an even higher concentration of obstacles, protein diffusivity was shown to be more reduced as for swollen cells.15 Such findings further stress the relevance of high biomass concentration and excluded-volume effects for protein diffusion inside the cellular environment. Yet, despite the increased interest in the consequences of macromolecular crowding, knowledge on the effect of crowding on protein diffusion beyond the general slow-down of diffusion rates remains still sparse. In addition to the effect of obstacles on molecular mobility, binding of proteins to other proteins or cell compartments17,20 may additionally retard diffusion.In the absence of binding events, short-time (in-cage) translational displacements are governed by local hydrodynamic effects that depend on the pure-solvent viscosity,22 whereas long-time translational diffusion provides sufficient averaging over different local surroundings, combined with a multitude of statistically independent encounters of the caged tracer particle with other host particles. Then, the friction experienced by tracer particles can be expected to scale with the macroscopic (zero-shear) solution viscosity η(c), such that the long-time diffusion coefficient DL may be considered to behave as predicted by the generalized Stokes–Einstein (GSE) relation23–26
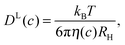 | (1) |
The validity of eqn (1) has been demonstrated for concentrated monodisperse colloids23,25 as well as for colloidal mixtures26,27 and even soft colloid systems.28 However, for charge-stabilized colloids deviations have been noticed.24,29 For proteins under macromolecular crowding the applicability of the GSE relationship is either confirmed10,30,31 or shown to be invalid,31,32 depending on the specific proteins and crowding agents used. In a recent study,13 we have demonstrated that concentrated single-component protein solutions follow the GSE relationship independently of the presence or absence of time-stable oligomers, i.e. size polydispersity. Studies of protein behavior in which crowding is realized by open random-coil structures such as Ficoll,33,34 dextran35,36 or other (semi)flexible polymers,37,38 however, have to be distinguished from those studying crowding by globular proteins: at intermediate to high concentrations relevant for crowding effects, random-coil polymers interpenetrate each other, leading to long-range entanglement and mesh-size effects that are of different physical nature as compared to crowding by globular particles.39,40 Thus, in the presence of random-coil polymers, protein diffusion is often33,36,37,41,42 but not always34 found to be faster than predicted by the solution viscosity, because the latter is much more affected by entanglement effects than the local diffusivity.
Here, we investigate a protein model mixture of bovine serum albumin (BSA) and the Src-homology 3 (SH3) domain, and show that concentration-dependent, transient binding can account for an apparent violation of the GSE relationship in crowded protein solutions. The SH3 domain and BSA were initially chosen due to their different sizes, combined with the potential affinity of SH3 to bind to proline and arginine rich regions like PxxP and RxxR motives43,44 (where x can be any amino acid). Both motives are found on the surface of BSA. These features suggest that our model mixture can be taken to represent a typically polydisperse mixture of distinct proteins subject to protein-specific interactions. Additionally, we provide evidence that the diffusivity of small molecules such as dioxane or water does not represent a reliable means to estimate the effective viscosity of highly concentrated protein solutions, challenging theory-based interpretations of protein (or similar macro-solute) diffusivity.
Materials and methods
Materials
The SH3 domain of human amphiphysin II/Bin145 and BSA were studied both as single-protein solutions and in mixtures. The SH3 domain has a molecular weight of about 10 kDa only, and was 13C and 15N enriched. BSA (molecular weight of 66.4 kDa) was used in unlabeled form. In mixtures, the mass ratio of SH3 to BSA was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, resulting in a molar ratio of SH3 to BSA of about 3
2, resulting in a molar ratio of SH3 to BSA of about 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. To assess potential specific binding between the two proteins, an 1H–15N HSQC spectrum of 3 mg ml−1 SH3 was recorded in presence and absence of BSA, the latter at a concentration of 6 mg ml−1 and 19.8 mg ml−1, corresponding to a molar ratio of SH3
1. To assess potential specific binding between the two proteins, an 1H–15N HSQC spectrum of 3 mg ml−1 SH3 was recorded in presence and absence of BSA, the latter at a concentration of 6 mg ml−1 and 19.8 mg ml−1, corresponding to a molar ratio of SH3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BSA of about 3
BSA of about 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. For this particular sample, 225 mM sodium phosphate buffer at pH 7.4 was used to avoid differences in the pH value between the samples. However, comparing the 1H–15N HSQC spectra of the SH3 domain with and without adding BSA revealed no significant changes in the chemical shifts, indicating that no detectable amount of time-stable SH3–BSA complexes are formed under dilute conditions.
1, respectively. For this particular sample, 225 mM sodium phosphate buffer at pH 7.4 was used to avoid differences in the pH value between the samples. However, comparing the 1H–15N HSQC spectra of the SH3 domain with and without adding BSA revealed no significant changes in the chemical shifts, indicating that no detectable amount of time-stable SH3–BSA complexes are formed under dilute conditions.
SH3 (Src-Homology 3) Bin1 was adopted from amphiphysin II. For recombinant expression of SH3, the gen of the AmpII/SH3 domain was cloned into a pET14b vector; the plasmid was then transformed into BL21(DE3) cells. Overexpression was induced with 1 mM IPTG at OD600 0.7 before growing for three hours at 37 °C. After harvesting, the cell pellet was resuspended in 50 mM sodium phosphate, 300 mM NaCl, 20 mM imidazol and 1 mM DTT at pH 8.0, containing protease inhibitor (Sigma Aldrich, product number P2714). Cells were lysed using lysozyme for 30 min, further treated in a microfluidic fluidizer and clarified by centrifugation. The supernatant was loaded on a nickel Sepharose column, washed with resuspension buffer and eluted with a gradient up to 350 mM imidazol. Fractions containing SH3 were pooled and treated with thrombin to cleave the His6-tag, where a second nickel column was used to separate cleaved from non-cleaved SH3. After that the flow through was purified using size exclusion (S75) chromatography, in which SH3 containing fractions were again pooled, dialyzed for removing salt, and then lyophilized. Blue-native PAGE depicted the presence of SH3 monomers only.
Fatty acid-free bovine serum albumin (BSA) was received from Sigma-Aldrich (product number A7030) as lyophilized powder, and was dissolved in D2O without further purification. Unpurified, commercial BSA contains about 50% permanent oligomers that likely arise from cystein-related disulfide bonds, see ref. 46 and also ref. 47 for evidence regarding the sample used.
In our previous studies of the Brownian dynamics of concentrated BSA solutions,13,47 no buffer was added to avoid screening of electrostatic interactions among the proteins. To compare with our previous results, the diffusion measurements presented herein were performed under the same conditions, i.e. the proteins were dissolved in pure D2O. With increasing concentration of the BSA–SH3 mixture, only a slight shift of the pD was observed (6.0 at lowest concentration to 6.4 at highest concentration). After the measurements of protein diffusion were completed, 1% of dioxane was added to the samples containing the protein mixtures for also measuring the diffusivity of small probe molecules in presence of highly concentrated proteins.
Isotope-filtered pulsed-field gradient (PFG) NMR
Translational diffusion measurements using the pulsed-gradient stimulated-echo (PGSTE) pulse sequence were performed on an Avance II spectrometer from Bruker (Karlsruhe, Germany) at 400 MHz 1H resonance frequency, equipped with a Diff60 probehead. The PFG NMR diffusion decays were in all cases singly exponential within experimental precision, as confirmed by fits to| A(g) = A(0)·exp(−γ2g2DLδ2(Δ − δ/3)), | (2) |
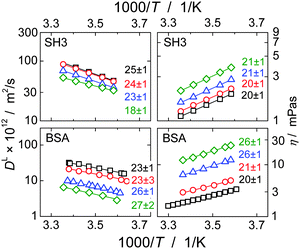
PFG-NMR diffusion experiments are potentially biased by T2 filtering effects. The STE pulse sequence consists of three parts: encoding of the signal, the diffusion period, and signal decoding. During the encoding and decoding periods of the experiment, transverse (T2) relaxation reduces the NMR-signal according to 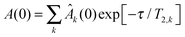 , where T2,k and Âk are the transverse relaxation time and the intrinsic intensity (before T2 relaxation) of the individual protein proton sites, respectively, and τ = 2 × 3.6 ms is the overall time span of the encoding and decoding periods of the NMR pulse sequence during which T2 relaxation occurs. T2 relaxation times are inversely proportional to the rotational correlation time of the particle. Larger particles with consequently longer rotational correlation times have – averaged over the different proton sites of the protein – shorter transverse relaxation times T2 than smaller particles. If T2 is comparable to or even shorter than τ (as is the case in concentrated protein solutions) and the solution is polydisperse, the signal obtained can be biased by monomers instead of representing the full ensemble average. This is the case for the BSA fraction, see below and ref. 13. Assuming a log-normal distribution of relaxation times, the median relaxation time represents the most populated one. For BSA and SH3 in mixture, the median relaxation time ranges between only 0.5 ms at high concentration and low temperature, and 5 ms at low concentration and high temperature. For comparison, SH3 at a concentration of 15 mg ml−1 has a temperature-dependent relaxation time ranging between 7 and 13 ms. For transverse relaxation data of concentrated BSA, see ref. 47.
, where T2,k and Âk are the transverse relaxation time and the intrinsic intensity (before T2 relaxation) of the individual protein proton sites, respectively, and τ = 2 × 3.6 ms is the overall time span of the encoding and decoding periods of the NMR pulse sequence during which T2 relaxation occurs. T2 relaxation times are inversely proportional to the rotational correlation time of the particle. Larger particles with consequently longer rotational correlation times have – averaged over the different proton sites of the protein – shorter transverse relaxation times T2 than smaller particles. If T2 is comparable to or even shorter than τ (as is the case in concentrated protein solutions) and the solution is polydisperse, the signal obtained can be biased by monomers instead of representing the full ensemble average. This is the case for the BSA fraction, see below and ref. 13. Assuming a log-normal distribution of relaxation times, the median relaxation time represents the most populated one. For BSA and SH3 in mixture, the median relaxation time ranges between only 0.5 ms at high concentration and low temperature, and 5 ms at low concentration and high temperature. For comparison, SH3 at a concentration of 15 mg ml−1 has a temperature-dependent relaxation time ranging between 7 and 13 ms. For transverse relaxation data of concentrated BSA, see ref. 47.
Viscosity measurements
Steady-shear viscosities were measured using the capillary microfluid viscometer m-VROC (Rheosense, Sam Ramon, CA) via detection of the fluid pressure gradient along the capillary, applying a shear rate of 2000 s−1. When decreasing the shear rate to 100 s−1, no change in viscosity was detected, yet the signal-to-noise ratio decreased due to a lower pressure gradient inside the capillary. To avoid a bias by isotope effects, samples for viscosity measurements were also prepared with D2O.Isothermal titration calorimetry
To measure the interaction between SH3 and BSA, isothermal titration calorimetry (ITC) measurements were performed, titrating BSA into an SH3 solution. Measurements were performed on a VP-ITC calorimeter (Microcal LLC, Northampton, MA) at 20 °C. To separate dilution effects, BSA was also titrated into pure buffer as a reference.Results and discussion
Single-protein solutions
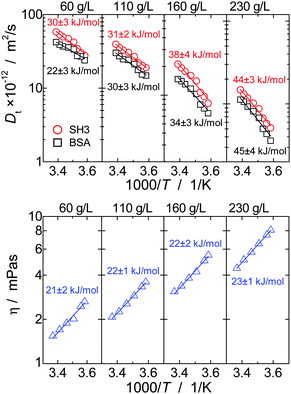
In single-protein solutions, both proteins behave as predicted from the GSE equation, eqn (1); see Fig. 1(a). Using eqn (1), the hydrodynamic radii for SH3 and BSA are calculated to be 2.0 nm and 3.4 nm,13 respectively. These values are in accordance with the predictions of 2.2 nm for SH3 using the HydroPro software50 (applied to protein data bank file 1BB9) and the known value of 3.44 nm for the BSA monomer.51 As indicated by the hydrodynamic size obtained, the PFG-NMR diffusion signal of BSA provides the translational displacement of mostly the monomers within the polydisperse (monomers and oligomers) surrounding.13 A very important observable is the temperature dependence of translational diffusion and viscosity (Fig. 2): for both quantities and for both proteins, the activation energy EA was found to be in the range of 18–27 kJ mol−1. These values of around 20 kJ mol−1 agree well with the activation energy of the viscous flow of pure water,52 indicating that local hydrodynamic interactions with the solvent dominate viscosity and translational diffusion. Somewhat enhanced activation energies at higher protein concentrations (e.g. BSA) suggest somewhat increased energetic barriers for particles diffusing in a crowded environment: under such conditions, surrounding particles have to get out of the way of the tracer particle to allow for translational particle rearrangements,53 and further, confined, surface-related water fractions arise. For SH3 diffusion, the decrease of EA may result from partial unfolding54,55 at high concentration and highest temperatures. This effect is expected to increase the ensemble-averaged hydrodynamic radius, and thus reduces diffusivity. The validity of eqn (1) is in accordance with colloid science concepts23 and agrees with our study13 on single-protein solutions (lysozyme, BSA, αB-crystallin).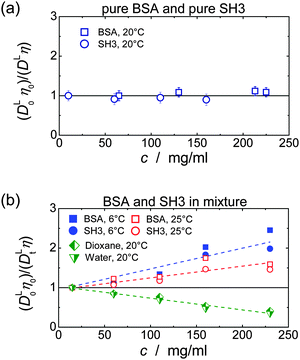 | ||
| Fig. 1 Test of the applicability of the GSE relation in concentrated solutions of (a) only SH3 or only BSA, and (b) in mixtures of SH3 and BSA, including the behavior of water and dioxane. At a fixed temperature, applicability of the GSE relationship requires DLη = const. (solid horizontal line). Note that increased (DL0η0)/(DLη) = RH,app/RH,0 suggest an increase in apparent hydrodynamic size. Data of pure BSA are taken from ref. 13. In part (b) error bars were skipped for clarity; dashed lines are linear fits to indicate the trend. In each case, the lowest concentration measured was used for normalization (DL0η0). | ||
 | ||
| Fig. 2 Temperature dependence of translational long-time diffusion coefficients DL (left) and viscosity (right) of the single-protein solutions in an Arrhenius plot. Numbers next to the data points give the activation energy and fitting error in kJ mol−1 as obtained from fitting the experimental data (solid lines). Protein concentrations are 10 mg ml−1 (squares), 60 mg ml−1 (circles), 110 mg ml−1 (triangles) and 160 mg ml−1 (rhombs) for SH3, and, for BSA, 65 mg ml−1 (squares), 130 mg ml−1 (circles), 213 mg ml−1 (triangles) and 255 mg ml−1 (rhombs). Data on translational diffusion of BSA as well as its viscosity at 213 mg ml−1 were taken from our study on single-protein solutions.13 | ||
SH3 and BSA in mixtures
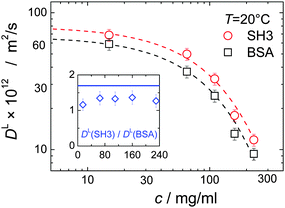
In mixtures, the diffusion coefficients of SH3 and BSA are different but have similar concentration dependencies (Fig. 3). Now, however, neither BSA nor SH3 follows the prediction of the GSE relation, see Fig. 1(b). Instead, with increasing protein concentration an increasing value of (DLη)−1 ∝ RH,app is observed at both 6 °C and 25 °C, meaning that translational diffusion is more retarded than expected from the solution viscosity η(c). Thus, the apparent, concentration-dependent hydrodynamic radius RH,app is about twice as large at high protein concentrations as in dilute solution. As follows from the measurements on single-protein solutions, neither the difference in size or shape between the two proteins, nor the presence of permanent oligomers (BSA) can account for this violation of the GSE relationship; see also ref. 13.Remember that in the long-time limit of diffusion, the tracer particle is subject to a multitude of statistically independent encounters with surrounding host particles, meaning that translational diffusion is averaged over different micro-environments. This renders long-time translational diffusion of colloidal particles sensitive to the macroscopic viscosity.26 The deviating behavior of the protein mixture from the behavior of both ordinary colloidal particles – that typically show GSE behavior23,25–28 – and single-protein solutions suggests that inter-protein interactions and/or concentration-dependent binding are of critical importance for the mixture of BSA and SH3, accounting for apparent hydrodynamic radii that seemingly increase with increasing protein concentration.
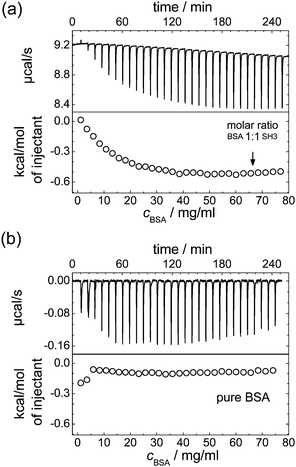
Indeed, for the mixtures of SH3 and BSA, ITC reveals an increasing protein binding tendency with increasing protein concentration, see Fig. 4: adding BSA to SH3 results in an exothermal process that becomes more pronounced with increasing concentration of BSA until saturation is reached. This increasing reactivity with increasing concentration indicates concentration-induced binding. Dilution of BSA in absence of SH3 does not reveal such an effect; besides the free energy of dilution, no indication of an exothermal event is observed.
Considering that, at least in dilute solutions amenable to high-resolution NMR, we were not able to detect direct indications for site-specific binding, we should also consider more general, crowding-related reasons for protein self- and hetero-association.56,57 Bound states generally require less space than individual, monomeric proteins. Thus, entropic excluded-volume effects can also account for increased inter-protein binding affinity. The difference in size between SH3 and BSA combined with the high protein concentration renders this depletion interaction particularly relevant. The depletion effect promotes a clustering of the larger particles, such that the presence of SH3 may cause BSA molecules to form transient clusters. However, the diffusivity of the smaller SH3 is more affected by the transient binding, as seen from the ratio of the diffusion coefficients DL(SH3)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DL(BSA), which is smaller than expected from the hydrodynamic radii (inset in Fig. 3). This is contrary to the expectation based upon a depletion attraction that should only affect the larger BSA.
DL(BSA), which is smaller than expected from the hydrodynamic radii (inset in Fig. 3). This is contrary to the expectation based upon a depletion attraction that should only affect the larger BSA.
Theory58 predicts that dimerization provides an energy gain in the order of kBT in case that 10–30% of the totally available volume is occupied by other particles. Indeed, an experimental study59 showed that crowding stabilizes protein–protein binding by about 1 kcal mol−1, i.e. by 1–2kBT. Given the non-specific nature of crowding-induced complex formation combined with its low binding energy, such complex formation can only be considered to be transient rather than permanent.
Irrespective of the potential (non-)specificity of the BSA–SH3 interaction, it is clear that, if the lifetime of transient binding is faster than or comparable to the experimental time scale of diffusion (of the order of 20 ms), the trajectory of the tracer particle will average over bound and unbound states.60 Thus, it will provide an effective, but enlarged hydrodynamic size that increases monotonically with the overall protein concentration. Our observations are consistent with this picture in that mono-exponential diffusion decays according to eqn (2) were observed in all cases, i.e., only a single diffusion coefficient is detected. We stress that T2-filtering effects cannot explain our observations: as long as bound and unbound populations are exchanging on the 20 ms timescale of the diffusion delay Δ, a potential T2 bias would not affect the measured result. Note that T2 of an 1H protein signal integrated over a broad chemical shift range is generally non-exponential due to differences in spin–spin dipolar couplings and differences in the local internal mobility of side chains, such that a size polydispersity (that may be stable on the shorter 1 ms timescale of the transverse encoding delay δ) cannot simply be judged on the basis of simple T2 decays.
The concept of crowding-induced transient binding is most directly corroborated by the temperature dependence of translational diffusion, see Fig. 5: for both BSA and SH3, the apparent activation energy EA of translational diffusion is significantly increased by a factor of about 1.5 to 2 as compared to the single-protein solutions. The apparent EA thus reflects the thermodynamics of the binding equilibrium. As we lack information on the specificity and stoichiometry of the binding and the structures of the transient protein assemblies, it is not possible to provide a more detailed analysis of the measured values. However, the effect of the binding equilibrium, with bound states being favored at lower temperature, is directly supported by the fact that the deviations from the GSE prediction are more pronounced at lower temperatures; see again Fig. 1(b).
For viscosity, in turn, the apparent activation energy matches within the experimental precision the value found for only BSA and only SH3. In contrast to translational diffusion, viscosity does not depend on hydrodynamic sizes of the individual diffusing particles, but is determined by the overall volume fraction of all dispersed particles. The extent to which (unspecific) binding reduces the volume occupied by the proteins thus appears to be reasonably small, and, as a result, the effect of oligomerization on the apparent EA is much weaker for viscosity than for translational diffusion.
We finally stress that our general observation is in qualitative agreement with previous work. In studies in which tracer protein diffusion was studied in the presence of another protein species, long-time translational diffusion was either found to be slower than expected from viscosity,31,32 or the validity of the GSE equation was retained.30 In contrast, for the case of crowding by globular proteins, we are not aware of any studies reporting on protein translational diffusion being faster than expected from the macro-viscosity.
Diffusion of small probe molecules
Fig. 1(b) clearly demonstrates that the concentration dependence of dioxane and water diffusion is qualitatively different from that of the proteins. Thus, it is immediately clear that small molecules are not reliable reporters on the viscosity experienced by highly concentrated macromolecules. Instead, the small solvent molecules diffuse faster than predicted from the SE relation, at least with regards to the (macroscopic) solution viscosity. Under crowding conditions, these small probe molecules diffuse in an environment of much larger surrounding particles, which renders the validity of the effective-medium approach questionable with regards to estimating the macroscopic dispersion viscosity. On the time-scale of translational motion of the small probe molecules, proteins appear as quasi-static objects that obstruct the diffusion of the much smaller solvent molecules, which is otherwise governed by the pure-solvent viscosity. Such a scenario is known to go along with a linear decrease of the translational diffusion coefficient with the volume fraction ϕ of obstructing particles,61| DL = DL0 (1 − βϕ), | (3) |
![[small beta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c3.gif)
![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) c). Here,
c). Here, ![[small beta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c3.gif) = βSH3·ϕSH3/(ϕSH3 + ϕBSA) + βBSA·ϕBSA/(ϕSH3 + ϕBSA) and
= βSH3·ϕSH3/(ϕSH3 + ϕBSA) + βBSA·ϕBSA/(ϕSH3 + ϕBSA) and ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) = θSH3·cSH3/c + θBSA·cBSA/c are independent of the overall protein concentration c = cSH3 + cBSA since the ratio of SH3 to BSA molecules is the same for all concentrations. Fig. 6 confirms the expected linear obstruction effect with protein concentration for water and dioxane diffusion.
= θSH3·cSH3/c + θBSA·cBSA/c are independent of the overall protein concentration c = cSH3 + cBSA since the ratio of SH3 to BSA molecules is the same for all concentrations. Fig. 6 confirms the expected linear obstruction effect with protein concentration for water and dioxane diffusion.
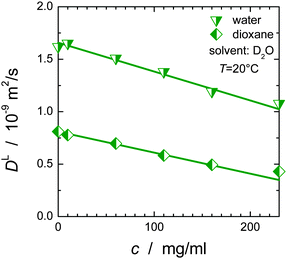 | ||
| Fig. 6 Obstruction effect for water and dioxane as a function of the overall protein concentration c. The diffusion coefficient of dioxane at zero protein concentration was calculated via the Stokes–Einstein relation using RH = 2.12 Å62 and ηD2O = 1.25 mPa s; for water the diffusion coefficient of 2.02 × 10−9 m2 s−1 at 20 °C63 was corrected by a factor of 1.25 to account for the different viscosity of D2O and H2O. | ||
The linear decrease of the diffusivity of small molecule stands in stark contrast to the (approximately) exponential slow-down of protein diffusion with increasing protein concentration; cf.Fig. 3 and ref. 53, 64 and 65. Likewise, the (macroscopic) solution viscosity commonly increases more than linearly with protein concentration.66,67
For simple liquids, in which solute and solvent are of equal or similar size, the validity of the SE relationship can often be retained via introducing slip boundary conditions,68,69i.e., the viscous friction ξ in DL = kBT/ξ scales as ξ = 4πηRH rather than the usual case of ξ = 6πηRH (stick boundary conditions). However, the maximal factor of 2/3, even when taken to vary between this value and 1 as a function of concentration, cannot account for such a difference in the concentration dependence of the diffusivity of solvent molecules and the macroscopic viscosity (and protein diffusion).
For small molecules, the deviation from SE behavior is reminiscent of neutral solutes in ionic liquids, where the solute-to-solvent size ratio plays a key role.70–73 Despite noting that charge–charge interactions are much more relevant for ionic liquids as for the diffusivity of water in presence of proteins, the deviations from SE behavior are similar in origin. In ionic liquids, regions of locally increased charge concentration exist next to regions of lower charge density, accounting for dynamical heterogeneity.71,72 Depending on the size of the tracer particle relative to the length scale of such heterogeneity, the effect is either averaged out, recovering SE behavior,72 or the neutral solute is small enough to predominately diffuse within regions of high mobility, accounting for diffusion rates higher than expected from the macroscopic viscosity. Although dynamical heterogeneity is not of relevance for long-range diffusion of water or dioxane in protein solutions, the structurally inhomogeneous surroundings (large, almost immobile proteins compared to the small solvent molecules) provide a similar scenario as for ionic liquids: despite of the obstruction effect mediated by the proteins, the environment probed by small solvent particles is dominated by the solvent itself, and contrasts with the (sterical) hindrance relevant for the proteins. Whereas a small molecule escapes a “macromolecular cage” almost effortlessly, proteins are much more sensitive to macromolecular caging, introducing dynamic correlations on larger scales, and thus experience a stronger retardation in diffusion than does water or dioxane.
This latter effect even holds with regards to the hydration shell of the proteins: the life-time of water molecules within the hydration shell is usually on the timescale of picoseconds,74 such that trapping of a water molecule within the hydration shell does not significantly hinder water diffusion. Thus, small probe molecules experience a local, solvent-related viscosity with some obstruction by the presence of the proteins, rather than being sensitive to the (macroscopic) dispersion viscosity. As a result, the GSE relationship cannot be applied (see Fig. 1(b)). Notably, this effect can already be seen at low concentrations, although the deviation is reasonably weak. On the other extreme, in case of a hydrated lyophilized protein powder, confinement effects become relevant even for small molecules, and surface effects must be taken into account.75
Protein diffusion within an entangled polymer matrix is phenomenologically similar to diffusion of water or dioxane under macromolecular crowding. Indeed, protein diffusion is usually faster than predicted by the GSE relationship in the presence of Ficoll or other unstructured polymers.33,36,37 For globular proteins crowded by other globular proteins, size effects are usually not that dramatic, such that protein diffusion is well described by the macroscopic (zero-shear) viscosity,13 given that no transient binding occurs.
Conclusions
In the absence of transient binding, long-time self-diffusion scales with the solution viscosity. Such a behavior is expected on the basis of established concepts in colloid science, and was demonstrated here for single-protein solutions of the SH3 domain and BSA, the latter even having a distribution in size and shape of the Brownian particles. In both cases, the activation energies of translational diffusion and macro-viscosity coincide within experimental uncertainty, being close to the activation energy for viscous flow of pure water. In contrast, upon mixing SH3 and BSA, translational diffusion of either species was found to be single-component but more retarded than expected from the solution viscosity: the hydrodynamic radius thus appeared to increase with concentration, indicating the relevance of attractive inter-protein interactions and concentration-dependent, transient binding.While specific binding sites could not be resolved in 1H–15N HSQC NMR spectra of a necessarily rather dilute solution of isotope-labeled SH3 in the presence of BSA, calorimetric measurements did prove an exothermal reaction between SH3 and BSA. The relevance of transient binding is most clearly corroborated by the observed temperature dependence of translational diffusion. In a mixture of both proteins, the apparent activation energy increased significantly with protein concentration, with values being notably larger than the again nearly constant activation energy of the macroscopic viscosity of the same mixture. This is in line with the fact that solution viscosity mainly depends on the overall volume fraction of the solutes rather than on individual particle sizes (Einstein model). The relevance of transient binding is further supported by the fact that the apparent increase in hydrodynamic radius with concentration was found to be larger at low temperatures, at which the binding equilibrium is shifted towards the bound state.
Moreover, we showed that translational diffusion of small probe molecules (water, dioxane) does not allow for conclusions on the viscosity relevant for long-time translational diffusion of highly concentrated proteins: the local viscosity probed by dioxane or water is in-between the pure solvent viscosity and the macroscopic solution viscosity, and is mainly affected by geometric obstruction effects.
Acknowledgements
We are grateful to Alexey Krushelnitsky for very helpful discussions, and thank Sebastian Kirschke for preparatory work during his Bachelor thesis, implementing and testing the pulse sequence for isotope-filtered PFG NMR. Funding of this work was provided by the Deutsche Forschungsgemeinschaft (DFG) in the framework of the collaborative research center SFB/TRR 102 (project A08). We also acknowledge significant investments in our NMR facility by the European Regional Development Fund (ERDF) of the European Union.References
- A. B. Fulton, How crowded is the cytoplasm?, Cell, 1982, 30, 345–347 CrossRef CAS PubMed
.
- S. B. Zimmerman and S. O. Trach, Estimation of macromolecule concentrations and excluded volume effects for the cytoplasm of Escherichia coli, J. Mol. Biol., 1991, 222, 599–620 CrossRef CAS PubMed
.
- R. J. Ellis and A. P. Minton, Cell biology: Join the crowd, Nature, 2003, 425, 27–28 CrossRef CAS PubMed
.
- R. J. Ellis, Macromolecular crowding: obvious but underappreciated, Trends Biochem. Sci., 2001, 26(10), 597–604 CrossRef CAS PubMed
.
- R. J. Ellis, Macromolecular crowding: an important but neglected aspect of the intracellular environment, Curr. Opin. Struct. Biol., 2001, 11, 114–119 CrossRef CAS PubMed
.
- O. Medalia, I. Weber, A. S. Frangakis, D. Nicastro, G. Gerisch and W. Baumeister, Macromolecular architecture in eukaryotic cells visualized by cryoelectron tomography, Science, 2002, 298, 1209–1213 CrossRef CAS PubMed
.
- H. X. Zhou, G. N. Rivas and A. P. Minton, Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences, Annu. Rev. Biophys., 2008, 37, 375–397 CrossRef CAS PubMed
.
- S. Klumpp, M. Scott, S. Pedersen and T. Hwa, Molecular crowding limits translation and cell growth, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(42), 16754–16759 CrossRef CAS PubMed
.
- B. Doliwa and A. Heuer, Cage effect, local anisotropies, and dynamic heterogeneities at the glass transition: A computer study of hard spheres, Phys. Rev. Lett., 1998, 80(22), 4915–4918 CrossRef CAS
.
- M. Roos, S. Link, J. Balbach, A. Krushelnitsky and K. Saalwächter, NMR-detected Brownian dynamics of αB-crystallin over a wide range of concentrations, Biophys. J., 2015, 108, 98–106 CrossRef CAS PubMed
.
- T. J. O'Leary, Concentration dependence of protein diffusion, Biophys. J., 1987, 52, 137–139 CrossRef
.
- T. Ando and J. Skolnick, Crowding and hydrodynamic interactions likely dominate in vivo macromolecular motion, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(43), 18457–18462 CrossRef CAS PubMed
.
- M. Roos, M. Ott, M. Hofman, S. Link, E. Rössler, J. Balbach, A. Krushelnitsky and K. Saalwächter, under revision.
- K. Luby-Phelps, Cytoarchitecture and physical properties of cytoplasm: volume, viscosity, diffusion, intracellular surface area, Int. Rev. Cytol., 2000, 192, 189–221 CAS
.
- J. W. Wojcieszyn, R. A. Schlegel, E.-S. Wu and K. A. Jacobson, Diffusion of injected macromolecules within the cytoplasm of living cells, Proc. Natl. Acad. Sci. U. S. A., 1981, 78(7), 4407–4410 CrossRef CAS
.
- R. Swaminathan, C. P. Hoang and A. S. Verkman, Photobleaching recovery and anisotropy decay of green fluorescent protein GFP-S65T in solution and cells: cytoplasmic viscosity probed by green fluorescent protein translational and rotational diffusion, Biophys. J., 1997, 72(4), 1900–1907 CrossRef CAS PubMed
.
- J. Lippincott-Schwartz, E. Snapp and A. Kenworthy, Studying Protein Dynamics in Living Cells, Nat. Rev. Mol. Cell Biol., 2001, 2, 444–456 CrossRef CAS PubMed
.
- A. S. Verkman, Solute and macromolecule diffusion in cellular aqueous compartments, Trends Biochem. Sci., 2002, 27, 27–33 CrossRef CAS PubMed
.
- M. Kumar, M. S. Mommer and V. Sourjik, Mobility of Cytoplasmic, Membrane, and DNA-Binding Proteins in Escherichia coli, Biophys. J., 2010, 98, 552–559 CrossRef CAS PubMed
.
- R. D. Phair and T. Misteli, High mobility of proteins in the mammalian cell nucleus, Nature, 2000, 404, 604–609 CrossRef CAS PubMed
.
- A. Partikian, B. Ölveczky, R. Swaminathan, Y. Li and A. S. Verkman, Rapid Diffusion of Green Fluorescent Protein in the Mitochondrial Matrix, J. Cell Biol., 1998, 140, 821–829 CrossRef CAS PubMed
.
- F. Roosen-Runge, M. Hennig, F. Zhang, R. M. J. Jacobs, M. Sztucki, H. Schober, T. Seydel and F. Schreiber, Protein self-diffusion in crowded solutions, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(29), 11815–11820 CrossRef CAS PubMed
.
- P. N. Segre, S. P. Meeker, P. N. Pusey and W. C. K. Poon, Viscosity and structural relaxation in suspensions of hard-sphere colloids, Phys. Rev. Lett., 1995, 75(5), 958–961 CrossRef CAS PubMed
.
- A. J. Banchio, G. Nägele and J. Bergenholtz, Viscoelasticity and generalized Stokes–Einstein relations of colloidal dispersions, J. Chem. Phys., 1999, 111(18), 8721–8740 CrossRef CAS
.
- A. J. Banchio, J. Bergenholtz and G. Nägele, Rheology and dynamics of colloidal suspensions, Phys. Rev. Lett., 1999, 82(8), 1792–1795 CrossRef CAS
.
- G. H. Koenderink and A. P. Philipse, Rotational and translational self-diffusion in colloidal sphere suspensions and the applicability of generalized Stokes-Einstein relations, Langmuir, 2000, 16, 5631–5638 CrossRef CAS
.
- W. Richtering and H. Müller, Comparison between Viscosity and Diffusion in Monodisperse and Bimodal Colloidal Suspensions, Langmuir, 1995, 11, 3699–3704 CrossRef CAS
.
- S. Gupta, J. Stellbring, E. Zaccarelli, C. N. Likos, M. Camargo, P. Holmqvist, J. Allgaier, L. Willner and D. Richter, Validity of the Stokes-Einstein relation in soft colloids up to the glass transition, Phys. Rev. Lett., 2015, 115, 128302 CrossRef PubMed
.
- A. Imhof, A. van Blaaderen, G. Maret, J. Mellema and J. K. G. Dhont, A comparison between the long-time self-diffusion and low shear viscosity of concentrated dispersions of charged colloidal silica spheres, J. Chem. Phys., 1994, 100, 2170–2181 CrossRef CAS
.
- P. Licinio and M. Delaye, Mutual and self-diffusion in concentrated α-crystallin protein dispersion. A dynamic light-scattering study, J. Phys., 1988, 49, 975–981 CAS
.
- Y. Wang, C. Li and G. J. Pielak, Effects of proteins on protein diffusion, J. Am. Chem. Soc., 2010, 132(27), 9392–9397 CrossRef CAS PubMed
.
- S. Zorilla, M. A. Hink, A. J. Visser and M. P. Lillo, Translational and rotational motions of proteins in a protein crowded environment, Biophys. Chem., 2007, 125, 298–305 CrossRef PubMed
.
- N. A. Busch, T. Kim and V. A. Bloomfield, Tracer diffusion of proteins in DNA Solutions. 2. Green fluorescent protein in crowded DNA solutions, Macromolecules, 2000, 33, 5932–5937 CrossRef CAS
.
- E. Dauty and A. S. Verkman, Molecular crowding reduces to a similar extent the diffusion of small solutes and macromolecules: measurement by fluorescence correlation spectroscopy, J. Mol. Recognit., 2004, 17, 441–447 CrossRef CAS PubMed
.
- D. Lavalette, M. A. Hink, M. Tourbez, C. Tétreau and A. J. Visser, Proteins as micro viscosimeters: Brownian motion revisited, Eur. Biophys. J., 2006, 35, 517–522 CrossRef CAS PubMed
.
- S. P. Zustiak, R. Nossal and D. L. Sackett, Hindered diffusion in polymeric solutions studied by fluorescence correlation spectroscopy, Biophys. J., 2011, 101, 255–264 CrossRef CAS PubMed
.
- Y. Y. Kuttner, N. Kozer, E. Segal, G. Schreiber and G. Haran, Separating the Contribution of Translational and Rotational Diffusion to Protein Association, J. Am. Chem. Soc., 2005, 127(27), 15138–15144 CrossRef CAS PubMed
.
- C. Li, Y. Wang and G. J. Pielak, Translational and rotational diffusion of a small globular protein under crowded conditions, J. Phys. Chem. B, 2009, 113, 13390–13392 CrossRef CAS PubMed
.
- A. Soranno, I. Koenig, M. B. Borgia, H. Hofmann, F. Zosel, D. Nettels and B. Schuler, Single-molecule spectroscopy reveals polymer effects of disordered proteins in crowded environments, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(13), 4874–4879 CrossRef CAS PubMed
.
- J. Danielsson, X. Mu, L. Lang, H. Wang, A. Binolfi, F.-X. Theillet, B. Bekei, D. T. Logan, Ph. Selenko, H. Wennerström and M. Oliveberg, Thermodynamics of protein destabilization in live cells, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(40), 12402–12407 CrossRef CAS PubMed
.
- H. Tanaka, I. Yoshizaki, S. Takahashi, M. Yamanaka, S. Fukuyama, M. Sato, S. Sano, M. Motohara, T. Kobayashi, S. Yoshitomi and T. Tanaka, Diffusion coefficient of the protein in various crystallization solutions: the key to growing high-quality crystals in space, Microgravity Sci. Technol., 2006, 18(3–4), 91–94 CrossRef CAS
.
- A. B. Goins, H. Sanabria and M. N. Waxham, Macromolecular Crowding and Size Effects on Probe Microviscosity, Biophys. J., 2008, 95, 5362–5373 CrossRef CAS PubMed
.
- K. Elliott, D. Sakamuro, A. Basu, W. Du, W. Wunner, P. Staller, S. Gaubatz, H. Zhang, E. Prochownik, M. Eilers and G. C. Prendergast, Bin1 functionally interacts with Myc and inhibits cell proliferation via multiple mechanisms, Oncogene, 1999, 18, 3564–3573 CrossRef CAS PubMed
.
- V. Anggono and P. J. Robinson, Syndapin I and endophilin I bind overlapping proline-rich regions of dynamin I: role in synaptic vesicle endocytosis, J. Neurochem., 2007, 102, 931–943 CrossRef CAS PubMed
.
- S. Suetsu, K. Toyooka and Y. Senju, Subcellular membrane curvature mediated by the BAR domain superfamily proteins, Semin. Cell Dev. Biol., 2010, 21, 340–349 CrossRef PubMed
.
- P. G. Squire, P. Moser and C. T. O'Konski, The hydrodynamic properties of bovine serum albumin monomer and dimer, Biochemistry, 1968, 7, 4261–4272 CrossRef CAS PubMed
.
- M. Roos, M. Hofmann, S. Link, M. Ott, J. Balbach, E. Rössler, K. Saalwächter and A. Krushelnitsky, The “long tail” of the protein tumbling correlation function: observation by 1H NMR relaxometry in a wide frequency and concentration range, J. Biomol. NMR, 2015, 63, 403–415 CrossRef CAS PubMed
.
- E. O. Stejskal and J. E. Tanner, Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient, J. Chem. Phys., 1965, 42, 288–292 CrossRef CAS
.
- M. L. Tillet, M. A. Horsfield, L.-Y. Lian and T. J. Norwood, Protein-ligand interactions measured by 15N-filtered diffusion experiments, J. Biomol. NMR, 1999, 13, 223–232 CrossRef
.
- J. G. de la Torre, M. L. Huertas and B. Carrasco, Calculation of hydrodynamic properties of globular proteins from their atomic-level structure, Biophys. J., 2000, 78, 719–730 CrossRef CAS
.
- I. Axelsson, Characterization of proteins and other macromolecules by agarose gel chromatography, J. Chromatogr. A, 1978, 152(1), 21–32 CrossRef CAS
.
- R. A. Horne, R. A. Courant, D. S. Johnson and F. F. Margosian, The activation energy of viscous flow of pure water and sea water in the temperature region of maximum density, J. Phys. Chem., 1965, 69, 3988–3991 CrossRef CAS
.
- N. Muramatsu and A. P. Minton, Tracer diffusion of globular proteins in concentrated protein solutions, Proc. Natl. Acad. Sci. U. S. A., 1988, 85, 2984–2988 CrossRef CAS
.
- O. Zhang and J. D. Forman-Kay, Structural characterization of folded and unfolded states of an SH3 domain in equilibrium in aqueous buffer, Biochemistry, 1995, 34, 6784–6794 CrossRef CAS PubMed
.
- A. E. Smith, L. Z. Zhou, A. H. Gorensek, M. Senske and G. J. Pielak, In-cell thermodynamics and a new role for protein surfaces, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(7), 1725–1730 CrossRef CAS PubMed
.
- S. B. Zimmerman and A. P. Minton, Macromolecular crowding: biochemical, biophysical, and physiological consequences, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 27–65 CrossRef CAS PubMed
.
- A. P. Minton, Implications of macromolecular crowding for protein assembly, Curr. Opin. Struct. Biol., 2000, 10, 34–39 CrossRef CAS PubMed
.
- O. G. Berg, The influence of macromolecular crowding on thermodynamic activity: solubility and dimerization constants for spherical and dumbbell-shaped molecules in a hard-sphere mixture, Biopolymers, 1990, 30, 1027–1037 CrossRef CAS PubMed
.
- J. Batra, K. Xu, S. Qin and H.-X. Zhou, Effect of macromolecular crowding on protein binding stability: modest stabilization and significant biological consequences, Biophys. J., 2009, 97, 906–911 CrossRef CAS PubMed
.
- T. Geyer, Mixing normal and anomalous diffusion, J. Chem. Phys., 2012, 137, 115101 CrossRef PubMed
.
- R. Kimmich, F. Klammler, V. D. Skirda, I. A. Serebrennikova, A. I. Maklakov and N. Fatkullin, Geometrical restrictions of water diffusion in aqueous protein systems. A study using NMR field-gradient techniques, Appl. Magn. Reson., 1993, 4, 425–440 CrossRef CAS
.
- D. K. Wilkins, S. B. Grimshaw, V. Receveur, C. M. Dobson, J. A. Jones and L. J. Smith, Hydrodynamic Radii of Native and Denatured Proteins Measured by Pulse Field Gradient NMR Techniques, Biochemistry, 1999, 38, 16424–16431 CrossRef CAS PubMed
.
- M. Holz, S. R. Heil and A. Sacco, Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate 1H NMR PFG Measurements, Phys. Chem. Chem. Phys., 2000, 2, 4740–4742 RSC
.
- T. J. O'Leary, Concentration dependence of protein diffusion, Biophys. J., 1987, 52, 137–139 CrossRef
.
- J. Han and J. Herzfeld, Macromolecular diffusion in crowded solutions, Biophys. J., 1993, 65, 1155–1161 CrossRef CAS PubMed
.
- P. Pradipasena and C. Rha, Effect of concentration on apparent viscosity of a globular protein solution, Polym. Eng. Sci., 1977, 17(12), 861–864 CAS
.
- W. J. Galush, L. N. Le and J. M. R. Moore, Viscosity Behavior of High-Concentration Protein Mixtures, J. Pharm. Sci., 2012, 110(3), 1012–1020 CrossRef PubMed
.
- B. J. Alder, D. M. Gass and T. E. Wainwright, Studies in Molecular Dynamics. VIII. The Transport Coefficients for a Hard-Sphere Fluid, J. Chem. Phys., 1970, 53, 3813–3826 CrossRef CAS
.
- F. Ould-Kaddour and D. Levesque, Molecular-dynamics investigation of tracer diffusion in a simple liquid: Test of the Stokes-Einstein law, Phys. Rev. E, 2000, 63, 011205 CrossRef PubMed
.
- A. Kaintz, G. Baker, A. Benesi and M. Maroncelli, Solute Diffusion in Ionic Liquids, NMR Measurements and Comparisons to Conventional Solvents, J. Phys. Chem. B, 2013, 117, 11697–11708 CrossRef CAS PubMed
.
- J. C. Araque, S. K. Yadav, M. Shadeck, M. Maroncelli and C. J. Margulis, How Is Diffusion of Neutral and Charged Tracers Related to the Structure and Dynamics of a Room-Temperature Ionic Liquid? Large Deviations from Stokes-Einstein Behavior Explained, J. Phys. Chem. B, 2015, 119, 7015–7029 CrossRef CAS PubMed
.
- J. C. Araque, J. J. Hettige and C. J. Margulis, Ionic liquids-Conventional solvent mixtures, structurally different but dynamically similar, J. Chem. Phys., 2015, 143, 134505 CrossRef PubMed
.
- Y. Kimura, Y. Kida, Y. Matsushita, Y. Yasaka, M. Ueno and K. Takahashi, Universality of Viscosity Dependence of Translational Diffusion Coefficients of Carbon Monoxide, Diphenylacetylene, and Diphenylcyclopropenone in Ionic Liquids under Various Conditions, J. Phys. Chem. B, 2015, 119, 8096–8103 CrossRef CAS PubMed
.
- V. P. Denisov and B. Halle, Protein hydration dynamics in aqueous solution, Faraday Discuss., 1996, 103, 227–244 RSC
.
- M. Rosenstihl, K. Kämpf, F. Klameth, M. Sattig and M. Vogel, Dynamics of interfacial water, J. Non-Cryst. Solids, 2015, 407, 449–458 CrossRef CAS
.
Footnote |
| † Present address: Deutsches Diabetes Zentrum, 40225 Düsseldorf, Germany. |
| This journal is © the Owner Societies 2016 |