Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Experimentally probing the libration of interfacial water: the rotational potential of water is stiffer at the air/water interface than in bulk liquid†
Yujin
Tong
,
Tobias
Kampfrath
and
R. Kramer
Campen
 *
*
Fritz Haber Institute of the Max Planck Society, Faradayweg 4-6, 14195 Berlin, Germany. E-mail: campen@fhi-berlin.mpg.de; Fax: +49 (0)30 8413 5106; Tel: +49 (0)30 8413 5230
First published on 15th June 2016
Abstract
Most properties of liquid water are determined by its hydrogen-bond network. Because forming an aqueous interface requires termination of this network, one might expect the molecular level properties of interfacial water to markedly differ from water in bulk. Intriguingly, much prior experimental and theoretical work has found that, from the perspective of their time-averaged structure and picosecond structural dynamics, hydrogen-bonded OH groups at an air/water interface behave the same as hydrogen-bonded OH groups in bulk liquid water. Here we report the first experimental observation of interfacial water's libration (i.e. frustrated rotation) using the laser-based technique vibrational sum frequency spectroscopy. We find this mode has a frequency of 834 cm−1, ≈165 cm−1 higher than in bulk liquid water at the same temperature and similar to bulk ice. Because libration frequency is proportional to the stiffness of water's rotational potential, this increase suggests that one effect of terminating bulk water's hydrogen bonding network at the air/water interface is retarding rotation of water around intact hydrogen bonds. Because in bulk liquid water the libration plays a key role in stabilizing reaction intermediates and dissipating excess vibrational energy, we expect the ability to probe this mode in interfacial water to open new perspectives on the kinetics of heterogeneous reactions at aqueous interfaces.
Introduction
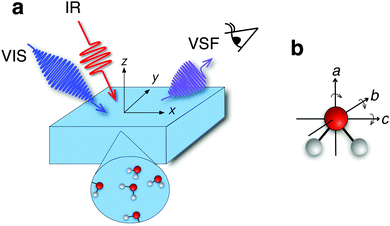
The chemical and physical properties of liquid water at the air/water interface control a wide variety of environmental, biological, and technological processes.1–3 Many of the properties of bulk liquid water, e.g. its phase diagram, its density maximum in the liquid phase and its high specific heat capacity and viscosity relative to other liquids, are known to sensitively depend on water's hydrogen-bonding network. Since this network is terminated at the air/water interface, interfacial water molecules must be differently coordinated than those in bulk,4 one might expect that the properties of interfacial water differ significantly from those of the bulk liquid. Probing many macroscopic properties of the air/water interface, e.g. surface tension and surface potential, is relatively straightforward. In contrast, it is challenging to experimentally probe the manner in which water's hydrogen-bond network, and molecular-level structure and dynamics evolve as one moves from bulk to the air/water interface.Much work in hydrogen-bonded systems has shown that the OH stretch frequency sensitively reports on local environment.5 Unfortunately, applying conventional vibrational spectroscopies such as infrared absorption or spontaneous Raman scattering to probe interfacial water is generally impossible. Typically, the response of water molecules at the interface is overwhelmed by that of the much larger number in bulk. This challenge was first overcome by Shen and coworkers more than twenty years ago when they probed the OH stretch response of the 1–2 layers of water at the air/water interface6 employing the interface-specific, laser-based technique, known as vibrational sum-frequency (VSF) spectroscopy. In a VSF measurement (see Fig. 1a), a polarization is induced in water by a pulsed infrared (IR) field whose frequency is resonant with a molecular vibration. These oscillating dipoles then interact with an additional non-resonant field at visible frequencies (VIS) that upconverts only the emission from interfacial water molecules because they lack the local inversion symmetry of bulk.7
Conducting a VSF measurement of the air/water interface with the IR incident field tuned to OH stretch frequencies gives an intensity spectrum with large features at ≈3150, 3400 and 3710 cm−1 in IR frequency.6 This spectrum differs dramatically from the OH stretch spectrum measured in IR absorption of bulk liquid water. Here, only a single peak is apparent that is centered at ≈3400 cm−1.8 The 3710 cm−1 feature apparent in the VSF spectrum has been, uncontroversially, assigned to non-hydrogen-bonded OH groups that point towards the vapor phase. While the two lower-frequency features are known to correspond to OH groups that donate hydrogen bonds, understanding the manner in which they report on interfacial molecular structure and dynamics has proven challenging. Based on the similarity of the center frequencies of these features to those of the IR spectrum of ice and liquid water, a number of initial studies assigned the two peaks to quasi-static structural types of interfacial water: ice-like and liquid-like.6,9–11 However, more recent experimental and computational studies all appear to rule out the notion that these two peaks are the result of structural heterogeneity in interfacial water.12–19 While the appropriate assignment is still controversial, collecting VSF spectra of the OD stretch of HOD in H2O at the air/water interface clarifies that the OH stretch line shape of hydrogen bonded interfacial water strongly resembles the OH stretch spectral response of the bulk liquid.12,13,16,17,20 Additionally, simulations of both time-averaged water structure, e.g. hydrogen-bond distance (O–H⋯O) and angle (∠O–H⋯O), and picosecond structural dynamics (i.e. the change of OH groups to new hydrogen bond acceptors and the rotation of intact hydrogen bonded pairs21) also find interfacial hydrogen-bonded OH groups behave similarly to those in bulk liquid water.14,22–25
These results are surprising. They suggest that terminating bulk water's hydrogen bond network has few consequences for hydrogen bond donating OH groups at an air/water interface. From an experimental point of view, this conclusion requires inferring the spatial arrangement of water molecules by their perturbation of an intramolecular vibration: the OH stretch. In principle, probing intermolecular vibrations is a more direct path to this insight. In bulk, the highest-frequency intermolecular vibration is water's libration (i.e. frustrated rotation): the frequency of which is proportional to the stiffness of the potential of mean force describing water's rotation about intact hydrogen bonds (see Fig. 1b). As noted above, from a simulation point of view most studies of the air/water interface have focussed on either time-averaged structure or picosecond structural dynamics. Such long timescale dynamics reflect changes in network topology, hydrogen bonds break and reform on ps timescales, but do not tell us whether the stiffness of the intact hydrogen bonded network changes as one moves from bulk to the interface.
Probing the libration of interfacial water addresses much of the limitations of prior experiment and simulation. From an experimental perspective it clearly complements and extends prior work characterising the OH stretch of interfacial water by more directly addressing water's intermolecular potential. From the perspective of simulation it complements the prior work described above by directly addressing the properties of the intact hydrogen-bonded network at the air/water interface. In addition to the insight it offers into water structure and dynamics a deeper understanding of water's libration at interfaces is of interest in its own right. Much prior work in bulk has shown that this mode plays an essential role in the flow of excess vibrational energy (e.g. from excited OH stretch modes to heat26–28) and in many aqueous phase chemical reactions (e.g. the localization of the excess electron in water29–31). The ability to probe the libration at aqueous interfaces should allow significant insight into the kinetics and mechanisms of these and similar processes in heterogeneous aqueous phase chemistry.2,3,32,33
Here, then, we employ VSF spectroscopy to experimentally characterize, for the first time, the libration of interfacial water. We find that the libration frequency of interfacial water is significantly higher than bulk liquid water at the same temperature. This observation suggests water's rotational potential stiffens on moving from the bulk liquid to the air/water interface.
Results and discussion
Experimental observable
To do so, we constructed the experiment shown schematically in Fig. 1 and collected a VSF spectrum in the IR frequency range 680–1050 cm−1. The technical details of our VSF spectrometer have been described previously,34 and are reproduced here, along with details specific to the current study, in the ESI.† The results of this measurement are shown in Fig. 2a. Note that we have plotted the intensity of the emitted VSF light (IVSF) divided by the intensity of the incident infrared (IIR) to account for the fact that the power of our incident infrared field is frequency dependent. Clearly, this spectrum shows a striking feature centered at ≈875 cm−1. To confirm this feature is a property of interfacial water, we performed a variety of control experiments. To verify the surface was contaminant free, we collected VSF spectra in this frequency range at the air/D2O, and CH and OH stretch frequency ranges at the air/H2O interface. To verify the signal was, in fact, sum-frequency emission, we confirmed that it was emitted at the angle expected from wave-vector conservation,35 and that IVSF depended linearly on the intensity of the VIS and IR beams. All control experiments thus strongly suggest that the spectral feature we observe is a property of interfacial H2O (see Section 1 of the ESI† for details).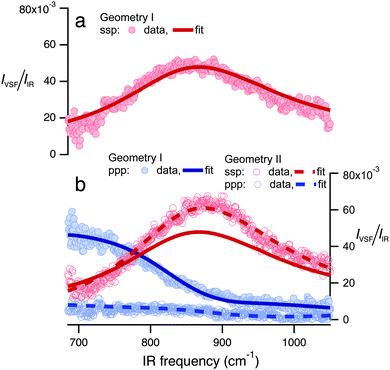 | ||
| Fig. 2 I VSF/IIR plotted as a function of incident IR frequency for spectra collected in (a) geometry I under the ssp polarization condition and (b) in geometry I under the ppp, and geometry II under both ssp and ppp. Solid and dashed lines are fits to the data using the line-shape model described in the text. The fit of the spectra shown in (a) is reproduced in (b) for comparison. All spectra shown have been normalized to account for the frequency-dependent IR intensity and to account for intensity variations between experimental configurations (see Section 2 of the ESI† for details). | ||
Note that the IVSF/IIR spectrum shown in Fig. 2a contains not only the vibrational response of interfacial water molecules but also depends on the incident angles and polarizations of all beams. The interfacial vibrational information is contained in the dependence of interfacial water's nonlinear susceptibility (χ(2)) on the frequency of the incident infrared field. As is shown in eqn (1), however, in addition to χ(2), IVSF/IIR depends on the well-known Fresnel coefficients (L) describing the reflection and transmission of all fields at an interface and their polarizations (ê is the unit polarization vector), the spectrum of the visible pulse (EVIS, ⊗ indicates a convolution), and the emission angle of the VSF field (θVSF).36–38
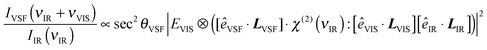 | (1) |
The Fresnel coefficients depend on the incident angles of the fields, their polarizations and the frequency-dependent, refractive indices of water and air. Their functional form has been well described previously and is reproduced, along with the complete expressions for the reflected VSF signal, in Section 2 of the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36–38 For purposes of this study the key point is that they are known independently of our measurements. Thus, calculating the Fresnel coefficients and independently measuring the spectrum of our visible pulse, i.e. EVIS, we can extract χ(2) from the data.
36–38 For purposes of this study the key point is that they are known independently of our measurements. Thus, calculating the Fresnel coefficients and independently measuring the spectrum of our visible pulse, i.e. EVIS, we can extract χ(2) from the data.
We quantify χ(2) by following prior workers and assume it is a coherent superposition of a nonresonant contribution (χ(2)nr), and one or more Lorentz-type resonances (χ(2)r):39
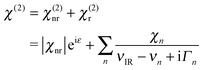 | (2) |
Because water's reflectivity is strongly frequency-dependent over 680–1050 cm−1, one would expect a dramatic change in measured IVSF/IIR as a function of angles and polarizations of the incident beams. If our line-shape model is correct, these changes should be entirely captured in the Fresnel coefficients: data collected under different incident beam angles and polarizations should be well described by the same χ(2) (i.e. the same parameters in eqn (2)). As shown in Fig. 2a and b, we find that measuring our sample with different beam incident angles and polarizations leads to drastic changes in IVSF/IIR but that all spectra can be well described with a single resonance with the same center frequency, line width and amplitude: the drastic differences in the measured spectra are quantitatively described by changes in Fresnel coefficients. The center frequency of the resulting resonance is 834 cm−1. We emphasize that assuming χ(2)r = 0 results in a qualitative misfit of the data (see Section 4.1 of the ESI† for more details).
Assignment
Having demonstrated that we probe an 834 cm−1 resonance of interfacial water, we turn to the vibrational response of the bulk liquid to help in this mode's assignment. Water's libration is the closest in frequency to our observed feature (in bulk liquid water no other mode is within a factor of two in energy40). Probed via IR absorption, in bulk liquid water it has a center frequency of ≈670 cm−1 at 25 °C. On cooling, it narrows and blue-shifts by ≈165 cm−1 until the formation of ice.28,41–43 Probed via spontaneous Raman scattering, the spectral response of water's libration is more complicated. At 25 °C, modes are apparent at 450, 550, and 722 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 (where the 450 cm−1 is IR inactive). However, the quantitative trend with cooling is the same: spectral weight shifts to higher frequencies with cooling until reaching ice where modes are apparent at 682, 799 and 920 cm−1.45,46 As shown in Fig. 3 we find that our observed spectral weight blue-shifts on cooling from 23 to 0 °C, similar to both bulk-sensitive techniques.
44 (where the 450 cm−1 is IR inactive). However, the quantitative trend with cooling is the same: spectral weight shifts to higher frequencies with cooling until reaching ice where modes are apparent at 682, 799 and 920 cm−1.45,46 As shown in Fig. 3 we find that our observed spectral weight blue-shifts on cooling from 23 to 0 °C, similar to both bulk-sensitive techniques.
 | ||
| Fig. 3 I VSF/IIR as a function of infrared frequency collected under the ssp polarization condition at 0° and 23 °C. | ||
While there are no prior VSF measurements of the libration at liquid water interfaces, two published computational studies have reported VSF spectra of the air/water interface at these frequencies. Both Perry et al. and Nagata et al. find a single broad peak, qualitatively similar to that of the IR absorption in bulk water.47,48 Quantitatively, however, the results of the two studies differ. Perry et al.'s findings agree remarkably well with our measured response: the librational mode of water at the air/water interface is blue-shifted ≈200 cm−1 relative to that of bulk water.47 Similar to our results (see Fig. 2) they predict the resonant intensity observed under the ssp polarization condition to be ≈4× larger than that under ppp. In contrast, Nagata and coworkers, as part of a study on the bend of water at the air/water interface, found the interfacial librational spectral response quantitatively similar to bulk.48 However, their sensitivity tests and prior studies by others49 strongly suggest that the spatial truncation scheme adapted to maximize computational efficiency, while suitable for study of the bending mode of interfacial water, is not appropriate for accurate description of the libration.
To summarise, we have demonstrated that the feature apparent at 875 cm−1 in our VSF spectra is the result of a resonance of interfacial water centered at 834 cm−1. Based on (i) the similarity in the center frequency of χ(2)r to that of the libration of bulk water measured via IR absorption and spontaneous Raman scattering, (ii) the similar temperature dependence of the resonance we observe and bulk water's libration, and (iii) the close correspondence between our measured signal and that predicted for the libration of interfacial water by Perry et al.,47 we assign the 834 cm−1 resonance to the libration of water at the air/water interface.
Before moving onto the implications of this observation it is worth noting that in bulk water the libration of D2O is shifted by ≈170 cm−1 to lower energies than that of H2O.41 Should the feature we observe be the libration of interfacial H2O, and the change of libration frequency when changing from H2O to D2O be similar in bulk liquid water and at the air/water interface, we would expect that probing the air/D2O interface in the 700–1050 cm−1 should reveal only the high frequency shoulder of a mode centered at lower frequencies. Our measurements (see Section 3 of the ESI†) are consistent with this expectation, further suggesting that the resonance we observe at the air/H2O interface is the libration of interfacial water.
Implications for interfacial water structure
The fact that the libration changes frequency as one moves from bulk liquid to the air/water interface while the OH stretch, and time-averaged structure and ps structural dynamics extracted from simulation, do not, suggests that this resonance provides new insight into interfacial water structure. Because the existence of a libration in liquid water is a consequence of the hindering of water's rotation by hydrogen bonds, the libration frequency is a measure of the ease of changing hydrogen bond angles for an intact hydrogen bond. Alternatively, the libration frequency is proportional to the stiffness of water's rotational potential while hydrogen bonded. To understand why water's libration at the air/water interface should differ significantly in frequency from that of the same mode in the bulk liquid, but many other observables differ little between these two environments, we first review work developing a microscopic picture of how the OH stretch relates to water structure.As emphasized by Geissler in a recent review,50 and following work by a number of other groups,51–55 the OH stretch frequency of water molecules decreases on moving from gas to liquid due to coupling to low-frequency modes and the magnitude of this change is proportional to the local electric field on an OH group's hydrogen atom projected in the direction of the OH bond. The change in OH stretch frequency (i.e. Δνg→lOH) is thus quite sensitive to the hydrogen-bond distance (Δνg→lOH ∝ 1/(O–H⋯O)2), much less sensitive to the hydrogen-bond angle (Δνg→lOH ∝ (cos∠O–H⋯O)), and relatively insensitive to the presence of additional water molecules, i.e. three-body and higher interactions. In this simplified picture, the linewidth of the OH stretch spectral response is the result of static disorder: OH groups do not change frequency on the time scale of light absorption. Calculations of the full VSF spectral response suggest this approximation is surprisingly accurate, accounting for motional narrowing is not necessary to qualitatively reproduce experimental VSF spectra.56 Thus, the OH stretch frequency reports principally on hydrogen-bond distance and a decrease in frequency indicates a decrease in distance.
Because VSF studies of the OH stretch at the air/water interface (when studying isotopically diluted H2O) find a center frequency of the OH stretch similar to bulk liquid water,20 this logic implies that hydrogen bond distances should be the same in both environments. Indeed simulations of average hydrogen bond distance and angle at the air/water interface confirm this picture.25 In addition to studying time averaged structural properties, atomistic simulation can be straightforwardly used to study the structural dynamics of water. Such studies in bulk have clarified that water's hydrogen bond network breaks and reforms rapidly, i.e. transfer of a hydrogen bond from an old to a new acceptor, so-called hydrogen bond exchange, takes ≈100 fs, but infrequently, i.e. once every several ps, and involves the concerted motion of >3 water molecules.21,22 Similar work at the air/water interface has shown that the mechanism by which hydrogen bonds break and reform is quite similar to bulk liquid and that such reforming of water's hydrogen bond network also occurs on ps timescales.25 While it thus seems clear that changes in libration frequency need not be related to changes in slower structural dynamics, it is less clear that there should be no relation between hydrogen bond distance and the stiffness of water's rotational potential. Certainly at least both of these observables describe the hydrogen-bonded state.
Computational studies of the gas-phase water dimer make clear, e.g. see Scott and Vanderkoi,57 that in the gas phase as the two waters approach each other the OH rotational potential is stiffened. As a result OH stretch frequency and libration frequency are strongly anti-correlated: with decreasing hydrogen bond distance OH stretch frequency decreases and libration frequency increases. For a gas phase water dimer the most energetically favorable hydrogen bonding distance and angle depends only on the relative position of the two molecules. It is not immediately obvious that such a 2-body character describes the intermolecular potential in, and thus that such a OH stretch/libration frequency correlation should extend to, liquid water.
X-ray, neutron and thermodynamic studies of bulk liquid water demonstrate that with decreasing temperature hydrogen bonds increase in strength and hydrogen bond distance decreases.58–60 Consistent with these results, with decreasing temperature OH stretch frequency shifts to lower energies.40 As discussed above, and also consistent with the trend expected from the dimer, with decreasing temperature the libration frequency shifts to higher energies.41 That is, with stronger hydrogen bonding in liquid water hydrogen-bond distance shortens and the rotational potential stiffens. While the correlation of the temperature-dependent changes in libration and OH stretch frequency of liquid water thus resemble those of the dimer, intriguingly, Fayer and coworkers have demonstrated that at low temperatures the 2-body character of the intermolecular potential does not.61 In particular, they show that with cooling, i.e. stronger hydrogen bonding, water's rotational potential increasingly changes from a 2-body to multi-body character.61 This change is rationalized by noting that water's structural correlations also increase dramatically with decreasing temperature.62,63 Consistent with the logic of Geissler and coworkers described above, OH stretch frequencies are relatively insensitive to this change in character of water's intermolecular potential. Fayer and coworkers observe it only via a temperature dependent decoupling of the librational contribution to the OH orientational correlation function and OH stretch frequency.
Given this understanding of bulk liquid water it seems reasonable to ask whether an air/water interface also induces structural correlations. Simulation studies clarify that, while hydrogen bond distances are quite similar at the air/water interface and in bulk liquid water, structural correlations are dramatically enhanced (this is immediately evident from the fact that interfacial water molecules have a preferential orientation with respect to an external reference frame while those in bulk do not).25,64 Armed with both of these observations it is perhaps unsurprising that when moving from bulk liquid water to the air/water interface the OH stretch frequency is constant but the libration frequency is not. Evidently, forming the air/interface induces structural correlations similar to those found when cooling liquid water without the decrease in hydrogen bond distance.
It is finally worth noting that, while the frequency and polarization dependence of our measured interfacial libration are well predicted by one of the two published studies of the librational response of VSF spectra of water at the air/water interface, much work clearly remains to be done. For example, while both theory studies find that the libration of water at the air/water interface, similar to bulk IR absorption measurements, is only a single spectral feature,47,48 we cannot rule out the possibility that there is a second librational resonance of interfacial water at frequencies <650 cm−1 (i.e. outside the detection window of our current experimental set up). Similarly, while our data are well described by a single, homogeneously broadened resonance, we cannot rule out the possibility of inhomogeneous broadening due either to librations of double hydrogen-bond donors at multiple and distinct frequencies, distinct librations of singly hydrogen-bond donating species or other forms of structural heterogeneity.37,65–69 We also cannot rule out the possibility such populations exist and do not contribute to our observed VSF signal due to orientational effects. From an experimental point of view, it is clear that extending our VSF measurements to significantly lower IR frequencies, e.g. 400 cm−1, and conducting 2D IR/VSF measurements over this frequency range would substantially constrain much of this uncertainty. Additionally quantifying the OH stretch rotational anisotropy at the air/water interface in a frequency and polarisation resolved IR pump/VSF probe scheme, extending the experimental concept of Fayer and coworkers to interfaces, would directly address whether the character of the intermolecular potential at the air/water interface differs from that in bulk at the same temperature.61,70 All of these measurements are technically demanding and the object of current work in our group. Despite these limitations, our current study offers a new observable describing the structure and dynamics of water at the air/water interface.
Conclusions
The observation that the frequency of the libration of interfacial water is blue-shifted by 165 cm−1 relative to that in bulk liquid water suggests that the potential of mean force underlying water rotation is significantly stiffer at the air/water interface than in bulk. In contrast, much prior experiment and simulation investigating the time averaged structure and picosecond structural dynamics of hydrogen-bonded OH groups at the air/water interface find that, from the perspective of these observables, interfacial water is similar to bulk liquid water. There is no contradiction between these apparently discordant viewpoints. Water's OH stretch frequency is principally sensitive to hydrogen bond distance while libration frequency is proportional to the stiffness of water's rotational potential around intact hydrogen bonds: each observable samples different aspects of water's intermolecular potential. Similarly, water's picosecond structural dynamics involve the breaking and reforming of hydrogen bonds and require concerted motions of >3 water molecules. These motions are substantially less frequent than those of water's rotational libration, they occur at THz frequencies, and are thus not sampled in our spectral window.In this study we describe a novel probe of the intact hydrogen bond network of interfacial water: interfacial water's libration. In addition to the insight into water physics it offers, the ability to probe interfacial water's libration immediately suggests a number of intriguing avenues of future research. As has been well documented in bulk, the water's libration is both important in understanding the dissipation of excess vibrational energy26–28 and in many aqueous phase chemical reactions. Probing the interfacial libration makes it possible to gain similar mechanistic insights into vibrational relaxation and heterogeneous chemistry at aqueous interfaces.2,3,32,33
References
- M. G. Cacace, E. M. Landau and J. J. Ramsden, Q. Rev. Biophys., 1997, 30, 241–277 CrossRef CAS PubMed.
- E. M. Knipping, M. J. Lakin, K. L. Foster, P. Jungwirth, D. J. Tobias, R. B. Gerber, D. Dabdub and B. J. Finlayson-Pitts, Science, 2000, 288, 301–306 CrossRef CAS PubMed.
- A. Laskin, D. J. Gaspar, W. Wang, S. W. Hunt, J. P. Cowin, S. D. Colson and B. J. Finlayson-Pitts, Science, 2003, 301, 340–344 CrossRef CAS PubMed.
- G. N. I. Clark, C. D. Cappa, J. D. Smith, R. J. Saykally and T. Head-Gordon, Mol. Phys., 2010, 108, 1415–1433 CrossRef CAS.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- Q. Du, R. Superfine, E. Freysz and Y. R. Shen, Phys. Rev. Lett., 1993, 70, 2313–2316 CrossRef CAS PubMed.
- Y. R. Shen, Nature, 1989, 337, 519–525 CrossRef CAS.
- H. J. Bakker and J. L. Skinner, Chem. Rev., 2010, 110, 1498–1517 CrossRef CAS PubMed.
- Q. Du, E. Freysz and Y. Shen, Science, 1994, 264, 826–828 CrossRef CAS PubMed.
- D. Gragson and G. Richmond, J. Phys. Chem. B, 1998, 102, 3847–3861 CrossRef CAS.
- M. Shultz, C. Schnitzer, D. Simonelli and S. Baldelli, Int. Rev. Phys. Chem., 2000, 19, 123–153 Search PubMed.
- M. Sovago, R. K. Campen, G. W. H. Wurpel, M. Müller, H. J. Bakker and M. Bonn, Phys. Rev. Lett., 2008, 100, 173901 CrossRef PubMed.
- M. Sovago, R. K. Campen, G. W. H. Wurpel, M. Muller, H. J. Bakker and M. Bonn, Phys. Rev. Lett., 2008, 101, 139402 CrossRef.
- B. M. Auer and J. L. Skinner, Chem. Phys. Lett., 2009, 470, 13–20 CrossRef CAS.
- M. Bonn, H. J. Bakker, Y. Tong and E. H. G. Backus, Biointerphases, 2012, 7, 1–5 CrossRef PubMed.
- S. Nihonyanagi, S. Yamaguchi and T. Tahara, J. Am. Chem. Soc., 2010, 132, 6867–6869 CrossRef CAS PubMed.
- S. Nihonyanagi, T. Ishiyama, T.-k. Lee, S. Yamaguchi, M. Bonn, A. Morita and T. Tahara, J. Am. Chem. Soc., 2011, 133, 16875–16880 CrossRef CAS PubMed.
- Z. Zhang, L. Piatkowski, H. J. Bakker and M. Bonn, Nat. Chem., 2011, 3, 888–893 CrossRef CAS PubMed.
- K.-i. Inoue, S. Nihonyanagi, P. C. Singh, S. Yamaguchi and T. Tahara, J. Chem. Phys., 2015, 142, 212431 CrossRef PubMed.
- M. Sovago, R. K. Campen, H. J. Bakker and M. Bonn, Chem. Phys. Lett., 2009, 470, 7–12 CrossRef CAS.
- D. Laage and J. T. Hynes, J. Phys. Chem. B, 2008, 112, 14230–14242 CrossRef CAS PubMed.
- P. Liu, E. Harder and B. J. Berne, J. Phys. Chem. B, 2005, 109, 2949–2955 CrossRef CAS PubMed.
- I.-F. W. Kuo, C. J. Mundy, B. L. Eggimann, M. J. McGrath, J. I. Siepmann, B. Chen, J. Vieceli and D. J. Tobias, J. Phys. Chem. B, 2006, 110, 3738–3746 CrossRef CAS PubMed.
- T. D. Kühne, T. A. Pascal, E. Kaxiras and Y. Jung, J. Phys. Chem. Lett., 2011, 2, 105–113 CrossRef PubMed.
- A. Vila Verde, P. G. Bolhuis and R. K. Campen, J. Phys. Chem. B, 2012, 116, 9467–9481 CrossRef CAS PubMed.
- S. Ashihara, N. Huse, A. Espagne, E. Nibbering and T. Elsaesser, Chem. Phys. Lett., 2006, 424, 66–70 CrossRef CAS.
- F. Ingrosso, R. Rey, T. Elsaesser and J. T. Hynes, J. Phys. Chem. A, 2009, 113, 6657–6665 CrossRef CAS PubMed.
- J. Petersen, K. B. Møller, R. Rey and J. T. Hynes, J. Phys. Chem. B, 2013, 117, 4541–4552 CrossRef CAS PubMed.
- B. C. Garrett, D. A. Dixon, D. M. Camaioni, D. M. Chipman, M. A. Johnson, C. D. Jonah, G. A. Kimmel, J. H. Miller, T. N. Rescigno, P. J. Rossky, S. S. Xantheas, S. D. Colson, A. H. Laufer, D. Ray, P. F. Barbara, D. M. Bartels, K. H. Becker, J. Kit H Bowen, S. E. Bradforth, I. Carmichael, J. V. Coe, L. R. Corrales, J. P. Cowin, M. Dupuis, K. B. Eisenthal, J. A. Franz, M. S. Gutowski, K. D. Jordan, B. D. Kay, J. A. LaVerne, S. V. Lymar, T. E. Madey, C. W. McCurdy, D. Meisel, S. Mukamel, A. R. Nilsson, T. M. Orlando, N. G. Petrik, S. M. Pimblott, J. R. Rustad, G. K. Schenter, S. J. Singer, A. Tokmakoff, L.-S. Wang, C. Wittig and T. S. Zwier, Chem. Rev., 2005, 105, 355–389 CrossRef CAS PubMed.
- D. Zhu, L. Zhang, R. E. Ruther and R. J. Hamers, Nat. Mater., 2013, 12, 836–841 CrossRef CAS PubMed.
- J. Savolainen, F. Uhlig, S. Ahmed, P. Hamm and P. Jungwirth, Nat. Chem., 2014, 6, 697–701 CrossRef CAS PubMed.
- Y. Jung and R. A. Marcus, J. Am. Chem. Soc., 2007, 129, 5492–5502 CrossRef CAS PubMed.
- B. Abel, Annu. Rev. Phys. Chem., 2013, 64, 533–552 CrossRef CAS PubMed.
- Y. Tong, J. Wirth, H. Kirsch, M. Wolf, P. Saalfrank and R. K. Campen, J. Chem. Phys., 2015, 142, 054704 CrossRef PubMed.
- A. G. Lambert, P. B. Davies and D. J. Neivandt, Appl. Spectrosc. Rev., 2005, 40, 103–145 CrossRef CAS.
- X. Zhuang, P. B. Miranda, D. Kim and Y. R. Shen, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12632–12640 CrossRef CAS.
- H.-F. Wang, W. Gan, R. Lu, Y. Rao and B.-H. Wu, Int. Rev. Phys. Chem., 2005, 24, 191–256 Search PubMed.
- Y. Tong, A. Vila Verde and R. K. Campen, J. Phys. Chem. B, 2013, 117, 11753–11764 CrossRef CAS PubMed.
- C. Bain, P. B. Davies, T. H. Ong, R. N. Ward and M. A. Brown, Langmuir, 1991, 7, 1563–1566 CrossRef CAS.
- Y. Maréchal, J. Mol. Struct., 2011, 1004, 146–155 CrossRef.
- H. R. Zelsmann, J. Mol. Struct., 1995, 350, 95–114 CrossRef CAS.
- J. E. Bertie and Z. Lan, Appl. Spectrosc., 1996, 50, 1047–1057 CrossRef CAS.
- M. W. Severson, J. P. Devlin and V. Buch, J. Chem. Phys., 2003, 119, 4449–4457 CrossRef CAS.
- G. E. Walrafen, J. Chem. Phys., 1967, 47, 114 CrossRef CAS.
- P. Benassi, V. Mazzacurati, M. Nardone, M. A. Ricci, G. Ruocco, A. de Santis, R. Frattini and M. Sampoli, Mol. Phys., 1987, 62, 1467–1481 CrossRef CAS.
- P. T. T. Wong and E. Whalley, J. Chem. Phys., 1975, 62, 2418–2425 CrossRef CAS.
- A. Perry, C. Neipert, C. Ridley, B. Space and P. B. Moore, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 050601(R) CrossRef PubMed.
- Y. Nagata, C.-S. Hsieh, T. Hasegawa, J. Voll, E. H. G. Backus and M. Bonn, J. Phys. Chem. Lett., 2013, 1872–1877 CrossRef CAS PubMed.
- M. Heyden, J. Sun, H. Forbert, G. Mathias, M. Havenith and D. Marx, J. Phys. Chem. Lett., 2012, 3, 2135–2140 CrossRef CAS PubMed.
- P. L. Geissler, Annu. Rev. Phys. Chem., 2013, 64, 317–337 CrossRef CAS PubMed.
- J. Sadlej, V. Buch, J. K. Kazimirski and U. Buck, J. Phys. Chem. A, 1999, 103, 4933–4947 CrossRef CAS.
- S. A. Corcelli, C. P. Lawrence and J. L. Skinner, J. Chem. Phys., 2004, 120, 8107–8117 CrossRef CAS PubMed.
- J. Eaves, A. Tokmakoff and P. Geissler, J. Phys. Chem. A, 2005, 109, 9424–9436 CrossRef CAS PubMed.
- T. Hayashi, T. la Cour Jansen, W. Zhuang and S. Mukamel, J. Phys. Chem. A, 2005, 109, 64–82 CrossRef CAS PubMed.
- F. Paesani, S. S. Xantheas and G. A. Voth, J. Phys. Chem. B, 2009, 113, 13118–13130 CrossRef CAS PubMed.
- B. M. Auer and J. L. Skinner, J. Chem. Phys., 2008, 129, 214705 CrossRef CAS PubMed.
- J. N. Scott and J. M. Vanderkooi, Water, 2010, 2, 14–28 Search PubMed.
- T. Lazaridis and M. Karplus, J. Chem. Phys., 1996, 105, 4294–4316 CrossRef CAS.
- G. Hura, J. M. Sorenson, R. M. Glaeser and T. Head-Gordon, J. Chem. Phys., 2000, 113, 9140–9148 CrossRef CAS.
- A. K. Soper, Chem. Phys., 2000, 258, 121–137 CrossRef CAS.
- D. E. Moilanen, E. E. Fenn, Y.-S. Lin, J. L. Skinner, B. Bagchi and M. D. Fayer, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 5295–5300 CrossRef CAS PubMed.
- E. B. Moore and V. Molinero, J. Chem. Phys., 2009, 130, 244505 CrossRef PubMed.
- A. Nilsson, C. Huang and L. G. M. Pettersson, J. Mol. Liq., 2012, 176, 2–16 CrossRef CAS.
- R. S. Taylor, L. X. Dang and B. C. Garrett, J. Phys. Chem., 1996, 100, 11720–11725 CrossRef CAS.
- P. Wernet, D. Nordlund, U. Bergmann, M. Cavalleri, M. Odelius, H. Ogasawara, L. Naslund, T. Hirsch, L. Ojamae, P. Glatzel, L. Pettersson and A. Nilsson, Science, 2004, 304, 995–999 CrossRef CAS PubMed.
- C. Huang, K. T. Wikfeldt, T. Tokushima, D. Nordlund, Y. Harada, U. Bergmann, M. Niebuhr, T. M. Weiss, Y. Horikawa, M. Leetmaa, M. P. Ljungberg, O. Takahashi, A. Lenz, L. Ojamae, A. P. Lyubartsev, S. Shin, L. G. M. Pettersson and A. Nilsson, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15214–15218 CrossRef CAS PubMed.
- A. Taschin, P. Bartolini, R. Eramo, R. Righini and R. Torre, Nat. Commun., 2013, 4, 2401 CAS.
- C.-S. Hsieh, M. Okuno, J. Hunger, E. H. G. Backus, Y. Nagata and M. Bonn, Angew. Chem., Int. Ed., 2014, 53, 8146–8149 CrossRef CAS PubMed.
- A. Taschin, P. Bartolini, R. Eramo, R. Righini and R. Torre, J. Chem. Phys., 2014, 141, 1–13 CrossRef PubMed.
- C.-S. Hsieh, R. K. Campen, A. C. Vila Verde, P. Bolhuis, H.-K. Nienhuys and M. Bonn, Phys. Rev. Lett., 2011, 107, 116102 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Full description of the theoretical expressions of the reflected VSF signal, the procedure to normalize the signal to account for the spectral profile of the incident IR field, the procedure to quantitatively compare between the different experimental geometries, a description of the control experiments and a description of the details of the quantitative line shape analysis. See DOI: 10.1039/c6cp01004k |
| This journal is © the Owner Societies 2016 |