Open Access Article
Open Access ArticleHydrogen dynamics in β-Mg(BH4)2 on the picosecond timescale
Luca
Silvi
 *a,
Eva
Röhm
b,
Maximilian
Fichtner
b,
Winfried
Petry
a and
Wiebke
Lohstroh
a
*a,
Eva
Röhm
b,
Maximilian
Fichtner
b,
Winfried
Petry
a and
Wiebke
Lohstroh
a
aHeinz Maier-Leibnitz Zentrum (MLZ) und Physik Department E13, Technische Universität München, Lichtenbergstr. 1, 85748, Garching, Germany. E-mail: luca.silvi@frm2.tum.de
bKarlsruher Institut für Technology, Institut für Nanotechnologie, P. O. Box 3640, D-76021 Karlsruhe, Germany
First published on 26th April 2016
Abstract
A quasielastic neutron scattering study on β-Mg(BH4)2 has been performed to investigate the hydrogen dynamics on the picosecond time-scale. Both vibrational and rotational motions of the [BH4]− tetrahedra contribute to the signal at low energy transfers. A comprehensive analysis of the elastic and quasielastic incoherent structure factors allowed the separation of different parts. Below 200 K, vibrations and rotations (around the C2 or C3 symmetry axis of the [BH4]− tetrahedra) are well separated. Above that temperature, a transition is observed in the vibrational part, and the spectral weight is shifted towards the quasielastic region. The dynamic transition is not accompanied by any structural phase change but we suggest that it is correlated with the anomalous thermal expansion that has been reported for β-Mg(BH4)2 [Filinchuk, et al., Chem. Mater., 2009, 21, 925].
1 Introduction
Complex borohydrides are compounds composed of a metal cation (e.g. Li, Mg, Ca, or K) and a tetrahedral unit [BH4]. This material class has been the subject of intensive studies due to its promising hydrogen storage capacity. For example, magnesium borohydride (Mg(BH4)2) is characterized by a gravimetric and volumetric storage density of 14.9 wt% and 90 kg m−3 H2;1,2 moreover, the material is interesting due to its overall reaction enthalpy ΔH, and the reported values (for desorption to MgH2) are in the range of −40 to −57 kJ mol−1 H23,4 which is suitable for storage applications. However, reaction kinetics is sluggish and Mg(BH4)2 decomposes only at 600 K in a multi-step process5,6 and its limited reversibility7 makes it unsuitable for practical applications.Magnesium borohydride exists in various crystalline forms, as recently discovered and characterized by X-ray and neutron scattering techniques.8–10 Among the observed polymorphs of Mg(BH4)2, namely α, β, γ and δ-phases, the low-temperature (LT) α-phase and the high-temperature (HT) β-phase are the most commonly investigated for hydrogen storage applications;7 the crystal structures are shown in Fig. 1.
 | ||
| Fig. 1 Crystal structure of α- (left) and β-Mg(BH4)2 (right) along the c axis: magnesium atoms are represented by orange spheres, boron by green and hydrogen by gray spheres. In both phases, Mg atoms are surrounded by four [BH4] units in a strongly deformed tetrahedral environment.11 | ||
The structure of α-Mg(BH4)2 has been identified by X-ray and neutron scattering techniques to be a hexagonal lattice with P6122 space group symmetry and a unit cell volume of 3434 Å3.11 The α-polymorph is stable up to 490 K and, at higher temperatures, it transforms irreversibly into the β-phase.12,13 The latter has an orthorhombic Fddd crystal structure symmetry with a larger unit cell volume of 7543 Å3 and it is metastable when cooled down to room temperature (and below). In comparison to the β-phase, the α-phase is less dense (3%) and it contains some unoccupied voids (37 Å3) along the (00z) direction which are not present in the β-polymorph.
The hexagonal P6122 structure is characterized by six non-equivalent [BH4]− positions, whereas in the orthorhombic Fddd structure the non-equivalent positions decrease to five. In both phases, Mg atoms are surrounded by four [BH4] tetrahedra leading to a strongly distorted tetrahedral environment, and, at the local level, the [BH4] groups are facing the Mg atoms via two opposite edges of the tetrahedra, leading to an almost linear configuration Mg–B–Mg and a bidentate orientation of Mg with respect to the bridging hydrogens11,12 (Fig. 2).
The decomposition of β-Mg(BH4)2 has been studied extensively for hydrogen storage applications and various pathways have been observed both experimentally and theoretically, depending on the applied hydrogen pressure and temperature conditions.6,14 In order to improve the slow kinetics, Mg(BH4)2 has been mixed with additives, mainly metal salts such as CaF2, ZnF2 and TiF3,15 ScCl316 or NbF5.17 Moreover, the mixtures with other borohydrides (e.g. Li(BH4)) have been investigated in detail.18 Noteworthily, in the latter case, it is possible to reverse the structural phase transition from the β- to α-phase during cooling of the sample, although the mechanism is not entirely understood.
Despite the numerous studies, a full understanding of the ground state structures, hydrogen bonding and gas release is still missing. Extensive theoretical calculations show that the ground state is energetically almost degenerated and a variety of different structures that are very close in energy have been proposed, among them the experimentally found α-phase.19 A recent work20 showed that, including van der Waals interactions, the lowest energy structure is the experimentally observed α-phase. Conversely, Caputo et al.,21 using a computational methodology combining cluster optimization, simulated annealing based crystal structure prediction, periodic DFT total energy calculations and symmetry group relations analysis, found other crystal structures with lower energies. Still, the question about theoretically predicted and experimentally observed structures is open. The β-phase is energetically less favourable than the α-phase, as shown by DFT calculations,22–24 but the origin of the non-reversibility of the structural phase transition is not clear yet. For the alkaline borohydrides LiBH4,25 NaBH426 and KBH4,27 it has been observed from quasielastic neutron scattering (QENS) experiments that the driving force for the structural phase transition is an order–disorder transition of the [BH4] units, whereas for Ca(BH4)2 it was suggested that the [BH4] librations drive the structural phase transition.28 Apparently, the dynamics of the [BH4] units plays a crucial role in understanding the thermal properties of alkaline and earth alkaline borohydrides.
For Mg(BH4)2, nuclear magnetic resonance (NMR) experiments29,30 revealed a complex reorientational dynamic involving at least three jump processes in α-Mg(BH4)2, and a variety of thermally activated processes in β-Mg(BH4)2 with a distribution of activation energies. QENS experiments performed on β-Mg(BH4)231 showed the reorientation of the [BH4] tetrahedra on two different characteristic timescales, using backscattering and indirect geometry time-of-flight spectroscopy. From the elastic incoherent structure factor (EISF) (which correlates with the spatial distribution of the hydrogens in the long time average), it was suggested that the [BH4] units exhibit hindered rotations around the 2-fold C2 and 3-fold C3 symmetry axis of the [BH4] units, respectively (see Fig. 2) on a timescale of hundreds of picoseconds.
The aim of the present work is to investigate the hydrogen dynamics in an extended dynamic range, i.e. to address the picosecond timescale and extend the momentum transfer (Q) to larger values to shed further light on the hydrogen dynamics in β-Mg(BH4)2. In particular, the evaluation of the EISF and the quasielastic incoherent structure factor (QISF) at large Q values enables the discrimination of different reorientational geometries. Moreover, QENS experiments might reveal a significant contribution of vibrational motions in the experimentally probed time-window.
2 Experimental
Quasielastic neutron scattering (QENS) has been performed on β-Mg(BH4)2. The material has been prepared as described in previous work.32 The high neutron absorption cross-section of natural boron was avoided using isotope enriched 11B. For the measurements, approx. 200 mg of β-Mg(11BH4)2 was mounted into an Aluminium flat cell, yielding a neutron transmission of ∼90%. Quasielastic neutron scattering experiments have been performed using a cold time-of-flight spectrometer TOFTOF33,34 at the Heinz Maier-Leibnitz Zentrum (MLZ) in Munich, Germany. Two different wavelengths of incoming neutrons were selected: the first at λ1 = 2.5 Å yielding an energy resolution of 450 μeV (FWHM) of the elastic line and an accessible elastic momentum transfer Q from 0.5 to 4.2 Å−1, and the second at λ2 = 6 Å, with an energy resolution of 48 μeV (FWHM) and an elastic momentum transfer from 0.2 to 2 Å−1. The sample was mounted at 135° with respect to the incoming neutron beam and the measurements were performed at temperatures ranging from 11 to 500 K. The raw time-of-flight data were converted to the scattering function S(Q,ω) by the following procedure: the data were normalized to the incoming neutron flux and the empty container signal was subtracted taking into account self-shielding and self-absorption factors. After normalizing to a vanadium standard measurement, the energy transfer was calculated and a correction of energy dependent detector efficiency was performed. The momentum transfer Q was calculated and the spectra have been grouped into bins of equal ΔQ. For the analysis, detector angles of the aluminium Bragg peaks arising from the sample environment were excluded.3 Results and discussion
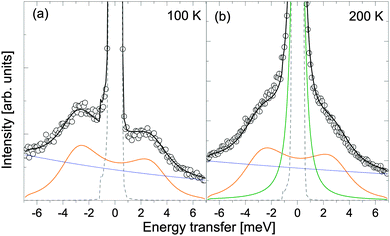
The results of QENS measurements are shown in Fig. 3 and 4 for the two wavelengths and a chosen Q-value. For both instrument settings, the sample has been cooled down to 11 K. At this temperature, the measured width of the elastic peak at zero energy transfer reflects the instrumental resolution function. With increasing temperature, a quasielastic broadening is observed, and its intensity increases with increasing temperature. Note that the two incoming wavelengths λ probe different characteristic timescales and hence the observed quasielastic signals could be caused by different underlying motions. Besides the quasielastic broadening, the data probing the shorter timescales (λ = 2.5 Å) show distinct low energy (vibrational) inelastic peaks at ΔE = ±3.2 meV for temperatures below 300 K. The energy transfer of this excitation is constant for all Q. At 300 K and above, the quasielastic signal becomes very strong and the inelastic excitation cannot be resolved in the spectra. | ||
| Fig. 3 S(Q,ω) at 6 Å of β-Mg(BH4)2 at 11, 200, 300 and 500 K. The black solid lines represent the fit of the data according to eqn (11). (gray dashed line) 11 K (resolution), (blue rhombus) 200 K, (green square) 300 K, and (red triangle) 500 K. The vertical error bars denote ±1σ. | ||
 | ||
| Fig. 4 S(Q,ω) of β-Mg(BH4)2, measured at 2.5 Å and at 11, 100, 200 and 500 K. The black solid lines represent the fit of the data according to eqn (11) and (14). (gray line) 11 K (resolution), (blue circle) 100 K, (green square) 200 K, and (red triangle) 500 K. Datasets measured at 300 and 400 K have been omitted for clarity. The vertical error bars denote ±1σ. | ||
The first attempt to separate the vibrational and quasielastic signals was carried out by following the procedure proposed by Cusack et al.35 In the harmonic approximation, the vibrational frequency distribution is temperature independent, and the Debye–Waller factor and the Bose occupation number relate the data taken at different temperatures. Outside the QENS region, the relation with low temperature data and high temperature data is then given by:
 | (1) |
 | ||
| Fig. 5 Ratio between high temperature data and low temperature data (T = 100 K) at λ = 2.5 Å: (blue squares) 200 K, (green circles) 300 K, (red triangles) 500 K. Data at 400 K have been omitted for clarity. The line represents the right hand-side of eqn (1), using Uvib = 0.0001 × T [K] Å2. The vertical error bars denote ±1σ. | ||
The vibrational displacement Uvib in eqn (1) is temperature dependent and the best agreement with the data is obtained for Uvib = 0.0001 × T [K] Å2. Clearly at 200 K the quasielastic signal falls to zero beyond ∼2 meV. Above ∼2 meV, the signal is described to a good approximation by the harmonic temperature scaling, whereas above 300 K, the agreement with the approximation is only found for energies above ∼8 meV. This is an indication of a transition in the vibrational modes that affects the quasielastic region. A clear separation of these two contributions is not possible and the vibrational part cannot be subtracted for analysis of the quasielastic data. Therefore, a more complex approach was chosen, as outlined below.
The same analysis for the 6 Å data is shown in Fig. 6. Above ∼2 meV the quasielastic signal falls off, showing a good agreement with the right hand side of eqn (1) and hence in this case, the vibrational part could be treated as flat background contribution.
 | ||
| Fig. 6 Ratio between high temperature data and low temperature data (T = 100 K) at λ = 6 Å: (blue squares) 200 K, (green circles) 300 K, (red triangles) 500 K. Data at 400 K have been omitted for clarity. The line represents the right hand-side of eqn (1), using Uvib = 0.0001 × T [K] Å2. The vertical error bars denote ±1σ. | ||
3.1 Data analysis
Due to the large hydrogen incoherent scattering cross-section, the experiments almost exclusively probe hydrogen dynamics. In the incoherent approximation, the scattering function S(Q,ω) can be written as:| S(Q,ω) = Strans(Q,ω) ⊗ Srot(Q,ω) ⊗ Svib(Q,ω), | (2) |
| Imeas ∝ [Srot(Q,ω) ⊗ Svib(Q,ω)] ⊗ Res(Q,ω) + b(Q). | (3) |
The fraction of elastically scattered neutrons
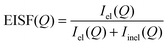 | (4) |
The experimental S(Q,ω) has been analysed as outlined in Appendix A, and from that the EISF, QISFQE and QISFinel have been derived for each dataset. For the three quantities it is:
| EISF = B(Q)[p + (1 − p)A0(Q)] | (5) |
| QISFQE = B(Q)(1 − p)[1 − A0(Q)] | (6) |
| QISFinel = 1 − B(Q), | (7) |
 | (8) |
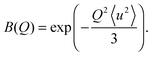 | (9) |
3.2 Data analysis for λ = 6 Å
For the analysis of the measurements performed at λ = 6 Å, the spectra have been fitted up to 2 meV. The vibrational part is then described by a flat background (see beginning of this section) and in all the fit functions the correct dependence of the detailed balance factor has been taken into account. For T ≥ 200 K, the data show a clear quasielastic component and two Lorentzians in eqn (11) are necessary to describe the experimental points: the first one with a half width half maximum (HWHM) Γ1 < 0.1 meV and a second, broader one with a Γ2 > 0.3 meV. For both Lorentzians, Γ1 and Γ2 do not show any Q-dispersion, however, the widths are increasing with temperature, indicating thermally activated motions localized in space.37 A summary of the results for Γ1 and Γ2 can be found in Table 1.| T [K] | Γ 1 [meV] | Γ 2 [meV] |
|---|---|---|
| 100 | — | — |
| 200 | 0.033 ± 0.002 | 0.33 ± 0.05 |
| 300 | 0.073 ± 0.011 | 0.35 ± 0.04 |
| 400 | 0.08 ± 0.008 | 0.50 ± 0.06 |
| 500 | 0.11 ± 0.02 | 0.55 ± 0.08 |
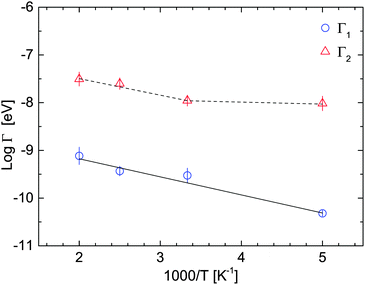
Fig. 7 shows Γ1 and Γ2 as a function of the temperature (on a logarithmic scale), together with the fit of the Arrhenius expression:
 | (10) |
The elastic incoherent structure factor (EISF) has been calculated using eqn (4), and the results are plotted in Fig. 8. Also shown are the theoretically expected Q-dependence of the EISF for rotations around the C2/C3 axis and the tumbling motion. At 300 K and above, the EISF is independent of temperature, indicating that the spatial distribution of the hydrogen atoms does not change in the probed time- and space window, however the increasing Γ1,2 confirms that reorientation processes become faster with increasing temperature. The functional Q-dependence will be discussed later in the paper, in connection with the results obtained for the 2.5 Å-measurements.
 | ||
| Fig. 8 Measured EISFs at 6 Å: (blue circles) 200 K, (magenta triangles) 300 K, (yellow rhombus) 400 K, and (red stars) 500 K. The dashed line represents the rotational diffusion model for C2/3 rotations (eqn (8)), whereas the dotted line represents the tumbling motions, according to eqn (17). The dash-dot line is a combination of the C2 and C3 rotations, and the dash–dot–dot line is a combination of C2/3 rotation with tumbling motions (see the text for details). The vertical error bars denote ±1σ. | ||
3.3 Data analysis for λ = 2.5 Å
Analysis of the data obtained at 2.5 Å (see Fig. 4) is more complex due to the observed distinct inelastic contribution close to the quasielastic region. These excitations are occurring around ∼±3.2 meV, and they have been also reported in ref. 38, and were tentatively ascribed to lattice phonons. The spectra have been fitted using the functions listed in Table 2 to represent the elastic, quasielastic and vibrational contributions, and the results of the fits are shown in Fig. 9 and 10. In the instrumental resolution function measured at 11 K (see Fig. 4), the inelastic excitation appears in the energy-loss side of the neutron and therefore only the central peak has been used as a resolution Res(Q,ω) in eqn (3).| T [K] | Fit functions |
|---|---|
| 100 | δ + DHO + background |
| 200 | δ + L2 + DHO + background |
| >300 | δ + L2 + L3 |
At 100 and 200 K, data show clearly inelastic peaks close, but still separated from the quasielastic region. The vibrational part is modelled using a damped harmonic oscillator (DHO, with a frequency ωq, eqn (14)) and the jump rotational part according to eqn (11). The starting values for the jump rotational part are taken from the 6 Å data (Γ2), and the values found are in agreement with the 6 Å data with 10% variation.
At temperature T ≥ 300 K, data are not showing any visible inelastic peaks. At this temperature we presume an over-damped DHO which is indistinguishable from a Lorentzian shape function in the measured energy transfer range. Therefore, the inelastic contribution had been described by a Lorentzian L3 (characterised by Γ3 (see Fig. 10 and 11)).
ω q represents the characteristic frequency of individual [BH4] units, since we probe the incoherent scattering cross-section. Apparently, the lattice potential of all five different [BH4] sites is similar, yielding distinct peaks. Inelastic neutron scattering (INS) measurements on β-Mg(BH4)238 show a complex vibrational structure extending over a wide range of energies. A structured low-energy band (between 3 and 38 meV) has been reported and it was tentatively assigned to lattice phonons. The inelastic peaks detected in this work around ±3.2 meV are in agreement with this previous study, thus confirming a superposition of vibrational and quasielastic signals at low energy transfers. At higher temperatures, the vibrational diffusion becomes over-damped and is described in our analysis by L3. Vibrational and rotational reorientations are occurring on similar timescales: the characteristic frequency extracted for vibration is νvib ∼ 0.8 ps−1, which is in the same order of magnitude as rotational frequency τrot−1 from Γ2.
The EISF, QISFQE and QISFinel are calculated from the elastic, quasielastic and inelastic intensities, normalized to the total intensity. The results are summarized in Fig. 12. With increasing temperature, the fraction of elastically scattered neutrons (EISF) decreases, but no oscillating behaviour characteristic for rotational reorientations around the C2 or C3 axis is observed. This is expected, since no separation of vibrational and rotational parts was done. The solid lines in Fig. 12 are a global fit (at each temperature) to eqn (5)–(7) to extract the parameters 〈u2〉, p and dB–H. Due to the structureless behaviour at relatively high Q of the EISF, this information cannot be obtained from the fraction of the elastically scattered neutrons alone, but the global fit procedure was necessary. For the data analysis, the QE components have been assumed to be described by C2/3 reorientation (see eqn (8)), in agreement with low temperature data collected at 6 Å and with the previously proposed reorientational mechanisms.31
 | ||
| Fig. 12 EISF (black squares), QISFinel (blue triangles), and QISFL1 (red circles) from 100 K to 500 K. Solid lines represent the fit to the data according to eqn (5)–(7). In (a) 100 K, (b) 200 K, (c) 300 K, (d) 400 K and (e) 500 K. The vertical error bars denote ±1σ. | ||
The agreement with the experimental data is quite satisfactory confirming that the chosen approach for the analysis of the data allows us to extract the rotational and vibrational parts. The mean square displacement (MSD) 〈u2〉 and dB–H are shown in Fig. 13 and 14.
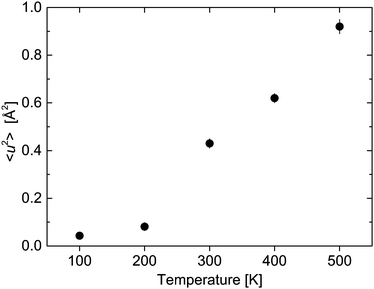 | ||
| Fig. 13 Mean square displacement 〈u2〉 as a function of temperature. The vertical error bars denote ±1σ. | ||
 | ||
| Fig. 14 Distance between boron and hydrogen atoms as a function of temperature. The vertical error bars denote ±1σ. | ||
3.4 Discussion
Previously, Blanchard et al.31 reported three thermally activated processes in β-Mg(BH4)2 with activation energies: 39 ± 0.5, 76 ± 5 and 214 ± 4 meV from QENS data in the observation timescale of hundreds of picoseconds. In their work, the faster jump process with the lowest activation energy had been attributed to the rotation around the C2∥ axis (see Fig. 2), energetically more favourable because of the [BH4] bidentate configuration with respect to the Mg ions, although its weight was rather low (15% of the QENS intensity). NMR measurements on β-Mg(BH4)230 are not showing discrete activation energies, but a broad distribution, centred around 138 ± 5 meV with a distribution width of ΔEa = 36 ± 3 meV.In this work, at longer timescales (6 Å-measurement), two reorientational processes with different time constants are detected. For the slower one, the activation energy has been calculated to be Ea = 32 ± 1 meV and Γ0 = 0.22 meV, in agreement with previous QENS and DFT calculations.31 We tentatively assign a C2∥ reorientation, energetically more favorable with respect to C3 rotations due to the bidentate configuration between Mg and H atoms. The other process is one order of magnitude faster (τ−1 ∼ 0.5–1 ps−1), but it shows a discontinuity at around 300 K and therefore its activation energy has not been determined. Γ2 is also of rotational origin, but its temperature dependence most likely reflects the transition in the vibrational part. The transition is also visible in the EISF, where, for temperatures above 200 K, the deviation from simple reorientational motions (like C2/C3 rotations) becomes significant (see Fig. 8). Other reorientation processes (like tumbling motions (eqn (17))) or other combinations (convolution between C2 and C3 rotations, or between C2 and tumbling motions) also do not describe the measured EISF obtained for the 6 Å measurement.
Similarly, in the same temperature regime, the data measured at 2.5 Å show the transition from an under-damped harmonic oscillator observed at 100 and 200 K to the over-damped regime above that temperature. The damping Γq and the HWHM Γ3 are plotted in Fig. 11. At 300 K and above, the vibrational inelastic scattering overlaps with the quasielastic region, and therefore the EISF reflects the merging of the two contributions.
The transition from the under-damped to the over-damped DHO is visible in the parameters extracted from the data analysis. The mean square displacement shows a step like increase from 200 K to 300 K and above (Fig. 13). The large values of 〈u2〉 (Fig. 13) differ from the harmonic contribution Uvib that has been estimated at the beginning of this section. Uvib characterizes fast vibrations of single nuclei around their lattice position (Debye–Waller factor), whereas we attribute 〈u2〉 to confined vibrational modes that originate from movements of the entire [BH4] unit around their equilibrium position. Therefore, the MSD 〈u2〉 describes in first approximation, the sum of contributions of localized atom vibrations and phonon band vibrations of the host lattice. For the lattice term, it is supposed that the hydrogen atoms follow the motions of the host lattice atoms.36
The rotational part, described by L2, is detected at 200 K and above. The scattering intensity follows eqn (6), as shown in Fig. 12. At 200 K, only a fraction 1 − p, with p = 0.47 ± 0.08, is undergoing reorientational motions, whereas at higher temperature, all [BH4] are reorienting and therefore in eqn (5) and (6), p is zero. The distances dB–H extracted are in the range of crystallographic values measured using X-ray and neutron diffractions11,12 (Fig. 14). From the analysis, we could assign the quasielastic rotational component to a C2 reorientation mechanism.
From the analysis of the 2.5 Å data, it became obvious that vibrational modes are contributing significantly to the observed intensities at low energy transfers. However, since the 6 Å-data are sensitive to longer timescales, it can be expected that 〈u2〉 has different values. Similarly, we suppose that the analysis of the 6 Å data, especially the functional dependence of the EISF at 300 K and above, reflects the overlap of vibrational intensity with the quasielastic region. The limited momentum transfer Q available in the 6 Å measurements makes the analysis of the EISF and QISFs quite harsh and was therefore not attempted.
Hydrogen dynamics has been studied in several borohydride compounds in order to elucidate the connection with the crystal structure and dynamics. In alkali borohydrides, like LiBH4,39,40 NaBH4 and KBH4,41,42 the rotational reorientation is correlated with a crystal structure transition from an ordered (low-temperature) to a disordered (high-temperature) phase. In NaBH4 and LiBH4, hydrogen motions become faster as soon as the disordered state is reached. In the disordered phase of KBH4, the hydrogen reorientation (jump rotation around the C4-fold axis) is similar to the one found in NaBH4. In LiBH4, the [BH4] dynamics changes from an C3 reorientation mechanism to a disordered reorientational model involving all four H atoms, as soon as the structural transition from orthorhombic (LT) to hexagonal (HT) is approached.43 Moreover, it has been suggested that the anomalous evolution of the lattice parameters as a function of temperature is associated with a pre-transition behaviour.44 Another mechanism in the crystal structure transition is found in Ca(BH4)2,45 which is mainly driven by librations. Internal vibrations strongly affect the free energy and therefore drive the crystal phase transition.
In β-Mg(BH4)2, we observe a dynamic transition between 200 K and 300 K: in the rotational part, at 300 K all [BH4] units take part in the reorientation while only hindered rotations are observed at 200 K; additionally, a transition from the under-damped to over-damped DHO is observed in that temperature range. The change in dynamics seems not to be connected to any structural phase transition. However, a recent study on β-Mg(BH4)246 showed highly anisotropic, non-uniform thermal expansion of the lattice. In particular, the b-lattice parameter showed a maximum at around 275 K, while for the a-lattice parameter a minimum value at approximately 200 K was observed. Moreover, the authors found that the refined atomic displacements did not detectably decrease with lower temperature. Our findings suggest a strong correlation between [BH4] dynamics and the structural environment. The partial covalent character of β-Mg(BH4)2 appears to be connected with the crystal vibrational dynamics, in an intermediate position between ionic bonded borohydrides (LiBH4 and NaBH4) to the more covalently bonded Ca(BH4)2.
4 Conclusions
In this work, QENS experiments have been performed on β-Mg(BH4)2 probing two different time-scales in order to explore the hydrogen dynamics, and in particular possible reorientations of the [BH4] units. At longer timescales (up to 16 ps, 6 Å), two different rotation motions have been detected. The slower one has an apparent activation energy of 32 ± 3 meV. The second reorientation motion is also assigned to a rotational reorientation around C2∥ or C2⊥, however its temperature dependence is influenced by the underlying vibrations as it became obvious from the investigations at faster observation times. Below 300 K, a distinct DHO signal appears in the measured data whereas at 300 K and above, it overlaps with the quasielastic signal. A transition from an under-damped to an over-damped regime is plausible. This transition in the scattering intensity strongly affects the EISF, QISFQE and QISFinel and the vibrational and rotational motions could only be separated using a global fitting approach. From the experimental results, on both timescales, no long range diffusion of the [BH4] units has been detected. In conclusion, the whole hydrogen dynamics in the picosecond timescale is dominated by both local rotational and vibrational reorientations occurring on similar timescales.Appendix A
The experimental data were analysed by a combination of rotational and vibrational reorientations (see eqn (3)). The scattering function Srot(Q,ω) for jump rotational processes is described as the sum of a δ-function (representing the elastic line) and a series of Lorentzian functions Ln(Γn,ω): | (11) |
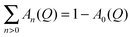 . The time of the jump is assumed to be instantaneous. In the case of hindered rotations, that is a fraction of atoms (p) not taking part in the reorientation, eqn (11) becomes:
. The time of the jump is assumed to be instantaneous. In the case of hindered rotations, that is a fraction of atoms (p) not taking part in the reorientation, eqn (11) becomes: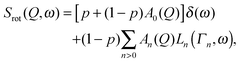 | (12) |
In the harmonic approximation, the vibrational scattering function Svib(Q,ω) can be written in a general form as the sum of elastic and inelastic terms:
| Svib(Q,ω) = B(Q)δ(ω) + [1 − B(Q)]Sinelvib(Q,ω), | (13) |
 | (14) |
The prefactor B(Q) (Debye–Waller factor) generally depends on the phonon density of states and it is related to the mean square displacement of the atoms,48 in this case hydrogen. In the case of harmonic vibrations and only one type of scatterer, a general expression is given by
 | (15) |
For purely rotational reorientations of the tetrahedra [BH4] in Mg(BH4)2, around the C2 or C3 symmetry axis (see Fig. 2), the EISF (identical to A0) is given by (in the powder average):
 | (16) |
 | (17) |
Following the general expression of eqn (3), in the case of a single reorientation process (eqn (12) with n = 1), and no translational Strans, S(Q,ω) becomes:
| S(Q,ω) = B[p + (1 − p)A0]δ(ω) + B(1 − p)A1L(ω) + [p + (1 − p)A0](1 − B)Sinelvib(ω) + (1 − B)(1 − p)A1[Sinelvib(ω) ⊗ L(ω)], | (18) |
| EISF = B(Q)[p + (1 − p)A0(Q)] | (19) |
| QISFQE = B(Q)(1 − p)[1 − A0(Q)] | (20) |
| QISFinel = 1 − B(Q). | (21) |
Acknowledgements
L. S. thanks Joachim Wuttke (Forschungszentrum Jülich (JCNS) and Heinz Maier-Leibnitz Zentrum (MLZ)) for the helpful discussion.References
- Y. Nakamori, K. Miwa, A. Ninomiya, H. Li, N. Ohba, S. Towata, A. Züttel and S. Orimo, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 045126 CrossRef.
- K. Chłopek, C. Frommen, A. Léon, O. Zabara and M. Fichtner, J. Mater. Chem., 2007, 17, 3496–3503 RSC.
- H.-W. Li, K. Kikuchi, Y. Nakamori, N. Ohba, K. Miwa, S. Towata and S. Orimo, Acta Mater., 2008, 56, 1342–1347 CrossRef CAS.
- T. Matsunaga, F. Buchter, P. Mauron, M. Bielman, Y. Nakamori, S. Orimo, N. Ohba, K. Miwa, S. Towata and A. Züttel, J. Alloys Compd., 2008, 459, 583–588 CrossRef CAS.
- G. L. Soloveichik, Y. Gao, J. Rijssenbeek, M. Andrus, S. Kniajanski, R. C. Bowman Jr., S.-J. Hwang and J.-C. Zhao, Int. J. Hydrogen Energy, 2009, 34, 916–928 CrossRef CAS.
- N. Hanada, K. Chlopek, C. Frommen, W. Lohstroh and M. Fichtner, J. Mater. Chem., 2008, 18, 2611–2614 RSC.
- G. Severa, E. Rönnebro and C. M. Jensen, Chem. Commun., 2010, 46, 421–423 RSC.
- M. Paskevicius, M. P. Pitt, C. J. Webb, D. A. Sheppard, U. Filsø, E. M. Gray and C. E. Buckley, J. Phys. Chem. C, 2012, 116, 15231–15240 CAS.
- Y. Filinchuk, B. Richter, T. R. Jensen, V. Dmitriev, D. Chernyshov and H. Hagemann, Angew. Chem., Int. Ed., 2011, 50, 11162–11166 CrossRef CAS PubMed.
- W. I. F. David, S. K. Callear, M. O. Jones, P. C. Aeberhard, S. D. Culligan, A. H. Pohl, S. R. Johnson, K. R. Ryan, J. E. Parker, P. P. Edwards, C. J. Nuttall and A. Amieiro-Fonseca, Phys. Chem. Chem. Phys., 2012, 14, 11800–11807 RSC.
- Y. Filinchuck, R. Černý and H. Hagemann, Chem. Mater, 2009, 21, 925–933 CrossRef.
- J.-H. Her, P. W. Stephens, Y. Gao, G. L. Soloveichik, J. Rijssenbeek, M. Andrus and J.-C. Zhao, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63, 561–568 CAS.
- R. Černý, Y. Filinchuk, H. Hagemann and K. Yvon, Angew. Chem., Int. Ed., 2007, 46, 5765–5767 CrossRef PubMed.
- J. Yang, X. Zhang, J. Zheng, P. Song and X. Li, Scr. Mater., 2011, 64, 225–228 CrossRef CAS.
- Z. Zhang, H. Wang, J. Liu and M. Zhu, Thermochim. Acta, 2013, 560, 82–88 CrossRef CAS.
- R. J. Newhouse, V. Stavila, S.-J. Hwang, L. E. Klebanoff and J. Z. Zhang, J. Phys. Chem. C, 2010, 114, 5224–5232 CAS.
- A. Al-Kukhun, H. T. Hwang and A. Varma, Int. J. Hydrogen Energy, 2012, 37, 17671–17677 CrossRef CAS.
- E. G. Bardají, Z. Zhao-Karger, N. Boucharat, A. Nale, M. J. van Setten, W. Lohstroh, E. Röhm, M. Catti and M. Fichtner, J. Phys. Chem. C, 2011, 115, 6095–6101 Search PubMed.
- B. Dai, D. S. Sholl and J. K. Johnson, J. Phys. Chem. C, 2008, 112, 4391–4395 CAS.
- A. Bil, B. Kolb, R. Atkinson, D. G. Pettifor, T. Thonhauser and A. N. Kolmogorov, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 224103 CrossRef.
- R. Caputo, A. Kupczak, W. Sikora and A. Tekin, Phys. Chem. Chem. Phys., 2013, 15, 1471–1480 RSC.
- V. Ozolins, E. H. Majzoub and C. Wolverton, Phys. Rev. Lett., 2008, 100, 135501 CrossRef CAS PubMed.
- J. Voss, J. S. Hummelshøj, Z. Łoodziana and T. Vegge, J. Phys.: Condens. Matter, 2009, 21, 012203 CrossRef CAS PubMed.
- X.-F. Zhou, A. R. Oganov, G.-R. Qian and Q. Zhu, Phys. Rev. Lett., 2012, 109, 245503 CrossRef PubMed.
- Y. Filinchuk, D. Chernyshov and R. Černý, J. Phys. Chem. C, 2008, 112, 10579–10584 CAS.
- W. H. Stockmayer and C. C. Stephenson, J. Chem. Phys., 1953, 21, 1311–1312 CrossRef CAS.
- G. Renaudin, S. Gomes, H. Hagemann, L. Keller and K. Yvon, J. Alloys Compd., 2004, 375, 98–106 CrossRef CAS.
- A. Borgschulte, R. Gremaud, A. Züttel, P. Martelli, A. Remhof, A. J. Ramirez-Cuesta, K. Refson, E. G. Bardají, W. Lohstroh, M. Fichtner, H. Hagemann and M. Ernst, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 024102 CrossRef.
- A. V. Skripov, A. V. Soloninin, O. A. Babanova, H. Hagemann and Y. Filinchuk, J. Phys. Chem. C, 2010, 114, 12370–12374 CAS.
- A. V. Soloninin, O. A. Babanova, A. V. Skripov, H. Hagemann, B. Richter, T. R. Jensen and Y. Filinchuk, J. Phys. Chem. C, 2012, 116, 4913–4920 CAS.
- D. Blanchard, J. B. Maronsson, M. D. Riktor, J. Kheres, D. Sveinbjørnsson, E. G. Bardají, A. Léon, F. Juranyi, J. Wuttke, K. Lefmann, B. C. Hauback, M. Fichtner and T. Vegge, J. Phys. Chem. C, 2012, 116, 2013–2023 CAS.
- K. Chłopek, C. Frommen, A. Léon, O. Zabara and M. Fichtner, J. Mater. Chem., 2007, 17, 3496–3503 RSC.
- T. Unruh, J. Neuhaus and W. Petry, Nucl. Instrum. Methods Phys. Res., Sect. A, 2007, 580, 1414–1422 CrossRef CAS.
- W. Lohstroh and Z. Evenson, Journal of large-scale research facilities JLSRF, 2015, 1, 1–3 CrossRef.
- S. Cusack and W. Doster, Biophys. J., 1990, 58, 243–251 CrossRef CAS PubMed.
- R. Hempelmann, Quasielastic Neutron Scattering and Solid State Diffusion, Clarendon Press, 2000 Search PubMed.
- M. Bée, Quasielastic Neutron Scattering, Adam Hilger, 1988 Search PubMed.
- A. Giannasi, D. Colognesi, L. Ulivi, M. Zoppi, A. J. Ramirez-Cuesta, E. G. Bardají, E. Röhm and M. Fichtner, J. Phys. Chem. A, 2010, 114, 2788–2793 CrossRef CAS PubMed.
- A. V. Skripov, A. V. Soloninin, Y. Filinchuk and D. Chernyshov, J. Phys. Chem. C, 2008, 112, 18701–18705 CAS.
- N. Verdal, T. J. Udovic and J. J. Rush, J. Phys. Chem. C, 2012, 116, 1614–1618 CAS.
- O. A. Babanova, A. V. Soloninin, A. P. Stepanov, A. V. Skripov and Y. Filinchuk, J. Phys. Chem. C, 2010, 114, 3712–3718 CAS.
- N. Verdal, M. R. Hartman, T. Jenkins, D. J. DeVries, J. J. Rush and T. J. Udovic, J. Phys. Chem. C, 2010, 114, 10027–10033 CAS.
- N. Verdal, T. J. Udovic, J. J. Rush, H. Wu and A. V. Skripov, J. Phys. Chem. C, 2013, 117, 12010–12018 CAS.
- H. Hagemann, Y. Filinchuk, D. Chernyshov and W. van Beek, Phase Transitions, 2009, 82, 344–355 CrossRef CAS.
- D. Blanchard, M. D. Riktor, J. B. Maronsson, H. S. Jacobsen, J. Kehres, D. Sveinbjörnsson, E. G. Bardají, A. Léon, F. Juranyi, J. Wuttke, B. C. Hauback, M. Fichtner and T. Vegge, J. Phys. Chem. C, 2010, 114, 20249–20257 CAS.
- Y. Filinchuk, R. Černý and H. Hagemann, Chem. Mater., 2009, 21, 925–933 CrossRef CAS.
- B. Fåk and B. Dorner, Phys. B, 1997, 234, 1107–1108 CrossRef.
- S. Lovesey, Theory of Neutron Scattering from Condensed Matter, Clarendon Press, 1986 Search PubMed.
- A. A. Maradudin and P. A. Flinn, Phys. Rev., 1963, 129, 2529–2547 CrossRef CAS.
| This journal is © the Owner Societies 2016 |


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−
exp(−