 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural effect of glyme–Li+ salt solvate ionic liquids on the conformation of poly(ethylene oxide)†
Zhengfei
Chen
a,
Samila
McDonald
a,
Paul A.
Fitzgerald
b,
Gregory G.
Warr
b and
Rob
Atkin
*a
aPriority Research Centre for Advanced Fluids and Interfaces, Newcastle Institute for Energy and Resources, The University of Newcastle, Callaghan, NSW 2308, Australia. E-mail: rob.atkin@newcastle.edu.au
bSchool of Chemistry, The University of Sydney, Sydney, NSW 2006, Australia
First published on 11th May 2016
Abstract
The conformation of 36 kDa polyethylene oxide (PEO) dissolved in three glyme–Li+ solvate ionic liquids (SILs) has been investigated by small angle neutron scattering (SANS) and rheology as a function of concentration and compared to a previously studied SIL. The solvent quality of a SIL for PEO can be tuned by changing the glyme length and anion type. Thermogravimetric analysis (TGA) reveals that PEO is dissolved in the SILs through Li+–PEO coordinate bonds. All SILs (lithium triglyme bis(trifluoromethanesulfonyl)imide ([Li(G3)]TFSI), lithium tetraglyme bis(pentafluoroethanesulfonyl)imide ([Li(G4)]BETI), lithium tetraglyme perchlorate ([Li(G4)]ClO4) and the recently published [Li(G4)]TFSI) are found to be moderately good solvents for PEO but solvent quality decreases in the order [Li(G4)]TFSI ∼ [Li(G4)]BETI > [Li(G4)]ClO4 > [Li(G3)]TFSI due to decreased availability of Li+ for PEO coordination. For the same glyme length, the solvent qualities of SILs with TFSI− and BETI− anions ([Li(G4)]TFSI and [Li(G4)]BETI) are very similar because they weakly coordinate with Li+, which facilitates Li+–PEO interactions. [Li(G4)]ClO4 presents a poorer solvent environment for PEO than [Li(G4)]BETI because ClO4− binds more strongly to Li+ and thereby hinders interactions with PEO. [Li(G3)]TFSI is the poorest PEO solvent of these SILs because G3 binds more strongly to Li+ than G4. Rheological and radius of gyration (Rg) data as a function of PEO concentration show that the PEO overlap concentrations, c* and c**, are similar in the three SILs.
Introduction
Ionic liquids (ILs) are salts with melting points below 100 °C. ILs have attracted great research interest owing to their remarkable combination of physicochemical properties including negligible vapour pressure, high ionic conductivity, non-flammability, high thermal stability and large electrochemical window.1–10Solvate ionic liquids (SILs) form when addition of a ligand molecule to a salt results in the formation of complex cations (or anions) and thereby reduces the melting point to less than 100 °C. A series of SILs prepared from mixtures of alkali metal (Li+, Na+ and K+) salts and oligoethers (or glymes, CH3(OCH2CH2)nOCH3, abbreviated as Gn) have been reported and characterised, in which the glyme molecules coordinate the alkali ions via their ether oxygens.11–18 Li+ based SILs are attractive electrolytes for secondary lithium ion batteries due to their high lithium content.19
In Li+–glyme SILs, the glyme molecules bind to the Li+ ion to produce large complex cations. SILs are defined as “good” or “poor” depending on the relative coordination strengths of the glyme and anion with Li+. In a good SIL, strong and long lived [Li(glyme)]+ cations are formed, resulting in negligible free glyme. Conversely, in a poor SIL, Li+–anion interactions are stronger than Li+–glyme interactions, and there can be up to 90% uncoordinated free glyme in the SIL.14 Good SILs have properties similar to a conventional IL, whereas the properties of poor SILs are like those of concentrated salt solutions.20 Henderson et al. studied the ionic association of different glymes (G1 to G4) in a variety of lithium salts, illustrating the effects of ionic association strength of the salts and the coordinating glyme length on the formation of solvate ionic liquids.21–23 In general, good SILs are more likely to form when the ionic association strength in the salt is relatively weak. The length of glyme has a more complex effect, however, it appears that the SILs with longer glyme are more stable, as they are more slowly exchangeable.21
The structure and interactions of equimolar mixtures of glyme and Li+ salt (bis(trifluoromethylsulfonyl)imide (TFSI), nitrate or trifluoroacetate salts) have recently been examined using molecular dynamic simulations.24 It was found that glyme–Li+ interactions were dominant in the mixture of glyme (G3 or G4)–LiTFSI (good solvate ILs) but were much less in the other two salts. A subsequent experimental study of the bulk structure of a good SIL ([Li(G4)]TFSI) and poor SIL (lithium tetraglyme nitrate ([Li(G4)]NO3)) has been completed by our group using neutron diffraction and empirical potential structure refinement (EPSR) simulated fits.18 In [Li(G4)]TFSI, the coordination number between Li+–G4 is 2–3 times higher than that for Li+–anion, whereas the coordination number is lower in [Li(G4)]NO3. This produces Li+ rich and depleted regions.
Conventional electrolytes in secondary Li+ batteries are limited by the use of volatile and flammable organic solvents for lithium salts.25 Polymer electrolytes (PEs) have been explored as replacements for organic solvents due to their negligible volatility and high thermal stability.26,27 Poly(ethylene oxide) (PEO) is one of the most popular PEs as it is stable to Li+ metal electrodes. PEO coordinates with Li+via ether oxygens, which leads to high Li+ transference numbers.28–30 However, the conductivities of PEs is only about 10% of typical conventional electrolytes because PEs are usually gels or solids. Recently, researchers have added conventional ILs to PEs in order to improve ionic conductivity and transport properties with some promising results.29,31 Kido et al. recently studied the ionic conductivity of SIL–polymer mixtures, showing greatly enhanced ionic conductivity (by an order of magnitude) compared to conventional PEs.32 The very high Li+ content of SILs suggests that their addition to PEs could improve charge storage and overall battery performance in addition to ionic conductivity. Therefore, understanding the mechanism of PEO dissolution in SILs, and how solvent quality varies with changes in the glyme length and anion type, is of both applied and fundamental importance.
The polymer radius of gyration (Rg), which is the average root-mean-squared distance of any point in the polymer coil from its centre of mass, is determined by the solvent quality which is categorised as poor, theta (θ) or good.33 In a good solvent, polymer chains are expanded (swollen) because interactions between the solvent and the polymer are energetically favourable. In a poor solvent, polymer chains are collapsed as polymer–polymer interactions are preferred over polymer–solvent interactions. In a theta solvent, the excluded volume expansion is cancelled and the chains adopt their random flight conformations (ideal chains). Rg is related to the Flory exponent (ν) by Rg = K(Mw)ν, where K is a constant based on the polymer type and Mw is the polymer molecular weight. Generally, for a good, theta and poor solvent, ν = 0.6, 0.5 and 0.33, respectively.
In moderately good (i.e. between a theta and good solvent) or good solvents, polymer solutions can generally be divided into three regimes: dilute, semi-dilute and concentrated regimes.33 In the dilute regime, the polymer coils are fully swollen by solvent, and Rg is almost independent of concentration. In the semi-dilute regime, there is overlap of neighbouring polymer coils, so Rg decreases with increasing polymer concentration, and the intra-chain excluded volume effect is reduced. In the concentrated regime, Rg is once again relatively constant as a function of polymer concentration. Here the high frequency of inter-chain polymer–polymer interactions means that the theta condition is reached, as the polymer essentially solvates itself. The crossover concentrations from dilute to semi-dilute, and semi-dilute to concentrated, are denoted c* and c**, respectively.
PEO is soluble in several imidazolium based aprotic ILs34–40 due to hydrogen bonding with the imidazolium cations.41 For the protic ILs ethylammonium nitrate (EAN) and propylammonium nitrate (PAN),42,43 PEO dissolves via hydrogen bonding between the ether oxygen and alkylammonium hydrogens. While PAN is a theta solvent for PEO, EAN is a moderately good solvent.
Recently, we reported the first study of PEO conformation dissolved in a SIL, [Li(G4)]TFSI, from the dilute through to the concentrated regime.44 [Li(G4)]TFSI was found to be a poorer solvent for PEO than water (a good solvent), but better than both EAN and PAN. The solvent quality of the SIL was attributed to coordination bonds between PEO and Li+, which is very different from both aprotic and protic ILs, where conventional hydrogen bonding is key.34–38,41,45
In this work, we examine the relationships between the chemical structure of the SIL and the solvent environment it provides for PEO using small angle neutron scattering (SANS), thermogravimetric analysis (TGA), and rheology. For SANS, at high concentrations, a mixture of hydrogenous and deuterated PEO is used to satisfy zero average contrast (ZAC) conditions, which allows Rg to be extracted despite significant overlap of neighbouring polymer coils.33,44,46,47 The present study will examine the effect of (1) shortening the glyme length from G4 to G3, (2) increasing the anion size from TFSI− to bis(pentafluoroethanesulfonyl)imide (BETI−) and (3) employing a poor SIL ([Li(G4)]ClO4) as the solvent on PEO conformation.
Experimental section
The SILs [Li(G3)]TFSI, [Li(G4)]BETI, and [Li(G4)]ClO4 were prepared by mixing equimolar triglyme (G3) or tetraglyme (G4) (Sigma Aldrich) with lithium bis(trifluoromethanesulfonyl)imide (Li[TFSI], Sigma Aldrich), lithium bis(pentafluoroethanesulfonyl)imide (Li[BETI], Fluorochem) or lithium perchlorate (Li[ClO4], Sigma Aldrich), respectively, at 50 °C with constant stirring on a hot plate overnight to form a clear liquid. The SILs were dried at 120 °C for 3 hours. The water contents determined by Karl Fischer titration were 0.02 wt% for [Li(G3)]TFSI, 0.01 wt% for [Li(G4)]BETI and 0.1 wt% for [Li(G4)]ClO4.Fully deuterated poly(ethylene oxide) (d-PEO, Mw = 36 kDa, PDI = 1.05) was purchased from Polymer Source (Canada). The corresponding hydrogenous poly(ethylene oxide) (h-PEO, Mw = 34 kDa, PDI = 1.05) was obtained from Fluka. d-PEO–SIL, d,h-PEO–SIL, and h-PEO–SIL solutions from 0.1 to ∼11 wt% (1 to 150 mg mL−1) were prepared several days prior to measurement to ensure complete mixing. No phase separation was observed for any sample.
Molecular weights were determined using size exclusion chromatography (SEC) on a Shimadzu CBM-20A liquid chromatography system with an Agilent Polargel-M guard column and three Phenomenex Phenogel 5 μm columns (10e3A/10e4A/10e5A) at 50 °C. The eluent was dimethylacetamide at a flow rate of 1.0 mL min−1, injections were 100 μL, and detection was with a Shimadzu RID-10A differential refractive index detector. Samples were filtered through a 0.45 μm pore polytetrafluoroethylene (PTFE) membrane prior to injection. The SEC was calibrated with poly(methyl methacrylate) standards (PDI < 1.1), which was adjusted using an 11.4 kDa PEO standard that was pre-determined using a Bruker MALDI-TOF mass spectrometer.
Small angle neutron scattering (SANS) experiments were conducted using the QUOKKA beamline48 at ANSTO (Australia) using 1 mm path-length Hellma Cells. The incident neutron wavelength was 5.0 Å. Two sample-to-detector distances of 2 m and 12 m with count time 30 min and 120 min, respectively, were used to provide a q range of 0.006 to 0.34 Å−1. These count times are ∼16 times longer than would normally be necessary for deuterated solvents on a high flux instrument such as QUOKKA, but are necessary here because of the high incoherent scattering due to the high hydrogen content of our solvents. After subtraction of the solvent scattering, the uncertainties in scattered intensities are less than 1.5%. Raw 2D SANS data were reduced to 1D data in IGOR Pro with reduction procedures provided by NIST modified for use on QUOKKA.49 In order to produce the PEO–SIL data on an absolute scale, the empty beam and an empty 1 mm Hellma cell were run before measurement and subtracted from the PEO–SIL SANS data. The pure SILs were run under the same conditions as PEO–SIL solutions and the solvent backgrounds were subtracted from the PEO–SIL solutions during the data reduction process. All experiments were carried out at 25 °C except for the PEO–[Li(G4)]BETI solutions which were analysed at 30 °C to ensure the samples were liquid.
Shear rate dependent viscosities of PEO–SIL solutions were measured on a TA Instruments AR-G2 rheometer using the cone and plate arrangement with a cone of 40 mm diameter and angle of 1°59′36′′ by increasing the shear rate from 1 to 1000 s−1. All measurements were maintained at 25 °C except for PEO–[Li(G4)]BETI solutions which were measured at 30 °C. A thermogravimetric analysis (TGA) of 5 wt% PEO in each SIL was performed on a TG/TDA analyser (PerkinElmer) from room temperature to 600 °C at a heating rate of 10 °C min−1 under nitrogen gas flow (20 mL min−1).
SANS data analysis
The method for analysing the reduced SANS data was described in detail in the previous work.44 Generally, the coherent neutron cross section per unit volume, I(q), for solutions of identical deuterated and hydrogenous polymers is given by:33| I(q)/nN2 = φ(1 − φ)(bH − bD)2P(q) + [φbD + (1 − φ)bH − bs(vp/vs)]2S(q) | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where λ is the neutron wavelength and 2θ is the scattering angle; n and N are the number density and degree of polymerization of the polymer molecules; bH, bD, and bs are the neutron scattering lengths of the hydrogenous monomer units, deuterated monomer units and the solvent, respectively; vp/vs is the ratio of specific volumes for polymer and solvent; and φ is the volume fraction of deuterated polymer chains.
θ, where λ is the neutron wavelength and 2θ is the scattering angle; n and N are the number density and degree of polymerization of the polymer molecules; bH, bD, and bs are the neutron scattering lengths of the hydrogenous monomer units, deuterated monomer units and the solvent, respectively; vp/vs is the ratio of specific volumes for polymer and solvent; and φ is the volume fraction of deuterated polymer chains.
When the polymer chains are fully deuterated (φ = 1), the first term of the right-hand side of eqn (1) is zero. This allows the characteristic dimensions to be determined from S(q). Fits to the data using the polymer excluded volume effect (eqn (2) and (3))50 yield apparent Rg and the Flory exponent (ν) as a function of polymer concentration. This approach is generally useful in the relatively low polymer concentration regime, but is also used in the concentrated region, see below, where this model reduces to the Debye equation for a Gaussian polymer by setting ν = 0.5 (see eqn (6)).
 | (2) |
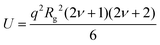 | (3) |
The correlation length or “blob size” (ξ), is independent of the molecular weight but decreases with increasing polymer concentration.51ξ can be determined from S(q) using the Ornstein–Zernike formula:52
| I(q) = I0/(1 + q2ξ2) | (4) |
 | (5) |
At higher polymer concentrations, zero average contrast (ZAC) between the polymer and solvent is achieved by mixing hydrogenous and deuterated PEO such that φ = 0.16 for [Li(G3)]TFSI, 0.2 for [Li(G4)]BETI and 0.06 for [Li(G4)]ClO4 (see ESI,† Table S1 for the neutron scattering length densities). This means that φbD + (1 − φ)bH = bs(vp/vs), so that the second term of the right-hand side of eqn (1) is zero, and Rg is determined from P(q) only. The unperturbed chain dimension in theta condition or melt can be determined by the Debye equation:33
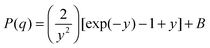 | (6) |
Results
The SANS patterns for d-PEO dissolved in [Li(G3)]TFSI, [Li(G4)]BETI and [Li(G4)]ClO4 at PEO concentrations from 1 to 50 mg mL−1 are shown in Fig. 1. The SANS spectra for the pure solvents are shown in ESI,† Fig. S1, and are featureless over the q range probed in this work. As expected, the scattering intensity increases with increasing PEO concentration. Data fits using the excluded volume model (eqn (2) and (3)) are also shown in Fig. 1 (solid curves) and the fitting parameters for each system (apparent radius of gyration, Rg, and Flory exponent, ν) are listed in Tables 1–3, respectively, together with correlation lengths, ξ, derived from fits to the Ornstein–Zernike formula (eqn (4)). Fits are shown in the ESI† in Fig. S2.| d-PEO conc. (mg mL−1) | Apparent Rg (Å) | ξ (Å) | ν |
|---|---|---|---|
| 1.5 | 65 | 43 | 0.513 |
| 2.8 | 66 | 43 | 0.515 |
| 4.4 | 62 | 41 | 0.505 |
| 8.7 | 55 | 37 | 0.505 |
| 13.5 | 50 | 33 | 0.505 |
| 20.0 | 44 | 29 | 0.505 |
| 34.3 | 35 | 23 | 0.505 |
| 49.0 | 29 | 19 | 0.505 |
| d-PEO conc. (mg mL−1) | Apparent Rg (Å) | ξ (Å) | ν |
|---|---|---|---|
| 1.5 | 72 | 48 | 0.538 |
| 2.8 | 66 | 43 | 0.529 |
| 4.1 | 64 | 42 | 0.515 |
| 8.8 | 58 | 38 | 0.526 |
| 13.2 | 52 | 34 | 0.521 |
| 19.7 | 47 | 30 | 0.524 |
| 34.6 | 37 | 24 | 0.513 |
| 48.2 | 30 | 19 | 0.513 |
| d-PEO conc. (mg mL−1) | Apparent Rg (Å) | ξ (Å) | ν |
|---|---|---|---|
| 1.3 | 71 | 48 | 0.524 |
| 2.5 | 65 | 42 | 0.524 |
| 3.7 | 66 | 43 | 0.524 |
| 8.2 | 58 | 39 | 0.510 |
| 12.6 | 54 | 36 | 0.510 |
| 17.8 | 48 | 32 | 0.515 |
| 30.4 | 41 | 27 | 0.513 |
| 45.0 | 34 | 23 | 0.503 |
The apparent Rg of PEO in [Li(G3)]TFSI is 65 Å at 1.5 mg mL−1, and decreases with increasing PEO concentration. The same PEO is slightly more swollen in [Li(G4)]BETI (Rg = 72 Å) and [Li(G4)]ClO4 (Rg = 71 Å), but these also shrink with increasing concentration (c) across the range examined. Correlation lengths consistently follow the same trend as apparent Rg for all PEO concentrations in these SILs, which is also seen in the aqueous systems.54 As the polymer concentration increases, more inter-chain interactions occur and adjacent polymer chains are closer together, thus reducing ξ.
At the lowest PEO concentrations examined, the Flory exponents (ν) of 0.513, 0.538, and 0.524 are found for [Li(G3)]TFSI, [Li(G4)]BETI, and [Li(G4)]ClO4, respectively. At higher PEO concentrations, ν decreases to a near constant value (0.5) with increasing PEO concentration as polymer–polymer interactions increase and solvent–polymer interactions decrease.
These results are also consistent with our previous study of [Li(G4)]TFSI;44 in the most dilute solutions and at comparable concentrations, apparent Rg of 69 Å, ξ = 45 Å and ν = 0.54 are identical to those found here for [Li(G4)]BETI. This is not surprising given the chemical similarity between the anions.
Zimm plots (Kc/I(q) vs. (q2 + c), eqn (5)) for the low concentration SANS data are shown in Fig. 2. Extrapolations to c = 0 and q2 = 0 in Fig. 2 are used to determine the fully swollen (infinite dilution) Rg,55 which are 77 Å, 79 Å and 84 Å for PEO in [Li(G3)]TFSI, [Li(G4)]ClO4 and [Li(G4)]BETI, respectively, and again close to the previously obtained value of 86 Å in [Li(G4)]TFSI.44 This confirms that swelling of the PEO chains by the solvent increases in the order [Li(G3)]TFSI < [Li(G4)]ClO4 < [Li(G4)]BETI ∼ [Li(G4)]TFSI, consistent with the Flory exponent values.
Zimm plot analysis also yields second virial coefficients (A2) between 0.4 and 0.7 × 10−3 cm3 mol g−2 for the three SILs. This is consistent with 0.7 × 10−3 cm3 mol g−2 obtained in [Li(G4)]TFSI (Mw = 38 kDa PEO),44 but much smaller than that found in water (A2 = 2.2 × 10−3 cm3 mol g−2, Mw = 38 kDa PEO)56 and the aprotic IL [BMIm]BF4 (A2 = 2.0 × 10−3 cm3 mol g−2, Mw = 27.3 kDa PEO),39 which are good solvents for PEO. However, the solvent quality of these SILs is better than that of the protic IL EAN, which has a much smaller A2 value of 1.6 × 10−6 cm3 mol g−2 (Mw = 38 kDa PEO), and is closer to a theta solvent for PEO.43 Therefore, our analysis reveals that SILs are moderately good solvents for PEO.
At high PEO concentrations, Rg cannot be determined through the excluded volume model because of inter-chain interactions,47 so the zero average contrast (ZAC) method is used. SANS results for PEO in [Li(G3)]TFSI, [Li(G4)]BETI and [Li(G4)]ClO4 at PEO concentrations from 50 to 150 mg mL−1 with corresponding fits to the Debye model (eqn (6)) are shown in Fig. 3, with best-fit parameters listed in Table 4.
| PEO–[Li(G3)]TFSI | PEO–[Li(G4)]BETI | PEO–[Li(G4)]ClO4 | |||
|---|---|---|---|---|---|
| PEO conc. (mg mL−1) | R g (Å) | PEO conc. (mg mL−1) | R g (Å) | PEO conc. (mg mL−1) | R g (Å) |
| 49.5 | 66 | 50.9 | 63 | 44.8 | 66 |
| 72.4 | 65 | 67.2 | 62 | 70 | 64 |
| 115.6 | 65 | 100.3 | 60 | 110 | 64 |
| 152.2 | 64 | 129.5 | 62 | 140 | 64 |
At high PEO concentrations, Rg = 65 ± 2 Å is independent of the SIL and PEO concentration within experimental uncertainty. The Rg value (∼65 ± 2 Å) for the PEO is close to the measured chain size of 70 Å for the same Mw in the melt,57 indicating that these solutions in the concentrated regime have already achieved the limiting Rg value for that of the melt. Viscosities of PEO–SIL solutions at various PEO concentrations were measured as a function of shear rate from 1 to 1000 s−1 (see ESI,† Fig. S3). The viscosities of pure [Li(G3)]TFSI, [Li(G4)]BETI and [Li(G4)]ClO4 are consistent with previous reports.15 For the SIL–PEO systems, viscosity increases notably with increasing PEO concentration, and slight shear thinning was observed at shear rates above 200 s−1. This is typical for PEO in various ILs such as EAN and PAN,58 and also in water,59 but the microscopic explanation of shear thinning is still a matter of debate.60
The c* and c** concentrations, which define the transitions from the dilute to semi-dilute and semi-dilute to concentrated regimes, can be determined from slope changes in plots of apparent Rg, ξ, or viscosity as a function of polymer concentration.44 In Fig. 4, apparent Rg and ξ for PEO decrease slightly at low PEO concentrations, then follows an apparent Rg ∼ c−0.25 dependence at higher PEO concentrations. Note that this is an apparent Rg, and is not expected to follow Rg ∼ c−0.125,61 as stated in the experimental section. The concentration at which the slope changes is c*, and gives values of 16, 12 and 14 mg mL−1 for [Li(G3)]TFSI, [Li(G4)]BETI and [Li(G4)]ClO4 respectively. These experimental values can be compared to c* values calculated from Rg at infinite dilution using c* = (Mw/NA)/(4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Rg3/3), and give corresponding values of 31, 24 and 29 mg mL−1 respectively. The experimental values are about a factor of two smaller than the calculated values, but within the difference of about one experimental data point. Rg at higher PEO concentrations is determined from ZAC data, which enabled c** to be measured at 50, 43 and 45 mg mL−1 for [Li(G3)]TFSI, [Li(G4)]BETI and [Li(G4)]ClO4 respectively.
Rg3/3), and give corresponding values of 31, 24 and 29 mg mL−1 respectively. The experimental values are about a factor of two smaller than the calculated values, but within the difference of about one experimental data point. Rg at higher PEO concentrations is determined from ZAC data, which enabled c** to be measured at 50, 43 and 45 mg mL−1 for [Li(G3)]TFSI, [Li(G4)]BETI and [Li(G4)]ClO4 respectively.
Viscosity as a function of polymer concentration is also shown in Fig. 4 for the three PEO–SIL systems. In the dilute regime, viscosity increases weakly with polymer concentration as chains are mostly isolated. In the semi-dilute regime, the viscosity increases more steeply due to increasing entanglement of polymer chains. In the concentrated regime, the polymer–polymer interactions are dominant, which results in a much sharper increase in the viscosity with increasing concentration. The crossovers c* (from dilute to semi-dilute) and c** (from semi-dilute to concentrated), determined from the viscosity trend agree very well with those determined from Rg, as shown in Fig. 4.
For the same polymer, better solvent quality leads to a smaller c* and c** as the polymer chains are more extended. The crossover concentrations therefore show that the solvent quality for PEO increases in the order of [Li(G3)]TFSI < [Li(G4)]ClO4 < [Li(G4)]TFSI ∼ [Li(G4)]BETI. The c* for the same PEO polymer in EAN was reported as between 24 and 60 mg mL−1,43 suggesting that EAN is a poorer solvent than the SILs.
TGA curves for 5 wt% PEO in pure glyme (G3 or G4) and the three SILs are shown in Fig. 5. The data for PEO in G3 and G4 are similar to that for the pure glymes15 until the decomposition temperatures of 167 °C for G3 and 206 °C for G4 are reached.15 Above these temperatures, approximately 5 wt% of the total mass (PEO polymer) is retained until the PEO begins to decompose at ∼340 °C. This confirms no strong interactions between PEO and the pure glymes, consistent with only weak dispersion interactions between ethylene oxide groups.
 | ||
| Fig. 5 TGA curves of 5 wt% PEO in pure glymes and SILs under N2 flow. Note: the 5 wt% PEO in G4 data (dashed line) was reproduced from our previous work44 for comparison. | ||
TGA profiles for the PEO–SILs solutions are similar to those of pure SILs15 over the entire temperature range. All PEO–SIL solutions exhibit thermal stability up to ∼200 °C, as shown in Fig. 5. For PEO in the good SILs, [Li(G3)]TFSI and [Li(G4)]BETI, there is a gradual decrease in weight due to glyme decomposition above 200 °C and PEO above 350 °C until almost all mass is lost at ∼420 °C. The remaining mass is residual carbon. For the PEO in the poor SIL [Li(G4)]ClO4, weight loss is more rapid above 200 °C due to the markedly greater amount of free glyme.15 At 341 °C, 30 wt% of the original mass remains, which is equal to the sum of PEO and LiClO4, i.e. all of the glyme has been removed. At higher temperatures, PEO begins to decompose, and LiClO4 decomposition commences at 390 °C.62 The 12 wt% mass fraction present at temperatures greater than 470 °C and its white appearance is consistent with decomposition of LiClO4 into LiCl.62
Discussion
The conformation of a polymer in solution is dictated by the solvent quality, which is governed by the balance of polymer–polymer and polymer–solvent interactions. Fits to the SANS data (Rg coil size and Rg at infinite dilution, Flory exponent ν) revealed that the three SILs are moderately good solvents, with solvent quality increasing in the order [Li(G3)]TFSI < [Li(G4)]ClO4 < [Li(G4)]TFSI ∼ [Li(G4)]BETI. Trends in viscosity as a function of concentration confirm this order.[Li(G3)]TFSI is a poorer solvent for PEO than either [Li(G4)]TFSI or [Li(G4)]BETI. In pure Li+–glyme SILs, the glyme molecules compete with the anion for Li+.14,15 It has previously been shown that the Li+–O distance of ∼2.2 Å in [Li(G4)]TFSI is reduced to ∼2.0 Å in [Li(G3)]TFSI,16 indicating tighter Li+–glyme binding. Tighter binding leads to higher ionicity (cation–anion separation)16,63 and higher viscosity.15,63 For PEO to be solvated by the SIL it must compete effectively for Li+ coordination sites with both the glyme and anion. Molecular Dynamics simulations have shown that the number of anions not attached to any Li+ doubles from 6% in [Li(G3)]TFSI to 12.2% in [Li(G4)]TFSI,24 meaning that anions are more strongly associated with Li+ in [Li(G3)]TFSI. Tighter binding of G3 to Li+ than G4 means that Li+ is less available to bind PEO, resulting in poorer solvency.
Employing the same glyme length enables the effect of the anion on PEO solvation to be assessed. The solvent quality for PEO for G4 based SILs is [Li(G4)]TFSI ∼ [Li(G4)]BETI > [Li(G4)]ClO4. Henderson et al. reported the association strength for LiX salts in glymes is BETI− ∼ TFSI− < ClO4−.21 This means ClO4− coordinates much more strongly to Li+ than the other two anions. While BETI− is slightly larger than TFSI− due to its two additional CF2 groups, it has similar coordination strength. Therefore, Li+ is similarly available to bind with PEO in [Li(G4)]TFSI and [Li(G4)]BETI, but less so in [Li(G4)]ClO4, consistent with the trends in solvent quality.
The solvent quality of PEO dissolved in its monomeric liquids, ethylene glycol and monoglyme has been studied using rheology and photon correlation spectroscopy (PCS).64 The polymer–solvent and solvent–solvent interactions were greatly influenced by the number of H-bond donors available in the solvent, with increased H-bond capacity leading to better solvency. This is consistent with our observations. Given that lithium acts a hydrogen bond donor, as the Li+ concentration per unit volume increases (from [Li(G4)]ClO4 to [Li(G4)]TFSI and [Li(G4)]BETI) the solvent quality increases.
Strong coordination of ClO4− with Li+ means that [Li(G4)]ClO4 is a poor SIL, with around 20% free glyme.14 This means PEO in [Li(G4)]ClO4 can be solvated by both free glyme as well as complex cation and anion. Given that the TGA data confirms that interaction between G4 and PEO are weak, this will also contribute to [Li(G4)]ClO4 being a poorer solvent.
Coordination between the Li and glyme leads to a greater thermal stability for the three SILs up to ∼200 °C.14,15 For PEO–[Li(G4)]ClO4, the more severe mass loss is due to the weaker coordination between glyme and Li+.15 At 341 °C, 30 wt% of the mass is retained which is equal to the sum of PEO and LiClO4. The great similarity in the thermal behaviour between the PEO–SIL solutions and their respective SILs suggests that PEO does not completely replace the glyme from Li+,44 irrespective of the change of the structure on the SIL.
We argued in our previous work that the dissolution of PEO in [Li(G4)]TFSI was via the coordination between Li+ and PEO.44 Typical coordination numbers for LiX–PEO complexes are 4 to 6.65,66 Recent molecular dynamics simulations suggest that the average coordination number (Li+/O) in both [Li(G3)]TFSI and [Li(G4)]TFSI is 5, with 1 and 0.5 oxygens contributed from the anion, respectively.13 Therefore, in SILs such as [Li(G3)]TFSI and [Li(G4)]TFSI, it is more likely that PEO is solvated by displacing the anion from the coordination sphere of lithium ions, and we expect that solvation in [Li(G4)]BETI will be similar. The recent work on thermal, ionic and electrochemical properties of PEO–[Li(G4)]TFSI by Kido et al. showed that some Li–PEO complex could also form,32 which may effect the PEO structure.
Conclusions
PEO is dissolved in [Li(G3)]TFSI, [Li(G4)]BETI and [Li(G4)]ClO4via the coordination between PEO ether oxygens and Li+, although interactions between PEO and free glyme may also play a role in [Li(G4)]ClO4. All three solvate ionic liquids are moderately good solvents for PEO as revealed by the Flory exponent values, Zimm analysis, and viscosity behaviour.Solvent quality increases in the order of [Li(G3)]TFSI < [Li(G4)]ClO4 < [Li(G4)]BETI ∼ [Li(G4)]TFSI. The Rg values and the crossover concentrations determined from trends in Rg and viscosity as a function of PEO concentration show that PEO conformation in the SILs is similar, and much less affected by changing ion structures compared to that in common ionic liquids.67 This is likely a consequence of the mechanism of solvation being coordination bonds with Li+ ions in SILs rather than hydrogen bonds in conventional ILs.
PEO must compete with anion and glyme for Li+ coordination sites to be solvated. If there is a stronger coordination between Li+ and the anion (ClO4−vs. TFSI− or BETI−) or Li+ and glyme (e.g. G3 vs. G4), then the solvent quality is poorer for PEO. For the same glyme length, weakly coordinating anions (good SILs) are better solvents than strongly coordinating anions (poor SILs) because the lithium ion is more available for binding PEO. The poor SIL contains a substantial proportion of free glyme which could also contribute to poorer solvation because glyme–PEO interactions are weak.
Acknowledgements
GGW and RA acknowledge support from Australian Research Council Discovery Projects, and RA acknowledges ARC for a Future Fellowship. The authors wish to thank ANSTO for the provision of small angle neutron scattering beamtime (Proposal 4452). This work benefitted from software developed by the DANSE project under NSF award DMR-0520547.References
- T. Welton, Coord. Chem. Rev., 2004, 248, 2459–2477 CrossRef CAS
.
- D. R. MacFarlane, N. Tachikawa, M. Forsyth, J. M. Pringle, P. C. Howlett, G. D. Elliott, J. H. Davis, M. Watanabe, P. Simon and C. A. Angell, Energy Environ. Sci., 2014, 7, 232–250 CAS
.
- Z. Chen, P. A. FitzGerald, Y. Kobayashi, K. Ueno, M. Watanabe, G. G. Warr and R. Atkin, Macromolecules, 2015, 48, 1843–1851 CrossRef CAS
.
- Z. Chen, Y. Kobayashi, G. B. Webber, K. Ueno, M. Watanabe, G. G. Warr and R. Atkin, Langmuir, 2015, 31, 7025–7031 CrossRef CAS PubMed
.
- T. L. Greaves and C. J. Drummond, Chem. Soc. Rev., 2008, 37, 1709–1726 RSC
.
- A. Dolan, R. Atkin and G. G. Warr, Chem. Sci., 2015, 6, 6189–6198 RSC
.
- R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS PubMed
.
- J. Sweeney, G. B. Webber and R. Atkin, Phys. Chem. Chem. Phys., 2015, 17, 26629–26637 RSC
.
- D. Wakeham, P. Niga, C. Ridings, G. Andersson, A. Nelson, G. G. Warr, S. Baldelli, M. W. Rutland and R. Atkin, Phys. Chem. Chem. Phys., 2012, 14, 5106–5114 RSC
.
- O. Werzer and R. Atkin, Phys. Chem. Chem. Phys., 2011, 13, 13479–13485 RSC
.
- T. Mandai, K. Yoshida, S. Tsuzuki, R. Nozawa, H. Masu, K. Ueno, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2015, 119, 1523–1534 CrossRef CAS PubMed
.
- T. Tamura, T. Hachida, K. Yoshida, N. Tachikawa, K. Dokko and M. Watanabe, J. Power Sources, 2010, 195, 6095–6100 CrossRef CAS
.
- S. Tsuzuki, W. Shinoda, M. Matsugami, Y. Umebayashi, K. Ueno, T. Mandai, S. Seki, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2015, 17, 126–129 RSC
.
- K. Ueno, R. Tatara, S. Tsuzuki, S. Saito, H. Doi, K. Yoshida, T. Mandai, M. Matsugami, Y. Umebayashi, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2015, 17, 8248–8257 RSC
.
- K. Ueno, K. Yoshida, M. Tsuchiya, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2012, 116, 11323–11331 CrossRef CAS PubMed
.
- K. Yoshida, M. Nakamura, Y. Kazue, N. Tachikawa, S. Tsuzuki, S. Seki, K. Dokko and M. Watanabe, J. Am. Chem. Soc., 2011, 133, 13121–13129 CrossRef CAS PubMed
.
- B. McLean, H. Li, R. Stefanovic, R. J. Wood, G. B. Webber, K. Ueno, M. Watanabe, G. G. Warr, A. Page and R. Atkin, Phys. Chem. Chem. Phys., 2015, 17, 325–333 RSC
.
- T. Murphy, S. K. Callear, N. Yepuri, K. Shimizu, M. Watanabe, J. N. Canongia Lopes, T. Darwish, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2016 10.1039/C6CP00176A
.
- C. Zhang, A. Yamazaki, J. Murai, J.-W. Park, T. Mandai, K. Ueno, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2014, 118, 17362–17373 CAS
.
- T. Mandai, K. Yoshida, K. Ueno, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2014, 16, 8761–8772 RSC
.
- W. A. Henderson, J. Phys. Chem. B, 2006, 110, 13177–13183 CrossRef CAS PubMed
.
- W. A. Henderson, N. R. Brooks, W. W. Brennessel and V. G. Young, Chem. Mater., 2003, 15, 4679–4684 CrossRef CAS
.
- W. A. Henderson, N. R. Brooks and V. G. Young, Chem. Mater., 2003, 15, 4685–4690 CrossRef CAS
.
- K. Shimizu, A. A. Freitas, R. Atkin, G. G. Warr, P. A. FitzGerald, H. Doi, S. Saito, K. Ueno, Y. Umebayashi, M. Watanabe and J. N. Canongia Lopes, Phys. Chem. Chem. Phys., 2015, 17, 22321–22335 RSC
.
- K. Xu, Chem. Rev., 2014, 114, 11503–11618 CrossRef CAS PubMed
.
- D. T. Hallinan and N. P. Balsara, Annu. Rev. Mater. Res., 2013, 43, 503–525 CrossRef CAS
.
- W. H. Meyer, Adv. Mater., 1998, 10, 439–448 CrossRef CAS PubMed
.
- E. Quartarone, P. Mustarelli and A. Magistris, Solid State Ionics, 1998, 110, 1–14 CrossRef CAS
.
- J. H. Shin, W. A. Henderson and S. Passerini, J. Electrochem. Soc., 2005, 152, A978–A983 CrossRef CAS
.
- J. Xi, X. Qiu, M. Cui, X. Tang, W. Zhu and L. Chen, J. Power Sources, 2006, 156, 581–588 CrossRef CAS
.
- J.-H. Shin, W. A. Henderson and S. Passerini, Electrochem. Commun., 2003, 5, 1016–1020 CrossRef CAS
.
- R. Kido, K. Ueno, K. Iwata, Y. Kitazawa, S. Imaizumi, T. Mandai, K. Dokko and M. Watanabe, Electrochim. Acta, 2015, 175, 5–12 CrossRef CAS
.
- G. Cheng, W. W. Graessley and Y. B. Melnichenko, Phys. Rev. Lett., 2009, 102, 157801 CrossRef CAS PubMed
.
- H.-N. Lee and T. P. Lodge, J. Phys. Chem. Lett., 2010, 1, 1962–1966 CrossRef CAS
.
- S. K. Chaurasia, R. K. Singh and S. Chandra, J. Raman Spectrosc., 2011, 42, 2168–2172 CrossRef CAS
.
- L. T. Costa and M. C. C. Ribeiro, J. Chem. Phys., 2006, 124, 184902 CrossRef PubMed
.
- J. M. Harner and D. A. Hoagland, J. Phys. Chem. B, 2010, 114, 3411–3418 CrossRef CAS PubMed
.
- Z. F. Bai, M. W. Nagy, B. Zhao and T. P. Lodge, Langmuir, 2014, 30, 8201–8208 CrossRef CAS PubMed
.
- A. Triolo, O. Russina, U. Keiderling and J. Kohlbrecher, J. Phys. Chem. B, 2006, 110, 1513–1515 CrossRef CAS PubMed
.
- H.-N. Lee, N. Newell, Z. Bai and T. P. Lodge, Macromolecules, 2012, 45, 3627–3633 CrossRef CAS
.
- N. Winterton, J. Mater. Chem., 2006, 16, 4281–4293 RSC
.
- J. A. Smith, G. B. Webber, G. G. Warr, A. Zimmer, R. Atkin and O. Werzer, J. Colloid Interface Sci., 2014, 430, 56–60 CrossRef CAS PubMed
.
- O. Werzer, G. G. Warr and R. Atkin, J. Phys. Chem. B, 2011, 115, 648–652 CrossRef CAS PubMed
.
- Z. Chen, P. A. FitzGerald, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2015, 17, 14872–14878 RSC
.
- J. Mondal, E. Choi and A. Yethiraj, Macromolecules, 2014, 47, 438–446 CrossRef CAS
.
- J. S. King, W. Boyer, G. D. Wignall and R. Ullman, Macromolecules, 1985, 18, 709–718 CrossRef CAS
.
- M. Benmouna and B. Hammouda, Prog. Polym. Sci., 1997, 22, 49–92 CrossRef CAS
.
- E. P. Gilbert, J. C. Schulz and T. J. Noakes, Phys. B, 2006, 385–386(part 2), 1180–1182 CrossRef CAS
.
- S. R. Kline, J. Appl. Crystallogr., 2006, 39, 895–900 CrossRef CAS
.
- B. Hammouda, Adv. Polym. Sci., 1993, 106, 87–133 CrossRef CAS
.
- M. Adam and M. Delsanti, Macromolecules, 1977, 10, 1229–1237 CrossRef CAS
.
-
H. E. Stanley, Introduction to Phase Transitions and Critical Phenomena, Oxford University Press, Oxford, 1971 Search PubMed
.
- B. H. Zimm, J. Chem. Phys., 1945, 13, 141–145 CrossRef CAS
.
- B. Hammouda and D. L. Ho, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 2196–2200 CrossRef CAS
.
- C. B. Shogbon, J.-L. Brousseau, H. Zhang, B. C. Benicewicz and Y. A. Akpalu, Macromolecules, 2006, 39, 9409–9418 CrossRef CAS
.
- K. Devanand and J. C. Selser, Macromolecules, 1991, 24, 5943–5947 CrossRef CAS
.
- L. J. Fetters, D. J. Lohse, D. Richter, T. A. Witten and A. Zirkel, Macromolecules, 1994, 27, 4639–4647 CrossRef CAS
.
- J. A. Smith, G. B. Webber, G. G. Warr and R. Atkin, J. Phys. Chem. B, 2013, 117, 13930–13935 CrossRef CAS PubMed
.
- V. Gauri and K. Koelling, Rheol. Acta, 1997, 36, 555–567 CrossRef CAS
.
- X. Xu, J. Chen and L. An, J. Chem. Phys., 2014, 140, 174902 CrossRef PubMed
.
- M. Daoud, J. P. Cotton, B. Farnoux, G. Jannink, G. Sarma, H. Benoit, C. Duplessix, C. Picot and P. G. de Gennes, Macromolecules, 1975, 8, 804–818 CrossRef CAS
.
- K. H. Stern, J. Phys. Chem. Ref. Data, 1974, 3, 481–526 CrossRef CAS
.
- T. Tamura, K. Yoshida, T. Hachida, M. Tsuchiya, M. Nakamura, Y. Kazue, N. Tachikawa, K. Dokko and M. Watanabe, Chem. Lett., 2010, 39, 753–755 CrossRef CAS
.
- V. Crupi, A. Faraone, G. Maisano, D. Majolino, P. Migliardo, V. Venuti and V. Villari, J. Chem. Phys., 2000, 112, 5205–5211 CrossRef CAS
.
- J. D. Londono, B. K. Annis, A. Habenschuss, O. Borodin, G. D. Smith, J. Z. Turner and A. K. Soper, Macromolecules, 1997, 30, 7151–7157 CrossRef CAS
.
- G. Mao, M.-L. Saboungi, D. L. Price, M. B. Armand and W. S. Howells, Phys. Rev. Lett., 2000, 84, 5536–5539 CrossRef CAS PubMed
.
- T. Ueki and M. Watanabe, Bull. Chem. Soc. Jpn., 2012, 85, 33–50 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp00919k |
| This journal is © the Owner Societies 2016 |




