Identification and H(D)-bond energies of C–H(D)⋯Cl interactions in chloride–haloalkane clusters: a combined X-ray crystallographic, spectroscopic, and theoretical study

Abstract

The cationic (1,3,5-triazapentadiene)Pt^II complex [Pt{NH=C(N(CH₂)₅)N(Ph)C(NH₂)=NPh}₂]Cl₂ ([1]Cl₂) was crystallized from four haloalkane solvents giving [1][Cl₂(CDCl₃)₄], [1][Cl₂(CHBr₃)₄], [1][Cl₂(CH₂Cl₂)₂], and [1][Cl₂(C₂H₄Cl₂)₂] solvates that were studied by X-ray diffraction. In the crystal structures of [1][Cl₂(CDCl₃)₄] and [1][Cl₂(CHBr₃)₄], the Cl⁻ ion interacts with two haloform molecules via C–D⋯Cl⁻ and C–H⋯Cl⁻ contacts, thus forming the negatively charged isostructural clusters [Cl(CDCl₃)₂]⁻ and [Cl(CHBr₃)₂]⁻. In the structures of [1][Cl₂(CH₂Cl₂)₂] and [1][Cl₂(C₂H₄Cl₂)₂], cations [1]²⁺ are linked to a 3D-network by a system of H-bondings including one formed by each Cl⁻ ion with CH₂Cl₂ or C₂H₄Cl₂ molecules. The lengths and energies of these H-bonds in the chloride–haloalkane clusters were analyzed by DFT calculations (M06 functional) including AIM analysis. The crystal packing noticeably affected the geometry of the clusters, and energy of C–H⋯Cl⁻ hydrogen bonds ranged from 1 to 6 kcal mol⁻¹. An exponential correlation (R² > 0.98) between the calculated Cl⁻⋯H distances and the energies of the corresponding contacts was found and used to calculate hydrogen bond energies from the experimental Cl⁻⋯H distances. Predicted energy values (3.3–3.9 kcal mol⁻¹ for the [Cl(CHCl₃)₂]⁻ cluster) are in a reasonable agreement with the energy of the Cl₃C–H⋯Cl⁻ bond estimated using ATRFTIR spectroscopy (2.7 kcal mol⁻¹).

---

1 Introduction

The research area of non-covalent interactions, including e.g. hydrogen bondings (HBs), has experienced enormous progress due to their implementation in supramolecular chemistry, crystal engineering, and structural biology.^1–6 In particular, relatively weak C–H⋯X⁻ HBs have been intensively studied both theoretically and experimentally^7–12 mostly because of their applications in asymmetric catalysis and design of artificial anion receptors.^13–15 Owing to the ubiquitous role of chloride ions in biological systems, C–H⋯Cl⁻ interactions are of special interest. Both aromatic and aliphatic C–H donors can be involved in such interactions^9,10,14,16 and, e.g., HBs are responsible for the formation of anionic clusters with methane and halomethane molecules [Cl(CH_xHal_4−x)_n]⁻ (n = 1–10); their existence was predicted theoretically and these clusters were also detected experimentally by mass-spectrometry.^17–19 Chloride–haloalkane clusters attract attention as useful models for studying both hydrogen and halogen bondings, and they are relevant for the construction of the potential energy surface of ion-molecular S_N2 reactions.^20–23 The structure and the stability of these clusters in the gas phase are widely studied by spectroscopic and theoretical methods.^7,8,16,17,24

Chloride ions are also known to form short contacts with various HB donors including haloalkane molecules (e.g. chloroform and dichloromethane) in the solid state. Although structural data on these C–H⋯Cl⁻ interactions are easily available from the CCDC database, they have rarely been studied^12,25,26 and, to our knowledge, in contrast to the gas phase, the energy of these HBs in the solid state has never been evaluated.

In the framework of our ongoing project on reactions of metal-bound substrates bearing C≡N bonds, we developed a synthetic procedure allowing the facile generation of cationic (1,3,5-triazapentadiene)Pt^II complexes having halides as counterions (Fig. 1).²⁷

Fig. 1 Graphical view of [1]Cl₂.

Upon crystallization, these cationic species are capable of forming crystal structures that easily incorporate solvent molecules (such as CHCl₃,²⁸ MeNO₂,²⁹ ROH,³⁰ or H₂O³¹) in a way that these complexes and their associates (e.g. halogen- or hydrogen bonded) can be studied by conventional X-ray crystallography supported by quantum-chemical calculations. In particular, crystallization of (1,3,5-triazapentadiene)Pt^II complexes from chloroform (or its mixtures with some other solvents) led to the formation of the anionic chloroform clusters [Cl(CHCl₃)_n]⁻ (n = 2, 3).²⁸ In continuation of that study, we employed four different halogenated solvents (deuterochloroform, bromoform, dichloromethane, and 1,2-dichloroethane) to obtain new solvates and used X-ray diffraction to explore the geometry of the formed chloride–haloalkane clusters. We also conducted quantum-chemical calculations to estimate the energy of intermolecular contacts.

A similar methodology was used in the studies of association of halides with various donors from both experimental^{18,19,32–34} and theoretical^16,18,24,35 viewpoints. We used this combined experimental and theoretical approach in the studies of halide–alcohol,³⁰ halide–nitromethane,²⁹ and chloride–chloroform²⁸ clusters in solvated platinum(II) complexes.

As a result of the present study, an exponential correlation was proposed between interatomic H⋯Cl⁻ distances and energies of the corresponding HBs. We also used ATRFTIR spectroscopy to experimentally assess the energy of C–H⋯Cl⁻ HBs in the clusters. All our results are discussed in sections that follow.

2 Results and discussion

Deuterochloroform, bromoform, dichloromethane, and 1,2-dichloroethane solvates, viz. [1][Cl₂(CDCl₃)₄], [1][Cl₂(CHBr₃)₄], [1][Cl₂(CH₂Cl₂)₂], and [1][Cl₂(C₂H₄Cl₂)₂], respectively, were obtained upon crystallization of [1]Cl₂ (Fig. 1) from the corresponding haloalkane. All these solvates were studied by single-crystal X-ray diffraction (Fig. S1–S4, Table S1, ESI†). Geometric parameters of [1]²⁺ in all four structures are similar to each other and are not unusual (Fig. 2 and Table S2, ESI†).^27–31

Fig. 2 View of [1]²⁺ in the structure of [1][Cl₂(CDCl₃)₄] with the atom numbering scheme. Only H atoms that are involved in the N–H/D⋯Cl⁻ and C–H/D⋯Cl⁻ HBs are shown; all other H atoms are omitted for clarity.

Depending on co-crystallized haloalkane these four complexes demonstrate different types of intermolecular contacts. In the next sections, we describe the structural features of the solvates obtained from X-ray diffraction experiments along with geometric characteristics of the optimized model clusters calculated using the DFT method. Then, we discuss the results of AIM analysis and compare the calculated energies of the observed chloride–haloalkane contacts with the experimental data on the thermal stability of the solvates and energies of the C–H/D⋯Cl⁻ bonds obtained using solid state ATRFTIR spectroscopy.

Structures of the deuterochloroform and bromoform solvates

In general, the systems of intermolecular HBs in the deuterochloroform and bromoform solvates are almost identical. As depicted in Fig. 3, in both cases the Cl⁻ anion is involved in five HBs giving rise to a distorted square-pyramidal environment. In both structures, two non-equivalent haloform molecules are bound to the same Cl⁻ giving the slightly asymmetric dimeric clusters [Cl(CDCl₃)₂]⁻ (Fig. 3, left) and [Cl(CHBr₃)₂]⁻ (Fig. 3, right).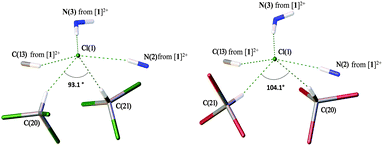

Fig. 3 Pyramidal environment of Cl⁻ in the structures of [1][Cl₂(CDCl₃)₄] (left) and [1][Cl₂(CHBr₃)₄] (right).

Deuterochloroform solvate [1][Cl₂(CDCl₃)₄] is structurally isotypic to the previously reported chloroform solvate [1][Cl₂(CHCl₃)₄].²⁸ According to the CCDC data, chloride is prone to forming short contacts with co-crystallized chloroform molecules and the formation of dimeric and even trimeric H-bonded clusters in the solid state is not unique (Fig. S7, ESI†). In contrast, chloride–bromoform clusters have never been previously identified and reported. In the dimeric chloride–chloroform clusters, the angle between two chloroform molecules varies in the range of 70–180°, and the majority of [Cl(CHCl₃)₂]⁻ clusters feature the ∠HClH angle in a more narrow interval of 70–110° (Fig. S8, ESI†). This is in a good agreement with the values observed for the studied solvates, i.e. 93.2° for [1][Cl₂(CHCl₃)₄], 93.1° for [1][Cl₂(CDCl₃)₄], and 104.1° for [1][Cl₂(CHBr₃)₄].

In the crystal structure of [1][Cl₂(CDCl₃)₄], the anionic [Cl(CDCl₃)₂]⁻ clusters are additionally linked to [1]²⁺ by two HBs via the Cl(6) atom (Fig. S5, ESI†). Although no such additional bonding was found in the crystal structure of [1][Cl₂(CHBr₃)₄] (Fig. S6, ESI†), both [1][Cl₂(CDCl₃)₄] and [1][Cl₂(CHBr₃)₄] demonstrate evident similarity of intermolecular packing giving rise to 2D-layered systems (Fig. 4). The HB geometric parameters for these solvates are summarized in Tables 1 and 2.

Fig. 4 A view of 2D layers running along the ab plane in the structures of [1][Cl₂(CDCl₃)₄] (left) and [1][Cl₂(CHBr₃)₄] (right).

Table 1 HB parameters for [1][Cl₂(CDCl₃)₄] [Å and °]

D–H⋯A	d(H⋯A)	d(D⋯A)	∠(DHA)
Symmetry transformations used to generate equivalent atoms: #1 x − 1/2, −y + 1/2, −z + 1.
N(2)–H(2N)⋯Cl(1)#1	2.56	3.385(2)	155.8
N(3)–H(3N)⋯Cl(1)	2.19	3.168(2)	175.3
C(20)–D(20)⋯Cl(1)	2.43	3.367(2)	156.8
C(21)–D(21)⋯Cl(1)	2.44	3.428(2)	167.5
C(13)–H(13)⋯Cl(1)	2.72	3.637(2)	160.5
C(2)–H(2)⋯Cl(6)#1	2.81	3.641(2)	146.1
C(16)–H(16A)⋯Cl(6)	2.95	3.665(2)	129.7

---

Table 2 HB parameters for [1][Cl₂(CHBr₃)₄] [Å and °]

D–H⋯A	d(H⋯A)	d(D⋯A)	∠(DHA)
Symmetry transformations used to generate equivalent atoms: #1 x − 1/2, −y + 1/2, −z + 1.
N(2)–H(2)⋯Cl(1)	2.71	3.537(6)	157.1
N(3)–H(3A)⋯Cl(1)#1	2.29	3.160(7)	168.1
C(13)–H(13)⋯Cl(1)#1	2.83	3.758(8)	165.3
C(20)–H(20)⋯Cl(1)	2.42	3.361(10)	155.5
C(21)–H(21)⋯Cl(1)	2.36	3.319(10)	160.0

---

Structure of the dichloromethane and dichloroethane clusters

Both solvates exhibit similar patterns of intermolecular interactions (Fig. 5), which are, in turn, noticeably different from those observed in haloform solvates [1][Cl₂(CHCl₃)₄], [1][Cl₂(CDCl₃)₄], and [1][Cl₂(CHBr₃)₄] (Fig. 3). In the crystal structures of [1][Cl₂(CH₂Cl₂)₂] and [1][Cl₂(C₂H₄Cl₂)₂], each Cl⁻ interacts with only one haloalkane molecule via HB, and complex systems of intermolecular HBs link cations [1]²⁺ into 3D-networks (Fig. S9 and S10, ESI†), which is strikingly different from the 2D-layered structure of the haloform solvates.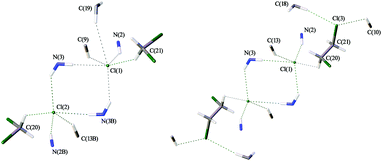

Fig. 5 The systems of HBs leading to the 3D-network of [1][Cl₂(CH₂Cl₂)₂] (left) and [1][Cl₂(C₂H₄Cl₂)₂] (right).

In the case of [1][Cl₂(CH₂Cl₂)₂], the system is asymmetric (Fig. 5, left). One of two chloride ions is involved in five HBs, including one C–H⋯Cl(1)⁻ contact with a CH₂Cl₂ molecule, three N–H⋯Cl⁻ HBs and a weak C–H⋯Cl⁻ HB. The second chloride is involved in six interactions forming an additional weak C–H⋯Cl⁻ HB (Table 3). In the case of [1][Cl₂(C₂H₄Cl₂)₂], the structure is symmetric and each chloride is involved in five HBs (Fig. 5, right). In contrast to [1][Cl₂(CH₂Cl₂)₂], each dichloroethane molecule in [1][Cl₂(C₂H₄Cl₂)₂] forms three weak HBs, viz. as a proton donor with the Cl⁻ anion and as a proton acceptor forming C–H⋯Cl(3) HBs with two neighboring complexes [1]²⁺ (Table 4).

Table 3 HB parameters for [1][Cl₂(CH₂Cl₂)₂] [Å and °]

D–H⋯A	d(H⋯A)	d(D⋯A)	∠(DHA)
Symmetry transformations used to generate equivalent atoms: #1 −x + 1, −y, −z + 1; #2 −x + 1, −y + 1, −z + 1; #3 −x + 2, −y + 1, −z + 1; #4 −x + 2, −y, −z + 1.
N(2B)–H(2B)⋯Cl(2)	2.47	3.323(7)	164.4
N(3B)–H(3B′)⋯Cl(1)#1	2.45	3.244(7)	150.1
N(3B)–H(3B′′)⋯Cl(2)#2	2.43	3.229(7)	151.8
N(2)–H(2)⋯Cl(1)	2.66	3.392(7)	141.1
N(3)–H(3′)⋯Cl(2)#3	2.46	3.220(7)	144.9
N(3)–H(3′′)⋯Cl(1)#4	2.40	3.226(7)	155.9
C(9)–H(9)⋯Cl(1)#4	2.79	3.595(9)	142.5
C(13B)–H(13B)⋯Cl(2)#2	2.89	3.741(10)	149.5
C(19)–H(19)⋯Cl(1)#4	2.91	3.840(8)	157.0
C(21)–H(21B)⋯Cl(1)	2.58	3.451(11)	146.4
C(20)–H(20B)⋯Cl(2)	2.58	3.313(11)	130.9

---

Table 4 HB parameters for [1][Cl₂(C₂H₄Cl₂)₂] [Å and °]

D–H⋯A	d(H⋯A)	d(D⋯A)	∠(DHA)
Symmetry transformations used to generate equivalent atoms: #1 −x, −y − 1, −z; #2 x, y − 1, z.
N(2)–H(2)⋯Cl(1)#1	2.52	3.343(9)	155.7
N(3)–H(3A)⋯Cl(1)#2	2.52	3.264(9)	142.2
N(3)–H(3B)⋯Cl(1)	2.57	3.389(10)	154.7
C(13)–H(13)⋯Cl(1)	2.82	3.685(11)	151.3
C(18)–H(18B)⋯Cl(3)	2.81	3.703(11)	150.3
C(10)–H(10)⋯Cl(3)#2	2.85	3.473(11)	124.1
C(20)–H(20A)⋯Cl(1)	2.83	3.423(12)	119.4

---

According to the CCDC data (Fig. S11, ESI†), CH₂Cl₂ similar to CHCl₃ forms a variety of H-bonded clusters with Cl⁻. Generally, the number of contacts that Cl⁻ can form in the solid state seems to be limited by steric factors and only rarely exceeds five (Fig. S7 and S11, ESI†). In the studied clusters, the haloform molecules (CHCl₃ and CHBr₃) form H-bonded dimers occupying two of five sites in the pyramidal environment of Cl⁻, which results in the 2D-layered structure of [1][Cl₂(CHCl₃)₄], [1][Cl₂(CDCl₃)₄], and [1][Cl₂(CHBr₃)₄]. By contrast, dichloromethane and dichloroethane molecules form only one HB and therefore each Cl⁻ can form an additional N(3)–H⋯Cl⁻ HB with the third complex [1]²⁺ leading to a 3D-network in the packing of [1][Cl₂(CH₂Cl₂)₂] and [1][Cl₂(C₂H₄Cl₂)₂]. Taking into account the plausible anticooperative character of HBs in such systems, the above effect might result from a difference in the relative stability of C–H⋯Cl⁻ contacts formed by Cl⁻ with haloalkane molecules in comparison with the N(3)–H⋯Cl⁻ interaction. Indeed, analysis of geometric characteristics (viz. H⋯Cl⁻ distances and C–H⋯Cl⁻ angles; Tables 1–4) of the C–H⋯Cl⁻ contacts indicates that haloform molecules (CHCl₃ and CHBr₃) form shorter and more linear bondings with the Cl⁻ ion than those formed by dichloroalkanes (CH₂Cl₂ and C₂H₄Cl₂).

This observation suggests that in the latter case the formed HBs are weaker (Scheme 1). This assumption is in accord with the lower CH acidity of CH₂Cl₂ and C₂H₄Cl₂ molecules in comparison with haloforms and was further confirmed by theoretical and experimental studies of HB geometries and energies in the solvates (see later).

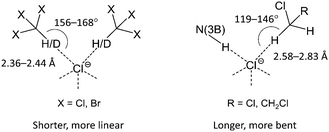Scheme 1 Haloform molecules (CHCl₃, CDCl₃, and CHBr₃) form shorter and more linear contacts with Cl⁻ than dichloroalkanes (CH₂Cl₂, C₂H₄Cl₂).

Quantum-chemical study of geometry and energy of HBs

All short contacts between Cl⁻ and various proton donor C and N atoms in the clusters are likely caused by HBs. However, some of these bonds are significantly non-linear and positions of the H atoms in the X-ray structures are inherently imprecise. In order to clarify the situation and quantitatively estimate the energies of Cl⁻⋯H contacts, we carried out theoretical DFT calculations combined with the topological analysis of the electron density distribution (AIM method).³⁶ The performed full geometry optimization procedure also allows the analysis of the geometrical features of these clusters in the gas phase.

We focused on the study of the isolated solvates [1]₂[Cl(CHCl₃)₂], [1]₂[Cl(CHBr₃)₂], [1]₃[Cl(CH₂Cl₂)], and [1]₃[Cl(C₂H₄Cl₂)] (see Fig. S12–S15, ESI†) because these systems contain all types of HBs that are discussed in the experimental part and constitute reasonable models from the viewpoint of computational costs. If the crystal packing effects are significant, the structures should change appreciably on going from the solid state to the gas phase, otherwise the short contacts (i.e. HBs) are expected to be preserved in the isolated form.³⁷

The results of our theoretical calculations are summarized in Table 5 and depicted in Fig. S12–S15 (ESI†). As can be inferred from comparison of the calculated parameters with the crystallographic data (Tables 1–4), optimized structures of the isolated complexes are in reasonable agreement with the structural data. In general, chloride anions form several HBs with the CH and NH moieties of [1]²⁺ and are involved in anticooperative C–H⋯Cl⁻ interactions with one or two solvent molecules. As expected, the exact calculated values of bond distances and angles are somewhat different from the experimental values (Table S3, ESI†). In several cases, calculations predict also a different number of contacts formed by each chloride (Fig. 6 and 7).

Table 5 Energies of Cl⁻⋯H/D–C contacts calculated from the Cl⁻⋯H/D distances

Solvate	Bond	d(Cl^−⋯H/D), Å	E ^acorr, kcal mol^−1
a Data adopted from ref. 28.
[1][Cl2(CHCl3)4]^a	C(20)–H(20)⋯Cl(1)	2.43	3.87
	C(21)–H(21)⋯Cl(1)	2.46	3.60
	C(13)–H(13)⋯Cl(1)	2.72	1.90
[1][Cl2(CDCl3)4]	C(20)–D(20)⋯Cl(1)	2.43	3.87
	C(21)–D(21)⋯Cl(1)	2.44	3.78
	C(13)–H(13)⋯Cl(1)	2.72	1.90
[1][Cl2(CHBr3)4]	C(13)–H(13)⋯Cl(1)#1	2.83	1.45
	C(20)–H(20)⋯Cl(1)	2.42	3.97
	C(21)–H(21)⋯Cl(1)	2.36	4.60
[1][Cl2(CH2Cl2)2]	C(9)–H(9)⋯Cl(1)#4	2.79	1.60
	C(13B)–H(13B)⋯Cl(2)#2	2.89	1.25
	C(19)–H(19)⋯Cl(1)#4	2.91	1.19
	C(21)–H(21B)⋯Cl(1)	2.58	2.68
	C(20)–H(20B)⋯Cl(2)	2.58	2.68
[1][Cl2(C2H4Cl2)2]	C(13)–H(13)⋯Cl(1)	2.82	1.49
	C(20)–H(20A)⋯Cl(1)	2.83	1.45

---

Fig. 6 Geometry of the [Cl(CHCl₃)₂]⁻ (left) and [Cl(CHBr₃)₂]⁻ (right) clusters according to DFT calculations (see Fig. 3 for comparison).

Fig. 7 Geometry of the Cl⁻ environment in [1]₃[Cl(CH₂Cl₂)] (left) and [1]₃[Cl(C₂H₄Cl₂)] (right) according to DFT calculations (see Fig. 5 for comparison).

In [1]₂[Cl(CHCl₃)₂], the Cl⁻⋯H–C(21)Cl₃ contact is elongated by 0.11 Å, whereas the other Cl⁻⋯H contacts are shortened (by 0.01–0.35 Å) as compared to the solid state structural data. In [1]₂[Cl(CHBr₃)₂], the Cl⁻⋯H–N(3)H, Cl⁻⋯H–C(19)H, and Cl⁻⋯H–C(20)Br₃ contacts are shortened (by 0.13–0.43 Å), whereas the length of the other short Cl⁻⋯H contacts remains virtually unchanged. Apart from that, two additional contacts, viz. Cl⁻⋯H–C(15)H and Cl⁻⋯H–C(19)H, were found in comparison with the solid state structure (Fig. 6). In [1]₃[Cl(CH₂Cl₂)], the Cl⁻⋯H–C(20)HCl₂, Cl⁻⋯H–N(3B)H, and Cl⁻⋯H–C(15)H bonds are elongated upon geometry optimization (by 0.07–0.42 Å), while other Cl⁻⋯H contacts are shortened (by 0.10–0.27 Å) or remain unchanged. Finally, for [1]₃[Cl(C₂H₄Cl₂)] we observed elongation of the Cl⁻⋯H–N(3′)H bond (by 0.07 Å) and shortening of the other contacts (by 0.07–0.41 Å). Thus, one can conclude that the crystal packing has a noticeable effect on the geometrical features of the studied clusters, while qualitatively all studied systems remain rather similar.

Topological analysis of the electron density distribution (AIM method)³⁶ of [1]₂[Cl(CHCl₃)₂], [1]₂[Cl(CHBr₃)₂], [1]₃[Cl(CH₂Cl₂)], and [1]₃[Cl(C₂H₄Cl₂)] indicates the low magnitude of the electron density, positive values of the Laplacian, and positive or very close to zero values of the energy density in appropriate bond critical points (3, −1) (Table S3, ESI†). All these values are typical for HBs.³⁸ We have defined the energies of the computed contacts according to the procedures proposed by Espinosa et al.³⁹ (E^a_bond) and Vener et al.⁴⁰ (E^b_bond), and some of them (i.e. one of the Cl⁻⋯H–CCl₃, Cl⁻⋯H–N(3)H, and Cl⁻⋯H–N(2) contacts in the [1]₂[Cl(CHCl₃)₂] cluster; Cl⁻⋯H–CBr₃ and Cl⁻⋯H–N(3)H contacts in the [1]₂[Cl(CHBr₃)₂] cluster; one of the Cl⁻⋯H–N(3)H contacts in [1]₃[Cl(CH₂Cl₂)] and [1]₃[Cl(C₂H₄Cl₂)] clusters) can be classified as HBs of moderate strength (4.04–8.47 kcal mol⁻¹) mainly due to electrostatic interactions following the classification by Jeffrey⁴¹ (“strong” H-bonds: 40–15 kcal mol⁻¹, “moderate” H-bonds: 15–4 kcal mol⁻¹, and “weak” H-bonds:<4 kcal mol⁻¹).

The other Cl⁻⋯H contacts are weak (0.94–3.14 kcal mol⁻¹) and determined mostly by dispersion and some electrostatic interactions. The balance between Lagrangian kinetic energy G(r) and potential energy density V(r) at the bond critical points (3, −1) can shed light on the nature of hydrogen bonds. If the ratio −G(r)/V(r) > 1 is satisfied, the nature of appropriate interaction is purely non-covalent (i.e. a combination of dispersion and electrostatic interactions);⁴² if −G(r)/V(r)<1, some covalent components are present. Based on this criterion, one can state that the covalent component is present only in “moderate” H-bonds and absent in cases of “weak” H-bonds (Table S3, ESI†). It is noteworthy that in the case of [1]₃[Cl(CH₂Cl₂)] we were unable to locate an appropriate bond critical point (3, −1) for Cl⁻⋯H–C(20)HCl₂ weak HB (Fig. 7, left). For [1]₃[Cl(C₂H₄Cl₂)], we found bond critical points (3, −1) corresponding to the three additional weak interactions, viz. Cl⁻⋯H–C(21)H, Cl⁻⋯H–C(15)H, and Cl⁻⋯H–C(6), that were not observed experimentally (Fig. 7, right).

Calculated energies of Cl⁻⋯H–C bonds were plotted against the lengths of Cl⁻⋯H contacts (see Fig. 8 for E^a_bond and Fig. S16, ESI† for E^b_bond). Data points were fitted by an exponential function, leading to the following equations:

E^a_bond = 1516.9 × e^{−2.457×d(Cl−⋯H)}, R² = 0.9849 (1)

E^b_bond = 539.3 × e^{−2.067×d(Cl−⋯H)}, R² = 0.9825 (2)

Fig. 8 The correlation between theoretically calculated Cl⁻⋯H distances (Å) and E^a_bond energies (kcal mol⁻¹) of the C–H/D⋯Cl⁻ contacts. Data points are taken from Table 5. Only the C–H/D⋯Cl⁻ contacts with appropriate bond critical points established by AIM analysis were considered.

As follows from the obtained correlations (1) and (2), the energies of the Cl⁻⋯H–C contacts exponentially decrease with growing Cl⁻⋯H distances. Good correlations (R² values exceeded 0.98) allowed the calculation of energies of all experimentally observed Cl⁻⋯H–C short contacts (Table 5). Calculated energy values using this approach (E^a_corr and E^b_corr) vary in the range of 1.19–4.60 kcal mol⁻¹, which is slightly lower than the values obtained for the Cl⁻⋯H–CCl₃ and Cl⁻⋯H–CBr₃ contacts using the AIM method (Table S3, ESI†).

The results of this theoretical study indicate that in the studied clusters the energy of the Cl⁻⋯H–C bonding significantly varies depending on the co-crystallized haloalkane. Being rather strong in the case of chloroform and bromoform (up to 4.4 and 6.0 kcal mol⁻¹, respectively), it drastically decreases in the case of dichloroethane (less than 1.9 kcal mol⁻¹). Moreover, in the case of dichloromethane, no HB was verified by AIM analysis. The results of our calculations also confirm the inequivalence of haloform molecules within the chloride–haloform dimeric clusters [Cl(CHX₃)₂]⁻ (X = Cl, Br) indicating a noticeable difference in energy and geometry of the Cl⁻⋯H–C bondings formed by each of the two molecules (Table S3, ESI† and Fig. 6).

Energies of C–H⋯Cl⁻ HBs in some chloride–haloalkane clusters in the gas phase have been previously assessed theoretically^7,16 and also measured experimentally.^43–45 According to the data summarized in Table 6, the energies vary from 4.7 to 19.5 kcal mol⁻¹ depending on chloromethane and the number of formed HBs. As can be inferred from the inspection of data compiled in Table 6, the energy of HBs within the clusters gradually decreases when the number of contacts is growing; this phenomenon is known as HB cooperativity/anticooperativity. One can expect that for the studied systems that involve up to 8 contacts per Cl⁻ (established by AIM analysis) the energy of an individual C–H⋯Cl⁻ bond should be markedly lower than experimentally determined energy for the isolated clusters in the gas phase (14.7 kcal mol⁻¹ for [Cl(CHCl₃)₂]⁻ and 14.8 kcal mol⁻¹ for [Cl(CH₂Cl₂)]⁻). The energy values obtained as a result of our theoretical study (from 1.45 kcal mol⁻¹ in [1][Cl₂(C₂H₄Cl₂)₂] to 4.60 kcal mol⁻¹ in [1][Cl₂(CHBr₃)₄]) agree with this assumption.

Table 6 Thermochemical and theoretically calculated values of C–H⋯Cl⁻ HB energies for the anionic clusters [Cl(CH_4−xCl_x)_n]⁻ (x = 1–3; n = 1–8) in the gas phase

Cluster	n	E(C–H⋯Cl^−), kcal mol^−1
		ΔHexp	ΔEcalc	ΔHcalc
a Ref. 18. b Ref. 45. c Ref. 43 .d Ref. 44.e Ref. 16.f Ref. 7.
[Cl(CHCl3)n]^−	1	−19.5 ± 0.2^a	−19.6^e	−19.6^e
		−19.1 ± 0.7^b
		−18.1^c^,^d
	2	−14.7 ± 0.2^a
	3	−11.8 ± 0.2^a
[Cl(CH2Cl2)n]^−	1	−14.8 ± 0.2^a	−15.3^e	−15.1^e
		−15.5^b	−18.24^f
		−15.8^d
	2	−13.1 ± 0.2^a
	3	−9.7 ± 0.2^a
	4	−9.0 ± 0.2^a
	5	−7.7 ± 0.2^a
[Cl(CH3Cl)n]^−	1	−11.7 ± 0.2^a	−11.5^e	−11.7^e
		−8.6^b	−13.82^f
		−12.2 ± 2.0^d
	2	−11.1 ± 0.2^a
	3	−8.4 ± 0.2^a
	4	−7.6 ± 0.2^a
	5	−6.2 ± 0.2^a
	6	−5.8 ± 0.2^a
	7	−4.8 ± 0.2^a
	8	−4.7 ± 0.2^a

---

ATRFTIR studies of the chloroform and dichloromethane solvates

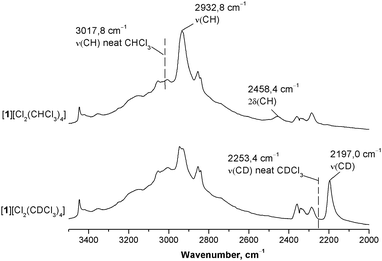
To quantitatively assess and compare the energy of C–H⋯Cl⁻ HBs in the chloroform and dichloromethane solvates we used ATRFTIR spectroscopy. It is well known that the formation of HBs by the CH group of CHCl₃ with medium–strong proton acceptors shifts the ν(CH) stretching band to lower frequencies and the δ(CH) band to higher frequencies, while intensities of both bands increase.^46,47 The value of the frequency shift increases with growth of the HB energy⁷ and thus can be used to assess it. In order to assign these bands in the IR spectrum of [1][Cl₂(CHCl₃)₄], we compared this spectrum with that of the CDCl₃ analog (see Fig. S17–S21, ESI†). As these two solvates are structurally isotypic, their IR spectra differ mainly in the position of ν(CH)/ν(CD) and δ(CH)/δ(CD) bands (Fig. 9 and Fig. S21, ESI†). In both spectra, a significant red shift of the ν(CH)/ν(CD) bands is observed as compared to the spectra of neat solvents (Δν of approx. 86 and 56 cm⁻¹ for CHCl₃ and CDCl₃, respectively) indicating the formation of medium-to-strong HBs.^2,48 Apart from that, the value of the isotope effect calculated as a ν(CH):ν(CD) ratio is lower in the case of the solvate than in the case of neat chloroform (1.335 and 1.340, respectively). Reduced values of the isotope effect are characteristic of the formation of HBs.^49,50 Thus, in [1][Cl₂(CHCl₃)₄] and [1][Cl₂(CDCl₃)₄], the IR spectra in combination with X-ray structures clearly indicate the formation of medium-to-strong HB between the CH group of CHCl₃ and Cl⁻. The resolution of the IR spectra did not allow the discrimination of two C–H⋯Cl⁻ bonds, which are non-equivalent according to both X-ray data and theoretical calculations.

Fig. 9 ATRFTIR spectra (3500–2000 cm⁻¹) of [1][Cl₂(CHCl₃)₄] and [1][Cl₂(CDCl₃)₄].

When discussing hydrogen bond spectroscopic and geometric parameters, one can rely heavily on the experimental data available. However, when discussing hydrogen bond energies, one is limited predominantly by the computational results, as direct measurement of H-bond energy values is a notoriously complicated task. To quantitatively evaluate the energy of the formed C–H⋯Cl⁻ hydrogen bonds, we applied the correlation reported by Wendler et al.:⁵¹

E(C–H⋯A) = 0.13 × Δν(CH) (3)

According to the proposed equation, the frequency shift (Δν) of 86 cm⁻¹ corresponds to the energy of approx. 2.7 kcal mol⁻¹. The application of computationally obtained correlation to our systems is justified by the fact that it gives energy values which are in a reasonable agreement with the estimates from AIM analysis for the isolated model complexes. Concerning the applicability of eqn (3) to the systems with multiple H-bonds, one should keep in mind that the changes in energy upon formation of multiple H-bonds are reflected by the spectroscopic parameters of individual H-bonds and the energy-spectroscopy correlation is likely to hold.

To estimate the energy of the C–H⋯Cl⁻ bond in the CH₂Cl₂ solvate, the same procedure was applied to [1][Cl₂(CH₂Cl₂)₂] and its deuterated analog [1][Cl₂(CD₂Cl₂)₂] (Fig. 10 and Fig. S22, ESI†). In this case, we were unable to identify bands corresponding to ν(CH) in the spectrum of [1][Cl₂(CH₂Cl₂)₂] and therefore the ν(CD) bands were used to evaluate the energy. As expected, an increase in intensity of both ν_as(CD) and ν_s(CD) bands was observed giving evidence for the involvement of CD₂Cl₂ in the formation of HBs. However, as seen from the comparison of the data given in Fig. 9 and 10, intensities of ν_as(CD) and ν_s(CD) bands in the spectrum of [1][Cl₂(CD₂Cl₂)₂] are much lower than that of the ν(CD) band in the spectrum of [1][Cl₂(CDCl₃)₄]. Moreover, both ν_as(CD) and ν_s(CD) bands are only slightly shifted (by 10–15 cm⁻¹) to lower frequencies as compared to the spectrum of neat CD₂Cl₂. These observations indicate that, in the studied systems, C–H⋯Cl⁻ HBs formed by CH₂Cl₂ are much weaker than in the case of CHCl₃, and the energy of the former contact estimated using eqn (3) is lower than 1 kcal mol⁻¹.

Fig. 10 ATRFTIR spectra (3500–2000 cm⁻¹) of [1][Cl₂(CH₂Cl₂)₂] and [1][Cl₂(CD₂Cl₂)₂].

In agreement with the results of quantum-chemical calculations, analysis of ATRFTIR data indicates that in [1][Cl₂(CH₂Cl₂)₂], dichloromethane is only weakly bound to Cl⁻. These results are also in good agreement with structural data that favor weaker interaction of CH₂Cl₂ and C₂H₄Cl₂ molecules with Cl⁻ as compared to that in [1][Cl₂(CDCl₃)₄] and [1][Cl₂(CHBr₃)₄].

3 Experimental

Synthesis

[1][Cl₂(CDCl₃)₄], [1][Cl₂(CHCl₃)₄], [1][Cl₂(CHBr₃)₄], [1][Cl₂(CH₂Cl₂)₂], [1][Cl₂(CD₂Cl₂)₂], and [1][Cl₂(C₂H₄Cl₂)₂] were obtained via the previously described procedure⁵² using CDCl₃, CD₂Cl₂, CHBr₃, or C₂H₄Cl₂ (that were used as received) and CHCl₃ or CH₂Cl₂ (freshly distilled) as solvents. The colorless crystalline precipitates were separated by filtration or decantation, washed with several portions of the corresponding solvent and kept under the layer of the solvent.

ATRFTIR spectroscopy

Attenuated total reflectance (ATR) FTIR spectra were recorded using a Nicolet 6700 Fourier-spectrometer equipped with a Smart iTR unit for single-bounce ATR with ZnSe crystals (the angle of incidence is 42°). A Ge/KBr beam splitter and a DTGS TEC detector were used to obtain spectra with 2 cm⁻¹ resolution in the range of 4000–575 cm⁻¹. The spectra of the pure crystal were used as a reference and these spectra were analyzed without any correction.

X-ray structure determinations

The crystals of all complexes were immersed in cryo-oil, mounted in a Nylon loop, and measured at a temperature of 100 K. The X-ray diffraction data were collected on a Nonius KappaCCD, Bruker Kappa Apex II, or Bruker Smart Apex II diffractometer using Mo Kα radiation (λ = 0.71073 Å). The Denzo-Scalepack⁵³ or APEX2⁵⁴ software packages were used for cell refinements and data reductions. The structures were solved either by direct methods using the SHELXS-97⁵⁵ or SIR-97⁵⁶ software or by the charge flipping method using superflip program with the Olex2⁵⁷ graphical user interface. A semi-empirical absorption correction (SADABS)⁵⁸ was applied to all data. Structural refinements were carried out using SHELXL-97.⁵⁵ In [1][Cl₂(CHBr₃)₄], the Br atoms of one of the CHBr₃ solvent molecules were disordered over two sites with occupancies of 0.82 and 0.18. The disordered Br atoms were restrained so that their U_ij components approximate to isotropic behavior. Also, in [1][Cl₂(C₂H₄Cl₂)₂], the C5 and C6 atoms were restrained so that their U_ij components approximate to isotropic behavior. In [1][Cl₂(CDCl₃)₄] and [1][Cl₂(CH₂Cl₂)₂], the NH and NH₂ hydrogen atoms were located from the difference Fourier map but constrained to ride on their parent atom, with U_iso = 1.5U_eq (parent N-atom). Other hydrogen atoms were positioned geometrically and constrained to ride on their parent atoms, with C–H = 0.95–0.99 Å, N–H = 0.88 Å, and U_iso = 1.2U_eq (parent atom). The crystallographic details are summarized in Table S1 (ESI†).

Computational details

The full geometry optimization of [1]₂[Cl(CHCl₃)₂], [1]₂[Cl(CHBr₃)₂], [1]₃[Cl(CH₂Cl₂)], and [1]₃[Cl(C₂H₄Cl₂)] has been carried out at the DFT level of theory using the M06 functional⁵⁹ with the help of the Gaussian-09⁶⁰ program package. The experimental X-ray geometries were used as starting points for the theoretical optimization procedure. The calculations were carried out using a quasi-relativistic Stuttgart pseudopotential that described 60 core electrons and the appropriate contracted basis set⁶¹ for the platinum atoms and the 6-31G(d) basis set for other atoms. The M06 functional is much less time-consuming than the MP2 method used by us previously;^28,29 at the same time, the M06 functional describes reasonably weak dispersion forces and non-covalent interactions.^62,63 No symmetry operations have been applied. The Hessian matrix was calculated analytically to prove the location of correct minima (no imaginary frequencies). The topological analysis of the electron density distribution with the help of the atoms in molecules (AIM) method developed by Bader has been performed by using the Multiwfn program (version 3.3.4).⁶⁴

4 Final remarks

As shown by this and the previous studies,^28–31 various (1,3,5-triazapentadiene)M^II complexes represent a simple and useful system allowing the study of non-covalent anion interactions by conventional X-ray diffraction supported by theoretical calculations. Since C–H⋯Cl⁻ hydrogen bonds are of special interest, we used the (1,3,5-triazapentadiene)Pt^II system to study weak interactions of Cl⁻ with four different haloalkanes, viz. CDCl₃, CHBr₃, CH₂Cl₂, and C₂H₄Cl₂. We found that in the case of CDCl₃ and CHBr₃, similar to CHCl₃,²⁸ each chloride anion interacts with two haloform molecules giving the negatively charged clusters [Cl(CHX₃)₂]⁻, whereas in the cases of weaker HB donors CH₂Cl₂ and C₂H₄Cl₂, only one C–H⋯Cl⁻ contact was observed between Cl⁻ and the co-crystallized chloroalkane.

Although C–H⋯Cl⁻ HBs formed by chloroform and dichloromethane molecules are relatively well known and many examples (albeit unprocessed in a vast majority of cases) of such interactions can be retrieved from the CCDC database, C–H⋯Cl⁻ hydrogen bonds formed by CHBr₃ and C₂H₄Cl₂ molecules are far less studied. Only nine examples of C–H⋯Cl⁻ contacts involving dichloroethane molecule were retrieved from the Cambridge Crystallographic Database (Table S5, ESI†), and no such interactions were detected for bromoform meaning that the chloride–bromoform clusters [Cl(CHBr₃)₂]⁻ are the first example of such interactions reported in the literature.

In the case of chloroform, bromoform, and dichloroethane solvates, the existence of C–H⋯Cl⁻ HBs was further confirmed by theoretical analysis (AIM method). Energy of the observed C–H⋯Cl⁻ HBs was assessed both theoretically by the AIM method and experimentally using IR spectroscopy and these energies vary in the range of 1–6 kcal mol⁻¹. The combined theoretical (AIM method) and ATRFTIR study revealed that, in the chloride–haloalkane clusters, dichloromethane and dichloroethane form significantly weaker C–H⋯Cl⁻ HBs than haloform molecules (CHCl₃, CDCl₃, and CHBr₃). These results are in accord with the X-ray data and shed light on the drastic difference in the intermolecular packing between the 2D-layered structure of haloform solvates and 3D-networks observed for [1][Cl₂(CH₂Cl₂)₂] and [1][Cl₂(C₂H₄Cl₂)₂].

In this work, we used multidisciplinary combined and complementary experimental and theoretical approaches that allow bypassing certain limitations of the X-ray diffraction method in the studies of hydrogen bond systems, viz. inability of accurate evaluation of H-bond energies. We proposed the exponential correlation (R² > 0.98) between the calculated Cl⁻⋯H distances and the energies of the corresponding contacts. This correlation can be used to obtain hydrogen bond energies from the crystallographically predicted Cl⁻⋯H distances without the additional involvement of resource- and time-consuming quantum-chemical calculations. We also found another correlation, viz. between spectroscopic observables and energies of individual H-bonds in systems with multiple cooperatively or anti-cooperatively coupled H-bonds. It is believed that these correlations should be beneficial for both crystallography and physical chemistry communities.

Acknowledgements

TVS is grateful to Saint Petersburg State University for the postdoctoral fellowship (12.50.1560.2013). PVG, ASN, and VYK thank Russian Foundation for Basic Research for support of their studies (grants 15-03-01563, 16-33-60063, and 16-03-00441). ATRFTIR studies were performed at the Center for Geo-Environmental Research and Modeling (GEOMODEL) of Research Park of Saint Petersburg State University within the framework of Russian Foundation for Basic Research grant 14-03-00111 (PMT and REA). The authors are grateful to Prof. Dr A. G. Starikov (Southern Scientific Center of Russian Academy of Sciences, Rostov-on-Don, Russian Federation) for providing computational facilities and also for valuable comments. We also thank Prof. Dr E. S. Shubina for useful advices and helpful discussion.

Notes and references

1. G. Desiraju and T. Steiner, The Weak Hydrogen Bond: In Structural Chemistry and Biology, Oxford University Press, 2001.
2. J. Joseph and E. D. Jemmis, J. Am. Chem. Soc., 2007, 129, 4620–4632.
3. K. Choi and A. D. Hamilton, Coord. Chem. Rev., 2003, 240, 101–110.
4. P. A. Gale, S. E. García-Garrido and J. Garric, Chem. Soc. Rev., 2008, 37, 151–190.
5. P. A. Gale and R. Quesada, Coord. Chem. Rev., 2006, 250, 3219–3244.
6. H. J. Schneider, Angew. Chem., Int. Ed., 2009, 48, 3924–3977.
7. E. S. Kryachko and T. Zeegers-Huyskens, J. Phys. Chem. A, 2002, 106, 6832–6838.
8. B. Nepal and S. Scheiner, Chem. – Eur. J., 2015, 21, 1474–1481.
9. V. S. Bryantsev and B. P. Hay, J. Am. Chem. Soc., 2005, 127, 8282–8283.
10. C. Coletti and N. Re, J. Phys. Chem. A, 2009, 113, 1578–1585.
11. B. P. Hay and R. Custelcean, Cryst. Growth Des., 2009, 9, 2539–2545.
12. L. Brammer, E. A. Bruton and P. Sherwood, Cryst. Growth Des., 2001, 1, 277–290.
13. Y. Li and A. H. Flood, Angew. Chem., Int. Ed., 2008, 47, 2649–2652.
14. J. Cai and J. L. Sessler, Chem. Soc. Rev., 2014, 43, 6198–6213.
15. O. B. Berryman, A. C. Sather, B. P. Hay, J. S. Meisner and D. W. Johnson, J. Am. Chem. Soc., 2008, 130, 10895–10897.
16. L. Pedzisa and B. P. Hay, J. Org. Chem., 2009, 74, 2554–2560.
17. Z. M. Loh, R. L. Wilson, D. A. Wild, E. J. Bieske and M. S. Gordon, J. Phys. Chem. A, 2005, 109, 8481–8486.
18. K. Hiraoka, T. Mizuno, T. Iino, D. Eguchi and S. Yamabe, J. Phys. Chem. A, 2001, 105, 4887–4893.
19. S. Denifl, F. Zappa, I. Maehr, A. Mauracher, M. Probst, T. D. Maerk and P. Scheier, J. Am. Chem. Soc., 2008, 130, 5065–5071.
20. I. Szabó and G. Czakó, J. Phys. Chem. A, 2015, 119, 3134–3140.
21. E. J. Bieske and O. Dopfer, Chem. Rev., 2000, 100, 3963–3998.
22. J. Xie, R. Otto, J. Mikosch, J. Zhang, R. Wester and W. L. Hase, Acc. Chem. Res., 2014, 47, 2960–2969.
23. D. A. Wild and E. J. Bieske, Int. Rev. Phys. Chem., 2003, 22, 129–151.
24. P. Botschwina, R. Oswald and V. Dyczmons, Int. J. Mass Spectrom., 2007, 267, 308–314.
25. X. Xie and R. E. McCarley, Inorg. Chem., 1997, 36, 4011–4016.
26. G. Espino, F. A. Jalón, B. R. Manzano, M. Pérez-Manrique, K. Mereiter and D. Quiñonero, Supramol. Chem., 2012, 24, 787–798.
27. P. V. Gushchin, M. R. Tyan, N. A. Bokach, M. D. Revenco, M. Haukka, M.-J. Wang, C.-H. Lai, P.-T. Chou and V. Y. Kukushkin, Inorg. Chem., 2008, 47, 11487–11500.
28. P. V. Gushchin, G. L. Starova, M. Haukka, M. L. Kuznetsov, I. L. Eremenko and V. Y. Kukushkin, Cryst. Growth Des., 2010, 10, 4839–4846.
29. P. V. Gushchin, M. L. Kuznetsov, Q. Wang, A. A. Karasik, M. Haukka, G. L. Starova and V. Y. Kukushkin, Dalton Trans., 2012, 41, 6922.
30. P. V Gushchin, M. L. Kuznetsov, M. Haukka and V. Y. Kukushkin, J. Phys. Chem. A, 2014, 118, 9529–9539.
31. M. N. Kopylovich, E. A. Tronova, M. Haukka, A. M. Kirillov, V. Y. Kukushkin, J. J. R. Fraústo Da Silva and A. J. L. Pombeiro, Eur. J. Inorg. Chem., 2007, 4621–4627.
32. W. H. Robertson, E. G. Diken, E. A. Price, J.-W. Shin and M. A. Johnson, Science, 2003, 299, 1367–1372.
33. K. Giles and E. P. Grimsrud, J. Phys. Chem., 1993, 97, 1318–1323.
34. D. a Wild, K. T. Kuwata, C.-K. Wong, J. D. Lobo, A. Deev, T. S. Schindler, M. Okumura and E. J. Bieske, J. Phys. Chem. A, 2010, 114, 4762–4769.
35. D. A. Wild and T. Lenzer, Phys. Chem. Chem. Phys., 2004, 6, 5122–5132.
36. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990.
37. A. A. Melekhova, A. S. Novikov, K. V. Luzyanin, N. A. Bokach, G. L. Starova, V. V. Gurzhiy and V. Y. Kukushkin, Inorg. Chim. Acta, 2015, 434, 31–36.
38. I. Rozas, I. Alkorta and J. Elguero, J. Am. Chem. Soc., 2000, 122, 11154–11161.
39. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
40. M. V. Vener, A. N. Egorova, A. V. Churakov and V. G. Tsirelson, J. Comput. Chem., 2012, 33, 2303–2309.
41. G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, Oxford, 1997.
42. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529.
43. K. E. Sahlstrom, W. B. Knighton and E. P. Grimsrud, J. Phys. Chem. A, 1997, 101, 1501–1508.
44. J. W. Larson and T. B. McMahon, J. Am. Chem. Soc., 1984, 106, 517–521.
45. R. C. Dougherty, J. Dalton and J. David roberts, Org. Mass Spectrom., 1974, 8, 77–79.
46. K. S. Rutkowski, S. M. Melikova, R. E. Asfin, B. Czarnik-Matusewicz and M. Rospenk, J. Mol. Struct., 2014, 1072, 32–37.
47. K. S. Rutkowski, A. Karpfen, S. M. Melikova, W. A. Herrebout, A. Koll, P. Wolschann and B. J. van der Veken, Phys. Chem. Chem. Phys., 2009, 11, 1551–1563.
48. N. S. Golubev, G. S. Denisov, S. Macholl, S. N. Smirnov, I. G. Shenderovich and P. M. Tolstoy, Z. Phys. Chem., 2008, 222, 1225–1245.
49. D. C. Daniel and J. L. Mchale, J. Phys. Chem. A, 1997, 101, 3070–3077.
50. A. Nowak, Large Molecules – Structure and Bonding, 1974, vol. 18, pp. 177–216.
51. K. Wendler, J. Thar, S. Zahn and B. Kirchner, J. Phys. Chem. A, 2010, 114, 9529–9536.
52. P. V Gushchin, M. L. Kuznetsov, M. Haukka, M. Wang, A. V Gribanov and V. Y. Kukushkin, Inorg. Chem., 2009, 48, 2583–2592.
53. Z. Otwinowski and W. Minor, in Methods in Enzymology, Macromolecular Crystallography, Part A, ed. C. W. Carter and J. Sweet, Academic Press, New York, USA, 1997, vol. 276, pp. 307–326.
54. APEX2 - Software Suite for Crystallographic Programs, Bruker AXS, Inc., Madison, WI, USA, 2009.
55. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
56. A. Altomare, M. C. Burla, M. Camalli, G. L. Cascarano, C. Giacovazzo, A. Guagliardi, A. G. G. Moliterni, G. Polidori and R. Spagna, J. Appl. Crystallogr., 1999, 32, 115–119.
57. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
58. G. M. Sheldrick, SADABS - Bruker AXS scaling and absorption correction, Bruker AXS, Inc., Madison, Wisconsin, USA, 2008.
59. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
60. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. J. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013.
61. D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141.
62. L. A. Burns, A. Vázquez-Mayagoitia, B. G. Sumpter and C. D. Sherrill, J. Chem. Phys., 2011, 134, 084107.
63. M. Sumimoto, Y. Kawashima, D. Yokogawa, K. Hori and H. Fujimoto, Int. J. Quantum Chem., 2013, 113, 272–276.
64. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.

---

Footnote

† Electronic supplementary information (ESI) available: Crystallographic data and additional ATRFTIR spectra. CCDC 1401547–1401550. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6cp00861e

---