Open Access Article
Open Access ArticleTuning of dye optical properties by environmental effects: a QM/MM and experimental study†
Gianluca
Del Frate
a,
Fabio
Bellina
b,
Giordano
Mancini
a,
Giulia
Marianetti
a,
Pierpaolo
Minei
b,
Andrea
Pucci
 b and
Vincenzo
Barone
*a
b and
Vincenzo
Barone
*a
aScuola Normale Superiore, Piazza dei Cavalieri 7, I-56126 Pisa, Italy. E-mail: vincenzo.barone@sns.it
bDipartimento di Chimica e Chimica Industriale, Università di Pisa, via Moruzzi 13, I-56124 Pisa, Italy
First published on 10th March 2016
Abstract
The present work is aimed at a deeper investigation of two recently synthesized heteroaromatic fluorophores by means of a computational multilayer approach, integrating quantum mechanics (QM) and molecular mechanics (MM). In particular, dispersion of the title dyes in a polymer matrix is studied in connection with potential applications as photoactive species in luminescent solar concentrators (LSCs). Molecular dynamics simulations, based on accurate QM-derived force fields, reveal increased stiffness of these organic dyes when going from CHCl3 solution to the polymer matrix. QM/MM computations of UV spectra for snapshots extracted from MD simulations show that this different flexibility permits explaining the different spectral shapes obtained experimentally for the two different environments. Moreover, the general spectroscopic trends are reproduced well by static computations employing a polarizable continuum description of environmental effects.
1 Introduction
Commodity materials based on thermoplastic polymers derived from oil or renewable resources are everyday expanding their range of applications, thanks to their excellent thermo-mechanical properties, chemical stability, easy processing, sustainability and low cost.1 A new class of materials is nowadays even more rapidly evolving due to the development of modern technologies that require combinations of properties. This great interest towards functional materials has driven a wide investigation on the design and development of new “intelligent” systems with unique mechanical and optical properties.2–4 Several specific features can be finely tuned by an appropriate combination of a polymeric matrix with different molecular entities, by means of dispersion5 or covalent functionalization.6,7 Such materials can be envisaged as stimuli responsive devices, which can find widespread applications in various fields.8,9 Many external factors, such as pressure, temperature, pH, viscosity or radiation, can in fact, alter the system's response.10 Owing to these characteristics, optical responsive materials can be exploited in renewable energy technologies; over the last three decades increasing interest has been devoted to light harvesting devices. Recent findings on global warming11 and nonrenewable energy resources have stimulated increasing interest towards the employment of alternative ways for energy. Sunlight stands indeed as an ideal asset that can be taken advantage of. Luminescent solar concentrators (LSCs) represent a way to decrease the cost of solar photovoltaics.12 LSCs consist of a fluorescent dye dispersed in a thin slab of polymeric material. Upon solar irradiation, a fraction of the emitted light is collected at the edges of the device where photovoltaic cells are located.13 Organic fluorescent dyes bearing π-conjugated electron-donor and electron-acceptor moieties exhibit intra-molecular charge-transfer (ICT)14 properties, and can therefore show the optical properties required by LSCs, such as high quantum yield and large Stokes shift.15Selection of the best molecular structure for such applications is not easily driven by a strategy based on experimental data alone, which can be very approximate. Therefore, computational modeling finds increasing use to carry out systematic studies aimed to gain a deeper understanding of the chemical–physical properties responsible for the experimental optical features. As a matter of fact, computational approaches nowadays allow simulation of spectral shapes at a very reasonable cost and with good results.16 It is therefore not surprising that many and different computational methods, aimed at the reproduction of photophysical properties of organic probes dispersed in – or covalently bounded to – several environments,17–21 have been recently reported: such methods, trying to reveal subtle phenomena that take place at the atomic level, hard to detect by means of experimental techniques alone, are becoming an invaluable tool to support experiments. However, the modeling of environmental effects, is often a crucial step, and it needs to be taken into account in order to correctly describe the photophysics of a target molecule: charge density can rearrange as a consequence of the electric field generated by the surrounding environment. Moreover, the conformational equilibrium of flexible molecules is often strongly tuned by solvent effects. Unfortunately, it is still arduous to treat the solvent using very accurate quantum mechanical (QM) calculations, because of the computational cost of including a large reservoir of molecules constituting the environment. For these reasons, during the last few decades different approaches have been developed to deal with solvation, ranging from implicit methods, such as the so-called Polarizable Continuum Models (PCM),22 to more demanding procedures, such as Monte Carlo (MC), and both classical and ab initio molecular dynamics (MD) simulations, which explicitly feature solvent molecules in their spatial coordinates.23–27
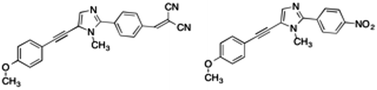
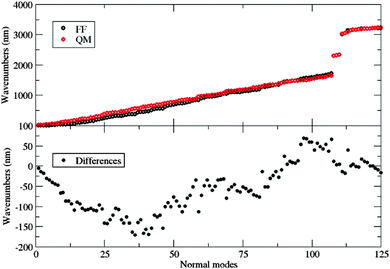
In a previous work,28 a new class of alkynylimidazole-based fluorophores has been studied as promising luminescent dyes in LSCs. UV-Vis spectra of these molecules in tetrahydrofuran (THF) solution as well as in a poly(methyl methacrylate) (PMMA) thin film were experimentally determined, suggesting an enhanced rigidity of the investigated fluorophores in the polymer matrix. Absorption spectra were simulated in good agreement with experimental data, using the CAM-B3LYP long-range corrected hybrid density functional, in conjunction with the PCM to take bulk environmental effects into account. Moreover, a fast and reliable computational protocol was developed to simulate absorption and emission spectra of such luminescent species when dispersed in the rigid, polymeric environment: starting from the ground-state energy minimum, the main dihedral angle (i.e., the one between the phenyl and the imidazole moieties) was fixed at its ground-state value during the excitation (mimicking in such a way the caging effects of the hydrophobic bundle), while all other internal coordinates have been relaxed. As already stated, bulk electrostatic effects were taken into account by the PCM. As is well known, PCM offers the unquestionable advantage of providing an overall and reliable description of the surrounding environment, which is mainly characterized by its dielectric constant. However, the continuum method fails in the treatment of specific solute–solvent interactions, which depend on the spatial coordinates of the two interacting components.29 For this reason, in the present study, a recently developed protocol21 was applied to address with improved accuracy the description of the polymeric bundle, and compared to the cheaper “static” approach described above in the reproduction of spectroscopic properties. The proposed approach involves computational methodologies ranging from MD simulations, based on accurate force fields (FF), to full QM calculations, and explicitly simulating the surrounding solvent (the PMMA matrix, in this study). As is well known, FF based simulations manage to mimic the dyes in a realistic environment, and follow the time-evolution of the whole system to its most likely configurations over time scales longer than 100 ns. However, since variations in the chromophore's structure significantly affect the computation of its spectroscopic properties, highly accurate and reliable FF parameters are required. For this reason the FF parameterization of the dye used in this work was performed using JOYCE,30,31 and all the intra-molecular parameters needed to describe the chromophore in its ground state were specifically derived from QM calculations by fitting optimized energies, gradients and Hessian matrices. Two different alkynylimidazole-based fluorophores bearing a different electron withdrawing group were investigated for their potential application in LSCs, namely the novel 5-((4-dicyanovinyl)ethynyl)-1-methyl-2-(4-nitrophenyl)-1H-imidazole, a, and the already reported25 5-((4-methoxy)ethynyl)-1-methyl-2-(4-nitrophenyl)-1H-imidazole, b (Fig. 1). Alkynylimidazoles a and b were prepared according to a simple reaction sequence, starting from 1-methyl-1H-imidazole.
Evidence for the reduced flexibility of these organic dyes when dispersed in a polymeric bundle is gathered by comparison with chloroform solution, employing classical MD simulations. Then, attention is focused on reproducing absorption spectra in PMMA, and, in particular, on the comparison between different representations of the polymeric environment during such spectroscopic calculations.
2 Experimental section
2.1 Materials
Melting points were recorded on a hot-stage microscope (Reichert Thermovar). NMR spectra were recorded at room temperature at 400 MHz (1H) and 100 MHz (13C) and were referenced to TMS or the residual solvent's signal. All reactions were performed under an argon flow. 1-Methyl-1H-imidazole was purified by distillation at reduced pressure. N-Bromosuccinimide (NBS) was purified by crystallization from water. All other commercially available reagents and solvents were used as received. 5-((4-Methoxyphenyl)ethynyl)-1-methyl-2-(4-nitrophenyl)-1H-imidazole (b) was prepared and characterized as reported in our previous work. Poly(methylmethacrylate) (PMMA, Aldrich, Mw = 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, acid number < 1 mg KOH per g) density = 1.17 g mL−1 (T = 25 °C).
000 g mol−1, acid number < 1 mg KOH per g) density = 1.17 g mL−1 (T = 25 °C).
2.2 4-(1-Methyl-1H-imidazol-2-yl)benzaldehyde
A modification of the literature procedure for the Pd- and Cu-mediated C-2 direct arylation of 1-substituted-1H-imidazole with aryl bromides was adopted.32,33 A solution of 1-methyl-1H-imidazole (3.75 mmol, 82.1 mg, 300 μL), Pd(OAc)2 (28 mg, 0.05 mmol), CuI (952 mg, 5 mmol), CsOAc (960 mg, 5 mmol) and 4-bromobenzaldehyde (463 mg, 2.5 mmol) in DMA (15 mL) was stirred at 110 °C for 72 h. After cooling to room temperature, the reaction mixture was diluted with AcOEt (100 mL) and poured into a saturated aqueous NH4Cl solution (100 mL). NH4OH (5 mL) was added and the resulting mixture was stirred in open air for 0.5 h, then extracted with AcOEt (3 × 20 mL). The collected organic extracts were washed with water (2 × 20 mL), dried over anhydrous Na2SO4, and concentrated under reduced pressure. The crude reaction product was purified by flash chromatography on silica gel using EtOAc as an eluent to give 4-(1-methyl-1H-imidazol-2-yl)benzaldehyde as a yellow solid (206 mg, 44% yield): m.p. 43–44 °C. 1H NMR (400 MHz, CDCl3): δ = 10.04 (s, 1H), 7.95 (m, 2H), 7.82 (m, 2H), 7.16 (d, J = 1.2 Hz, 1H), 7.02 (d, J = 1.2 Hz, 1H), 3.80 (s, 3H). 13C NMR (100 MHz, CDCl3): δ = 191.7, 146.3, 136.2, 135.9, 129.1 (2C), 128.9, 128.8 (2C), 123.3, 34.8 ppm. MS (EI) m/z (%): 187 (12), 186 (100), 185 (95), 157 (23), 156 (20).2.3 4-(5-((4-Methoxyphenyl)ethynyl)-1-methyl-1H-imidazol-2-yl)benzaldehyde
According to our recently reported procedure,34 NBS (140 mg, 0.39 mmol) was added in one portion to a solution of 4-(1-methyl-1H-imidazol-2-yl)benzaldehyde (142 mg, 0.8 mmol) in DMF (8 mL), and the resulting mixture was stirred in the dark at room temperature for 12 h. Then, Pd(PPh3)2Cl2 (12 mg, 0.016 mmol, 2 mol%), CuI (6 mg, 0.032 mmol, 4 mol%), 4-ethynylanisole (200 μL, 1.5 mmol), and piperidine (240 μL, 2.4 mmol) were sequentially added under a stream of argon. The resulting reaction mixture was stirred at 80 °C for 4 h, then cooled to room temperature and treated with EtOAc (50 mL) and saturated aqueous NH4Cl (50 mL). The resulting biphasic mixture was stirred for 30 minutes in open air, then extracted with EtOAc (3 × 10 mL). The organic extracts were collected, washed with water (3 × 10 mL) and brine (10 mL), dried over anhydrous Na2SO4, filtered and concentrated under reduced pressure. The crude reaction product was purified by flash chromatography on silica gel using a mixture of toluene and AcOEt (6/4) as an eluent, to give the title compound as a pale orange solid (125 mg, 52% yield): m.p. 119–121 °C. 1H NMR (400 MHz, CDCl3): δ = 10.10 (s, 1H), 8.02 (m, 2H), 7.91 (m, 2H), 7.49 (m, 2H), 7.47 (s, 1H) ppm, 6.93 (m, 2H), 3.89 (s, 3H), 3.87 (s, 3H). 13C NMR (100 MHz, CDCl3): δ = 191.7, 160.3, 146.8, 136.4, 135.8, 134.1, 132.9 (2C), 130.2 (2C), 128.7 (2C), 119.3, 114.6, 114.0 (2C), 97.5, 76.2, 55.4, 33.3 ppm. MS (EI) m/z (%): 317 (23), 316 (100), 315 (29), 207 (10).2.4 5-((4-Methoxyphenyl)ethynyl)-1-methyl-2-(4-dicyanovinylphenyl)-1H-imidazole (a)
According to a literature procedure,35 4-(5-((4-ethoxyphenyl)ethynyl)-1-methyl-1H-imidazol-2-yl)benzaldehyde (64 mg, 0.2 mmol) was reacted with malononitrile (20 mg, 0.3 mmol) in EtOH (7 mL) and a catalytic amount (5 drops) of triethylamine. The reaction mixture was stirred at room temperature for 12 h, then concentrated under reduced pressure to obtain the required product as a bright orange powder (60 mg, 83% yield): m.p. 158–159 °C. 1H NMR (400 MHz, CDCl3): δ = 8.04 (m, 2H), 7.93 (m, 2H), 7.82 (s, 1H), 7.50 (m, 2H), 7.48 (s, 1H), 6.93 (m, 2H), 3.92 (s, 3H), 3.87 (s, 3H). 13C NMR (100 MHz, CDCl3): δ = 160.2, 158.8, 146.0, 134.3, 133.0 (2C), 131.1 (2C), 130.7, 129.0 (2C), 120.0, 114.2 (2C), 113.7 (2C), 112.6, 108.8, 97.9, 83.0, 75.9, 55.4, 33.4 ppm. MS (EI) m/z (%): 365 (30), 364 (100), 349 (23), 281 (38), 208 (18), 207 (61).2.5 Preparation of polymer films for optical studies
Different dye/PMMA thin films were prepared by drop casting, i.e. pouring a 0.8 mL chloroform solution containing 30 mg of the polymer and the proper amount of dye to obtain concentrations in the range of 0.05–2.2 wt% over a 35 × 50 mm area of a glass surface. The glass slides were cleaned with chloroform and immerged in 6 M HCl for at least 12 h, then they were rinsed with water, acetone and isopropanol and dried for 8 h at 120 °C. Solvent evaporation was performed on a warm hot plate (about 30 °C) and in a closed environment. The film thickness was measured by a Starrett micrometer to be 25 ± 5 microns.3 Computational details
3.1 General approach
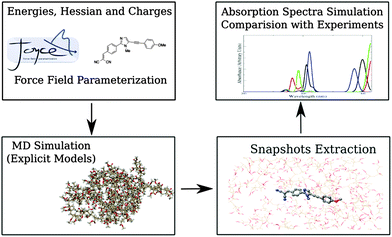
The applied computational protocol (sketched in Fig. 2), already tested in previous studies,21,23 can be summarized as follows:(1) QM calculations are performed to sample the conformational space of the considered dyes to find their global minimum. Energies, first and second derivatives, are computed, together with CM536 point charges. Next, partial geometry optimizations are performed, constraining specific internal coordinates at selected values, in order to describe soft degrees of freedom (i.e., flexible dihedrals). The obtained data are then used to optimize FF parameters.
(2) Reliable models for both PMMA and CHCl3 are built, by means of MM methods using FF parameters taken from the literature. MD simulation of the fluorophores in the two different considered environments (i.e., in the real sized polymer matrix and in CHCl3 solution) are then performed and analyzed.
(3) Sufficient number of statistically uncorrelated snapshots is extracted from the MD trajectories, once the inspection of the internal motions of the dyes indicates that the accessible conformations have been sampled with sufficient accuracy.
(4) Absorption spectra are finally computed and compared on one hand with experiments and on the other hand with the results obtained using a polarizable continuum representation of the environment (i.e., the polymeric matrix).
3.2 QM calculations
QM calculations were performed to (i) obtain reference structures, for parameterizing classical FFs, and to (ii) compute absorption spectra.For both compounds a and b, global energy minima were located at the DFT level, using the B3LYP exchange–correlation functional and the SNSD basis set.37,38 To reproduce experimental conditions, solvent effects were taken into account by means of the conductor-like variant of PCM (C-PCM).39 In particular, butanoic acid was considered as the solvent, because of its dielectric constant (2.9931) similar to that of PMMA (3–3.3). Moreover, the Hessian matrix and harmonic vibrational frequencies were evaluated on the computed global minimum. In order to describe flexible terms in the fluorophores FFs and QM energy scans along flexible dihedrals were performed, all the other geometrical parameters being optimized at fixed values of the soft variable spaced by 30°. The structures obtained from those relaxed scans were then used by JOYCE software in order to fit dihedral FF parameters. Absorption spectra were computed for several (roughly, two-hundred for compound) statistically uncorrelated snapshots, extracted from MD simulations running in the polymeric environment. Environmental effects were taken into account by the so-called electrostatic embedding (EE)40,41 in which all the retained PMMA atoms are represented by their OPLS42 point charges. At larger distances, bulk solvent effects were accounted for by means of the PCM. Electronic transitions were computed using the TD-DFT method, and considering the six lowest electronic states for each snapshot. The CAM-B3LYP functional and the SNSD basis set were used: this combination, in fact, has already been shown to be suitable for these kinds of systems.
All the QM calculations were performed using the Gaussian 09 suite of programs.43
3.3 Force field parameterizations
As stated above, JOYCE software was used to obtain accurate intra-molecular FFs for a and b. The analytical form, Eintra, includes the standard bonded and non-bonded contributions, namely:| Eintra = Estretch + Ebend + ERtorsion + Eftorsion + Enb | (1) |
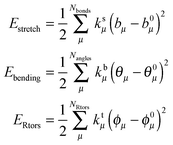 | (2) |
The potential around flexible dihedrals (Ftors) is usually described by the leading terms of a Fourier series:
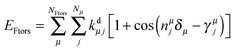 | (3) |
The last term in eqn (1) represents non-bonded interactions, consisting of Lennard-Jones and Coulomb contributions, i.e.
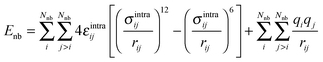 | (4) |
FF parameters are obtained using JOYCE through the minimization of the following merit function Ig:
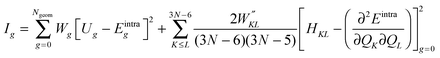 | (5) |
For all the considered dyes, LJ parameters were transferred directly from the OPLS FF and atomic charges were set to their CM5 values computed at the global energy minimum. The OPLS FF was used to describe the PMMA polymer matrix, and the general Amber FF (GAFF)44 for CHCl3.
3.4 Molecular modeling and MD simulations
A random sequence of atactic PMMA, in a completely linear conformation, was built by using an in-house Python (http://www.python.org) script, thus obtaining a real-sized macromolecule of approximately 300 kDa (therefore, having 2920 monomers of methacrylic acid). Such conformation was then minimized using the conjugate gradient algorithm, until an energy threshold of 0.5 kJ mol−1 was reached. A replica of this minimized conformation was added and rotated, with the aim of increasing the complexity of the system. Preliminary MD runs were performed in vacuo, to equilibrate the polymer: the simulation time-step was initially set to 0.1 fs for the first 200 ps and then increased to 0.5 fs for the remaining 4.8 ns. A 14 Å cutoff was applied for both the electrostatic and the van der Waals (vdW) interactions. When a curled conformation was eventually reached by the polymer, periodic boundary conditions were applied in all the directions and the dye was manually introduced inside the polymer matrix and kept frozen at its equilibrium conformation. The system was coupled to a thermal bath at 300 K and to a pressure bath at 1 bar through weak coupling schemes,45 thus running in the NPT ensemble. Coupling constants were set to 0.1 ps and 0.5 ps, respectively. vdW forces were computed applying a cutoff distance of 13 Å, whereas long-range electrostatic interactions were treated with the particle mesh Ewald (PME) method. After 20 ns of MD simulation, the final density was found to be lower than 1.00 g cm−3, pretty far from the average experimental value (1.17–1.19 g cm−3). To achieve a mass density closer to the experimental range, all the angles' force constant values were reduced by 50%. Moreover, the coupling constant to the barostat was reduced from 0.5 to 0.1 ps. Under these conditions, after 20 ns of simulation, a density value of 1.20 g cm−3 was obtained. Such collapsed structure was finally re-equilibrated by restoring the system under the initial conditions. After 5 ns, the density value was detected to be stable at 1150 kg m−3 (a reasonable value taking into account the complexity of the simulated system).The starting coordinates for the liquid chloroform box setup were taken from the coordinate file available on the Virtual Chemistry server.46 CM5 charges were computed on the CHCl3 molecule, modeling the environment (CHCl3) with PCM. The box size was tripled, passing from 1000 to 3174 CHCl3 molecules. The LINCS constraining algorithm47 was applied to all the chemical bonds. A first equilibration in the NPT ensemble of 2.0 ns was performed, using a time-step of 0.2 fs for the first 500 ps and 2.0 fs for the last 1.5 ns.
Two sets of MD simulations were performed: on the solvated and the polymer-embedded dye. Thus, to study dyes a and b, a total of four MD simulations were performed. For the polymer matrix, MD was carried out in the NPT ensemble to match the experimental conditions, and using the same conditions already mentioned for the PMMA modeling step. The last snapshot coming from the PMMA-density equilibration was used as the starting conformation. The fluorophore was “unfrozen”, and the total sampling time was set to 50 ns. The time-step was set to 2 fs and all the bonds were constrained at their initial value by means of the LINCS algorithm. System coordinates were saved every ps. The simulations in the chloroform solution were performed in the NVT ensemble, at 300 K. The total sampling time was set again to 50 ns. All the chemical bonds of the dye and the solvent were constrained.
All the simulations described above were performed using GROMACS 4.6.5.48
3.5 Absorption spectra calculations
Transition energies obtained for the MD snapshots were broadened by means of Gaussian functions, using a half width at half maximum (HWHM, and indicated as Δv in eqn (6)) of 0.25 eV. This value was chosen to match experimental data. For a generic snapshot c, the spectrum is then computed as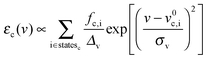 | (6) |
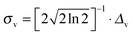 , v0c,i and fc,i are the excitation energy and the dimensionless oscillator strength of the considered i excitation, respectively. For an appropriate comparison with the experiments, the obtained spectra are plotted in the wavelength domain (εc(λ)). The final absorption spectrum is obtained by averaging the individual signals, according to
, v0c,i and fc,i are the excitation energy and the dimensionless oscillator strength of the considered i excitation, respectively. For an appropriate comparison with the experiments, the obtained spectra are plotted in the wavelength domain (εc(λ)). The final absorption spectrum is obtained by averaging the individual signals, according to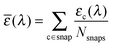 | (7) |
4 Results
4.1 Fluorophore force fields
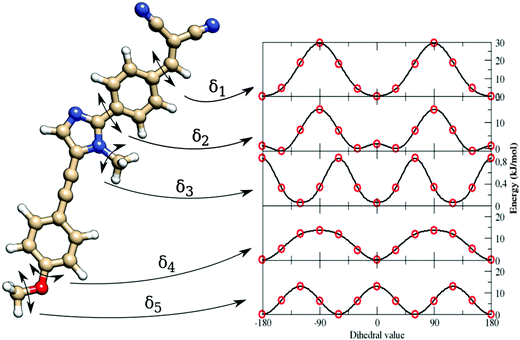
As indicated in Section 3.3, van der Waals (vdW) parameters were directly transferred from published force fields. For both a and b, CM5 charges were computed at geometries optimized in butanoic acid at the DFT/PCM level.No strong differences were found on the two minima, as shown in Fig. 3, where the a and b minima structures are superimposed. In particular, values of 28° and 30° for the dihedral angle between the imidazole and the pull-phenyl was found for a and b, respectively. Starting from a, and as already mentioned in Section 3.3, the parameterization was performed through the minimization of eqn (5) for each scanned internal coordinate, obtaining an overall standard deviation of 0.00624 kJ mol−1. The same equilibrium geometrical parameters and force constants were used for equivalent internal coordinates only if contained within the same molecular block, e.g. the phenyl-pull or the phenyl-push moiety. The flexibility of the molecule under examination does not permit the use of only the absolute energy minimum to obtain a reliable FF. Therefore, a reference QM scan was performed for all the dihedral angles that could affect the overall conformation (and indicated in Fig. 4 as δ1–5), using the procedure already described in the section devoted to computational details. The obtained energy profiles for the five dihedral angles are shown in Fig. 4, where single point energies calculated at the QM level are compared to their FF counterparts.
The good agreement between both levels of theory (see Fig. 4) points out that our FF performs a remarkable job in reproducing the structures and relative energies of different conformers. All the potential energy curves along the five torsional angles are symmetric about the origin. The δ1 and δ4 dihedral angles show energy minima at 0° and 180°, i.e. for planar arrangements of the whole molecule. The largest geometry variations are related to the δ2 dihedral angle, which shows four different energy minima at ±30° and ±150°. However, planar conformers (0° and 180°) are also quite stable due to the significant electron delocalization between the two connected rings. The capability of the FF of a to reproduce the vibrational behavior of the molecule was checked by comparing QM and FF harmonic frequencies. Fig. 5 shows that the QM trend is well reproduced by the FF calculations, with a root-mean square deviation of 82 cm−1, which can be considered satisfactory for the purposes of the present study.
 | ||
| Fig. 5 Top: Computed vibrational frequencies (both at the QM and FF levels) of fluorophore a. Bottom: Differences between the two descriptions. | ||
With the aim of developing a FF also for the b dye, a somewhat different strategy was used: FF parameters for the common, planar structure were simply transferred from a to b. Then, reference geometrical parameters and force constants relative to the nitro group were computed for the b molecule, freezing all the other parameters at the values optimized for a. The results related to the parameterization of the torsion of the nitro group are shown in Fig. 6. The full FF parameter set can be found in the ESI.†
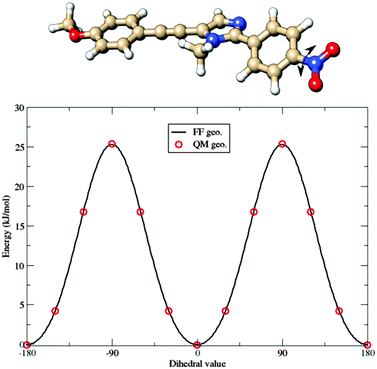 | ||
| Fig. 6 Comparison between QM (red circles) and Joyce FF (continuous line) potential energy curves governing the torsion of the nitro group in the b fluorophore. | ||
4.2 MD simulation analysis
The enhanced rigidity of the fluorophores upon dispersion in the polymer bundle was postulated in ref. 28 to explain the reduced efficiency of quenching effects. In fact, quantum yields determined in solution and PMMA have essentially the same value (≈0.1): while this parameter in solution is widely affected by large conformational changes that take place between the ground and the excited states, in the polymer matrix these structural conversions are not allowed. The goal of the MD simulations is therefore two-fold: on the one hand they permit the generation of statistically uncorrelated snapshots on which spectroscopic properties can be computed and, on the other hand, they also permit demonstrating, at an atomistic level, the reduced flexibility of the dispersed molecules, due to polymer caging effects. In the following we will explicitly consider only the dye a, whereas the results of dye b are given in the ESI.†Interesting aspects are evidenced by inspection of Fig. 7.
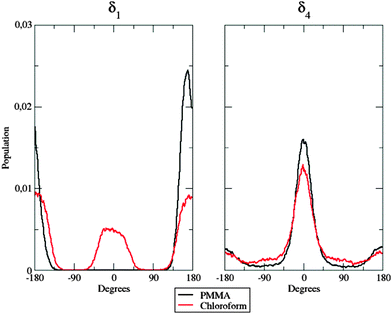 | ||
| Fig. 7 Population distribution of the δ1 (left panel) and the δ4 (right panel) flexible dihedrals in the two considered environments. | ||
In the left panel, it is easy to note differences among the behavior of the dye when dispersed in the polymer matrix and in solution: in the former case, δ1 is frozen at approximately 180°, whereas both planar conformations (0° and 180°) are populated in the latter case. This fact could be due to the hindering effect exhibited by the polymer chains: their steric hindrance prevents the dye from any conformational rearrangement along the considered dihedral, since such torsion implies the movement of a large and bulky group (the dicyanovinyl moiety). Concerning next δ4 (right panel in Fig. 7), no significant differences were found between the two different environments: nonetheless, in PMMA, the population is more peaked at 0° than in chloroform solution, highlighting again the constraining effect of the polymer matrix. This trend is confirmed by the behavior of δ2.
As a matter of fact, the inter-conversion between the allowed conformations of δ2 is much faster in CHCl3 than inside the polymer (Fig. 8, left panel): indeed, during the considered 50 ns, only two well-defined transitions from one conformer to the other were observed, the first one occurring after more than 15 ns.
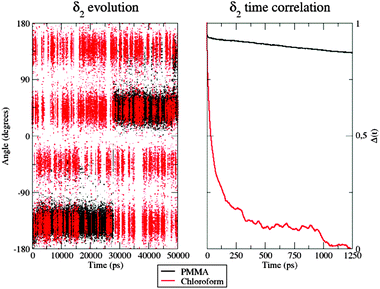 | ||
| Fig. 8 Left: Time evolution of the δ2 dihedral in the PMMA matrix (black) and chloroform solution (red). Right: Time correlation of the δ2 dihedral in the two environments. | ||
Furthermore, in CHCl3, the four different conformers of the dye show comparable populations. In contrast, it is clear that 50 ns are not sufficient to obtain a fully equilibrated population of all the energy minima when the dye is within the PMMA thin film, because of the very slow structural conversions allowed by the polymeric entanglement. This observation was also confirmed by looking at the δ2 time autocorrelation function (ACF), computed as
Δ(t) = cos[δ2(t0 + t)]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos[δ2(t0)] cos[δ2(t0)] | (8) |
Further evidence of different flexibilities of the investigated dye among the PMMA chains and the chloroform solutions was provided by the analysis of other structural features, such as (i) the radius of gyration and (ii) the distance between the pull- and the push-phenyl rings, placed at the ends of the dye. Such parameters give an overall description of the internal mobility of the fluorophore in the medium under examination. The radius of gyration is well known to provide a rough measure of the compactness of a structure, and has been calculated as
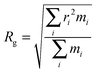 | (9) |
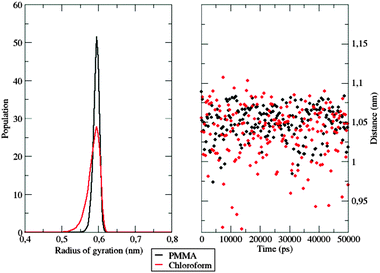 | ||
| Fig. 9 Left: Normalized gyration radius distribution of the investigated dye among the sampled time in the two different simulations. Right: Distance evolution between the two phenyl rings. | ||
The hardness encountered by the dye is evident in the polymer simulation, where the radius of gyration is stable at 0.6 nm. Similar conclusions can be drawn by looking at the evolution of the distance between the push- and the pull-moieties during the simulation. As shown in Fig. 9, right panel, the polymer does not allow the dispersed molecule to relax along its major axis, thus keeping the distance between the two considered groups around 1.05 nm for the whole time span. In contrast, in the chloroform solution, the distance between the two considered groups oscillates frequently during the simulation, thanks to the higher flexibility of the surrounding environment.
The computation of dynamic properties in the two different media could permit gaining further insights also concerning the effects of the considered environments on the fluorophore's dynamics. The mean square displacement (MSD) of the center of mass of a was computed for both simulations as
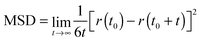 | (10) |
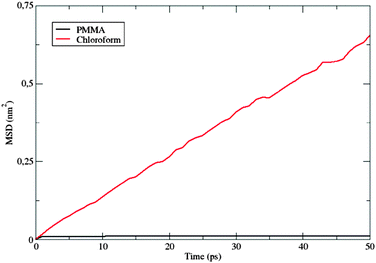
Fig. 10 shows the MSD variation during the first 50 ps.
The behavior of the dye in chloroform is typical for a molecular solute in a liquid solvent, where a diffusive regime is quickly approached. In contrast, in the polymer matrix, the MSD value suddenly reaches a plateau: the solute is trapped, its motion being strongly hindered by the surrounding PMMA cage, which delays the establishment of a diffusive regime. Moreover, the absence of a sub-diffusive behavior indicates that the polymer chains are also not diffusing, i.e. the polymer behaves as a plastic, thin film.
4.3 UV absorption spectra
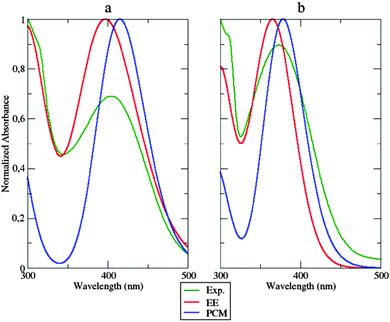
All the results analyzed in Section 4.2 point out a strong rigidity of the dyes induced by the caging effect of the polymeric matrix. It is, therefore, natural to assume that structural changes between the ground and excited electronic states are severely restricted in the polymer bundle. Keeping this in mind, it seems reasonable to simulate polymer hindering effects by the previously adopted28 static approach, where the δ2 dihedral angle is fixed to its ground-state value and bulk polymer effects are taken into account by the PCM. MD simulations permit checking this simplified model by looking at the populations of the different conformers along the time. The results (see Section 4.2, Fig. 8 – left panel) clearly show that not all the low energy conformers are equally populated. Inter-conversions ruled by the δ2 dihedral are very slow, because of the caging effect of the polymer, so that 50 ns are not sufficient to reach equilibrium values of these populations. In order to obtain a more homogeneous collection of conformers for computing equilibrium spectroscopic properties, one additional MD simulation was performed: in this case the starting configuration of the considered dye was symmetrized along the δ2 dihedral angle. Then, absorption spectra were computed, in the case of the dye within the polymer, by averaging single signals, computed at the TD-DFT level, from snapshots extracted from the NPT-MD simulations at constant time intervals of 500 ps. In each of the extracted snapshots, all the atoms of PMMA residues which had at least one atom within 15 Å from the fluorophore have been replaced by the respective atomic charge (according to the OPLS FF).Computed UV absorption spectra for the fluorophore a are reported in Fig. 11, left panel.
Both the approaches mentioned above (the static and the dynamic one) were applied and compared with experiments. Inspection of Fig. 11 shows that both the static and dynamic approaches overestimate the absorbance intensity at the maximum absorption wavelength. Nonetheless, the dynamic approach reproduces very well the first peak at approximately 300 nm, whose intensity is underestimated in the static model. This last approach shifts the absorption wavelength by about 11 nm, while the same experimental peak is underestimated by 7 nm using the dynamic approach. The same observations could be extended to system b (Fig. 11, right panel). The overall shape of the experimental spectrum is again better reproduced by the dynamic simulation than by its static counterpart. The two approaches show, instead, comparable errors (of opposite sign) concerning the position of the peak maximum.
Computational and experimental findings are summarized in Table 1. Globally, inspection of the shape of the computed spectra evidences a good match with experiments, especially concerning the decay slope. Furthermore, the good agreement between the results obtained from atomistic and continuous descriptions of the environment suggests the absence of strong specific solute–solvent interactions (especially of electrostatic origin). Although the dynamic atomistic approach improves the reproduction of the spectral shape (especially in the area under 350 nm), it is worth noticing that PCM performs a remarkable job in simulating the main features of the polymer embedding, permitting a preliminary semi-quantitative analysis of general trends by a fast approach.
| System | Method | Absorption peak (nm) |
|---|---|---|
| a in PMMA | Experimental | 404 |
| Static approach (PCM) | 415 | |
| Dynamic approach (EE) | 397 | |
| b in PMMA | Experimental | 373 |
| Static approach (PCM) | 378 | |
| Dynamic approach (EE) | 365 | |
5 Conclusions
Purposely tailored FFs have enabled us to follow the time evolution of two alkynylimidazole fluorophores when dispersed in a PMMA matrix intended to be part of a sunlight-harvesting device. Careful analysis of MD trajectories highlighted an overall rigidity of such hetero-aromatic molecular structures, due to the presence of the polymer chains, which hindered inter-conversions between different low-energy conformers. Analogous simulations in chloroform solution showed, instead, a significant flexibility of the dyes. These results confirm the hypothesis advanced recently to explain the different behavior of these dyes in solution and in the polymeric matrix.Next, the attention was focused on the computation of absorption spectra of the same fluorophores within the polymer matrix. This was achieved by using two different methods, i.e. (i) a static approach, where spectroscopic computations were made only on the conformational minimum, modeling the environment using a polarizable continuum model (PCM), and (ii) a dynamic approach, where the same computations were made on several snapshots extracted from the MD trajectories, and explicitly representing the polymer through the so-called electrostatic embedding (EE). Even if a more correct reproduction of absorption spectra was achieved by the application of the second, more demanding, protocol, it has to be noticed that a static approach also works pretty well. In particular, the static protocol is confirmed in this work to be a very useful tool in virtual screening campaigns, where the best structures for the above-mentioned applications have to be chosen by fast yet sufficiently accurate methods. It is, however, apparent that reliable optical features can be obtained using only force fields tailored for the correct reproduction of both structural and electrostatic (here by means of CM5 charges) properties.
The proposed approaches could also be extended to the simulation of emission spectra: the validity of the CAM-B3LYP theoretical scheme in the computation of emission properties is currently under investigation in our group, together with the parameterization of ad hoc FFs for the excited states of the two tested dyes, to be used during MD simulations in the dynamic approach. Future applications of the proposed procedures could also cover the inclusion of new, polar polymer matrices, as well as other condensed-phase environments, in order to further assess the validity of implicit and explicit models.
Acknowledgements
The research leading to the results had received funding from the European Union's Seventh Framework Programme (FP7/2007–2013) under grant agreement no. ERC-2012-AdG-320951-DREAMS. The authors thank the DREAMS Lab technical staff for managing the computing facilities at SNS and Nicola De Mitri for useful discussions.References
- J. Harmsen and J. B. Powell, Sustainable Development in the Process Industries: Cases and Impact, John Wiley & Sons, Inc., Hoboken, New Jersey, 2010 Search PubMed.
- K. E. Geckeler and R. Edward, Functional Nanomaterials, American Scientific Publisher, Stevenson Ranch, California, 2006 Search PubMed.
- X. D. Liu, A. R. Esker, M. Haeussler, C. Kim, P. Lucas, M. Matsunaga, N. Nishi, J. J. Robin, B. Z. Tang, D. A. Wang, M. Yamada and H. Yu, Functional Materials and Biomaterials, Adv. Polym. Sci., Springer-Verlag, Berlin, Heidelberg, 2007, vol. 209 Search PubMed.
- F. Ciardelli, G. Ruggeri and A. Pucci, Chem. Soc. Rev., 2013, 42(3), 857–870 RSC.
- S. K. Yesodha, C. K. S. Pillai and N. Tsutsumi, Prog. Polym. Sci., 2004, 29, 45–74 CrossRef CAS.
- G. S. Kumar and D. C. Neckers, Chem. Rev., 1989, 89, 1915–1925 CrossRef CAS.
- A. Natansohn and P. Rochon, Chem. Rev., 2002, 102, 4139–4176 CrossRef CAS PubMed.
- S. L. R. Barker, D. Ross, M. J. Tarlov, M. Gaitan and L. E. Locascio, Anal. Chem., 2000, 72, 5925–5929 CrossRef CAS PubMed.
- K. Komori, H. Matsui and T. Tatsuma, Bioelectrochemistry, 2005, 65, 129–134 CrossRef CAS PubMed.
- A. Pucci, G. Ruggeri and R. Bizzarri, Soft Matter, 2011, 7, 3689–3700 RSC.
- J. Houghton, Global Warming, Cambridge University Press, 3rd edn, 2005 Search PubMed.
- W. G. van Sark, Renewable Energy, 2013, 49, 207–210 CrossRef CAS.
- M. G. Debije and P. P. C. Verbunt, Adv. Energy Mater., 2012, 2, 12–35 CrossRef CAS.
- F. Bures, RSC Adv., 2014, 4, 58826–58849 RSC.
- B. C. Rowan, L. R. Wilson and B. S. Richards, IEEE J. Sel. Top. Quantum Electron., 2008, 14, 1312–1322 CrossRef CAS.
- J. Bloino, J. Phys. Chem. A, 2015, 119, 5269–5287 CrossRef CAS PubMed.
- S. Fantacci, F. De Angelis, A. Sgamellotti, A. Marrone and N. Re, J. Am. Chem. Soc., 2005, 127, 14144–14145 CrossRef CAS PubMed.
- V. Barone, J. Bloino, S. Monti, A. Pedone and G. Prampolini, Phys. Chem. Chem. Phys., 2011, 13, 2160–2166 RSC.
- G. Prampolini, F. Bellina, M. Biczysko, C. Cappelli, L. Carta, M. Lessi, A. Pucci, G. Ruggeri and V. Barone, Chem. – Eur. J., 2013, 19, 1996–2004 CrossRef CAS PubMed.
- N. A. Murugan, R. Apostolov, Z. Rinkevicius, J. Kongsted, E. Lindahl and H. Agren, J. Am. Chem. Soc., 2013, 135, 13590–13597 CrossRef CAS PubMed.
- N. De Mitri, G. Prampolini, S. Monti and V. Barone, Phys. Chem. Chem. Phys., 2014, 16, 16573–16587 RSC.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105(8), 2999–3094 CrossRef CAS PubMed.
- N. De Mitri, S. Monti, G. Prampolini and V. Barone, J. Chem. Theory Comput., 2013, 9, 4507–4516 CrossRef CAS PubMed.
- M. Pu and T. Privalov, Chem. – Eur. J., 2015, 21, 17708–17720 CrossRef CAS PubMed.
- M. Sulpizi, P. Carloni, J. Hutter and U. Rothlisberger, Phys. Chem. Chem. Phys., 2003, 5, 4798–4805 RSC.
- O. Crescenzi, M. Pavone, F. De Angelis and V. Barone, J. Phys. Chem. B, 2005, 109, 445–453 CrossRef CAS PubMed.
- N. A. Murugan, J. Phys. Chem. B, 2011, 115, 1056–1061 CrossRef CAS PubMed.
- V. Barone, F. Bellina, M. Biczysko, J. Bloino, T. Fornaro, C. Latouche, M. Lessi, G. Marianetti, P. Minei, A. Panattoni and A. Pucci, Phys. Chem. Chem. Phys., 2015, 17, 26710–26723 RSC.
- O. B. Malcioglu, A. Calzolari, R. Gebauer, D. Varsano and S. Baroni, J. Am. Chem. Soc., 2011, 133, 15425–15433 CrossRef CAS PubMed.
- I. Cacelli and G. Prampolini, J. Chem. Theory Comput., 2007, 3, 1803–1817 CrossRef CAS PubMed.
- V. Barone, I. Cacelli, N. De Mitri, D. Licari, S. Monti and G. Prampolini, Phys. Chem. Chem. Phys., 2013, 15, 3736–3751 RSC.
- F. Bellina, C. Calandri, S. Cauteruccio and R. Rossi, Tetrahedron, 2007, 63, 1970–1980 CrossRef CAS.
- F. Bellina, M. Lessi and C. Manzini, Eur. J. Org. Chem., 2013, 5621–5630 CrossRef CAS.
- F. Bellina, M. Lessi, G. Marianetti and A. Panattoni, Tetrahedron Lett., 2015, 56, 3855–3857 CrossRef CAS.
- K. Danel and L. J. T'suen, ARKIVOC, 2002, 1, 12–18 Search PubMed.
- A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 527–541 CrossRef CAS PubMed.
- V. Barone, P. Cimino and E. Stendardo, J. Chem. Theory Comput., 2008, 4, 751–764 CrossRef CAS PubMed.
- V. Barone and P. Cimino, J. Chem. Theory Comput., 2009, 5, 192–199 CrossRef CAS PubMed.
- M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- G. G. Hall and C. M. Smith, Int. J. Quantum Chem., 1984, 25, 881–890 CrossRef CAS.
- C. M. Smith and G. G. Hall, Theor. Chem. Acc., 1986, 69, 63–69 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, J. Bloino, B. G. Janesko, A. F. Izmaylov, F. Lipparini, G. Zheng, J. L. Sonnenberg, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, P. V. Parandekar, N. J. Mayhall, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian Development Version, Revision I.03, Gaussian, Inc., Wallingford, CT, 2014 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25(9), 1157–1174 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. van Gunsteren, A. Di Nola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- http://virtualchemistry.org/, accessed December 2015.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- D. van der Spoel, E. Lindahl, B. Hess and GROMACS development team, GROMACS User Manual version 4.6.5, 2013, http://www.gromacs.org Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: (i) Force field parameters for the a and b fluorophores and (ii) MD simulation analysis of the b fluorophore. See DOI: 10.1039/c6cp00841k |
| This journal is © the Owner Societies 2016 |