Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ozone uptake on glassy, semi-solid and liquid organic matter and the role of reactive oxygen intermediates in atmospheric aerosol chemistry†
Thomas
Berkemeier
*a,
Sarah S.
Steimer
bc,
Ulrich K.
Krieger
c,
Thomas
Peter
c,
Ulrich
Pöschl
a,
Markus
Ammann
b and
Manabu
Shiraiwa
*a
aMax Planck Institute for Chemistry, Multiphase Chemistry Department, 55128 Mainz, Germany. E-mail: t.berkemeier@mpic.de; m.shiraiwa@mpic.de
bPaul Scherrer Institute, Laboratory of Environmental Chemistry, 5232 Villigen PSI, Switzerland
cETH Zurich, Institute for Atmospheric and Climate Science, 8092 Zurich, Switzerland
First published on 7th April 2016
Abstract
Heterogeneous and multiphase reactions of ozone are important pathways for chemical ageing of atmospheric organic aerosols. To demonstrate and quantify how moisture-induced phase changes can affect the gas uptake and chemical transformation of organic matter, we apply a kinetic multi-layer model to a comprehensive experimental data set of ozone uptake by shikimic acid. The bulk diffusion coefficients were determined to be 10−12 cm2 s−1 for ozone and 10−20 cm2 s−1 for shikimic acid under dry conditions, increasing by several orders of magnitude with increasing relative humidity (RH) due to phase changes from amorphous solid over semisolid to liquid. Consequently, the reactive uptake of ozone progresses through different kinetic regimes characterised by specific limiting processes and parameters. At high RH, ozone uptake is driven by reaction throughout the particle bulk; at low RH it is restricted to reaction near the particle surface and kinetically limited by slow diffusion and replenishment of unreacted organic molecules. Our results suggest that the chemical reaction mechanism involves long-lived reactive oxygen intermediates, likely primary ozonides or O atoms, which may provide a pathway for self-reaction and catalytic destruction of ozone at the surface. Slow diffusion and ozone destruction can effectively shield reactive organic molecules in the particle bulk from degradation. We discuss the potential non-orthogonality of kinetic parameters, and show how this problem can be solved by using comprehensive experimental data sets to constrain the kinetic model, providing mechanistic insights into the coupling of transport, phase changes, and chemical reactions of multiple species in complex systems.
1 Introduction
Organic compounds are ubiquitous in the earth's atmosphere and constitute a major fraction of atmospheric particulate matter.1–3 Finely dispersed submicron particles affect climate by scattering sunlight and serving as nuclei for cloud droplets and ice crystals4 and play a key role in air quality and public health by reducing visibility and posing adverse health effects.5,6 Most organic aerosols arise from oxidation of volatile organic compounds followed by condensation of oxidation products, so-called secondary organic aerosols (SOA).2,3,7 After formation, organic aerosols are still subject to chemical processing by reactive trace gases such as ozone,8,9 ammonia,10 the hydroxyl11–13 or nitrate radical,14,15 influencing chemical composition16–18 and particle size distribution,19 and hence, affecting hygroscopicity,20–22 viscosity,23 gas-particle partitioning,24–26 radiative properties,27 and toxicity.28 The rate of chemical reactions occurring in aerosol particles depends strongly on their phase state,8–11,18,29 which varies from liquid to solid depending on composition30–32 and ambient conditions such as temperature and relative humidity.33–39 Accordingly, diffusivity of organic molecules40 and trace gases penetrating the organic matrix41–44 decreases significantly under cold or dry conditions.Accurate description of the multiphase reaction kinetics of these systems is vital for understanding the rates at which compounds degrade and oxidants are consumed. Kinetic models commonly evaluate single steps that may limit reaction rate such as mass transfer or chemical reaction. Classical resistor models are computationally inexpensive, but only describe certain aspects of the reaction system in distinct limiting cases.45,46 These models have difficulty in describing systems which are driven by multiple rate-limiting processes or transition between limiting cases.47 Hence, the important subset of cases where both the bulk material and the trace gas show diffusion limitation (“counter-diffusion case”) cannot be properly described.
Kinetic flux models resolve this problem by tracking reactant concentration as a function of depth,48–51 which leads to a better description of the processing of organic material in the atmosphere.8,12,15 However, they are computationally more expensive and rely on a set of kinetic parameters of which not all are directly accessible by experiment. Due to the high number of input parameters, kinetic flux models applied to small data sets are usually not fully constrained, leaving large flexibility in the possible range of input parameters yielding the same or similar model output.12,47 The two possible solutions to this problem are (i) reduction of the kinetic input parameter set and thus simplification of the kinetic model and loss of information or (ii) extension of the dimensions of the experimental input data set. Added dimensions can be additional experimental observables (e.g. reactant concentrations in gas and particle phase, viscosity, system size, refractive indices) or can be varied environmental conditions (reactant concentrations, system size, temperature, relative humidity) or simply an extended observation time scale to encompass more rate-limiting processes.47,52 A kinetic parameter can only be determined if a related process affects the measured quantity. Care must be taken in case parameters depend on environmental conditions (e.g. bulk diffusion coefficients depend on both RH and temperature separately).
These criteria of a wide range of experimental dimensions are fulfilled in a recent study by Steimer et al., who investigated ozonolysis of shikimic acid as model system for chemical processing of organic aerosols.53 The cyclohexene derivative shikimic acid contains a single double bond that serves as target for ozone. Due to the closed ring structure, ozonolysis does not lead to fragmentation and thus volatilization of the oxidation products. The structural formula of shikimic acid is displayed in Fig. 1A. Pure shikimic acid exhibits a glassy solid phase state with a glass transition temperature of 327 K.54 Due to the plasticizing effect of water, shikimic acid is expected to cover the full range of (semi-)solid phase states at atmospherically relevant RHs. The experimental study by Steimer et al. clearly demonstrated the limitations of classical methods for analysis of heterogeneous kinetics, which motivates the application of the kinetic multi-layer model for aerosol surface and bulk chemistry (KM-SUB)49 to the kinetic data set in this study. In order to cope with the extended set of kinetic parameters of the kinetic flux model, we apply a global optimization method including a genetic algorithm to find an optimal correlation between model and experiment.
2 Methods
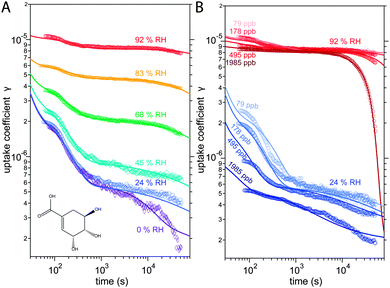
The kinetic experiments have been reported in detail by Steimer et al. and will be described only briefly in the following.53 Experiments were performed in an atmospheric pressure coated wall flow reactor (48 cm length, 1.2 cm inner diameter) with long reaction times and atmospherically relevant oxidant concentrations as detailed. The temperature in the reactor was held constant by a thermostat-controlled cooling jacket and RH was adjusted by directing gas flows through tempered water reservoirs.Measurements were performed at an O3 concentration of 178 ppb at 6 different relative humidities: 0, 24, 45, 69, 83 and 92% RH. At 24 and 92%, measurements were conducted at three additional O3 concentrations of 89, 495 and 1985 ppb, giving a total of 12 distinct experimental conditions. The measurement results are ozone uptake coefficients γ, which represent the probability that ozone molecules colliding with a surface are subsequently taken up by the condensed phase.55 The experimental data is shown Fig. 1.
2.1 Kinetic model
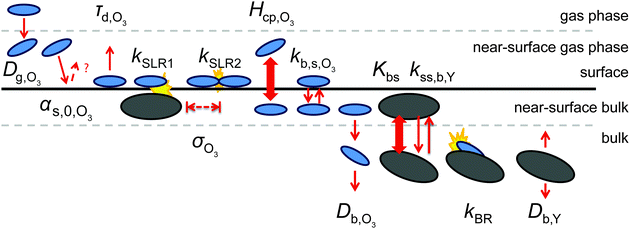
We use the kinetic multi-layer model of aerosol surface and bulk chemistry, KM-SUB, which provides a depth-resolved description of mass transport and chemical reaction in aerosol particles and surface films.49 KM-SUB resolves the following processes explicitly: gas-phase diffusion, adsorption and desorption, surface–bulk exchange, bulk diffusion of trace gas (X) and bulk material (Y) as well as chemical reactions at the surface and in the bulk. The following three reaction pathways are considered for ozone loss in the KM-SUB representation of the reaction system: a bimolecular surface layer reaction between adsorbed ozone and surface-exposed shikimic acid (SLR1), a bulk reaction between both reactants (BR) and the self-reaction of two ozone molecules adsorbed to the surface (SLR2). Secondary reactions involving oxidation products are neglected for simplicity.For this study, several modifications have been applied to the original KM-SUB model as outlined below. The kinetic behaviour of a reaction system is described in this modified version of KM-SUB by the thirteen kinetic parameters given in Table S1 (ESI†). Fig. 2 illustrates the microscopic representations of the processes covered with KM-SUB in this study.
Similar to previous studies26,47 a near-surface gas-phase layer (extending one mean free path λX of the gas molecules from the surface) has been added to explicitly resolve diffusion of gas molecules to the surface. The gas phase diffusion flux Jdiff from the flow tube centre with far from surface trace gas concentration [X]g to the near-surface gas phase layer with concentration [X]gs is described following the Knopf–Pöschl–Shiraiwa approach for gas phase diffusion in cylindrical reactors.56
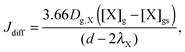 | (1) |
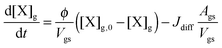 | (2) |
Bulk diffusion is treated as first order process, following Fick's first law of diffusion.55 While Fickian diffusion is a continuum approach that strictly only applies if molecular motion can be described by random motion of an ensemble of molecules, continuum conditions can always be generated by choosing sufficiently small layer sizes. At low diffusivity and high reactivity, however, the spatial extension of diffusion gradients approaches the molecular length scale, which can induce effects related to coarseness of matter in reaction–diffusion systems. To consider these effects, we chose a lower limit for bulk layer thickness of 0.3 nm, congruent with previous work.57
In contrast to the original KM-SUB, the quasi-stationary surface layer (ss) has a certain extent into the particle and hence also constitutes the near-surface bulk. The surface concentration of bulk material (i.e., shikimic acid), [Y]ss, can be interpreted as concentration of reactive sites (i.e. C–C double bonds) accessible by surface-adsorbed molecules. This entity depends crucially on molecular structure and orientation: molecules may spread out at the surface or form a densely packed monolayer. The reactive site of a molecule in the surface layer might not be facing upwards but be directed away from the surface and may not undergo a surface layer-type reaction.58 Thus, we define the surface-accessible fraction of reactive sites by defining a surface equilibrium constant Kbs that relates an equilibrium near-surface bulk concentration [Y]b1,eq to an equilibrium surface concentration [Y]ss,eq. Kbs can be interpreted as a depth to which surface-adsorbed ozone molecules can still react with near-surface bulk molecules without undergoing a phase transfer into the bulk phase.
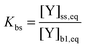 | (3) |
| kb,ss,Y = kss,b,Y(1 − θss)Kbs | (4) |
2.2 Global optimization algorithm
In order to obtain a common kinetic parameter set describing all experimental data sets, we used a global fitting method combining a uniformly-sampled Monte-Carlo (MC) search with a genetic algorithm (GA).12,47 In the MC search, kinetic input parameters for KM-SUB were varied randomly within individual bounds. All measurements were fitted simultaneously by the model and the correlation between modelled uptake coefficient γmod(t) and experimentally determined uptake γexp(t) evaluated in a least-squares fashion. For each experimental data set i, the residual ri was calculated in log-space to account for the large range of γ observed during the experiments.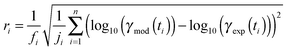 | (5) |
In total, we varied 11 parameters, 6 of which were allowed to increase or decrease monotonically over 6 steps in relative humidity. Thus, a total of 41 distinct parameter values were obtained during optimization to the experimental data. Optimization of such a large parameter set is computationally expensive and only feasible on a computer cluster for models like KM-SUB. In a typical optimization 10 million single KM-SUB model runs were performed, requiring about 2 days of computation time on 120 CPUs. After global optimization, a 1D local optimization (golden cut search) was performed to check for local convergence. In this step, the monotonicity restraint of the parameter's RH dependence was not applied. To decrease computation time, the initial global fit was conducted without gas-phase diffusion and gas-phase loss corrections, which accelerated computation by a factor of 10. The obtained result was then optimised locally to re-fit to the experimental data including the additional minor correction terms.
3 Results and discussion
3.1 Uptake data and global optimization results
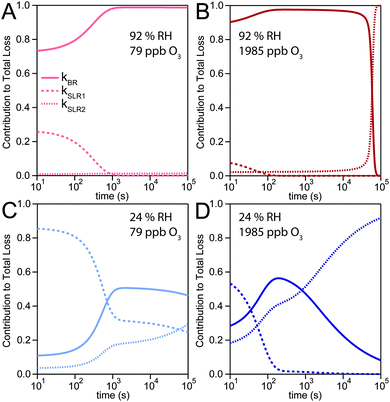
The experimental uptake coefficients53 and the corresponding KM-SUB results obtained with the MCGA algorithm are shown in Fig. 1. Panel A shows a clear increase in γ upon increase in RH, consistent with recent experimental data.8,32 In panel B, the effect of changing gas-phase ozone concentration is displayed for 24% RH (blue lines) and 92% RH (red lines): at high [O3]g, a lower γ is observed. The correlation between model and experiment is high overall, achieving a low total residual R of 0.020 according to eqn (5).The plot of uptake data against time reveals a step profile in which several plateaus can be identified. The first prominent plateau in the experimental data occurs at around 100 s and transitions into a second plateau at around 1000 s. In the low RH data we can also find signs for a third plateau at ∼5 × 104 s reaction time. This can be understood by the model results shown in Fig. 3, which details the contribution of the three pathways of ozone loss (SLR1, SLR2, BR) to the total ozone loss at 24 and 92% RH for 79 and 1985 ppb [O3]g in the kinetic model.
Until around 1000 s reaction time, surface reaction between ozone and shikimic acid (SLR1, dashed lines) contributes significantly to the overall ozone loss under all conditions. We thus term the initial plateau the surface reaction plateau. This is consistent with previous resistor model descriptions and justified by its inverse O3 concentration dependence.53 The integral uptake within this period corresponds roughly to a monolayer of shikimic acid.53 The relative contribution of SLR1 is highest at low [O3]g and dry RH. However, the absolute rate of surface reaction is almost independent of RH and rather a function of [O3]g.
The contribution of SLR1 becomes very low after 1000 s due to depletion of shikimic acid at the surface except in the case of low [O3]g and low RH (panel C), where surface reaction remains substantial as transport of bulk material Y to the surface is sufficiently fast and bulk reaction sufficiently slow to maintain a high quasi-stationary concentration of surface-exposed molecules. After 1000 s, bulk reaction (BR, solid lines) dominates the overall uptake for the majority of the investigated cases. Thus, the second plateau in the experimental uptake data can be termed as the bulk reaction plateau. The model result again confirms the assignment of this kinetic regime based on qualitative arguments with the resistor model.53 Self-reaction between two ozone molecules at the surface (SLR2, dotted lines) is present at all times and shows a high relative contribution when the overall ozone uptake is low (γ < ∼10−6). When the bulk material is used up or strongly shielded by unreactive product, SLR2 will dominate the ozone loss, creating a third plateau on the reaction coordinate, the self-reaction plateau. Note that this case cannot be introduced into a classical resistor model.53 At lower RH, model and experiment deviate slightly at reaction times > 2 × 104 s. This data might however be influenced by a drift of the baseline concentration of ozone (see discussion in ref. 53). This is evident from the curvature of the experimental data after 2 × 104 s: while some of the uptake data at low RH are right-bent (drop in γ accelerates) as is especially pronounced in the 0% RH data set, others are left-bent (drop in γ halts) as can be seen in the 495 ppb and 1985 ppb data set at 24% RH.
The 1985 ppb data set at 92% RH (dark red markers in Fig. 1) shows an important feature that is fully captured by the KM-SUB model: due to fast reaction in the liquid film at high RH and a high ozone concentration, shikimic acid is depleted in the flow reactor which causes a steep drop in γ after about 104 s of ozone exposure, providing an important constraint on the magnitude of the bulk reaction rate coefficient, kBR.
3.2 Kinetic regimes of the reaction system
In addition to characterization of the three major pathways of ozone loss, a full determination of the kinetic regime of a reaction system is required for identification of the physical or chemical processes limiting overall gas uptake.47,66 We characterise the regime by three classification parameters:20 the contribution of surface reaction to the total chemical loss rate (STLR), the saturation ratio assessing the supply of reactants from the gas phase (SR) and a mixing parameter assessing the extent of spatial heterogeneity in the particle phase (MP). The kinetic regimes and limiting cases defined by these criteria can be visualised in a “kinetic cube”, in which each axis corresponds to one of the three classification parameters. At the extremes of the classification parameters (vertices of the kinetic cube), we find the limiting cases usually used in kinetic modelling studies such as a bulk reaction with well-mixed reactants (Brx) or a surface reaction limited by diffusion of bulk material to the surface (Sbd).47 For these cases we assign term-symbol like identification symbols that reveal the predominant reaction location (“G”as phase, “S”urface or “B”ulk) and the limiting process (rx: chemical reaction, bd: bulk diffusion, mt: mass transfer, gd: gas diffusion) of the reaction system. A more detailed description of the concept of kinetic regimes and the kinetic cube can be found in Berkemeier et al.47 and in the ESI† (Section A).A detailed look into the kinetic regime of the shikimic acid – ozone reaction system is provided in Fig. 4. Fig. 4A shows the temporal evolution of γ at 178 ppb ozone and 24% RH and highlights five distinctive points (yellow circles) on the reaction coordinate. Fig. 4B outlines the corresponding evolution of the kinetic regime in the kinetic cube. Fig. 4C shows a projection of the top plane of the kinetic cube (shaded area in panel B) and compares with the corresponding experiment at 92% RH to outline the differences in the kinetic regimes at higher RH.
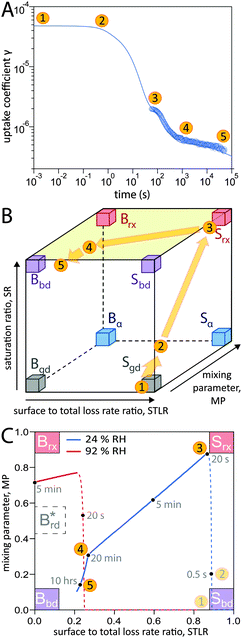 | ||
| Fig. 4 Temporal evolution of the reaction system's kinetic regime. (A) 5 characteristic points on the reaction coordinate. (B) These points lie on a trajectory through the kinetic cube,47 representing the change of the limiting process. From an initial gas-diffusion limited surface reaction (Sgd), the system transitions into a reaction-rate limited surface reaction (Srx). After an inflection point, the system evolves towards a bulk-diffusion limited bulk reaction (Bbd). (C) View at the top plane of the kinetic cube (marked green in panel b) with trajectories at 24% RH (blue solid line) and 92% RH (red solid line). Dashed lines are drawn while not in the top plane (SR < 0.8). | ||
At (1), the near-surface gas phase in the flow reactor is nearly depleted of O3 due to rapid adsorption of ozone, leading to an effective surface reaction in the absence of competition for adsorption sites. The ozone uptake is thus limited by gas-phase diffusion and falls into the limiting case Sgd. At (2), the saturation ratio SR has increased due to accumulation of O3 molecules, possibly in the form of reactive oxygen intermediates,62 at the surface. This process continues until (3) when the adsorbed molecules have reached an effective/dynamic Langmuir adsorption equilibrium with the gas phase, reflected by a mixing parameter MP close to 1. At this stage, ozone uptake and loss of bulk material are limited by chemical reaction at the surface and the system falls into the limiting case Srx. After 100 s of reaction time, depletion of surface-exposed bulk material causes a strong concentration gradient of shikimic acid in the bulk (decrease of MP) and bulk reaction becomes more important (decrease of STLR) as shown in Fig. 3. The system now strives towards a dynamic equilibrium at (4), in which bulk reaction and surface reaction are balanced (STLR ∼ 0.25) and bulk diffusion of both ozone and shikimic acid severely limits the reaction (MP < 0.4). From that point, changes in the kinetic regime occur very slowly. Over the next hours, the diffusion flux of bulk material to the surface is gradually reduced, as bulk material is increasingly depleted in the near-surface bulk, indicated by a slow decrease in STLR and MP. At (5), the system is mainly limited by bulk diffusion, almost reaching the corresponding limiting case Bbd.
Panel C shows that at higher RH (red dashed and solid line), a slightly different route is taken through the kinetic cube compared to the dry state (blue dashed and solid line). The contribution of bulk reaction increases quickly after the start of ozone exposure due to fast bulk diffusion. The system quickly reaches its dynamic equilibrium at a much higher value of MP (∼0.72). Ozone uptake is overall dominated by bulk reaction and diffusion and the system neither occupies a state where both reactants are well-mixed (i.e. Brx), nor a state where the reaction is only constrained to the near-surface bulk (traditional reacto-diffusive case, Brd*, ref. 47).
Even though in both cases described in Fig. 4C a dynamic equilibrium is reached after an initial phase of transient behaviour, the steady state behaviour is not compliant with standard limiting cases that can be described by analytical expressions of traditional resistor models.45–47,67,68 To our knowledge, no analytical expressions are available that describe a system driven by counter-diffusion of two reactive components (Bbd limiting case) as observed at low RH. While analytical expressions are well-known for the limiting cases Brx and Brd*, there is no simple model for cases that lie between the two extremes, as observed at high RH.
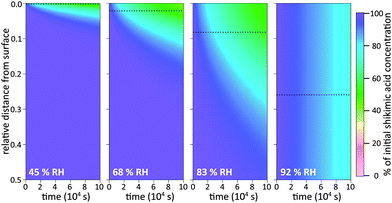
To illustrate these two types of diffusion behaviour, KM-SUB is used to create time-resolved depth profiles of bulk material as shown in Fig. 5. The analysis shows that under dry conditions shikimic acid is only degraded very close to the surface, in agreement with a study by Steimer et al. who showed no visible decay of bulk material using STXM microscopy.69 Even at 45% RH and after 105 seconds reaction time, only the topmost 5% of the 200 nm film show significant loss in bulk material. In this case the reacto-diffusive length of ozone (black dashed lines), i.e. the effective depth over which reaction occurs,70 is merely 0.3% of the total film thickness. Upon increase in RH, elevated bulk diffusion coefficients lead to a larger reaction zone of ozone and shikimic acid as indicated by a larger reacto-diffusive length and hence a broader band of reduced shikimic acid concentrations at the film surface (69% RH and 83% RH). Note that at these intermediate humidities, no chemical gradients were detected using STXM microscopy as particles were already well-mixed at and above 52% RH. This disagreement is most likely due to the uncertainty in determining Db,Y caused by reaction products that might alter the diffusion coefficient inside the organic matrix as discussed in Section 3.3 below. At 92% RH, shikimic acid is well-mixed in the model and ozone molecules reach almost the entire film depth, which is again consistent with STXM microscopy. These results on chemical gradients complement recent studies, which proposed the formation of chemical gradients in the oxidation of organic aerosol by OH12,44 and NO3.15 Our study shows chemical gradients even for the much slower reaction of organic aerosols with ozone.
3.3 Kinetic parameters obtained from global optimization
Fig. 6 shows the s-shaped humidity dependence of Db,O3 as determined by global optimization to the experimental data (solid circles). Such functional forms with a constant Db,O3 at low RH and a strong increase at medium RH are consistent with percolation theory,71 an approach commonly used to describe systems where small molecules percolate through a rigid matrix of larger molecules.8,19 Measurements of Db,H2O in shikimic acid by Steimer et al.59 (blue shadings) revealed overall higher diffusion coefficients and no s-shape of the Db,H2O curve. The Db,O3 curve however closely resembles the estimate of water diffusivity (Db,H2O) in α-pinene secondary organic aerosol (SOA) of similar oxidation state (molecular O/C ratio of 0.7) obtained with the semi-empirical method described in Berkemeier et al.42 (orange shadings). The values determined for Db,O3 are slightly shifted towards lower diffusivities compared to recent experimental data of less oxidised α-pinene SOA in ref. 54 (green shadings) and ref. 72 (purple shadings), but show the same qualitative shape. The difference is in line with the results of Berkemeier et al.,42 who predicted a decrease in diffusion rates upon chemical ageing, i.e. by an increase in molecular O/C ratio. At a molecular O/C ratio of 0.5, the estimated diffusion coefficients of Berkemeier et al.42 coincide with the results of Lienhard et al.,54 who determined the molecular O/C ratio of their SOA samples to 0.53. A part of the difference between Db,H2O and Db,O3 can be attributed to the molecular size of ozone, which is almost three times larger than water.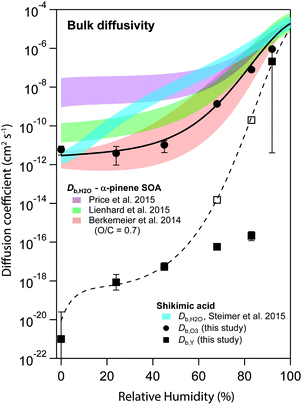 | ||
| Fig. 6 Humidity dependence of the bulk diffusion coefficients of ozone (Db,O3, black circles) and shikimic acid (Db,Y, black squares) as determined by global optimization to the experimental data set. The black solid and the dashed line represent a fit to a Vignes-type equation for ozone and shikimic acid, respectively. Open square markers indicate model runs including product effects, consistent with the Vignes-type fit. Blue shadings are measurements of water diffusivity in shikimic acid as measured by Steimer et al.59 Red shadings indicate an estimate of water diffusivity in SOA corresponding to the molecular O/C ratio of shikimic acid.42 Measurements on SOA at slightly lower molecular O/C ratio have been performed by Price et al. (purple shadings) and Lienhard et al. (green shadings).54,72 | ||
Hence, results are closely related, even though the method of determining diffusion coefficients in this paper is conceptually very different to the established methods for determination of water diffusion coefficients in organic material. In previous work using a steady-state approach, it was not possible to reconcile diffusion coefficients from RH-dependent kinetic data.53
The Db,O3 curve can be fitted as a function of molar organic fraction xorg by the Vignes-type eqn (6) used in Lienhard et al.,54
| Db = (Dwb)α(1−xorg)(Dorgb)αxorg | (6) |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α = xorg2(C + 3D − 4Dxorg) α = xorg2(C + 3D − 4Dxorg) | (7) |
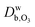 and
and 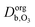 are the ozone diffusivity in pure water and pure organics, respectively. The equation uses a correction factor α that has the form of an activity coefficient. The parameters for eqn (6) and (7) used in this study are listed in Table S3 (ESI†).
are the ozone diffusivity in pure water and pure organics, respectively. The equation uses a correction factor α that has the form of an activity coefficient. The parameters for eqn (6) and (7) used in this study are listed in Table S3 (ESI†).
Fig. 6 also includes the humidity dependence of Db,Y, which shows many orders of magnitude lower values than Db,O3. Db,Y increases from ∼10−20 cm2 s−1 to 10−7 cm2 s−1 upon increase of RH, reflecting that the phase state of shikimic acid changes from amorphous solid over semi-solid to liquid (moisture-induced phase transformation73), compliant with earlier work.39 The dashed black line represents a fit using the Vignes-type equation. Note that a good fit was only obtained neglecting the values at 68 and 83% RH. At this intermediate humidity, Db,Y needs to be ∼10−17 cm2 s−1 to explain the slow reduction in γ at long reaction times seen in the experimental data (cf.Fig. 1) as Db,Y controls the slope of this reduction (cf. Fig. S1, ESI†). Such low diffusivity would lead to incomplete mixing of bulk material in the model (as discussed in Fig. 5 and Section 3.2), which is not in line with previous results by Steimer et al.,69 who observed well-mixed particles during ozonolysis down to 67% RH using STXM microscopy. This disparity may be caused by product effects not captured by the kinetic model: A slight decrease in Db,O3 or Hcp,O3 over time could lead to a similar deceleration of reaction kinetics. A recent study has shown that oxidative processing of organic aerosols can lead to an increase of viscosity, and hence decrease of bulk diffusivity according to the Stokes–Einstein relation.23 Also, polar products could preferentially adsorb to the surface, blocking surface sites and reducing surface–bulk transport rates. Such product effects reducing diffusivities cannot be distinguished in the model from incomplete transport of shikimic acid to the surface. Test runs with composition-dependent Db,O3 showed that the values of Db,Y indicated by the open square markers in Fig. 6 could be supported by the model if Db,O3 would decrease over the course of the 16 h experiment by factors of 5 and 2.5 at 68% RH and 83% RH, respectively. In this scenario, no diffusion gradients would be present in shikimic acid at 68% and 83% RH (Fig. S2, ESI†), which is in contrast to the results shown in Fig. 6, but consistent with STXM experiments.53 A thorough discussion of the effect of reaction products on reactive uptake is however beyond the scope of this study as laboratory experiments only measured gas-phase ozone concentrations. The very low values for Db,Y obtained in this study at medium to high RH values should hence be handled with reservation.
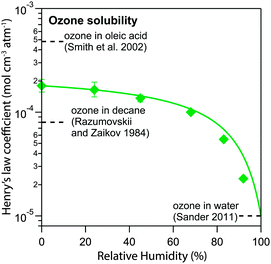
Fig. 7 shows the humidity dependence of the Henry's law coefficient of ozone, Hcp,O3, which is used to describe the saturation concentration of ozone in the organic matrix. Henry's law coefficients (green diamonds) were found to decrease with decreasing organic weight fraction, worg, following a logarithmic mixing rule (green solid line), eqn (8). 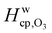 and
and 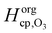 are the Henry's law coefficients of ozone in pure water74 and pure organics, respectively.
are the Henry's law coefficients of ozone in pure water74 and pure organics, respectively.
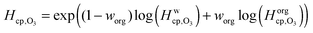 | (8) |
The value of 1.8 × 10−4 mol cm−3 atm−1 determined for 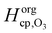 seems reasonable compared to Henrys law coefficients for decane75 and oleic acid67 (dashed black lines in Fig. 7).
seems reasonable compared to Henrys law coefficients for decane75 and oleic acid67 (dashed black lines in Fig. 7).
The organic acid thus shows an effect similar to the salting-out behaviour known for inorganic solutes, but acts in the opposite direction (“salting-in”) comparable to other organic solvents investigated previously such as acetic acid.76 Error bars in Fig. 6 and 7 represent the interval in which a model parameter can be varied until the total residual R increases by 20%.
Note that these 1-dimensional degrees of freedom are measures of parameter sensitivity and do not consider interactions between model parameters, which will be discussed in Section 3.4. The optimization yielded a bulk reaction rate coefficient kBR of 4.4 × 10−18 cm3 s−1, which compares well to literature values for similarly functionalised molecules such as maleic acid (1.7 × 10−18 cm3 s−1) or fumaric acid (1.0 × 10−17 cm3 s−1) in aqueous solution.77 The value is also consistent with the bulk reaction rate coefficient of 6.1 × 10−18 cm3 s−1 obtained by steady-state analysis.53
The surface reaction rate coefficient for ozonolysis of shikimic acid kSLR1 (8.5 × 10−16 cm2 s−1) is found to be one order of magnitude higher than the ozone self-reaction rate coefficient kSLR2 (4.3 × 10−17 cm2 s−1). A self-reaction of ozone at the particle surface could not be captured by steady-state analysis using the resistor model approach, leading to overall lower correlation to the experimental data especially at dry RH, or an overestimation of bulk diffusion coefficients at low RH.53 Including such a self-reaction adds a constant loss term that enables to describe the experimental data at dry RH while staying consistent with data obtained using other experimental techniques.59,69
The bulk–surface partitioning parameter Kbs also shows humidity-dependence and ranges from 2.0–9.3 × 10−9 cm, indicating that the relative amount of molecules accessible by surface adsorbed reactants increases with humidity. This suggests that shikimic acid molecules are slightly surface active and enrich at the surface of more dilute aqueous solutions. Note that while Kbs spans almost one order of magnitude, the surface concentration increases only by 84% over the entire humidity range due to overall dilution of the aqueous solution. The moderate increase could be due to a packing effect: at low RH, molecules might show a random orientation toward the particle surface, while at high RH molecules may form a structured outer layer on top of the aqueous solution. In addition, the mobility of the surface monolayer could play a significant role: at low RH, surface molecules may be immobile and a reactive site that is directed away from the surface would be inaccessible by adsorbed reactants. Such a molecule would not be able to undergo surface layer reaction, which effectively reduces the surface concentration of reaction sites irrespective of the concentration of surface molecules. These findings are supported by Vieceli et al.,58 who demonstrated the importance of molecular orientation and double bond orientation in alkene ozonolysis systems at different phase states using molecular dynamics simulations. A different interpretation of this enhanced surface reactivity could be influence of water molecules on the chemical reaction as has been observed in the ozonolysis of maleic acid78 and phosphocholine.79 This would however require existence of a long-lived reaction intermediate whose decomposition can be induced with water molecules and serves as rate-determining step in the reaction mechanism. We discuss the possibility of such reaction intermediates in Section 3.5.
Analysis of the rate coefficients for surface–bulk exchange kb,s,O3 and kss,b,Y reveals that the exchange process cannot be described simply by means of diffusion. The surface–bulk exchange rates are accelerated compared to the rates of bulk diffusion layer at low RH and are found to be overall less dependent on RH. Such surface layers of enhanced mobility are well-known in quasi-liquid surface layers of solid surfaces.60 At low RH, the surface–bulk-exchange rates had thus little influence on calculation results. At higher RH, kb,s,O3 approaches the value expected for a pure diffusive process, whereas kss,b,Y behaves differently: surface–bulk exchange is slowed down heavily at 92% RH compared to the analogous diffusion process. Hence, replenishment of bulk molecules on the surface is at low RH limited by bulk transport and at high RH limited by bulk–surface exchange. A possible reason is the replacement of shikimic acid molecules at the surface by more polar products, preventing an effective surface reaction after depletion of the initial surface layer. Such a low surface–bulk exchange rate was necessary to describe the experimental data, as otherwise the surface reaction plateau, clearly visible in the experimental data, was not reproduced by the model.
3.4 Uniqueness of the kinetic parameter set
Even though a kinetic parameter set was found to fit an experimental data set sufficiently well, these parameters might not constitute the only set generating the same model output and hence not be a unique solution of the optimization problem. If a subset of parameters is mutually dependent, different combinations of these parameters will give an identical result. It is then not guaranteed that a fitted parameter value equals its physical counterpart. In the following we will refer to such parameter pairs or sets as non-orthogonal parameters. We show that the problem of non-orthogonality can often be overcome by fitting many data sets obtained at various experimental conditions and over long time spans. Two parameters might only differ in their influence on the calculation result at specific points during the reaction course (Fig. S1 and S3, ESI†) or show a different effect on the model output under varying experimental conditions.The existence of non-orthogonal parameter sets was investigated for many combinations of input parameters by distributing the parameters on two axes and calculating the total residual R as a 2D contour map. Parameters λi were varied by a factor f(λi) yielding λi′ = f(λi) λi with f(λi) spanning four orders of magnitude from 0.01 to 100. Parameters on the same axis were varied uniformly. A few selected results computed at 24% RH are shown as contour plots in Fig. 8. By far the most common result of this analysis was a distinct minimum in which also the global fitting result (red cross) fell. An example for this is Fig. 8A, which shows a 2D contour map for the parameters τd,O3 and σO3. While both parameters control the Langmuir adsorption equilibrium concentration of ozone at the surface and are thus potentially non-orthogonal, a distinct minimum was found. The two parameters decouple as experimental data with multiple ozone gas phase concentrations is used and τd,O3 and σO3 behave differently upon change in [O3]g.
 | ||
| Fig. 8 Total residual R (colour bar) between experimental data and KM-SUB model results in the local environment of the best fitting parameter set (red crosses, cf. Table S2, ESI†). The best fit parameters λi were multiplied by a factor f(λi) and the residual calculated after eqn (5) and R = ∑ri, to obtain the depicted contour lines. Panel A shows a distinct minimum in R, indicating that an optimum value for both σO3 and τd,O3 was found in the 2D subspace. Panel B shows that when kBR, Db,O3 and kb,s,O3 are varied uniformly against Hcp,O3, a stretched out unconfined minimum is obtained and the parameters are thus non-orthogonal and hence not uniquely defined. Panel C showcases that the same dependence is not observed for subsets of these parameters. Panel D shows that diffusivities of O3 and shikimic acid are not interchangeable. | ||
Non-orthogonality was observed when kBR, kb,s,O3 and Db,O3 were varied uniformly and plotted against Hcp,O3 in Fig. 8B. This finding shows that the values of the parameters Hcp,O3, kBR, kb,s,O3 and Db,O3 cannot be uniquely determined unless any of the parameters is constrained. Note that only the simultaneous increase of the diffusion and reaction parameters can compensate the increase in Hcp,O3, for smaller subsets of the parameters full non-orthogonality was not observed (Fig. 8C). Hence, constraining one of these parameters would determine all others. Since the Henry's law coefficient of ozone can be constrained fairly well in the aqueous solution, the 92% RH data set can be used to constrain all other parameters. By assuming a Hcp,O3 between 1–3 × 10−5 mol cm−3 atm−1, kBR can be constrained between 3 × 10−18 and 1 × 10−17 cm2 s−1, Db,O3 between 2–6 × 10−6 cm2 s−1 and kb,s,O3 between 14.5–43.5 cm s−1. The diffusion coefficients Db,O3 and Db,Y were also found to be orthogonal (Fig. 8D). Note that with a larger subset of parameters, the chance of finding non-orthogonal input parameters can be higher. We tested up to four parameters in two dimensions, as this was the maximum computationally feasible. We cannot exclude that more flexibility exists in the choice of kinetic input parameters reproducing the experimental data.
Another way of detecting dependencies between input parameters λi is to use sensitivity coefficients S(λi). Once sensitivity coefficients are obtained this technique is computationally much more efficient as no further model evaluations are needed. A short description of normalised sensitivity coefficients and the method is given in the supplement (Section B). However, no additional co-dependence of parameters was detected using this method.
3.5 ROI reaction mechanism
The desorption lifetime of ozone and the effective molecular cross section of physisorbed ozone are not compliant with a pure physical adsorption process of ozone. In the following we will suggest an alternative reaction mechanism including the formation of reactive oxygen intermediates (ROI) to explain this behaviour.The desorption lifetime of ozone, τd,O3, was determined to be 5.3 × 10−4 s, which is many orders of magnitude larger than the values of order nanoseconds estimated by molecular dynamics simulations63 and density functional theory.80 Thus, this value must be an effective value that represents additional processes such as decomposition of ozone and formation of long-lived reactive oxygen intermediates (ROI).62,81 A physisorption process with unusually long desorption lifetime also leads to artefacts in the simulation data at the sub-minute time scale: a long residence time leads to high initial uptake of ozone onto the organic film, causing the flow tube to deplete on ozone. The experimental data however shows no evidence for full depletion of ozone in the early stages of the experiment,53 which can only be realised in the kinetic model using desorption lifetimes in the sub-microsecond time range.
The effective molecular cross section of physisorbed ozone, σO3, is found to be 2.4 × 10−14 cm2, which is higher than the geometrical value of 1.5 × 10−15 cm2, hence effectively reducing the number of sorption sites for ozone. As discussed in Section 2.1 this might be due to electrostatic repulsion of adsorbed molecules or dictated by surface morphology, i.e. ozone molecules adsorbing only to certain structural features of the surface. The corresponding maximum surface concentration of adsorbed ozone of 2.4 × 1013 cm−2 closely resembles the coverage of surface-accessible double bonds of 1–2 × 1013 cm−2 expected from the surface cross section of shikimic acid σY, suggesting that surface-adsorbed molecules may interact with the double bond of shikimic acid and pointing towards formation of ROI on the surface.
Formation of ROI on the surface as a form of ozone chemisorption can also explain the emergence of an additional plateau in the experimental data at very low values of γ: while O3 molecules are unlikely to react with another directly by simple collision, decomposition into ROI and subsequent recombination of two chemisorbed O3 molecules could effectively lead to self-reaction of O3 and explain the non-zero uptake of O3 onto dry shikimic acid at long reaction times (Fig. 1).
The accepted mechanism of alkene ozonolysis in both, gas and condensed phases, involves formation of a trioxyl diradical (primary ozonide, PO), following the Criegee mechanism.82–84 The PO further decomposes to a Criegee intermediate and a carbonyl compound.82 The following chemical mechanism (R1–R3) was used to draw a simplified picture of this rather complicated surface chemistry. Subscripts s and ss denote species adsorbed in the sorption layer or surface-exposed in the quasi-static surface layer, respectively. For ozone from the sorption layer we assume a desorption lifetime of 3.2 × 10−9 s, corresponding to a physisorption energy of 20 kJ mol−1.62
| O3(s) + Y(ss) → ROI-1(ss) | (R1) |
| ROI-1(ss) → O3(s) + Y(ss) | (R2) |
| ROI-1(ss) → product | (R3) |
Quantum mechanical calculations suggest an activation barrier of ∼60 kJ mol−1 for the reaction of PO to Criegee intermediates.86–88 Our model results agree well with these calculations and the corresponding energy profile is shown in Fig. 9.62
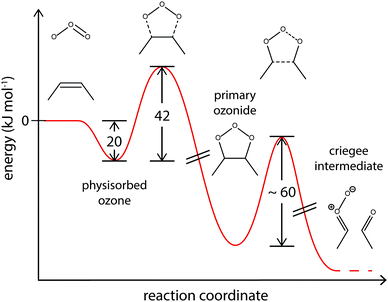 | ||
| Fig. 9 Suggested energy profile for the surface reaction of shikimic acid with ozone, following a Criegee-type mechanism. The model parameters obtained with global optimization give activation energies of 20 kJ mol−1 for desorption of physisorbed oxygen and 42 kJ mol−1 for formation of the reactive oxygen intermediate. This intermediate reacts to Criegee intermediates and carbonyl compounds.85–87 | ||
Note that since no experimental data for decay of the bulk material Y was available, kR2 and kR3 and the corresponding activation energies could not be uniquely constrained, and hence the identity of the reactive intermediate not unerringly identified. In an alternative formulation of this mechanism, a reversible π-complex between ozone and the double bond could also function as reactive intermediate.83,84
While reconciling ozone adsorption properties, the above mechanism cannot fully describe the stable long-term uptake of ozone observed in the experiments under dry conditions since shikimic acid is depleted at the surface under these conditions, hampering the formation of ROI (Fig. S4, ESI†).
Ozone decomposition is known to occur on aromatic surfaces62 and even on inert surfaces such as mineral dust,88 demanding an alternative pathway for ozone chemisorption. We thus tested a mechanism involving a second ROI, which can be thought of as oxygen adatom, whose formation is independent of double bond concentration. Formation and consumption of O2 was neglected in these calculations as its concentration can be assumed constant.
| O3(s) → ROI-2(s) + O2(s) | (R4) |
| ROI-2(s) + O2(s) → O3(s) | (R5) |
| ROI-2(s) + Y(ss) → product | (R6) |
| ROI-2(s) + ROI-2(s) → O2(s) | (R7) |
4 Summary and outlook
Multiphase chemistry of ozone plays an important role in degradation and chemical transformation of atmospheric marker substances. The phase state of organic aerosols is expected to vary as a function of environmental conditions such as temperature and relative humidity. Shikimic acid appears to be a good model compound for organic aerosol, as it similarly adopts a (semi)-solid to liquid phase state depending on RH. We demonstrate that phase state strongly affects the rate of reactive uptake and chemical ageing of organic aerosols. The KM-SUB analysis shows that the predominant kinetic regimes change as a function of time and relative humidity and reveals that even the quasi-stationary states along the reaction coordinate cannot be properly described with resistor or simple kinetic models, i.e. without the use of depth-resolved computation. Even though depth-resolved computation may be too expensive for large-scale atmospheric models, KM-SUB can be used to develop simple but robust parameterizations for atmospheric models.The model simulations suggest the formation of reactive oxygen intermediates, likely primary ozonides or O atoms, at the particle surface. Such intermediates can explain the low sorption site density and the long effective desorption lifetime of ozone needed in Langmuir–Hinshelwood type descriptions of this system. The ROIs provide potential pathways for the self-reaction and catalytic destruction of ozone needed to explain the long-term uptake observed under dry conditions.
The ROI-related pathways of ozone degradation at the surface, together with the amorphous solid phase state of organic matter under cold and dry conditions, may help to explain how reactive organic compounds in the bulk of atmospheric aerosol particles are effectively shielded from degradation by ozone. The apparent abundance and longevity of ROIs has implications for human health as they can generate cytotoxic free radicals and cause oxidative stress upon inhalation of particulates.90
For future experimental studies, the effect of temperature on reactive gas uptake would be of major interest as temperature affects not only the particle phase state, but also the rates of chemical reactions. Simultaneous detection of both oxidant uptake and decay of bulk material would further constrain the kinetic parameter set. We suggest the use of kinetic flux models alongside future laboratory experiments to detect kinetic regimes and push the reaction system into various cases of well-understood kinetic behaviour through choice of experimental conditions. Large data sets under wide experimental conditions would help to constrain the optimization parameter space and to identify processes necessary for accurate description of the kinetic data. Additional measurements of experimentally accessible physical parameters such as Henry's law and diffusion coefficients as function of humidity and temperature would hereby strongly facilitate the global optimization of models to large experimental data sets. Experiments (or simulations) on the sub-second time scale might help to shine further light on surface adsorption processes. To reveal details about the chemical reaction mechanism, spectroscopic techniques sensitive to short-lived and radical species need to be applied in conjunction with further kinetic experiments and modelling studies to identify the important intermediate species and their interactions.
Acknowledgements
This work was funded by the Max Planck Society (MPG) and the EU project PEGASOS. T. B. was supported by the Max Planck Graduate Center with the Johannes Gutenberg-Universität Mainz (MPGC). M. Ammann acknowledges support by the Swiss National Science Foundation (grant no. 163074). We would like to thank Andrew J. Huisman, Claudia Marcolli, Daniel M. Lienhard, Peter Spichtinger, Andrea Pozzer and Rolf Sander for helpful discussions.Notes and references
- M. Kanakidou, et al. , Atmos. Chem. Phys., 2005, 5, 1053–1123 CrossRef CAS.
- M. Hallquist, et al. , Atmos. Chem. Phys., 2009, 9, 5155–5235 CrossRef CAS.
- J. L. Jimenez, et al. , Science, 2009, 326, 1525–1529 CrossRef CAS PubMed.
- M. O. Andreae and D. Rosenfeld, Earth-Sci. Rev., 2008, 89, 13–41 CrossRef.
- U. Pöschl, Angew. Chem., Int. Ed., 2005, 44, 7520–7540 CrossRef PubMed.
- U. Pöschl and M. Shiraiwa, Chem. Rev., 2015, 115, 4440–4475 CrossRef PubMed.
- P. J. Ziemann and R. Atkinson, Chem. Soc. Rev., 2012, 41, 6582–6605 RSC.
- M. Shiraiwa, et al. , Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11003–11008 CrossRef CAS PubMed.
- S. Zhou, et al. , Faraday Discuss., 2013, 165, 391–406 RSC.
- M. Kuwata and S. T. Martin, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 17354–17359 CrossRef CAS PubMed.
- J. H. Slade and D. A. Knopf, Geophys. Res. Lett., 2014, 41, 5297–5306 CrossRef CAS.
- A. M. Arangio, et al. , J. Phys. Chem. A, 2015, 119, 4533–4544 CrossRef CAS PubMed.
- J. H. Kroll, et al. , J. Phys. Chem. A, 2015, 119, 10767–10783 CrossRef CAS PubMed.
- I. J. George and J. P. D. Abbatt, Nat. Chem., 2010, 2, 713–722 CrossRef CAS PubMed.
- M. Shiraiwa, U. Pöschl and D. A. Knopf, Environ. Sci. Technol., 2012, 46, 6630–6636 CrossRef CAS PubMed.
- Y. Rudich, N. M. Donahue and T. F. Mentel, Annu. Rev. Phys. Chem., 2007, 58, 321–352 CrossRef CAS PubMed.
- M. R. Alfarra, et al. , Atmos. Chem. Phys., 2012, 12, 6417–6436 CAS.
- B. Wang, et al. , J. Phys. Chem. A, 2015, 119, 4498–4508 CrossRef CAS PubMed.
- M. Shiraiwa, et al. , Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 11746–11750 CrossRef CAS PubMed.
- Y. Rudich, Chem. Rev., 2003, 103, 5097–5124 CrossRef CAS PubMed.
- F. D. Pope, et al. , Environ. Sci. Technol., 2010, 44, 6656–6660 CrossRef CAS PubMed.
- A. T. Lambe, et al. , Atmos. Chem. Phys., 2011, 11, 8913–8928 CAS.
- N. A. Hosny, et al. , Chem. Sci., 2016, 7, 1357–1367 RSC.
- T. D. Vaden, et al. , Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 2190–2195 CrossRef CAS PubMed.
- J. P. D. Abbatt, A. K. Y. Lee and J. A. Thornton, Chem. Soc. Rev., 2012, 41, 6555–6581 RSC.
- M. Shiraiwa, et al. , Phys. Chem. Chem. Phys., 2013, 15, 11441–11453 RSC.
- J. Laskin, et al. , Anal. Chem., 2010, 82, 2048–2058 CrossRef CAS PubMed.
- R. D. McWhinney, et al. , Environ. Sci. Technol., 2011, 45, 2131–2136 CrossRef CAS PubMed.
- C. Pfrang, M. Shiraiwa and U. Pöschl, Atmos. Chem. Phys., 2011, 11, 7343–7354 CAS.
- D. A. Knopf, L. M. Anthony and A. K. Bertram, J. Phys. Chem. A, 2005, 109, 5579–5589 CrossRef CAS PubMed.
- C. Kidd, et al. , Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 7552–7557 CrossRef CAS PubMed.
- F. H. Marshall, et al. , Chem. Sci., 2016, 7, 1298–1308 RSC.
- B. Zobrist, et al. , Atmos. Chem. Phys., 2008, 8, 5221–5244 CrossRef CAS.
- B. J. Murray, et al. , Nat. Geosci., 2010, 3, 233–237 CrossRef CAS.
- A. Virtanen, et al. , Nature, 2010, 467, 824–827 CrossRef CAS PubMed.
- T. Koop, et al. , Phys. Chem. Chem. Phys., 2011, 13, 19238–19255 RSC.
- E. Saukko, et al. , Atmos. Chem. Phys., 2012, 12, 7517–7529 CrossRef CAS.
- R. M. Power, et al. , Chem. Sci., 2013, 4, 2597–2604 RSC.
- L. Renbaum-Wolff, et al. , Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8014–8019 CrossRef CAS PubMed.
- E. Abramson, et al. , Phys. Chem. Chem. Phys., 2013, 15, 2983–2991 RSC.
- H. J. Tong, et al. , Atmos. Chem. Phys., 2011, 11, 4739–4754 CrossRef CAS.
- T. Berkemeier, et al. , Atmos. Chem. Phys., 2014, 14, 12513–12531 Search PubMed.
- H. C. Price, et al. , Atmos. Chem. Phys., 2014, 14, 3817–3830 CrossRef.
- J. F. Davies and K. R. Wilson, Chem. Sci., 2015, 6, 7020–7027 RSC.
- B. J. Finlayson-Pitts and J. N. Pitts, Chemistry of the upper and lower atmosphere, Academic Press, San Diego, California, 1999 Search PubMed.
- D. R. Worsnop, et al. , Geophys. Res. Lett., 2002, 29, 57 CrossRef.
- T. Berkemeier, et al. , Atmos. Chem. Phys., 2013, 13, 6663–6686 Search PubMed.
- G. D. Smith, et al. , J. Phys. Chem. A, 2003, 107, 9582–9587 CrossRef CAS.
- M. Shiraiwa, C. Pfrang and U. Pöschl, Atmos. Chem. Phys., 2010, 10, 3673–3691 CrossRef CAS.
- M. Shiraiwa, et al. , Atmos. Chem. Phys., 2012, 12, 2777–2794 CrossRef CAS.
- P. Roldin, et al. , Atmos. Chem. Phys., 2014, 14, 7953–7993 Search PubMed.
- C. Pfrang, M. Shiraiwa and U. Pöschl, Atmos. Chem. Phys., 2010, 10, 4537–4557 CAS.
- S. S. Steimer, et al. , Phys. Chem. Chem. Phys., 2015, 17, 31101–31109 RSC.
- D. M. Lienhard, et al. , Atmos. Chem. Phys., 2015, 15, 13599–13613 CrossRef CAS.
- U. Pöschl, Y. Rudich and M. Ammann, Atmos. Chem. Phys., 2007, 7, 5989–6023 CrossRef.
- D. A. Knopf, U. Pöschl and M. Shiraiwa, Anal. Chem., 2015, 87, 3746–3754 CrossRef CAS PubMed.
- B. Zobrist, et al. , Phys. Chem. Chem. Phys., 2011, 13, 3514–3526 RSC.
- J. Vieceli, O. L. Ma and D. J. Tobias, J. Phys. Chem. A, 2004, 108, 5806–5814 CrossRef CAS.
- S. S. Steimer, et al. , Atmos. Meas. Tech., 2015, 8, 2397–2408 CrossRef.
- M. D. Ediger and J. A. Forrest, Macromolecules, 2014, 47, 471–478 CrossRef CAS.
- W. J. Massman, Atmos. Environ., 1998, 32, 1111–1127 CrossRef CAS.
- M. Shiraiwa, et al. , Nat. Chem., 2011, 3, 291–295 CrossRef CAS PubMed.
- J. Vieceli, et al. , J. Phys. Chem. B, 2005, 109, 15876–15892 CrossRef CAS PubMed.
- S. Takahama and L. M. Russell, J. Geophys. Res.: Atmos., 2011, 116, D02203 CrossRef.
- J. Julin, et al. , J. Phys. Chem. A, 2013, 117, 410–420 CrossRef CAS PubMed.
- M. Shiraiwa, et al. , Atmos. Chem. Phys., 2014, 14, 8323–8341 Search PubMed.
- G. D. Smith, et al. , J. Phys. Chem. A, 2002, 106, 8085–8095 CrossRef CAS.
- J. D. Hearn, A. J. Lovett and G. D. Smith, Phys. Chem. Chem. Phys., 2005, 7, 501–511 RSC.
- S. S. Steimer, et al. , Atmos. Chem. Phys., 2014, 14, 10761–10772 Search PubMed.
- D. R. Hanson, A. R. Ravishankara and S. Solomon, J. Geophys. Res.: Atmos., 1994, 99, 3615–3629 CrossRef CAS.
- T. Murata, M. S. Lee and A. Tanioka, J. Colloid Interface Sci., 1999, 220, 250–254 CrossRef CAS PubMed.
- H. C. Price, et al. , Chem. Sci., 2015, 6, 4876–4883 RSC.
- E. Mikhailov, et al. , Atmos. Chem. Phys., 2009, 9, 9491–9522 CrossRef CAS.
- R. Sander, Atmos. Chem. Phys., 2015, 15, 4399–4981 CAS.
- S. D. Razumovskii and G. E. Zaikov, Ozone and its reactions with organic compounds, Elsevier, Amsterdam, 1984 Search PubMed.
- A. K. Bin, Ozone: Sci. Eng., 2006, 28, 67–75 CrossRef CAS.
- J. Hoigne and H. Bader, Water Res., 1983, 17, 173–183 CrossRef CAS.
- P. J. Gallimore, et al. , Atmos. Chem. Phys., 2011, 11, 12181–12195 CrossRef CAS.
- C. W. Dilbeck and B. J. Finlayson-Pitts, Phys. Chem. Chem. Phys., 2013, 15, 1990–2002 RSC.
- A. Maranzana, et al. , J. Phys. Chem. A, 2005, 109, 10929–10939 CrossRef CAS PubMed.
- U. Pöschl, et al. , J. Phys. Chem. A, 2001, 105, 4029–4041 CrossRef.
- L. Vereecken, D. R. Glowacki and M. J. Pilling, Chem. Rev., 2015, 115, 4063–4114 CrossRef CAS PubMed.
- E. R. Altwicker and J. Basila, Tetrahedron, 1973, 29, 1969–1974 CrossRef CAS.
- W. G. Alcock and B. Mile, J. Chem. Soc., Chem. Commun., 1976, 5–6, 10.1039/c39760000005.
- M. Olzmann, et al. , J. Phys. Chem. A, 1997, 101, 9421–9429 CrossRef CAS.
- C. A. Taatjes, D. E. Shallcross and C. J. Percival, Phys. Chem. Chem. Phys., 2014, 16, 1704–1718 RSC.
- K. T. Kuwata, et al. , J. Phys. Chem. A, 2010, 114, 9192–9204 CrossRef CAS PubMed.
- C. R. Usher, A. E. Michel and V. H. Grassian, Chem. Rev., 2003, 103, 4883–4940 CrossRef CAS PubMed.
- J. McCabe and J. P. D. Abbatt, J. Phys. Chem. C, 2009, 113, 2120–2127 CAS.
- S. Enami, M. R. Hoffmann and A. J. Colussi, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 7365–7369 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp00634e |
| This journal is © the Owner Societies 2016 |