Reactivity of atomically dispersed Pt²⁺ species towards H₂: model Pt–CeO₂ fuel cell catalyst

Abstract

The reactivity of atomically dispersed Pt²⁺ species on the surface of nanostructured CeO₂ films and the mechanism of H₂ activation on these sites have been investigated by means of synchrotron radiation photoelectron spectroscopy and resonant photoemission spectroscopy in combination with density functional calculations. Isolated Pt²⁺ sites are found to be inactive towards H₂ dissociation due to high activation energy required for H–H bond scission. Trace amounts of metallic Pt are necessary to initiate H₂ dissociation on Pt–CeO₂ films. H₂ dissociation triggers the reduction of Ce⁴⁺ cations which, in turn, is coupled with the reduction of Pt²⁺ species. The mechanism of Pt²⁺ reduction involves reverse oxygen spillover and formation of oxygen vacancies on Pt–CeO₂ films. Our calculations suggest the existence of a threshold concentration of oxygen vacancies associated with the onset of Pt²⁺ reduction.

---

1. Introduction

Hydrogen fuel cells (FCs) have attracted significant attention during the last few years as environmentally friendly power sources for a variety of small to medium-scale applications, including automotive vehicle propulsion or even chip-integrated micro-devices.^1–3 The high demand for noble metals is among the major challenges associated with low-temperature FC technology. Recently, it was shown that novel catalytic materials containing atomically dispersed Pt²⁺ species^4–8 on the surface of nanostructured CeO₂ are highly efficient anode catalysts for hydrogen FCs.^8–10

The mechanism of H₂ activation on nanostructured CeO₂ containing ionic Pt²⁺, however, remains controversial. One of the reasons is that the role of atomically dispersed Pt²⁺ on CeO₂ has not been studied individually, i.e. in the absence of other active species such as Pt⁴⁺, Pt⁰, and oxygen vacancies.^11–13 For instance, most of the studies employed Pt-doped CeO₂ materials in the form of solid solutions, Ce_1−xPt_xO_2−δ, prepared by the solution combustion method.^11,12 This preparation method yields oxygen vacancies as the result of charge compensation upon substitution of Ce⁴⁺ ions by Pt²⁺ in the Ce_1−xPt_xO_2−δ solid solution.^12,14 In the most stable configuration, the Pt²⁺ is displaced from the Ce⁴⁺ site to adopt a square planar arrangement with four lattice oxygen ions and one oxygen vacancy is formed per Pt²⁺ site.¹⁵ In Ce_1−xPt_xO_2−δ catalysts, the charge compensating oxygen vacancy is located within the square planar arrangement of Pt²⁺ ions forming a Pt–O₃ moiety.^5,12 In the corresponding configuration, Pt²⁺ has three Pt–O bonds with a length of about 200 pm.^5,12

In contrast to the combustion solution method, physical vapor deposition (PVD) and radio frequency magnetron sputtering yield a Pt–O₄ moiety without the oxygen vacancies.⁸ It was found that Pt²⁺ is anchored on the CeO₂ support at {100} nanofacets, which form so-called O₄ nanopockets, abundant at the surface of nanostructured cerium oxide.⁸ Here, the oxide support serves as a polydentate ligand for Pt²⁺ species and their binding can be described similarly to that in classical coordination compounds.¹⁶ The formation of the Pt–O₄ moiety is not accompanied by creation of the charge compensating oxygen vacancy. Instead, two Ce⁴⁺ cations are reduced to Ce³⁺ per one Pt²⁺ site. The corresponding Ce³⁺ ions can be re-oxidized to Ce⁴⁺ in an oxygen atmosphere during the catalyst preparation. The exceptionally high stability of the Pt–O₄ moiety^8,17 is likely to be responsible for the excellent durability of the Pt–CeO₂ based anode catalyst even under dynamic operation conditions.^9,10

In the present study we provide new insights into the mechanism of hydrogen activation on Pt²⁺–CeO₂ in the absence of oxygen vacancies and identify the active sites for hydrogen dissociation. Our model catalyst approach allows us to isolate Pt²⁺ sites as well as to control the amount of metallic Pt⁰ in the Pt–CeO₂ films. We employed high-resolution synchrotron photoelectron spectroscopy (SRPES) and resonant photoemission spectroscopy (RPES) to monitor the oxidation states of Pt²⁺ and Ce⁴⁺ ions with ultimate surface sensitivity.

2. Materials and methods

2.1. Experimental details: SRPES and RPES

High-resolution SRPES experiments were performed at the Materials Science Beamline (MSB), Elettra synchrotron light facility in Trieste, Italy. The MSB, with a bending magnet source provides synchrotron light in the energy range of 21–1000 eV. The ultrahigh vacuum (UHV) end-station (base pressure 1 × 10⁻¹⁰ mbar) is equipped with a multichannel electron energy analyzer (Specs Phoibos 150), a rear view low energy electron diffraction (LEED) optics, a sputter gun (Ar), and a gas inlet system. The basic setup of the chamber includes a dual Mg/Al X-ray source.

The Pt–CeO₂ oxide films were prepared on a well-ordered CeO₂(111) buffer layer grown on a single crystal Cu(111) substrate. Cu(111) (MaTecK GmbH, 99.999%) was cleaned by several cycles of Ar⁺ sputtering (300 K, 60 min) and annealing (723 K, 5 min) until no traces of carbon or any other contaminant were found in the photoelectron spectra. Then, an epitaxial CeO₂(111) layer was deposited onto the clean Cu(111) substrate by PVD of Ce metal (Goodfellow, 99.99%) in an oxygen atmosphere (p_O2 = 5 × 10⁻⁵ Pa, Linde, 99.999%) at 523 K. This preparation method¹⁸ yielded a continuous, stoichiometric CeO₂(111) film with a thickness of 1.5 nm as determined from the attenuation of the Cu 2p_3/2 intensity. In the next step, the mixed Pt–CeO₂ films were prepared by means of simultaneous PVD of Ce and Pt (Goodfellow, 99.99%) metals in an oxygen atmosphere (p_O2 = 5 × 10⁻⁵ Pa) onto the CeO₂(111)/Cu(111) at 110 K. The low deposition temperature results in a growth of Pt–CeO₂ nanoparticles on the CeO₂(111) film.⁸

The Pt concentration of 5%, 15% and 18% per volume of the mixed layers was achieved by using different Pt/Ce deposition rate ratios. The deposition rate ratios were determined from the ratios of nominal thicknesses of Pt to CeO₂ deposited during the same period of time. All Pt–CeO₂/CeO₂(111) were deposited onto a 1.5 nm thick CeO₂(111) buffer layer at 110 K and maintained a nominal thickness of Pt–CeO₂ film of 0.3 nm.

During the course of experiments, all Pt–CeO₂/CeO₂(111) samples were briefly annealed at 700 K followed by cooling to 110 K. This treatment eliminated the less stable Pt⁴⁺ species yielding exclusively Pt²⁺ for 5% Pt–CeO₂ film. For 15% and 18% Pt–CeO₂, Pt²⁺ is formed together with metallic Pt⁰ particles of different size (see ref. 8 for details). Then, the Pt–CeO₂/CeO₂(111) samples were exposed to 50 L of H₂ (2.67 × 10⁻⁵ Pa, 250 s) at different temperatures between 110 and 700 K. Hydrogen (Linde 99.999%) was dosed by backfilling the UHV chamber.

The Pt 4f spectra were acquired with photon energies of 180 eV. The binding energies in the spectra acquired with synchrotron radiation were calibrated with respect to the Fermi level. Additionally, Al Kα radiation (1486.6 eV) was used to measure O 1s, Ce 3d, Pt 4f, and Cu 2p_3/2 core levels. All spectra were acquired at constant pass energy and at an emission angle for the photoelectrons of 20° or 0° with respect to the sample normal, while using the X-ray source or synchrotron radiation, respectively. All spectral components were fitted with a Voigt profile. Pt 4f spectra were fitted by doublet peaks with a spin–orbit splitting of 3.30 eV and a fixed branching ratio of 1.33. Cu 3p spectra were fitted by a doublet with a fixed spin–orbit splitting of 2.42 eV and a fixed branching ratio of 2. A combination of a linear and Shirley background was subtracted from Pt 4f spectra.

Valence band spectra were acquired at three different photon energies, 121.4, 124.8, and 115.0 eV, that correspond to the resonant enhancements in Ce³⁺, Ce⁴⁺ ions, and to off-resonance conditions, respectively. Analysis of the spectra obtained with these photon energies forms the basis of RPES.^19,20 The ratio between the corresponding resonant intensities, D(Ce³⁺)/D(Ce⁴⁺), denoted as a Resonant Enhancement Ratio (RER) is a direct measure of the degree of reduction of cerium oxide and can be used to quantify the concentration of Ce³⁺ ions in the films.²¹ All SRPES data were processed using KolXPD fitting software.²² The values of total spectral resolution were 1 eV (Al Kα), 200 meV (hν = 115–180 eV), 400 meV (hν = 410 eV) and 650 meV (hν = 650 eV). During the experiment, the sample temperature was controlled by a DC power supply passing a current through Ta wires holding the sample. Temperatures were monitored by a K-type thermocouple attached to the back of the sample.

2.2. Computational details: model Pt²⁺ sites on extended ceria surfaces

The theoretical study of the adsorption and dissociation of H₂ on model Pt sites at extended CeO₂ surfaces was based on the density functional theory (DFT) calculations employing the Perdew–Burke–Ernzerhof (PBE)²³ generalized gradient approximation (GGA) for the exchange and correlation (XC) functional. In line with previous studies,^24–26 the ions were described with Vanderbilt's ultrasoft pseudopotentials,²⁷ while the crystal wavefunction and density were expanded with a plane-wave basis set limited by energy cutoffs of 40 and 320 Ry, respectively. It is well established that the usual local and gradient-corrected approximations of the XC functional cannot describe the correct insulating electronic structure of ceria-based materials.^24,28,29 This is because the electron self-interaction effects arising from the high localization of the Ce 4f electrons are not properly cancelled out by these XC approximations. The addition of an on-site Hubbard U term to the GGA functional (GGA+U) has been proven to be a practical and efficient method to simulate ceria-based systems.^24,28,29 For the periodic surface-slab calculations we used the GGA+U method as implemented by Cococcioni and de Gironcoli,³⁰ employing a value of the parameter U = 4.5 eV in line with previous works.^24,25,31 Integrals in the Brillouin zone were calculated at the Γ point. These calculations were performed using the Quantum Espresso package.³²

The CeO₂(111) surface was modeled with 3 O–Ce–O tri-layers separated by more than 12 Å of vacuum normal to the surface. The coordinates of the lowermost tri-layer were constrained to their bulk-like optimized positions, while all other atoms were allowed to relax during the structural optimizations. The Pt₆ cluster supported on the CeO₂(111) surface was modeled as described in ref. 26. The CeO₂ surface step was modeled with a vicinal surface exposing (110) facets between (111) terraces, and was described with monoclinic periodic slabs separated by more than 10 Å of vacuum in the direction perpendicular to the (111) terrace and labeled as step I in the ref. 33. The dimensions of the cell were 17.97 × 11.67 Å along the [11̄2] and [11̄0] directions, where the [11̄0] direction is parallel to the step edge. The vicinal surface slabs were 3 CeO₂ tri-layers thick. It has been shown that this thickness is sufficient to converge the structural and thermodynamic step properties.³³ The Pt²⁺ ion at this step edge was obtained by adsorbing a Pt atom at the hollow site of the (110) facet of the vicinal surface. During the geometry optimization, the atomic positions of the lowermost CeO₂ tri-layer were constrained as well as those of the Ce atoms in the central tri-layer, except for the Ce atoms below the step edge. All structures were relaxed by minimizing the atomic forces, until the maximum component of the residual forces on each ion was less than 0.02 eV Å⁻¹.

To compute the minimum energy path for H₂ dissociation we employed the Climbing-Image Nudge-Elastic-Band method³⁴ using the Broyden scheme. These calculations were performed in the supercells described above including up to 17 replica images.

2.3. Computational details: model Pt²⁺ sites on ceria nanoparticles

The adsorption of atomic Pt on the {100} sites resulting in the formation of the Pt–O₄ moiety on the ceria nanoparticles (NPs) has been investigated by means of periodic spin-polarized density functional calculations using the VASP code.^35–37 In line with previous studies,^19,38–40 present calculations of ceria NP systems have been performed using the PW91⁴¹ XC potential corrected with a value of U = 4 eV. The valence states were represented using plane-wave basis set with a cut-off of 415 eV for the kinetic energy. The core-valence electrons interaction has been described through the projector augmented wave method.⁴² Only the Γ-point has been used to sample the reciprocal space. The electron density was self-consistently converged with a 10⁻⁴ eV total energy threshold and structures were optimized until forces acting on all atoms were smaller than 0.02 eV Å⁻¹. Formation energies of n oxygen vacancies in mPt–Ce₄₀O₈₀ models were calculated with respect to the energy of O₂ molecule, E(O₂), as follows: E_vac = {E(mPt–Ce₄₀O_80−n) + n/2[E(O₂)] − E(mPt–Ce₄₀O₈₀)}/n. Whereas ceria NPs of many different shapes and sizes coexist in experiments, simulated models have to be restricted to a model selected from a variety of low-energy nanoparticulate systems.^39,40,43 We have chosen the NP Ce₄₀O₈₀ to represent in a qualitative fashion properties of the experimentally treated nanostructures. Our benchmark calculations have shown, for instance, that increasing the NP to Ce₈₀O₁₆₀ insignificantly affects the adsorption of metal atoms.⁸ Note also that the increase of the U-value to 4.5 eV (the value used in the calculations of the extended ceria surfaces, see Section 2.2) will strengthen the binding of Pt atom to the O₄ site on the NP Ce₄₀O₈₀ by only 4%.⁸

3. Results and discussion

3.1. Reactivity of Pt–CeO₂ films towards molecular hydrogen

Pt 4f spectra obtained from 5%, 15%, and 18% Pt–CeO₂ films prepared by physical vapor co-deposition of Pt and Ce metals in an oxygen atmosphere onto CeO₂/Cu(111) buffer layer followed by a brief annealing to 700 K in UHV are shown in Fig. 1 (top traces).

Fig. 1 Pt 4f spectra obtained from 5% Pt–CeO₂ (a), 15% Pt–CeO₂ (b), and 18% Pt–CeO₂ (c) films prepared by co-deposition of Pt and Ce in an oxygen atmosphere at 110 K on CeO₂(111)/Cu(111) films followed by a brief annealing to 700 K (top spectra) and subsequently exposed to 50 L of hydrogen at different temperatures. The Cu 3p signal originates from the underlying Cu(111) substrate. The spectra were acquired with photon energy of 180 eV.

The Pt 4f spectrum obtained from 5% Pt–CeO₂ film contains a single spin–orbit doublet at 73.0 eV (Pt 4f_7/2) associated with Pt²⁺ species in a square planar coordination, i.e. Pt–O₄ moiety.⁸ A second broad spin–orbit doublet arises from the underlying Cu(111) substrate at 75.1 eV (Cu 3p_3/2). Earlier we reported that Pt⁴⁺ ions formed in small amounts on Pt–CeO₂ films prepared by PVD at 110 K are largely eliminated by annealing above 300 K in UHV.^8,44 Besides the major contribution from Pt²⁺ species, two additional spin–orbit doublets emerge in the Pt 4f spectra obtained from 15% and 18% Pt–CeO₂ films at 71.1–71.2 (Pt 4f_7/2) and 72.0 eV (Pt 4f_7/2). We associate the corresponding peaks with the presence of metallic (Pt⁰) and oxidized Pt particles (Pt*). We assume that the Pt⁰ particles on the samples with 15% and 18% Pt are partially covered by atomic oxygen due to the reverse oxygen spillover triggered by annealing.^19,26 The same phenomenon likely leads to oxidation of smaller Pt particles resulting in the Pt* component in the spectra of both 15% and 18% Pt–CeO₂ films.⁴⁵ Earlier a similar component was detected by Hatanaka et al.⁴⁶ and Wu et al.⁴⁷ at 72.1 eV in the spectra of small oxidized Pt clusters supported on CeO₂.

Previous calculations based on DFT predicted that the dissociation of molecular H₂ on pristine CeO₂(111) surfaces leads to surface hydroxylation and reduction of cerium cations.^48–51 The dissociation of H₂ is associated with a high activation barrier (∼1.0 eV)^48–50 and therefore requires high pressures (∼10⁵ Pa)^52–56 and/or elevated temperatures. In our previous studies, however, we did not observe any activity of noble-metal-free CeO₂(111) towards H₂ dissociation under the conditions of a UHV model experiment (<10⁻⁴ Pa).⁵⁷ This observation suggests that the reaction rate of hydrogen dissociation on pure CeO₂(111) under the UHV conditions is too low to yield measurable changes in the oxidation state of cerium cations.

In order to detect whether H₂ dissociation is possible on the Pt–CeO₂ films, we monitored the oxidation states of both Pt and Ce cations. In particular, we employed resonant photoemission spectroscopy²⁰ to quantify the oxidation state of Ce cations with high surface sensitivity (see Methods). The Pt 4f spectra obtained from 5%, 15%, and 18% Pt–CeO₂ films exposed to hydrogen at different temperatures are shown in Fig. 1. The corresponding development of the relative concentrations of Pt²⁺, Pt⁰, and Pt* along with Ce³⁺ are plotted in Fig. 2. We found that interaction of H₂ with the 5% Pt–CeO₂ film does not cause reduction of Pt²⁺ or Ce⁴⁺ (Fig. 2a and d). This observation strongly suggests that the Pt²⁺ sites do not facilitate dissociation of molecular hydrogen under the experimental conditions employed.

Fig. 2 Relative concentrations of Pt²⁺, Pt⁰, Pt* per total Pt content (a–c) and Ce³⁺ per total number of Ce and RERs (d–f) on 5% Pt–CeO₂ (a and d), 15% Pt–CeO₂ (b and e), and 18% Pt–CeO₂ (c and f) films as a function of temperature during annealing under exposure to 50 L H₂. The circled data points were obtained prior to the hydrogen exposure.

To clarify this experimental finding we performed DFT calculations to compare the reaction pathways and the energetics for H₂ dissociation on both the Pt²⁺ (Fig. 3, red line) and the CeO₂(111) surface sites (Fig. 3, black line). The Pt–CeO₂ system was modeled as a low-energy vicinal surface exposing CeO₂(111) terraces and step edges along the [11̄0] direction.³³ We found that Pt atoms bind at step facets forming planar Pt–O₄ moieties that have structural and electronic properties very similar to Pt–O₄ species identified on ceria nanoparticles.⁸ Our present calculations show that the activation energy for H₂ dissociation at the Pt²⁺ sites is even larger than the barrier on the pristine CeO₂(111) surface.

Fig. 3 Minimum energy paths for H₂ dissociation on the pristine CeO₂(111) surface (black, adapted with permission from ref. 51. Copyright 2015 American Chemical Society), the ionic Pt²⁺ sites (red), and the supported Pt₆ cluster (green) – middle panel. The top and bottom panels display the initial (IS), transition (TS), and final (FS) states of H₂ dissociation on the Pt²⁺–CeO₂ and Pt₆/CeO₂(111) systems. The activation energies in TS states (open symbols) are given in parentheses. Ce⁴⁺, Ce³⁺, and O²⁻ ions are displayed as yellow, brown, and red spheres, respectively.

Compared to the value of 1.0 eV calculated for the pristine CeO₂(111) surface,⁵¹ the barrier increases to 1.2 eV in the presence of the Pt²⁺ sites at the steps. The lower propensity towards H₂ adsorption on these Pt²⁺ sites can be explained by electrostatic arguments as proposed by García-Melchor and López.⁴⁸ The higher activation energy calculated for the Pt²⁺ sites implies that H₂ desorption is strongly favored against dissociation, in accordance with the experiment showing no activity for the 5% Pt–CeO₂ system.

In sharp contrast to the 5% Pt–CeO₂, we detected facile reduction of Pt²⁺ species coupled with the reduction of Ce⁴⁺ on both 15% and 18% Pt–CeO₂ samples upon reaction with H₂ at elevated temperatures (see Fig. 1b, c, 2b, c, e and f). Eventually, all Pt²⁺ species are reduced quantitatively to metallic Pt⁰. Remarkably, very small amounts of Pt⁰ turned out to be sufficient to initiate the reduction process (see Fig. 1b, 2b and e). Note that such small amounts of metallic Pt⁰ as are present on the 15% Pt–CeO₂ film (corresponding to a nominal coverage of less than 0.05 Å Pt) could be hardly detected by conventional X-ray photoelectron spectroscopy. Quite consistently, our DFT simulations show that sub-nm sized Pt clusters supported on ceria are, indeed, highly active for H₂ dissociation. For instance, we calculated an activation energy of ∼0.3 eV (Fig. 3, green line) for Pt₆ particle supported on CeO₂(111), which can be easily overcome even at low temperature.

3.2. The mechanism of Pt²⁺ reduction in the presence of metallic Pt particles

In view of the high stability of the Pt–O₄ moiety,⁸ the observed reduction of Pt²⁺ sites upon reaction with hydrogen may appear surprising. However, we reported previously that the adsorption of atomic hydrogen, leading to hydroxylation of the oxygen ions of the Pt–O₄ moiety and reduction of Ce⁴⁺ results in destabilization and, possibly, in reduction of Pt²⁺ species.⁸ In the presence of metallic Pt⁰ on Pt–CeO₂, atomic hydrogen could spillover from Pt particles to the support leading to hydroxylation of the Pt–O₄ moiety. In fact, the calculated reaction pathway on Pt₆/CeO₂ (Fig. 3, final state bottom panels) suggests the tendency for H to migrate to the cluster periphery and accumulate at the boundary in contact with the oxide support.

On Pt/CeO₂(111) model catalysts, reversible hydrogen spillover is typically indicated by an increase of the RER between 190 and 260 K by about ΔRER = 0.3.⁵⁷ On both the 15% and the 18% Pt–CeO₂ samples (Fig. 2e and f) the corresponding effect is much weaker. Therefore, we assume that there is only little tendency for hydrogen spillover from the metallic Pt particles to the oxide for the Pt–CeO₂ catalysts employed in the present work. This suggests that hydrogen spillover and hydroxylation of Pt–O₄ are not the key steps in Pt²⁺ reduction during the reaction with H₂.

Thus, the mechanism of Pt²⁺ reduction is likely to be associated with the formation of oxygen vacancies upon reverse oxygen spillover¹⁹ from Pt–CeO₂ to the Pt particles. Upon exposure to H₂ the spilt-over oxygen is continuously removed from the Pt particles by reaction with hydrogen and formation of water which desorbs immediately. This reaction channel leads to formation of oxygen vacancies accompanied by the reduction of Ce⁴⁺. The corresponding scenario is consistent with the absence of hydroxyl groups in the O 1s spectra on 15% and 18% Pt–CeO₂ films exposed to H₂ above 350 K (data not shown). The developments of the Pt²⁺ (Fig. 2b and c) and the Ce³⁺ (Fig. 2e and f) concentrations show that reduction of Ce⁴⁺ slightly precedes the reduction of Pt²⁺. This suggests that the Pt²⁺ ions are destabilized in the presence of oxygen vacancies and at sufficiently high vacancy concentration are eventually reduced to Pt⁰.

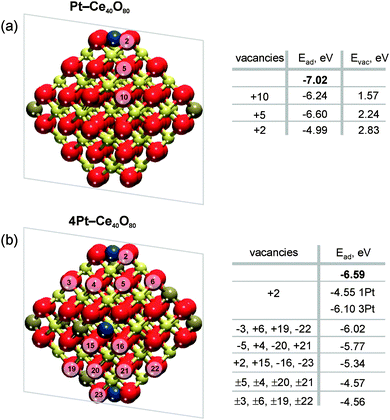
Indeed, our DFT calculations show that the formation of oxygen vacancies notably lowers the adsorption energy of Pt atom in Pt–Ce₄₀O₈₀ and 4Pt–Ce₄₀O₈₀ NPs (see Fig. 4). The stability of Pt²⁺ depends on various parameters such as the proximity of the oxygen vacancies, their number, the Pt²⁺ concentration, and the distribution of Ce³⁺ ions (see ESI† for details).

Fig. 4 Adsorption energies of atomic Pt in the 2+ state, E_ad, without (n = 0) and with n (n > 0) oxygen vacancies on (a) Pt–Ce₄₀O_80−n and (b) 4Pt–Ce₄₀O_80−n nanoparticle models. E_ad values calculated in the absence of oxygen vacancies are shown in bold. The transparent planes cut the nanoparticles into two halves. The vacancies with the signs “+” and “−” are located in front of and behind the planes, respectively. The sign “±“indicates two symmetric oxygen vacancies located in front of and behind the transparent planes. For the 4Pt–Ce₄₀O_80−n nanoparticle (b), the formation of one oxygen vacancy at the position +2 leads to significant decrease of E_ad of one Pt²⁺ in the proximity of the vacancy (1Pt) while the remaining three Pt²⁺ species (3Pt) are influenced less significantly. Formation energies of oxygen vacancies, E_vac, in Pt–Ce₄₀O₈₀ model (a) were calculated with respect to the energy of O₂ molecule.

The criterion for Pt²⁺ being stable against formation of metallic particles is that the magnitude of adsorption energy of atomic Pt, E_ad, is larger than the bulk cohesive energy value of Pt (−5.85 eV).⁵⁸ For isolated Pt²⁺ in the {100} O₄ nanopocket of stoichiometric CeO₂ this is clearly the case (E_ad = −7.02 eV). The formation of a single oxygen vacancy in a position outside the {100} nanopocket (Pt–Ce₄₀O₇₉, vacancy positions +5 or +10, see Fig. 4) is not energetically sufficient to trigger the reduction of Pt²⁺ cations. The same holds in the case where four vacancies have been created outside the pockets on NP with four Pt²⁺ ions (4Pt–Ce₄₀O₇₆, vacancy positions −3, 6, 19, −22 or +4, −5, −20, 21, see Fig. 4).

The adsorption energy of atomic Pt in the 2+ state falls dramatically below the cohesive energy (to −4.55 or −4.99 eV) if a single vacancy is created inside the square pocket (position +2). Such decrease is a direct consequence of the loss of the square-planar coordination for the Pt²⁺ cations. However, the vacancy formation energy is strongly enhanced at the pocket sites themselves (see Tables S1 and S2, ESI†). This suggests that, at least initially, the oxygen vacancies will be formed preferentially outside the Pt–O₄ moiety. If two of such oxygen vacancies are created per Pt²⁺ ion, we indeed find configurations in which the Pt²⁺ adsorption energy falls well below the cohesive energy. This is the case, for instance, upon creation of eight oxygen vacancies in the 4Pt–Ce₄₀O₈₀ system (4Pt–Ce₄₀O₇₂, vacancy position ±4, ±5, ±20, ±21 or ±3, ±6, ±22, ±19, see Fig. 4). Thus, DFT calculations indicate that the onset of Pt²⁺ reduction occurs when approximately two oxygen vacancies are created per each Pt²⁺ site.

Interestingly, a rough estimation of the ratio between the concentrations of oxygen vacancies and the Pt²⁺ cations at the onset of Pt²⁺ reduction can be obtained from the experimental data (see ESI,† Table S3). The concentration of oxygen vacancies produced by oxygen spillover can be calculated from the temperature dependent change in the Ce³⁺ concentration, taking into account that two Ce³⁺ ions are produced per oxygen vacancy (note that the Ce³⁺ ions present at low temperature originate from the charge transfer from metallic particles without the generation of oxygen vacancies).^19,59 As well, a certain number of Ce³⁺ ions emerge upon the redox reaction between Pt and CeO₂ during the growth of Pt²⁺–CeO₂ films.⁸ In addition we have to take into account the consumption of Pt²⁺ ions because the reduction of one Pt²⁺ ion leads to formation of two additional Ce⁴⁺ centers, which subsequently may be reduced to Ce³⁺ by formation of one oxygen vacancy. Taking both contributions into account, we obtain a ratio of 1.5 between the concentration of the oxygen vacancies and the concentration of Pt²⁺ ions in the temperature region between 450 and 500 K, where the onset of Pt²⁺ reduction is observed (see ESI† for details of the evaluation procedure). It is noteworthy that this value is in fairly good agreement with the results of our DFT calculations.

4. Conclusions

We have studied H₂ activation on Pt–CeO₂ model catalysts under UHV conditions by means of SRPES, RPES, and DFT calculations. The isolated Pt²⁺ sites on the catalyst surface are found to be inactive towards H₂ dissociation. The activation of H₂ on Pt–CeO₂ requires trace amounts of metallic Pt⁰ to be present on the surface. The low reactivity of the Pt²⁺ sites is manifested by a high activation barrier for H₂ dissociation which exceeds even the barrier on pristine CeO₂(111). In the presence of small amounts of metallic Pt⁰, the surface becomes very active towards hydrogen dissociation and Pt²⁺ is rapidly reduced. The proposed reduction mechanism involves reverse spillover of oxygen from the Pt–CeO₂ support to the Pt⁰ particles followed by the clean-off reaction with hydrogen. Reduction of the ceria support subsequently leads to substantial destabilization of the ionic Pt²⁺ species. Once a threshold concentration of oxygen vacancies is reached, Pt²⁺ is reduced and metallic Pt particles are formed.

Author contributions

Y. L., A. N., T. S., M. V., and N. T. performed the SRPES and RPES experiments. K. C. P. contributed to the SRPES and RPES experiments and operation of the experimental facilities. J. L. and V. M. supervised the experimental work. Y. L., A. N., and J. L. were involved in the analysis of the experimental data. A. F., M. F. C. and F. R. N. performed the computational modelling supervised by K. M. N. and S. F. All co-authors were involved in the preparation of the manuscript.

Acknowledgements

This work was funded by the European Community (FP7-NMP.2012.1.1-1 project ChipCAT, Reference No. 310191), by the Deutsche Forschungsgemeinschaft (DFG) within the Excellence Cluster “Engineering of Advanced Materials” in the framework of the excellence initiative, by Spanish MINECO (grants CTQ2012-34969 and CTQ2015-64618-R), by the Generalitat de Catalunya (grants 2014SGR97 and XRQTC), and by the Czech Science Foundation (grant 15-06759S). The authors acknowledge a support by the COST Action CM1104 “Reducible oxide chemistry, structure and functions”. Computer resources, technical expertise and assistance were provided by the Red Española de Supercomputación and by the ISCRA initiative of the CINECA consortium. Y. L., A. N., M. V., N. T., and K. C. P. thank Elettra for excellent working conditions and support.

References

1. R. F. Service, Science, 2002, 296, 1222–1224.
2. L. Carrette, K. A. Friedrich and U. Stimming, ChemPhysChem, 2000, 1, 162–193.
3. M. Z. Jacobson, W. G. Colella and D. M. Golden, Science, 2005, 308, 1901–1905.
4. M. Flytzani-Stephanopoulos and B. C. Gates, Annu. Rev. Chem. Biomol. Eng., 2012, 3, 545–574.
5. M. S. Hegde, G. Madras and K. C. Patil, Acc. Chem. Res., 2009, 42, 704–712.
6. E. W. McFarland and H. Metiu, Chem. Rev., 2013, 113, 4391–4427.
7. M. S. Hegde and P. Bera, Catal. Today, 2015, 253, 40–50.
8. A. Bruix, Y. Lykhach, I. Matolínová, A. Neitzel, T. Skála, N. Tsud, M. Vorokhta, V. Stetsovych, K. Ševčiková, J. Mysliveček, R. Fiala, M. Václavů, K. C. Prince, S. Bruyere, V. Potin, F. Illas, V. Matolín, J. Libuda and K. M. Neyman, Angew. Chem., Int. Ed., 2014, 53, 10525–10530.
9. R. Fiala, M. Vaclavu, M. Vorokhta, I. Khalakhan, J. Lavková, V. Potin, I. Matolínová and V. Matolín, J. Power Sources, 2015, 273, 105–109.
10. R. Fiala, M. Vaclavu, A. Rednyk, I. Khalakhan, M. Vorokhta, J. Lavkova, V. Potin, I. Matolinova and V. Matolin, Catal. Today, 2015, 240(part B), 236–241.
11. G. Dutta, U. V. Waghmare, T. Baidya and M. S. Hegde, Chem. Mater., 2007, 19, 6430–6436.
12. P. Bera, K. R. Priolkar, A. Gayen, P. R. Sarode, M. S. Hegde, S. Emura, R. Kumashiro, V. Jayaram and G. N. Subbanna, Chem. Mater., 2003, 15, 2049–2060.
13. B. D. Mukri, U. V. Waghmare and M. S. Hegde, Chem. Mater., 2013, 25, 3822–3833.
14. M. Nolan, J. Mater. Chem., 2011, 21, 9160–9168.
15. D. O. Scanlon, B. J. Morgan and G. W. Watson, Phys. Chem. Chem. Phys., 2011, 13, 4279–4284.
16. A. G. Hu, K. M. Neyman, M. Staufer, T. Belling, B. C. Gates and N. Rosch, J. Am. Chem. Soc., 1999, 121, 4522–4523.
17. H. A. Aleksandrov, K. M. Neyman and G. N. Vayssilov, Phys. Chem. Chem. Phys., 2015, 17, 14551–14560.
18. F. Šutara, M. Cabala, L. Sedláček, T. Skála, M. Škoda, V. Matolín, K. C. Prince and V. Cháb, Thin Solid Films, 2008, 516, 6120–6124.
19. G. N. Vayssilov, Y. Lykhach, A. Migani, T. Staudt, G. P. Petrova, N. Tsud, T. Skála, A. Bruix, F. Illas, K. C. Prince, V. Matolín, K. M. Neyman and J. Libuda, Nat. Mater., 2011, 10, 310–315.
20. V. Matolin, I. Matolinova, L. Sedlacek, K. C. Prince and T. Skala, Nanotechnology, 2009, 20, 215706.
21. T. Staudt, Y. Lykhach, N. Tsud, T. Skála, K. C. Prince, V. Matolín and J. Libuda, J. Catal., 2010, 275, 181–185.
22. J. Libra, KolXPD: Spectroscopy Data Measurement and Processing, http://www.kolibrik.net/science/kolxpd/, Accessed 15.03.2015, 2015.
23. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
24. S. Fabris, G. Vicario, G. Balducci, S. de Girancoli and S. Baroni, J. Phys. Chem. B, 2005, 109, 22860–22867.
25. L. Szabová, O. Stetsovych, F. Dvořák, M. Farnesi Camellone, S. Fabris, J. Mysliveček and V. Matolín, J. Phys. Chem. C, 2012, 116, 6677–6684.
26. F. R. Negreiros and S. Fabris, J. Phys. Chem. C, 2014, 118, 21014–21020.
27. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
28. J. Paier, C. Penschke and J. Sauer, Chem. Rev., 2013, 113, 3949–3985.
29. M. V. Ganduglia-Pirovano, J. L. F. Da Silva and J. Sauer, Phys. Rev. Lett., 2009, 102, 026101.
30. M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105.
31. L. Szabova, M. F. Camellone, M. Huang, V. Matolin and S. Fabris, J. Chem. Phys., 2010, 133, 234705.
32. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
33. S. M. Kozlov, F. Viñes, N. Nilius, S. Shaikhutdinov and K. M. Neyman, J. Phys. Chem. Lett., 2012, 3, 1956–1961.
34. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
35. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
36. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
37. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
38. G. N. Vayssilov, A. Migani and K. Neyman, J. Phys. Chem. C, 2011, 115, 16081–16086.
39. A. Migani, G. N. Vayssilov, S. T. Bromley, F. Illas and K. M. Neyman, Chem. Commun., 2010, 46, 5936–5938.
40. A. Migani, G. N. Vayssilov, S. T. Bromley, F. Illas and K. M. Neyman, J. Mater. Chem., 2010, 20, 10535–10546.
41. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
42. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
43. M. A. Sk, S. M. Kozlov, K. H. Lim, A. Migani and K. M. Neyman, J. Mater. Chem. A, 2014, 2, 18329–18338.
44. A. Neitzel, Y. Lykhach, T. Skála, N. Tsud, M. Vorokhta, D. Mazur, K. C. Prince, V. Matolín and J. Libuda, Phys. Chem. Chem. Phys., 2014, 16, 24747–24754.
45. D. J. Miller, H. Öberg, S. Kaya, H. Sanchez Casalongue, D. Friebel, T. Anniyev, H. Ogasawara, H. Bluhm, L. G. M. Pettersson and A. Nilsson, Phys. Rev. Lett., 2011, 107, 195502.
46. M. Hatanaka, N. Takahashi, N. Takahashi, T. Tanabe, Y. Nagai, A. Suda and H. Shinjoh, J. Catal., 2009, 266, 182–190.
47. T. Wu, X. Pan, Y. Zhang, Z. Miao, B. Zhang, J. Li and X. Yang, J. Phys. Chem. Lett., 2014, 5, 2479–2483.
48. M. García-Melchor and N. López, J. Phys. Chem. C, 2014, 118, 10921–10926.
49. D. Fernández-Torre, J. Carrasco, M. V. Ganduglia-Pirovano and R. Pérez, J. Chem. Phys., 2014, 141, 014703.
50. G. Vicario, G. Balducci, S. Fabris, S. de Gironcoli and S. Baroni, J. Phys. Chem. B, 2006, 110, 19380–19385.
51. F. R. Negreiros, M. F. Camellone and S. Fabris, J. Phys. Chem. C, 2015, 119, 21567–21573.
52. S. Bernal, J. J. Calvino, G. A. Gifredo, J. M. Rodriguez-Izquiero, V. Perrichon and A. Laachir, J. Catal., 1992, 137, 1–11.
53. A. Laachir, V. Perrichon, A. Badri, J. Lamotte, E. Catherine, J. C. Lavalley, J. El Fallah, L. Hilaire, F. Le Normand, E. Quéméré, G. N. Sauvion and O. Touret, J. Chem. Soc., Faraday Trans., 1991, 87, 1601–1609.
54. G. Vilé, B. Bridier, J. Wichert and J. Pérez-Ramírez, Angew. Chem., Int. Ed., 2012, 51, 8620–8623.
55. M. Boaro, M. Vicario, C. de Leitenburg, G. Dolcetti and A. Trovarelli, Catal. Today, 2003, 77, 407–417.
56. J. Carrasco, G. Vilé, D. Fernández-Torre, R. Pérez, J. Pérez-Ramírez and M. V. Ganduglia-Pirovano, J. Phys. Chem. C, 2014, 118, 5352–5360.
57. Y. Lykhach, T. Staudt, M. Vorokhta, T. Skála, V. Johánek, K. C. Prince, V. Matolín and J. Libuda, J. Catal., 2012, 285, 6–9.
58. C. Kittel, Introduction to Solid State Physics, Wiley, 8th edn, 2004.
59. Y. Lykhach, M. Kozlov, T. Skála, A. Tovt, V. Stetsovych, N. Tsud, F. Dvořák, V. Johánek, A. Neitzel, J. Mysliveček, S. Fabris, V. Matolín, K. M. Neyman and J. Libuda, Nat. Mater., 2016, 15 DOI:10.1038/nmat4500.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp00627b

---