Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cysteine containing dipeptides show a metal specificity that matches the composition of seawater†
Luca
Belmonte
,
Daniele
Rossetto
,
Michele
Forlin
,
Simone
Scintilla
,
Claudia
Bonfio
and
Sheref S.
Mansy
 *
*
CIBIO, University of Trento, via Sommarive 9, Povo, Italy. E-mail: mansy@science.unitn.it
First published on 10th May 2016
Abstract
Model prebiotic dipeptide sequences were identified by bioinformatics and DFT and molecular dynamics calculations. The peptides were then synthesized and evaluated for metal affinity and specificity. Cysteine containing dipeptides were not associated with metal affinities that followed the Irving–Williams series but did follow the concentration trends found in seawater.
Life as we know depends on metal ions. Approximately half of all proteins are metalloproteins,1 and central metabolism is dependent on metal centres for enzymatic catalysis. Considering the abundance of metals on Earth, it is reasonable to expect that metal ions directly participated in the emergence of life. However, it is unclear at what point metal ions began to impact the sequence of polymers found in cellular life today.
Analyses of extant life can allow for the reconstruction of past evolutionary events but are rarely able to give insight into processes that occurred before the advent of the last universal common ancestor. Partly for this reason, model prebiotic chemical reactions are used to understand how the constraints imposed by chemistry and physics lead to the emergence of cellular life. Here we attempt to merge these two approaches by using protein sequence and structural data to infer prebiotically plausible peptides and then test these peptides for metal binding activity using density functional theory (DFT) and molecular dynamic calculations and affinity measurements. Furthermore, a focus was placed on cysteine containing peptides so that insight could be gained into the role of iron–sulphur clusters in the origin of life. Iron–sulphur clusters are thought to be one of the most ancient cofactors found in biology and are involved in fundamental physiological processes in all living cells. Iron–sulphur clusters are typically coordinated by cysteine side-chains.2 Early Earth was rich in metals and sulfur,3 and plausible prebiotic syntheses of amino acids4 and peptides5 have been described.
To assess the ligand preference of metal ions coordinated with proteins, 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 sequences of structures of proteins deposited in the protein data bank were analysed for iron, iron–sulphur cluster, cobalt, nickel, copper, and zinc ion coordination. Polynuclear iron–sulphur clusters showed a strong preference for cysteine ligation, accounting for 77.9% and 96.6% of the ligation of [2Fe–2S] and [4Fe–4S] clusters, respectively (Fig. S1, ESI†). Only 4.9% of proteins coordinating a mononuclear iron ion had a cysteine ligand. Zn2+ coordination also showed a strong preference for ligation by a cysteine (37%). The remaining mononuclear centres in the 2+ oxidation state showed a preference for histidine ligation, with cysteine binding accounting for a smaller fraction of the structures (Fig. S1, ESI†).
600 sequences of structures of proteins deposited in the protein data bank were analysed for iron, iron–sulphur cluster, cobalt, nickel, copper, and zinc ion coordination. Polynuclear iron–sulphur clusters showed a strong preference for cysteine ligation, accounting for 77.9% and 96.6% of the ligation of [2Fe–2S] and [4Fe–4S] clusters, respectively (Fig. S1, ESI†). Only 4.9% of proteins coordinating a mononuclear iron ion had a cysteine ligand. Zn2+ coordination also showed a strong preference for ligation by a cysteine (37%). The remaining mononuclear centres in the 2+ oxidation state showed a preference for histidine ligation, with cysteine binding accounting for a smaller fraction of the structures (Fig. S1, ESI†).
To probe whether the amino acid sequences in the immediate vicinity of metal ligands were important for metal ion coordination, the frequency of residues immediately preceding (−1) and following (+1) cysteine ligands was evaluated. The analysis showed that some residues were strongly selected in both −1 and +1 positions for all the metal ions tested, including glutamate, lysine, glutamine, methionine, cysteine, and tryptophan. The +1 position showed a preference for smaller side-chains, with a glycine residue being the most favoured following cysteine ligated iron, nickel, and zinc cations (Fig. S2, ESI†). Although copper ions showed some preference for glycine, the most favoured residues to occupy the +1 position for this metal ion were alanine and threonine. Co2+ showed no preference for glycine and instead was dominated by leucine at the +1 position. The position preceding the ligating cysteine was enriched in valine for all the metal ions tested except for copper. However, valine was only the most preferred residue at the −1 position for iron ions.
Next, the sequence and structural data were used to build a model of metal-binding dipeptides. First, the minimal coordination spheres of the transition metal ions were built by taking the coordinates of the iron ion and the methanethiolate (CH3S−) tetrahedral unit of the cysteine ligands of Clostridium pasteurianum rubredoxin6 (Protein Data Bank ID: 1IRO). The metal centre of the resulting [(CH3S)4Fe]2− molecule was then substituted with divalent cobalt, nickel, copper, and zinc and the geometries optimized by DFT calculations at the B3LYP/TZV+(2d,p) level of theory for the ligands and the LANL2TZ+ plus Effective Core Potential (ECP)7,8 basis set for the metal cations. Difficulties with DFT calculations were shown in the past for complexes containing two interacting transition metals.9 Mononuclear metal centres are much simpler. Furthermore, calculations using B3LYP were approximately two-fold faster than by using PW91 and PBE0 and showed only slight differences in energies between 0.016% and 0.042% (Fig. S3 and S4, ESI†). Metal ions were placed in a high spin configuration because of coordination to soft thiolate ligands. The effect of solvent was accounted for by the polarizable continuum model (PCM).10 The ab initio Merz–Kollman method11,12 was used for the Molecular Electrostatic Potential (MEP) rather than DFT. Lennard-Jones potential parameters were calculated by fitting the potential energy functions obtained by moving the metal dications towards a single methanethiolate.13,14 For these Lennard-Jones calculations, the Møller–Plesset perturbation theory (MP2) was used rather than DFT (Fig. S5 and Table S1, ESI†). All calculations were performed using GAMESS-US.15 Interaction energies were calculated in the gas phase using MP2.
The calculated structures (Fig. 1) superimposed with a RMSD of 0.26 Å, 0.25 Å, 0.38 Å, and 0.38 Å for divalent iron, cobalt, nickel, and zinc, respectively, on the ligand sphere of analogous centres in proteins (Fig. S6, ESI†). Although complexes of Cu2+ with four methanethiolates typically assume a square planar geometry, DFT calculations gave Cu2+ in a tetrahedral geometry. This effect was likely due to entrapment in a local minimum on the potential energy surface close to the starting geometry. Calculations with Cu+ resulted in structures inconsistent with Cu+ proteins deposited in the protein data bank. We thus discarded copper ions from further analyses. MP2 calculations were also used to determine the interaction energies of the divalent metals in a tetrahedral geometry with four methanethiolate ligands, which resulted in a distribution that followed the Irving–Williams series, i.e. Fe2+ < Co2+ < Ni2+ > Zn2+ (Fig. 2).
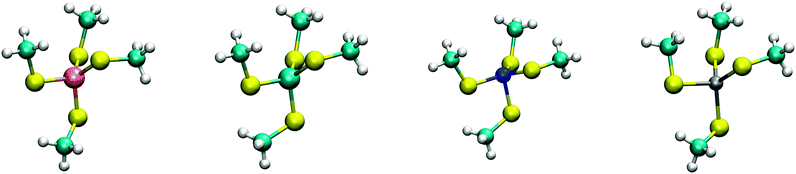 | ||
| Fig. 1 DFT optimized structures of [(CH3S)4M]2− complexes. From left to right, Fe2+, Co2+, Ni2+, and Zn2+ high spin complexes are shown with multiplicities of 5, 4, 3, and 1, respectively. | ||
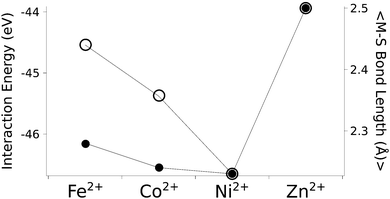 | ||
| Fig. 2 The calculated interaction energy and bond length between metal ions and methanethiolates. Associated plots of charge and force constants can be found in Fig. S7 (ESI†). Filled circles represent average metal–sulphur bond lengths, while open circles represent interaction energies in the gas phase. | ||
Next, X-Cys and Cys-X dipeptides were designed based on the frequency of their appearance in metalloprotein entries in the protein data bank (Fig. S2, ESI†). Both high frequency (His-Cys, Val-Cys, Gly-Cys, Cys-Gly, Cys-Thr, Cys-Leu, Cys-Pro) and low frequency (Cys-Tyr, Cys-Val, Cys-Ile, Cys-Phe, Cys-Trp) dipeptides were evaluated. It was not possible to run DFT calculations, because of the dimensions of these larger complexes. Therefore, the parameters from DFT calculations were used for molecular dynamics simulations of cysteine and cysteine-containing dipeptide sequences. In order to better approximate the behaviour of the molecules during molecular dynamics, the bonded and non-bonded interactions were recalculated and remapped for both the metal centres and the methanethiolates. All of the complexes were solvated in water, neutralized and equilibrated for 20 ps. The complexes were heated to 298 K in a stepwise manner. A constant pressure of 1 atm was used to have an isothermal–isobaric (NPT) ensemble. Long-range electrostatic interactions were calculated using the Ewald approximation and periodic boxes (PBC). The SHAKE16 procedure was employed to constrain the hydrogen atoms. The Ewald sum was computed using the Particle-Mesh Ewald (PME).17 Molecular dynamics simulations were run with NAMD.18
Unlike the ab initio calculations with methanethiolate ligands, the data from molecular dynamics on metal coordinated dipeptides did not fit the Irving–Williams series. Complexes with a RMSD greater than 4.5 Å from molecular dynamics simulation trajectories were discarded19 (Fig. 3 and Fig. S8, ESI†). Of the thirteen complexes analysed, only seven dipeptides and cysteine passed this criterion. Generally, across the different dipeptides and cysteine, the Ni2+ complexes possessed higher internal energies (that is, Ni2+ complexes assumed less stable conformations) than the other transition metal complexes, whereas the Zn2+ complexes gave the lowest internal energies. In between these two extremes, Fe2+ was associated with a less stable conformation than Co2+.
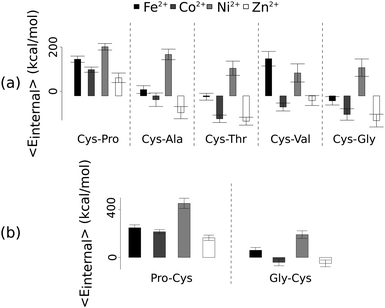 | ||
| Fig. 3 Average internal energies of the metal–peptide complexes calculated from molecular dynamics simulations. Cysteine was either at the amino- (a) or carboxy- (b) terminus. | ||
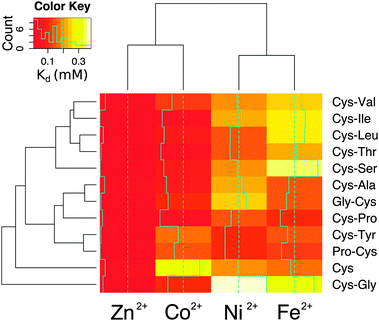
To determine whether the energies calculated from molecular dynamics correlated with measurements in the laboratory, each dipeptide was synthesized following standard Fmoc-based solid-phase peptide synthesis procedures. Peptide composition was confirmed using mass spectrometry (Fig. S9, ESI†). Considering that free peptide termini could act as metal ligands, the amino- and carboxy-termini were blocked by acetylation and amidation, respectively, to avoid interactions that the molecular dynamics calculations could not take into account. All of the peptides were soluble in water except for Cys-Trp. Metal binding was assessed by calculating the dissociation constant from titrations with Co2+, Fe2+, and Ni2+ monitored by UV-visible spectrophotometry. Zn2+ binding was quantified by monitoring the displacement of bound Co2+ (Table S2 and Fig. S10, ESI†). The trend in metal ion affinity for each dipeptide was more similar to molecular dynamics calculations with dipeptides than with the ab initio calculations with methanethiolate ligands. Generally, the affinity for Zn2+ was the highest, followed by Co2+, Ni2+, and then Fe2+. This trend was previously observed with hindered thiolate ligands and was explained by taking into consideration the combined effect of covalent (more important for Co2+ and Cu2+) and ionic (more important for Zn2+) contributions to the bond energy.20 Importantly, the affinities measured by metal ion titrations correlated with the average internal energies calculated from molecular dynamics (Fig. S11, ESI†). The correlation was improved when only taking into account complexes with a completely buried prosthetic centre (Table S3, ESI†).
The affinity and selectivity of the dipeptides were influenced by the sequence composition. For example, Cys-Tyr and Pro-Cys were the only peptides that bound Ni2+ with greater affinity than both Co2+ and Fe2+. The extent of metal preference also varied. The affinity of Cys-Ala for Zn2+ was 3-fold greater than for Fe2+, whereas the difference was 30-fold for Cys-Ile. The reasons for the differences between the dipeptides were not readily apparent. Also, no significant correlation was found between the sequences found adjacent to the protein ligands in the protein data bank and the measured affinities. There was a correlation, however, between the metal ions. Zn2+ and Co2+ affinities (Pearson correlation coefficient = 0.75) and Ni2+ and Fe2+ affinities (Pearson correlation coefficient = 0.68) for the dipeptides were significantly correlated (Fig. S12, ESI†). This is consistent with the fact that Co2+ functions as a useful biochemical and spectroscopic substitute for Zn2+in vitro, and nickel–iron sulphur clusters naturally exist in proteins. The similarities between nickel and iron dications may also reflect an ability to interact with the oxygen and nitrogen moieties in addition to the sulphur of cysteine. Cys and Cys-Gly deviated the most from the remaining peptides (Fig. 4).
The metal ion composition of proteins is thought to reflect the environment from which the protein emerged.21,22 Although it is difficult to know the metal ion concentrations on prebiotic Earth, iron ions were likely present at higher concentrations, since Fe2+ is much more soluble than the Fe3+ found today in the ocean. Additionally, cellular life may have emerged from a specific niche environment not well described by overall, average conditions. Today seawater contains trace amounts (nanomolar to subnanomolar concentrations) of the transition metals investigated here. None of the tested dipeptides was able to bind the transition metals with strong enough affinity to form a complex in seawater. Nevertheless, the dipeptide–metal affinity trends match the metal concentration trends of seawater23 and do not follow the Irving–Williams series. For example, in seawater, iron is the transition metal at the highest concentration, and most of the dipeptides bound iron with lower affinity than the other metal cations. More specifically, the concentration trend in seawater is iron > nickel > cobalt > zinc ions,23 and the measured dissociation constants of cysteine containing dipeptides were generally iron > nickel > cobalt > zinc ions. That is, the higher the metal ion concentration, the higher the metal–peptide dissociation constant (i.e. the lower the affinity), which correlates well with what is typically found for modern protein folds.24 Proteins do not evolve tighter metal binding than what is necessary.
Currently, there are not enough data to understand how metal–peptide affinities could result in a selective advantage. If, however, a specific metal–peptide complex was beneficial to a protocell, perhaps due to an associated catalytic activity,25 then a protocell that encapsulated such a complex could out compete protocells containing a less active peptide.26 To better probe the relevance of metallopeptides in the origin of life, studies on catalytic activity and a broader investigation of model prebiotic peptidyl ligands will be needed.
Conclusions
Cysteine containing dipeptides show a metal specificity that is not observed with less hindered, small molecule, thiolate ligands. Therefore, even short peptide sequences may have been better suited to coordinate metal ions on the prebiotic Earth than competing, non-biologically relevant small molecules. As short peptide sequences increased in length and folding complexity, the properties of the polypeptides must have changed. This is likely why the dipeptide metal affinities did not correlate with the sequence frequencies found in metalloproteins. Nevertheless, insight into model prebiotic sequences can be gained by using quantum mechanics and molecular dynamics as a guide. The combined results arising from these computational methodologies were consistent with the general metal ion specificity of dipeptide, cysteine containing sequences measured in the laboratory and matched the metal ion distribution of seawater.Acknowledgements
This work was supported by the Simons Foundation (290358), the Armenise-Harvard Foundation, COST action CM1304, and CIBIO.Notes and references
- A. J. Thomson and H. B. Gray, Bio-inorganic chemistry, Curr. Opin. Chem. Biol., 1998, 2, 155–158 CrossRef CAS PubMed.
- H. Beinert, Iron–sulfur proteins: ancient structures, still full of surprises, JBIC, J. Biol. Inorg. Chem., 2000, 5, 2–15 CrossRef CAS PubMed.
- W. L. Griffin, et al., The world turns over: Hadean–Archean crust–mantle evolution, Lithos, 2014, 189, 2–15 CrossRef CAS.
- S. L. Miller, A production of amino acids under possible primitive earth conditions, Science, 1953, 117, 528–529 CAS.
- G. Danger, R. Plasson and R. Pascal, Pathways for the formation and evolution of peptides in prebiotic environments, Chem. Soc. Rev., 2012, 41, 5416 RSC.
- Z. Dauter, K. S. Wilson, L. C. Sieker, J.-M. Moulis and J. Meyer, Zinc-and iron-rubredoxins from Clostridium pasteurianum at atomic resolution: a high-precision model of a ZnS4 coordination unit in a protein, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 8836–8840 CrossRef CAS.
- P. J. Hay and W. R. Wadt, Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- W. R. Wadt and P. J. Hay, Ab initio effective core potentials for molecular calculations. Potentials for main group elements Na to Bi, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- E. Decolvenaere, M. J. Gordon and A. Van der Ven, Testing Predictions from Density Functional Theory at Finite Temperatures: β2-Like Ground States in Co–Pt, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 085119, 1–8 Search PubMed.
- B. Mennucci, Polarizable continuum model, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 386–404 CrossRef CAS.
- K. M. Merz, Analysis of a large data base of electrostatic potential derived atomic charges, J. Comput. Chem., 1992, 13, 749–767 CrossRef CAS.
- U. C. Singh and P. A. Kollman, An approach to computing electrostatic charges for molecules, J. Comput. Chem., 1984, 5, 129–145 CrossRef CAS.
- R. H. Stote and M. Karplus, Zinc binding in proteins and solution: a simple but accurate nonbonded representation, Proteins: Struct., Funct., Bioinf., 1995, 23, 12–31 CrossRef CAS PubMed.
- E. Ahlstrand, D. Spångberg, K. Hermansson and R. Friedman, Interaction energies between metal ions (Zn2+ and Cd2+) and biologically relevant ligands, Int. J. Quantum Chem., 2013, 113, 2554–2562 CrossRef CAS.
- M. W. Schmidt, et al., General atomic and molecular electronic structure system, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- J.-P. Ryckaert, A. Bellemans, G. Ciccotti and G. V. Paolini, Shear-rate dependence of the viscosity of simple fluids by nonequilibrium molecular dynamics, Phys. Rev. Lett., 1988, 60, 128 CrossRef CAS PubMed.
- U. Essmann, et al., A smooth particle mesh Ewald method, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- J. C. Phillips, et al., Scalable molecular dynamics with NAMD, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- V. A. Voelz, G. R. Bowman, K. Beauchamp and V. S. Pande, Molecular Simulation of ab initio Protein Folding for a Millisecond Folder NTL9 (1–39), J. Am. Chem. Soc., 2010, 9, 1526–1528 CrossRef PubMed. et al.
- S. I. Gorelsky, Spectroscopic and DFT Investigation of [M{HB(3,5-iPr2pz)3}(SC6F5)] (M = Mn, Fe, Co, Ni, Cu, and Zn) Model Complexes: Periodic Trends in Metal–thiolate Bonding, Inorg. Chem., 2005, 44, 4947–4960 CrossRef CAS PubMed.
- M. A. Saito, D. M. Sigman and F. M. M. Morel, The bioinorganic chemistry of the ancient ocean: the co-evolution of cyanobacterial metal requirements and biogeochemical cycles at the Archean–Proterozoic boundary?, Inorg. Chim. Acta, 2003, 356, 308–318 CrossRef CAS.
- C. L. Dupont, S. Yang, B. Palenik and P. E. Bourne, Modern proteomes contain putative imprints of ancient shifts in trace metal geochemistry, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 17822–17827 CrossRef CAS PubMed.
- D. R. Lide, CRC handbook of chemistry and physics, CRC press, 2004 Search PubMed.
- J. A. Cowan, Metal activation of enzymes in nucleic acid biochemistry, Chem. Rev., 1998, 98, 1067–1088 CrossRef CAS PubMed.
- M. Gorlero, et al., Ser-His catalyses the formation of peptides and PNAs, FEBS Lett., 2009, 583, 153–156 CrossRef CAS PubMed.
- K. Adamala and J. W. Szostak, Competition between model protocells driven by an encapsulated catalyst, Nat. Chem., 2013, 5, 495–501 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp00608f |
| This journal is © the Owner Societies 2016 |