Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Facilitated diffusion in the presence of obstacles on the DNA
David
Gomez
*a and
Stefan
Klumpp
ab
aMax Planck Institute of Colloids and Interfaces, Science Park Golm, 14424 Potsdam, Germany. E-mail: david.gomez@mpikg.mpg.de; Tel: +49 331 567-9622
bInstitute for Nonlinear Dynamics, Georg-August University Göttingen, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
First published on 22nd March 2016
Abstract
Biological functions of DNA depend on the sequence-specific binding of DNA-binding proteins to their corresponding binding sites. Binding of these proteins to their binding sites occurs through a facilitated diffusion process that combines three-dimensional diffusion in the cytoplasm with one-dimensional diffusion (sliding) along the DNA. In this work, we use a lattice model of facilitated diffusion to study how the dynamics of binding of a protein to a specific site (e.g., binding of an RNA polymerase to a promoter or of a transcription factor to its operator site) is affected by the presence of other proteins bound to the DNA, which act as ‘obstacles’ in the sliding process. Different types of these obstacles with different dynamics are implemented. While all types impair facilitated diffusion, the extent of the hindrance depends on the type of obstacle. As a consequence of hindrance by obstacles, more excursions into the cytoplasm are required for optimal target binding compared to the case without obstacles.
I. Introduction
Processing of the genetic information is to a very large extent dependent on the sequence-specific binding of proteins to DNA. Examples include binding of transcription factors to specific operator sites and binding of RNA polymerases to promoters.1 Sequence-specificity is typically not perfect, and binding motifs therefore are typically ‘fuzzy’, with a range of different sequences displaying comparable affinities for the protein and an even larger range showing weak affinity.2 In addition, binding of DNA-binding proteins (DBPs) to DNA usually has an electrostatic component that is independent of the sequence, i.e. non-specific. For that reason both the equilibrium binding pattern and the binding kinetics of DBPs can be quite complex.3 Nevertheless, DBPs find their functional binding sites (of size ∼10–30 bp1,4) with remarkable efficiency despite the large number of non-specific binding sites (∼106 in the genome of E. coli) that compete for binding with the functional site. In a seminal work, Riggs et al. measured the in vitro rate at which the lac repressor finds its promoter, and they found that under certain conditions, the lac repressor binds to its target at faster rates than the simple three dimensional diffusion limit.5 To explain this phenomena, Berg, Winter and von Hippel proposed the so called facilitated diffusion model,6,7 in which such high binding rates are achieved if the DBP undergoes a combination of three-dimensional (3D) excursions in the bulk solution, together with one-dimensional (1D) sliding on the DNA. This theoretical model has been strongly supported by experimental techniques that directly showed the number of basepairs scanned via 1D sliding,8–10 and the average fraction of time the DBP remains bound to the DNA before unbinding.11,12Since it was proposed, facilitated diffusion has been the subject of much theoretical,13–18 experimental4,19–24 and computational25–27 efforts. Interest in facilitated diffusion has been renewed by the direct observation of facilitated diffusion in bacterial cells using single-molecule techniques.11,12 One key feature that is different in cells compared to in vitro is that the cytoplasm is not a dilute solution, but a rather crowded environment that can be occupied up to 40% by macromolecules.28,29 The presence of these macromolecules (crowders) inside the cells has effects on diffusion,30–32 enzymatic reactions,33–36 protein folding37–40 and gene expression.41–43 In addition, the DNA itself is also covered with proteins that bind to the DNA in order to perform functions such as transcription, DNA repair and gene regulation.1,44–46 Moreover, the DNA itself is spatially organized and compacted by histones in eukaryotes and nucleoid-associated proteins in bacteria.47,48 Thus, the DNA is also highly occupied (∼30%) by DBPs that affect the facilitated diffusion process. So far, only a few of the theoretical studies have included the impact of these macromolecules on the promoter finding dynamics.49–53
In this paper we address the effects of obstacles bound to the DNA in facilitated diffusion, i.e. in the promoter search of RNA polymerase or the search of a transcription factor for its functional binding site. We use a lattice model to study the facilitated diffusion, first in the free case without crowders and then in the presence of obstacles on the DNA. Specifically, we consider three different types of obstacles characterized by different dynamics on the DNA. We show that, for all types, facilitated diffusion is impaired when the DNA occupation fraction increases, but the strength of the effect depends on the type of obstacle. The lattice model we use aims to create a clear conceptual understanding of the facilitated diffusion rather than to provide a detailed computational description of the process. The method is, however, applicable more generally.
II. Lattice model for simulating facilitated diffusion
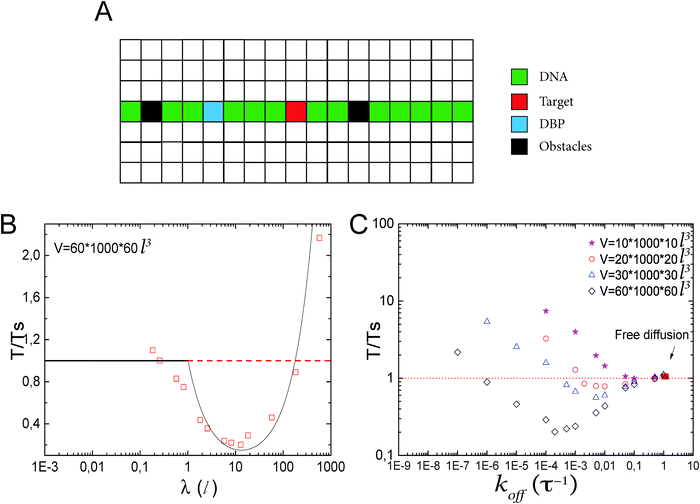
Facilitated diffusion is studied using Monte Carlo simulations of particles on a 3D lattice with periodic boundary conditions. The simulation box has a total volume V = mx × my × mzl3, where l is the lattice spacing, chosen as the linear extension of the smallest particle type. A DNA molecule is implemented as a linear arrangement of lattice sites along the y axis with x = z = (mx/2)l = (mz/2)l. The system contains a target (e.g., a promoter or a regulatory binding site) and two types of particles: One DBP searching for the target and obstacles on the DNA, see Fig. 1A. All particles are taken to occupy exactly one lattice site. We take the target to be static, and its position is randomly chosen among the DNA lattice sites. The DBP is initially placed randomly in the bulk solution, whereas the obstacles are placed on DNA lattice sites, occupying a fraction of DNA equal to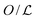 , where O is the number of obstacles and
, where O is the number of obstacles and 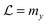 the length of the DNA template. Here, obstacles are considered to be only on the DNA and they are not allowed to unbind and diffuse in the bulk solution.
the length of the DNA template. Here, obstacles are considered to be only on the DNA and they are not allowed to unbind and diffuse in the bulk solution.
 | ||
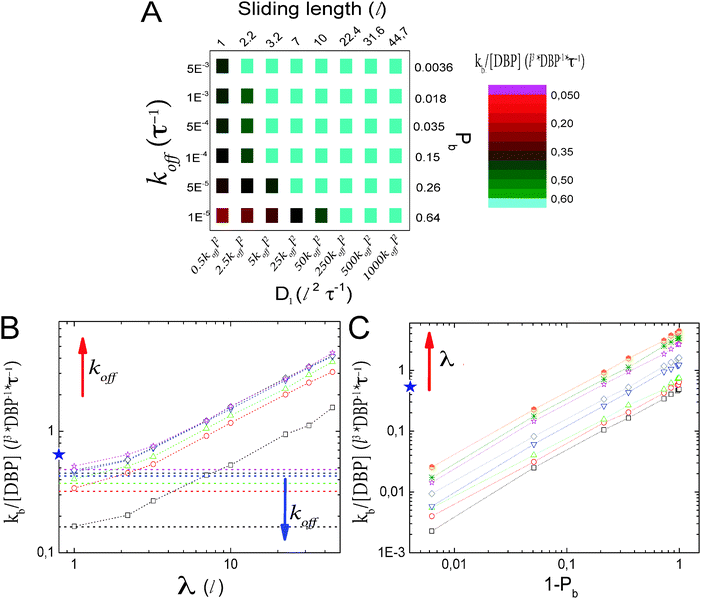
| Fig. 1 Lattice model for facilitated diffusion: (A) schematic view of the model. DBP (light blue) diffuses by hopping either to one of the six nearest neighboring lattice sites (3D) or to one of the two neighboring lattice sites if it is sliding on the DNA (1D), which is represented by the green line of lattice sites. O obstacles (black) are placed on the DNA. Their dynamics depend on the type of obstacle (see the text), but in all cases they are not allowed to perform excursions to the bulk solution. Molecules have square geometry and diffusion is only allowed if the destination site is unoccupied. Note that the simulations use a three-dimensional lattice rather than the two-dimensional one depicted schematically here. (B) Search time (normalized by the search time Ts in the absence of non-specific binding of the DBP to the DNA) as a function of the sliding length λ. Data points are simulation results, and the line is the ratio between eqn (5) and Ts = V/4Da. (C) T/Ts for different DNA concentrations, plotted as a function of the unbinding rate koff. Different minimal search times and optimal unbinding rates are observed for different DNA concentrations. | ||
In our implementation, the DBP can either diffuse in the bulk solution or slide on the DNA. If the DBP is in the bulk solution, at each simulation time step (of duration τ), it moves to each neighboring site with a probability of 1/6. Thus, DBP diffuses in the bulk solution with diffusion constant D3 = l2/(6τ). If one of the neighboring sites is part of the DNA and it is free, the move is always accepted, and the DBP is placed onto the DNA. In contrast, if the DNA site is occupied by an obstacle, the move is rejected and the DBP stays in the bulk solution (since obstacles are not allowed to unbind, and moves within the bulk solution are always unhindered). Thus, no interactions other than steric repulsion are considered between the DBP and the obstacles.
If the DBP is bound to the DNA, it can either diffuse on the DNA or unbind from it with a rate koff. If the DBP diffuses on the DNA, it performs a 1D random walk along the y axis with diffusion constant D1. Unless stated otherwise, we choose D1 = D3/10, as 1D diffusion is typically slower than 3D diffusion.9,11 Since we are interested in the effects that obstacles on the DNA have on the facilitated diffusion process, we implement three types of obstacles with different dynamics on the DNA: (i) static (immobile) obstacles, (ii) obstacles that diffuse on the DNA with a diffusion constant D1, and (iii) obstacles that both diffuse and unbind from the DNA. Facilitated diffusion is expected to be affected differently by these three types of obstacles. 1D diffusion of both the DBP and the mobile obstacles is implemented as follows: if the destination site of a move is already occupied by another molecule, the move is rejected and the position is not updated. Position update of different molecules is performed in a random-sequential fashion: In every simulation step, we update the DBP position together with O randomly chosen obstacles, in such a way that on average all particles are updated once per simulation step.
1D diffusion takes places until the DBP unbinds from the DNA with probability Poff. Thus, Poff determines the rate at which the DBP unbinds from the DNA, koff = Poffτ−1. We note that experimentally, the unbinding rate is typically varied via the salt concentration,23,24 because non-specific binding to DNA is typically of electrostatic nature and can be screened by large salt concentrations, resulting in large values of Poff.
In our simulations, the DBP finds the target either by 3D diffusion, if hopping from the bulk to one of the six neighboring lattice sites of destination happens to be the target, or by 1D diffusion if one of the two neighboring lattice sites is the target. Once the target has been found, we record the search time, and the DBP is randomly placed in the bulk solution.
III. Facilitated diffusion without obstacles
We start by considering the reference case of facilitated diffusion without obstacles on the DNA. This has been extensively studied in the past, both theoretically and computationally.13–18,25–27 In particular, it is well known that the efficiency of facilitated diffusion strongly depends on DNA concentration, D1 and salt concentration (koff).26,50,54 The lattice model allows us to modulate these parameters and also provides a rather intuitive interpretation of the facilitated diffusion mechanism.To begin with, we simulate facilitated diffusion in lattices of different sizes, thus effectively varying the DNA concentration. We keep the length of the simulation box (the direction parallel to the DNA) fixed at my = 1000l, but vary the box width in the other two dimensions (mx = mz = L = 10, 20, 30 and 60l). Simulations are run until 2000 target finding events have taken place. In order to quantify the efficiency of facilitated diffusion in comparison to the free 3D diffusion case, we consider the ratio of the average search times T/Ts. Here, T is the average time for finding the target by facilitated diffusion, and Ts is the average time for finding the target via free 3D diffusion in the absence of DNA. Thus, if this ratio is less than one, facilitated diffusion is more efficient than the free diffusion case, whereas if the ratio exceeds one, it would be better for the system to find the target by simple 3D diffusion.
The essence of facilitated diffusion can be understood based on the following simple argument: the rate for target finding is diffusion-limited and thus given by k = γDa, and the corresponding search time T = (kc)−1, where D is the diffusion coefficient, a the size of the target, and c = 1/V the concentration of the DBP (in our scenario a single one). γ is a numerical prefactor, which is γ = 4π in the classical Smoluchowski result,55 and γ = 4 in our lattice model, where the target is a site on the DNA. Thus, the average time for target finding is obtained as T = 1/k = V/(γDa). The presence of the DNA has two different effects on the DBP dynamics, which can both be understood by introducing effective parameters: on one hand, transient binding to the DNA effectively slows down diffusion. Since diffusion along the DNA is typically slow, one can interpret binding to the DNA as pauses in 3D diffusion. These pauses can be incorporated into an effective diffusion coefficient
| Deff = D3(1 − Pb), | (1) |
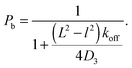 | (2) |
On the other hand, sliding along the DNA effectively increases the size of the target. To reach the target, the DBP does not need to bind to the target site directly, but may also bind close to the target and slide there by 1D diffusion. The average distance, over which the DBP slides along the DNA while bound, is given by
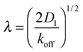 | (3) |
Taken together, the two effects lead to
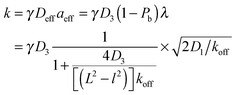 | (4) |
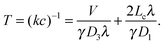 | (5) |
An important feature of this result is that the search time is non-monotonic as a function of the DNA binding strength. This feature has been a hallmark of facilitated diffusion, which has been at the center of many theoretical studies,6,7,14,15,17 and which was confirmed experimentally by varying the salt concentration.23,24 Based on our simple argument above, it can be interpreted as arising from the opposite effects of increasing the strength of non-specific binding on the effective diffusion coefficient and the effective target size.
Fig. 1C shows T/Ts as a function of koff for four different DNA concentrations. In all the cases, a non-monotonic behavior is observed as the value of koff is modulated. For low values of koff, ratios larger than one are obtained, reflecting mostly the effective reduction in the 3D diffusion constant. Thus, in this parameter range, 3D diffusion in the absence of DNA is more effective that facilitated diffusion. For intermediate values of koff, a minimum in the T/Ts ratio is observed. In this case, sliding on the DNA indeed facilitates binding to the promoter, due to the effectively larger target size, i.e. λ + l. For high values of koff, the T/Ts ratio gets close to one, as DNA binding is weak and has only a small effect.
In the case of V = 60 × 1000 × 60l3, the optimal value of koff is found to be 0.0002τ−1. Then, the DBP diffuses on average over a sliding length of λ ≃ 11l. With the obtained optimal value of koff we can obtain the probability that the DBP is bound to the DNA Pb = 0.48, see eqn (1). Thus, on average, the DBP spends approximately the same time bound to the DNA as diffusing freely in the bulk solution. This is in agreement with Marko's model, which predicts that the fraction of time the DBP spends on the DNA is the same fraction of time it spends in the bulk solution.14 Notably, the latter prediction is not general and in cases with high DNA concentration it is no longer valid. For example, when taking the case of V = 10 × 1000 × 10l3, we find that the optimal unbinding rate is koff = 0.1τ−1. When substituting the latter value of koff into eqn (2), we obtain that Pb = 0.063. Here, the very frequent DBP–DNA non-specific binding events drastically reduce D3 if the DBP spends a relatively long time on the DNA. Thus, the optimal DBP dynamics is the one at which the DBP spends most of the time in the bulk solution with very short sliding events on the DNA, see the pink data in Fig. 1B.
Though similar qualitative behavior in facilitated diffusion is observed at all DNA concentrations, large quantitative differences are obtained. As the DNA concentration increases, the minimum in the T/Ts ratio gets close to one, and the optimal koff value shifts to the right. This shows that at large DNA concentrations, it is more efficient for the system to tune the koff parameter to large values, and thus, decrease Pb.
Eqn (5) suggests that there are two relevant parameters of facilitated diffusion, the binding probability Pb and the sliding length λ. Each of these parameters determines the strength of one of the two effects of non-specific DNA binding. They are related to the microscopic parameters koff and D1, but using these two parameters does not separate the two effects. Experimentally, modulation of the parameters via salt concentration modulates koff and thereby acts via both effects.
As a check of the parameter dependencies indicated by eqn (5), we systematically vary Pb and λ. This is done microscopically by modulating koff with the D1/koff ratio fixed and D1 for constant koff, respectively. The results are shown in Fig. 2. The color map in Fig. 2A shows the rate for target binding as a function of both parameters. Light blue color indicates parameter combinations for which ‘facilitated diffusion’ is indeed optimal, i.e. the combination of 3D and 1D diffusion is more efficient than free 3D diffusion (T/Ts < 1). It is rather inefficient if the DBP remains bound to the DNA for long time without scanning the DNA. The dependencies on the individual parameters are shown in Fig. 2B and C, respectively. Fig. 2B shows the promoter finding rate as a function of the sliding length for constant values of koff and, thus, Pb. The horizontal lines represent the limiting case where the DBP binds to the DNA but does not diffuse along it (D1 = 0). The star indicates the finding rate in the absence of DNA. As expected from eqn (5), the rate increases linearly with increasing sliding length (except for sliding lengths λ ≲ l, where the effective target sizes becomes ≃l). The linear increase is seen for all values of koff. The plot also shows that sufficiently large sliding lengths are needed in order for the binding rate to exceed the free binding rate in the absence of DNA. The minimal required sliding length for facilitation increases with increasing Pb or decreasing koff.
Fig. 2C shows the finding rate as a function of (1 − Pb), the probability that the DBP is free in solution, for constant sliding length. For low values of (1 − Pb), the DBP frequently binds non-specifically to the DNA. These events effectively reduce the 3D diffusion constant to Deff = D3(1 − Pb). In agreement with this expectation, the finding rate increases linearly with the probability to be unbound, 1 − Pb.
IV. Effect of obstacles on the DNA
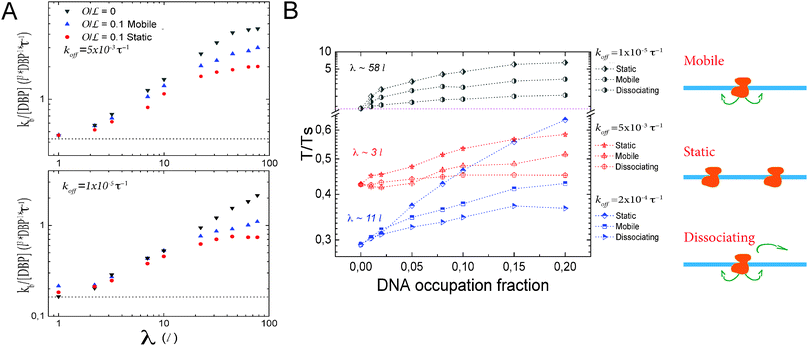
Next, we consider the impact that obstacles on the DNA have on facilitated diffusion. To that end, we implement three types of obstacles with different dynamics: obstacles of the first type diffuse on the DNA, but do not unbind. We set the crowders to diffuse on the DNA with the same 1D diffusion constant D1 as the DBP. The obstacles can transiently occupy the target position, making it inaccessible for the DBP, independent of whether the DBP arrives via 3D diffusion or 1D sliding. The second type of obstacles that we consider are static (D1 = 0), with obstacles regularly spaced on the DNA. In this case, we make sure that the target is placed on a free DNA lattice site between the obstacles. Obstacles of type three also diffuse on the DNA, again with the same diffusion constant as the DBP, but, in addition, these obstacles can dissociate from the DNA with a rate kObstoff. In these simulations, we do not track diffusion of unbound obstacles in the bulk. Rather, when an obstacle dissociates from the DNA, we immediately place a new obstacle on a random position of the DNA in order to keep the DNA occupation fraction constant, see the representation of the obstacles in Fig. 3. The obstacle that dissociates is removed from the simulation.Based on the two effects of (non-specific) binding to DNA discussed above, one can argue that obstacles on the DNA affect target finding only through the effective target size. By contrast, obstacles or crowders in the solution, which we do not consider here, would mostly affect it via the effective diffusion, although one can also expect an increase in the target size (due to crowding-enhanced binding to the DNA, which increases the sliding length25,26). Obstacles on the DNA that act as barriers for sliding effectively reduce the sliding length and thus the target size. Thus one can estimate an effective target size to be the smaller one of the two length scales of this system, the sliding length on one hand, and the average distance between obstacles on the other.
However, Fig. 3A shows that the dynamics of the roadblock also matter for the results. Here, we run simulations for two different values of koff, koff = 0.005τ−1 and 0.00001τ−1, at 10% DNA occupation. Shown data are for obstacle types one and two. The plot shows the target finding rate as a function of λ when modulating D1. Lines represent the limiting case of D1 = 0. As D1 increases, the finding rate becomes larger. For λ ≃ 3l the promoter finding rate starts to differ between the different types of obstacles. On one hand, at 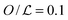 there is an obstacle every 10 lattice sites if they are static. Thus, as D1 increases, the search scenario becomes effectively one in which the DBP finds a target of size aeff = 10l, with an effective three dimensional diffusion constant Deff. On the other hand, if obstacles diffuse on the DNA, aeff fluctuates and can transiently be reduced or increased. Thus, saturation takes place at larger values of λ. We note that this average size depends on the obstacles' one-dimensional diffusion constant.
there is an obstacle every 10 lattice sites if they are static. Thus, as D1 increases, the search scenario becomes effectively one in which the DBP finds a target of size aeff = 10l, with an effective three dimensional diffusion constant Deff. On the other hand, if obstacles diffuse on the DNA, aeff fluctuates and can transiently be reduced or increased. Thus, saturation takes place at larger values of λ. We note that this average size depends on the obstacles' one-dimensional diffusion constant.
In Fig. 3B we plot the T/Ts ratio as a function of the fractional occupation of the DNA by obstacles, for three different values of koff, koff = 0.005, 0.0002 and 0.00001τ−1. These values correspond to sliding lengths of λ ≃ 3l, 11l and 58l, respectively. We note that in all cases, the presence of obstacles has a negative effect on facilitated diffusion, even for intermediate values of koff at low occupation fractions.
In general, static obstacles have the largest impact on facilitated diffusion, because they effectively trap the DBP once it has been bound non-specifically to the DNA. In this case the only way that the DBP can overcome an obstacle is to unbind from the DNA. Thus, the negative effect of static obstacles on the T/Ts ratio becomes larger as the unbinding rate koff decreases. Type-1 obstacles have the second largest effect on facilitated diffusion. Here, even though obstacles trap the DBP in regions where the target may not be present, this trapping changes as the obstacles diffuse on the DNA, making the target accessible to the DBP, even if it remains bound to the DNA for long time. However, 1D diffusion is effectively slowed down by obstacles on the DNA. The effect of the obstacles decreases as the DBP unbinding rate increases. Type-3 obstacles have the weakest effect on facilitated diffusion. In this case, the DBP can access the target in the same way as for type one. Since the obstacles can unbind from the DNA, the trapping effect is weaker and the DBP can scan larger sections of DNA. Thus, the impact of this type of obstacle on facilitated diffusion is more modest.
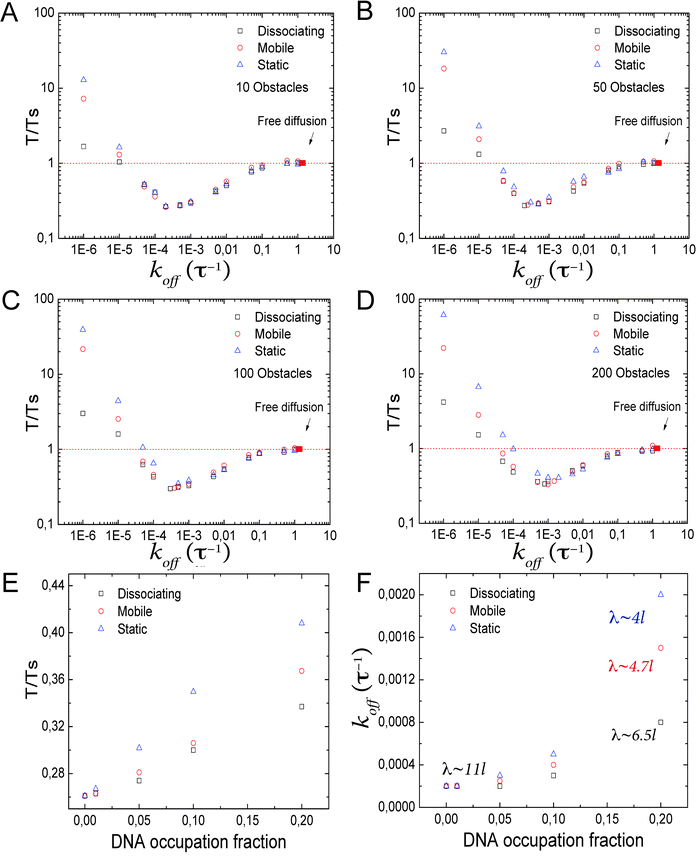
Interestingly, for different types of obstacles and DBP unbinding rates, the T/Ts ratios can get close and even cross (Fig. 3B). To take a better look into this issue, we reconstruct the facilitated diffusion plot for different levels of fractional DNA occupation, and obtain the koff value at which facilitated diffusion is optimal, see Fig. 4A–D. As can be observed, the minimum shifts towards higher values of koff and higher values of T/Ts. Next, we plot in Fig. 4E the optimal values of the T/Ts ratio as a function of DNA occupation. Static obstacles have the strongest effects on facilitated diffusion, and the dissociating obstacles the weakest. In Fig. 4F, we plot the corresponding values of koff at which facilitated diffusion is the most effective. Here, as the DNA occupation increases, the DBP needs to bind less tightly and scan smaller sections of DNA at every 1D sliding excursion. This suggests that in order to be as efficient as possible, the DBP has to spend more time in the bulk solution than on the DNA. Specifically, we showed above that in the absence of obstacles on the DNA, the DBP spends on average ≃50% of the total search time bound to the DNA. In the presence of static obstacles occupying 20% of the DNA, the average time the DBP spends bound to the DNA under optimal conditions is decreased to only 9%.
V. Concluding remarks
In this paper, we used a simple computational approach to study the promoter finding process via facilitated diffusion. We used lattice simulations to revisit how the promoter finding process is affected when modulating different parameters in our simulations. Non-specific binding to the DNA effectively reduces diffusion in the bulk and thereby the diffusion-limited binding to the target. At the same time, sliding along the DNA effectively increases the size of the target. The competition of these two effects leads to a characteristic maximum in the binding rate. This maximum is very sensitive to the concentration of DNA, D1, koff and λ. The lattice model provides a rather intuitive picture of these situations as well as an efficient computational implementation of facilitated diffusion.In addition, we have studied the effects that different types of obstacles have on the facilitated diffusion process. In general, since the DBP is (at least transiently) trapped between two obstacles, its sliding length is reduced, decreasing effectively the target size. Beyond that, our results suggest that obstacles with different dynamics on the DNA have different effects on facilitated diffusion, with static obstacles affecting the finding rate the most. In order to be as efficient as possible, the DBP has to modulate its interaction with the DNA, and spend more time in the bulk solution. The methods we used here can be applied more generally and there are a number of possible extensions to this work, such as addressing the effects of crowders on the bulk solution on the facilitated diffusion process. Other aspects of facilitated diffusion will require more detailed molecular approaches, for example the effect of DNA flexibility and supercoiling, which are difficult to implement in the lattice model. The latter has been shown to have an effect on target search kinetics with more rapid target finding for a coiled DNA conformation than for stretched DNA conformations.56–58 Studying the interplay of the DNA conformation and obstacles will be a task for future work.
References
- D. F. Browning and S. J. Busby, The regulation of bacterial transcription initiation, Nat. Rev. Microbiol., 2004, 2(1), 57–65 CrossRef CAS PubMed.
- G. D. Stormo, DNA binding sites: representation and discovery, Bioinformatics, 2000, 16(1), 16–23 CrossRef CAS PubMed.
- U. Gerland, J. D. Moroz and T. Hwa, Physical constraints and functional characteristics of Transcription Factor-DNA interaction, Proc. Natl. Acad. Sci. U. S. A., 2002, 99(19), 12015–12020 CrossRef CAS PubMed.
- F. Wang, S. Redding, I. J. Finkelstein, J. Gorman, D. R. Reichman and E. C. Greene, The promoter-search mechanism of Escherichia coli RNA polymerase is dominated by three-dimensional diffusion, Nat. Struct. Mol. Biol., 2013, 20(2), 174–181 CAS.
- A. Riggs, S. Bourgeois and M. Cohn, The lac repressor-operator interactions. III. Kinetic studies, J. Mol. Biol., 1970, 53, 401 CrossRef CAS PubMed.
- O. G. Berg, R. B. Winter and P. H. von Hippel, Diffusion-driven mechanisms of protein translocation on nucleic acids. 1. Models and theory, Biochemistry, 1981, 20, 6929–6948 CrossRef CAS PubMed.
- P. H. von Hippel and O. G. Berg, Facilitated target location in biological systems, J. Biol. Chem., 1989, 264, 675–678 CAS.
- S. G. Erskine and S. E. Halford, Reactions of the EcoRV restriction endonuclease with fluorescent oligodeoxynucleotides: identical equilibrium constants for binding to specific and non-specific DNA, J. Mol. Biol., 1998, 275, 759–772 CrossRef CAS PubMed.
- Y. M. Wang, R. H. Austin and E. C. Cox, Single Molecule Measurements of Repressor Protein 1D Diffusion on DNA, Phys. Rev. Lett., 2006, 97, 048302 CrossRef CAS PubMed.
- S. Cranz, C. Berger, A. Baici, I. Jelesarov and H. R. Bosshard, Monomeric and dimeric bZIP transcription factor GCN4 bind at the same rate to their target DNA site, Biochemistry, 2004, 43, 718–727 CrossRef CAS PubMed.
- J. Elf, G.-W. Li and X. S. Xie, Probing transcription factor dynamics at the single-molecule level in a living Cell, Science, 2007, 316(5828), 1191–1194 CrossRef CAS PubMed.
- P. Hammar, P. Leroy, A. Mahmutovic, E. G. Marklund, O. G. Berg and J. Elf, The lac repressor displays facilitated diffusion in living cells, Science, 2012, 336(6088), 1595–1598 CrossRef CAS PubMed.
- I. M. Sokolov, R. Metzler, K. Pant and M. C. Williams, Target search of N sliding proteins on a DNA, Biophys. J., 2005, 89, 895 CrossRef CAS PubMed.
- S. E. Halford and J. F. Marko, How do site-specific DNA-binding proteins find their targets?, Nucleic Acids Res., 2004, 32(10), 3040–3052 CrossRef CAS PubMed.
- M. Bauer and R. Metzler, Generalized facilitated diffusion model for DNA-binding proteins with search and recognition states, Biophys. J., 2012, 102, 2321 CrossRef CAS PubMed.
- K. V. Klenin, H. Merlitz, J. Langowski and C.-X. Wu, Facilitated diffusion of DNA-binding proteins, Phys. Rev. Lett., 2006, 96, 018104 CrossRef PubMed.
- M. Slutsky and L. A. Mirny, Kinetics of protein-DNA interaction: facilitated target location in sequence-dependent potential, Biophys. J., 2004, 87(6), 4021–4035 CrossRef CAS PubMed.
- A. B. Kolomeisky, Physics of protein-DNA interactions:mechanisms of facilitated target search, Phys. Chem. Chem. Phys., 2013, 13, 2088–2095 RSC.
- H. Kabata, O. Kurosawa, I. Arai, M. Washizu, S. A. Margarson, R. E. Glass and N. Shimamoto, Visualization of single molecules of RNA polymerase sliding along DNA, Science, 1993, 262(5139), 1561–1563 CAS.
- N. P. Stanford, M. D. Szczelkun, J. F. Marko and S. E. Halford, One- and three-dimensional pathways for proteins to reach specific DNA sites, EMBO J., 2000, 19(23), 6546–6557 CrossRef CAS PubMed.
- S. Reddinga and E. C. Greene, How do proteins locate specific targets in DNA?, Chem. Phys. Lett., 2013, 570, 1–11 CrossRef PubMed.
- L. J. Friedman, J. P. Numm and J. Gelles, RNA polymerase approaches its promoter without long-range sliding along DNA, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(24), 9740–9745 CrossRef CAS PubMed.
- R. B. Winter, O. G. Berg and P. H. von Hippel, Diffusion-driven mechanisms of protein translocation on nucleic acids. 3. The Escherichia coli lac repressor-operator interaction: kinetic measurements and conclusions, Biochemistry, 1981, 20, 6961–6977 CrossRef CAS PubMed.
- D. M. Gowers, G. G. Wilson and S. E. Halford, Measurementof the contributions of 1D and 3D pathways to the translocation of a protein along DNA, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 15883–15888 CrossRef CAS PubMed.
- C. A. Brackley, M. E. Cates and D. Marenduzzo, Intracellular Facilitated Diffusion: Searchers, Crowders, and Blockers, Phys. Rev. Lett., 2013, 111, 108101 CrossRef CAS PubMed.
- R. K. Das and A. B. Kolomeisky, Facilitated search of proteins on DNA: correlations are important, Phys. Chem. Chem. Phys., 2010, 12, 2999–3004 RSC.
- A. Marcovitz and Y. Levy, Sliding dynamics along DNA: a molecular perspective, Innovations in Biomolecular Modeling and Simulation, RSC, Biomolecular Sciences 24, 2012, ch. 10, pp. 237–262 Search PubMed.
- S. B. Zimmerman and S. O. Trach, Estimation of macromolecule concentrations and excluded volume effects for the cytoplasm of Escherichia coli, J. Mol. Biol., 1991, 222, 599–620 CrossRef CAS PubMed.
- D. S. Cayley and M. T. Record Jr, Large changes in cytoplasmic biopolymer concentration with osmolality indicate that macromolecular crowding may regulate proteinDNA interactions and growth rate in osmotically stressed Escherichia coli K-12, J. Mol. Recognit., 2004, 17, 488–496 CrossRef PubMed.
- N. Muramatsu and A. P. Minton, Tracer diffusion of globular proteins in concentrated protein solutions, Proc. Natl. Acad. Sci. U. S. A., 1988, 85, 2984–2988 CrossRef CAS.
- J. Han and J. Herzfeld, Macromolecular diffusion in crowded solutions, Biophys. J., 1993, 65, 1155–1161 CrossRef CAS PubMed.
- J. S. Kim and A. Yethiraj, Effects of macromolecular crowding on reaction rates: a computational and theoretical study, Biophys. J., 2009, 96, 1333–1340 CrossRef CAS PubMed.
- D. Gomez and S. Klumpp, Biochemical reactions in crowded environments: revisiting the effects of volume exclusion with simulations, Front. Phys., 2015, 3, 45 Search PubMed.
- B. K. Derham and J. J. Harding, The effect of the presence of globular proteins and elongated polymers on enzyme activity, Biochim. Biophys. Acta, 2006, 1764, 1000–1006 CrossRef CAS PubMed.
- M. G. S. Norris and N. Malys, What is the true enzyme kinetics in the biological system? An investigation of macromolecular crowding effect upon enzyme kinetics of glucose-6-phosphatase dehydrogenase, Biochem. Biophys. Res. Commun., 2011, 405, 388–392 CrossRef CAS PubMed.
- H.-X. Zhou, G. Rivas and A. P. Minton, Macromolecular crowding and confinement: Biochemical, biophysical, and potential physiological consequences, Annu. Rev. Biophys., 2008, 37, 375–397 CrossRef CAS PubMed.
- B. van den Berg, R. J. Ellis and C. M. Dobson, Effects of macromolecular crowding on protein folding and aggregation, EMBO J., 1999, 18(24), 6927–6933 CrossRef CAS PubMed.
- M. S. Cheung, D. Klimov and D. Thirumalai, Molecular crowding enhances native state stability and refolding rates of globular proteins, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(13), 4753–4758 CrossRef CAS PubMed.
- J. Mittal and R. B. Best, Dependence of Protein Folding Stability and Dynamics on the Density and Composition of Macromolecular Crowders, Biophys. J., 2010, 98, 315–320 CrossRef CAS PubMed.
- D. Gnutt, M. Gao, O. Bryski, M. Heyden and S. Ebbinghaus, Effekte des Volumenausschlusses in lebenden Zellen, Angew. Chem., 2015, 127, 2578–2581 CrossRef.
- H. Matsuda, G. G. Putzel, V. Backman and I. Szleifer, Macromolecular crowding as a regulator of gene transcription, Biophys. J., 2014, 106, 1801–1810 CrossRef CAS PubMed.
- M. J. Morelli, R. J. Allen and P. R. ten Wolde, Effects of macromolecular crowding on genetic networks, Biophys. J., 2011, 101, 2882–2891 CrossRef CAS PubMed.
- C. Tan, S. Saurabh, M. P. Bruchez, R. Schwartz and P. LeDuc, Molecular crowding shapes gene expression in synthetic cellular nanosystems, Nat. Nanotechnol., 2013, 8, 602–608 CrossRef CAS PubMed.
- S. P. Haugen, W. Ross and R. L. Gourse, Advances in bacterial promoter recognition and its control by factors that do not bind DNA, Nat. Rev. Microbiol., 2008, 6, 507–519 CrossRef CAS PubMed.
- E. Nudler, RNA polymerase active center: the molecular engine of transcription, Annu. Rev. Biochem., 2009, 78, 335–361 CrossRef CAS PubMed.
- R. M. Saecker, M. T. Record and P. L. Dehaseth, Mechanism of bacterial transcription initiation: RNA polymerase-promoter binding, isomerization to initiation-competent open complexes, and initiation of RNA synthesis, J. Mol. Biol., 2011, 412, 754–771 CrossRef CAS PubMed.
- C. L. Peterson and M. A. Laniel, Histones and histone modifications., Curr. Biol., 2004, 14(14), R546–R551 CrossRef CAS PubMed.
- S. C. Dillon and C. J. Dorman, Bacterial nucleoid-associated proteins, nucleoid structure and gene expression, Nat. Rev. Microbiol., 2010, 8, 185–195 CrossRef CAS PubMed.
- Y. Meroz, I. Eliazar and J. Klfter, Facilitated diffusion in a crowded environment: from kinetics to stochastics, J. Phys. A: Math. Theor., 2009, 42, 434012 CrossRef.
- A. Marcovitz and Y. Levy, Obstacles may facilitate and direct DNA search by proteins, Biophys. J., 2013, 104, 2042–2050 CrossRef CAS PubMed.
- G.-W. Li, O. G. Berg and J. Elf, Effects of macromolecular crowding and DNA looping on gene regulations kinetics, Nat. Phys., 2009, 5, 294–297 CrossRef CAS.
- A. Mahmutovic, O. G Berg and J. Elf, What matters for lac repressor search in vivo – Sliding, Hopping, Intersegment Transfer, Crowding on DNA or Recognition?, Nucleic Acids Res., 2015, 43(7), 3454–3464 CrossRef CAS PubMed.
- L. Liu and K. Luo, Molecular crowding effect on dynamics of DNA-binding proteins search for their targets, J. Chem. Phys., 2014, 141, 225102 CrossRef PubMed.
- O. Givaty and Y. Levy, Protein Sliding Along DNA: Dynamics and Structural Characterization, J. Mol. Biol., 2009, 385, 1087–1097 CrossRef CAS PubMed.
- M. V. Smoluchowski, Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen, Z. Phys. Chem., 1917, 92, 129–168 Search PubMed.
- B. van den Broek, M. A. Lomholt, S.-M. J. Kalisch, R. Metzler and G. J. L. Wuite, How DNA coiling enhances target localization by proteins, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(41), 15738–15742 CrossRef CAS PubMed.
- D. M. Gowers and S. E. Halford, Protein motion from nonspecific to specific DNA by three-dimensional routes aided by supercoiling, EMBO J., 2003, 22, 1410–1418 CrossRef CAS PubMed.
- M. A. Lomholt, B. van den Broek, S. M. Kalisch, G. J. Wuite and R. Metzler, Facilitated diffusion with DNA coiling, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(20), 8204–8208 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2016 |