Open Access Article
Open Access ArticlePredictive thermodynamics for ionic solids and liquids†
Leslie
Glasser
*a and
H. Donald Brooke
Jenkins
*b
aNanochemistry Research Institute, Department of Chemistry, Curtin University, Perth 6845, Western Australia, Australia. E-mail: l.glasser@curtin.edu.au; Fax: +61 8 9266-4699; Tel: +61 8 9848-3334
bDepartment of Chemistry, University of Warwick, Coventry, West Midlands CV4 7AL, UK. E-mail: h.d.b.jenkins@warwick.ac.uk; Fax: +44 (0)2476-466-747; Fax: +44 (0)2476-524-112; Tel: +44 (0)2476-466-747 Tel: +44 (0)2476-523-265
First published on 26th May 2016
Abstract
The application of thermodynamics is simple, even if the theory may appear intimidating. We describe tools, developed over recent years, which make it easy to estimate often elusive thermodynamic parameter values, generally (but not exclusively) for ionic materials, both solid and liquid, as well as for their solid hydrates and solvates. The tools are termed volume-based thermodynamics (VBT) and thermodynamic difference rules (TDR), supplemented by the simple salt approximation (SSA) and single-ion values for volume, Vm, heat capacity,  , entropy,
, entropy,  , formation enthalpy, ΔfH°, and Gibbs formation energy, ΔfG°. These tools can be applied to provide values of thermodynamic and thermomechanical properties such as standard enthalpy of formation, ΔfH°, standard entropy,
, formation enthalpy, ΔfH°, and Gibbs formation energy, ΔfG°. These tools can be applied to provide values of thermodynamic and thermomechanical properties such as standard enthalpy of formation, ΔfH°, standard entropy, 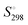 , heat capacity, Cp, Gibbs function of formation, ΔfG°, lattice potential energy, UPOT, isothermal expansion coefficient, α, and isothermal compressibility, β, and used to suggest the thermodynamic feasibility of reactions among condensed ionic phases. Because many of these methods yield results largely independent of crystal structure, they have been successfully extended to the important and developing class of ionic liquids as well as to new and hypothesised materials. Finally, these predictive methods are illustrated by application to K2SnCl6, for which known experimental results are available for comparison. A selection of applications of VBT and TDR is presented which have enabled input, usually in the form of thermodynamics, to be brought to bear on a range of topical problems. Perhaps the most significant advantage of VBT and TDR methods is their inherent simplicity in that they do not require a high level of computational expertise nor expensive high-performance computation tools – a spreadsheet will usually suffice – yet the techniques are extremely powerful and accessible to non-experts. The connection between formula unit volume, Vm, and standard thermodynamic parameters represents a major advance exploited by these techniques.
, heat capacity, Cp, Gibbs function of formation, ΔfG°, lattice potential energy, UPOT, isothermal expansion coefficient, α, and isothermal compressibility, β, and used to suggest the thermodynamic feasibility of reactions among condensed ionic phases. Because many of these methods yield results largely independent of crystal structure, they have been successfully extended to the important and developing class of ionic liquids as well as to new and hypothesised materials. Finally, these predictive methods are illustrated by application to K2SnCl6, for which known experimental results are available for comparison. A selection of applications of VBT and TDR is presented which have enabled input, usually in the form of thermodynamics, to be brought to bear on a range of topical problems. Perhaps the most significant advantage of VBT and TDR methods is their inherent simplicity in that they do not require a high level of computational expertise nor expensive high-performance computation tools – a spreadsheet will usually suffice – yet the techniques are extremely powerful and accessible to non-experts. The connection between formula unit volume, Vm, and standard thermodynamic parameters represents a major advance exploited by these techniques.
Introduction
Consider what obliges one to attempt to estimate the properties of a known inorganic material or predict the properties of an as-yet unprepared material. Examine the complexities! There are about 100 chemical elements, which combine to form about 100 million already-known compounds, of which some 10% could be classified as inorganic/mineral.1 There remains an almost limitless range of possible combinations as yet unexplored. By contrast, the most comprehensive current crystallographic databases report data on only about one million of these organic compounds and on only about one-quarter of a million inorganic compounds.2 Ionic liquids are combinations of such a broad range of cations and anions so that the in-principle possible number of such liquids is of the order of 1018 (although the realistically possible number is orders of magnitude smaller) – already, some 1000 have been reported in the literature.3 On the other hand, thermodynamic data is available for only some 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 compounds, of which about 60% (20
000 compounds, of which about 60% (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) are inorganic (see ESI† for a list of thermodynamic data compendia). Thus, the chance of finding the property data one seeks is miniscule; add to this, the need to obtain data on as-yet unprepared material, such as might be required for a proposed synthesis. As a consequence, a number of simple empirical rules have been developed for a variety of thermodynamic properties (see Table 1).
000) are inorganic (see ESI† for a list of thermodynamic data compendia). Thus, the chance of finding the property data one seeks is miniscule; add to this, the need to obtain data on as-yet unprepared material, such as might be required for a proposed synthesis. As a consequence, a number of simple empirical rules have been developed for a variety of thermodynamic properties (see Table 1).
| Rule | Thermodynamic property | Value | Ref. |
|---|---|---|---|
| Dulong and Petit and Neumann–Kopp summation: heat capacity | C p, per mole for atoms in solids | ≈3R ≈ 25 J K−1 mol−1 where R is gas constant | 4 |
| Trouton: vaporization |
ΔvapS° for organic molecules and non-polar liquids
ΔvapH° for organic molecules and non-polar liquids For hydrogen bonding in liquids |
ΔvapS°/J K−1 mol−1 ≈ 85
ΔvapH°/kJ mol−1 ≈ 85Tb/K T b = boiling point ΔvapH°/kJ mol−1 > 85Tb/K |
|
| Walden: fusion | ΔfusS° for rigid non-spherical molecules | ≈20–60 J K−1 mol−1 | |
| Richards: fusion | ΔfusS° for rigid spherical molecules | ≈7–14 J K−1 mol−1 | 5 |
| Glasser & Jenkins: Cp, for silicate anions | Single ion heat capacity, Cp, for silicate anions | ≈13.8n where n is the number of atoms contained within the silicate anion | 6 |
| Glasser & Jenkins: Cp for general anions | Single ion heat capacity, Cp for general anions | ≈17n where n is the number of atoms contained within the anion | 6 |
| Westwell, Searle, Wales & Williams: sublimation enthalpy from melting point | ΔsublH° for molecules that do not possess internal rotors, such as long chain organic molecules |
ΔsublH°/kJ mol−1 = 0.188Tm/K + 0.522
T m = melting point R 2 = 0.90 |
7 |
| Westwell, Searle, Wales & Williams: sublimation enthalpy from boiling point | ΔsublH° for molecules that do not possess internal rotors, such as long chain organic molecules |
ΔsublH°/kJ mol−1 = 0.119Tb/K + 1.38
T b = boiling point R 2 = 0.96 |
|
| Westwell, Searle, Wales & Williams: vaporization enthalpy of solids | ΔvapH° for molecules that do not possess internal rotors, such as long chain organic molecules |
ΔvapH°/kJ mol−1 = 0.166Tm/K − 3.99
T m = melting point R 2 = 0.86 |
|
| Westwell, Searle, Wales & Williams: vaporization enthalpy of liquids | ΔvapH° for molecules that do not possess internal rotors, such as long chain organic molecules |
ΔvapH°/kJ mol−1 = 0.108Tb/K − 5.08
T b = boiling point R 2 = 0.98 |
|
| Westwell, Searle, Wales & Williams: Tb from Tm | T b from Tm for molecules that do not possess internal rotors, such as long chain organic molecules |
T
b/K = 1.52Tm/K + 14.5
T b = boiling point T m = melting point R 2 = 0.86 |
|
| Westwell, Searle, Wales & Williams: vaporization and sublimation enthalpies | ΔvapH° for molecules that do not possess internal rotors, such as long chain organic molecules |
ΔvapH°/kJ mol−1 = 0.889ΔsublH°/kJ mol−1 − 4.75
R 2 = 0.98 |
|
| Kempster & Lipson; Glasser & Jenkins: formula unit volume | V m mainly for organic solids | V m ≈ 0.018 nm3 per atom | 8 |
| V m for water | V m ≈ 0.0245 nm3 | (see Table 3)9 | |
The most basic data that needs to be obtained for this essentially unlimited set of materials is thermodynamic because such data informs us of the stability of the materials, our ability to synthesise them, and to maintain their integrity. In the absence of published data, the question then arises as to how one should proceed in order to obtain that data.
The most fundamental approach would be through quantum mechanical (QM) calculation,10 where one considers in detail how the fundamental particles of which a material consists, such as atoms and electrons, interact with one another through electrostatic forces, charge transfer, van der Waals (dispersion) interactions, electron correlation, and so forth. While such an approach has yielded important results, it is complex, uses expensive computation facilities, and requires considerable expertise in both application and interpretation. At a somewhat simpler level, density functional theory (DFT)11 has reduced the complexity of QM methods and, hence, their cost by relating the energetics to the more readily computable electron density of the material and using functions of the electron density function (that is, functionals) to derive experimentally observable results. DFT has found increasing favour in recent years in providing useful results but difficulties remain in dealing with dispersion and electron correlation. Thus, in stark contrast to the VBT approach, these QM approaches require considerable expertise to execute and interpret reliably.
A rational response has been to collect data on related materials and use that data to extrapolate (or interpolate) in order to estimate the properties of the material under investigation. We illustrate this approach in some general terms first, and then focus on an approach which we have termed volume-based thermodynamics (VBT)12,13 together with the thermodynamic difference rule (TDR),9,14–16 both of which we and colleagues have developed and fostered over the last two decades. These empirical procedures have proven to have great generality and utility, and have been widely implemented for ionic solids and liquids,17 as also illustrated in a list of applications in the final section of this paper. One further very successful method is the “Simple Sum Approximation” (SSA)18 where the thermodynamic properties of a complex ionic, such as MgSiO3, is treated as a sum of its components, being the oxides MgO and SiO2 in this case.
Prediction basically relies on the combination, through the Gibbs relation, of enthalpy, H, and entropy, S, contributions:19
| ΔG = ΔH − TΔS | (1) |
 , and hence, viaeqn (1) lead to the prediction of ΔfG° for individual materials as well as ΔrG° for a reaction of interest. It is often of little concern that such estimates may not be highly precise, since the purpose of thermodynamic prediction may, in many instances, simply be one of assessing synthetic feasibility or otherwise, i.e., simply whether ΔrG is negative (feasible) or positive (infeasible in principle, although a small positive value, say ∼20 kJ mol−1, does not preclude formation of useful proportions of product which can be extracted from the reaction system).20 Furthermore, experimentally-derived thermodynamic values themselves can have considerable uncertainties.21–23 The actual mathematics required is minimal yet quantitative interpretation results. This review summarises VBT, TDR, SSA, and single-ion additivity, and highlights many of their successes – indeed, the scope of their application has proved to be quite remarkable – and directs the reader to numerous applications where these procedures have played a significant role in yielding the thermodynamics.
, and hence, viaeqn (1) lead to the prediction of ΔfG° for individual materials as well as ΔrG° for a reaction of interest. It is often of little concern that such estimates may not be highly precise, since the purpose of thermodynamic prediction may, in many instances, simply be one of assessing synthetic feasibility or otherwise, i.e., simply whether ΔrG is negative (feasible) or positive (infeasible in principle, although a small positive value, say ∼20 kJ mol−1, does not preclude formation of useful proportions of product which can be extracted from the reaction system).20 Furthermore, experimentally-derived thermodynamic values themselves can have considerable uncertainties.21–23 The actual mathematics required is minimal yet quantitative interpretation results. This review summarises VBT, TDR, SSA, and single-ion additivity, and highlights many of their successes – indeed, the scope of their application has proved to be quite remarkable – and directs the reader to numerous applications where these procedures have played a significant role in yielding the thermodynamics.
In essence, VBT [together with its isomegethic (“equal size”) rule,24 which vastly extends its application to new and hypothesised materials] relates the formula unit volumes, Vm, of materials, however measured or estimated, to their thermodynamic quantities, thereby leading to practical prediction. TDR uses the differences between related materials to predict values for other similar materials, while the additive SSA and single-ion values (and also TDR, in a slightly more complex way) demonstrate that the properties of complex materials may be estimated by summing the corresponding properties of their component parts.
Group additivity methods
Group methods operate by assuming that a material (typically, but not exclusively, an organic molecule) contains independent entities (such as single bonds, double bonds, alcohol, amine, etc.) whose thermodynamic property values can be summed to produce a property value for the whole material, but supplemented by other terms to allow for the interactions between and among groups. (An extensive list of group methods is presented in our ESI.†) The most developed of these are termed Benson group methods.25 In order to permit broad application of the methods, it has been necessary to develop hundreds of group terms, with the further complication of the necessity for the user to identify suitable groups within the material under consideration. Many computer programs incorporate these methods, often as preliminary steps to a more complex analysis. The NIST WebBook26 provides a free service which implements the Benson group additivity scheme for gas-phase organic molecules.Group methods have also been developed for ionic systems, by identifying constituent cations and anions whose properties are summed to provide the overall property value sought. The results are most reliable when based on related materials. In general, these methods have not received wide acceptance.
Volume-based thermodynamics
Early thermodynamic property-size relations were generally based upon ion radii since the alkali metal and halide monatomic ions of the most important alkali halides are spherical and radius, which could be quite readily established from X-ray data, was the most obvious measure of relative ion size. An important equation in this context was the Kapustinskii relation27 for lattice potential energy, UPOT: | (2) |
Mallouk, Bartlett and coworkers28–31 presented some relationships between formula unit volume, Vm and thermodynamic properties (notably lattice energy, UPOT, as a function of Vm−1/3) and standard entropy,  (as a function of Vm) but only for a handful of MX (1
(as a function of Vm) but only for a handful of MX (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) simple salts. Jenkins, Roobottom, Passmore and Glasser32 explored these relationships further, by (i) replacing the distance sum with the equivalently-dimensioned cube-root of the formula unit volume, Vm1/3, and (ii) using a generalisation of the charge product33 into an ionic strength factor-type summation, I:
1) simple salts. Jenkins, Roobottom, Passmore and Glasser32 explored these relationships further, by (i) replacing the distance sum with the equivalently-dimensioned cube-root of the formula unit volume, Vm1/3, and (ii) using a generalisation of the charge product33 into an ionic strength factor-type summation, I:
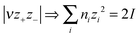 | (3) |
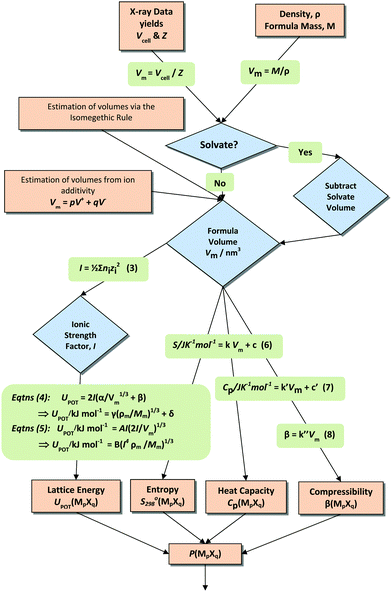
Scheme 1 summarises the processes and equations which use material volumes to produce thermodynamic values.
Lattice energies for a large database of simple ionic solids could be reliably correlated using this linear VBT function:34
 | (4, Scheme 1) |
Equivalent equations may be couched in terms of density, ρm, and formula mass, Mm:
| UPOT/kJ mol−1 = γ(ρm/Mm)1/3 + δ | (4, Scheme 1) |
| UPOT/kJ mol−1 = B(I4ρm/Mm)1/3 | (5, Scheme 1) |
For lattice energies greater than 5000 kJ mol−1, which includes most minerals, a limiting version35 of this equation exists which contains no empirical constants whatsoever and yet satisfactorily predicts lattice energies up to 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 and probably beyond:
000 kJ mol−1 and probably beyond:
| UPOT = AI(2I/Vm)1/3 | (5, Scheme 1) |
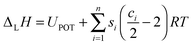 | (9) |
 | ||
| Fig. 1 Born–Haber–Fajans cycle for solids and aqueous solutions of formula MpXq. IP = ionisation potential; EA = electron affinity; lattice enthalpy (ΔLH) and enthalpies of formation (ΔfH), sublimation (ΔsublH), dissociation (ΔdissH), hydration (ΔhydrH), and solution (ΔsolnH) are involved. UPOT represents the lattice potential energy. In the formula for ΔLH, m depends on p and q and the nature of the ions Mq+ and Xq− (see eqn (9) in text).36 | ||
Using these approaches, it becomes simple to evaluate the lattice energies, UPOT (and enthalpies of formation, ΔfH°, via the Born–Haber–Fajans relation) of ionic solids.
Thermodynamic difference rule (TDR)
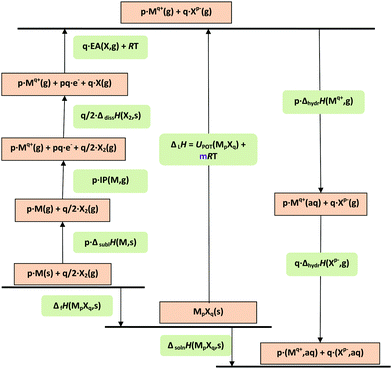
The thermodynamic difference rule, TDR, is a complementary set of procedures which utilizes additive connections among related materials.9,12–16Scheme 2 shows the steps by which TDR is usually applied. The technique is extremely powerful as a result of its ability to enable estimates to be made of thermodynamic data not otherwise available.| P(MpXq·nL,s) − P(MpXq,s) = nθP(L, s–s) | (11a) |
| P(MpXq·mL,s) − P(MpXq·nL,s) = (m − n)θP(L, s–s) | (11b) |
| UPOT(MpXq·nH2O,c) − UPOT(MpXq,c) = nθU(H2O) | (12) |
| Material | Ionic strength factor, I | α/kJ mol−1 (nm3 formula unit−1)−1/3 | β/kJ mol−1 | Mean absolute error (%) |
|---|---|---|---|---|
| a C p values have been estimated for 799 materials, ranging from small ionics to large mineral structures. Poor outliers may be avoided by using the lesser of the calculated value from eqn (7) and the approximate limiting Dulong–Petit value of 25 × m J K−1 mol−1, where m = number of atoms in the formula unit (cf.Table 1). | ||||
| Lattice energy from volume data, UPOT/kJ mol−1 = 2I(α/Vm1/3 + β) (4) | ||||
MX (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
1 | 117 | 52 | 4 |
MX2 (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
3 | 134 | 61 | |
M2X (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
3 | 165 | −30 | |
MX (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
4 | 119 | 60 | |
| MpXq | ½(pq2 + qp2) | 139 | 28 | |
| Material | Ionic strength factor, I | γ/kJ mol−1 cm−1 | δ/kJ mol−1 | Mean absolute error (%) |
|---|---|---|---|---|
| Lattice energy from density data, UPOT/kJ mol−1 = γ(ρ/M)1/3 + δ (5) | ||||
MX (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
1 | 1981.2 | 103.8 | 4 |
MX2 (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
3 | 8375.6 | −178.8 | |
M2X (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
3 | 6764.3 | 365.4 | |
MX (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
4 | 6864.0 | 732.0 | |
| MpXq | ½(pq2 + qp2) | 2347.6 × I | 55.2 × I | |
| k/J K−1 mol−1 (nm−3 formula unit) | c/J K−1 mol−1 | Mean absolute error (%) | |
|---|---|---|---|
| Entropy, S/J K−1 mol−1 = kVm + c (6) | |||
| Anhydrous ionic salts | 1360 ± 56 | 15 ± 6 | 12 |
| Hydrated ionic salts | 1579 ± 30 | 6 ± 6 | 7.4 |
| Organic liquids | 1133 ± 7 | 44 ± 2 | 5.7 |
| Organic solids | 774 ± 21 | 57 ± 6 | 10.4 |
| k′/J K−1 mol−1 (nm−3 formula unit) | c′/J K−1 mol−1 | Mean absolute error (%) | |
|---|---|---|---|
| Heat capacity, Cp/J K−1 mol−1 = k′Vm + c′ (7) | |||
| Non-framework silicates | 1465 | 11 | |
| General ionic solidsa | 1322 | −0.8 | 24.5 |
| Ionic liquids | 1037 | 45 | |
| k′′/GPa−1 (nm−3 formula unit) | Mean absolute error (%) | |
|---|---|---|
| Isothermal compressibility, β/GPa−1 = k′′Vm (8) | ||
| General ionic solids (no alkali halides) | 0.634 | 12 |
| Perovskites | 0.472 | 7 |
Room-temperature ionic liquids
Room-temperature ionic liquids (RTILs)38–41 can replace organic solvents used for the dissolution of both polar and non-polar solutes and for processing or extraction of materials, while also having useful catalytic features.42 ILs are low-polluting, with low combustibility, good thermal stability and low vapour pressures. They have high viscosities, and their liquid range can often cover several hundred degrees. The range of their applications has been extended by use of mixtures of IL's43 and as supercritical fluids.44As their name implies, they are usually liquid at ambient temperatures and consist solely of ionic species. In order to reduce the lattice energy of their crystalline state and hence their melting point, one or sometimes both of their cations and anions need to be large and their cations also often have low symmetry. The cations are generally organic with long-chain features and buried charges, such as the pyrollidinium, methylimidazolium and pyridinium cations (see Fig. 2) while the anions, such as BF4−, PF6−, or NTf2− [formula: (CF3SO2)2N−] have diffuse charges.
 | ||
| Fig. 2 Principal cations involved in important ionic liquids. (I) Imidazolium cations, (II) pyridinium cations, (III) tetraalkylammonium cations, (IV) tetraalkylphosphonium cations, and (V) pyrollidinium cations. | ||
Since there are, as noted above, many possible combinations of cation and anion, it becomes possible to consider designing ionic liquids to purpose. Although early QSAR predictions45–47 were not always regarded as satisfactory,48 molecular volume49 has emerged as an important observable. Thus, Glasser38 has estimated a VBT-based entropy for ionic liquids, derived from correlations for both inorganic solids and organic liquids:
| S (J K−1 mol−1) = 1246.5(Vm/nm3) + 29.5 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ionic liquids, with amended constants (eqn (4), Scheme 1): I = 1, α = 8326 kJ nm mol−1 and β = 157 kJ mol−1.
1 ionic liquids, with amended constants (eqn (4), Scheme 1): I = 1, α = 8326 kJ nm mol−1 and β = 157 kJ mol−1.
VBT relations have now been used to establish other physical thermodynamic properties, independent of crystal structure, such as liquid entropy,53 melting point,54–56 heat capacity57 and critical micelle concentration (c.m.c.).58 A recent review by Beichel59 cites relevant literature from the Krossing laboratory; in order to emphasize lack of reliance on any experimental input at all, this group has introduced the term “augmented volume-based thermodynamics”.
An explanation for the simple volume relations
The striking simple relations to volume involved in VBT, almost independent of structure, upon which we have reported invite some explanation. We suggest that the bulk thermodynamic properties derive from the interactions between the particles involved (complex ions or even molecules) rather than within those particles.60 For ionic materials, the interactions are largely coulombic (electrostatic or Madelung energies) with lesser contributions from specific repulsion and van der Waals-type interactions so that (to the approximation inherent in our correlations) the interactions are similar, independent of the specific species involved and also independent of structure. At this level of approximation we have found that the thermodynamic values that emerge prove adequate, in the majority of cases, for deciding questions of alternative synthetic routes for the preparation of inorganic materials.As we have noted above, an important consequence of the independence of structure is that these relations apply equally to pure liquids as to solids, so that they can be applied to the increasingly important class of ionic liquids.38
Madelung energies – for known structures
The coulombic (or Madelung) energy, EM, of a material of known structure is readily calculated by means of standard computer programs, such as GULP61 and EUGEN.62 This energy corresponds to separating the constituent ions into independent gas phase ions against coulombic forces only. We have observed63 that the resulting Madelung energy is closely related to the corresponding lattice energy, in the form| UPOT/kJ mol−1 = 0.8518EM + 293.9 | (14) |
Eqn (14) thus provides a further simple direct means for obtaining lattice energies, apart from VBT. However, the Madelung calculation comes into its own when applied to an ionic system with structures containing covalently-bonded complexes, such as K2SnCl6. If the complex ion, SnCl62− in this case, is treated as a “condensed ion”, with all the ion charge placed on the central atom (thus Sn2−) and the ligands given zero charge (Cl0), then we are effectively dealing with a system which decomposes to 2K+(g) + Sn2−(g) when the Madelung energy, now EM′, is supplied. For this system
| UPOT/kJ mol−1 = 0.963EM′ | (15) |
From these values, we can determine a formation energy for the “condensed ion” complex (see example below).
Isomegethic rule
Our isomegethic (“equal size”) rule24 states that “ionic salts of the same empirical chemical formula having identical charge states (i.e., lattice ionic strength factors, I) will have approximately equal formula unit volumes, Vm.” Since I, Vm and stoichiometry are then approximately identical, isomegethic compounds will have almost identical lattice potential energies too.As an illustration, consider the relation:
| Vm(NO+ClO4−) ≈ Vm(NO2+ClO3−) ≈ Vm(ClO2+NO3−) | (14a) |
| UPOT(NO+ClO4−) ≈ UPOT(NO2+ClO3−) ≈ UPOT(ClO2+NO3−) | (14b) |
Single-ion values
Since it is seldom that all the desired thermodynamic values are available to generate the desired data, we have prepared sets of internally consistent single-ion values which may be used additively to generate otherwise absent data, collected in Table 4. An early example of this procedure is provided by the work of Latimer67,68 in developing single ion entropy estimates.| Cation | Volume/nm3 | C p(298)ion/J K−1 mol−1 | −ΔfH(298)/kJ mol−1 | −ΔfG(298)/kJ mol−1 | Anion | Volume/nm3 | C p(298)ion/J K−1 mol−1 | −ΔfH(298)/kJ mol−1 | −ΔfG(298)/kJ mol−1 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| NH4+ | 0.0356 | 67.0 | F− | 0.014 | 20.6 | 5 | 5.0 | ||||
| Li+ | 0.0067 | 19.4 | 21.1 | 308.7 | 259.8 | Cl− | 0.0298 | 36.1 | 23.5 | 110.8 | 113.7 |
| Na+ | 0.0158 | 37.2 | 29.7 | 278.3 | 232.2 | Br− | 0.0363 | 48.6 | 26.6 | 66.3 | 70.6 |
| K+ | 0.0277 | 50.5 | 31.4 | 316 | 258.7 | I− | 0.0488 | 56.8 | 28.3 | −8.2 | 0.0 |
| Rb+ | 0.0341 | 63.1 | 31.3 | 311.7 | 257.4 | N3− | 0.0416 | 54.8 | |||
| Cs+ | 0.042 | 69.2 | 31.7 | 315.4 | 260.4 | O2− | 0.0134 | 7.4 | |||
| Ag+ | 29.9 | OH− | 0.0184 | 20.7 | 21.2 | 228.6 | 247.9 | ||||
| Mg2+ | 0.0049 | 20.5 | 26.1 | 491.4 | 374 | S2− | 0.032 | 22.1 | |||
| Ca2+ | 0.0201 | 32.5 | 28.9 | 579.8 | 468.2 | ClO3− | 70.1 | 68.5 | |||
| Sr2+ | 0.0213 | 37.9 | 30.3 | 627.2 | 558.7 | BrO3− | 76.1 | 39.7 | |||
| Ba2+ | 0.027 | 55.1 | 30.2 | 655 | 570.1 | CO32− | 0.0426 | 52.6 | 57.5 | 594.3 | 582.7 |
| Mn2+ | 30.4 | 262.9 | 161.3 | NO3− | 0.0492 | 78.5 | |||||
| Fe2+ | 0.0067 | 38.6 | 31.8 | 138.5 | 32.3 | PO43− | 0.057 | 71.8 | |||
| Zn2+ | 0.0125 | 37.3 | SO42− | 0.0611 | 74.3 | 71.5 | 812.2 | 802.3 | |||
| Cu2+ | 0.0053 | 33.5 | ClO4− | 0.0619 | 105.8 | 134.9 | |||||
| Ni2+ | 0.0004 | 29.6 | 126.7 | MnO4− | 0.0665 | ||||||
| Co2+ | 0.0019 | 39.5 | 32.0 | 161.8 | AsO43− | 0.0658 | |||||
| Fe3+ | 0.0061 | 28.2 | 208.2 | 60.0 | VO43− | 0.0663 | |||||
| Al3+ | 17.3 | 20.9 | 630.1 | 462.5 | Fe(CN)64− | 219.8 | |||||
| La3+ | 28.8 | 785.9 | 595.3 | ||||||||
| Cr3+ | 31.0 | 282.1 | 85.6 | ||||||||
| Fe3+ | 30.7 | SiO32− | 57.58 | 1056.9 | 1090.1 | ||||||
| Sc3+ | 0.0035 | SiO44− | 68.93 | 1198.5 | 1300.8 | ||||||
| Lu3+ | 0.0102 | SiO56− | 82.18 | 1344.4 | 1520.9 | ||||||
| Yb3+ | 0.0111 | Si2O52− | 101.86 | 1962.7 | 1920.0 | ||||||
| Tm3+ | 0.011 | Si2O76− | 127.4 | 2246.4 | 2361.2 | ||||||
| Er3+ | 0.0126 | Si2O1012− | 162.2 | ||||||||
| Y3+ | 0.0131 | Si3O108− | 182.77 | 3315.1 | 3476.7 | ||||||
| Dy3+ | 0.0137 | Si5O1816− | 317.21 | 5660.3 | 6050.0 | ||||||
| Tb3+ | 0.0148 | Si4O116− | 213.09 | 4098.6 | 4108.7 | ||||||
| Gd3+ | 0.0133 | ||||||||||
| Eu3+ | 0.0146 | ||||||||||
| Sm3+ | 0.0164 | ||||||||||
| Si4+ | 24.5 | ||||||||||
| Ti4+ | 35.2 | H2O | 0.0245 | 40.9 | 41.3 | 285.8 | 237.1 |
An example set of predictive thermodynamic calculations: K2SnCl6
We here provide a set of results for the material dipotassium hexachlorostannate, K2SnCl6, where we have deliberately selected the difficult case of a partially covalent material for which experimental thermodynamic values are available for comparison. This demonstrates some of the weaknesses of these predictive methods against some of their strengths in that they may provide a wide range of otherwise unavailable thermodynamic values.| KCl | SnCl4 | K2SnCl6 | 2KCl + SnCl4 | % Diff | 2KCl + SnCl4 → K2SnCl6 | |
|---|---|---|---|---|---|---|
| ΔfH°(25 °C,s)/kJ mol−1 | −436.7 | −517.0 | −1482.0 | −1390.4 | −6.2 | −91.6 |
| S°(25 °C,s)/J K−1 mol−1 | 82.7 | 265.0 | 371.0 | 430.4 | 16.0 | −59.4 |
| ΔfG°(25 °C,s)/kJ mol−1 | −461.3 | −596.0 | −1592.6 | −1518.7 | −4.6 | −73.9 |
| C p(25 °C,s)/J K−1 mol−1 | 51.4 | 157.2 | 221.1 | 260.1 | 17.6 | −39.0 |
For the SSA to be accurate, it is necessary that the reaction to form product should yield zero (or small) thermodynamic differences. As may be seen from the final column in Table 5, the reaction 2KCl + SnCl4 → K2SnCl6 produces non-zero differences, so that the SSA results (3rd last column) are not accurate, but may be useful as a general guide when the thermodynamic values are unknown.
The constants used in the following calculations are selected from Table 2.
(a) Formula unit volume,70Vm/nm3 = Vcell/Z = 1.0057/4 = 0.2514
(b) Ionic strength factor, 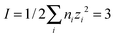 (eqn (3))
(eqn (3))
(c) Lattice (potential) energy, UPOT/kJ mol−1 = 2I(α/Vm1/3 + β) (eqn (4)) = 2 × 3 (165/0.25141/3 − 30) = 1389 (cf. Born–Haber–Fajans cycle value71 = 1390, Fig. 3)
(d) Standard entropy, S/J K−1 mol−1 = kVm + c (eqn (6)) = 1360 × 0.2514 + 15 = 356.9 (cf. 371.0, diff. 3.9%, Table 5)
(e) Heat capacity, Cp/J K−1 mol−1 = k′Vm + c′ (eqn (7)) = 1322 × 0.2514 − 0.8 = 331.6 (cf. 221.1, diff. −33%, Table 5) (Neumann–Kopp atom additive value6 for 9 atoms = 25 × 9 = 225: diff. 1.7%)
Comment: the VBT value calculated for Cp considerably exceeds the 9-atom limiting Neumann–Kopp value, which we propose is a preferred value (see Table 2). This suggests that the rigid covalent SnCl62− structure corresponds to too-large a volume compared with a close-packed strictly ionic system. Correspondingly, the predicted entropy is also too large. By contrast, in calculating the lattice energy, any volume error is minimised by the use of a cube-root volume.
(f) ΔfH(SnCl62−,g)/kJ mol−1 = UPOT(K2SnCl6,s)71 + ΔfH(K2SnCl6,s)69 − 2ΔfH(K+,g)71 = (1390) + (−1482) − 2(514) = −1120 (cf.65 −1156, diff. 3.1%)
(g) Madelung energy72 for K2SnCl6(s), EM/kJ mol−1 = 9322 converted to UM/kJ mol−1 = 0.8518 × 9322 + 293.9 = 8234
Comment: see Born–Haber–Fajans cycle, Fig. 3.
(h) Madelung energy, assuming the “condensed ion”72 SnCl62−, EM′/kJ mol−1 = 1613.7 converted to UPOT/kJ mol−1 = 0.963 × 1614 = 1554
Comment: this result may be compared with the value noted in (c) above of 1390 kJ mol−1 (+11%).
Comment: see Born–Haber–Fajans cycle, Fig. 3.
(i) By difference, dissociation energy to independent ions, ΔdissH(SnCl62−,g) = 5199 kJ mol−1
Comment: this is a “new” value, not previously reported.
(j) Lattice energy/kJ mol−1 to form independent gaseous ions 2 × K+ (ΔfH = 2 × 541.0),69 6 × Cl− (ΔfH = 6 × −227.6),69 and Sn4+ (ΔfH = 9320.7)65 = 7501, diff. 10% from (g).
Conclusion
Neither volume-based thermodynamics (VBT) nor the thermodynamic difference rule (TDR), together with their supporting quantities, require a high level of computational expertise nor expensive high-performance computation tools – a spreadsheet will usually suffice – yet the techniques are extremely powerful and accessible to non-experts. Table 2 summarises correlation equations between formula unit volume, Vm, and various thermodynamic properties, together with measures of anticipated errors. These correlation equations provide ready access to otherwise unavailable thermodynamic data, as also rapid checks of published data. The results should always be treated with appropriate caution by checking against known values for related materials.Applications of volume-based thermodynamics, VBT, and the thermodynamic difference rule, TDR
In rough chronological order, we present a selection of applications of VBT and TDR which have enabled input, usually in the form of thermodynamics, to be brought to bear on a range of topical problems, often “state of the art”. These present a diverse range of applications for our techniques. The message for the reader is that:• VBT and TDR can be applied in numerous situations;
• Their application can lead to surprising new results as well as confirmatory ones;
• The basic application is usually very straightforward (Table 6).
| Volume Based Thermodynamics (VBT) or Difference Rule (TDR) specific application | Topic treated | Ref. |
|---|---|---|
| Thermodynamics of new homopolyatomic cation salts of sulfur and selenium. | A study designed to investigate hitherto unknown homopolyatomic cation species of sulfur and selenium (e.g., S82+ and Se82+). The crystalline salt, S8(AsF6)2 and its selenium analogue were predicted, prior to synthesis, to be lattice-stabilised in the solid state relative to the corresponding AsF6− salts of their stoichiometrically possible dissociation. | 73 |
| The fluoride ion affinity of AsF5 and standard enthalpy of formation, ΔfH(AsF6−,g). | Two different values for ΔfH°(AsF6−,g) had been published in the literature at the time of our investigation. The first estimate was made by Bartlett, et al. Jenkins, Krossing, Passmore and co-workers estimated ΔfH(AsF6−,g) using the thermochemical data for the salts [NF4+][BF4−], [NF4+][SbF6−], and [NF4+][AsF6−], obtaining a value which was lower than Bartlett et al.'s value. This lower standard enthalpy of formation implied a lower fluoride ion affinity of AsF5. In order to decide which value (433 or 467 kJ mol−1) is likely to be the more accurate, we modelled the fluoride ion affinity using ab initio methods and concluded a most likely value to be: 430.5 ± 5.5 kJ mol−1. In a further, later, study further FIA values were assigned. | 74–76 |
| Thermodynamics of stabilisation of S2+, Se2+ and Te2+ ions in the solid state. | In a study on the solvated salt S4(AsF6)2·AsF3 we found, using the TDR, that the solvated salt: S4(AsF6)2·AsF3 was more stable than the unsolvated salt, S4(AsF6)2 or more stable than the decomposition products of S4(AsF6)2·AsF3 (which are 2S2AsF6 (c) and AsF3(l)). Such systems could not have been examined thermodynamically in this way other than by using VBT and TDR because of the complexity of the lattices involved. | 77 |
| Study of fluoride ion donor ability. |
Here was studied the ability of fluoride ion donors, C+F−(s), to donate a fluoride ion to an acceptor, A(g). The trend among experimentalists attempting to synthesise increasingly more effective fluoride ion donors:
C+F−(s) + A(g) → C+AF−(g) had been to increase the cation size further and further but this study, guided by VBT, showed that there was very little gained by size increases beyond a critical level. Here VBT played a defining role in that it led to an abortion of certain synthetic work which was taking a particular (unfruitful) avenue of development. |
78 and 79 |
| Application of VBT and TDR to assessment of the relative stabilities of bisulfite (HSO3−) and metabisulfite (S2O52−) salts. |
Although the bisulfites, MHSO3 (M = Li, Na, and K), are widely believed to be stable compounds, they have never been obtained as solids. VBT suggests that the cation volumes, Vm(M+) are insufficiently large to stabilize the HSO3− ion relative to the metabisulfite, S2O52− ion. Crystalline compounds, originally thought to be NaHSO3 and KHSO3, were eventually identified to be metabisulfites, Na2S2O5 and K2S2O5. The fact that RbHSO3 and CsHSO3 can be isolated, whilst attempts to crystallize MHSO3 (M = Li, Na, K) lead to the formation of M2S2O5:
2MHSO3(s) → M2S2O5(s) + H2O(l) has been explained using volume-based thermodynamics, VBT. |
80 |
| Use of VBT to identify thermodynamics of complex reactions and to assist in discerning the probable synthetic route of formation of products. |
This application illustrates the level of sophistication of the thermochemistry that can be dealt with using VBT. Here the synthesis of the salts NO[Al(OR)4], R = C(CF3)2Ph and C(CF3)3 by metathesis reaction of NO[SbF6] and the corresponding Li[Al(OR)4] salts in liquid sulfur dioxide solution were studied and the complete thermodynamics involved in the reaction (in the liquid sulfur dioxide medium):
3NO(g) + NO2(g) + Li[Al(OR)4](s) → NO[Al(OR)4](s) + LiNO3(s) + N2O(g) was analysed using VBT, whereupon it was seen that an unfavourable disproportionation reaction: 2NO2(g) → NO+(g) + NO3−(g) is more than compensated for by the disproportionation enthalpy of the reaction: 3NO(g) → N2O(g) + NO2(g) and the lattice energy of LiNO3(s). Evidence is presented that the reaction proceeds via a complex of Li+ with NO, NO2 (or their dimers) and N2O. |
81 |
| Assessment of the stability of N5+ salts. | The nitrogen-rich energetic salts, N5+N3− and N5+N5− were initially seen as having enormous potential as environmentally clean (friendly) rocket propellants and aircraft fuels offering the possibility of cheap travel. Their potential captured the excitement of the media. However, in a theoretical study, VBT coupled with ab initio calculations for the species N3, N3−, N5+ and N5− showed that neither N5+N3− or N5+N5− could be stabilised thermodynamically and that they would decompose instantaneously into N3 radicals and nitrogen gas. | 82 and 83 |
| VBT and Prussian blue – a contribution to evolving technology. | This study examined the solid-state thermodynamics of the cation exchanges that occur in electrochromic reactions of Prussian Blue. These electrochemically induced changes of valence that result in striking color changes constitute the process of electrochromism, a modern evolving technology in which final “best formulations” are yet being sought. Our study provided an incisive thermodynamic clarification of an ill-understood ion exchange that accompanies the early electrochromic cycles. The results showed by how much the exchange of interstitial Fe3+ ions by alkali metal ions, as exemplified by K+, is thermodynamically favoured. | 84 |
| Use of VBT to investigate the thermodynamics of a new binary fluoro metal dianion [Ti4F19]2− prepared by autoionisation of TiF4 by cation complexation with crown ethers. | This application of VBT shows how the methodology can be applied to investigate new and complex problems in thermodynamics. Following the successful preparation of the new Ti4F192− anion, this application was used to guide synthetic endeavour by studying whether the Ti4F192− anion is more able to form salts with mono or dications. To investigate this we considered two reactions: 2MTi2F9(s) → M2Ti4F18(s) (the target reaction, for which we needed to estimate ΔH ≈ ΔG) and the gas phase dimerisation reaction: 2Ti2F9−(g) → Ti4F182−(g). | 85 |
| Hypothetical compounds – nitryl chlorate and its possible preparation. | Volume-based thermodynamics (VBT) has examined the attempted preparation of the salt, nitryl chlorate: [NO2][ClO3]. Nitrosyl perchlorate, [NO][ClO4], is a known and stable salt which provoked attempts to synthesize the isomeric nitryl chlorate, [NO2][ClO3]. Our isomegethic rule assigns these two materials to have similar lattice potential energies. Silver chlorate, Ag[ClO3], was reacted with nitryl hexafluoroantimonate, [NO2][SbF6] (in nitromethane) at room temperature. Silver hexafluoroantimonate, Ag[SbF6] was identified as one of the reaction products but no [NO2][ClO3] was detected. Nitric acid, HNO3, was found as a side product and it was concluded that this was possibly caused by the presence of traces of water within the nitromethane solvent employed. After three attempts, we failed to prepare the target material, [NO2][ClO3]. However VBT calculations tend to confirm that [NO2][ClO3] is formed but then decomposes in neat Ag[ClO3] and [NO2][SbF6]. | 86 |
| Novel, state-of-the-art, selenium chemistry | This study represents state of the art chemistry and an extremely complex problem. Here 77Se NMR spectroscopy, DFT and MO computations, coupled with VBT and TDR estimations, were utilised to investigate the reversible dissociation of solid Se6I2(AsF6)2·2SO2 in liquid SO2 into solutions containing 1,4-Se6 I22+ in equilibrium with Se42+, Se82+ and Se102+ and seven binary selenium–iodine cations. The study also provided preliminary evidence for the existence and stability of the 1,1,4,4-Se4Br42+ and cyclo-Se7Br+ cations. | 87 |
| Predicted stabilities for noble-gas fluorocation salts using VBT. | In the few situations in noble gas (Ng) chemistry where thermochemical facts are known, VBT can be used to validate and confirm these. This provides further evidence that, in predictive mode, results from VBT can provide a reliable guide to thermodynamic possibilities. The lattice energies, standard enthalpies, and Gibbs energies of formation for salts containing the NgF+, Ng2F3+, XeF3+, XeF5+, Xe2F11+, and XeOF3+ (Ng = Ar, Kr, Xe) cations were estimated using crystallographic and estimated ion volumes. VBT was able, in this way, to provide estimates and predict stabilities – albeit sometimes with quite large uncertainties in the estimated data. While, for example, the stabilities of [XeFn][Sb2F11] (n = 2, 3) and [XeF][AsF6] were confirmed with respect to dissociation to the xenon fluoride and the pnictogen pentafluoride, the stabilities of [XeF3][AsF6] and [XeF3][As2F11] were shown to be marginal under standard conditions. | 88 |
| The thermodynamic hydrate difference rule (HDR) applied to materials at the inorganic–organic interface. | The thermodynamic hydrate difference rule (HDR) is shown here also to apply equally well to formate, carbonate, acetate, glycolate and oxalate salts and their hydrates. | 89 |
| The thermodynamic difference rule and the thermodynamics of hydration (and solvation) of inorganic solids and the existence/absence of certain hydrates. |
The thermodynamics of the formation of solid and liquid inorganic hydrates and ammoniates was examined in this application, suggesting that hydration is always marginally thermodynamically favourable.
More detailed consideration further demonstrated that the mean value of ΔrG per mole of water addition, from anhydrous parent to hydrate within a sequence, increases consistently toward zero, becoming progressively less favorable as the degree of hydration, n, increases, and is also broadly independent of any structural features of the materials. |
90 |
| VBT determination of ionicity or covalency within structures. | The question as to why [P(C6H5)4]+N3− and [As(C6H5)4]+N3− exist as ionic salts whilst [Sb(C6H5)4]+N3− and [Bi(C6H5)4]+N3− are covalent solids was examined. The estimations provided an unexpected answer! | 91 |
| Interpolation of thermodynamic data for sulfur compounds and use of VBT to examine possible synthetic routes and subsequent stability. | Using VBT the values of ΔfG led us to a tentative proposal for the synthesis of Na2SO2. The stability of Na2SO2 however raises doubts and Na2SeO2 emerges as a more attractive target material for synthesis. We predict its synthesis will be easier and that it is stable to disproportionation into Na2Se and Na2SeO4. (Subsequently to the publication of this paper it was preliminarily reported to Vegas verbally that Na2SO2 has indeed been possibly identified in aqueous solution). | 92 |
| Tetraanionic nitrogen-rich tetrazole-based salts | Study of energetics using VBT | 93 |
| (TDAE)(O2SSSSO2)(s) examined using VBT and containing the very first polythionite anion, OSSSSO22−. | Synthesis of (TDAE)(O2SSSSO2). | 94 |
| Examination of VBT in respect of estimation of lattice energies of salts containing the 5,5′-(tetrazole-1N-oxide)2− anion. | Investigation of energetics of defence materials. | 95 |
| Use of TDR to examine thermochemical data for arsenic and phosphorus compounds. | Arsenic oxides/hydrates conform exactly to the TDR whilst analogous phosphorus oxides/hydrates do not. Comments on enthalpies of formation of phosphates. | 96 and 97 |
Acknowledgements
LG and HDBJ thank their respective institutions for providing facilities for the execution of this work. Witali Beichel (Freiburg) is thanked for helpful discussion on ILs. The Curtin University Library is thanked for providing the means by which this article is available in Open Access.References
- Chemical Abstracts Service, CAS Content, http://https://www.cas.org/content/cas-databases, accessed May, 2016.
- L. Glasser, Crystallographic Information Resources, J. Chem. Educ., 2016, 93, 542–549 CrossRef CAS.
- E. I. Izgorodina, Towards large-scale, fully ab initio calculations of ionic liquids, Phys. Chem. Chem. Phys., 2011, 13, 4189–4207 RSC.
- G. W. Castellan, Physical Chemistry, Addison-Wesley, Reading, MA, 2nd edn, 1971 Search PubMed.
- B. Wunderlich, Pure Appl. Chem., 1989, 61, 1347–1351 CrossRef CAS.
- L. Glasser and H. D. B. Jenkins, Ambient Isobaric Heat Capacities, Cp,m, for ionic solids and liquids: an Application of Volume-Based Thermodynamics (VBT), Inorg. Chem., 2011, 50, 8565–8569 CrossRef CAS PubMed.
- M. S. Westwell, M. S. Searle, D. J. Wales and D. H. Williams, J. Am. Chem. Soc., 1995, 117, 5013–5015 CrossRef CAS.
- C. J. E. Kempster and H. Lipson, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3674 CrossRef CAS.
- H. D. B. Jenkins and L. Glasser, Difference rule - A new thermodynamic principle: Prediction of standard thermodynamic data for inorganic solvates, J. Am. Chem. Soc., 2004, 126, 15809–15817 CrossRef CAS PubMed.
- L. Piela, Ideas of quantum chemistry, Elsevier, Amsterdam, 2013 Search PubMed.
- W. Koch and M. C. Holthausen, A chemist's guide to density functional theory, Wiley-VCH, Weinheim, New York, 2001 Search PubMed.
- L. Glasser and H. D. B. Jenkins, Predictive thermodynamics for condensed phases, Chem. Soc. Rev., 2005, 34, 866–874 RSC.
- L. Glasser and H. D. B. Jenkins, Volume-Based Thermodynamics: A Prescription for Its Application and Usage in Approximation and Prediction of Thermodynamic Data, J. Chem. Eng. Data, 2011, 56, 874–880 CrossRef CAS.
- H. D. B. Jenkins and L. Glasser, Thermodynamic Difference Rules: A Prescription for their Application and Usage to Approximate Thermodynamic Data, J. Chem. Eng. Data, 2010, 55, 4231–4238 CrossRef CAS.
- H. D. B. Jenkins, L. Glasser and J. F. Liebman, The Thermodynamic Hydrate Difference Rule (HDR) Applied to Salts of Carbon-Containing Oxyacid Salts and Their Hydrates: Materials at the Inorganic–Organic Interface, J. Chem. Eng. Data, 2010, 55, 4369–4371 CrossRef CAS.
- L. Glasser and H. D. B. Jenkins, The thermodynamic solvate difference rule: Solvation parameters and their use in interpretation of the role of bound solvent in condensed-phase solvates, Inorg. Chem., 2007, 46, 9768–9778 CrossRef CAS PubMed.
- L. Glasser, Thermodynamic estimation: Ionic materials, J. Solid State Chem., 2013, 206, 139–144 CrossRef CAS.
- C. H. Yoder and N. J. Flora, Geochemical applications of the simple salt approximation to the lattice energies of complex materials, Am. Mineral., 2005, 90, 488–496 CrossRef CAS.
- H. D. B. Jenkins, Chemical Thermodynamics – at a glance, Blackwell Publishing, Oxford, 2008 Search PubMed.
- L. Glasser, Correct Use of Helmholtz and Gibbs Function Differences, ΔA and ΔG: The van't Hoff Reaction Box, J. Chem. Educ., 2016, 93, 978–980 CrossRef CAS.
- H. S. Elliott, J. F. Lehmann, H. P. A. Mercier, H. D. B. Jenkins and G. J. Schrobilgen, X-ray Crystal Structures of XeF·MF6 (M = As, Sb, Bi), XeF·M2F11 (M = Sb, Bi) and Estimated Thermochemical Data and Predicted Stabilities for Noble-Gas Fluorocation Salts using Volume-Based Thermodynamics, Inorg. Chem., 2010, 49, 8504–8523 CrossRef CAS PubMed.
- L. V. Gurvich, Reference books and data banks on the thermodynamic properties of individual substances, Pure Appl. Chem., 1989, 61, 1027–1031 CrossRef CAS.
- H. Nyman, T. Talonen, A. Roine, M. Hupa and J. Corander, Statistical Approach to Quality Control of Large Thermodynamic Databases, Metall. Mater. Trans. B, 2012, 43, 1113–1118 CrossRef CAS.
- H. D. B. Jenkins, L. Glasser, T. M. Klapötke, M. J. Crawford, K. K. Bhasin, J. Lee, G. J. Schrobilgen, L. S. Sunderlin and J. F. Liebman, The ionic isomegethic rule and additivity relationships: Estimation of ion volumes. a route to the energetics and entropics of new, traditional, hypothetical, and counterintuitive ionic materials, Inorg. Chem., 2004, 43, 6238–6248 CrossRef CAS PubMed.
- N. Cohen and S. W. Benson, Estimation of heats of formation of organic compounds by additivity methods, Chem. Rev., 1993, 93, 2419–2438 CrossRef CAS.
- P. J. Linstrom and W. G. Mallard, NIST Chemistry WebBook, http://webbook.nist.gov/chemistry/, accessed April, 2016.
- A. F. Kapustinskii, Lattice energy of ionic crystals, Q. Rev., Chem. Soc., 1956, 10, 283–294 RSC.
- T. E. Mallouk, G. L. Rosenthal, R. Muller, R. Brusasco and N. Bartlett, Fluoride ion affinities of germanium tetrafluoride and boron trifluoride from thermodynamic and structural data for (SF3)2GeF6, ClO2GeF5, and ClO2BF4, Inorg. Chem., 1984, 23, 3167–3173 CrossRef CAS.
- T. E. Mallouk, PhD thesis, University of Berkeley, CA, 1983.
- C. Shen, R. Hagiwara, T. E. Mallouk and N. Bartlett, in ACS Symp. Ser. No. 555, ed. J. Thrasher and S. Strauss, ACS, Washington, DC, 1994, pp. 26–39 Search PubMed.
- D. Gibler, PhD thesis, Princeton University, NJ, 1974.
- H. D. B. Jenkins, H. K. Roobottom, J. Passmore and L. Glasser, Relationships among ionic lattice energies, molecular (formula unit) volumes, and thermochemical radii, Inorg. Chem., 1999, 38, 3609–3620 CrossRef CAS PubMed.
- L. Glasser, Lattice Energies of Crystals with Multiple Ions - a Generalised Kapustinskii Equation, Inorg. Chem., 1995, 34, 4935–4936 CrossRef CAS.
- H. D. B. Jenkins and L. Glasser, Volume-based thermodynamics: Estimations for 2
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 salts, Inorg. Chem., 2006, 45, 1754–1756 CrossRef CAS PubMed.
2 salts, Inorg. Chem., 2006, 45, 1754–1756 CrossRef CAS PubMed. - L. Glasser and H. D. B. Jenkins, Lattice energies and unit cell volumes of complex ionic solids, J. Am. Chem. Soc., 2000, 122, 632–638 CrossRef CAS.
- H. D. B. Jenkins, Thermodynamics of the Relationship between Lattice Energy and Lattice Enthalpy, J. Chem. Educ., 2005, 82, 950–952 CrossRef CAS.
- P. Vieillard, Thermodynamics of Hydration in Minerals: How to Predict These Entities, in Thermodynamics – Fundamentals and Its Application in Science, ed. R. Morales-Rodriguez, InTech, 2012 Search PubMed.
- L. Glasser, Lattice and phase transition thermodynamics of ionic liquids, Thermochim. Acta, 2004, 421, 87–93 CrossRef CAS.
- H. D. B. Jenkins, Ionic liquids – an overview, Sci. Prog., 2011, 94, 265–297 CrossRef CAS PubMed.
- H. D. B. Jenkins, Recent initiatives in experimental thermodynamic studies on ionic liquids [IL] – the emergence of a standard thermochemical database for ILs, Sci. Prog., 2011, 94, 184–210 CrossRef CAS PubMed.
- C. Robelin, Models for the thermodynamic properties of molten salt systems: Perspectives for ionic liquids, Fluid Phase Equilib., 2016, 409, 482–494 CrossRef CAS.
- J. P. Hallett and T. Welton, Room-Temperature Ionic Liquids: Solvents for Synthesis and Catalysis. 2, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS PubMed.
- H. Niedermeyer, J. P. Hallett, I. J. Villar-Garcia, P. A. Hunt and T. Welton, Mixtures of ionic liquids, Chem. Soc. Rev., 2012, 41, 7780–7802 RSC.
- S. Keskin, D. Kayrak-Talay, U. Akman and Ö. Hortaçsu, A review of ionic liquids towards supercritical fluid applications, J. Supercrit. Fluids, 2007, 43, 150–180 CrossRef CAS.
- A. R. Katritzky, R. Jain, A. Lomaka, R. Petrukhin, M. Karelson, A. E. Visser and R. D. Rogers, Correlation of the Melting Points of Potential Ionic Liquids (Imidazolium Bromides and Benzimidazolium Bromides) Using the CODESSA Program [J. Chem. Inf. Comput. Sci., 2002, 42, 225–231], J. Chem. Inf. Model., 2005, 45, 533–534 CrossRef CAS.
- A. R. Katritzky, A. Lomaka, R. Petrukhin, R. Jain, M. Karelson, A. E. Visser and R. D. Rogers, QSPR Correlation of the Melting Point for Pyridinium Bromides, Potential Ionic Liquids, J. Chem. Inf. Comput. Sci., 2002, 42, 71–74 CrossRef CAS PubMed.
- M. Deetlefs, K. R. Seddon and M. Shara, Predicting physical properties of ionic liquids, Phys. Chem. Chem. Phys., 2006, 8, 642–649 RSC.
- D. Wileńska, I. Anusiewicz, S. Freza, M. Bobrowski, E. Laux, S. Uhl, H. Keppner and P. Skurski, Predicting the viscosity and electrical conductivity of ionic liquids on the basis of theoretically calculated ionic volumes, Mol. Phys., 2015, 113, 630–639 CrossRef.
- J. M. Slattery, C. Daguenet, P. J. Dyson, T. J. S. Schubert and I. Krossing, How to predict the physical properties of ionic liquids: A volume-based approach, Angew. Chem., Int. Ed., 2007, 46, 5384–5388 CrossRef CAS PubMed.
- K. E. Gutowski, J. D. Holbrey, R. D. Rogers and D. A. Dixon, Prediction of the formation and stabilities of energetic salts and ionic liquids based on ab initio electronic structure calculations, J. Phys. Chem. B, 2005, 109, 23196–23208 CrossRef CAS PubMed.
- K. E. Gutowski, R. D. Rogers and D. A. Dixon, Accurate thermochemical properties for energetic materials applications. I. Heats of formation of nitrogen-containing heterocycles and energetic precursor molecules from electronic structure theory, J. Phys. Chem. A, 2006, 110, 11890–11897 CrossRef CAS PubMed.
- K. E. Gutowski, R. D. Rogers and D. A. Dixon, Accurate thermochemical properties for energetic materials applications. II. Heats of formation of imidazolium-, 1,2,4-triazolium-, and tetrazolium-based energetic salts from isodesmic and lattice energy calculations, J. Phys. Chem. B, 2007, 111, 4788–4800 CrossRef CAS PubMed.
- H. D. B. Jenkins and L. Glasser, Standard absolute entropy,
 , values from volume or density. 1. Inorganic materials, Inorg. Chem., 2003, 42, 8702–8708 CrossRef CAS PubMed.
, values from volume or density. 1. Inorganic materials, Inorg. Chem., 2003, 42, 8702–8708 CrossRef CAS PubMed. - I. Krossing, J. M. Slattery, C. Daguenet, P. J. Dyson, A. Oleinikova and H. Weingartner, Why are ionic liquids liquid? A simple explanation based on lattice and solvation energies, J. Am. Chem. Soc., 2006, 128, 13427–13434 CrossRef CAS PubMed.
- U. Preiss, S. Bulut and I. Krossing, In Silico Prediction of the Melting Points of Ionic Liquids from Thermodynamic Considerations: A Case Study on 67 Salts with a Melting Point Range of 337 °C, J. Phys. Chem. B, 2010, 114, 11133–11140 CrossRef CAS PubMed.
- U. P. Preiss, W. Beichel, A. M. T. Erle, Y. U. Paulechka and I. Krossing, Is Universal, Simple Melting Point Prediction Possible?, ChemPhysChem, 2011, 12, 2959–2972 CrossRef CAS PubMed.
- U. Preiss, J. M. Slattery and I. Krossing, In Silico Prediction of Molecular Volumes, Heat Capacities, and Temperature-Dependent Densities of Ionic Liquids, Ind. Eng. Chem. Res., 2009, 48, 2290–2296 CrossRef CAS.
- U. Preiss, C. Jungnickel, J. Thoming, I. Krossing, J. Luczak, M. Diedenhofen and A. Klamt, Predicting the Critical Micelle Concentrations of Aqueous Solutions of Ionic Liquids and Other Ionic Surfactants, Chem. – Eur. J., 2009, 15, 8880–8885 CrossRef CAS PubMed.
- W. Beichel, U. P. Preiss, S. P. Verevkin, T. Koslowski and I. Krossing, Empirical description and prediction of ionic liquids' properties with augmented volume-based thermodynamics, J. Mol. Liq., 2014, 192, 3–8 CrossRef CAS.
- L. Glasser and H. A. Scheraga, Calculations on Crystal Packing of a Flexible Molecule: Leu-Enkephalin, J. Mol. Biol., 1988, 199, 513–524 CrossRef CAS PubMed.
- J. D. Gale, GULP: A computer program for the symmetry-adapted simulation of solids, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- E. I. Izgorodina, U. L. Bernard, P. M. Dean, J. M. Pringle and D. R. MacFarlane, The Madelung Constant of Organic Salts, Cryst. Growth Des., 2009, 9, 4834–4839 CAS.
- L. Glasser, Solid-State Energetics and Electrostatics: Madelung Constants and Madelung Energies, Inorg. Chem., 2012, 51, 2420–2424 CrossRef CAS PubMed.
- H. D. B. Jenkins and J. F. Liebman, Volumes of solid state ions and their estimation, Inorg. Chem., 2005, 44, 6359–6372 CrossRef CAS PubMed.
- Y. Marcus, Ion Properties, Marcel Dekker, New York, 1997 Search PubMed.
- Y. Marcus, Ions in Solution and their Solvation, Wiley, 2015 Search PubMed.
- W. M. Latimer, Methods of Estimating the Entropies of Solid Compounds, J. Am. Chem. Soc., 1951, 73, 1480–1482 CrossRef CAS.
- P. J. Spencer, Estimation of thermodynamic data for metallurgical applications, Thermochim. Acta, 1998, 314, 1–21 CrossRef CAS.
- Outotec, HSC Chemistry 8, http://www.outotec.com/en/Products--services/HSC-Chemistry/, accessed April, 2016.
- National Institute for Materials Science, AtomWork Inorganic Material Database, http://crystdb.nims.go.jp/index_en.html, accessed June, 2016.
- in CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press, Boca Raton, 2015 Search PubMed.
- L. Glasser, Simple Route to Lattice Energies in the Presence of Complex Ions, Inorg. Chem., 2012, 51, 10306–10310 CrossRef CAS PubMed.
- T. S. Cameron, R. J. Deeth, I. Dionne, H. B. Du, H. D. B. Jenkins, I. Krossing, J. Passmore and H. K. Roobottom, Bonding, structure, and energetics of gaseous E82+ and of solid E8(AsF6)2 (E = S, Se), Inorg. Chem., 2000, 39(25), 5614–5631 CrossRef CAS PubMed.
- S. Brownridge, I. Krossing, J. Passmore, H. D. B. Jenkins and H. K. Roobottom, Recent advances in the understanding of the syntheses, structures, bonding and energetics of the homopolyatomic cations of Groups 16 an 17, Coord. Chem. Rev., 2000, 197, 397–481 CrossRef CAS.
- H. D. B. Jenkins, H. K. Roobottom and J. Passmore, Estimation of enthalpy data for reactions involving gas phase ions utilizing lattice potential energies: Fluoride ion affinities (FIA) and pF(-) values of mSbF5(I) and mSbF5(g) (m = 1, 2, 3), AsF5(g), AsF5·SO2(c). Standard enthalpies of formation: ΔHf°(SbmF5m+1−, g) (m = 1, 2, 3), ΔHf°(AsF6−, g), and ΔHf°(NF4+, g), Inorg. Chem., 2003, 42(9), 2886–2893 CrossRef CAS PubMed.
- H. D. B. Jenkins, I. Krossing, J. Passmore and I. Raabe, A computational study of SbnF5n (n = 1–4) - Implications for the fluoride ion affinity of nSbF5, J. Fluorine Chem., 2004, 125(11), 1585–1592 CrossRef CAS.
- T. S. Cameron, I. Dionne, H. D. B. Jenkins, S. Parsons, J. Passmore and H. K. Roobottom, Preparation, X-ray Crystal Structure Determination, Lattice Potential Energy, and Energetics of Formation of the Salt S4(AsF6)2·AsF3 Containing the Lattice-Stabilized Tetrasulfur [2+] Cation. Implications for the Understanding of the Stability of M42+ and M2+ (M = S, Se, and Te) Crystalline Salts, Inorg. Chem., 2000, 39(10), 2042–2052 CrossRef CAS PubMed.
- K. O. Christe and H. D. B. Jenkins, Quantitative measure for the “nakedness” of fluoride ion sources, J. Am. Chem. Soc., 2003, 125(31), 9457–9461 CrossRef CAS PubMed.
- K. O. Christe and H. D. B. Jenkins, Quantitative measure for the “nakedness” of fluoride ion sources, J. Am. Chem. Soc., 2003, 125, 14210 CrossRef CAS.
- H. D. B. Jenkins and D. Tudela, New methods to estimate lattice energies – Application to the relative stabilities of bisulfite (HSO3−) and metabisulfite (S2O52−) salts, J. Chem. Educ., 2003, 80(12), 1482–1487 CrossRef CAS.
- A. Decken, H. D. B. Jenkins, G. B. Nikiforov and J. Passmore, The reaction of LiAl(OR)4 R = OC(CF3)2Ph, OC(CF3)3 with NO/NO2 giving NO·Al(OR)4, LiNO3 and N2O. The synthesis of NO·Al(OR)4 from LiAl(OR) and NO.SbF6 in sulfur dioxide solution, Dalton Trans., 2004,(16), 2496–2504 RSC.
- D. A. Dixon, D. Feller, K. O. Christe, W. W. Wilson, A. Vij, V. Vij, H. D. B. Jenkins, R. M. Olson and M. S. Gordon, Enthalpies of Formation of Gas-Phase N3, N3−, N5+, and N5− from Ab Initio Molecular Orbital Theory, Stability Predictions for N5+N3− and N5+N5−, and Experimental Evidence for the Instability of N5+N3−, J. Am. Chem. Soc., 2004, 126(3), 834–843 CrossRef CAS PubMed.
- K. O. Christe, A. Vij, W. W. Wilson, V. Vij, D. A. Dixon, D. Feller and H. D. B. Jenkins, N5+N5− allotrope is California dreaming, Chem. Br., 2003, 39(9), 17 Search PubMed.
- D. R. Rosseinsky, L. Glasser and H. D. B. Jenkins, Thermodynamic clarification of the curious ferric/potassium ion exchange accompanying the electrochromic redox reactions of Prussian blue, iron(III) hexacyanoferrate(II), J. Am. Chem. Soc., 2004, 126(33), 10472–10477 CrossRef CAS PubMed.
- A. Decken, H. D. B. Jenkins, C. Knapp, G. B. Nikiforov, J. Passmore and J. M. Rautiainen, The autoionization of [TiF4] by cation complexation with [15]crown-5 to give [TiF2([15]crown-5)][Ti4F18] containing the tetrahedral [Ti4F18]2− ion, Angew. Chem., Int. Ed., 2005, 44, 7958–7961 CrossRef CAS PubMed.
- K. K. Bhasin, M. J. Crawford, H. D. B. Jenkins and T. M. Klapötke, The volume-based thermodynamics (VBT) and attempted preparation of an isomeric salt, nitryl chlorate: NO2·ClO3, Z. Anorg. Allg. Chem., 2006, 632(5), 897–900 CrossRef CAS.
- S. Brownridge, L. Calhoun, H. D. B. Jenkins, R. S. Laitinen, M. P. Murchie, J. Passmore, J. Pietikainen, J. M. Rautiainen, J. C. P. Sanders, G. J. Schrobilgen, R. J. Suontamo, H. M. Tuononen, J. U. Valkonen and C. M. Wong, 77Se NMR Spectroscopic, DFT MO, and VBT Investigations of the Reversible Dissociation of Solid (Se6I2)[AsF6]2·2SO2 in Liquid SO2 to Solutions Containing 1,4-Se6I22+ in Equilibrium with Sen2+ (n = 4, 8, 10) and Seven Binary Selenium Iodine Cations: Preliminary Evidence for 1,1,4,4-Se4Br42+ and cyclo-Se7Br+, Inorg. Chem., 2009, 48(5), 1938–1959 CrossRef CAS PubMed.
- H. S. Elliott, J. F. Lehmann, H. P. A. Mercier, H. D. B. Jenkins and G. J. Schrobilgen, X-ray Crystal Structures of XeF.MF6 (M = As, Sb, Bi), XeF·M2F11 (M = Sb, Bi) and Estimated Thermochemical Data and Predicted Stabilities for Noble-Gas Fluorocation Salts using Volume-Based Thermodynamics, Inorg. Chem., 2010, 49(18), 8504–8523 CrossRef CAS PubMed.
- H. D. B. Jenkins, L. Glasser and J. F. Liebman, The Thermodynamic Hydrate Difference Rule (HDR) Applied to Salts of Carbon-Containing Oxyacid Salts and Their Hydrates: Materials at the Inorganic–Organic Interface, J. Chem. Eng. Data, 2010, 55(10), 4369–4371 CrossRef CAS.
- L. Glasser and F. Jones, Systematic Thermodynamics of Hydration (and of Solvation) of Inorganic Solids, Inorg. Chem., 2009, 48(4), 1661–1665 CrossRef CAS PubMed.
- K. O. Christe, R. Haiges, J. A. Boatz, H. D. B. Jenkins, E. B. Garner and D. A. Dixon, Why Are [P(C6H5)4]+N3− and [As(C6H5)4]+N3− Ionic Salts and Sb(C6H5)4N3 and Bi(C6H5)4N3 Covalent Solids? A Theoretical Study Provides an Unexpected Answer, Inorg. Chem., 2011, 50, 3752–3756 CrossRef CAS PubMed.
- A. Vegas, J. F. Liebman and H. D. B. Jenkins, Unique thermodynamic relationships for ΔfH° and ΔfG° for crystalline inorganic salts. I. Predicting the possible existence and synthesis of Na2SO2 and Na2SeO2, Acta Crystallogr., Sect. B: Struct. Sci., 2012, 68, 511–527 CrossRef CAS PubMed.
- D. Srinivas, V. Ghule, K. Muralidharan and H. D. B. Jenkins, Tetraanionic Nitrogen-Rich Tetrazole-Based salts, Chem. – Asian J., 2013, 8, 1023–1028 CrossRef CAS PubMed.
- P. Bruna, A. Decken, S. Greer, F. Grein, H. D. B. Jenkins, B. Mueller, J. Passmore, T. A. P. Paulose, J. M. Rautiainen and S. Richardson, Synthesis of (TDAE)(O2SSSSO2) and Discovery of (TDAE)(O2SSSSO2)(s) containing the first polythionite anion, Inorg. Chem., 2013, 52, 13651–13662 CrossRef CAS PubMed.
- L. Glasser, H. D. B. Jenkins and T. M. Klapötke, Is the VBT Approach valid for estimation of the lattice enthalpy of salts containing the 5,5′-(Tetrazole-1N-oxide)2−?, Z. Anorg. Allg. Chem., 2014, 640, 1297–1299 CrossRef CAS.
- H. D. B. Jenkins, D. Holland and A. Vegas, Thermodynamic data for crystalline arsenic and phosphorus compounds, M2O5·nH2O reexamined using the Thermodynamic Difference Rules, Thermochim. Acta, 2016, 633, 24–30 CrossRef CAS.
- H. D. B. Jenkins, D. Holland and A. Vegas, An assessment of the TDR for mixed inorganic oxides and comments on the enthalpies of formation of phosphates, Thermochim. Acta, 2015, 601, 63–67 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Lists of predictive thermodynamic group estimation methods, and of thermodynamic databases. See DOI: 10.1039/c6cp00235h |
| This journal is © the Owner Societies 2016 |