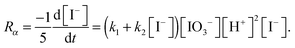How imperfect mixing and differential diffusion accelerate the rate of nonlinear reactions in microfluidic channels

Abstract

In this paper, we show experimentally that inside a microfluidic device, where the reactants are segregated, the reaction rate of an autocatalytic clock reaction is accelerated in comparison to the case where all the reactants are well mixed. We also find that, when mixing is enhanced inside the microfluidic device by introducing obstacles into the flow, the clock reaction becomes slower in comparison to the device where mixing is less efficient. Based on numerical simulations, we show that this effect can be explained by the interplay of nonlinear reaction kinetics (cubic autocatalysis) and differential diffusion, where the autocatalytic species diffuses slower than the substrate.

---

I. Introduction

Over the past decade, microfluidics has evolved into a rapidly growing, innovative field of research, with immense impact in many areas of technology and daily application.¹ This includes not only the miniaturization of conventional chemical processing but also numerous applications in biology and medicine.² The invention of PDMS-based soft lithography has greatly accelerated this development of microfluidic applications,³ which often include combinations with electrical and mechanical devices as well as variants of different polymer materials and porous substrates.^4–7

The use of microfluidic devices typically implies that the Reynolds number will be small, i.e., fluid flows will be laminar, due to the small dimensions of the channels. In this case, no turbulent mixing will occur, so that mixing inside the microchannels will exclusively rely on diffusion, an inherently slow process.⁸ This has stimulated ongoing research efforts to enhance mixing in microfluidic devices based on a wide spectrum of different approaches.^9,10 These include variations in the channel geometry and surface compositions as well as ultrasonic, electric, magnetic, and thermal effects see Lee et al.¹¹ and references therein.

For linear reactions, insufficient mixing may limit the reaction speed. If the reactants are segregated in different regions of the fluid, the reaction will be limited to the interface of the non-mixed regions, where all reactants are present. However, in these regions, the reactants will be eventually depleted as a consequence of the reaction. New material has to be transported to the interface by diffusion, which will slow down the overall progress of the reaction.¹² For turbulent flows a large body of work has been devoted to study these problems, in particular, with the help of numerical simulations.^13–15 In the case of nonlinear autocatalytic reactions, the relation between mixing and reaction rate is more difficult to predict. For example the rate of mixing can change the occurrence of a bifurcation, resulting in abrupt qualitative changes of the dynamics.^16,17

In this article, we will systematically study how the progress of a nonlinear reaction depends on the mixing conditions. We will focus on clock reactions, which can be seen as the most basic class of nonlinear chemical reactions. Clock reactions are reactions in which the concentrations of reaction products remain low over a longer period of time that is known as the induction period. After the induction period, a sudden rapid change in the concentrations occurs. A combination of two mechanisms, inhibition and autocatalysis, leads to this type of behavior.¹⁸ In more complex reaction networks with additional kinetic features, clock reactions also form the basis of oscillatory kinetics.¹⁹ Here, we use the prototypical example of an autocatalytic clock reaction, the iodate–arsenous acid reaction. This reaction is the sum of two well-known reactions, the Dushman reaction,²⁰

IO₃⁻ + 5I⁻ + 6H⁺ → 3I₂ + 3H₂O,

and the Roebuck reaction,²¹

H₃AsO₃ + I₂ + H₂O → 2I⁻ + H₃AsO₄ + 2H⁺.

The rate-limiting step is the Dushman reaction, for which the rate is given by

A detailed account of the chemistry behind this clock reaction can be found in Hanna et al.²² The rate constants are such that the quadratic autocatalysis dominates only if the concentration of I⁻ is less than about 10⁻⁶ M. This clock reaction is known to produce traveling waves,²² and these waves have been used to study the effect of reaction-diffusion on convection.²³

In this paper, we study the effect of different mixing conditions on the iodate–arsenous acid clock reaction. In particular, we compare mixing experiments under batch conditions with results from experiments in microfluidic devices, where the reaction is operated under flow conditions. The paper is organized as follows. Section II is devoted to materials and methods. In Section III, we show the experimental results, where we first concentrate on experiments in microtiter plates and then move to results from microfluidic systems. A discussion of the results is provided in Section IV, where we present numerical simulations of a generic reaction scheme with cubic autocatalysis and differential diffusion.

II. Experimental

Reagents

Potassium iodide and potassium iodate in ACS grade were purchased from Carl-Roth GmbH, Karlsruhe, Germany. Disodium phosphate, sulfuric acid and arsenic trioxide in ACS grade were purchased from Sigma Aldrich, Darmstadt, Germany. Starch in pure grade and citric acid monohydrate (98%) was purchased from neolab, Heidelberg, Germany. Potassiumdihydrogenphosphate and fluoresceinisothiocyanate in ACS grade were purchased from Merck, Darmstadt, Germany. Sodium hydroxide in ACS grade was purchased from AppliChem GmbH, Darmstadt, Germany.

The used arsenous acid was prepared as follows. 0.98 g As₂O₃ were dissolved in 35 ml bidistilled water adjusted to pH 12.7 with NaOH. After complete dissolution, the solution was adjusted to pH 2.0 with sulfuric acid to obtain a 0.2 mol l⁻¹ stock solution of arsenous acid. All experiments were done with a clock solution prepared from equal amounts of 0.046 mol l⁻¹ arsenous acid and 0.15 mol l⁻¹ aqueous potassium iodate solution. The pH of the reaction was adjusted with 0.1 mol l⁻¹ NaOH solution and stabilized between 2.6 and 6.8 with McIllvane citrate buffer solution.²⁴ To each reaction solution, 0.1% of soluble starch indicator was added to visualize the triiodide as a dark blue color. The ratio of concentrations of arsenous acid to iodate were chosen to R = 0.3, so that iodate was in excess and the reaction ends in a state of completely dark color.²⁵

Determination of induction period in a microtiter plate

To obtain statistically reliable results for the induction period of the autocatalytic iodate–arsenous acid clock reaction, we performed multiple parallel experiments using 96 well microtiter plates (Brand GmbH & Co. KG, Wertheim, Germany). In each case, equal amounts (80 μl) of arsenic acid and iodate solution were placed in columns of 8 wells. In each column of 8 wells, the autocatalytic reaction was then started simultaneously by adding 80 μl of KI inducer solution with a 8-tip Eppendorf-pipette. The same protocol was chosen for different inducer concentrations. The induction period was manually measured with a stop watch (neolab, Heidelberg, Germany).

Microfluidics

The microfluidic channel was manufactured from polydimethylsiloxane (PDMS) by soft lithography as introduced by Duffy et al.²⁶ Briefly, a silicium wafer was coated with photoresist (SU-8 2050, microresist, Germany) in a vacuum spin coater (WS-400BX-6NPP/Lite, Laurell, North Wales, USA) to predefined height. After prebaking, the coated wafer was illuminated with a UV lamp (Tamarack PRX 500, San Francisco, USA) through a photomask (JD-Phototools, Hitchin, United Kingdom) with the channel layout as shown in Fig. S3A (ESI†). After postbaking, the structure was developed in dev-600mr developer (microresist, Berlin, Germany) until all non-illuminated photoresist was removed. After cleaning with 2-propanol and drying at room temperature, the wafer was ready to use for the microchannel manufacturing process. The dimensions of the microstructure used in our experiments are given in the Fig. S5 (ESI†).

For microfluidic chip fabrication, PDMS elastomer (Sylgard 184-Kit, Dow Corning, Wiesbaden, Germany) was mixed with curing agent in a 1 : 10 ratio. The elastomer/curer mixture was poured onto the structured silicon wafer and the PDMS was polymerized at 95 °C in a laboratory oven (Thermofischer, Germany). After cooling to room temperature over night, the chip was cut with a scalpel out of the PDMS block on top of the wafer, inlet and outlet holes were punched into the PDMS with a syringe needle, and the PDMS block with the channel structure was plasma bonded to a glass cover slip in a vacuum plasma oven (Harrick, Ithaca, USA). The completely assembled chip can be seen in Fig. S3B (ESI†). The microchannel was filled with pure water and stored at room temperature until use. The required solutions of the clock reaction were stored separately in Hamilton 250 μl microsyringes (Harvard Apparatus, Holliston, USA) to avoid an uncontrolled initiation of the autocatalytic reaction and connected to the inlet structures in the PDMS microfluidic chip via PTFE tubings. During experiments, the solutions were pumped simultaneously through the microchannels with a PHD Ultra micropump (Harvard Apparatus, Holliston, USA).

Image acquisition and processing

We observed the autocatalytic iodate–arsenous acid clock reaction in the microfluidic channel under an inverse IX71 microscope (Olympus, Hamburg, Germany). An Edmund DIN4 objective (magnification 0.1, Edmund Optics GmbH, Karlsruhe, Germany) was used. Image acquisition was done with an ORCA-ER camera (C4742-80, Hamamatsu, Herrsching, Germany) mounted to the microscope. Data was stored as picture stacks in *.avi formate using the Xcellence-Pro-Software (Olympus, Hamburg, Germany). For the fluorescence measurements a fluorescence filter (FITC-Filter, Olympus, Hamburg, Germany) was placed in the optical pathway. For further analysis, the image stacks were imported to the image processing program ImageJ (Java opensource, http://imagej.nih.gov/ij/).

Determination of induction period in the microchannel

The induction period of the iodate–arsenous acid clock reaction in the microchannel was determined from the flow speed and the downstream position of the black triiodide–starch band as shown in Fig. 2B. The flow speed was calculated from the channel dimensions and the pumping rate of the PHD ultra micropump (Harvard Apparatus). The downstream position of the iodine–starch band was measured with ImageJ. A baseline was defined directly behind the inlet region of the channel as shown in Fig. 2A and the distance to the color band was measured in micrometers along the centerline. The induction period in the microchannel was then calculated by dividing the downstream distance of the triiodide–starch band by the flow speed and compared to the induction periods measured in the microtiter plate experiments.

Mathematical modeling

Numerical simulations of the cubic autocatalytic reaction A + 2B → 3B with a rate k₁ were run in 1-dimensional domains of length L = 50 space units. We used an explicit Euler scheme for temporal integration with a time step of 0.01 time units. A three-point approximation was used for the Laplacian term with equidistant grid points at a distance of 0.1 space units.

III. Results

The iodate–arsenous acid clock reaction

Here, we used the iodate–arsenous acid clock reaction as a prototypical nonlinear chemical system to explore the interplay of nonlinear kinetics and mixing under different conditions. Before systematically exploring the influence of mixing on the reaction rate, we characterized its dependence on the pH value and the arsenous acid concentration. To obtain statistically reliable results, we performed multiple parallel experiments using 96 well microtiter plates, see Materials and methods. In Fig. S1 (ESI†), the induction period is shown as a function of the inducer concentration (KI) for different pH values (A) and different concentrations of arsenous acid (B). In all cases, the induction time is decreased for increasing KI concentration as expected. For a given KI concentration, an increase in the proton concentration speeds up the reaction. Similarly, an increase in the arsenous acid concentration also speeds up the reaction but is limited to a maximum speed set by the Dushman reaction.

Efficient mixing prolongs the induction time of the clock reaction in a batch reactor

We now turn to the influence of mixing on the induction period. First, we systematically changed the mixing conditions under batch conditions. Again, we used 96 well plates to perform large numbers of parallel experiments with the iodate–arsenous acid clock reaction under batch conditions. The 96 well plates were now placed on a shaker to enhance mixing of the educts after addition of the inducer (KI). Different mixing conditions were created by running the shaker for different periods of time after addition of the inducer. In Fig. 1A, the dependence of the induction period on the shaking time is shown. We observed that longer shaking time, i.e., an increased degree of mixing, resulted in prolonged induction periods. Thus more efficient mixing slowed down the clock reaction.

Fig. 1 Induction period of the clock reaction under batch conditions, measured in a 96 well microtiterplate. (A) Different mixing conditions were established in a 240 μl volume by changing the shaking time on a microtiterplate shaker. The induction period is clearly increased for longer shaking times. (B, left) The viscosity of the 10 mM KI inducer solution was changed by adding 2 mg ml⁻¹ agarose. (B, middle) The viscosity of all solutions was changed by adding 2.5 mg ml⁻¹ agarose. (B, right) Control experiment in aqueous solution without agarose.

A similar result was obtained when changing the rotational speed of the shaker while keeping the shaking time constant. For an increased rotational speed of the shaker, a higher degree of mixing is reached during a given time. Consequently, the induction period of the clock reaction was increased for increasing stirring speeds as can be seen in Fig. S2 in the ESI.† At 500 rpm, the maximal induction period was reached. Further increasing the rotational speed of the shaker did not increase the induction period beyond this saturation value.

As an additional control, we changed the viscosity of the reaction medium to confirm that less efficient mixing indeed results in a speed-up of the reaction. We compared the induction period of the iodate–arsenous acid clock reaction in aqueous solution with the induction period in experiments, where (i) the viscosity of the KI inducer solution was changed by addition of agarose, and (ii) the viscosity of all solutions was changed equally by addition of agarose. The results are displayed in Fig. 1B, showing that only in the case of a more viscous KI inducer solution, the induction period of the clock reaction is considerably reduced.

Laminar flow conditions in a microfluidic channel may accelerate the induction time of the clock reaction

Under batch conditions, the inducer solution is added with a micropipette to the well containing the iodate–arsenous acid mixture. Drops of inducer solution fall into the well and mix with the clock solution as a consequence of convection and diffusion. Longer shaking periods or increased rotational speed of the shaker will enhance fluid convection within the well and thus promote the mixing process. On average, this results in a prolonged induction period of the clock reaction. However, the fluid dynamical details of the mixing process in each well are different and not well controlled. In order to mix the inducer with the clock solution in a well-controlled and reproducible manner, we performed experiments in a microfluidic chip, where flow conditions are strictly laminar (low Reynolds number regime) and mixing takes place by diffusion between adjacent fluid layers in the laminar flow. In particular, microfluidics allows us to change the mixing time in a well-controlled fashion by systematically modifying the geometry of the microfluidic channel.

Layout and operation of the microfluidic chip are explained in Fig. 2 and Fig. S3 (ESI†). The two components of the clock solution and the inducer solution are introduced into the chip via separate tubings (inlets A–C in Fig. 2A). At a rectangular junction, the three components are merged and flow together down the main channel of the chip. Due to the laminar flow conditions, the three liquids will not mix but remain in separate layers as they flow along the main channel. Only gradually, the three components will mix by lateral diffusion between the adjacent layers, as the fluid moves downstream. As the chip is operated under continuous flow conditions, different locations downstream the main channel correspond to different points in time along the reaction coordinate.

Fig. 2 Clock reaction in a microfluidic environment. (A) Layout of the channel junction in the upstream part of the chip. Iodate (inlet A), arsenous acid (inlet B), and iodide (inlet C) were pumped via separate inlets into the chip and merged inside the main channel. (B) The induction time of the clock inside the microchannel was determined by measuring the distance of the dark iodine band to the baseline along the center line, see also (A). (C) Induction period of the clock reaction for different flow speeds compared to induction period under batch conditions in a microtiter plate. Concentration of the inducer KI is 50 mM and the pH value is 5.2 in all cases. Under flow conditions, the induction period is clearly shortened. (D) With increasing inducer concentration, the difference in the induction period between flow and batch conditions is reduced until, for inducer concentrations above 40 mM, the reaction proceeds faster in the 96 well plate as compared to the microchannel. Here, the pH value is 3.8.

When introducing the iodate–arsenous acid clock reaction into the chip, a stationary color band will emerge some distance downstream of the channel junction, where the clock solutions are merged with the inducer solution, see Fig. 2B. For a constant flow speed in the channel, the induction period of the clock reaction can be directly calculated from the downstream distance between the junction and the color band. In Fig. 2C, the induction period is shown for different flow speeds in comparison to the induction period under batch conditions. Here, an inducer concentration of 50 mM was used. Under laminar flow conditions, the induction period grows when increasing the flow speed from 0.18 μl min⁻¹ to 0.24 μl min⁻¹. However, in all cases considered here, it was clearly accelerated compared to the batch conditions in the microtiter plate. For increased inducer concentration, the difference in the induction periods under batch and flow conditions becomes less pronounced until, for inducer concentrations above 40 mM, the situation reverses and the induction period under batch conditions is shorter compared to the microflow, see Fig. 2D.

In the microfluidic channel, mixing will proceed much slower than in the well plate, due to the strictly laminar flow conditions. The shorter induction periods that we observe in the microchannel for inducer concentrations below 40 mM are thus in line with our findings reported in the previous section, where increased mixing was found to prolong the induction period. Also, with increased flow speed, we expect that mixing occurs faster due to Taylor dispersion. The increase in induction period with increasing flow speed thus fits into the same picture.

Enhanced diffusive mixing in a microfluidic channel prolongs the induction time of the clock reaction

To confirm that more efficient mixing indeed slows down the reaction, we changed the geometry of the microfluidic channel so that diffusive mixing is enhanced. In Fig. 3A and B, both channel geometries are shown. On the left hand side (A), the channel design that was used in the previous section is displayed. On the right hand side (B), the modified design can be seen, where obstacles have been introduced in the upper part of the channel to enhance diffusive mixing between adjacent layers in the laminar flow. To visualize the mixing process, a fluorescein solution was introduced into the middle inlet. It can be clearly seen that in the presence of the obstacles, mixing is strongly enhanced, resulting in an almost uniform fluorescein distribution downstream of the obstacles. For comparison, the fluorescence profiles perpendicular to the flow direction are displayed in Fig. 3C for both channels downstream of the channel junction. They confirm that mixing progresses much faster in the channel with obstacles (red line) as compared to the channel geometry without obstacles in the inlet region (blue line).

Fig. 3 Mixing efficiency in a microchannel without (A) and with obstacles (B) in the inlet region. A fluorescein solution was introduced through the central inlet on the left, water was pumped into the side inlets (top and bottom). In both cases, a flow speed of 0.1 μl min⁻¹ was used in the main channel (0.033 μl min⁻¹ through each inlet). An overlay of brightfield and fluorescence images is shown. (C) Fluorescence intensity profiles in the microchannel without (blue line, see also A) and with obstacles (red line, see also B). Intensity profiles were taken perpendicular to the flow direction, 600 μm downstream of the last obstacle in (B), and at the same downstream location in (A). (D) Induction time in the microchannel without (red dashed line) and with obstacles (black solid line) in the inlet region. For comparison also the induction period in the microtiter plate is shown (dashed blue line).

After characterizing the mixing conditions, we ran the clock reaction under flow conditions in both channel geometries to compare the induction periods. The components of the clock reaction and the inducer solution were introduced through separate inlets as described in the previous section. In Fig. 3D, the induction periods in the channel without and with obstacles in the inlet region are shown for different concentrations of the inducer KI. At inducer concentrations below 50 mM, the induction period is prolonged in the channel with obstacles, i.e., under conditions of enhanced mixing. For comparison also the induction periods under batch conditions in the 96 well plate are displayed. Here, the induction period is even longer than in the channel with obstacles. By comparing the induction periods in microchannels with different mixing conditions we confirmed that for low inducer concentrations, enhanced mixing prolongs the induction period, i.e., slows down the progress of this nonlinear chemical reaction.

IV. Discussion

Intuitively, we expect that proper mixing promotes the progress of a chemical reaction, whereas imperfect mixing may potentially result in a slow-down. Here, we have observed the opposite behavior. The induction period of the nonlinear iodate–arsenous acid clock reaction is shortened under conditions of imperfect mixing, while enhanced mixing leads to a slower reaction progress. How can we explain these findings?

The iodate–arsenous acid reaction can be described by two reactions, namely the Dushman reaction and the Roebuck reaction.²² The rate of the Dushman reaction, which is the slowest of these processes (rate limiting reaction), is given by the sum of a simple autocatalytic process and a cubic autocatalytic process in iodide (I⁻). The simple autocatalytic process, however, is only dominant at very low concentrations of I⁻ (about 10⁻⁶ M).²² Some of the intermediates of the reaction are I₂ and I⁻. In addition, starch is present in the reaction mixture, so that the complex S–I₃⁻ is formed, visible as a strong blue color. Complex formation will slow down the effective diffusion of the activator iodide.²² We therefore decided to study the effect of changes in the activator diffusivity in a generic nonlinear reaction with cubic autocatalysis,

To mimic our experiments, where progress of the iodate–arsenous acid clock reaction was studied under different mixing conditions, we performed numerical simulations based on the following reaction-diffusion system,

and compared the results for homogeneous (well-mixed) initial conditions with a situation where the two components were initially separated. In the latter case, we systematically changed the diffusion coefficient of the activator. The results are shown in Fig. 4. Both the concentrations of the autocatalytic specie B (red) and of the substrate A (blue) are displayed (see Fig. S4 in the ESI† for an explanation of how Fig. 4 was constructed). The data shown in Fig. 4 clearly demonstrate how a combination of cubic autocatalysis with slow diffusion of the autocatalytic specie can explain an accelerated reaction in the case of imperfect mixing, i.e. for initially separated reactants as in the microfluidic device. In the case of the microchannel experiment, slow diffusion of the autocatalytic species results in a diffusive mixing zone close to the interface of the initially segregated reactants, where the components of the clock encounter an inducer concentration close to the value of the non-mixed inducer solution. In contrast, in the microtiter plate turbulent mixing will rapidly disperse the inducer, so that, for low and moderate concentrations of the inducer solution, the clock reaction is triggered more rapidly in the microchannel. Only with increasing concentration of the inducer solution, turbulent mixing will take longer to disperse the more concentrated drop of inducer solution, so that beyond a critical concentration (40 mM in the example shown in Fig. 2D), the clock reaction is triggered faster in the microtiter plate than in the microfluidic channel.

Fig. 4 Mixing and diffusion influence the induction period of a generic reaction with cubic autocatalysis. (a) Well-mixed initial conditions, (b–d) initially separated reactants with diffusion coefficients of the autocatalytic specie of (b) D_b = D_a, (c) D_b = (1/10)D_a, and (d) D_b = (1/100)D_a. Red represents high concentrations of the autocatalyst B, while blue represents high concentration of the substrate A. The size of the space-time plots is 50 space units (horizontal) × 200 time units (downwards). The initial concentrations of A and B are [A] = 1 and [B] = 0.01 throughout the system in (a), while they are [A] = 0 and [B] = 0.02 in the left half and [A] = 2 and [B] = 0 in the right half of the system for (b–d). The rate of the reaction is k₁ = 10, the diffusion coefficient of A is set to D_a = 1.

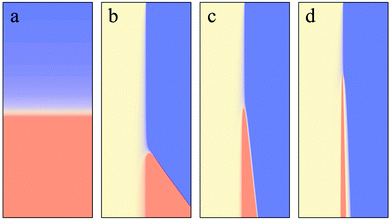
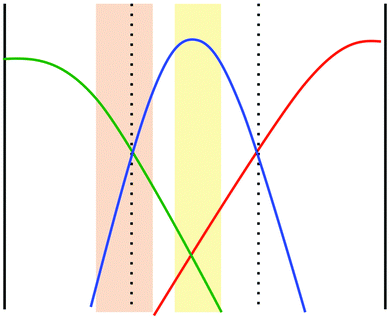
To what extent does the scenario of a reduced diffusivity of the autocatalytic species apply to the specific situation in our experiments described above? It is known that the product of the iodate–arsenous acid reaction depends on the ratio of concentrations of the reactants. For [As(III)]₀ > 3[IO₃⁻]₀ the product will be I⁻ aside from H₃AsO₄, whereas for [As(III)]₀ < 5/2[IO₃⁻]₀ the product will be I₂ again together with H₃AsO₄.²² In the microchannel experiments, iodate and iodide are introduced via the side inlets, whereas arsenous acid is pumped into the middle inlet. Due to lateral diffusion, the distribution of reactants inside the microchannel will form two regions, one where the main product is I⁻ and another in which I₂ is the main product. This is schematically shown in Fig. 5. The orange-shaded region corresponds to the region where [As(III)]₀ < 5/2[IO₃⁻]₀, i.e., where a high concentration of I₂ will emerge as the final product. In the yellow region, we have [As(III)]₀ > 3[IO₃⁻]₀, i.e., here the main product will be I⁻. Between these two regions a mixture of I₂ and I⁻ will be present and form a complex with starch, so that the diffusion of the autocatalytic species in this region will be diminished. In this way, we can indeed explain the accelerated induction periods that we observed in our microfluidic experiments based on an interplay of nonlinear kinetics and differences in diffusion coefficients, as demonstrated for a generic autocatalytic system in Fig. 4. Note that following this explanation, we expect a dependence of the induction period on the channel width. In particular, we expect that an enlarged channel will result in a prolonged induction period because iodate (inlet A) and iodide (inlet C) need to diffuse over a longer distance perpendicular to the flow in order to initiate the reaction.

Fig. 5 Schematic of the concentration profiles of iodate (green), arsenous acid (blue) and iodide (red). The region shaded in yellow corresponds to a region where the product is iodide (I⁻), while in the region shaded in orange the main product is iodine (I₂).

Acknowledgements

RN and CB thank the Bundesministerium für Bildung und Forschung (BMBF) for funding in the framework of the Impulszentrum für integrierte Bioanalyse (Taschentuchlabor). IB acknowledges financial support by the Alexander von Humboldt-Foundation.

References

1. P. Tabeling, Introduction to Microfluidics, Oxford University Press, USA, 2010.
2. K. Ohno, K. Tachikawa and A. Manz, Microfluidics: Applications for analytical purposes in chemistry and biochemistry, Electrophoresis, 2008, 29, 4443–4453.
3. J. C. McDonald, et al., Fabrication of microfluidic systems in poly(dimethylsiloxane), Electrophoresis, 2000, 21, 27–40.
4. E. Verpoorte and N. F. de Rooij, Microfluidics meets MEMS, Proc. IEEE, 2003, 91, 930–953.
5. T. Thorsen, S. J. Maerkl and S. R. Quake, Microfluidic Large-Scale Integration, Science, 2002, 298, 580–584.
6. A. W. Martinez, S. T. Phillips and G. M. Whitesides, Three-dimensional microfluidic devices fabricated in layered paper and tape, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 19606–19611.
7. R. R. Niedl and C. Beta, Hydrogel-driven paper-based microfluidics, Lab Chip, 2015, 15, 2452–2459.
8. T. M. Squires and S. R. Quake, Microfluidics: Fluid physics at the nanoliter scale, Rev. Mod. Phys., 2005, 77, 977–1026.
9. J. D. Tice, H. Song, A. D. Lyon and R. F. Ismagilov, Formation of Droplets and Mixing in Multiphase Microfluidics at Low Values of the Reynolds and the Capillary Numbers, Langmuir, 2003, 19, 9127–9133.
10. A. J. Bae, C. Beta and E. Bodenschatz, Rapid switching of chemical signals in microfluidic devices, Lab Chip, 2009, 9, 3059–3065.
11. C.-Y. Lee, C.-L. Chang, Y.-N. Wang and L.-M. Fu, Microfluidic Mixing: A Review, Int. J. Mol. Sci., 2011, 12, 3263–3287.
12. J. M. Ottino, The Kinematics of Mixing: Stretching, Chaos, and Transport, Cambridge University Press, 1989.
13. P. E. Dimotakis, Turbulent Mixing, Annu. Rev. Fluid Mech., 2005, 37, 329–356.
14. H. Pitsch, Large-Eddy Simulation of Turbulent Combustion, Annu. Rev. Fluid Mech., 2006, 38, 453–482.
15. C. Beta, K. Schneider, M. Farge and H. Bockhorn, Numerical study of mixing of passive and reactive scalars in two-dimensional turbulent flows using orthogonal wavelet filtering, Chem. Eng. Sci., 2003, 58, 1463–1477.
16. I. R. Epstein, The consequences of imperfect mixing in autocatalytic chemical and biological systems, Nature, 1995, 374, 321–327.
17. J. C. Roux, P. De Kepper and J. Boissonade, Experimental evidence of nucleation induced transition in a bistable chemical system, Phys. Lett. A, 1983, 97, 168–170.
18. J. Billingham and D. J. Needham, Mathematical modelling of chemical clock reactions, J. Eng. Math., 1993, 27, 113–145.
19. S. K. Scott, Oscillations, Waves, and Chaos in Chemical Kinetics, Oxford University Press, 1994.
20. S. Dushman, The Rate of the Reaction between Iodic and Hydriodic Acids, J. Phys. Chem., 1903, 8, 453–482.
21. J. R. Roebuck, The Rate of the Reaction between Arsenious Acid and Iodine in Acid Solutions; the Rate of the Reverse Reaction; and the Equilibrium between Them, J. Phys. Chem., 1901, 6, 365–398.
22. A. Hanna, A. Saul and K. Showalter, Detailed studies of propagating fronts in the iodate oxidation of arsenous acid, J. Am. Chem. Soc., 1982, 104, 3838–3844.
23. J. A. Pojman, I. R. Epstein, T. J. McManus and K. Showalter, Convective effects on chemical waves. 2. Simple convection in the iodate–arsenous acid system, J. Phys. Chem., 1991, 95, 1299–1306.
24. T. C. McIlvaine, A Buffer Solution for Colorimetric Comparison, J. Biol. Chem., 1921, 49, 183–186.
25. L. Forštová, H. Ševčíková, M. Marek and J. H. Merkin, Electric field effects on selectivity of reactions within propagating reaction fronts, Chem. Eng. Sci., 2000, 55, 233–243.
26. D. C. Duffy, J. C. McDonald, O. J. A. Schueller and G. M. Whitesides, Rapid Prototyping of Microfluidic Systems in Poly(dimethylsiloxane), Anal. Chem., 1998, 70, 4974–4984.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp00224b

---