Dielectric relaxation behavior in antiferroelectric metal organic framework [(CH₃)₂NH₂][Fe^IIIFe^II(HCOO)₆] single crystals

Abstract

The fundamental aspects of the relaxation dynamics in niccolite-type, mixed valence metal–organic framework, multiferroic [(CH₃)₂NH₂][Fe³⁺Fe²⁺(HCOO)₆] single crystals have been reported using dielectric relaxation spectroscopy covering eight decades in frequency (10⁻² ≤ f ≤ 10⁶) in the temperature range 120 K ≤ T ≤ 250 K. The compound shows antiferroelectric to paraelectric phase transition near T = 154 K with the relaxor nature of electric ordering. The temperature dependent dielectric response in modulus representation indicates three relaxation processes within the experimental window. The variable range hopping model of small polarons explains the bulk non-Debye type conductivity relaxation. The fastest relaxation with activation energy E_a = 0.17 eV is related to progressive freezing of the reorientation motions of DMA⁺ cations. X-ray diffraction data revealed that complete freezing of orientational and translational motions of DMA⁺ cations occurs well below phase transition temperature. These experimental observations are fundamentally important for the theoretical explanation of relaxation dynamics in niccolite-type metal–organic frameworks.

---

Introduction

The quest to design suitable multifunctional materials that display coexistence of electric and magnetic ordering in a single phase is an active area of current research.¹ In this context and among different classes of multifunctional materials, metal–organic frameworks (MOFs) with general formula [(CH₃)₂NH₂][M(HCOO)₃] (where M = Mg, Zn, Mn, Ni, Co, Fe) are promising type-I multiferroic materials which crystallize in a perovskite-like topology.^2–9 These materials are drawing remarkable research interest due to their intriguing fundamental physics and potential applications in novel multifunctional devices. These compounds show lower magnetic ordering at 8–36 K (except for Zn and Mg analogues) compared to electric ordering at 160–270 K.^2–7 In 2011 Fu et al. reported the dielectric hysteresis loop for dimethylammonium cobalt formate and confirmed that the low-temperature phases of the Co-compound and its Mn, Ni and Fe analogues are ferroelectric.⁹ Furthermore, experimental investigations indicate that phase transitions in these compounds are related to the ordering of dimethylammonium ions (DMA⁺) in the cavities of the framework. Other promising multiferroic MOFs are ammonium metal formats with general formula [NH₄][M(HCOO)₃] (where M = Mg, Zn, Mn, Ni, Co, Fe).^10–15 These compounds crystallize in the chiral topology with the space group P6₃22 (D₆⁶).^10–12 They exhibit electric order at 191–255 K, associated with a decrease of symmetry to P6₃ (C₆⁶).^10–12 The observation of the good dielectric hysteresis loop below T_c confirmed that the low-temperature structures of these materials are ferroelectric.¹⁰

Recently, heterometallic MOFs of general formula [(CH₃)₂NH₂][Fe^IIIM^II(HCOO)₆] (M^II = Fe, Co, Mn, Mg, Ni, Zn, Cu) were discovered.^16–20 These compounds crystallize in the niccolite-like topology.^16–20 Except for the Cu analogue (C2/c space group),²⁰ all of them crystallize in the trigonal space group (P3̄1c).^16–19 It is worth noting that only the mixed-valence [(CH₃)₂NH₂][Fe^IIIFe^II(HCOO)₆] (DMFeFe) undergoes an order–disorder phase transition into an antiferroelectric R3̄c phase at 155 K.^16,19 This behavior is associated with the electronic contribution to the mechanism of the phase transition.¹⁹

We have recently reported the dielectric response of DMFeFe¹⁹ and these measurements revealed significant differences between MOFs crystallizing in perovskite- and niccolite-like topology.¹⁹ However, the measurements were performed on a polycrystalline sample; eventually a deeper analysis of the observed dielectric anomalies could not be performed. In this paper, we report a systematic study on the dielectric response of DMFeFe single crystals in order to understand the electrical conduction and dielectric relaxation behavior. In addition, the physical natures of the observed relaxation processes are also presented.

Experimental

Ambient pressure dielectric measurements of the examined sample were carried out using a Novocontrol analyzer. The dimensions of the crystals with crystallographic orientation [100] were of the order of 2 × 1 × 0.7 mm³. For electrical measurements, the samples was dried and painted with a silver electrode. The small signal of amplitude 1 V was applied across the sample. The temperature was controlled by the Novo-control Quattro system, by using a nitrogen gas cryostat. The measurements were taken every 1 K over the temperature range from 130 to 230 K. Temperature stability of the samples was better than 0.1 K.

The single-crystal X-ray diffraction data were collected in the temperature range of 100–160 K. The details concerning the crystal structure refinement and selected geometry as well as hydrogen-bond parameters are provided in the ESI,† Tables S1–S3.

Results and discussion

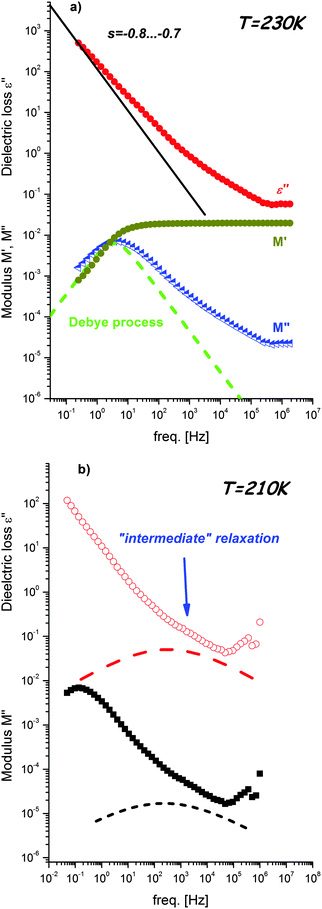
The thermal evolutions of dielectric permittivity, ε′, and loss, ε′′, at several frequencies for DMFeFe crystals are presented in Fig. 1. It is observed that ε′ increases monotonically with decreasing frequency at all the temperatures, which is a characteristic feature of polar dielectric materials. The graph clearly indicates that dielectric anomaly takes place near T = 154 K. It has been well established that this anomaly corresponds to the antiferroelectric to paraelectric phase transition in the material.¹⁹ Additionally, the anomaly in the temperature dependence of ε′ in the vicinity of the phase transition temperature shows strong frequency dispersion. This implies a relaxor nature of electric ordering in the niccolite-type MOF material. The peak maximum shifts towards the high temperature side with the increase in frequency and ε′(T) spectra merge at high temperatures near T = 190 K. The magnitude of the permittivity value at the transition temperature decreases with increasing frequency whereas that of loss follows reverse behavior. Literature reports of dielectric response for classical relaxor ferroelectric systems (i.e., PMN-PT, PZT) support these observations.²¹ In addition, it has to be emphasized that the relaxor nature of perovskite-type MOFs has already been reported by Tian et al.¹

Fig. 1 Temperature dependence of dielectric permittivity (upper panel) and dielectric loss (lower panel) for selected frequencies. The vertical dashed line indicates phase transition temperature. Inset: temperature dependence of the inverse permittivity for two frequencies.

Fig. 2 Frequency dependence of (a) dielectric permittivity, (b) dielectric loss and (c) imaginary part of the complex electric modulus in the temperature range from 248 K to 123 K. The inset focuses on loss spectra in the vicinity of the phase transition.

Fig. 3 (a) Comparison of the ε′′ spectra with M′ and M′′ spectra measurements at 230 K. The straight line represents slope equal −1 ionic conductivity. Dashed curves represent the Debye process. (b) The ε′′ and M′′ spectra collected at 210 K. Dashed curves represent (as guide for the eyes) the “intermediate” relaxation process masked by the conductivity part.

The transition from the antiferroelectric to paraelectric state is also clearly observed in frequency dependent dielectric permittivity and loss spectra (see Fig. 2). Inspection of the spectra shows existence of a marked relaxation process visible in the high frequency range below T = 163 K. The maximum of this process shifts to lower frequencies upon cooling. It should be emphasized that its amplitude starts decreasing in a close vicinity of the phase transition temperature and becomes about half order of magnitude lower for temperatures below T_c (Fig. 2b). However, during phase transition the shape of the process changes slightly from Debye-like above 154 K to slightly non-Debye below this temperature, i.e., it can be described by the Kohlraush–Williams–Watts process with exponent β_KWW = 0.9. The same temperature effect on this relaxation process can also be observed for electric modulus representation (Fig. 2c). Moreover, for this representation an additional process becomes evident in the low frequency region that also shifts to lower frequencies with decreasing temperature. Contrary to the faster relaxation, this slower process is not sensitive to phase transition. As presented in Fig. 3a, this relaxation is directly related to dc-conductivity of the material and it is possible to estimate conductivity relaxation times directly from electric modulus representation. Close inspection of the spectra presented in Fig. 3a reveals that the slope of the dc-conductivity part in the ε′′(f) dependence is lower than −1, the value typical for ionic conductivity. It can also be noticed that conductivity relaxation in the M′′(f) spectrum is markedly wider than the Debye relaxation. Both findings indicate that conductivity in the examined material has a different nature than simple ionic conductivity. Possible sources of this process will be discussed in further part of this section.

Fig. 3b presents comparison of the dielectric loss and modulus spectra recorded at 210 K. Close inspection of these data reveals that for both representations an additional, intermediate process between dc-conductivity and fast relaxation exists. This process is located close to the conductivity one and, due to its low amplitude, remains strongly overlapped by the conductivity part. For these reasons “intermediate” relaxation is observed as a change of power law dependence of ε′′(f) or M′′(f) at a high frequency wing of the dc-conductivity process. Due to the strong overlapping with the conductivity parts, it is difficult to estimate its shape and relaxation time.

The most reliable estimation of relaxation times for all processes was possible by separate fitting of the two regions of the dielectric spectra. The high frequency/low temperature fast relaxation was parameterized using the Cole–Cole functions , where τ and Δε denote the relaxation time and strength, respectively, and ε_∞ is the high-frequency contribution. In the case of the electric modulus, two Cole–Cole functions were used due to existence of the additional process from the slowest conductivity relaxation at M(f) spectra. Furthermore, dc-conductivity part of the loss spectra was parameterized according to the electrodynamics relation ε′′(f) = σ_dc/ε₀f^−s where s is the exponent describing departure from simple ionic temperature behavior with s = −1.

Using the information from fits, we have constructed the relaxation map of the examined material by plotting the relaxation time τ function of 10³/T. This relaxation map mirrors the dynamic properties of the system and the central feature of our investigation. The relaxation map (Fig. 4) clearly indicates that the thermal activation of slowest conductivity τ_σ relaxation spans through four decades in frequency. The τ_σ (T) dependence exhibited a clear convex curvature i.e., neither the classical Arrhenius nor the VFT-type behavior. Despite the curvature, it can be modeled in the first approximation using the Arrhenius relation , where τ₀, k_B and E_a denote relaxation time at the high temperature limit, Boltzmann constant and activation energy, respectively. It is evident that the experimental data fitted to Arrhenius law is fulfilled with E_a = 0.37 eV and the characteristic time τ₀ ≈ 10⁻⁹ s. This behavior has been described for several single crystals as evidence for the actuation of the small polaron hopping mechanism with a gradual decrease in electron–lattice coupling. The resolute convex curvature indicates a temperature dependent activation energy of τ_σ(T). Eventually, it is expected that activation energy, , is governed by the dimensionality (p) of conduction. The exponent value is equal to p = 1/4 for the three dimensional case of the conductivity process assuming a disordered crystal structure often observed in ABO₃-type materials. It is known that several perovskite manganites exhibit electric conductivity described in terms of the variable range hopping (VRH) model , where T₀ is related to the disorder energy which corresponds to variation in the local environment of the crystal lattice sites participating in the hopping process of the small polaron.²² The present experimental data are satisfactorily explained by the VRH model with T₀ = 1.15 × 10¹⁰ K, which confirms small polaron hopping. Comparing both Arrhenius dependence and VRH behavior, it can be concluded that both extrapolated theoretical loci deviate from each other approximately near phase transition temperature. This is a tentative indication on the sensitivity of conductivity relaxation time to phase transition temperature. The contribution of conduction (electrons or holes or protons) to dielectric polarization has been studied in many systems for both single crystals and polycrystalline ceramics.^23,24 Our experimental data show high magnitude of permittivity below f = 10 kHz throughout the temperature range of investigation (Fig. 2). It is expected that polarization can be greatly amplified by the interaction of the electrons, created by vacancies and the dielectric relaxation process. Under these circumstances, even at low concentration of the dipoles, the system could display a very high value of permittivity. In the investigated material, conductivity relaxation initiates from the contribution of the combination effect of electrical ordering of DMA⁺ cations in the framework, which couple with the conducting electrons. Therefore, an important role of the mixed ionic–polaronic conductivity mechanism is probable for this magnitude of activation energy of the slowest process, since it includes the charge carriers generated from the vacancies. As can be seen, above transition point T_c = 154 K nearly a Debye like conductivity relaxation feature is evident and relaxation frequency is proportional to (T − T_c) near T_c. The relaxation time bends upward far above T ≈ 190 K, showing “classical” critical slowing of the characteristic relaxation frequency in the neighborhood of T_c in the paraelectric phase. Very similar dielectric behaviors are observed due to the critical slowing-down of typical order–disorder-type ferroelectrics such as dimethylammonium cobalt formate and NaNO₂.⁹

Fig. 4 Arrhenius plot of the relaxation times for fast (upper panel) and conductivity (lower panel) relaxation processes observed in the sample. The vertical arrow indicates phase transition temperature.

It is important to note that the slowest process related to conductivity represents the bulk process in the crystal. The intermediate process appears as a shoulder to the slowest relaxation for both modulus and dielectric loss representation. Again, it is well known that the maxima in M′′(f) spectra are dominated by components with the smallest capacitance. The experimental data show that the capacitance corresponding to the bulk process is reasonably smaller than the shoulder (see Fig. 2). It is also important to note that the intermediate relaxation is almost temperature independent. The origin of this weak relaxation process is not clear. Since X-ray diffraction data discussed below show that DMA⁺ cations exhibit easy movements along the trigonal 3-fold axis, it might be related to slowing down of these movements upon cooling.

The fastest process, emerging at low temperatures, also exhibits an activation type of dynamics but with lower magnitude of activation energy than dc-conductivity relaxation, i.e., E_a = 0.17 eV and τ₀ = 10⁻¹² s. This process appears both in ε′′(f) and M′′(f) representations as well as develops the relaxation peak for temperatures lower than 163 K. It indicates the dipolar nature of the relaxation process. The physical nature and mechanism of this relaxation process in the examined material are attributed to the reorientational motion of DMA⁺ cations in the structure.

Indeed, previous dielectric studies of perovskite formate, DMNaFe, showed that the relaxation time of the fastest process related to reorientational motions of DMA⁺ cations also has a Debye shape with τ = 10⁻⁵ s at 166 K and E_a = 0.28 eV.²⁵ These data also showed a decrease of τ upon heating.²⁵ Fast relaxation time of about 10⁻⁷ s for the process related DMA⁺ cation was also reported for (CH₃)₂NH₂Al(SO₄)₂·6H₂O.²⁶ Note that this relaxation time is comparable to that observed in our DMFeFe crystals. The presented discussion indicates that the fast low-temperature relaxation is most likely related to progressive freezing of the reorientation motions of DMA⁺ cations. It should be emphasized that a shorter relaxation time found at the same temperatures for DMFeFe niccolite, when compared to DMNaFe perovskite, can be attributed to significant differences in the crystal structure of both structural types. Namely DMA⁺ cations have more space for motions in the niccolite structure due to the larger size of the cavities occupied by these cations and weaker bonding to the anionic framework via hydrogen bonds, when compared to the perovskite structure. As a result, these ions can exhibit faster reorientational motions in the niccolite structure and smaller activation energy is necessary to activate such motions.²⁵

Additionally, the detailed analysis of the DMFeFe crystal structure reveals that the DMA⁺ disorder in both phases has a more complex character than that previously reported. Fig. 5 illustrates the ordering of the template ions in the 160–100 K range. In the paraelectric phase DMA⁺ cations may adopt at least six different orientation states with equal probability (s.o.f. = 1/6). Splitting of the C and N positions through the ..2 axis and elongation of the carbon thermal ellipsoids at 160 K in the c direction indicate easy movements of counter-ions along the trigonal 3-fold axis. A similar behavior of DMA⁺ has been reported for DMMgFe.¹⁹ After phase transition the orientational disorder is lost but DMA⁺ ions still show disorder related to movement along the 3-fold axis. As a result, the number of possible states is reduced to three, except that two of them are symmetry related (A and A′ in Fig. 5). At 100 K the occupancy of the A and B positions is equal to 0.27(1) and 0.45(1), respectively. In each position the NH₂ groups are involved in N–H⋯O hydrogen bonds of similar strength with the anionic framework, Table S3 (ESI†). The decrease of displacement parameters with decreasing temperature together with a slight change of the occupancy factors between A and B sites (see Fig. S1, ESI†), may signify switching between the available A and B or A′ and B states, at least near phase transition temperature. The dynamical disorder evolves into a statistical one with a decrease in temperature and the latter one is preserved down to the helium temperatures. The model of the DMFeFe crystal structure from the neutron diffraction data collected at 40 K,¹⁸ based on the only one orientation state of DMA⁺, displays essentially elongated C and N displacement parameters indicating disorder which is not resolved. It is worth adding that although X-ray diffraction data reveal loss of the orientational disorder below T_c, previously reported IR data showed that broadening of the ρ(NH₂) mode due to disorder processes became negligible only below about 100 K.¹⁹ This behavior indicated that DMA⁺ cations retain some degree of orientational and translational freedom down to about 100 K, i.e., the complete freezing-in of these cations occurs well below T_c. A similar behavior was reported also for [(CH₃)₂NH₂][M(HCOO)₃] and [(CH₃)₂ND₂][M(HCOO)₃] perovskites (M = Mn, Ni).⁵

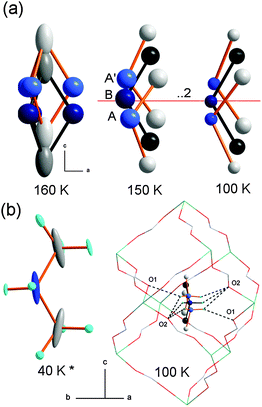Fig. 5 Ordering of DMA⁺ cations. (a) Dynamical disorder in the P3̄1c paraelectric phase (160 K) and possible positions in the R3̄c antiferroelectric phase (150 K, 100 K). (b) DMA⁺ at 40 K from ref. 18 and hydrogen bond interactions at 100 K. A and B denote symmetry independent states.

The most intriguing fact emerging from the activation plot presented in Fig. 4 is, however, the absence of any sign of phase transition at 154 K in the temperature dependence of the relaxation times of the fastest process. This transition was shown to be related to ordering of DMA⁺ cations below T_c due to slowing down of their reorientational motions upon cooling and freezing of these motions at low temperatures.¹⁹ Our dielectric data show that this transition is reflected by a marked change of the amplitude of the low temperature relaxation and their broadening, as was mentioned above, and one could expect that also the rate of this process will change during the transition. Surprisingly, inverse T dependence of the relaxation times related to this process remains smooth and continuous in the both phases (see Fig. 4). It is well-known that the value of E_a for the reorientational motions of organic cations confined by the host framework depends, among others, on the strength of hydrogen bonding and ionic interactions between the cation and the anionic framework.²⁷ The lack of any noticeable change in the E_a on going from the high-temperature to low-temperature phase of DMFeFe indicates, therefore, very similar confinement of DMA⁺ in both phases. Indeed, X-ray diffraction data reveal a very weak change of the unit cell volume due to the phase transition and small strengthening of hydrogen bonding in the low-temperature phase. It is worth adding that the lack of change in E_a during phase transitions was previously reported also for [NH₃(CH₂)₄NH₃][Co(HCOO)₃] niccolite-type formate.²⁸

Conclusions

On the basis of dielectric data which provide the direct access to the dynamic features of relaxation and conduction, collected for the examined sample, we have drawn the following conclusions.

(1) Complex modulus spectroscopy is an appropriate representation of dielectric data to understand the key features of conductivity relaxation and provide the potential connection to understand the microscopic origin of the processes.

(2) The examined sample showed the relaxor nature of electric ordering with transition temperature T = 154 K.

(3) The temperature dependent bulk conductivity relaxation with non-exponential nature is evidenced by variable range hopping of small polarons.

(4) The magnitude of activation energy for the fastest process is related to the orientational motion of DMA⁺.

(5) Detailed X-ray diffraction data revealed that DMA⁺ cations retain some degree of orientational and translational freedom down to about 100 K.

Acknowledgements

This research was partially supported by the National Science Center (Narodowe Centrum Nauki) in Poland under project No. DEC-2013/11/B/ST5/01058. Authors are deeply grateful for the financial support by the National Science Centre within the framework of the Maestro2 project (Grant No. DEC-2012/04/A/ST3/00337).

References

1. Y. Tian, A. Stroppa, Y. Chai, L. Yan, S. Wang, P. Barone, S. Picozzi and Y. Sun, Sci. Rep., 2014, 4, 6062.
2. P. Jain, V. Ramachandran, R. J. Clark, H. D. Zhou, B. H. Toby, N. S. Dalal, H. W. Kroto and A. K. J. Cheetham, J. Am. Chem. Soc., 2009, 131, 13625.
3. G. Rogez, N. Viart and M. Drillon, Angew. Chem., Int. Ed., 2010, 49, 1510.
4. R. Shang, S. Chen, Z. M. Wang and S. Gao, in Metal-Organic Framework Materials, ed. R. L. MacGillivray and C. M. Lukehart, John Wiley & Sons Ltd., 2014, pp. 221–238.
5. M. Mączka, A. Gągor, B. Macalik, A. Pikul, M. Ptak and J. Hanuza, Inorg. Chem., 2014, 53, 457.
6. M. Mączka, M. Ptak and L. Macalik, Vib. Spectrosc., 2014, 71, 98.
7. M. Mączka, W. Zierkiewicz, D. Michalska and J. Hanuza, Spectrochim. Acta, Part A, 2014, 128, 674.
8. B. Pato-Doldán, M. Sánchez-Andújar, L. C. Gómez-Aguirre, S. Yáñez-Vilar, J. Lopez-Beceiro, C. Gracia-Fernández, A. A. Haghighirad, F. Ritter, S. Castro-García and M. A. Señarís-Rodríguez, Phys. Chem. Chem. Phys., 2012, 14, 8498.
9. D. W. Fu, W. Zhang, H. L. Cai, Y. Zhang, J. Z. Ge, R. G. Xiong, S. D. Huang and T. Nakamura, Angew. Chem., Int. Ed., 2011, 50, 11947.
10. G. C. Xu, W. Zhang, X. M. Ma, Y. H. Hen, L. Zhang, H. L. Cai, Z. M. Wang, R. G. Xiong and S. Gao, J. Am. Chem. Soc., 2011, 133, 14948.
11. M. Mączka, A. Pietraszko, B. Macalik and K. Hermanowicz, Inorg. Chem., 2014, 53, 787.
12. R. Shang, G. C. Xu, Z. M. Wang and S. Gao, Chem. – Eur. J., 2014, 20, 1146.
13. M. Mączka, M. Ptak and S. Kojima, Appl. Phys. Lett., 2014, 104, 222903.
14. M. Mączka, P. Kadłubański, P. T. C. Freire, B. Macalik, W. Paraguassu, K. Hermanowicz and J. Hanuza, Inorg. Chem., 2014, 53, 9615.
15. M. Mączka, K. Szymborska-Małek, A. Ciupa and J. Hanuza, Vib. Spectrosc., 2015, 77, 17.
16. K. S. Hagen, S. G. Naik, B. H. Huynh, A. Masello and G. Christou, J. Am. Chem. Soc., 2009, 131, 7516.
17. J.-P. Zhao, B.-W. Hu, F. Lloret, J. Tao, Q. Yang, X.-F. Zhang and X.-H. Bu, Inorg. Chem., 2010, 49, 10390.
18. L. Cañadillas-Delgado, O. Fabelo, J. A. Rodríguez-Velamazán, M.-H. Lemėe-Cailleau, S. A. Mason, E. Pardo, F. Lloret, J.-P. Zhao, X.-H. Bu, V. Simonet, C. V. Colin and J. Rodríguez-Carvajal, J. Am. Chem. Soc., 2012, 134, 19772.
19. A. Ciupa, M. Mączka, A. Gągor, A. Sieradzki, J. Trzmiel, A. Pikul and M. Ptak, Dalton Trans., 2015, 44, 8846.
20. A. Ciupa, M. Mączka, A. Gągor, A. Pikul and M. Ptak, Dalton Trans., 2015, 44, 13234.
21. H. Wang, H. Xu, H. Luo and Z.-G. Ye, Appl. Phys. Lett., 2005, 87, 012904.
22. A. Molak, M. Paluch and S. Pawlus, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134207.
23. Ch. Ang, Z. Yu and L. E. Cross, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 228.
24. M. Maglione and M. Belkaoumi, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 2029.
25. M. Mczka, A. Pietraszko, L. Macalik, A. Sieradzki, J. Trzmiel and A. Pikul, Dalton Trans., 2014, 43, 17075.
26. R. Sobiestianskas, J. Grigas, V. Samulionis and E. F. Andreyev, Phase Transitions, 1991, 29, 167.
27. Z. Y. Du, T. T. Xu, B. Huang, Y. J. Su, W. Xue, C. T. He, W. X. Zhang and X. M. Chen, Angew. Chem., Int. Ed., 2015, 54, 914.
28. R. Shang, S. Chen, K. L. Hu, Z. C. Jiang, B. W. Wang, M. Kurmoo, Z. M. Wang and S. Gao, APL Mater., 2014, 2, 124104.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1. Temperature induced changes in the site occupation factor for the B position and the distance between the split nitrogen atoms. Fig. S2. The exemplary fitting of relaxation time. Tables S1–S3: The details concerning the crystal structure refinement and selected geometry as well as hydrogen-bond parameters. CIF and check CIF files for DMFeFe at 100, 125, 140, 150 and 160 K. See DOI: 10.1039/c6cp00064a

---