Large negative thermal expansion in non-perovskite lead-free ferroelectric Sn₂P₂S₆

Abstract

Functional materials showing both negative thermal expansion (NTE) and physical performance, such as ferroelectricity and magnetism, have been extensively explored in the past decade. However, among ferroelectrics a remarkable NTE was only found in perovskite-type PbTiO₃-based compounds. In this work, a large NTE of −4.7 × 10⁻⁵ K⁻¹ is obtained in the non-perovskite lead-free ferroelectric Sn₂P₂S₆ from 243 K to T_C (338 K). Structure refinements and first-principle calculations reveal the effects of the Sn(II) 5s–S 3p interaction on spontaneous polarization and its correlation with NTE. Then the mechanism of spontaneous volume ferroelectrostriction (SVFS) is verified and it could well elucidate the nature of NTE in ferroelectric Sn₂P₂S₆. This is the first case to demonstrate the unusual NTE behavior by SVFS in a non-perovskite lead-free ferroelectric material.

---

Introduction

As an intriguing property of solids, negative thermal expansion (NTE) has attracted enormous attention over the years.^1–3 These unusual materials, in which the volume (of unit cell) contracts upon heating, are fundamentally interesting and technologically important. To date, varieties of compounds including framework compounds,^1,4 ferroelectrics,⁵ magnetics,^6,7 and those with a valence change have been revealed with NTE features.⁸ By utilizing NTE materials to form either a single phase or a composite, the controllable coefficient of thermal expansion (CTE) of solids is highly expected which benefits equipment working at variable temperatures to reduce thermal failure. Moreover, smart materials or sensors could be realized through the interplay between elastic and physical properties during the unusual NTE progress in functional materials such as ferroelectrics and magnetics.

Different models have been proposed to elucidate NTE in such kinds of materials. Low-frequency vibration modes with a negative Grüneisen parameter are vital to the NTE in framework structures such as ZrW₂O₈.⁹ The magnetovolume effect (MVE) or the Invar effect is often triggered by Γ_5g magnetic transition.⁶ The spontaneous volume ferroelectrostriction (SVFS), a recently raised mechanism, is applied to the NTE in ferroelectrics.³ As being valuable to electronic technology, ferroelectrics showing NTE have been studied intensively in the past decade, however, only in PbTiO₃-based perovskite-type compounds. Actually, the NTE is quite rare among prototypic ferroelectrics. Most ferroelectrics exhibit normal volumetric expansion, for example, +2.8 × 10⁻⁵ K⁻¹ of BaTiO₃ (P4mm) and +3.8 × 10⁻⁵ K⁻¹ of LiNbO₃ (R3c).^10,11 The unusual NTE in ferroelectrics was first found in perovskite-type PbTiO₃ (P4mm) with an averaged volumetric CTE of −2.0 × 10⁻⁵ K⁻¹ (300–763 K).^12,13 Afterward, enhanced NTE was achieved by forming a solution with BiMO₃ (M = Fe, Zn_1/3Nb_2/3).³ Other ferroelectrics, especially the non-perovskite and lead-free ones, have not been concerned to NTE studies yet.

It is known that the Pb(II) 6s–O 2p interaction is essential for the large distortion as well as the NTE in PbTiO₃.^3,14 Besides, the divalent Sn(II) owns similar valence electronic configuration of 5s and could be ferroactive with some appropriate anions. Instead of oxides, the chalcogenide Sn₂P₂S₆ is a proper ferroelectric. The unit cell of Sn₂P₂S₆ adopting monoclinic P_n symmetry builds with rigid (P₂S₆) octahedra and two non-equivalent (SnS₈) polyhedra (Fig. 1a). The P_S vector lies in an ac-plane with a major component along the a-axis and a minor one along the c-axis (none along unique b-axis). It displays a moderate spontaneous polarization (P_S ∼ 14 μC cm⁻²) at room temperature and transforms into the paraelectric phase (P2₁/n) at T_C ∼ 339 K through a second-order phase transition.¹⁵ Axial thermal expansions of Sn₂P₂S₆ were once measured using a dilatometer with single crystals.^16,17 However, the resulted axial CTEs look quite discrepant (Fig. S5, ESI†) mainly because of the domain orientations in ferroelectric crystals, which act as an extrinsic effect involved in the dilatometric measurements. Moreover, the mechanism of the seeming NTE in Sn₂P₂S₆ is still unclear. In this work, we firstly reveal the nature of NTE in Sn₂P₂S₆ by determining the structure evolution and combining the first-principles calculations. Interestingly, the SVFS mechanism could well elucidate the NTE in Sn₂P₂S₆, which is the first NTE case in a non-perovskite lead-free ferroelectric material.

Fig. 1 (a) Unit cell and P_S vector of ferroelectric Sn₂P₂S₆. Short P–P and P–S bonds are omitted for clarity. (b) Evolutions of lattices and cell volume as a function of temperature (error bars are much smaller than labels). The volumetric coefficient of thermal expansion (CTE) is displayed with dashed lines. (c) Schematic of NTE in Sn₂P₂S₆. The scale of NTE is amplified. Arrows indicate intensely reduced Sn1–S distances as discussed below.

Experimental

The well crystalline Sn₂P₂S₆ powders with a grain size about 2 μm (Fig. S1, ESI†) were prepared in an evacuated sealed quartz tube.¹⁸ The ferroelectric–paraelectric phase transition temperature was confirmed to be 338 K using Differential Scanning Calorimetry (DSC) (Fig. S2, ESI†). The Raman spectrum was also carried out to verify the phase composition of the as-synthesized powders (Fig. S3, ESI†). Characterization of thermal expansion was performed using a high-resolution Panalytical X'Pert Powder X-ray Diffractometer (XRD, Cu Kα). Full patterns at non-ambient temperatures were collected in an Anton-Paar TTK450 chamber from 123 K to 423 K with a 10–30 K interval, and then conducted the Rietveld refinements with FULLPROF.¹⁹ Afterward, the effects of the Sn(II)–S interaction on both spontaneous polarization (P_S) and NTE are revealed using the first-principles calculations. The details of experiments, structure refinements and calculation processes are available in the ESI.†

Results and discussion

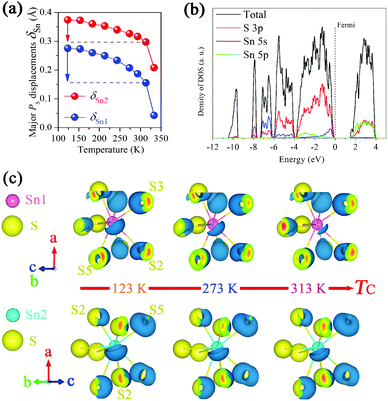
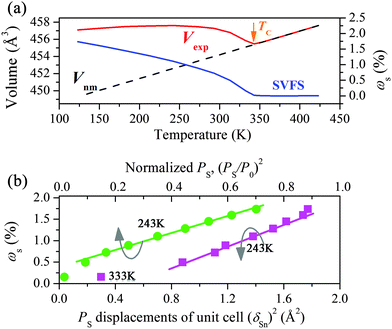
The obtained full XRD patterns were well refined using the starting structure model (ICSD-25357) reported by G. Dittmar (Fig. S4, ESI†). The typical R_wp is below 0.05 and the accurate lattice parameters are obtained (Table S1, ESI†). As shown in Fig. 1b, the evolution routes of a-, b-axis change abruptly at around 343 K, the temperature near the T_C. The major polar a-axis displays continuous contraction below T_C while the minor polar c-axis shows normal expansion. Another contraction along the non-polar b-axis is also observed from 273 K to T_C. In particular, the cell volume displays a remarkable NTE from 243 K to T_C and a minimum value at T_C. The averaged volumetric CTE is as large as −4.7 × 10⁻⁵ K⁻¹ within an appropriate 100 K temperature interval. Note that the strength of this NTE is competitive to that of several popular magnetics, such as −3.3 × 10⁻⁵ K⁻¹ of LaFe_10.6Si_2.4 (260–370 K) and −3.6 × 10⁻⁵ K⁻¹ of Mn₃Cu_0.5Ge_0.5N (280–365 K),^6,7 and also the superior one among ferroelectrics, −3.9 × 10⁻⁵ K⁻¹ of 0.4PbTiO₃–0.6BiFeO₃ (300–950 K).³ Besides the unusual NTE, the CTE of Sn₂P₂S₆ below 243 K is as low as +0.94 × 10⁻⁵ K⁻¹. In contrast, a robust one, +5.90 × 10⁻⁵ K⁻¹ appears in the paraelectric phase. Thus, the abnormally low CTE and NTE of volume below T_C must result from an additionally negative contribution relating to the spontaneous polarization (P_S) of the ferroelectric phase. Without ferroelectricity, the paraelectric phase expands as common materials due to the anharmonic atomic vibration.

It is known that the appearance of P_S in Sn₂P₂S₆ accompanies the relative displacements of Sn(II) cations to the charge center of the S₈ polyhedron, i.e., P_S displacement (δ_Sn), which could be acquired from a refined structure. The calculated major δ_Sn (along a-axis) at 293 K is 0.19 Å at the Sn1 site and 0.32 Å at the Sn2 site, close to the reported values (0.22 Å, 0.30 Å) of single crystals.²⁰Fig. 2a displays the temperature dependent major – δ_Sn. Both decrease upon heating and the one at the Sn1 site weakens much more considerably than that at the Sn2 site. In Sn₂P₂S₆ the hybridization between Sn 5s and S 3p is suggested to be crucial to ferroelectricity.²¹ To further investigate the above behaviors of δ_Sn and its correlation with NTE in Sn₂P₂S₆, first-principles calculations were performed to explore the varying Sn–S bonding character in the ferroelectric phase using the Vienna ab-initio simulation package (VASP). Several refined structures at 123 K, 273 K, and 313 K were calculated respectively without further optimization. The one at 373 K was also included to examine the case in the paraelectric phase.

Fig. 2 (a) Temperature dependent major P_S displacements (δ_Sn) at two non-equivalent Sn(II) sites. The maximum error is 0.014 Å for δ_Sn at 333 K, whose size is close to the circle label. (b) Calculated total DOS and PDOS of Sn 5s, 5p and S 3p according to the structure at 273 K. (c) Evolution of the asymmetrical electrons concentrating around Sn(II) sites below T_C. The isosurface of electron density is 0.0270 e Å⁻³.

As shown in Fig. 2b, the Sn 5s states hybridize with the S 3p states in several energy intervals, especially from −7.4 to −6.2 eV. The electronic distribution of these states clearly displays hybridization in several Sn–S bonds (Fig. S6, ESI†). Similar to the result of the Pb(II) 6s–O 2p interaction,²² only a small amount of Sn 5s states locates at the top of the valence band where the major S 3p states occupy. These top 5s states should be caused by 5s–3p mixing and relate to the antibonding states. The electrons calculated corresponding to the valence band maximum (VBM) show asymmetrical shapes around Sn(II) cations (Fig. 2c), pointing to these far sulfur anions and appropriately paralleling to the polar a-axis. This brings to mind the lone pair electrons (LPEs) exhibiting stereochemical activity. Our results coincide more with the revised concept of LPEs, in which it is the direct cation–anion interaction rather than the 5s/6s electrons that induces structure distortion.²² Here, we still refer to these hat-like electrons as LPEs. As the structure changes from 123 K to 313 K, the bonding states weaken slightly and similarly at two Sn(II) sites (Fig. S6, ESI†). Interestingly, these LPEs disappear markedly at the Sn1 site while not at the Sn2 site, matching well with the distinct evolution of P_S displacements as discussed. In the paraelectric structure, none of the LPEs could be seen around the Sn(II) cation (Fig. S7, ESI†). Thus the LPEs induced by the Sn(II)–S interaction contribute essentially to the local distortion and favor the appearance of ferroelectricity.

After the above studies, we can speculate how this NTE could happen. The Sn(II)–S interaction in the ferroelectric phase gives rise to anisotropic Sn–S bonding, i.e., short covalent and long ionic bonds (Fig. S6, ESI†). With rising temperature, the Sn(II)–S interaction is depressed by thermal vibrations and then the LPEs concentrating around the Sn(II) site become smaller until the phase transition at T_C. The electronic repulsion between these electrons and front sulfur anions is thus reduced, then the elongated Sn–S bonds are released, allowing those distant anions to move backward to the Sn(II) cations. This progress permits the contraction of these long Sn–S distances, which may lead to the NTE in terms of the crystal structure. Fig. 3 displays the temperature dependent bond lengths of Sn–S as a result of structure refinements. The two long bonds around the Sn1 site (Sn1–S2 & Sn1–S5-l) decrease much more rapidly than the ones around the Sn2 site (Sn2–S3-l & Sn2–S6), especially during the NTE region. This is consistent with the distinct evolution of LPEs at two Sn(II) sites. Moreover, the contraction of long ionic bonds around the Sn1 site looks severe than the elongation of short covalent ones. From 243 to 333 K, the long Sn1–S bonds contract by 0.25, 0.23 and 0.15 Å (7.6%, 6.5% and 4.7%), while the short ones elongate mostly by 0.17, 0.16 and 0.10 Å (5.7%, 5.6% and 3.4%), respectively. The contractions exceed the elongations by about 0.05 Å. Note that the contraction of the polar a-axis in this region is 0.035 Å, comparable with 0.05 Å. Thus we suggest that the asymmetric change of Sn1–S bonds finally triggers the NTE. Fig. 1c illuminates the progress of NTE in Sn₂P₂S₆.

Fig. 3 Temperature dependent bond lengths of Sn–S in Sn₂P₂S₆. The errors are less than 0.01 Å, smaller than the labels. The symbols “-s” and “-l” denote short covalent and long ionic Sn–S bonds respectively. The shadow regions indicate where the NTE occurs.

The NTE in Sn₂P₂S₆ was once ascribed to the negative Grüneisen coefficients of optical vibrations (γ_optic) as the case in ZrW₂O₈. Based on the thermal expansion behavior, the calculated γ_optic changes its sign around 200 K and gets more and more negative until the phase transition.²³ According to the relation k_BT = ℏω_i, where k_B is the Boltzmann constant and the ℏ is the reduced Planck constant, the modes accounting for the NTE should have approximate frequencies around 140 cm⁻¹. However, high-pressure Raman studies of Sn₂P₂S₆ show that almost all optical modes above 150 cm⁻¹ present positive γ_optic values.²⁴ Moreover, with increasing temperature, the weighted γ_optic should be more positive instead of being more negative since high-frequency optical vibrations tend to be active. Thus, the thermodynamic calculation conflicts with the experimental results. Therefore, the NTE in ferroelectric Sn₂P₂S₆ is difficult to be described simply through the Grüneisen model.

As a new case in non-perovskite lead-free ferroelectrics, it is necessary to further examine the correlation of NTE with the ferroelectricity in Sn₂P₂S₆ and see whether it is compatible to the SVFS mechanism. The contribution of P_S to the volume expansion in Sn₂P₂S₆, ω_s is calculated as (V_exp − V_nm)/V_nm × 100%, in which V_exp is the observed volume and V_nm is a nominal one extrapolated from the paraelectric phase (Fig. 4a). Then ω_s is plotted as the square of polarization as shown in Fig. 4b. It is unambiguous that the ω_s correlates strongly with both the squared P_S displacement, (δ_Sn)² and the (P_S/P₀)² (normalized P_S from literature data of Sn₂P₂S₆ crystals in ref. 25). The dominated linearity below T_C well suggests that the P_S correlates inherently with the ω_s and governs the negative contribution to the cell volume. Hence, the SVFS mechanism is applicable to account for the NTE here. Actually, it is expected to see such a linearity between the ferroelectricity and the ω_s, since the LPEs impact the bond lengths and the P_S simultaneously as discussed above.

Fig. 4 (a) Temperature dependent V_exp, V_nm and magnitude of negative contribution to thermal expansion from ferroelectricity, ω_s. (b) Linear correlations of ω_s ∼ (P_S/P₀)² and ω_s ∼ (δ_Sn)². δ_Sn here is the total P_S displacement of Sn(II) cations in the single unit cell. The maximum error of (δ_Sn)² is 0.02 Ų at 333 K, smaller than the square label.

Though here the P_S is much inferior compared with the one in PbTiO₃ (14 vs. 60 μC cm⁻² at 300 K), the SVFS seems intense enough to trigger NTE in Sn₂P₂S₆. It is interesting to see both ferroelectrics, actually the sole two prototypic ones showing remarkable NTE, involve the s–p interaction (Pb–O and Sn–S) to generate the P_S. This well indicates the special role of this interaction and the LPEs in the NTE behavior of ferroelectrics, which is worthy of more studies. In addition, besides the NTE behavior, Sn₂P₂S₆ also displays semi-conductive character and could be easily grown into large crystals. These features, which are absent in PbTiO₃, permit more possibilities to design special materials or devices with the unusual NTE behavior.

Conclusions

In conclusion, the unusual negative thermal expansion in non-perovskite lead-free ferroelectric Sn₂P₂S₆ is carefully studied. A large NTE of −4.7 × 10⁻⁵ K⁻¹ is determined from 243 K to T_C (338 K). The evolution of P_S displacement and NTE progress are clarified by means of structure analyses and first-principles calculations. Then the NTE mechanism of spontaneous volume ferroelectrostriction (SVFS), which is developed from perovskite-type lead-based ferroelectrics, is firstly extended to the elucidation of NTE in non-perovskite and lead-free ferroelectric Sn₂P₂S₆. In addition, it is further suggested that s–p interaction and LPEs play a significant role in obtaining remarkable NTE in ferroelectrics. This work will considerably motivate the design of new ferroelectric and functional NTE materials.

Acknowledgements

This work is supported by NSFC (91022016, 21031005, 21590793, 21231001, 91422301), Program for Changjiang Scholars (IRT1207) and Funds for the Central Universities, China (Grant No. FRF-SD-13-008A).

Notes and references

1. T. A. Mary, J. S. O. Evans, T. Vogt and A. W. Sleight, Science, 1996, 272, 90–92.
2. K. Takenaka, Sci. Technol. Adv. Mater., 2012, 13, 013001.
3. J. Chen, L. Hu, J. Deng and X. Xing, Chem. Soc. Rev., 2015, 44, 3522–3567.
4. B. K. Greve, K. L. Martin, P. L. Lee, P. J. Chupas, K. W. Chapman and A. P. Wilkinson, J. Am. Chem. Soc., 2010, 132, 15496–15498.
5. J. Chen, K. Nittala, J. S. Forrester, J. L. Jones, J. Deng, R. Yu and X. Xing, J. Am. Chem. Soc., 2011, 133, 11114–11117.
6. K. Takenaka and H. Takagi, Appl. Phys. Lett., 2005, 87, 261902.
7. R. Huang, Y. Liu, W. Fan, J. Tan, F. Xiao, L. Qian and L. Li, J. Am. Chem. Soc., 2013, 135, 11469–11472.
8. M. Azuma, W. Chen, H. Seki, M. Czapski, S. Olga, K. Oka, M. Mizumaki, T. Watanuki, N. Ishimatsu, N. Kawamura, S. Ishiwata, M. G. Tucker, Y. Shimakawa and J. P. Attfield, Nat. Commun., 2011, 2, 347.
9. R. Mittal, S. L. Chaplot, H. Schober and T. A. Mary, Phys. Rev. Lett., 2001, 86, 4692–4695.
10. H. E. Kay and P. Vousden, Philos. Mag., 1949, 40, 1019.
11. S. C. Abrahams, H. J. Levinstein and J. M. Reddy, J. Phys. Chem. Solids, 1966, 27, 1019–1026.
12. G. Shirane and H. Sadao, J. Phys. Soc. Jpn., 1951, 6, 265–270.
13. X. Xing, J. Deng, J. Chen and G. Liu, Rare Met., 2003, 22, 1–4.
14. Y. Kuroiwa, S. Aoyagi, A. Sawada, J. Harada, E. Nishibori, M. Takata and M. Sakata, Phys. Rev. Lett., 2001, 87, 217601.
15. C. D. Carpentier and R. Nitsche, Mater. Res. Bull., 1974, 9, 1097–1100.
16. A. Say, O. Mys, A. Grabar, Y. M. Vysochanskii and R. Vlokh, Phase Transitions, 2009, 82, 531–540.
17. Y. M. Vysochanskii, T. Janssen, R. Currat, R. Folk, J. Banys, J. Grigas and V. Samulionis, Phase transitions in phosphorous chalcogenide ferroelectrics, Vilnius University Publishing House, Vilnius, 2008.
18. I. N. Rybina, T. G. Lupeiko, S. N. Svirskaya and A. A. Nesterov, Inorg. Mater., 2010, 46, 1242–1243.
19. J. Rodriguez-Carvajal, Abstracts of the Satellite Meeting on Powder Diffraction of the XV Congress of the IUCr, Toulouse, France, 1990, p. 127.
20. B. Scott, M. Pressprich, R. D. Willet and D. A. Cleary, J. Solid State Chem., 1992, 96, 294–300.
21. K. Glukhov, K. Fedyo, J. Banys and Y. M. Vysochanskii, Int. J. Mol. Sci., 2012, 13, 14356–14384.
22. D. J. Payne, R. G. Egdell, A. Walsh, G. W. Watson, J. Guo, P.-A. Glans, T. Learmonth and K. E. Smith, Phys. Rev. Lett., 2006, 96, 157403.
23. Y. Vysochanskii, A. Kohutych, R. Yevych and S. Perechinskii, AIP Conf. Proc., 2009, 209, 209–215.
24. V. V. Shchennikov, N. V. Morozova, I. Tyagur, Y. Tyagur and S. V. Ovsyannikov, Appl. Phys. Lett., 2011, 99, 212104.
25. R. M. Yevych and Y. M. Vysochanskii, Condens. Matter Phys., 2008, 11, 417–423.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp00011h

---