Open Access Article
Open Access ArticleLabel-free detection of DNA single-base mismatches using a simple reflectance-based optical technique†
G.
Nava‡
a,
E.
Ceccarello‡
a,
F.
Giavazzi
a,
M.
Salina
b,
F.
Damin
c,
M.
Chiari
c,
M.
Buscaglia
a,
T.
Bellini
a and
G.
Zanchetta
*a
aDipartimento di Biotecnologie Mediche e Medicina Traslazionale, Università degli Studi di Milano, via Fratelli Cervi 93, 20090 Segrate, Milano, Italy. E-mail: giuliano.zanchetta@unimi.it
bProxentia S.r.l., 20135 Milano, Italy
cIstituto di Chimica del Riconoscimento Molecolare (ICRM), C.N.R., Via Mario Bianco 9, 20131 Milano, Italy
First published on 12th April 2016
Abstract
Rapid and quantitative detection of the binding of nucleic acids to surface-immobilized probes remains a challenge in many biomedical applications. We investigated the hybridization of a set of fully complementary and defected 12-base long DNA oligomers by using the Reflective Phantom Interface (RPI), a recently developed multiplexed label-free detection technique. Based on the simple measurement of reflected light intensity, this technology enables to quantify the hybridization directly as it occurs on the surface with a sensitivity of 10 pg mm−2. We found a strong effect of single-base mismatches and of their location on hybridization kinetics and equilibrium binding. In line with previous studies, we found that DNA–DNA binding is weaker on a surface than in the bulk. Our data indicate that this effect is a consequence of weak nonspecific binding of the probes to the surface.
Introduction
The hybridization process, by which nucleic acid chains recognize and selectively bind to complementary strands, is at the basis of a whole range of biological processes.1 Furthermore, simple and robust detection and discrimination of nucleic acid sequences is of critical importance for various biomedical applications, ranging from gene expression profiling to determination of single point mutations to quantification of microRNAs as possible biomarkers for diseases.2–4 Along with biomedical investigation, the research aiming at the exploitation of DNA to realize nanostructures like scaffolds, drug carriers, or nanomachines – in brief DNA nanotechnology5 – is gaining increasing interest and critically relies on accurate detection, modelling and control of the hybridization process.In recent years, DNA microarrays, based on the recognition and hybridization of target sequences by surface immobilized single-stranded DNA (ssDNA) probes, have reached considerable success and widespread use for their versatility and massive data generation.6 However, conventional detection methods based on fluorescence emission of labelled targets fail to quantitatively assess concentrations and binding energies, which affects their reliability and reproducibility. Therefore, label-free methods enabling the quantitative detection of DNA binding while preserving multiplexing, scalability and cheapness appear to be of general interest.3
Here we apply for the first time to DNA–DNA recognition a recently proposed label-free optical technique, the Reflective Phantom Interface (RPI).7–10 The RPI is based on measuring the increase of reflected light intensity upon mass adsorption on a surface with extremely low initial reflectivity, which thus yields a high signal-to-noise ratio. We realize this condition by using a fluorinated material iso-refractive to water as a sensing substrate. Changes in reflectance allow the quantification of small variations in the amount of molecules at the interface, such as those produced by the binding of ligand target molecules to surface-immobilized receptor probes. This approach requires a particularly simple measuring procedure and experimental setup.8 We measure kinetic and equilibrium binding constants upon hybridization of probes and target DNA 12-mers, demonstrating a detection sensitivity of about 10 pg mm−2 of oligomers bound to the surface. The effect of a single nucleotide mismatch in the pairing sequence is easily discriminated and quantified.
In line with other observations of surface hybridization, we find a binding strength weaker than that expected in the bulk. Our data enable discriminating among the various potential causes of such a weakening.
Experimental
Substrate preparation
The fluorinated material used in this study (Hyflon AD60, Solvay Specialty Polymers, Italy) is an optically transparent, amorphous, glassy copolymer of tetrafluoroethylene and 2,2,4-trifluoro-5-trifluoromethoxy-1,3-dioxole containing 60 mol% of the cyclic comonomer, with a refractive index (nHyflon ≈ 1.327) very close to the typical buffered water value (nTrisHCl ≈ 1.335 under our experimental conditions), yielding a “background” reflectivity R0 ≲ 10−5. The bulk material was machined and mechanically lapped to obtain prisms with optical quality faces. The prisms were cleaned with distilled water and plasma treatment and then immersed for 30 min in a water solution of ammonium sulfate at 20% (wt/vol) saturation, containing 1% wt/vol of a different polymer, copoly (DMA-NAS-MAPS)11 that serves the two purposes of coating of the Hyflon surface and of providing a few nm-thick scaffold for the grafting of aminated molecules. The coated prisms were then rinsed with water and dried under vacuum at 80 °C. The estimated roughness of the substrate, between 0.1 and 1 μm, did not change upon such treatments, while its reflectivity only slightly increased – around 25% – without substantially affecting RPI sensitivity.DNA sequences
By taking advantage of the multiplexing capacity of the RPI, we prepared surfaces with multiple spots carrying various 12-base long DNA oligomers that interact with the same target sequence present in solution. Specifically, the target sequence is5′-ACGACAGTCCTG-3′ (12T) while the probe sequences are:
12FC: NH2-5′-CAGGACTGTCGT-3′, complementary to 12T;
12CM: NH2-5′-CAGGA![[A with combining low line]](https://www.rsc.org/images/entities/char_0041_0332.gif) TGTCGT-3′, with one central mismatch (underlined);
TGTCGT-3′, with one central mismatch (underlined);
12TM3: NH2-5′-CAGGACTGTCG![[A with combining low line]](https://www.rsc.org/images/entities/char_0041_0332.gif) -3′, with one mismatch at the 3′ terminal;
-3′, with one mismatch at the 3′ terminal;
12TM5: NH2-5′-![[A with combining low line]](https://www.rsc.org/images/entities/char_0041_0332.gif) AGGACTGTCGT-3′, with one mismatch at the 5′ terminal.
AGGACTGTCGT-3′, with one mismatch at the 5′ terminal.
To test the effect of the distance from the surface, we also studied sequences with polyA spacers on the tethered end (An-12FC: NH2-5′-(A)nCAGGACTGTCGT-3′, n = 6, 12).
Negative controls consisted of a sequence completely unrelated to 12FC, 23CTRL:
NH2-5′-GCCCACCTATAAGGTAAAAGTGA-3′.
All sequences were purchased from Integrated DNA Technologies, with HPLC purification.
DNA immobilization
After the coating with the copolymer, the sensing surface of the prism was functionalized with the aminated DNA sequences, and spotted using an automated noncontact dispensing system (sciFLEXARRAYERS5; Scienion AG).The DNA sequences were spotted in droplets at concentrations ranging from cS = 0.625 μM to cS = 20 μM in Tris-HCl buffer pH 8 to obtain different surface probe densities. Moreover, each spot had multiple replicates to provide better statistics. The prisms were then incubated overnight in a humid chamber at room temperature. The spotted prisms were immersed in a 50 mM ethanolamine solution (Tris HCl 10 mM, NaCl 150 mM, pH 8) for 30 minutes, rinsed with distilled water and dried before use. No further surface passivation was found necessary.
Hybridization experiments and data analysis
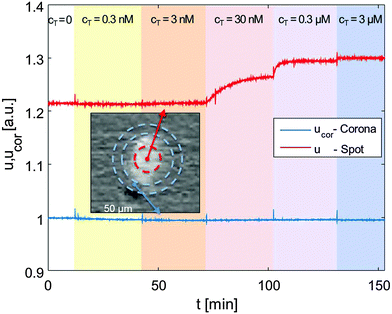
The details about the RPI optical setup can be found in ref. 7. The spotted prism was inserted into a standard glass cuvette and immersed in an incubation buffer consisting of Tris-HCl 10 mM, NaN3 0.02%, pH 8. Ionic strength was adjusted between 60 and 160 mM with added NaCl. The cuvette was kept at constant temperature through a thermalized holder.The sensing surface was illuminated using a LED source (HLMP-ED18-UX000; Avago Technologies) emitting at 450 nm – with a spectral half width of 17 nm. Reflected light was collected by a CCD camera (Stingray F-145B/C; Allied Technology). We acquired time-lapse videos of the surface with a rate of 1 frame per second, averaging every 5 consecutive frames. For each averaged frame, we extracted the intensity reflected by each spot and by its corresponding corona, as shown in Fig. 1 (inset picture). We then averaged the intensities of spots corresponding to identical conditions (probe type and spotting concentration), and of their coronas. Fig. 1 shows such intensities u (spots) and ucor (coronas) over time for 12FC probes.
Keeping the cell at 33 °C, we introduced in the cuvette, at given times (tC), increasing amounts of 12T, to produce a stepwise increase of target concentration, from cT = 0.3 nM to cT = 3 μM, as marked by the shadings in Fig. 1. After each increment in cT, the reflected intensity had a transient response corresponding to the DNA targets adhering to the surface.
The details about the analysis of reflectivity data can be found in the ESI.† In brief, the mean reflected intensity can be converted into the surface density of the mass present at the interface, σ, by describing the reflectance of a multi-layered structure.7 Specifically,
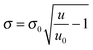 | (1) |
Results and discussion
Hybridization measurements using the RPI
The neat growth of u that follows the injections of target sequences, displayed in Fig. 1, is a clean indication that the RPI can effectively sense the binding process. Fig. 2a shows the surface density of the bound target, Δσ = σ − σ(t = 0) (eqn (1)) for the four different probes with the same length averaged over 4 spots each, plus the control probe which shows no sign of aspecific binding. The spots were produced with equal spotting concentration cS on the same chip. Therefore, the injection of 12T is the same for each probe and equal to the one reported in Fig. 1. Each increase of the target surface density Δσ after the injection time tC can be well fitted with a single exponential function (shown in Fig. 2a as black thin lines):Δσ(t) = ΔσC − ΔΔσ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(t − tC)/τC] exp[−(t − tC)/τC] | (2) |
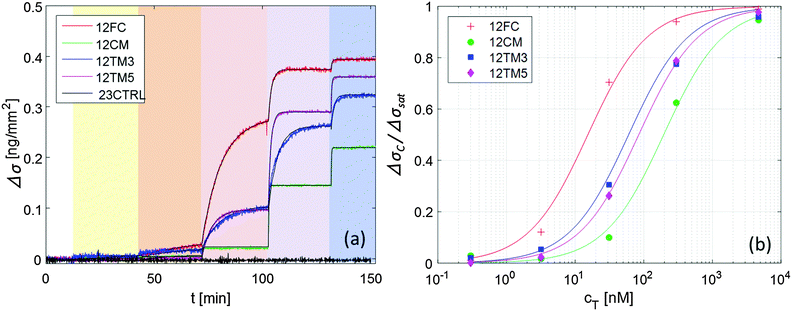 | ||
| Fig. 2 Increase of the surface density of bound target strand 12T, upon hybridization to different probes, for increasing concentration of 12T in solution (ionic strength INa = 160 mM, T = 33 °C, and cS = 6.25 μM). (a) Surface density signal averaged over 4 spots each; color shading for 12T addition is the same as in Fig. 1; black lines are fits with eqn (2). (b) Fraction of occupied binding sites for the 4 DNA probes upon increase of target concentration; lines are fits with the Langmuir model eqn (3). | ||
Fig. 2b shows the dependence of the equilibrium surface concentration ΔσC on cT, indicating growth and saturation. This behaviour suggests a first order adsorption mechanism. Indeed, ΔσC(cT) is well fitted by the expression expected for Langmuir adsorption isotherms:12
| ΔσC(cT) = ΔσsatcT/(cT + Kdiss) | (3) |
| Sequence | k on (s−1 nM−1) | k off (s−1) | K diss (nM) | K diss,L (nM) | K diss,NN (nM) |
|---|---|---|---|---|---|
| 12FC | 1.79 × 10−5 | 2.6 × 10−4 | 14.5 | 7 | 0.12 |
| 12TM3 | 2.02 × 10−5 | 1.4 × 10−3 | 68.8 | 30 | 0.30 |
| 12TM5 | 1.6 × 10−5 | 1.3 × 10−3 | 84.4 | 40 | 0.89 |
| 12CM | 14.1 × 10−5 | 2.63 × 10−2 | 187.1 | 228 | 12.9 |
In all linear two-state processes, Kdiss = koff/kon, with kon and koff being the association and dissociation kinetic coefficients, respectively. The measured τC depends on such coefficients as:12
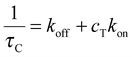 | (4) |
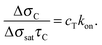 | (5) |
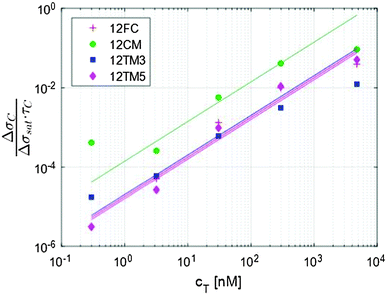 | ||
| Fig. 3 The initial slope of the exponential fit shown in Fig. 2a provides an evaluation of the kinetic association constant through eqn (5). | ||
Hybridization of sequences with single nucleotide mismatches
The traces shown in Fig. 2a display clear differences in the hybridization of the target strand to the four probes. The complete hybridization of 12FC leads to the largest σ increment when cT = 30 nM, while the sequences with a mismatch pair most significantly to the surface probes when cT = 300 nM. This difference corresponds to a different binding coefficient: as reported in Table 1, Kdiss markedly increases when mismatches are present in the sequence, of about 5 times if the defect is at the sequence terminal, and of about 13 times in the case of a central defect. The dependence of the thermodynamic stability of the duplexes on the mismatch position along the oligomer strands is a well-known property of nucleic acids.15,16 In Table 1, we report the values of Kdiss,NN, the dissociation coefficient computed for solution hybridization of the same sequences on the basis of the well-established nearest-neighbour model.13,14 The critical role of mismatch position along the sequence is confirmed by the computed values Kdiss,NN, which show the same scaling of Kdiss with the probe sequence. However, all the computed values are much lower than those measured via the RPI, indicating that bulk hybridization is stronger than surface hybridization, a phenomenon often observed in analogous experiments and discussed in a later section.The kinetic behaviour is also distinctly different in the four systems. A marked dependence of the hybridization kinetics on the mismatch position has also been previously reported.17 In the context of the experiments described here, this effect is particularly striking in the case of the hybridization with a central mismatch, in which binding takes place in a much shorter time than in the other cases. The quantitative analysis of such behaviour, Fig. 3 and Table 1, reveals that koff is much more sensitive to mismatches than kon. A pronounced increase of kon is only observed for the central mismatch, in contrast to the solution behaviour of shorter oligomers;17 however, also in this case, the increase of koff is larger. This appears reasonable, since kon mainly reflects the height of the entropic barrier that the two strands have to overcome to get close enough to each other to enable the formation of the duplex through the enthalpic gain of stacking and pairing.18 Accordingly, kon is expected to be much less sensitive to the quality of the pairing than koff, which is instead mainly determined by the enthalpy needed to unbind the two strands.
Effect of probe surface density and of ionic strength
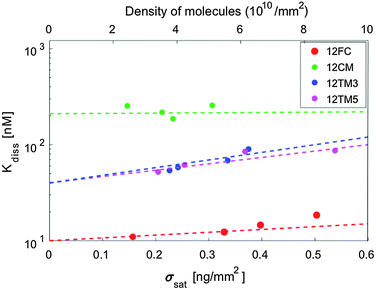
The hybridization curves of Fig. 2 were measured on spots of surface-immobilized probes that were all produced with equal cS. We attribute the differences in the Δσsat measured with the different probes to minor experimental differences in the spotting process. However, to explore the possible effects of probe surface crowding, we performed measurements analogous to those in Fig. 2 at different spotting concentrations, ranging from cS = 0.6 μM to cS = 25 μM, for all the different probes. Such concentrations correspond to probe surface densities in the range of 3–10 × 1010 molecules per mm2, as assessed from the measured σsat values (see Fig. S3 in the ESI†). The highest density of this range corresponds to about 1 probe per 10 nm2, a condition where the mean distance between neighbouring probes is in the order of their length.In Fig. 4 we plot Kdiss, determined by fitting ΔσC(cT) with Langmuir isotherms as in Fig. 2b; ΔσC(cT) is measured in spots having different surface concentrations of active probes, as expressed by Δσsat. While no clear trend is visible in the hybridization of 12CM, in the case of perfect pairing or terminal mismatches we can observe a slight but monotonic dependence, suggesting that binding may be weakened by crowding at the probe surface.19 Indeed, when the probes are at distance of contact to each other as is for the densest spots, it appears reasonable that hybridization is affected by their mutual electrostatic or steric hindrance. To take into account these effects, we report in Table 1 the values of Kdiss,L, the equilibrium coefficients obtained by extrapolating the measured Kdiss to limiting low probe concentrations along the lines in Fig. 4. Although these values have larger intrinsic uncertainty than Kdiss, it is quite clear that their values are still much higher than those for solution hybridization.
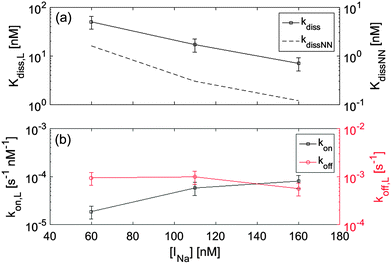
Ionic strength INa is very well known to significantly affect hybridization in the bulk. To explore analogous effects in surface hybridization, we performed measurements with the 12FC probes by changing the concentration of Na+ ions between 60 mM and 160 mM. In Fig. 5a, we compare measured values of dissociation constant Kdiss,L with the expected solution coefficients Kdiss,NN, finding a similar dependence on ionic strength. Fig. 5b shows the INa dependence of the kinetic coefficients. Data indicate that upon increasing INa, the strengthening of the duplex binding is mainly due to the increase of kon, while koff is only weakly affected, in agreement with previous single molecule measurements both in solution and at the surface.17,20
How does the surface affect binding?
Hybridization at the surface, as measured using the RPI, is weaker than its counterpart in the bulk. The ratio between Kdiss and Kdiss,NN ranges from about 15 – for a central pairing defect – to about 100 for the fully complementary binding.Systematic and relevant differences in the values of binding affinities and hybridization kinetics of DNA oligomers when measured in solution vs. on a sensor surface have been documented in a number of previous articles (see e.g.ref. 2 and 21 and references therein). Most of these studies have focused on immobilized oligomeric probes interacting with a long target strand, much longer than those considered here. In that case a major role is played by the molecular crowding at the surface, which follows the binding itself.22 However, important effects on affinities and kinetics were also found for oligomeric targets with length comparable to the ones we studied here.21,23,24
In line with what we observed using the RPI, previous investigations have found that even at low probe density – where crowding plays no role – and at large ionic strengths – where electrostatics is screened – binding can be orders of magnitude weaker than in solution, while the interaction is still well described by a Langmuir isotherm.25 Other studies have shown that the nature of the surface – hydrophobic vs. hydrophilic – also plays a complex role in the hybridization of DNA.26,27
Overall, the possible causes of the weakening of the hybridization free energy at the surface can be classified into two main groups: (i) effects due to target repulsion by the surface, and (ii) effects due to the competition of probe–target binding with nonspecific interactions of the probe and/or the target.
(i) Repulsive effects. Target repulsion by the surface can rise from electrostatic interaction with the surface-bound probes, targets or other ions. The data described above indicate that electrostatic effects should not be considered as the main origin of surface-induced duplex weakening: the ionic strength dependence is as expected in solution hybridization, and the probe density, which contributes to the surface charge density, has only a mild effect. It is also worth noticing that the roughly exponential dependence expressed by the lines in Fig. 4 agrees with predictions based on surface electrostatic repulsion,22 confirming that electrostatic repulsion is indeed detected, but with minor effects.
Alternatively, repulsion could be ascribed to the steric constraints imposed by the thin 3D polymeric matrix (around 85% of its volume is occupied by water), to which the probes are grafted. The targets might have to navigate into a molecularly crowded environment that limits the accessibility of the probes. This is expected to directly affect the kinetics of binding and unbinding. However, less obvious is the effect on the equilibrium of the interaction. As in the case of the electrostatic repulsion,25 the main effect can be described as an uneven partitioning of the targets between the bulk solution and the surface layer of immobilized probes. In this case, the concentration of target strands close to the surface cT,S is reduced with respect to the bulk concentration cT,V by cT,S/cT,V = exp(−μS/kBT), where μS is the chemical potential increment at the surface, that is the work required to transfer one target molecule from the bulk to the surface. This means that the apparent binding and kinetic coefficients measured by controlling cT,V are also modified by the same factor controlling the surface concentration. Since such a factor is in our case of the order of 100, this simple evaluation suggests a significant repulsive barrier of the order of 5 kBT. Should this barrier be interpreted as a reduction of the conformational volume Ω of the targets in the proximity of the probes (i.e. μS = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Ωvol/Ωsurf)), it would lead to the unrealistic conclusion that the phase space within the matrix is 100 times smaller than that in solution. To further test this notion, we checked the effect of placing a molecular spacer between the copolymer coating and the probe sequence to increase the distance of the docking sites from the coating polymer branches.28 This was done by inserting a 6- or 12-base long polyA tract on the tethered side of the 12FC probe. Rather than facilitating the hybridization, distancing the probe from the surface produced a slight decrease of the estimated affinities (Fig. S4 in the ESI†), likely due to enhanced crowding of the probes. Therefore, neither the electrostatic nor the steric repulsion of the polymer coating seem to provide a plausible origin of the observed weakening of the hybridization strength at the surface.
ln(Ωvol/Ωsurf)), it would lead to the unrealistic conclusion that the phase space within the matrix is 100 times smaller than that in solution. To further test this notion, we checked the effect of placing a molecular spacer between the copolymer coating and the probe sequence to increase the distance of the docking sites from the coating polymer branches.28 This was done by inserting a 6- or 12-base long polyA tract on the tethered side of the 12FC probe. Rather than facilitating the hybridization, distancing the probe from the surface produced a slight decrease of the estimated affinities (Fig. S4 in the ESI†), likely due to enhanced crowding of the probes. Therefore, neither the electrostatic nor the steric repulsion of the polymer coating seem to provide a plausible origin of the observed weakening of the hybridization strength at the surface.
(ii) Competitive effects. An alternative explanation of the reduced binding strength is the presence of other attractive interactions that compete with the probe–target interaction. These mainly include forms of nonspecific adhesion of the probes on the polymer support or sensor surface they are attached to. Surface–target interaction may also be present, but the identical nature of probes and targets suggests that these interactions, if present, are much more relevant to the probes, constrained to a continuous contact with the surface by their chemical bonds. Indeed, no sign of nonspecific adhesion of target strands was ever detected outside the functionalized spots. In principle, probe–probe interactions could also be present, as discussed in the context of different experiments.2 Complex probe–probe interactions mediated by targets have also been suggested.25 However, the weak dependence of binding strength on probe concentration that we observe suggests that no form of probe–probe interaction is actually playing a relevant role in our case, and thus points to probe–surface effects.
The competitive effect of probe–surface interaction can be estimated by a simple set of combined equilibrium equations:
| p·t0 = Kdiss,V·pt |
| p·s0 = KS·ps |
| p T = p + pt + ps | (6) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 3/3, with
3/3, with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≈ 3 nm being the length of the probe. From this estimate it follows that s0 ≥ 10 mM. Ignoring the surface contribution, one would write a similar set of equations as eqn (6) (without the second equation) and with an effective probe–target dissociation coefficient Kdiss,E, weakened by the competition with the surface. According to this simple model, Kdiss,E = Kdiss,V(1 + s0/KS). To obtain the factor of 100 suggested by the experiments, we would need a surface binding coefficient KS ≈ s0/100. This estimate yields KS ≥ 100 μM, a figure corresponding to a very weak interaction strength, well in the range of nonspecific binding coefficients. The fact that weak nonspecific interactions with the surface can have such a significant effect on the strong and selective DNA hybridization mechanism can thus be understood as ultimately due to the low entropic penalty associated with the adhesion of the probe to the surface to which it is already chemically connected. This description incorporates the notion that the probes are flexible and that hybridization is distributed along the whole chain, features specific to nucleic acids. Thus, in the presence of nonspecific interaction with the surface, the flexible probes can stick on it in a variety of patterns, all incompatible with the complete formation of a duplex, with which they thus compete.29 This marks a difference with protein ligand–receptor interactions occurring at a surface, which typically maintain the affinity they have in solution.
≈ 3 nm being the length of the probe. From this estimate it follows that s0 ≥ 10 mM. Ignoring the surface contribution, one would write a similar set of equations as eqn (6) (without the second equation) and with an effective probe–target dissociation coefficient Kdiss,E, weakened by the competition with the surface. According to this simple model, Kdiss,E = Kdiss,V(1 + s0/KS). To obtain the factor of 100 suggested by the experiments, we would need a surface binding coefficient KS ≈ s0/100. This estimate yields KS ≥ 100 μM, a figure corresponding to a very weak interaction strength, well in the range of nonspecific binding coefficients. The fact that weak nonspecific interactions with the surface can have such a significant effect on the strong and selective DNA hybridization mechanism can thus be understood as ultimately due to the low entropic penalty associated with the adhesion of the probe to the surface to which it is already chemically connected. This description incorporates the notion that the probes are flexible and that hybridization is distributed along the whole chain, features specific to nucleic acids. Thus, in the presence of nonspecific interaction with the surface, the flexible probes can stick on it in a variety of patterns, all incompatible with the complete formation of a duplex, with which they thus compete.29 This marks a difference with protein ligand–receptor interactions occurring at a surface, which typically maintain the affinity they have in solution.
Finally, we remark that a competition mechanism in surface binding appears to be consistent with both the lack of effects following the insertion of poly-A spacers, and with the observed kinetics. It is reasonable to expect that a competition with nonspecific binding should affect the association kinetics (kon), while leaving koff less affected.
Sensitivity of the RPI for DNA hybridization
Sensitivity represents one of the key elements for the performances of DNA detection techniques. The limit of detection given in terms of molar concentration of target in solution clearly depends on the strength of the interaction. Rather, a more relevant quantity for a surface-based method is the mass sensitivity. The minimum amount of target molecules that can be detected on the surface of the RPI system presented here was estimated considering the fluctuation of the signal. The limit of detection, corresponding to 3 times the standard deviation, is about 10 pg mm−2, which is equivalent to ∼2 × 109 molecules per mm2 or ∼2 × 106 molecules per spot for the dodecamers investigated.This value is comparable to those typically reported for surface plasmon resonance30,31 and others among the most sensitive label-free techniques.3,32
As for fluorescence-based methods, reported sensitivities are one to two orders of magnitude higher;33 however, it is often difficult to quantitatively relate fluorescence intensity to the amount of molecules actually captured on the surface,34 also for the limitations intrinsic to fluorescence emission like bleaching and quenching.35 Thus, the quantification of genetic expression levels by fluorescence requires complicated procedures, which may affect the reproducibility of the results.36 Conversely, despite the lower sensitivity, the RPI method offers a direct quantification of target concentration with minimum sample preparation and short time-to-result. Moreover, the direct access to the binding curves enables to exploit the large difference of hybridization kinetics observed between the fully complementary sequence and that presenting a central single-base mutation. Remarkably, as shown in Fig. 2a, in the target concentration range between 30 nM and 300 nM, the binding curves for the 12CM sequence are much faster and have lower amplitude than those for 12FC. This result suggests that considering the time slope of the surface binding measured by the RPI, a single-base mutation can be revealed in only a few minutes without washing steps or addition of labelling reagents.
Conclusions
We have applied the RPI, a novel label-free optical technique based on surface reflectance, to the detection and quantification of DNA oligomer hybridization. We find good sensitivity to binding events and high specificity for the presence and the position of pairing defects.The major points of this study are:
(i) The real-time access to the hybridization process provided by the RPI allows for the rapid and robust discrimination of single-nucleotide mismatches, based on both the kinetic and equilibrium properties of the binding events.
(ii) We addressed the origin of the weakening of the hybridization strength for surface-immobilized DNA, often observed in the literature. We interpret and model this effect as a result of very weak, non-specific probe–surface interactions.
The simplicity inherent to the RPI technology, combined with its multiplexing capability, can provide easy access to the investigation of DNA–DNA interactions occurring at surfaces and to the detection of specific sequences for diagnostic purposes.
Acknowledgements
We acknowledge support from MIUR grant “Building Materials with DNA bricks” (2010LKE4CC) and from EU (NAPES Project – NMP-2013-SMALL-7, Project no. 604241). We thank Solvay Solexis for kindly providing the Hyflon substrate and A. Baldo and S. Villa for experimental support. We also gratefully acknowledge useful discussions with R. Asselta, E. Paraboschi, G. Tagliabue and C. Battaglia and comments by referees which helped to improve the manuscript.Notes and references
- C. R. Calladine, H. R. Drew, B. F. Luisi, A. A. Travers, C. R. Calladine, H. R. Drew, B. F. Luisi and A. A. Travers, Understanding DNA, Elsevier, 2004 Search PubMed.
- A. N. Rao and D. W. Grainger, Biomater. Sci., 2014, 2, 436–471 RSC.
- E. Ozkumur, S. Ahn, A. Yalçin, C. A. Lopez, E. Cevik, R. J. Irani, C. DeLisi, M. Chiari and M. S. Unlü, Biosens. Bioelectron., 2010, 25, 1789–1795 CrossRef PubMed.
- W. Filipowicz, S. N. Bhattacharyya and N. Sonenberg, Nat. Rev. Genet., 2008, 9, 102–114 CrossRef CAS PubMed.
- T. Bellini, R. Cerbino and G. Zanchetta, Top. Curr. Chem., 2012, 318, 225–279 CrossRef CAS PubMed.
- F. Teles and L. Fonseca, Talanta, 2008, 77, 606–623 CrossRef CAS.
- F. Giavazzi, M. Salina, R. Cerbino, M. Bassi, D. Prosperi, E. Ceccarello, F. Damin, L. Sola, M. Rusnati, M. Chiari, B. Chini, T. Bellini and M. Buscaglia, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9350–9355 CrossRef CAS PubMed.
- F. Giavazzi, M. Salina, E. Ceccarello, A. Ilacqua, F. Damin, L. Sola, M. Chiari, B. Chini, R. Cerbino, T. Bellini and M. Buscaglia, Biosens. Bioelectron., 2014, 58, 395–402 CrossRef CAS PubMed.
- M. Salina, F. Giavazzi, R. Lanfranco, E. Ceccarello, L. Sola, M. Chiari, B. Chini, R. Cerbino, T. Bellini and M. Buscaglia, Biosens. Bioelectron., 2015, 74, 539–545 CrossRef CAS PubMed.
- M. Salina, F. Giavazzi, E. Ceccarello, F. Damin, M. Chiari, M. Ciuffo, G. P. Accotto and M. Buscaglia, Sens. Actuators, B, 2016, 223, 957–962 CrossRef CAS.
- G. Pirri, F. Damin, M. Chiari, E. Bontempi and L. E. Depero, Anal. Chem., 2004, 76, 1352–1358 CrossRef CAS PubMed.
- P. Atkins and J. de Paula, Physical Chemistry, W. H. Freeman, 2009 Search PubMed.
- J. SantaLucia, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 1460–1465 CrossRef CAS.
- R. Owczarzy, Y. You, B. G. Moreira, J. A. Manthey, L. Huang, M. A. Behlke and J. A. Walder, Biochemistry, 2004, 43, 3537–3554 CrossRef CAS PubMed.
- A. W. Peterson, L. K. Wolf and R. M. Georgiadis, J. Am. Chem. Soc., 2002, 124, 14601–14607 CrossRef CAS PubMed.
- J. SantaLucia and D. Hicks, Annu. Rev. Biophys. Biomol. Struct., 2004, 33, 415–440 CrossRef CAS PubMed.
- I. I. Cisse, H. Kim and T. Ha, Nat. Struct. Mol. Biol., 2012, 19, 623–627 CAS.
- F. Manyanga, M. T. Horne, G. P. Brewood, D. J. Fish, R. Dickman and A. S. Benight, J. Phys. Chem. B, 2009, 113, 2556–2563 CrossRef CAS PubMed.
- D. S. Dandy, P. Wu and D. W. Grainger, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 8223–8228 CrossRef CAS PubMed.
- N. F. Dupuis, E. D. Holmstrom and D. J. Nesbitt, Biophys. J., 2013, 105, 756–766 CrossRef CAS PubMed.
- R. Levicky and A. Horgan, Trends Biotechnol., 2005, 23, 143–149 CrossRef CAS PubMed.
- A. Halperin, A. Buhot and E. B. Zhulina, Biophys. J., 2005, 89, 796–811 CrossRef CAS PubMed.
- A. W. Peterson, Nucleic Acids Res., 2001, 29, 5163–5168 CrossRef CAS PubMed.
- Y. Gao, L. K. Wolf and R. M. Georgiadis, Nucleic Acids Res., 2006, 34, 3370–3377 CrossRef CAS PubMed.
- D. Irving, P. Gong and R. Levicky, J. Phys. Chem. B, 2010, 114, 7631–7640 CrossRef CAS PubMed.
- M. Kastantin and D. K. Schwartz, Small, 2013, 9, 933–941 CrossRef CAS PubMed.
- V. Chan, D. J. Graves and S. E. McKenzie, Biophys. J., 1995, 69, 2243–2255 CrossRef CAS PubMed.
- M. Shchepinov, Nucleic Acids Res., 1997, 25, 1155–1161 CrossRef CAS PubMed.
- A. B. Steel, R. L. Levicky, T. M. Herne and M. J. Tarlov, Biophys. J., 2000, 79, 975–981 CrossRef CAS PubMed.
- F. Yu, D. Yao and W. Knoll, Nucleic Acids Res., 2004, 32, e75 CrossRef PubMed.
- B. P. Nelson, T. E. Grimsrud, M. R. Liles, R. M. Goodman and R. M. Corn, Anal. Chem., 2001, 73, 1–7 CrossRef CAS PubMed.
- U. Rant, K. Arinaga, S. Scherer, E. Pringsheim, S. Fujita, N. Yokoyama, M. Tornow and G. Abstreiter, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 17364–17369 CrossRef CAS PubMed.
- T. Liebermann, W. Knoll, P. Sluka and R. Herrmann, Colloids Surf., A, 2000, 169, 337–350 CrossRef CAS.
- D. J. Fish, M. T. Horne, G. P. Brewood, J. P. Goodarzi, S. Alemayehu, A. Bhandiwad, R. P. Searles and A. S. Benight, Nucleic Acids Res., 2007, 35, 7197–7208 CrossRef CAS PubMed.
- L. Ramdas, K. Coombes, K. Baggerly, L. Abruzzo, W. E. Highsmith, T. Krogmann, S. Hamilton and W. Zhang, Genome Biol., 2001, 2 CrossRef CAS.
- S. Draghici, P. Khatri, A. C. Eklund and Z. Szallasi, Trends Genet., 2006, 22, 101–109 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Details about data analysis, effects of spotting concentration on probe surface density, and effects of polyA spacers on affinity estimates. See DOI: 10.1039/c5cp08017g |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2016 |