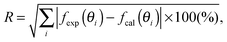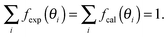Structure determination of the rutile-TiO₂(110)-(1 × 2) surface using total-reflection high-energy positron diffraction (TRHEPD)

Abstract

The exact structure of the rutile-TiO₂(110)-(1 × 2) surface, which had been under debate over the past 30 years, was investigated using the newly developed technique of total-reflection high-energy positron diffraction (TRHEPD), which is a positron counterpart of reflection high-energy electron diffraction (RHEED). The rocking-curves for the 00-spot obtained from the experimental diffraction patterns were compared to the curves for various models calculated with a full-dynamical theory. It was found that the rocking-curves matched those for a surface consisting of a Ti₂O₃ configuration, originally suggested by Onishi and Iwasawa [H. Onishi and Y. Iwasawa, Surf. Sci., 1994, 313, L783], but with a further modification of atomic positions close to the ones proposed by Wang et al. [Q. Wang, A. R. Oganov, Q. Zhu and X. F. Zhou, Phys. Rev. Lett., 2014, 113, 266101]. This result demonstrates that TRHEPD can distinguish between the existence and absence of the oxygen atoms on the topmost surface, and between the Ti atoms residing in positions at the interstitial-vertical sites and those at interstitial-horizontal sites.

---

Introduction

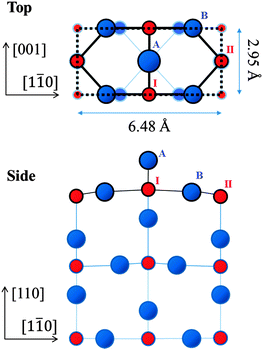
Titania (TiO₂) is a transition metal-oxide material used in a variety of applications including photo-catalysts,^1–3 metal–nanoparticle catalyst supports, gas sensors and corrosion-protective coating materials.^4–6 In these applications, knowledge of the structure of the surface is a critical factor in the understanding of the processes involved and in the appraisal of their functionality. Single-crystal TiO₂ surfaces have been studied extensively as a testing ground for molecule- and metal–nanoparticle adsorptions.^7–13 High-quality TiO₂ surfaces, obtained by mechanochemical polishing and in situ cleaning in ultra-high vacuum (UHV), have been used in the investigations above to elucidate the mechanisms of catalytic reactions on an atomic level.

Among the reconstructed rutile-TiO₂(110) surfaces, the (1 × 1) structure has been found to be the most stable.¹³ Its detailed atomic geometry has been studied intensively since the 1970s¹³ using a number of techniques such as low-energy electron diffraction (LEED),¹⁴ surface X-ray diffraction (SXRD)^15,16 and ab initio calculations with the density functional theory (DFT).^17,18Fig. 1 shows schematically the top and side views of the established (1 × 1) structure. The titanium (Ti) atoms labelled I are of six-fold coordination with oxygen (O) atoms, while those labelled II are of five-fold coordination. The protruding O atom labelled A, called the bridging oxygen, is of two-fold coordination. In addition, there are O atoms (one of which is labelled B on the diagram) of three-fold coordination; these are called in-plane oxygen atoms.

Fig. 1 Schematic top and side views of the established rutile-TiO₂(110)-(1 × 1) surface. The dotted rectangle indicates a (1 × 1) unit cell. Red and blue circles, labelled with Roman numerals and uppercase letters, represent Ti and O atoms, respectively. In the top view, Ti and O atoms at higher positions are depicted by circles with larger diameters.

It is known that the (1 × 1) structure transforms into (1 × 2) with a doubling of the periodicity along the [11̄0] direction upon high-temperature annealing in UHV. However, its detailed atomic configuration is yet to be determined. There has been much debate over the past 30 years about the precise structure of this surface, with several models proposed based on LEED observations,^19,20,23,28 scanning tunneling microscopy (STM) observations^20–22 and ab initio calculations.^21–29

The early studies interpreted the (1 × 2) structure to be one where alternate rows of the bridging oxygen (labelled A in Fig. 1) are missing from the (1 × 1) structure (missing-row model),¹⁹ as shown in Fig. 2(a). However, this model is now discounted.¹³ Onishi and Iwasawa proposed a Ti₂O₃(iv) model,²⁰ depicted in Fig. 2(b). In this model, the Ti atoms (labelled 1 and 2) reside in positions at the so-called interstitial-vertical (iv) sites.^20,23,24 They make up a double row along the [001] direction surrounded by the O atoms (labelled a-c-d and b-e-d), which form up into distorted tetrahedrons. An alternative Ti₂O₃ (Ti₂O₃(ih)) model, illustrated in Fig. 2(c), is also mentioned in ref. 24 and 28, where the Ti atoms (labelled 1 and 2) reside in positions at the interstitial-horizontal (ih) sites.²⁴ The vertical (z) coordinates of atomic positions are identical to those in the Ti₂O₃(iv) model (Fig. 2(b)). Pang et al. proposed a Ti₃O₅ model,²¹ as shown in Fig. 2(d), where all the atoms are placed in the bulk-like positions. Park et al. proposed a Ti₂O model,²² displayed in Fig. 2(e),²⁷ where the topmost Ti atoms making up a double row are of five-fold coordination. Recently, Wang et al.²⁵ investigated the reconstructions of the rutile-TiO₂(110) surface by using a global optimization method, called USPEX, which allowed for both structural and compositional variation. The stable structures they optimised include a modified Ti₂O₃(iv)-(1 × 2) configuration, as shown in Fig. 2(f). Here the vertical (z) coordinates of the atomic positions of the Ti atoms at the iv sites (labelled 1 and 2) are not the same in value; we call this the asymmetric-Ti₂O₃(iv) model.

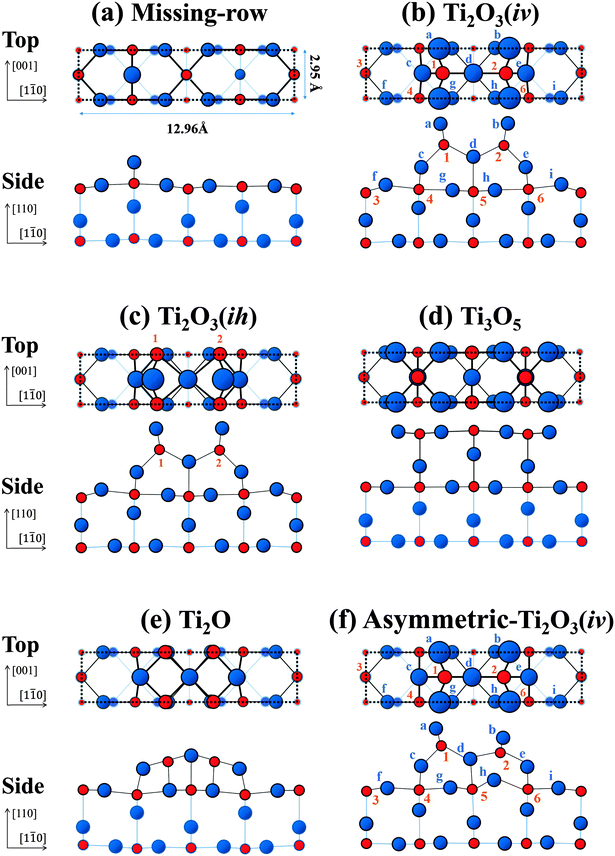Fig. 2 Schematic top and side views of structural models of the rutile-TiO₂(110)-(1 × 2) surface: (a) missing-row;²⁹ (b) Ti₂O₃(iv);²³ (c) Ti₂O₃(ih);²⁴ (d) Ti₃O₅;²¹ (e) Ti₂O;²⁷ and (f) asymmetric-Ti₂O₃(iv)²⁵ models. Each dotted rectangle indicates (1 × 2) unit cell. The red circles indicate Ti atoms, labelled with numbers in (b), (c) and (f), and the blue circles indicate O atoms, labelled with lowercase letters.

Note that the Ti atoms of the Ti₂O model (Fig. 2(e)) reside in positions at the (ih) sites, similar to the Ti₂O₃(ih) (Fig. 2(c)) models with only the topmost O atoms missing. The LEED analyses in the previous investigations did not identify this structural difference.²⁸

To determine which of these models is plausible for the structure of the rutile-TiO₂(110)-(1 × 2) surface, we have performed studies using total reflection high-energy positron diffraction (TRHEPD) which is the positron counterpart of reflection high-energy electron diffraction (RHEED).

When a positron beam impinges on a material surface at a glancing angle smaller than a certain critical value, it undergoes total-reflection because of the positive electrostatic potential inside the material.^30,31 Since the positrons do not penetrate into the bulk under this condition, the diffraction intensity depends entirely on the structure of the topmost surface. When the glancing angle is slightly larger than the critical value, the diffraction intensity depends on the immediate subsurface structure as well;³⁰ the positrons penetrate into the bulk, being refracted toward the surface, and those elastically scattered contribute to the diffraction pattern. There are no contributions in the observed diffraction patterns from the region deeper than the depth determined by the direction of the refracted beam and the mean free path for the inelastic scattering of the positrons.

This method was proposed by Ichimiya³¹ in 1992, and first demonstrated experimentally by Kawasuso and Okada³² in 1998 using a ²²Na-based positron beam. Recently a TRHEPD experiment station has been developed at the slow positron facility (SPF), KEK, where a linac-based, brightness-enhanced high-intensity beam³³ is employed. Diffraction intensities detected using this system are about two orders of magnitude greater³⁴ than those from the ²²Na-source ones, enabling more precise and efficient analyses.^30,34–36

Experimental

The details of the TRHEPD station at the KEK-SPF are described elsewhere,^33,34 with an overview of the method given here. A linac-based brightness-enhanced positron beam with an energy of 10 keV was impinged onto the samples (detailed below). The intensity of the incident beam was measured to be ∼10⁶ positrons/s, or ∼0.1 pA. A phosphor screen behind the micro-channel-plates detected the diffracted positrons. The TRHEPD patterns on the screen were recorded with a charge-coupled-device camera and the data obtained was stored on a personal computer. For the structural analysis, the glancing angle (θ) of incidence dependence of the 00-spot diffraction intensity, called the “rocking-curve”,³⁷ was extracted from a series of the TRHEPD patterns taken with an exposure time of 2.5 min each. The glancing angle was typically varied from 0.5° to ∼6° with a 0.1° step by rotating the sample.

In this study, rutile-TiO₂(110) crystals (5 × 10 × 0.5 mm³) with mechanochemically polished surfaces were provided by the Crystal Base Co., Ltd. The samples for the (1 × 1) surface were prepared in a UHV chamber (of base pressure 1 × 10⁻⁸ Pa) by a few cycles of Ar+ ion spattering (2 kV, 1 min at 5 × 10⁻⁴ Pa) at room temperature, followed by annealing with an O₂ exposure (∼875 K, 30 min at 1 × 10⁻⁶ Pa). The resulting single-domain and well-ordered (1 × 1) surfaces were ascertained using a RHEED apparatus installed in the chamber after the TRHEPD measurements. Samples were then treated with further annealing in UHV (∼1175 K, 30 min) to obtain the (1 × 2) surface. The resulting well-ordered (1 × 2) surfaces were similarly confirmed with RHEED after the TRHEPD measurements. There were no streak features noted in the diffraction patterns, which indicate that no transformations had taken place from the well-ordered (1 × 2) surface into the single-linked and/or the cross-linked (1 × 2) surface(s)^38,39 during this heat treatment.

No appreciable effects from beam irradiation or sample charge-up were observed during the TRHEPD measurements; this is attributed to the very low intensity of the positron beam (of ∼0.1 pA). It has been reported for this surface⁴⁰ that the use of a weak beam current (of nA regime) is necessary in LEED experiments to avoid damage, which has been observed when standard currents (of μA regime) were used. Since the surface sensitivity of the positron is much higher than that of the electron,⁴¹ TRHEPD measurements benefit from being able to use a much weaker beam than LEED.

For both the rutile-TiO₂(110)-(1 × 1) and the -(1 × 2) surfaces, rocking-curves were first obtained under a “one-beam” condition,³⁷ where the beam azimuthal angle was set at 23° off the [11̄0] direction. Since the low order in-plane diffractions are suppressed for the beam incidence from this direction, the variation of the 00-spot intensity is almost solely dependent on the z coordinates of the atomic positions. The reduced number of structural parameters allows a simplified and efficient analysis to be performed for the atomic configuration in the direction normal to the surface.

The discrimination between the Ti₂O₃(iv) and the Ti₂O₃(ih) models is not possible by the one-beam analysis since their atomic configurations normal to the surface are the same (see the side views of Fig. 2(b) and (c)). Many-beam measurements, where the beam azimuths were set at the [11̄0] and [001] directions, were also performed to determine the in-plane coordinates of the atoms. The 00-spot intensity in such a condition depends on in-plane coordinates of atomic positions,⁴² as well as the z coordinates which have been determined in the one-beam analysis.

Results and discussion

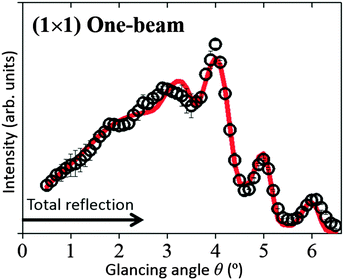
The open circles in Fig. 3 show the experimental rocking-curve obtained for the (1 × 1) surface in the one-beam condition. The experimental uncertainty of each point is shown by the bar on the circle, and indicates the root-mean-square deviation of the average of the intensity obtained experimentally over three separate runs. The rocking-curve was calculated using the structure determined by the SXRD analysis,¹⁶ adjusting the values of the parameters necessary for TRHEPD analysis,³⁷ which were: the averaged crystal potential (V_crys); the averaged imaginary potentials for Ti and O atoms via electronic excitations (ν_eTi, ν_eO); and those via phonon scattering (ν_pTi, ν_pO). The solid (red) curve in Fig. 3 shows the calculated result giving the best (lowest) value for the reliability factor (R)³⁷ of 0.9%. R is defined as
where f_exp(θ_i) and f_cal(θ_i) are the intensities of the experimental and calculated rocking-curves, respectively, normalized to

Fig. 3 The TRHEPD rocking-curve for the rutile-TiO₂(110)-(1 × 1) surface under the one-beam condition. The open circles denote experimental data. The uncertainty is shown by a bar on each circle. The red solid curve shows the calculated result.

The optimised values of the parameters are: V_crys = 19 V; ν_eTi = 1.8 V; ν_eO = 1.5 V; ν_pTi = 0.8 V; and ν_pO = 0.1 V. Further adjustments for the z coordinates of atomic positions (together with the parameter values) did not improve the R value. Thus, it has been reconfirmed by TRHEPD that the (1 × 1) structure determined by SXRD¹⁶ is valid. The critical angle for the total-reflection corresponding to the above V_crys value is 2.5° for the incident beam energy of 10 keV. The angular region for total-reflection is indicated by the line with an arrowhead in Fig. 3.

The open circles in Fig. 4(a) show the experimental data for the (1 × 2) surface in the one-beam condition. The calculated rocking-curves, using the z coordinates of the atomic positions proposed in ref. 21, 23, 25, 27 and 29 with the parameter values (V_crys, ν_eTi, ν_eO, ν_pTi and ν_pO) determined in the (1 × 1) analysis are also shown and are denoted as follows: the orange single-dotted-broken curve for the missing-row model²⁹ (Fig. 2(a)); the blue broken curve for the Ti₂O₃ models^20,23,24 (Fig. 2(b) and (c)); the purple double-dotted-broken curve for the Ti₃O₅ model²¹ (Fig. 2(d)); the green dotted curve for the Ti₂O model²⁷ (Fig. 2(e)); and the red solid curve for the asymmetric-Ti₂O₃ model²⁵ (Fig. 2(f)).

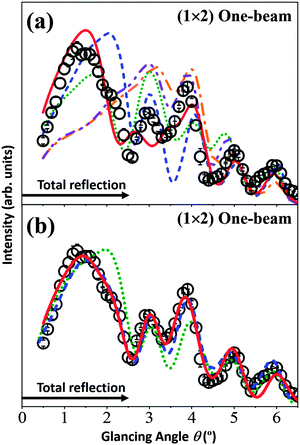Fig. 4 The TRHEPD rocking-curves for the rutile-TiO₂(110)-(1 × 2) surface under the one-beam condition. Open circles in (a) and (b) are the same experimental data. Uncertainties estimated as for the data in Fig. 3 are also shown. The single-dotted-broken (orange), broken (blue), double-dotted-broken (purple), dotted (green) and solid (red) curves are calculated results from the missing-row, the Ti₂O₃, the Ti₂O, the Ti₃O₅ and the asymmetric-Ti₂O₃ models, respectively, using the z coordinates (a) proposed in the original studies and (b) adjusted to give better R values.

Neither the missing-row (orange single-dotted-broken curve) model nor the Ti₃O₅ (purple double-dotted-broken curve) model reproduces the peak-shape in the total-reflection region around θ = 1.5°, giving poor R values of 7.1% and 6.9%, respectively. Therefore, these models were eliminated as possible candidates and are not shown further.

The Ti₂O₃ (blue broken curve), the Ti₂O (green dotted curve) and the asymmetric-Ti₂O₃ (red solid curve) models, giving R values of 4.6%, 5.3% and 3.1%, respectively, have a peak in the total-reflection region. Taking these three as the more likely contenders, their rocking-curves were recalculated to give better (smaller) R values by adjusting the z coordinates from those proposed;^23,25,27 the results are shown in Fig. 4(b) using the same key as in Fig. 4(a). The R values for the adjusted coordinates are 1.7% and 1.3% for the Ti₂O₃ and the asymmetric-Ti₂O₃ models, respectively, while 3.1% for the Ti₂O model.

The R values for the Ti₂O₃ and asymmetric-Ti₂O₃ models are small enough to be considered as good candidates for the (1 × 2) structure. That for the Ti₂O model is not small enough, reflecting the mismatch around θ = 1.5° and θ = 4.0°.

Thus, the z coordinates of the atomic positions predicted by the “Ti₂O₃” configurations, as shown in Fig. 2(b), (c) and (f), are essential for a correct (1 × 2) structural model. It is to be noted that TRHEPD has clearly distinguished between the presence (Fig. 2(b), (c) and (f)) and absence (Fig. 2(e)) of the oxygen atoms on the topmost surface. This is clear evidence for the high sensitivity of the technique to the topmost surface structure.

The adjusted z coordinates of the atomic positions for the Ti₂O₃ and the asymmetric-Ti₂O₃ models are listed under (z) in Table 1. The uncertainty of z for each atom is estimated as follows. First, the standard deviation of the R obtained, D_R, is calculated by using the R values between the rocking-curves for the individual measurement runs and that for their average (the D_R obtained was 0.6% in the present case). Then, R is calculated between the rocking-curve for the best fit structure and that for the structure where the z coordinate of the atom in question alone deviates by Δz from that of the best fit structure. The value of Δz, which makes R increase by D_R (0.6%), is assigned as the uncertainty of z for the atom in question.

Table 1 Adjusted x, y and z coordinates of atomic positions for the Ti₂O₃(iv) and the asymmetric-Ti₂O₃(iv) models. The label for each atom corresponds to those in Fig. 2(b) and (f) or Fig. 6(a) and (b). The z coordinates were determined through the one-beam analysis, while the x and y coordinates were determined through the many-beam analyses. The x = y = z = 0 is the position of the Ti(5) atom, when it is not relaxed. Displacements are given in units of Å

Coordinates of atomic positions for the Ti2O3(iv) and the asymmetric-Ti2O3(iv) models
Label	Ti2O3(iv)			Asymmetric-Ti2O3(iv)
	(x)	(y)	(z)	(x)	(y)	(z)
O(a)	−1.99 ± 0.13	1.48 ± 0.16	4.06 ± 0.07	−2.31 ± 0.16	1.48 ± 0.18	3.85 ± 0.09
O(b)	—	—	—	1.71 ± 0.16	1.48 ± 0.18	3.12 ± 0.10
O(c)	−3.37 ± 0.18	0.00 ± 0.22	1.32 ± 0.18	−3.12 ± 0.18	0.00 ± 0.26	1.40 ± 0.21
O(d)	−0.00 ± 0.28	0.00 ± 0.24	1.93 ± 0.16	−0.30 ± 0.32	0.00 ± 0.28	1.82 ± 0.17
O(e)	—	—	—	3.24 ± 0.32	0.00 ± 0.28	1.36 ± 0.22
O(f)	−5.30 ± 0.26	1.48 ± 0.27	0.03 ± 0.20	−5.22 ± 0.34	1.48 ± 0.32	−0.07 ± 0.24
O(g)	−1.25 ± 0.29	1.48 ± 0.28	0.22 ± 0.18	−1.36 ± 0.34	1.48 ± 0.32	−0.04 ± 0.25
O(h)	—	—	—	1.27 ± 0.36	1.48 ± 0.32	0.46 ± 0.23
O(i)	—	—	—	5.22 ± 0.36	1.48 ± 0.32	−0.08 ± 0.23
Ti(1)	−1.79 ± 0.06	0.00 ± 0.15	2.45 ± 0.06	−1.91 ± 0.08	0.00 ± 0.18	2.67 ± 0.07
Ti(2)	—	—	—	1.52 ± 0.10	0.00 ± 0.18	2.16 ± 0.08
Ti(3)	−6.48 ± 0.22	0.00 ± 0.24	−0.23 ± 0.14	−6.48 ± 0.26	0.00 ± 0.28	−0.11 ± 0.18
Ti(4)	−3.24 ± 0.16	1.48 ± 0.18	−0.11 ± 0.12	−3.24 ± 0.28	1.48 ± 0.28	−0.07 ± 0.19
Ti(5)	0.00 ± 0.19	0.00 ± 0.19	−0.08 ± 0.14	−0.08 ± 0.26	0.00 ± 0.26	−0.02 ± 0.20
Ti(6)	—	—	—	3.24 ± 0.28	1.48 ± 0.28	−0.06 ± 0.19

---

In order to distinguish which of the “Ti₂O₃” models (the Ti₂O₃ or the asymmetric-Ti₂O₃ with (iv) and (ih) configurations) matched the (1 × 2) structure, many-beam rocking-curves were analysed. The open circles in Fig. 5(a) show the experimental data obtained under a many-beam condition with the incident beam direction set along the [001] direction. In this condition, the rocking-curve is sensitive to the coordinates of the atomic positions perpendicular to the [001] direction⁴² (i.e. along the [11̄0] direction, as shown in Fig. 2 and 6), as well as the z ([110]) coordinates.

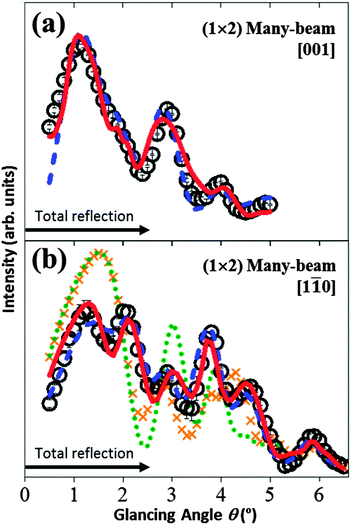Fig. 5 The TRHEPD rocking-curves for the rutile-TiO₂(110)-(1 × 2) surface under the many-beam conditions: (a) along the [001] direction; and (b) along the [11̄0] direction. Open circles denote the experimental data. Uncertainties determined as for the data in Fig. 3 are also shown. The calculated results are shown by the blue broken curves for the Ti₂O₃(iv) model, the red solid curves for the asymmetric-Ti₂O₃(iv) model, the green dotted curve for the Ti₂O₃(ih) model and the orange cross-pointed curve for the asymmetric-Ti₂O₃(ih) model. The results for the (ih) configuration are not shown in (a), because they coincide exactly with those for the corresponding (iv) configuration.

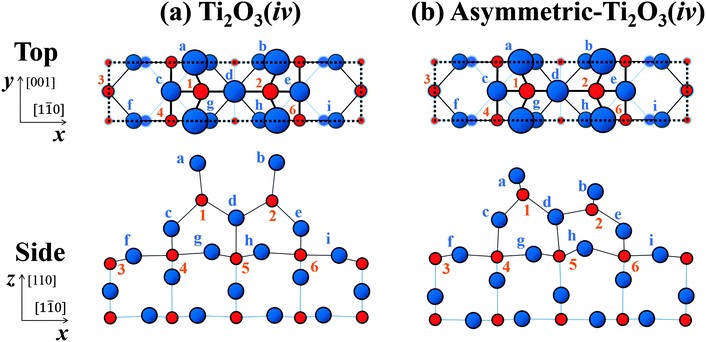Fig. 6 Schematic top and side views of the structures for (a) the Ti₂O₃(iv) and (b) the asymmetric-Ti₂O₃(iv) models after adjustment of the atomic positions. Each dotted rectangle indicates a (1 × 2) unit cell. The red circles labelled with numbers indicate Ti atoms and the blue circles labelled with lowercase letters indicate O atoms. Each is drawn in accordance with the x, y and z coordinates of atomic positions adjusted for the best (smallest) value of R within the model, as listed in Table 1.

The optimised results are shown by the blue broken curve for the Ti₂O₃(iv) model and the red solid curves for the asymmetric-Ti₂O₃(iv) model, where the in-plane coordinates along the [11̄0] direction are adjusted from those reported in ref. 23, 25, to give the best R values, while keeping the z coordinates fixed to those determined in the one-beam analysis.

The in-plane coordinates in question for those models with the respective (ih) configuration are identical to those with the (iv) configuration, since the in-plane coordinates along the [11̄0] direction are the same. The corresponding R values are 2.4% for the Ti₂O₃(iv, ih) model and 1.9% for the asymmetric-Ti₂O₃(iv, ih) models.

The open circles in Fig. 5(b) show the experimental data obtained under another many-beam condition with the incident beam direction set along the [11̄0] direction; the rocking-curve is sensitive to the coordinates of the atomic positions perpendicular to the [11̄0] direction⁴² (i.e. along the [001] and the z ([110]) directions, as shown in Fig. 2 and 6).

The calculated results are shown by the blue broken curve for the Ti₂O₃(iv) model, the red solid curve for the asymmetric-Ti₂O₃(iv) model, the green dotted curve for the Ti₂O₃(ih) model and the orange cross-pointed curve for the asymmetric-Ti₂O₃(ih) model. The corresponding R values are 1.7% for the Ti₂O₃(iv) model, 1.8% for the asymmetric-Ti₂O₃(iv) model, 6.4% for the Ti₂O₃(ih) model and 5.7% for the asymmetric-Ti₂O₃(ih) model.

From Fig. 5(b), it is clearly confirmed that the Ti atoms reside in positions at the interstitial-vertical (iv) sites,²⁴ and thus the model originally proposed by Onishi and Iwasawa²⁰ is more plausible for the (1 × 2) structure than that using the (ih) sites mentioned in ref. 24 and 28.

The schematic views of these optimised configurations are shown in Fig. 6(a) for the Ti₂O₃(iv) model and in Fig. 6(b) for the asymmetric-Ti₂O₃(iv) model. The in-plane coordinates of the atomic positions for these models optimized in the above many-beam analysis are added in Table 1: (x) along the [11̄0] direction; and (y) along the [001] direction. The uncertainties are estimated similarly to those of z coordinates.

In the case of the incident beam direction set along the [001] direction (Fig. 5(a)), the R value for the asymmetric-Ti₂O₃(iv) model, 1.9%, was better than that for the Ti₂O₃(iv), 2.4%, while the corresponding R values were almost the same in the case of the incident beam direction set along the [11̄0] direction (Fig. 5(b)). In addition, that on the one-beam analysis for the asymmetric-Ti₂O₃(iv) model, 1.3% was better than that for the Ti₂O₃(iv), 1.7% (Fig. 4(b)).

Our preliminary DFT calculation in fact shows that the Ti₂O₃(iv) model is unstable by 1.3 eV and the asymmetric-Ti₂O₃(iv) model is stable by 0.23 eV per (1 × 2) unit cell than the original Ti₂O₃(iv) model²³ because of the creation of the stable bond between the O(h) and the Ti(2) atoms. This result is consistent with the latest calculation²⁵ of Wang et al. by using the global optimization method, USPEX, allowing for both structural and compositional variation.

Thus, from the TRHEPD analysis and the theoretical results, the asymmetric-Ti₂O₃(iv) model is the best candidate for the (1 × 2) structure.

For the Ti₂O₃(iv) model in Fig. 6(a), the O(a)–Ti(1) bond length has become considerably longer than that of the O(c)–Ti(1) or the O(d)–Ti(1), which are: ∼2.2 Å for O(a)–Ti(1) (O(b)–Ti(2)); ∼1.9 Å for O(c)–Ti(1) (O(e)–Ti(2)); and ∼1.8 Å for O(d)–Ti(1) (O(d)–Ti(2)).

For the asymmetric-Ti₂O₃(iv) model, on the other hand, all the relevant bond lengths are almost the same. The O–Ti bond lengths in the higher distorted tetrahedron (labelled 1-a-c-d) which are: ∼1.9 Å for O(a)–Ti(1); ∼1.7 Å for O(c)–Ti(1); and ∼1.8 Å for O(d)–Ti(1), and those in the lower one (labelled 2-b-e-d) which are: ∼1.8 Å for O(b)–Ti(2); ∼1.9 Å for O(e)–Ti(2); and ∼1.8 Å for O(d)–Ti(2). The lower tetrahedron is more distorted than the higher one, but now closer to an octahedron. Such a local octahedral structure is often found in high valence transition metal oxides, like an orthorhombic MoO₃ structure.⁴³

This further reconstruction may have occurred owing to the general rules of the reduction of the density of state at Fermi level. We should mention the similarity in the asymmetric structure on the rutile-TiO₂(110)-(1 × 2) and those formed on the semiconductor surfaces of Si(001), Ge(001)⁴⁴ and GaAs(110) surfaces, where one may find the stabilisation of the surface band structure by the reduction of the density of state at the Fermi level.^44–46 Further theoretical work will reveal the origin of the similarity.

Conclusions

The TRHEPD rocking-curves for the rutile-TiO₂(110)-(1 × 2) surface were measured under the one-beam condition (incident beam 23° off the [11̄0] direction) and the many-beam conditions (incident beam along the [11̄0] and [001] directions). It has been revealed that the Ti₂O₃(iv) configuration, originally proposed by Onishi and Iwasawa,²⁰ is essentially correct, but some modifications as recently proposed by Wang et al.,²⁵ are necessary to explain the data. The best candidate for the structure of the rutile-TiO₂(110)-(1 × 2) surface, the asymmetric-Ti₂O₃(iv) model, is shown in Fig. 6(b) and the atomic coordinates are listed in Table 1.

Significantly, this work has clearly shown that the TRHEPD one-beam 00-spot rocking-curve can discern the existence of the oxygen atoms on the topmost surface and that the many-beam 00-spot rocking-curve can discriminate between Ti atoms residing in positions at the interstitial-vertical (iv) sites and those at interstitial-horizontal (ih) sites, demonstrating the usefulness of this technique as a surface science tool.

Acknowledgements

We thank the staff of the Photon Factory and the Accelerator Laboratory of KEK for their support in the operation of the slow positron facility under the approval of the Photon Factory Program Advisory Committee (Proposal No. 2013U002). This work has been carried out under the KEK-Hokkaido University Joint Research Program, and was partly supported by Grant-in-Aids for Scientific Research (S) No. 24221007 and for Young Scientists (B) 26800170 from JSPS. Professor A. Ichimiya and Professor Y. Horio are acknowledged for valuable comments and discussions.

Notes and references

1. A. Fujishima and K. Honda, Nature, 1972, 238, 37.
2. H. Ariga, T. Taniike, H. Morikawa, M. Tada, B. K. Min, K. Watanabe, Y. Matsumoto, S. Ikeda, K. Saiki and Y. Iwasawa, J. Am. Chem. Soc., 2009, 131, 14670.
3. A. Fujishima, K. Nakata, T. Ochiai, A. Manivannan and D. A. Tryk, Electrochem. Soc. Interface, 2013, 22, 51.
4. S. J. Tauster, S. C. Fung, R. T. K. Baker and J. A. Horsley, Science, 1981, 211, 1121.
5. B. Karunagaran, P. Uthirakumar, S. J. Chung, S. Velumani and E. K. Suh, Mater. Charact., 2007, 58, 680.
6. J. Huang and M. Haruta, in Bridging Heterogeneous and Homogeneous Catalysis: Concepts, Strategies, and Applications, ed. C. Li and Y. Liu, Wiley-VCH, Weinheim, 2014, pp. 397–424.
7. K. Asakura, in Catalysis, ed. J. J. Spivey and M. Gupta, RSC Publishing, Cambridge, 2012, vol. 24, p. 281.
8. D. W. Goodman, Catal. Lett., 2005, 99, 1.
9. K. Asakura, S. Takakusagi, H. Ariga, W.-J. Chun, S. Suzuki, Y. Koike, H. Uehara, K. Miyazaki and Y. Iwasawa, Faraday Discuss., 2013, 162, 165.
10. W.-J. Chun, K. Asakura and Y. Iwasawa, J. Phys. Chem. B, 1998, 102, 9006.
11. Y. Koike, W.-J. Chun, K. Ijima, S. Suzuki and K. Asakura, Mater. Trans., 2009, 50, 509.
12. W.-J. Chun, K. Miyazaki, N. Watanabe, Y. Koike, S. Takakusagi, K. Fujikawa, M. Nomura, Y. Iwasawa and K. Asakura, J. Phys. Chem. C, 2013, 117, 252.
13. U. Diebold, Surf. Sci. Rep., 2003, 48, 53.
14. R. Lindsay, A. Wander, A. Ernst, B. Montanari, G. Thornton and N. M. Harrison, Phys. Rev. Lett., 2005, 94, 246102.
15. G. Charlton, P. B. Howes, C. L. Nicklin, P. Steadman, J. S. G. Taylor, C. A. Muryn, S. P. Harte, J. Mercer, R. McGrath, D. Norman, T. S. Turner and G. Thornton, Phys. Rev. Lett., 1997, 78, 495.
16. G. Cabailh, X. Torrelles, R. Lindsay, O. Bikondoa, I. Joumard, J. Zegenhagen and G. Thornton, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 241403(R).
17. V. Swamya, J. Muscata, J. D. Galeb and N. M. Harrison, Surf. Sci., 2002, 504, 115.
18. V. Çelik, H. Ünal, E. Mete and Ş. Ellialtıoğlu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205113.
19. P. J. MøIIer and M.-C. Wu, Surf. Sci., 1989, 224, 265.
20. H. Onishi and Y. Iwasawa, Surf. Sci., 1994, 313, L783.
21. C. L. Pang, S. A. Haycock, H. Raza, P. W. Murray, G. Thornton, O. Gülseren, R. James and D. W. Bullett, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 1586.
22. K. T. Park, M. Pan, V. Meunier and E. W. Plummer, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245415.
23. M. Blanco-Rey, J. Abad, C. Rogero, J. Mendez, M. F. Lopez, J. A. Martin-Gago and P. L. de Andres, Phys. Rev. Lett., 2006, 96, 055502.
24. S. D. Elliott and S. P. Bates, Surf. Sci., 2001, 495, 211.
25. Q. Wang, A. R. Oganov, Q. Zhu and X. F. Zhou, Phys. Rev. Lett., 2014, 113, 266101.
26. S. D. Elliott and S. P. Bates, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 67, 035421.
27. H. Ünal, E. Mete and Ş. Ellialtıoğlu, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 115407.
28. M. Blanco-Rey, J. Abad, C. Rogero, J. Méndez, M. F. López, E. Román, J. A. Martín-Gago and P. L. de Andrés, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 081402(R).
29. K.-O. Ng and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 10544.
30. Y. Fukaya, M. Maekawa, A. Kawasuso, I. Mochizuki, K. Wada, T. Shidara, A. Ichimiya and T. Hyodo, Appl. Phys. Express, 2014, 7, 056601.
31. A. Ichimiya, Solid State Phenom., 1992, 28–29, 143.
32. A. Kawasuso and S. Okada, Phys. Rev. Lett., 1998, 81, 2695.
33. K. Wada, T. Hyodo, A. Yagishita, M. Ikeda, S. Ohsawa, T. Shidara, K. Michishio, T. Tachibana, Y. Nagashima, Y. Fukaya, M. Maekawa and A. Kawasuso, Eur. Phys. J. D, 2012, 66, 37.
34. M. Maekawa, K. Wada, Y. Fukaya, A. Kawasuso, I. Mochizuki, T. Shidara and T. Hyodo, Eur. Phys. J. D, 2014, 68, 165.
35. Y. Fukaya, I. Mochizuki, M. Maekawa, K. Wada, T. Hyodo, I. Matsuda and A. Kawasuso, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 205413.
36. I. Mochizuki, Y. Fukaya, A. Kawasuso, K. Yaji, A. Harasawa, I. Matsuda, K. Wada and T. Hyodo, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 245438.
37. A. Ichimiya, Surf. Sci., 1987, 192, L893.
38. R. A. Bennett, P. Stone, N. J. Price and M. Bowker, Phys. Rev. Lett., 1999, 82, 3831.
39. W. Busayaporn, PhD thesis, University of Manchester, 2010.
40. G. Charlton, PhD thesis, University of Manchester, 1997.
41. Y. Fukaya, A. Kawasuso and A. Ichimiya, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 193310.
42. Y. Horio, Y. Takakuwa and S. Ogawa, e-J. Surf. Sci. Nanotechnol., 2014, 12, 380.
43. L. Kihlborg, Least squares refinement of the crystal structure of molybdenum trioxide, Arkiv Kim, 1963, 21, 357.
44. D. J. Chadi, Phys. Rev. Lett., 1979, 43, 43.
45. C. Sánchez-Sánchez, M. G. Garnier, P. Aebi, M. Blanco-Rey, P. L. de Andres, J. A. Martín-Gago and M. F. López, Surf. Sci., 2013, 608, 92.
46. C. B. Duke, S. L. Richardson, A. Paton and A. Kahn, Surf. Sci., 1983, 127, L135.

---