Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nanometer-ranged attraction induced by multivalent ions between similar and dissimilar surfaces probed using an atomic force microscope (AFM)
Mohsen
Moazzami-Gudarzi
,
Gregor
Trefalt
,
Istvan
Szilagyi
,
Plinio
Maroni
and
Michal
Borkovec
*
Department of Inorganic and Analytical Chemistry, University of Geneva, Sciences II, 30 Quai Ernest-Ansermet, 1205 Geneva, Switzerland. E-mail: michal.borkovec@unige.ch; Tel: +41 22 3796405
First published on 24th February 2016
Abstract
Direct force measurements between positively charged amidine latex (AL) and negatively charged sulfate latex (SL) particles are carried out using an atomic force microscope (AFM). Forces between three different pairs, namely AL–AL, AL–SL, and SL–SL, are measured in solutions containing multivalent cationic aliphatic hexamines (N6) and in simple monovalent KCl solutions. The classical theory of Derjaguin, Landau, Verwey, and Overbeek (DLVO) can rationalize the observed force profiles very well, provided the PB equation is solved for the appropriate asymmetric electrolyte and charge regulation effects are included in the analysis. However, the DLVO description is typically valid only at distances beyond several nanometers. At shorter distances, a short-ranged non-DLVO attraction is present, which can be modeled with an exponential force profile. In KCl solutions, the range of this attraction is around 0.3 nm. In N6 solutions, the range of this attraction is about 1.0 nm in the SL–SL system, 0.6 nm in the AL–SL system, and 0.3 nm in the AL–AL system.
Introduction
Multivalent ions strongly affect interactions between charged colloidal particles in electrolyte solutions, and this aspect is essential for numerous applications, such as water purification, concrete hardening, or rheology of drilling fluids.1,2 Interactions in biological systems are equally strongly influenced by multivalent ions (e.g., phosphate, spermine, spermidine).3–5 For this reason, substantial effort is devoted to the investigation of the forces acting in such systems, both experimentally and theoretically. On the experimental side, one could recently witness the development of reliable tools capable of measuring forces between individual colloidal particles down to sub-nanometer distances. These methods include the colloidal probe technique based on the atomic force microscope (AFM)6–8 and video microscopy combined with optical or magnetic tweezers.9–12 These techniques were used to investigate the influence of multivalent ions on the forces acting between colloidal particles or inducing polyelectrolyte collapse.5,9,13 On the theoretical side, computer simulations and various approximation schemes (e.g., integral equations, density functionals) were employed to better understand the influence of electrostatic interactions on the forces acting between charged interfaces and those determining polyelectrolyte conformations in the presence of multivalent ions.3,4,14–16The classical view relies on the theory of Derjaguin, Landau, Verwey, and Overbeek (DLVO).17 This theory suggests that forces acting between colloidal particles are principally governed by van der Waals and double layer interactions, whereby the latter ones are being estimated by the Poisson–Boltzmann (PB) mean-field model. At the same time, however, one must postulate that multivalent ions specifically adsorb to the particle surface, thereby modifying the diffuse layer potential and, as a consequence, the double layer forces. The knowledge of the adsorption characteristics of these ions thus becomes essential within this approach.18
Modern theories treat electrostatic interactions between the ions beyond the mean-field PB approximation and include ion–ion correlation effects.14,15 An interesting consequence of this approach is that electrostatic interactions alone may lead to the adsorption of multivalent ions, and induce a charge reversal.16,19 However, researchers disagree whether additional specific interactions are relevant or not. Another significant prediction of such theories is that electrostatic interactions may induce additional attractive forces, which cannot be simply explained within the traditional DLVO theory.14,20 However, interaction forces between particles may further be influenced by additional effects, including finite ionic size, image charge contributions, or the shape of ions.15,21,22
The theoretical effort has been accompanied by numerous experimental studies, even though the latter activity was possibly less intense. Nevertheless, the surface force apparatus was used early on to study the influence of multivalent ions on the forces acting between mica surfaces.23 Reliable measurements involving colloidal particles and multivalent ions are relatively recent, and they mostly rely on the colloidal probe technique. Such force measurements involving a silica particle and an amino-functionalized substrate did provide evidence that multivalent counterions induce a charge reversal of the silica particle.24 These measurements further confirmed the close relation between double layer forces and ζ-potentials obtained from electrokinetic studies.16,25 Force measurements between two similar colloidal latex particles lead to similar conclusions.9,13,26 However, these experiments have further suggested that multivalent ions may induce additional attractive non-DLVO forces.13,27 While their origin could not yet be clearly established, they have an exponential distance dependence. However, so far such non-DLVO forces have not been reported in systems involving two oppositely charged surfaces in the presence of multivalent ions.
We have recently studied negatively charged colloidal particles in the presence of oligomeric aliphatic amines by electrokinetic techniques and direct force measurements.28,29 Under mildly acidic conditions, these oligoamines form multivalent ions due to partial ionization of the amino groups. In particular, pentaethylenehexamine (N6) leads to a substantial charge reversal and also induces the typical attractive non-DLVO force.28 For this reason, we decided to investigate the forces between oppositely charged particles in the presence of this oligoamine. In particular, we focus on positively charged amidine latex (AL) and negatively charged sulfate latex (SL). By quantitatively interpreting the forces acting between three different AL–AL, AL–SL, and SL–SL particle pairs, the present investigation goes substantially beyond the previous study, where only results for the SL–SL system were reported.28 By scanning a wide concentration range of N6, we are able to identify the attractive non-DLVO force in the asymmetric system for the first time.
Experimental
Materials
Positively charged amidine-terminated polystyrene latex (AL) and negatively charged sulfate-terminated polystyrene latex (SL) particles were purchased from Invitrogen. The mean diameters of AL and SL particles were 0.95 μm and 3.0 μm with relative polydispersities of 3.6% and 4.1%, respectively, as determined by the manufacturer by transmission electron microscopy. The aqueous stock particle suspensions were dialyzed until the conductivity of the surrounding solution reached that of pure water, which typically lasts about one week. A cellulose membrane having a cut-off of 50 kg mol−1 was used for both particles. In order to determine the particle concentration in the final dispersions, the light scattering intensities of dialyzed suspensions were calibrated through the ones without dialysis of known concentrations. AFM imaging was used to establish that the root-mean square roughness of both types of particles is <0.8 nm. The same particles were used in previous studies, where more details on the characterization can be found.28,30All measurements were performed in aqueous solutions prepared using Milli-Q water (Millipore) at room temperature of 21 ± 3 °C. Pentaethylenehexamine (N6) with the structural formula H2N(CH2CH2NH)4CH2CH2NH2 was purchased in basic form from Sigma-Aldrich. Stock solutions of N6 were prepared in the concentration range of 4–20 g L−1, and adjusted to pH 4.0 with HCl. The final concentration in stock solutions was measured using a total organic carbon and nitrogen analyzer (TOCV, Shimadzu). The solutions to be used in the experiments were prepared by dilution of stock solutions with a 1.0 mM KCl solution, which was also previously adjusted to pH 4.0 with HCl. N6 is not fully charged under these conditions and the precise ionic composition in solution was calculated based on the tabulated ionization constants at infinite dilution. This solution contains 1% of the species with a +3 charge, 88% with +4 charge, and 11% with +5 charge.28 The contour length of this molecule is 2.0 nm. This molecule assumes a coiled conformation in solution with a radius of gyration of <1 nm. Further experiments were performed in KCl solutions at pH 4.0.
Electrophoresis
The particle charge was studied by electrophoresis using ZetaNano ZS (Malvern Instruments, Worcestershire, UK). Particle suspensions were prepared at particle concentrations of about 80 mg L−1 in the appropriate solutions of N6 and/or KCl. The samples were equilibrated overnight and the average of at least 5 mobility measurements was taken. The electrophoretic mobility was converted to the electrokinetic potential (ζ-potential) using Henry's model. This model was found to be accurate within 10% for KCl when compared with the results of the standard electrokinetic model.17,31Electrophoresis experiments were used to demonstrate that N6 is almost entirely dissolved in solution and that the quantity adsorbed is negligible with respect to the one in the solution phase. Electrophoresis measurements were carried out at different particle concentrations for the SL system, which clearly indicate that N6 adsorbs and induces a charge reversal.28 One finds that the electrophoretic mobilities are independent of the particle concentration for the same N6 concentration, and therefore one can conclude that only a negligible fraction of N6 is adsorbed in the relevant range of particle concentrations.32 For the AL system, the electrophoretic mobility of the particles was compared for KCl and N6 solutions. The mobility values were converted to surface charge density using the standard electrokinetic model combined with the PB model and plotted versus the ionic strength. For the N6 solutions, the ionic strength was calculated by including the appropriate distribution of charged species discussed above. The data for both systems collapse, which suggests that the adsorption of N6 to AL particles is negligible.
Direct force measurements
Forces between a pair of latex particles were measured with the multiparticle colloidal probe technique. A closed-loop AFM (MFP-3D, Asylum Research) mounted on an inverted optical microscope (IX70, Olympus) was used. The glass plate fitting the bottom of the AFM fluid cell was cleaned in piranha solution consisting of a mixture of 98% H2SO4 and 30% H2O2 in a volumetric ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for 2 h. Subsequently, the plate was washed with pure water, dried in a stream of nitrogen, and treated for 20 min in an air-plasma (PDC-32G, Harrick, New York). The plate was finally silanized overnight in an evacuated container with hexamethyldisilazane (Alfa Aesar), and rinsed with pure water afterwards. A tipless cantilever was cleaned using the plasma cleaner and silanized in the same fashion, except that the silanization time was reduced to 2–3 h.
1 for 2 h. Subsequently, the plate was washed with pure water, dried in a stream of nitrogen, and treated for 20 min in an air-plasma (PDC-32G, Harrick, New York). The plate was finally silanized overnight in an evacuated container with hexamethyldisilazane (Alfa Aesar), and rinsed with pure water afterwards. A tipless cantilever was cleaned using the plasma cleaner and silanized in the same fashion, except that the silanization time was reduced to 2–3 h.
The silanized glass plate and the cantilever were then mounted in the AFM fluid cell, and a Teflon spacer was introduced to avoid mixing of the two types of latex particle suspensions during deposition. Colloidal suspensions of AL and SL at a particle concentration of about 100 mg L−1 were prepared and adjusted to pH 4.0. Initially, the AL suspension was injected into the cell on the left hand side of the spacer and left to deposit for about 1 h. The cell was then thoroughly flushed with 1.0 mM KCl solution of pH 4.0. Subsequently, the SL suspension was injected into the cell on the right hand side of the spacer and left to deposit for another hour, and the cell was flushed with the 1.0 mM KCl solution again. Finally, the spacer was removed and the cell was amply flushed with KCl or N6 solutions of the appropriate concentration, and left to equilibrate for at least 20 min.
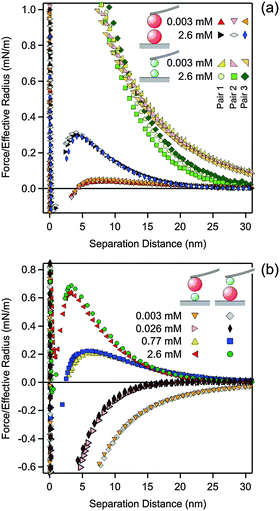
To perform the force measurements, the functionalized cantilever was approached to the substrate, and one particle was picked up by pressing the cantilever against the substrate. The AL and SL particles could be easily distinguished due to the different size. Once one of the particles was picked up, it was centered above another particle by observing the interference fringes using an optical microscope. Centering could be achieved with a lateral precision of about 50 nm. After aligning the particles, vertical approach–retraction cycles were recorded with a sampling rate of 5 kHz. The approach velocity was 500 nm s−1 and a cycle frequency of 0.5 Hz was used. For each particle pair, at least 100 cycles were recorded. The contact point was determined from the onset of the constant compliance region with a precision of about 0.5 nm. This region was perfectly linear, which confirms that the deformation of the latex particles is negligible in the contact region. The cantilever deflection was converted to forces by Hook's law with the spring constant of the cantilever. This constant was obtained from the frequency response of the cantilever and its lateral dimensions as proposed by Sader et al.33 The resulting values were about 0.1–0.4 N m−1 and were within 20% of the values obtained by the thermal noise method.7 The force profiles were obtained by down-sampling of the traces to 3 kHz and averaging the approach parts of the different cycles, resulting in a force resolution of about 0.5 pN. For better graphical display, the final force curves were further averaged in distance bins of 0.5 nm. At least 3 particle pairs were examined, and for these pairs the force curves were typically reproducible within 10%, see Fig. 1a. Within the same solution, the three different types of particle pairs could be realized in sequence, namely AL–AL or SL–SL in the two symmetric geometries (similar surfaces) and AL–SL in the asymmetric geometry (dissimilar surfaces). We have also compared results measured in two different geometries. First, an AL particle was attached to the cantilever and measured against a SL particle attached to the substrate. Second, a SL particle was attached to the cantilever and measured against an AL particle attached to the substrate. Both geometries gave very similar results as illustrated in Fig. 1b and they were both used to measure the force profiles in the asymmetric AL–SL systems.
Data analysis
The force profiles were interpreted in terms of a modified DLVO theory. The measured force profile was fitted to the following form:| F = FvdW + Fdl + Fatt | (1) |
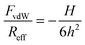 | (2) |
| Reff−1 = Rα−1 + Rβ−1 | (3) |
The double layer force was evaluated from the PB theory in the plate–plate geometry numerically. This theory describes the electrostatic potential profile ψ(x) as a function of the position x, whereby the two surfaces are located at x = ±h/2. The potential profile satisfied the PB equation
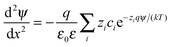 | (4) |
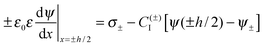 | (5) |
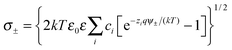 | (6) |
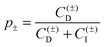 | (7) |
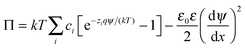 | (8) |
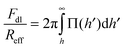 | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte, while in the N6 system for a respective mixture of 1
1 electrolyte, while in the N6 system for a respective mixture of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3
1, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 4
1, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 5
1, and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes. Displacement of the plane of origin of the double-layer with respect to the contact point by distances below 1 nm has small effects on the calculated force profiles in the concentration range considered. More details on the numerical procedure can be found elsewhere.34
1 electrolytes. Displacement of the plane of origin of the double-layer with respect to the contact point by distances below 1 nm has small effects on the calculated force profiles in the concentration range considered. More details on the numerical procedure can be found elsewhere.34
The short-ranged attractive non-DLVO force is modeled with a simple exponential profile
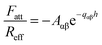 | (10) |
Results and discussion
We present direct force measurements between similar and dissimilar particle surfaces in the same electrolyte solutions carried out using the atomic force microscope (AFM). In particular, we study interactions between micrometer-sized positively charged amidine latex (AL) particles and negatively charged sulfate latex (SL) particles in the symmetric AL–AL and SL–SL as well as asymmetric AL–SL geometries. For brevity, we will sometimes denote the AL particles by a + sign and the SL particles by a − sign. This sign refers to the charge of the bare particle. These particles are mainly studied in solutions containing the aliphatic hexamine, denoted as N6, which adsorbs to the SL particles in a flat conformation and induces charge reversal.28 The three combinations ++, +−, and −− are realized in various electrolyte solutions in the same fluid cell. All experiments are carried out at pH 4.0, whereby N6 predominantly forms tetravalent cations. These experiments are further compared with those in monovalent KCl solutions.Monovalent salt solutions
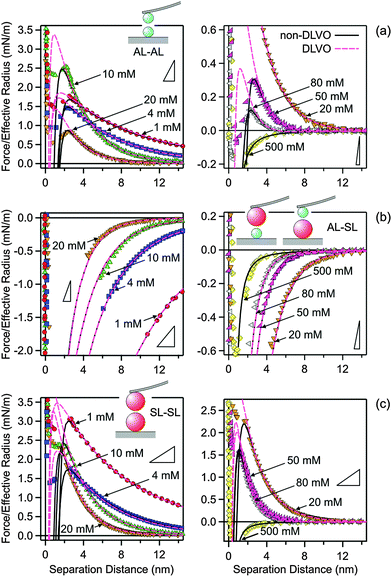
The measured force profiles in KCl solutions are shown in Fig. 2. The left column shows the measurements at low salt concentrations, while the right column shows the measurements at higher concentrations. The top row (Fig. 2a) shows the results for the symmetric AL–AL system, the middle row (Fig. 2b) for the asymmetric AL–SL system, and the bottom row (Fig. 2c) for the second symmetric SL–SL system. At high salt concentrations, the forces are attractive and very similar for all the different pairs studied. These attractive forces originate from van der Waals interactions. At lower salt concentrations, the forces are repulsive for the symmetric AL–AL and SL–SL systems, while they are attractive for the asymmetric AL–SL system. This behavior is typical for double-layer forces. The interacting particles bear the same charge for the symmetric systems, leading to electrostatic repulsion. For the asymmetric systems, the particles are oppositely charged, leading to electrostatic attraction. With increasing salt concentration, the electrostatic interactions are progressively screened, and their contribution disappears at higher concentrations, typically above 100 mM. This behavior is in agreement with DLVO theory. When the forces become strongly attractive, the force profile may not be accessible due to the mechanical jump-in instability of the cantilever. The triangles in Fig. 2 indicate the critical slopes that are given by the spring constant of the cantilever.The agreement with DLVO theory is only qualitative, however. Quantitative data analysis reveals that additional non-DLVO contributions are important at small separations, and they can be described with an attractive exponential force law given by eqn (10). Best fits of the experimental force profiles with DLVO theory including this non-DLVO contribution are shown as solid lines in Fig. 2. For comparison, results of the DLVO theory without additional attractive contributions are also shown as dashed lines. One observes that DLVO theory is insufficient to model the profiles at intermediate salt concentrations or at smaller distances, especially close to the jump-in occurring around 2 nm.
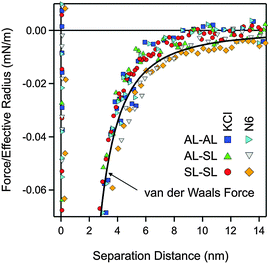
The quantitative data analysis was carried out according to the following strategy. Initially, van der Waals forces were studied at high salt concentrations, namely in 500 mM KCl solutions. These forces can be only reliably measured under these conditions, since otherwise they are masked by the repulsive double-layer forces. Under these conditions, the double layer interactions are fully screened. The results for the symmetric AL–AL and SL–SL, and the asymmetric AL–SL geometries are shown in Fig. 3. One observes that the data for the three systems coincide within experimental error. The distance dependence can be rather well described using eqn (2) with the common Hamaker constant of H = (3.5 ± 0.1) × 10−21 J. At larger distances, the experimentally observed force is somewhat weaker than the calculated one, probably due to retardation effects. The reported Hamaker constant is in line with previous studies of the same particles.28,30 The value is substantially smaller than the non-retarded value of 14.0 × 10−21 J calculated from the dielectric spectra of polystyrene and water from the Lifshitz theory.17,36 This discrepancy is caused by the combined effect of roughness and retardation, which has been discussed in detail for a similar type of latex particles elsewhere.37 These effects basically eliminate the salt dependence of the Hamaker constant. They further result in very similar Hamaker constants for the SL and AL particles, probably by coincidence.
Once the Hamaker constant was determined, the force profiles shown in Fig. 2 were quantified in three subsequent steps. In the first step, the force profiles involving the symmetric AL–AL pairs were analyzed (Fig. 2a). Initially, the DLVO theory was used, whereby the double layer forces are calculated using the non-linear PB equation for a simple electrolyte. This description is capable of quantifying the force profiles at larger distances, and yields good estimates of the surface properties, namely the diffuse layer potential and the regulation parameter. At shorter distances, however, the calculated force profiles are more repulsive than the experimental ones. This deficiency can be remedied by adding the exponential attractive non-DLVO contribution given by eqn (10) to the profile. With this modification, the resulting profiles describe the position of the jump-in reasonably well. At smaller distances than the position of the jump-in, the experimental force profiles become unreliable due to the existing mechanical instability and contributions from hydrodynamic interactions. By performing a least-squares fit with the model given by eqn (1), one obtains four different parameters, namely the diffuse layer potential ψ+, the regulation parameter p+, as well as the range and the amplitude of the non-DLVO force, namely q++−1 and A++. Among the fitted parameters, the regulation parameter and the range of the non-DLVO force remained relatively independent of the concentration, leading to the values p+ = 0.41 ± 0.03 and q++−1 = 0.35 ± 0.02 nm. Therefore, the AL–AL force profiles were refitted by keeping these quantities fixed to their average values, whereby the diffuse layer potential ψ+ and the amplitude of the non-DLVO force A++ were adjusted. During these and all subsequent fitting procedures, the Hamaker constant was fixed to H = 3.5 × 10−21 J and the salt concentration to the respective nominal value. The diffuse layer potential ψ+ was assumed to be positive, since ionized amidine groups bear a positive charge.
In the next step, the asymmetric AL–SL force profiles were analyzed (Fig. 2b). In this case, DLVO theory is sufficient to quantify the data. Thereby, the diffuse layer potential ψ+ and the regulation parameter p+ of the AL particle were fixed to the previously determined values for the AL–AL pairs, while the corresponding quantities were adjusted for the SL particles, namely ψ− and p−. Again, the regulation parameter shows no clear trends with the concentration, and is p− = 0.36 ± 0.07. This quantity was therefore fixed to the average value, and the entire series of force profiles was refitted, which yields the diffuse layer potential ψ− of the SL particles. The negative sign of the diffuse layer potential of the SL particles follows from the force profiles in the asymmetric setting unambiguously, since the AL particles are positively charged. These experimental data provide no evidence of an additional non-DLVO attraction, but we will come back to this point later. An earlier study reported a regulation parameter of 0.41 ± 0.03 for the same SL particles in the same electrolyte.28 This value is in good agreement with the presently reported one.
In the last step, the symmetric SL–SL force profiles were quantified (Fig. 2c). At this point, the surface properties of the SL particles, namely the diffuse layer potential ψ− and the regulation parameter p−, are known from the fit of the asymmetric situation, and it was comforting to see that DLVO theory predicts the force profiles at larger distances very well. At shorter distances, however, the forces are again more attractive than what is suggested by the DLVO theory, and this shortcoming can be again remedied by adding an attractive exponential non-DLVO contribution given by eqn (10). Therefore, the fitting of the SL–SL force profiles only involves the determination of the range and amplitude of this interaction, namely q−−−1 and A−−. The range was again relatively independent of the concentration, and yields an average value of q−−−1 = 0.32 ± 0.05 nm. The force profiles could be described well by fixing this parameter to the latter value and by fitting the amplitude A−− only.
The resulting parameters obtained from these fits are summarized in Table 1 and Fig. 4. Table 1 includes the parameters which can be assumed to be independent of the concentration, while Fig. 4 reports the concentration dependent ones.
| Solution | Regulation parameter | Range of non-DLVO exponential interaction | |||
|---|---|---|---|---|---|
| p + AL | p − SL | q ++ −1 (nm) AL–AL | q +− −1 (nm) AL–SL | q −− −1 (nm) SL–SL | |
| KCl | 0.41 ± 0.03 | 0.36 ± 0.07 | 0.35 ± 0.02 | — | 0.32 ± 0.05 |
| N6 | 0.38 ± 0.02 | Fig. 7b | 0.34 ± 0.02 | 0.56 ± 0.03 | 1.0 ± 0.1 |
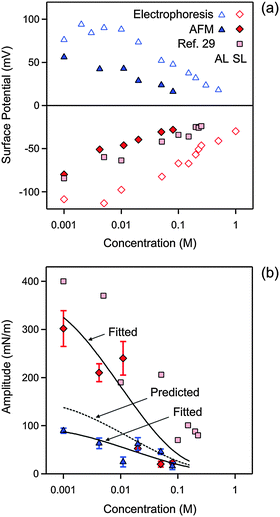 | ||
| Fig. 4 Concentration dependence of parameters obtained by fitting the experimental force profile with DLVO theory including the non-DLVO attraction in KCl solutions at pH 4.0. (a) Diffuse layer potential obtained from the present AFM measurements compared with the electrokinetic potential (ζ-potential) from electrophoresis. (b) Amplitude of the non-DLVO attraction. The two solid lines are empirical fitting functions of the amplitudes A++ and A−−, and the dotted line in between is the prediction for A+− using eqn (12). The corresponding data obtained from the symmetric SL–SL system in an earlier study28 are also shown. Table 1 shows the fitted parameters that are concentration independent. The error bars are indicated in (b), but they are comparable to the size of the data points in (a). | ||
First focus on the fitted diffuse layer potentials shown in Fig. 4a. The magnitude of the diffuse layer potential decreases with increasing salt concentration. This trend is expected on the basis of PB theory.17 The reported potentials for the SL particles compare well with a previous study, where these values were determined from the symmetric SL–SL particle pairs.28 The electrokinetic potential (ζ-potential) for the two types of particles is equally shown for comparison. These measurements confirm the signs of the potentials, as well as the overall trends. However, the magnitude of the electrokinetic potentials is substantially larger than the ones determined from the AFM experiment. These discrepancies are likely related to surface charge heterogeneities of the latex particles.38 These heterogeneities could induce an additional rotational motion of the particles, which would lead to an enhancement of the electrophoretic mobility.39 Similar discrepancies between diffuse layer potentials measured by AFM and electrophoresis were reported earlier in other latex particle systems.37,40 We suspect that AFM measurements provide a more reliable estimate of the diffuse layer potential, since the interaction force represents an equilibrium quantity, the entire profile is fitted to the model, and the consistency of the measured potentials can be tested independently. On the other hand, electrokinetic techniques require the interpretation of a dynamic quantity and provide only a one point measurement.31
The diffuse layer potentials of the SL particles were obtained from the force profiles in two different ways, namely from the analysis of the AL–AL and AL–SL systems as shown here, and from the symmetric SL–SL system discussed elsewhere28 (Fig. 4a). These two estimates agree very well, and this agreement confirms the self-consistency of the analysis of the force profiles in terms of DLVO theory. Good agreement between diffuse layer potentials obtained from a similar analysis of force profiles in symmetric and asymmetric systems was also reported in other systems.34 For this reason, we suspect that the AFM potentials represent more reliable estimates of the diffuse layer potential than the ones obtained from electrokinetics.
The nature of the attractive non-DLVO force, which can be described with an exponential law, resembles results from previous reports.13,27,35,40 In particular, an earlier study also analyzed short ranged forces between the same SL particles in the KCl electrolyte with an exponential force profile.28 That study reports the same range as reported here, and the measured amplitudes are very similar to the ones given here. The presently observed range is fully consistent with measurements using the surface force apparatus and theoretical calculations.35
Fig. 5 illustrates how the boundary conditions used in the PB calculations affect the force profiles. The respective parameters are summarized in Table 2. Focus on the leftmost column, where the force profiles in 4.0 mM KCl solution are shown. The other columns will be discussed later. The solid lines correspond to the results of DLVO theory including the non-DLVO attraction, while the dashed ones to DLVO theory alone. The underlying PB calculations rely on the CR approximation. The grey regions are delimited with the respective results for CC and CP boundary conditions that also include the non-DLVO attraction. The CC conditions lead to the most repulsive profile, while charge regulation makes the profile less repulsive. One observes that the nature of the boundary conditions is moderately important in all three different geometries.
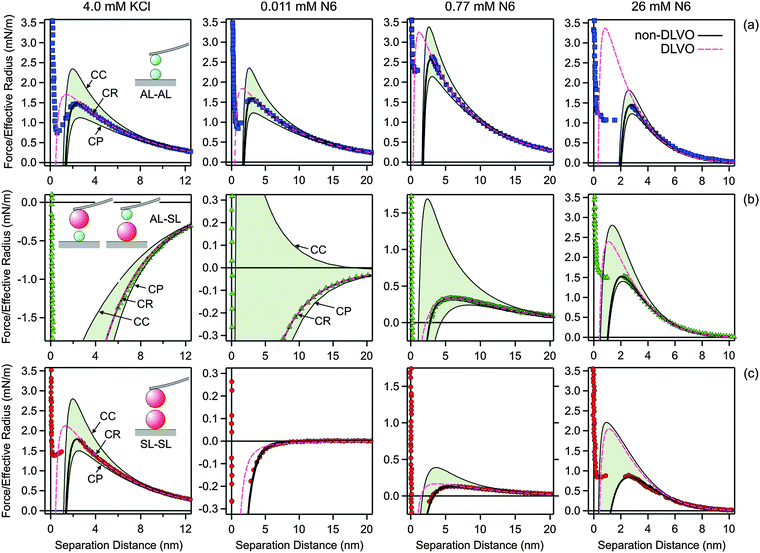 | ||
| Fig. 5 Comparison of selected experimental force profiles involving amidine latex (AL) and sulfate latex particles (SL) with DLVO theory with CR approximation and the one where the non-DLVO attraction is included. The grey regions are delimited by the corresponding profiles including the non-DLVO attraction with CC and CP conditions. The columns refer to different systems and concentration. The leftmost column 1 is for 4.0 mM KCl solution, while the remaining columns refer to N6 solutions with concentrations of the amino groups of 0.011 mM in column 2, 0.77 mM in column 3, and 26 mM in the rightmost column 4. The parameters used for calculations are given in Table 2. (a) AL–AL, (b) AL–SL, and (c) SL–SL. | ||
| Quantity | Symbol | KCl 4.0 mM | N6 0.011 mMa | N6 0.77 mMa | N6 26 mMa |
|---|---|---|---|---|---|
| a Concentration of amino groups. b The range of the interaction qαβ−1 is given in Table 1. | |||||
| Diffuse layer potential | ψ + (mV) | +44 | +56 | +68 | +41 |
| ψ − (mV) | −50 | −3.5 | +19 | +38 | |
| Regulation parameter | p + | 0.41 | 0.38 | 0.38 | 0.38 |
| p − | 0.36 | 0.13 | 0.08 | 0 | |
| Amplitude of non-DLVO interactionb | A ++ (mN m−1) | 65 | 380 | 480 | 800 |
| A +− (mN m−1) | 103 | 5.4 | 7.0 | 15 | |
| A −− (mN m−1) | 240 | 2.7 | 3.5 | 7.2 | |
Multivalent salt solutions
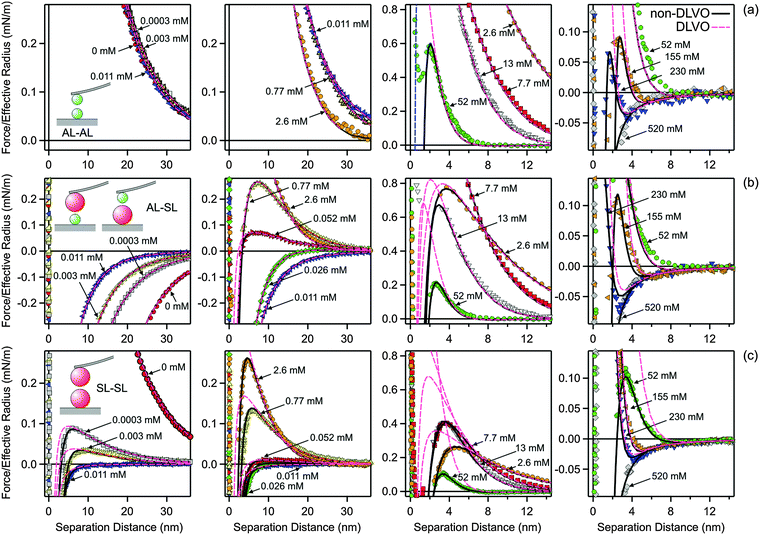
Forces between these particles in the presence of multivalent N6 cations are more complex due to the charge reversal of the SL particles.28,29 The force profiles measured at pH 4.0 and in the presence of 1.0 mM KCl for different N6 concentrations are summarized in Fig. 6. Again, the profiles for the different pairs of particles are given in different rows, namely AL–AL in the top row (Fig. 6a), AL–SL in the middle row (Fig. 6b), and SL–SL in the bottom row (Fig. 6c). The columns summarize increasing concentrations of N6 (from left to right). The concentrations in the N6 system always refer to the molar concentration of the amino groups. At very high concentrations, the forces are attractive for all different pairs, since they are dominated by van der Waals forces. As illustrated in Fig. 3, these attractive forces are identical to the ones observed in the KCl system within experimental error.For the symmetric AL–AL system (top row), the repulsive forces at lower N6 concentrations are dominated by double layer interactions between the positively charged particles. The situation resembles the one in monovalent KCl solution. This behavior can be understood due to the multivalent nature of the N6 cations. Highly charged co-ions are expelled from the proximity of the positively charged surface, and therefore they play only a minor role.
On the other hand, the forces acting between the AL–SL and SL–SL pairs in the presence of N6 oligomers are very different from the ones in monovalent salt solutions. This difference is due to the charge reversal induced by the adsorption of the N6 cations to the negatively charged SL particles. This charge reversal can be most clearly seen in the asymmetric AL–SL system. At low N6 concentrations, double layer interactions between the oppositely charged surfaces of the AL and SL particles induce attractive forces. As the N6 concentration is increased, the forces become repulsive. These repulsive forces are again caused by double layer interactions, but now the SL particles become positively charged. This charge reversal is caused by the strong adsorption of the multivalent N6 cations to the SL particle surface. With increasing N6 concentration, this repulsion becomes stronger due to progressive adsorption, but at even higher concentrations, it weakens again due to screening. At very high concentrations, the double layer interactions are completely screened, and the forces become attractive due to van der Waals interactions (Fig. 3). At the charge reversal point, which occurs at around 0.011 mM, the forces are more attractive, but mainly due to charge regulation effects.
The forces between SL–SL pairs are also strongly influenced by charge reversal. At low concentrations, the interactions are dominated by repulsive double layer forces, since the SL particles are negatively charged. When the concentration is increased, the surface undergoes a charge reversal at 0.011 mM. At the charge reversal point, the forces are attractive, as they are dominated by van der Waals interactions. At higher concentration, the surfaces become positively charged, and they repel again through double layer forces. When the concentration is increased further, the double layer forces are weakened by ionic screening, until they disappear completely and the forces become attractive again due to the dominance of van der Waals interactions.
While this mechanism is in line with DLVO theory, a quantitative comparison demonstrates that this theory cannot fully rationalize the data, see Fig. 6. This comparison again reveals the presence of an additional non-DLVO attraction, which can be modeled with an exponential force profile given by eqn (10). A similar fitting strategy as for the monovalent electrolyte was used. However, the double layer forces must be calculated using the non-linear PB equation for the appropriate electrolyte mixture, which includes multivalent cations as well as monovalent cations and anions. The ionic composition was kept fixed during the calculations. The same Hamaker constant as previously determined in the monovalent system was used. The model parameters were determined as follows. In a first step, the forces between AL–AL particles were quantified. Thereby, the surface properties, namely the diffuse layer potential ψ+ and the regulation parameter p+, as well as the parameters of the non-DLVO force, namely the range q++−1 and the amplitude A++, were fitted. The regulation parameter and the range showed no clear trends, with average values p+ = 0.38 ± 0.02 and q++−1 = 0.34 ± 0.02 nm. The profiles could be successfully fitted by fixing these parameters to their average values, and only adjusting ψ+ and A++. In a second step, the forces between AL–SL particles were investigated. Thereby, the surface parameters of the AL particles were fixed to the previously determined values. Therefore, the fitting process involved the surface properties ψ− and p−, and the parameters of the non-DLVO force q+−−1 and A+−. Within this series, the range q+−−1 remained approximately constant, and could be fixed to its average value of q+−−1 = 0.56 ± 0.03 nm. The remaining parameters, namely ψ−, p−, and A+−, had to be adjusted for each profile. In contrast to the monovalent situation, the regulation parameter p− could not be kept fixed within the concentration series, but could be constrained to p− > 0. In a third step, the forces between SL–SL were analyzed. The surface properties of the SL particles, namely ψ− and p−, were taken from the asymmetric system, and the fitting involved only the parameters of the short-ranged exponential non-DLVO force, namely its range q−−−1 and the amplitude A−−. The range could be again fixed to its average value of q−−−1 = 1.0 ± 0.1 nm, and the entire series could be rationalized with a single adjustable parameter, namely the amplitude A−−.
The resulting parameters are summarized in Table 1 and Fig. 7 and 8. Table 1 displays the parameters that remained fixed within the series, while the figures illustrate parameters that vary with the N6 concentration.
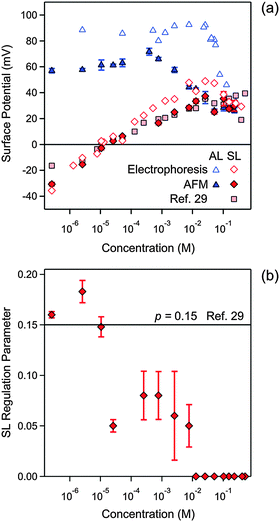 | ||
| Fig. 7 Concentration dependence of parameters obtained by fitting the experimental force profile with DLVO theory including the non-DLVO attraction in N6 solutions at pH 4.0. The concentration refers to molar concentration of the amino groups. (a) Diffuse layer potential obtained from the present AFM measurements compared with the electrokinetic potential (ζ-potential) from electrophoresis (b) and regulation parameter. The corresponding data obtained from the symmetric SL–SL system in an earlier study28 are also shown. Table 1 shows the fitted parameters that are concentration independent. The error bars are indicated in (b), but they are comparable to the size of the data points in (a). | ||
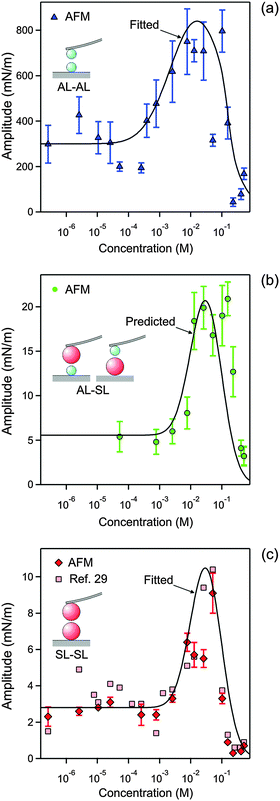 | ||
| Fig. 8 Concentration dependence of the amplitude of the non-DLVO attraction in N6 solutions at pH 4.0 obtained by fitting the force profiles measured with the AFM. The concentration refers to molar concentration of the amino groups. (a) AL–AL, (b) AL–SL, and (c) SL–SL. The lines in (a and c) are empirical fitting functions of the amplitudes A++ and A−−, and the one in (b) is the prediction of A+− with eqn (12). The corresponding data obtained from the symmetric SL–SL system in an earlier study28 are also shown in (c). Table 1 shows the fitted parameters that are concentration independent. | ||
Fig. 7 summarizes the concentration dependence of the surface properties. The diffuse layer potentials of the AL and SL particles are shown in Fig. 7a. The diffuse layer potentials obtained from the force measurements are compared with the electrokinetic potentials (ζ-potential) measured by electrophoresis. These values agree very well for the SL particles, but the electrokinetic potentials are larger for the AL particles. A similar disagreement was observed for the monovalent electrolyte (Fig. 4a) and for other latex particles.37,40 The diffuse layer potential of AL particles is positive, and goes through a weak maximum as a function of concentration. At high concentrations, this behavior resembles the monovalent case, and is characteristic of a surface, which interacts weakly with the ions present. For the SL particles, however, the potential strongly increases due to adsorption of the multivalent cationic N6 species. The diffuse layer potential vanishes at 0.011 mM, increases further, and after passing through a weak maximum it decreases again. The electrokinetic potentials now agree rather well with the diffuse layer potentials obtained by AFM. Such a charge reversal is characteristic of multivalent ions adsorbing to oppositely charged surfaces, and it was reported in similar systems earlier.24,28–30
The diffuse layer potentials of the SL particles obtained from the present analysis of the AL–AL and AL–SL systems compare favorably with the ones obtained from the symmetric SL–SL system as discussed elsewhere (Fig. 7a).28 This agreement again provides solid evidence of the self-consistency of the present DLVO analysis of the force profiles. In this situation, the diffuse layer potentials obtained from the AFM experiments also agree well with the electrokinetic ζ-potentials. The latter agreement probably results from the smoothing out of the surface charge heterogeneities through the adsorption of N6 oligomers.
In the presence of N6, the regulation parameter decreases with concentration for the SL particles, see Fig. 7b. Such a decrease is unusual, since in various other situations, the force profiles were compatible with a regulation parameter that was independent of concentration.30,41 A constant regulation parameter is also consistent with the force profiles in the present system, in particular, for monovalent salt solutions, and for the AL particles in the presence of N6 (Table 1). A previous study reported a concentration independent regulation parameter p− = 0.15 in the same SL–SL system containing N6 cations.28 While a constant regulation parameter is consistent with the data for the symmetric SL–SL system, but when this parameter is calculated from the asymmetric AL–SL system, one observes the decrease shown in Fig. 7b. This discrepancy illustrates the difficulties in estimating regulation parameters reliably, especially from data obtained in symmetric systems near a charge reversal.
The resulting parameters for the exponential non-DLVO attractive force are given in Table 1 and Fig. 8. For the AL–SL pairs, this additional force can only be reliably quantified for sufficiently high concentrations, roughly above 0.05 mM. The observed range for the AL–AL system of q++−1 = 0.34 ± 0.02 nm is well comparable with the values measured in the KCl electrolyte. For the SL–SL system, however, the range is substantially larger, namely q−−−1 = 1.0 ± 0.1 nm. For the AL–SL system, the range lies in between. Previous force measurements across electrolyte solutions containing multivalent counterions in symmetric systems indicate the presence of an additional non-DLVO attraction with a range of a few nm.13,27,28
The amplitudes determined for the AL–AL, AL–SL, and SL–SL pairs follow similar trends (Fig. 8). This amplitude remains relatively constant at low N6 concentrations, but then goes through a maximum located around 30 mM, and finally decreases sharply to vanishingly small values. The magnitude of the amplitude decreases with increasing range of attraction, namely in the sequence AL–AL, AL–SL, and SL–SL. The amplitudes for the short-ranged exponential attraction were equally extracted from the SL–SL data in a previous study, albeit assuming a constant regulation parameter.28 These values are also presented in Fig. 8c, and they agree with the present results very well. Previous measurements with latex particles in the presence of multivalent ions also report comparable strength of the short-ranged attraction and amplitudes passing through a maximum with increasing salt concentrations.13
Fig. 5 illustrates the major influence of boundary conditions in the PB calculations on the force profiles for the system containing N6. The parameters used in the calculations are given in Table 2. The column depicts force profiles for three different concentrations, namely 0.011 mM (column 2), 0.77 mM (column 3), and 26 mM (rightmost column 4). The shaded regions are again delimited with the results for CC and CP boundary conditions. The concentration of 0.011 mM reflects the charge neutralization point of the SL particles (Fig. 5, column 2). The forces in the AL–AL system are controlled by repulsive double layer forces, since these particles are highly charged. In this situation, the boundary conditions do play some role. For the SL–SL system, the forces are attractive, since the particles are neutral and their interaction is dominated by van der Waals forces and additional attractive non-DLVO forces. Since the double layer forces are negligible, the boundary conditions have no influence. The forces in the AL–SL system are attractive, but they are again dominated by double layer forces. In this case, however, boundary conditions are extremely important, since CC conditions lead to repulsion, while CP conditions to attraction. Therefore, the force profiles are highly sensitive to the regulation parameter of the SL particles, and this sensitivity permits that its value can be accurately extracted from such force profiles. The importance of the boundary conditions in similar asymmetric systems was also pointed out recently.26,30,41 The presence of an additional non-DLVO attraction is clearly evident in the SL–SL systems, since the observed attractive force is substantially stronger than the van der Waals force. Similar enhancement of the attraction by multivalent counterions at the charge neutralization point was also reported in other systems.27,28,30 This attractive force cannot be fitted with eqn (2) alone, but rather a superposition of eqn (2) and (10) is needed. For the concentration of 0.77 mM (Fig. 5, column 3), both particles are positively charged, but the surface charge density of the SL particle is small, while that of the AL particle is substantial. The force profiles for the AL–SL systems are again dominated by double layer forces, but they are repulsive at larger distances, while they become attractive upon approach. This characteristic shape can be well described by PB theory, provided one uses the correct values of the regulation parameters. In these situations, the boundary conditions are extremely important. For the concentration of 26 mM (Fig. 5, rightmost column 4), the effect of boundary conditions is relatively small for the AL–AL system, moderate for AL–SL, and largest for SL–SL. Under these conditions, however, the contribution of the non-DLVO attraction is substantial.
Mixing rule for the non-DLVO attraction
Given the ranges and amplitudes of the exponential non-DLVO attraction, one would like to have a simple mixing rule, which could predict the parameters of this force for the asymmetric system from the two symmetric ones. An arithmetic mean of the decay constants yields a relatively good estimate of the decay constant in the mixed system, namely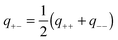 | (11) |
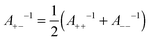 | (12) |
One can also investigate whether this simple mixing rule is consistent with the findings in the monovalent KCl system. Recall that an additional attractive component could not be identified between the AL–SL pairs, since the relevant part of the force curves was inaccessible due to the jump-in instability of the cantilever. Nevertheless, the data obtained in the symmetric systems can be used to calculate the effect of the non-DLVO attraction on the forces in the asymmetric system with the proposed mixing rules given in eqn (11) and (12). The predicted range of the exponential force for the AL–SL system is 0.33 nm, and the corresponding amplitudes are indicated in Fig. 4b. These parameters can be used to calculate the expected contribution of the non-DLVO forces in the AL–SL system, and the results are shown in Fig. 2. The contribution of the additional attraction is small, and cannot be seen on the scale of the graph. Still, the calculated force profiles that include the predicted non-DLVO force do not contradict the experimental data, and we conclude that the proposed mixing rule is also consistent with the data obtained in the monovalent KCl system.
One must stress, however, that this mixing rule is purely empirical, and this rule might not be applicable to other types of electrolytes or in other systems.
Conclusion
This study presents a comprehensive set of direct force measurements involving positively charged AL and negatively charged SL particles, particularly investigating forces between three different pairs, namely AL–AL, AL–SL, and SL–SL. Measurements in solutions containing multivalent cationic aliphatic amines N6 are compared with those in simple monovalent KCl solutions. In all situations, the DLVO theory is capable of describing the force profiles very well. To obtain good agreement with experiment, however, the PB equation must be solved for the appropriate asymmetric electrolyte and charge regulation effects must be included in the analysis. The observed force profiles cannot be rationalized without detailed consideration of charge regulation effects.However, the description by DLVO theory is only valid at distances beyond 5 nm. At shorter distances, one observes a short-ranged non-DLVO attraction, which can be modeled with an exponential force profile. In the monovalent system, the range of this attraction is around 0.3 nm. In the multivalent symmetric systems, the range of this attraction is about 1.0 nm in the SL–SL system, where the multivalent ions represent the counterions, but is again 0.3 nm in the AL–AL system, where the multivalent ions are the co-ions. For the first time, we were able to identify the non-DLVO attraction in the asymmetric AL–SL system. Here, we find an intermediate range of about 0.6 nm. The amplitude of this attraction decreases with increasing concentration for the monovalent system, while it passes through a maximum for the multivalent system. These findings are in line with previous reports.13,40 The origin of this attraction is currently not clear to us, but it could be related to ion–ion correlations, surface charge heterogeneities, hydrophobic forces, charge fluctuations, or electrolyte depletion.15,35,42,43 While ion–ion correlations represent an interesting possibility, theoretical studies suggest that the strength of these forces should increase with increasing salt concentrations,15,20 and the present experiments suggest a weakening of the additional attraction under these conditions. This observation points towards the importance of other forces as well.
Acknowledgements
This work was supported by the Swiss National Science Foundation and the University of Geneva.References
- B. Bolto and J. Gregory, Water Res., 2007, 41, 2301–2324 CrossRef CAS PubMed.
- B. Jonsson, A. Nonat, C. Labbez, B. Cabane and H. Wennerstrom, Langmuir, 2005, 21, 9211–9221 CrossRef PubMed.
- Y. Burak, G. Ariel and D. Andelman, Curr. Opin. Colloid Interface Sci., 2004, 9, 53–58 CrossRef CAS.
- M. O. Khan and B. Jonsson, Biopolymers, 1999, 49, 121–125 CrossRef CAS.
- K. Besteman, K. Van Eijk and S. G. Lemay, Nat. Phys., 2007, 3, 641–644 CrossRef CAS.
- W. A. Ducker, T. J. Senden and R. M. Pashley, Nature, 1991, 353, 239–241 CrossRef CAS.
- H. J. Butt, B. Cappella and M. Kappl, Surf. Sci. Rep., 2005, 59, 1–152 CrossRef CAS.
- G. Toikka, R. A. Hayes and J. Ralston, Langmuir, 1996, 12, 3783–3788 CrossRef CAS.
- C. Gutsche, U. F. Keyser, K. Kegler and F. Kremer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 031403 CrossRef CAS PubMed.
- J. Baumgartl, J. L. Arauz-Lara and C. Bechinger, Soft Matter, 2006, 2, 631–635 RSC.
- K. C. Neuman and A. Nagy, Nat. Methods, 2008, 5, 491–505 CrossRef CAS PubMed.
- D. R. Baselt, G. U. Lee, M. Natesan, S. W. Metzger, P. E. Sheehan and R. J. Colton, Biosens. Bioelectron., 1998, 13, 731–739 CrossRef CAS PubMed.
- F. J. Montes Ruiz-Cabello, G. Trefalt, Z. Csendes, P. Sinha, T. Oncsik, I. Szilagyi, P. Maroni and M. Borkovec, J. Phys. Chem. B, 2013, 117, 11853–11862 CrossRef PubMed.
- R. Kjellander and S. Marcelja, Chem. Phys. Lett., 1984, 112, 49–53 CrossRef CAS.
- A. Naji, M. Kanduc, J. Forsman and R. Podgornik, J. Chem. Phys., 2013, 139, 150901 CrossRef PubMed.
- A. Martin-Molina, C. Rodriguez-Beas, R. Hidalgo-Alvarez and M. Quesada-Perez, J. Phys. Chem. B, 2009, 113, 6834–6839 CrossRef CAS PubMed.
- W. B. Russel, D. A. Saville and W. R. Schowalter, Colloidal Dispersions, Cambridge University Press, Cambridge, 1989 Search PubMed.
- D. A. Sverjensky, Geochim. Cosmochim. Acta, 2006, 70, 2427–2453 CrossRef CAS.
- S. Raafatnia, O. A. Hickey, M. Sega and C. Holm, Langmuir, 2014, 30, 1758–1767 CrossRef CAS PubMed.
- J. Forsman, J. Phys. Chem. B, 2004, 108, 9236–9245 CrossRef CAS.
- K. Bohinc, J. M. A. Grime and L. Lue, Soft Matter, 2012, 8, 5679–5686 RSC.
- M. M. Hatlo and L. Lue, Soft Matter, 2008, 4, 1582–1596 RSC.
- R. M. Pashley, J. Colloid Interface Sci., 1984, 102, 23–35 CrossRef CAS.
- K. Besteman, M. A. G. Zevenbergen, H. A. Heering and S. G. Lemay, Phys. Rev. Lett., 2004, 93, 170802 CrossRef CAS PubMed.
- R. O. James and T. W. Healy, J. Colloid Interface Sci., 1972, 40, 53–64 CrossRef CAS.
- C. Zhao, D. Ebeling, I. Siretanu, D. van den Ende and F. Mugele, Nanoscale, 2015, 7, 16298–16311 RSC.
- O. Zohar, I. Leizerson and U. Sivan, Phys. Rev. Lett., 2006, 96, 177802 CrossRef PubMed.
- M. Moazzami-Gudarzi, G. Trefalt, I. Szilagyi, P. Maroni and M. Borkovec, J. Phys. Chem. C, 2015, 119, 15482–15490 CAS.
- I. Szilagyi, A. Polomska, D. Citherlet, A. Sadeghpour and M. Borkovec, J. Colloid Interface Sci., 2013, 392, 34–41 CrossRef CAS PubMed.
- F. J. Montes Ruiz-Cabello, G. Trefalt, P. Maroni and M. Borkovec, Langmuir, 2014, 30, 4551–4555 CrossRef CAS PubMed.
- A. V. Delgado, F. Gonzalez-Caballero, R. J. Hunter, L. K. Koopal and J. Lyklema, J. Colloid Interface Sci., 2007, 309, 194–224 CrossRef CAS PubMed.
- A. Mezei and R. Meszaros, Langmuir, 2006, 22, 7148–7151 CrossRef CAS PubMed.
- J. E. Sader, J. W. M. Chon and P. Mulvaney, Rev. Sci. Instrum., 1999, 70, 3967–3969 CrossRef CAS.
- F. J. Montes Ruiz-Cabello, G. Trefalt, P. Maroni and M. Borkovec, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 012301 CrossRef PubMed.
- S. H. Donaldson, A. Royne, K. Kristiansen, M. V. Rapp, S. Das, M. A. Gebbie, D. W. Lee, P. Stock, M. Valtiner and J. Israelachvili, Langmuir, 2015, 31, 2051–2064 CrossRef CAS PubMed.
- M. A. Bevan and D. C. Prieve, Langmuir, 1999, 15, 7925–7936 CrossRef CAS.
- M. Elzbieciak-Wodka, M. Popescu, F. J. Montes Ruiz-Cabello, G. Trefalt, P. Maroni and M. Borkovec, J. Chem. Phys., 2014, 140, 104906 CrossRef PubMed.
- J. D. Feick and D. Velegol, Langmuir, 2002, 18, 3454–3458 CrossRef CAS.
- J. L. Anderson, J. Colloid Interface Sci., 1985, 105, 45–54 CrossRef CAS.
- F. J. Montes Ruiz-Cabello, G. Trefalt, T. Oncsik, I. Szilagyi, P. Maroni and M. Borkovec, J. Phys. Chem. B, 2015, 119, 8184–8193 CrossRef CAS PubMed.
- I. Popa, P. Sinha, M. Finessi, P. Maroni, G. Papastavrou and M. Borkovec, Phys. Rev. Lett., 2010, 104, 228301 CrossRef PubMed.
- N. Adzic and R. Podgornik, Eur. Phys. J. E: Soft Matter Biol. Phys., 2014, 37, 49 CrossRef PubMed.
- R. A. Curtis and L. Lue, Curr. Opin. Colloid Interface Sci., 2015, 20, 19–23 CrossRef CAS.
| This journal is © the Owner Societies 2016 |