Improving dipolar recoupling for site-specific structural and dynamics studies in biosolids NMR: windowed RN-symmetry sequences

Abstract

Experimental characterization of one-bond heteronuclear dipolar couplings is essential for structural and dynamics characterization of molecules by solid-state NMR. Accurate measurement of heteronuclear dipolar tensor parameters in magic-angle spinning NMR requires that the recoupling sequences efficiently reintroduce the desired heteronuclear dipolar coupling term, fully suppress other interactions (such as chemical shift anisotropy and homonuclear dipolar couplings), and be insensitive to experimental imperfections, such as radio frequency (rf) field mismatch. In this study, we demonstrate that the introduction of window delays into the basic elements of a phase-alternating R-symmetry (PARS) sequence results in a greatly improved protocol, termed windowed PARS (wPARS), which yields clean dipolar lineshapes that are unaffected by other spin interactions and are largely insensitive to experimental imperfections. Higher dipolar scaling factors can be attained in this technique with respect to PARS, which is particularly useful for the measurement of relatively small dipolar couplings. The advantages of wPARS are verified experimentally on model molecules N-acetyl-valine (NAV) and a tripeptide Met-Leu-Phe (MLF). The incorporation of wPARS into 3D heteronuclear or homonuclear correlation experiments permits accurate site-specific determination of dipolar tensors in proteins, as demonstrated on dynein light chain 8 (LC8). Through 3D wPARS recoupling based spectroscopy we have determined both backbone and side chain dipolar tensors in LC8 in a residue-resolved manner. We discuss these in the context of conformational dynamics of LC8. We have addressed the effect of paramagnetic relaxant Cu(II)-EDTA doping on the dipolar coupling parameters in LC8 and observed no significant differences with respect to the neat sample permitting fast data collection. Our results indicate that wPARS is advantageous with respect to the windowless version of the sequence and is applicable to a broad range of systems including but not limited to biomolecules.

---

Introduction

Molecular dynamics is intimately linked to biological functions of proteins, nucleic acids, and macromolecular assemblies. Understanding the dynamics and connecting the motions to structure and molecular mechanisms is essential for our ability to gain fundamental understanding of biological systems and processes. Solid-state NMR (SSNMR) spectroscopy is uniquely positioned to provide dynamics information, with atomic resolution, in a broad range of systems, many of which are not accessible to other techniques.^1–6 Molecular motions can be studied through various SSNMR methods, including relaxation, exchange, and anisotropic tensorial interactions, all of which are sensitive to the dynamic modulation of the corresponding NMR observables. Anisotropic interactions, such as chemical shift and dipolar tensors, provide a wealth of information about the dynamics on timescales spanning nano- to milliseconds, including motional symmetries and amplitudes. In SSNMR, methods for recoupling of chemical shift anisotropy (CSA) and dipolar tensors are rapidly emerging, as evidenced by the growing body of literature on the subject.^7–45 Among the different approaches, the RN-symmetry based recoupling techniques, originally developed by Levitt and coworkers,^44,45 appear to be particularly versatile and promising due to their broad range of applicability in terms of experimental conditions (radio frequency (rf) fields, MAS frequencies) and the types of interactions that can be efficiently recoupled (CSA, dipolar, quadrupolar).^{9,12–18,24–26,28,32,41,43} While the basic RN-recoupling methods work sufficiently well, they suffer from the sensitivity to the rf field imperfections and contributions from other incompletely averaged interactions, such as ¹H CSA.¹⁴ Therefore, our laboratory has focused on the development of improved variants of RN-sequences, resulting in the recently developed phase-alternating method dubbed PARS.¹⁶ In this report, we present further improvement of the PARS technique for the recoupling of H–X dipolar interactions. We demonstrate that introduction of strategically timed delay periods (windows) into the RN elements of the PARS sequence results in a significant increase in the scaling factors thus permitting recoupling of smaller interactions and reduces the sensitivity of the sequence to rf field mis-sets and rf field inhomogeneity. The improved sequence is dubbed wPARS. We also demonstrate that this approach is compatible with proteins containing paramagnetic dopants (such as Cu(II)–EDTA), permitting considerable time savings due to the reduction of the effective T₁, the so-called PACC approach.^46–49 We validate these experiments on model compounds, N-acetyl-valine (NAV) and a tripeptide (MLF), and apply them in the context of 3D heteronuclear experiments to record in a residue-specific manner the dipolar couplings in dynein light chain 8 protein, LC8.

Experiments and methods

Materials

U–¹⁵N-labeled N-acetyl-valine (NAV) and U–¹³C,¹⁵N-Met-Leu-Phe (MLF) tripeptide were purchased from Cambridge Isotope Laboratories and used without any further purification or re-crystallization. U–¹³C,¹⁵N-dynein light chain (LC8) protein samples without and with Cu(II)-EDTA were prepared in our previous studies and used as-is.^50,51 Each sample was packed into a 1.6 mm Agilent MAS rotor for subsequent NMR experiments.

NMR spectroscopy

Experiments were conducted on a 14.1 T Varian InfinityPlus standard bore NMR spectrometer, with ¹H, ¹³C and ¹⁵N Larmor frequencies of 599.8, 150.8 and 60.8 MHz, respectively. A 1.6 mm triple-resonance Varian HXY MAS probe was used for the experiments performed at 14.1 T, and all spectra were recorded at the MAS frequency of 14 or 20 kHz, controlled to within ±5 Hz using a Varian MAS controller. The typical 90-degree pulse lengths were 2 μs (¹H), 3 μs (¹³C) and 3.3 μs (¹⁵N). To reduce sample heating during MAS, nitrogen gas was used for cooling, resulting in a final sample temperature of −18 °C for LC8 proteins and 22 °C for NAV and MLF. The ¹H–¹³C cross-polarization was performed with a linear amplitude ramp (90–110%) on ¹³C, the center of the ramp Hartmann–Hahn matched to the first spinning sideband. The contact time was 1.2 ms, and the recycle delay was 3 s. For typical wPARS-R10₁³ dipolar experiments conducted at the MAS frequency of 14 kHz, ¹H rf field strengths were 70 kHz (windowless), 93 kHz for the 25% window fraction (τ_win = 1.79 μs) and 140 kHz for the 50% window fraction (τ_win = 3.57 μs). Each rf field strength was optimized directly on the sample under study by finding the “zero” point for the fixed-length π pulse (0.5 × 10⁶/v_RF μs). A phase shift of 180° was used for alternating RN₀RN_π blocks, and a π pulse with a pulse length of 6.6 μs was applied on the ¹⁵N spin at the end of each RN block. High-power TPPM ¹H decoupling with an rf field strength of 105 kHz was used during the t₁, t₂ or t₃ acquisition periods. High-power CW ¹H decoupling was applied during the fpRFDR mixing period in the 3D experiments. A ¹³C rf field strength of 83.3 kHz was used during fpRFDR mixing. No phase sensitive detection was used for the t₁ dipolar evolution periods in all wPARS and DIPSHIFT 2D/3D experiments. All NMR data were processed with NMRPipe⁵² in a Mac environment using a standard protocol including sine-bell apodization, Fourier transform, phase correction and baseline correction in all dimensions. Additional relevant experimental and processing parameters are specified in the Table S1 of the ESI.†

Numerical simulations

All numerical simulations were performed using SIMPSON.⁵³ 168 REPULSION angles (α, β) and 13 γ angles were used to generate a powder average. The atomic coordinates for the model spin systems employed in the simulations were taken from the SSNMR structure of the leucine residue in the N-f-MLF-OH tripeptide (PDB ID 1Q7O).⁵⁴ The one-bond dipolar coupling constants for ¹H–¹³C and ¹H–¹⁵N were set as 24 049 and 10 500 Hz, respectively. J-couplings were ignored since their effects are negligible given their small sizes. Other parameters used in simulations were the same as in previous discussion or in the corresponding experiments. For all wPARS and wDIPSHIFT dipolar measurements on the model compounds and LC8 (for the backbone), single fitting was performed using the Minuit package in the SIMSON program. For side chain dipolar measurements on the LC8 sample, the fitting was performed with our previously reported Fortran script.¹⁴ The SIMPSON simulation scripts are provided in the ESI.†

Results and discussion

Windowed PARS: methodological considerations

Heteronuclear dipolar interaction can be conveniently reintroduced by rotor-synchronized pulse sequences possessing appropriate symmetry features under MAS. Unlike for cross-polarization based dipolar recoupling sequences, such as CPPI⁴² or LGCP,³⁹ most of the ¹H–¹⁵N or ¹H–¹³C dipolar recoupling techniques, such as REDOR,⁸ T-MREV8¹¹ and DIPSHIFT,²⁷ require application of rotor-synchronized rf field irradiation on the ¹H channel. The magnetization of ¹⁵N or ¹³C spins then evolves under the modulation of the reintroduced heteronuclear dipolar interactions. These recoupling sequences, except for REDOR, can suppress efficiently the strong ¹H–¹H homonuclear dipolar couplings. However, ¹H CSA interactions are partially recoupled, together with the heteronuclear dipolar couplings, during the application of rotor-synchronized recoupling pulses on the ¹H channel. This introduces an additional modulation on top of the dipolar-based evolution of ¹³C or ¹⁵N spins and the associated errors in the dipolar coupling constants extracted from such spectra. This error increases with the magnetic field strength and can be of the order of 10–15% at 19.95 T (850 MHz). Furthermore, the majority of the RN and CN symmetry based sequences (but not REDOR) are sensitive to the ¹H recoupling rf field imperfection, which could be the largest source of error in the accuracy of dipolar couplings determined with those methods. The ¹H rf field imperfection may be caused by the rf field inhomogeneity in the coil, time-dependent drifts of probe tuning conditions, or inaccurate experimental settings of the rf field due to electronic dead time influences or inaccurate power calibrations.

One approach to overcome the inaccuracies in the heteronuclear dipolar coupling measurements is the phase-alternating R-type symmetry (PARS) method reported by us recently.¹⁶ In this technique, the phase alternation introduced to the R-symmetry elements results in a drastic reduction of the residual ¹H CSA term, making PARS particularly beneficial at high magnetic fields (18.1 T and higher). For fast MAS conditions (60 kHz and higher), a cross-polarization with variable contact (CPVC) experiment was demonstrated to yield accurate dipolar couplings.³¹ CPVC was shown to be insensitive to the rf field inhomogeneity.

The motivation for the current study was to establish a heteronuclear dipolar recoupling method that would not only provide efficient suppression of the ¹H CSA but also lack sensitivity to the ¹H rf field imperfections, and be applicable over a wide range of MAS frequencies. As detailed below, the introduction of windowed delays into the appropriate-symmetry PARS sequences produces a method that exhibits the desired behavior. We call this approach windowed-PARS, or wPARS for short.

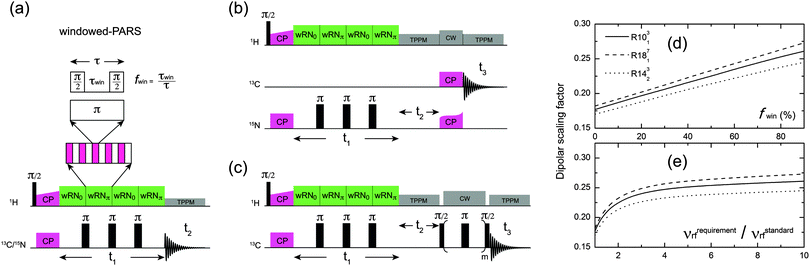
The implementation of wPARS recoupling as a non-constant time 2D sequence is illustrated in Fig. 1a. The recoupled ¹H–¹³C/¹⁵N dipolar evolution is modulated by the T₂′ decay of the ¹³C/¹⁵N spins during the t₁ period, which causes additional line broadening in the ¹H–¹³C/¹⁵N wPARS dipolar spectrum. Usually the decay rate of the T₂′ relaxation is much slower than the magnitude of the ¹H–¹³C/¹⁵N dipolar couplings expressed in frequency units (ca. 10–20 kHz). Therefore, in practice the T₂′ decay of ¹³C/¹⁵N spins does not affect the accuracy of the wPARS dipolar measurements and is simply represented by an empirical line broadening parameter used during the fitting of the wPARS dipolar line shape. Within this regular non-constant time wPARS scheme, the R-symmetry-based block, RN₀, and the π-phase shifted R-symmetry block, RN_π, are applied on the ¹H channel in an alternating fashion. The phases of the π pulses, which comprise the standard RN^v_n cycle RN₀, alternate between ϕ and −ϕ, where ϕ = πν/N, and RN_π has its phases shifted to ϕ + π and −ϕ + π. Both RN₀ and RN_π efficiently reintroduce the ¹H–¹³C/¹⁵N dipolar interactions as well as ¹H CSA (but with an opposite sign), since they possess the same symmetry properties, i.e. l = 2 and λ = 1. In the meantime, π pulses are applied on the X channel at the end of each RN block, and the inverse operation on the ¹³C/¹⁵N spins can restore the refocused ¹H–¹³C/¹⁵N dipolar interactions but not the ¹H CSA interaction. The windowless PARS technique is thus anticipated to yield accurate dipolar couplings whereas ¹H CSA interaction is fully suppressed. To improve the PARS sequence, a finite window (τ_win) with the fraction of f_win (0 ≤ f_win < 1) is inserted in the middle of the basic RN element (τ) splitting it into two π/2 pulses. This has the following consequences:

Fig. 1 (a) 2D ¹H–¹³C/¹⁵N wPARS pulse sequence. (b) 3D ¹H–¹⁵N(¹³C) wPARS pulse sequence. (c) 3D ¹H–¹³C(¹³C) wPARS pulse sequence. (d and e) Calculated dipolar scaling factors of windowed-RN sequences as a function of window fraction expressed as % (d) or ¹H rf field requirement corresponding to each window fraction in kHz (e), respectively.

(1) higher rf field is required to obey the symmetry rules that ensure selection of the desired interactions, and the ¹H rf field imperfection effect is then partly suppressed;

(2) the effective dipolar scaling factors of the basic RN sequences are improved by splitting the π pulses into two π/2 pulses, because the scaling factor is proportional to the integral of the reduced Wigner element whose maximum is π/2 for the single-quantum heteronuclear dipolar terms {l, m, λ, μ} = {2, ±2, 1, ±1}.⁷ Therefore, the scaling factor may be improved by turning the rf field off near π/2 pulses to give the single-quantum operator more time to accumulate in this favorable region. We note that the larger scaling factors in a recoupling sequence are useful when measuring relatively small dipolar couplings.

Fig. 1d shows the calculated scaling factors of the single-quantum R-symmetry heteronuclear dipolar recoupling sequences as a function of the window fraction of the RN element. The scaling factor at f_win = 0 corresponds to the regular windowless PARS or RN-DIPSHIT sequences. It can be seen that the scaling factors increase linearly with the window fraction, and, for instance, 26.6% enhancement can be achieved for R10₁³ with f_win = 0.5. The dependence of scaling factors on the required ¹H recoupling rf field strength for various window fractions is shown in Fig. 1e. The approximately exponential function suggests that efficient enhancement of the scaling factors occurs when the strength of the rf field is less than four times that of the conventional windowless PARS sequence, which corresponds to the window fraction of 0.75.

For application to large or complex systems, an additional isotropic chemical shift dimension is required to attain the necessary site resolution, and the 3D implementations of wPARS-based dipolar recoupling are illustrated in Fig. 1b and c, where heteronuclear ¹⁵N–¹³C and homonuclear ¹³C–¹³C magnetization transfers are introduced through SPECIFIC-CP and fpRFDR, respectively.

Simulations

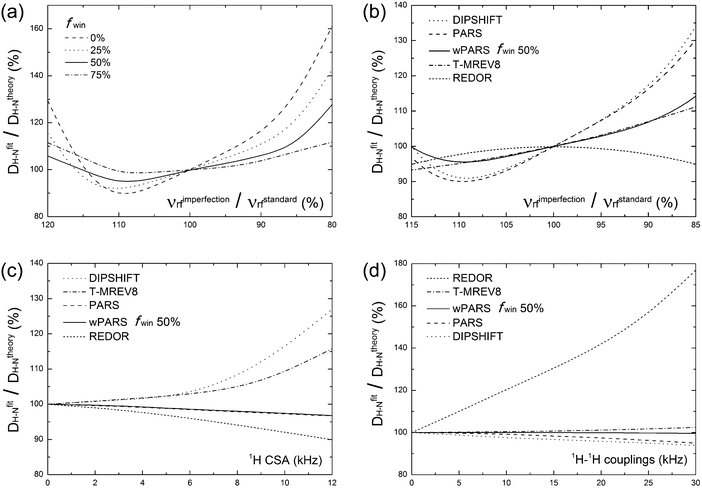
With the above considerations for the wPARS sequence design and the anticipated properties in mind, we have conducted numerical simulations to compare the performance of wPARS (50% window fraction) with other commonly used dipolar recoupling methods. Fig. 2 shows the error estimates for the simulated ¹H–¹⁵N dipolar parameters recorded by different recoupling sequences. We have used an ¹H–¹⁵N spin system described by an axially symmetric ¹H–¹⁵N dipolar interaction of ω_D = 10.5 kHz and considered the different extents of ¹H rf field mis-sets. We have incorporated ¹H CSA and ¹H–¹H homonuclear dipolar coupling parameters. We have then examined the effects on the dipolar line shapes recoupled by REDOR, T-MREV8, DIPSHIFT, PARS and wPARS with various window fractions. For RN sequences (DIPSHIFT, PARS and wPARS), the R10₁³ symmetry-based element was used. T-MREV8 was based on C5 type symmetry.

Fig. 2 (a) Simulations of errors (expressed in %) in the ¹H–¹⁵N dipolar coupling as a function of the ¹H rf field mismatch, shown as % of its correct theoretical value. Different window fractions of 0%, 25%, 50% and 75% were tested and are shown with solid, dashed, dotted and dashed-dotted lines, respectively. (b–d) Comparison of several popular dipolar measurement methods. Simulated errors (expressed in %) of the ¹H–¹⁵N dipolar coupling are plotted as functions of (b) the ¹H rf field mismatch, shown as % of its correct theoretical value; (c) the ¹H CSA variation in kHz; (d) the ¹H–¹H homonuclear coupling variation in kHz. Simulations were performed in a ¹H–¹⁵N two-spin system (for a, b and c) or a ¹H–¹H–¹⁵N three-spin system (d) with a MAS frequency of 14 kHz.

The numerical simulations indicate that the replacement of RN elements by windowed pulses can reduce the sensitivity to ¹H rf field imperfection. For this purpose, dipolar modulation curves were simulated for several ¹H rf field strengths ranging from 80% to 120% of the nominal theoretical field strength required for a proper synchronization of the symmetry-based sequence. As shown in Fig. 2a, the stability of the recoupling sequence increases when the window fraction is increased. With the window fraction of 75% or 50%, the error in the dipolar coupling determined by the windowed PARS is less than 10%, even with a huge mismatch of 15% with respect to the theoretical rf field strength. Such tolerance for rf field mismatch is unusual in practical NMR experiments. A drawback is that the wPARS sequence with 75% window fraction requires the rf field strength to be 4 times higher than that used in the regular PARS sequence, e.g., rf strength of 200 kHz would be needed for 75% windowed-R10₁³ sequences at the MAS frequency of 10 kHz. Such fields are generally too high to be attained with most commercial MAS NMR probes, and hence 50% windowed RN sequences present a practically suitable compromise in terms of performance and implementation with the available hardware.

The comparison of the wPARS performance to that of other recoupling methods was analyzed by simulations using the same spin system, and the results are presented in Fig. 2b–d. As shown in Fig. 2b, wPARS, T-MREV8 and REDOR sequences can efficiently suppress the effect of ¹H rf field imperfection. All three sequences employ a similar type of windowed recoupling elements, rendering them largely insensitive to ¹H rf field imperfections. On the other hand, as shown in Fig. 2c, only PARS and wPARS suppress the influence from ¹H CSA while other sequences are strongly dependent on the size and the orientation of the CSA tensor of the bonded proton. As discussed previously,¹⁴ with regular recoupling pulses on ¹H, either windowed or windowless, the recoupled ¹H CSA and ¹H–¹⁵N dipolar interactions would interfere with each other during the rotor period, which results in distorted dipolar line shapes and associated errors in the corresponding H–X dipolar parameters. As shown in Fig. 2d, REDOR is in addition susceptible to the effects of ¹H–¹H homonuclear dipolar couplings. This sensitivity stems from the ability of REDOR to partially recouple the homonuclear dipolar term even in the hard pulse limit, which is why the application of REDOR is limited to the isolated spin-pair cases or extensively deuterated systems.⁵⁵ On the contrary, for R-symmetry based recoupling sequences, such as R10₁³, the restricted selection rules result in efficient averaging of the 1st-order homonuclear dipolar couplings while the heteronuclear dipolar terms are reintroduced. It is also worth noting that wPARS exhibits almost no dependence on ¹H–¹H homonuclear dipolar couplings up to 30 kHz, while PARS or T-MREV8 shows slight dependence, which suggests that more efficient suppression on higher order ¹H–¹H homonuclear dipolar couplings can be obtained by wPARS.

Generally, among the dipolar recoupling methods discussed above, the windowed PARS sequence exhibits the most favorable properties, including efficient suppression of ¹H–¹H homonuclear dipolar and ¹H CSA interactions, as well as reduced sensitivity to rf field inhomogeneity. wPARS sequences do not require fast MAS conditions (MAS frequencies greater than 60 kHz), in contrast to CPVC based techniques. These features arguably make wPARS an optimal method for accurate measurements of heteronuclear couplings in a wide range of systems, including large biomolecules, as demonstrated below.

2D wPARS spectroscopy on model compounds: NAV and MLF

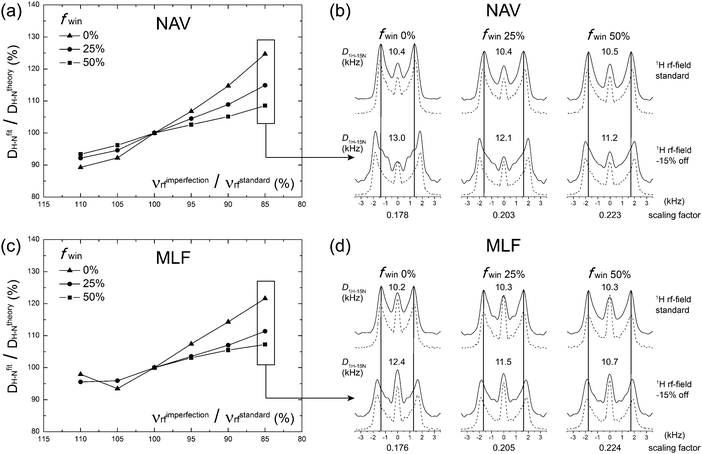
To verify the performance of the wPARS sequence, we first performed a series of experiments on U–¹⁵N-labeled N-acetyl-valine (NAV) and U–¹³C,¹⁵N-Met-Leu-Phe (MLF) tripeptide. A series of 2D NMR spectra were recorded where various windowed PARS-RN and DIPSHIFT-RN sequences were applied during the t₁ period.

Fig. 3a and c shows the plots of errors in the ¹H–¹⁵N dipolar couplings of NAV and MLF determined experimentally from wPARS spectra recorded with different window fractions, as a function of the ¹H rf field mismatch. The results demonstrate that, in agreement with numerical predictions, wPARS recoupling efficiently suppresses the influences from ¹H rf field imperfection and gives rise to undistorted ¹H–¹⁵N dipolar powder patterns. The experimental error depends on the window fraction to the degree predicted by the numerical simulations. In agreement with theory, the larger the window inserted into the RN elements, the lower the sensitivity of the wPARS to ¹H rf field imperfection. Typically, a 50% window fraction in PARS resulted in errors of less than 5% in the ¹H–¹⁵N dipolar couplings, when the mismatch of the rf field strength was in the range of ±10% from the theoretical value. It is important to note that the 5% error is generally of the same order as the systematic measurement errors. Therefore, 50% windowed PARS is basically insensitive to common ¹H rf field imperfections. A careful examination of the dipolar lineshapes recorded in the 50% wPARS with the matched and mismatched (by −15%) ¹H rf field indicates that the effect of the ¹H rf field imperfection is essentially negligible, except for a slight change in the central peak intensity (see Fig. 3b and d). The latter is the result of the contributions from partially unrefocused higher-order ¹H CSA Hamiltonian terms. As expected from numerical simulations, the introduction of the 50% window resulted in an increase of the heteronuclear dipolar scaling factors by ca. 25% compared to the conventional PARS spectra. As noted earlier, this improvement is particularly important for the measurements of small ¹H–¹³C/¹⁵N dipolar couplings (across multiple bonds or partially averaged due to dynamics).

Fig. 3 Experimental performance of wPARS 2D in the (a and b) NAV sample and (c and d) MLF sample. (a and c) Errors (expressed in %) in the ¹H–¹⁵N dipolar couplings plotted as a function of the ¹H rf field mismatch, shown as % of the correct theoretical value. Different window fractions of 0%, 25%, and 50% were tested and shown as filled squares, triangles and circles, respectively. (b and d) ¹H–¹⁵N dipolar line shapes extracted from 2D wPARS spectra recorded with different window fractions of 0%, 25%, and 50% at correct ¹H rf field and ¹H rf field mis-set by −15%. Experimental and fitted lineshapes are shown as solid and dashed lines, respectively. Experiments were performed with a MAS frequency of 14 kHz.

We note that an R element can be replaced with windowed pulses in the context of the conventional RN-DIPSHIFT experiment when ¹H CSA is negligible in the system of interest. Not surprisingly, a windowed RN-DIPSHIFT sequence also works well for the suppression of ¹H rf field imperfections and also exhibits increased dipolar scaling factors (see Fig. S1, ESI†).

Applications to proteins: dynein light chain 8

Since, as demonstrated in the previous sections, the wPARS dipolar splittings and line shape features are not affected to any significant extent by ¹H rf field imperfections, the sequence is very well suited for accurate measurements of ¹H–¹³C/¹⁵N dipolar parameters in proteins and other biological systems. Furthermore, as R10₁³-based wPARS dipolar line shapes are practically independent of the ¹H–¹H homonuclear dipolar couplings and ¹H CSA interactions, the dipolar asymmetry parameter (η_D) can be obtained experimentally. The knowledge of the latter is important as it reports on the presence and symmetry of motions occurring on timescales commensurate with the magnitude of the dipolar interaction.¹⁶

It is of interest to measure both ¹H–¹⁵N and ¹H–¹³C dipolar parameters as the latter report on the dynamics of side chains in proteins. ¹H–¹³C dipolar parameters can be conveniently measured in a 3D experiment, where the dipolar recoupling period is followed by a ¹³C–¹³C mixing step, such as fpRFDR, as reported previously³² and shown in Fig. 1c in the context of wPARS recoupling sequences.

To verify that performance of wPARS in the context of the 3D wPARS-fpRFDR experiment, we have compared 3D and 2D R10₁³-based ¹H–¹³C wPARS spectra on the MLF sample (Fig. 1a). As shown in Fig. S2 (ESI)†, the ¹H–¹³Cα dipolar line shapes for all residues in MLF extracted from the 2D spectrum are fully consistent with those obtained from ¹³Cα–¹³Cα, ¹³Cα–¹³Cβ and ¹³Cα–¹³Co cross-peaks in the 3D experiment. This result indicates that the fpRFDR mixing does not introduce any artifacts into the spectra, in accordance with the previous findings for a 3D CPVC-RFDR experiment.³²

To experimentally examine the application of wPARS in proteins, we have performed 3D experiments on dynein light chain, LC8, which has been extensively characterized in our laboratory.^24,50 We have examined two samples, nanocrystalline U–¹³C,¹⁵N-LC8 and the same preparation but doped with 5 mM Cu(II)–EDTA. The latter sample was studied by us previously in the context of experiments combining nonuniform sampling and paramagnetically assisted condensed data collection (NUS-PACC).⁵¹ The introduction of paramagnetic dopants permits large time savings due to dramatic reductions in T₁, which are particularly well realized in the context of fast MAS, where low-power decoupling can be used.^47–49 We have reported previously that the presence of 5 mM Cu(II)–EDTA does not have a significant effect on the LC8 spectra.⁵¹

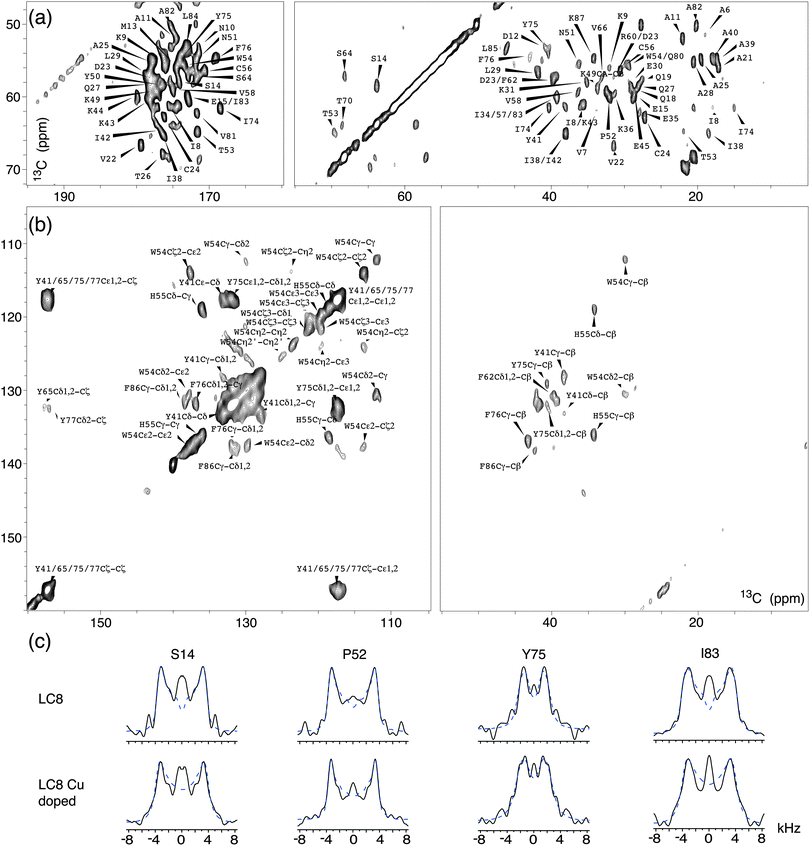
Fig. 4 shows expansions around several regions of the first 2D ¹³C–¹³C plane extracted from the 3D wPARS spectrum of LC8 prepared without Cu(II)–EDTA. The corresponding ¹H–¹³Cα dipolar line shapes for each residue were extracted along the third dimension in both 3D spectra. We obtained a total of 62 well-resolved wPARS dipolar patterns in each of the two samples, including 50 backbone and 12 side chain ¹H–¹³C line shapes. Representative experimental and fitted ¹H–¹³Cα dipolar line shapes for three LC8 residues are plotted in Fig. 4c. Note that the errors are less than ±5%.

Fig. 4 The 2D ¹³C–¹³C correlation planes extracted from the 3D R10₁³-based ¹H–¹³C(¹³C) wPARS spectrum recorded on U–¹³C,¹⁵N-LC8, with peak assignments shown for (a) aliphatic and (b) aromatic regions. (c) Representative dipolar line shapes extracted from 3D R10₁³-based ¹H–¹³C(¹³C) wPARS on U–¹³C,¹⁵N-LC8 (top) and Cu(II)–EDTA doped U–¹³C,¹⁵N-LC8 (bottom). Experimental and fitted lineshapes are shown as black solid and blue dashed lines, respectively. Experiments were performed with a MAS frequency of 20 kHz.

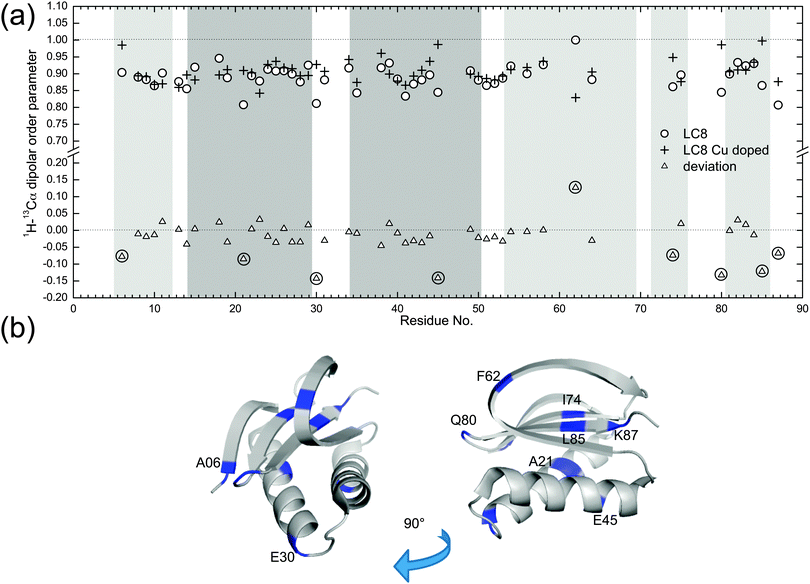
Fig. 5a shows the comparison of backbone ¹H–¹³C dipolar order parameters (DOP or S) of U–¹³C,¹⁵N-LC8 prepared with and without Cu(II)–EDTA, plotted as a function of the residue number. The rigid-limit dipolar coupling for one-bond ¹H–¹³C with a bond length of ∼1.09 Å is 22.8 kHz. Molecular motions occurring on timescales of 10⁻⁹–10⁻⁶ s give rise to reduced dipolar couplings. The results indicate that most ¹H–¹³C S are larger than 0.85, including those for the loop regions. Only a few residues, A21, E30 and K87, have DOP less than 0.85, indicating that these are somewhat flexible at the experimental temperature of −18 °C. The S values derived from wPARS are in overall strong agreement with our prior report, where S were derived from the conventional DIPSHIFT experiment.¹⁵ Comparing the results for the LC8 samples prepared with and without Cu(II)–EDTA, we find that, for the majority of the residues, Cu²⁺ had no noticeable effect on the dipolar order parameters, with the deviations being generally smaller than 0.06. These deviations correspond to 1.5 kHz for dipolar coupling, which is of the order of the fitting errors. The ¹H–¹³C dipolar line shapes for 50 representative backbone residues in LC8 samples with and without Cu doping are shown in Fig. S3 (ESI†).

Fig. 5 (a) ¹H–¹³Cα dipolar order parameters obtained experimentally with 3D R10₁³-based ¹H–¹³C(¹³C) wPARS for U–¹³C,¹⁵N-LC8 (empty circles) and Cu(II)–EDTA doped U–¹³C,¹⁵N-LC8 (crosses) plotted versus the residue number. The deviations between the two data sets are shown as empty triangles. The darker grey areas represent α-helices and the lighter grey areas represent β-sheets. (b) Cartoon representation of U–¹³C,¹⁵N-LC8 protein and the locations of residues for which dipolar couplings differ by more than 1.5 kHz for samples prepared with and without Cu(II)–EDTA.

There are 9 residues whose peaks are resolved and that show deviations in ¹H–¹³C dipolar order parameters greater than 0.06 in the presence of Cu(II)–EDTA, as illustrated in Fig. 5a. These residues are displayed in the context of the LC8 3D structure in Fig. 5b. The dipolar couplings measured for these residues in the Cu(II)–EDTA doped sample are greater than those without copper. Of these, E30, E45, and Q80 are located on the surface of LC8, and their side chains may be interacting with the dopant, affecting the dipolar couplings. Another possible source of error for these residues is the faster decay of ¹³C T₂ relaxation during the RFDR period caused by the presence of paramagnetic ions (see Fig. 1c). This is illustrated also in Fig. S4 (ESI†), showing the corresponding dipolar line shapes. There are no correlations between the relatively large dipolar order parameter deviations for the 9 residues and their chemical shift differences (Fig. S5, ESI†). The chemical shift perturbations are generally smaller than 0.2 ppm, in agreement with our previous observations.⁵¹

The combination of wPARS with fpRFDR allows us to determine not only the backbone dipolar order parameters but also those for the aromatic side chains, in a single 3D experiment. The aromatic side chain dipolar tensors are a sensitive probe of dynamics, and in LC8 many of the aromatic residues are mobile.³² The analysis of the side chain dynamics of the aromatic residues in U–¹³C,¹⁵N-LC8 is shown in Table S2 and Fig. S6 (ESI†). As discussed in our recent report,³² in the analysis of dipolar interactions of aromatic side chains, the dipolar asymmetry parameters η_D cannot be ignored. In Table S2 (ESI†), the ¹H–¹³C dipolar couplings and their corresponding dipolar asymmetry parameters η_D are shown for different residues. For H55 and W54 residues, the average ¹H–¹³C dipolar couplings are around 21 kHz, close to the rigid-limit ¹H–¹³C coupling of 22.8 kHz, and the corresponding η_D values are generally smaller than 0.4. This observation is consistent with our previous findings that these residues are nearly static.³² On the other hand, for F76, Y41 and Y75, the ¹H–¹³C dipolar couplings are smaller than 15 kHz, and the corresponding asymmetry parameters are 0.6 or higher. These values indicate that there are π-jumps occurring around the Cβ–Cγ (x-) axis of the aromatic ring, also consistent with our previous report.³² In this study,³² at room temperature, one additional kind of side chain motion for Phe and Tyr residues was also discussed, a ring displacement by a small angle along the z-axis. Such motions were not detected in our present study likely because the wPARS experiments were conducted at −18 °C, where the motions are more restricted compared with room temperature conditions. With respect to the influence of paramagnetic Cu(II)–EDTA doping on dipolar interaction parameters for the side chains of LC8, there are no significant differences observed in the presence of Cu(II)–EDTA, as shown in Table S2. This is in line with our findings for the ¹H–¹³C backbone order parameters.

Conclusions

In conclusion, the wPARS method enables accurate measurements of H–X heteronuclear dipolar couplings over a wide range of experimental conditions and MAS frequencies. wPARS suppresses efficiently the influences from the rf field imperfections, which the conventional PARS sequence could not accomplish. Due to the large increase in the effective dipolar scaling factors, wPARS enables determination of small dipolar couplings, which are observed in motionally averaged environments. The ability of wPARS to cleanly recouple dipolar interaction and efficiently suppress other terms also enables accurate determination of dipolar asymmetry parameters, which are essential for understanding the details of the anisotropic motions. The wPARS technique is readily applicable to site-specific measurements of backbone and side chain dipolar interaction parameters in proteins, as demonstrated on dynein light chain LC8. The experiment is compatible with paramagnetic doping conditions, yielding significant time savings due to the reduction of the spin–lattice relaxation time. We anticipate that wPARS will be a useful tool for probing molecular motions in a variety of systems, including but not limited to biological assemblies.

Acknowledgements

This work was supported by the National Institutes of Health, NIH Grants R01GM085306 and 1P30-GM110758-02 for the support of core research infrastructure at the University of Delaware.

References

1. A. McDermott, Annu. Rev. Biophys., 2009, 38, 385–403.
2. M. J. Knight, A. J. Pell, I. Bertini, I. C. Felli, L. Gonnelli, R. Pierattelli, T. Herrmann, L. Emsley and G. Pintacuda, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11095–11100.
3. A. Krushelnitsky, D. Reichert and K. Saalwachter, Acc. Chem. Res., 2013, 46, 2028–2036.
4. R. Linser, R. Sarkar, A. Krushelnitzky, A. Mainz and B. Reif, J. Biomol. NMR, 2014, 59, 1–14.
5. M. Lu, G. Hou, H. Zhang, C. L. Suiter, J. Ahn, I. J. Byeon, J. R. Perilla, C. J. Langmead, I. Hung, P. L. Gor'kov, Z. Gan, W. Brey, C. Aiken, P. Zhang, K. Schulten, A. M. Gronenborn and T. Polenova, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 14617–14622.
6. G. Hou, C. L. Suiter, S. Yan, H. Zhang and T. Polenova, Annu. Rep. NMR Spectrosc., 2013, 80, 293–357.
7. A. Gansmuller, J. P. Simorre and S. Hediger, J. Magn. Reson., 2013, 234, 154–164.
8. T. Gullion and J. Schaefer, J. Magn. Reson., 1989, 81, 196–200.
9. Y. Han, G. Hou, C. L. Suiter, J. Ahn, I. J. L. Byeon, A. S. Lipton, S. Burton, I. Hung, P. L. Gor'kov, Z. H. Gan, W. Brey, D. Rice, A. M. Gronenborn and T. Polenova, J. Am. Chem. Soc., 2013, 135, 17793–17803.
10. C. Herbst, P. Bellstedt, M. Gorlach and R. Ramachandran, J. Biomol. NMR, 2015, 62, 7–15.
11. M. Hohwy, C. P. Jaroniec, B. Reif, C. M. Rienstra and R. G. Griffin, J. Am. Chem. Soc., 2000, 122, 3218–3219.
12. G. Hou, I. J. Byeon, J. Ahn, A. M. Gronenborn and T. Polenova, J. Chem. Phys., 2012, 137, 134201.
13. G. Hou, S. Paramasivam, I. J. L. Byeon, A. M. Gronenborn and T. Polenova, Phys. Chem. Chem. Phys., 2010, 12, 14873–14883.
14. G. Hou, S. Paramasivam, S. Yan, T. Polenova and A. J. Vega, J. Am. Chem. Soc., 2013, 135, 1358–1368.
15. G. Hou, I. J. L. Byeon, J. Ahn, A. M. Gronenborn and T. Polenova, J. Am. Chem. Soc., 2011, 133, 18646–18655.
16. G. Hou, X. Lu, A. J. Vega and T. Polenova, J. Chem. Phys., 2014, 141.
17. G. Hou, S. Yan, S. Sun, Y. Han, I. J. L. Byeon, J. Ahn, J. Concel, A. Samoson, A. M. Gronenborn and T. Polenova, J. Am. Chem. Soc., 2011, 133, 3943–3953.
18. G. Hou, S. Yan, J. Trebosc, J. P. Amoureux and T. Polenova, J. Magn. Reson., 2013, 232, 18–30.
19. B. Hu, J. Trebosc, O. Lafon, Q. Chen, Y. Masuda, K. Takegoshi and J. P. Amoureux, ChemPhysChem, 2012, 13, 3585–3588.
20. K. Hu, W. Qiang, G. A. Bermejo, C. D. Schwieters and R. Tycko, J. Magn. Reson., 2012, 218, 115–127.
21. I. Hung and Z. Gan, J. Magn. Reson., 2011, 213, 196–199.
22. I. Karki, E. Mihaliuk and T. Gullion, Isr. J. Chem., 2014, 54, 163–170.
23. N. M. Loening, B. J. van Rossum and H. Oschkinat, Magn. Reson. Chem., 2012, 50, 284–288.
24. X. Lu, C. Guo, G. Hou and T. Polenova, J. Biomol. NMR, 2015, 61, 7–20.
25. X. Lu, O. Lafon, J. Trebosc, G. Tricot, L. Delevoye, F. Mear, L. Montagne and J. P. Amoureux, J. Chem. Phys., 2012, 137.
26. X. Lu, O. Lafon, J. Trebosc and J. P. Amoureux, J. Magn. Reson., 2012, 215, 34–49.
27. M. G. Munowitz, R. G. Griffin, G. Bodenhausen and T. Huang, J. Am. Chem. Soc., 1981, 103, 2529–2533.
28. E. Nimerovsky, R. Gupta, J. Yehl, M. Li, T. Polenova and A. Goldbourt, J. Magn. Reson., 2014, 244, 107–113.
29. Y. Nishiyama, R. Zhang and A. Ramamoorthy, J. Magn. Reson., 2014, 243, 25–32.
30. G. L. Olsen, A. Lupulescu, J. N. Dumez, L. Emsley and L. Frydman, Isr. J. Chem., 2014, 54, 154–162.
31. P. Paluch, T. Pawlak, J. P. Amoureux and M. J. Potrzebowski, J. Magn. Reson., 2013, 233, 56–63.
32. P. Paluch, T. Pawlak, A. Jeziorna, J. Trebosc, G. Hou, A. J. Vega, J. P. Amoureux, M. Dracinsky, T. Polenova and M. J. Potrzebowski, Phys. Chem. Chem. Phys., 2015, 17, 28789–28801.
33. M. K. Pandey, M. Malon, A. Ramamoorthy and Y. Nishiyama, J. Magn. Reson., 2015, 250, 45–54.
34. M. K. Pandey and Y. Nishiyama, J. Magn. Reson., 2015, 261, 133–140.
35. P. Schanda, B. H. Meier and M. Ernst, J. Am. Chem. Soc., 2010, 132, 15957–15967.
36. P. Schanda, B. H. Meier and M. Ernst, J. Magn. Reson., 2011, 210, 246–259.
37. K. O. Tan, A. B. Nielsen, B. H. Meier and M. Ernst, J. Phys. Chem. Lett., 2014, 5, 3366–3372.
38. Y. Umegawa, T. Yamaguchi, M. Murata and S. Matsuoka, Magn. Reson. Chem., 2015, 53, 514–519.
39. B. J. van Rossum, C. P. de Groot, V. Ladizhansky, S. Vega and H. J. M. de Groot, J. Am. Chem. Soc., 2000, 122, 3465–3472.
40. L. Vugmeyster, D. Ostrovsky and R. Fu, J. Magn. Reson., 2015, 259, 225–231.
41. Q. Wang, X. Lu, O. Lafon, J. Trebosc, F. Deng, B. Hu, Q. Chen and J. P. Amoureux, Phys. Chem. Chem. Phys., 2011, 13, 5967–5973.
42. X. Wu and K. W. Zilm, J. Magn. Reson., Ser. A, 1993, 102, 205–213.
43. S. Yan, H. Zhang, G. Hou, S. Ahmed, J. C. Williams and T. Polenova, J. Biol. Chem., 2015, 290, 1607–1622.
44. M. H. Levitt, in Encyclopedia of Nuclear Magnetic Resonance, ed. D. M. Grant and R. K. Harris, John Wiley & Sons, Ltd, Chichester, 2002, vol. 9, pp. 165–196.
45. A. Brinkmann and M. H. Levitt, J. Chem. Phys., 2001, 115, 357–384.
46. K. H. Mroue, N. MacKinnon, J. Xu, P. Zhu, E. McNerny, D. H. Kohn, M. D. Morris and A. Ramamoorthy, J. Phys. Chem. B, 2012, 116, 11656–11661.
47. S. Parthasarathy, Y. Nishiyama and Y. Ishii, Acc. Chem. Res., 2013, 46, 2127–2135.
48. N. P. Wickramasinghe, S. Parthasarathy, C. R. Jones, C. Bhardwaj, F. Long, M. Kotecha, S. Mehboob, L. W. M. Fung, J. Past, A. Samoson and Y. Ishii, Nat. Methods, 2009, 6, 215–218.
49. S. Laage, J. R. Sachleben, S. Steuernagel, R. Pierattelli, G. Pintacuda and L. Emsley, J. Magn. Reson., 2009, 196, 133–141.
50. S. Sun, A. H. Butterworth, S. Paramasivam, S. Yan, C. M. Lightcap, J. C. Williams and T. Polenova, Can. J. Chem., 2011, 89, 909–918.
51. S. Sun, S. Yan, C. Guo, M. Li, J. C. Hoch, J. C. Williams and T. Polenova, J. Phys. Chem. B, 2012, 116, 13585–13596.
52. F. Delaglio, S. Grzesiek, G. W. Vuister, G. Zhu, J. Pfeifer and A. Bax, J. Biomol. NMR, 1995, 6, 277–293.
53. M. Bak, J. T. Rasmussen and N. C. Nielsen, J. Magn. Reson., 2000, 147, 296–330.
54. C. M. Rienstra, L. Tucker-Kellogg, C. P. Jaroniec, M. Hohwy, B. Reif, M. T. McMahon, B. Tidor, T. Lozano-Perez and R. G. Griffin, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 10260–10265.
55. A. E. Bennett, C. M. Rienstra, J. M. Griffiths, W. Zhen, P. T. Lansbury and R. G. Griffin, J. Chem. Phys., 1998, 108, 9463–9479.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp07818k

---