 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Intramolecular structure and energetics in supercooled water down to 255 K
Felix
Lehmkühler
*ab,
Yury
Forov
c,
Thomas
Büning
c,
Christoph J.
Sahle
d,
Ingo
Steinke
ab,
Karin
Julius
c,
Thomas
Buslaps
d,
Metin
Tolan
c,
Mikko
Hakala
e and
Christian
Sternemann
c
aDeutsches Elektronen-Synchrotron DESY, Notkestr. 85, 22607 Hamburg, Germany. E-mail: felix.lehmkuehler@desy.de; Fax: +49 40 8998 2787; Tel: +49 40 8998 5671
bThe Hamburg Centre for Ultrafast Imaging, Luruper Chaussee 149, 22761 Hamburg, Germany
cFakultät Physik/DELTA, Technische Universität Dortmund, 44221 Dortmund, Germany
dESRF – The European Synchrotron, CS 40220, 38043 Grenoble Cedex 9, France
eDepartment of Physics, FI-00014 University of Helsinki, Finland
First published on 5th February 2016
Abstract
We studied the structure and energetics of supercooled water by means of X-ray Raman and Compton scattering. Under supercooled conditions down to 255 K, the oxygen K-edge measured by X-ray Raman scattering suggests an increase of tetrahedral order similar to the conventional temperature effect observed in non-supercooled water. Compton profile differences indicate contributions beyond the theoretically predicted temperature effect and provide a deeper insight into local structural changes. These contributions suggest a decrease of the electron mean kinetic energy by 3.3 ± 0.7 kJ (mol K)−1 that cannot be modeled within established water models. Our surprising results emphasize the need for water models that capture in detail the intramolecular structural changes and quantum effects to explain this complex liquid.
Introduction
The structure and properties of water are among the most fascinating topics in natural science. They have been discussed controversely for over one century. In particular, in the metastable supercooled state, water anomalies, become more pronounced.1–4 This includes various thermodynamic properties such as the heat capacity,5–8 isothermal compressibility9 and thermal expansion (see ref. 10 for an overview). In order to understand and connect these anomalies to the structural properties of liquid water, various scattering and spectroscopy techniques are frequently used covering ambient as well as supercooled conditions.2–4 Recently, an ultrafast X-ray scattering experiment under deep supercooling conditions indicated decreasing distortions of the hydrogen bonds, and the tetrahedral order became observable moving towards low-density liquid upon supercooling.11,12 Further experiments support coexisting water phases3,4,13 and an increase of interstitial water molecules in the hydrogen bond network.14 Beside such work studying the intermolecular hydrogen bond network, Raman spectroscopy is frequently used to obtain information on intramolecular bonding, guiding the way to the current understanding of intramolecular bonds in water ranging from water's boiling point down to supercooled conditions.15–19 Furthermore, deep-inelastic neutron scattering studies suggest a preferred delocalization of the proton, resulting in an excess of the proton's mean kinetic energy.20,21 These observations have been reconsidered recently,22,23 indicating a smooth change in kinetic energy. Nevertheless, the experimental results suggested influences of quantum nuclear effects on the water structure that have been addressed by recent simulation studies.24,25 However, a detailed view of the structure of liquid water and its connection to the water's anomalies is still pending.Here we study the structure of slightly supercooled water by means of X-ray Raman scattering (XRS) and X-ray Compton scattering. Upon supercooling down to 255 K, the XRS spectra taken in the vicinity of the oxygen K-edge show a change in the spectral shape suggesting an increase of tetrahedral order. Compton profile differences provide a more detailed insight into changes of energetics and structure on an intramolecular scale. Additional contributions to the experimental spectra are found that cannot be modeled by an expected temperature effect on hydrogen bonds for non-supercooled conditions. This is accompanied by a strong increase of the mean kinetic energy of the electrons. These results demonstrate the need for water models and simulations with special attention on the supercooled state that consider both intramolecular structural changes and quantum effects.
Experimental
Methods
In recent years, non-resonant inelastic X-ray scattering26 has become a standard technique to investigate liquid samples with special attention on water and water-based systems. Here, the study of absorption edges in the soft X-ray regime by hard X-rays, denoted as X-ray Raman scattering, provided ground-breaking results on the local structure of liquids and amorphous solids and extended results of conventional soft X-ray absorption experiments. In particular, studies of the oxygen K-edge in liquid and supercritical water,27–32 in different ices30,33–35 and water-based two-component systems36–39 challenged the question of water's microscopic structure.In X-ray Compton scattering experiments, inelastically scattered X-rays are probed at large energy and momentum transfers. In this regime, the impulse approximation26 becomes valid and the measured quantity of a liquid is proportional to the Compton profile for isotropic systems
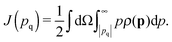 | (1) |
 | (2) |
Experimental setups
The XRS experiment was performed at the new beamline ID20 of the European Synchrotron Radiation Facility (ESRF).54 In total, we used 72 Si(660) analyzer crystals, resulting in an overall energy resolution of 0.6 eV. The crystals are grouped into six independent modules, each containing 12 crystals. Three modules were set to a scattering angle of 41°, two to 121° and one to 85°. In order to measure the oxygen K-edge at around 540 eV, the incident energy was varied between 10.21 keV and 10.245 keV to cover energy losses between 520 eV and 555 eV by setting the analyzer energy to Eana = 9.69 keV. Thus, the three scattering angles correspond to wave vector transfers of approximately 3.6 Å−1, 6.9 Å−1, and 8.8 Å−1, respectively. In this article, we will concentrate on the results taken at 3.6 Å−1. Ultrapure water (MilliQ, R > 18 MΩ) was filled into glass capillaries (2 mm diameter) that were sealed afterwards. The capilliaries were put to a sample chamber that allowed to access a large scattering-angle range and a broad temperature range. This chamber was evacuated to reduce background scattering and to guarantee stable temperature conditions. XRS spectra were taken at various temperatures between 293 K and 255 K and analyzed following the scheme discussed in ref. 54. To gain sufficient statistics, spectra were taken for at least 3 h at each temperature. To check for consistency, the procedure was repeated with freshly prepared samples.The Compton scattering experiment was performed at beamline ID15B of the European Synchrotron Radiation Facility (ESRF).55 The energy of the incident X-ray beam was 87.37 keV. The scattered intensity was measured using a 13-element Ge solid-state detector at a scattering angle of 152°. The momentum resolution was Δpq ≈ 1 atomic units (a.u.) at the Compton peak (pq = 0 a.u.). To achieve constant detector conditions, the incident flux was kept constant using an absorber feedback system. The obtained statistical accuracy was better than 0.035% units at pq = 0 a.u. within 0.03 a.u. momentum bin. Water was filled in glass capillaries of 2 mm thickness that were sealed afterwards by melting the glass. These capillaries were placed into a sample holder that was capable of covering temperatures down to 256 K. At each temperature, X-ray diffraction patterns were taken every 60 minutes to check whether or not the sample had frozen. The diffraction patterns show the same temperature behavior as discussed by Sellberg et al.11 To check the data for consistency, Compton spectra were saved every 10 minutes and checked for deviations larger than the statistical accuracy. The raw spectral data were corrected for absorption and the dead times of the detector before converting to the momentum scale by using the relativistic cross-section correction. Contributions from multiple scattering were corrected afterwards by taking the sample geometry into account. Finally, the positive and negative momentum sides of the Compton profiles were averaged.
Results and discussion
X-ray Raman scattering
First, we discuss the results of the XRS study. The extracted oxygen K-edges at four temperatures between T = 293 K and the supercooled temperature of T = 255 K are shown in Fig. 1. The edges are divided into three regimes:36,56 the preedge (A) around Eloss ≃ 535 eV energy loss, the main edge (B) around Eloss ≃ 538 eV and the post-edge (C) for Eloss ≃ 541 eV. The effects of structural properties and changes thereof on these spectral regions have been addressed frequently in the literature,27,29–31,34,36–38,56,57 leading to a current common sense of interpreting the oxygen K-edge. Typically, the occurrence of the preedge peak is connected to weakening or breaking of hydrogen bonds, in particular it is sensitive to the distortion of hydrogen bonds. The main edge feature increases when the temperature increases and reflects distorted hydrogen bonds, and the post-edge was found to reflect the tetrahedral order and strengthening of the hydrogen bonds. For instance, by comparing liquid water and hexagonal ice spectra one observes a decreased preedge peak due to less broken bonds in ice accompanied by a decreased main edge and an increase in the post-edge region originated by the lower density and the higher degree of tetrahedrally ordered molecules in ice, respectively.34,56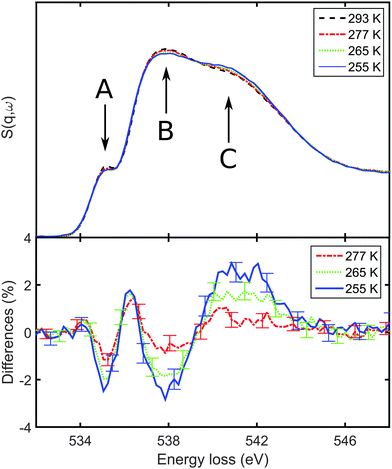 | ||
| Fig. 1 XRS spectra. Top: Oxygen K-edges for different temperatures. The pre-, main-, and postedge are indicated by A, B, and C, respectively. Bottom: Spectral differences with respect to T = 293 K. | ||
The spectra show a shift of spectral weight from the main edge to the post-edge region (region B to C) which is interpreted as the increase of tetrahedrality upon supercooling. In addition, the maximum in the preedge region (A) decreases slightly with decreasing temperature, suggesting less broken hydrogen bonds. Most importantly, this effect with decreasing temperature resembles data from non-supercooled water,30 suggesting a similar effect on the hydrogen bond network for supercooled and non-supercooled water. Analogous results have been reported recently in a X-ray absorption spectroscopy study at temperatures down to 264 K.32
Compton scattering
In order to obtain a more detailed insight into the quantitative intra- and intermolecular structural changes, Compton spectra were taken from supercooled water. The Compton profile differences with respect to the measurement at T = 277 K are shown in Fig. 2. The differences exhibit a pronounced minimum at pq = 0 a.u. and a maximum around pq = 1.4 a.u. The amplitude of these features increases with decreasing temperatures. First, the mean kinetic energies of the electrons were calculated from eqn (2). To be able to neglect contributions from the background, we discuss the change of energy Δ〈Ekin〉 = 〈Ekin(T)〉 − 〈Ekin(277 K)〉 as a function of temperature in Fig. 3. We observe a linear increase at low temperatures up to Δ〈Ekin〉 = (66 ± 20) kJ mol−1 at T = 256 K, which corresponds to a slope of −3.3 ± 0.7 kJ (mol K)−1. Above 277 K the energy changes only slightly reflecting the weak change of the hydrogen bond network due to the temperature increase. It is important to mention that the observed changes of the electron mean kinetic energy are in line with intramolecular bond length changes, as reported for different covalent bonds.58
with respect to the measurement at T = 277 K are shown in Fig. 2. The differences exhibit a pronounced minimum at pq = 0 a.u. and a maximum around pq = 1.4 a.u. The amplitude of these features increases with decreasing temperatures. First, the mean kinetic energies of the electrons were calculated from eqn (2). To be able to neglect contributions from the background, we discuss the change of energy Δ〈Ekin〉 = 〈Ekin(T)〉 − 〈Ekin(277 K)〉 as a function of temperature in Fig. 3. We observe a linear increase at low temperatures up to Δ〈Ekin〉 = (66 ± 20) kJ mol−1 at T = 256 K, which corresponds to a slope of −3.3 ± 0.7 kJ (mol K)−1. Above 277 K the energy changes only slightly reflecting the weak change of the hydrogen bond network due to the temperature increase. It is important to mention that the observed changes of the electron mean kinetic energy are in line with intramolecular bond length changes, as reported for different covalent bonds.58
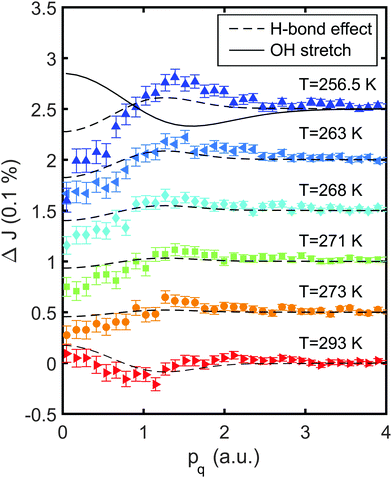 | ||
| Fig. 2 Compton profile differences ΔJ with respect to the spectra taken at T = 277 K. The dashed lines correspond to the ab initio temperature effect43 and the solid line represents a 1% stretch of the covalent OH bond. | ||
 | ||
| Fig. 3 Δ〈Ekin〉 = 〈Ekin(T)〉 − 〈Ekin(277 K)〉. The solid line is a linear fit with slope c = −3.3 ± 0.7 kJ (mol K)−1. | ||
Therefore, we model the Compton profile differences by calculated spectra in the framework of density functional theory from both ab initio molecular dynamics simulations and from water dimers. For a detailed overview of the models, see ref. 41–43.
The temperature effect on liquid water that we will employ in the following is obtained using the ab initio molecular dynamics model at non-supercooled temperatures, i.e., at room temperature and above.43 It is shown as dashed lines in Fig. 2. Here, the data of ref. 43 are scaled to the temperature differences of the present experiment. This temperature model fails to describe the data, both due to a different amplitude and a different shape with a maximum around p = 1.2 a.u.
The experimental observation of a maximum around pq = 1.4 a.u. and contributions up to pq ≈ 2.5 a.u. typically indicate changes on intramolecular length scales, such as OH bond length or bond angle variations.41,42 These contributions are not covered by any other changes of the local and molecular water structure, e.g., variation of density or hydrogen bond geometry. Differences of the OH bond lengths have also been reported as the dominating effect of deuteration,43 in water–ethanol mixtures,53 during freezing of clathrate hydrates,52 and in confined water.45 Upon supercooling, optical spectroscopy suggests stretching of the covalent OH bond lengths in liquid water as a consequence of the strengthening of the hydrogen bond network. Therefore, we compare the Compton profile differences with a 1% OH bond stretch as a solid line in Fig. 2. A linear change of the intramolecular OH bond length rOH was found to change the Compton profile differences linearly.37,42,52 This calculated difference fails to model neither the experimental data fully nor the remaining effect after consideration of the temperature effect on the H-bonds. Intra- or intermolecular structural changes which would be expressed in a similar Compton profile difference have been unreported in the literature so far, suggesting the need of improved water models, e.g., taking quantum effects into account.
Conclusions
Under supercooled conditions a strengthening of the hydrogen bond network of liquid water is expected. This is typically expressed by shortening of the hydrogen bond length between neighboring water molecules that is consequently accompanied by a stretching and a narrowing of the distribution of the effective intramolecular OH bond length, as discussed e.g. from the neutron scattering and infrared spectroscopy results.17,19,20 In contrast, our data indicate more complex structural effects upon supercooling. First, we found an increase of tetrahedral order during cooling by XRS. These observations are similar to the results obtained from non-supercooled water which are in line with a reduced number of broken hydrogen bonds, suggested both by continuous and mixture water models. Second, Compton profile differences suggest intramolecular structural changes upon supercooling accompanied by a significant change of the electron mean kinetic energy, uniquely probed by Compton scattering. In contrast to Compton scattering such changes have only a small impact on the XRS spectra, as XRS is sensitive to the unoccupied states (i.e. intermolecular bonding) and not to the intramolecular bonding (i.e. the occupied states). Thus, the XRS spectra cannot be modeled for the oxygen K edges with respect to intramolecular structural changes with the needed accuracy.37 It is important to mention that we find no indication for the appearance of interstitial molecules under supercooled conditions,14 which would result in an opposite effect on the XRS spectra56 and show significant additional contributions to the Compton differences at small pq.42While the XRS data are in line with the increase of tetrahedral order upon supercooling, the suggestion of intramolecular structural changes appears to be contradictive to the common understanding of the structure of supercooled water. Such an observation might be a fingerprint of quantum effects that emanate as effective bond length changes in the Compton profiles. Bond length changes have been indeed suggested by simulations,24 and have been interpreted as a result from quantum effects.59–61 In particular, the OH bond length was found to change when quantum effects are taken into account24 and a significant fraction of molecules exhibits transient autoprotolysis events.25 Quantum effects were, in addition, suggested as an explanation for the results of neutron Compton experiments on supercooled water,20,21 however, the statistical accuracy of such neutron experiments is not comparable to that of X-ray Compton data. This lack of statistical accuracy makes the extraction of qualitative bond parameters and thus a detailed access to quantum effects impossible in those experiments. In conclusion, our results demonstrate that already upon slight supercooling, one needs much more elaborate water models and simulations. They are specifically needed to properly capture the detailed intramolecular structural changes as well as the quantum effects under supercooled conditions. These features are uniquely probed by inelastic X-ray scattering techniques and may hold the key for a better understanding of the complex liquid.
Acknowledgements
This work has been supported by the Cluster of Excellence “The Hamburg Centre for Ultrafast Imaging’’ (CUI) funded by DFG (EXC 1074). IS was supported by the DFG within the framework of the graduate school 1355 “Physics with new advanced coherent radiation sources’’. YF and KJ acknowledge funding by the Cluster of Excellence RESOLV (EXC 1069) funded by DFG. TB thanks the BMBF (Project 05K13PE2 within FSP-302) and MERCUR (AN-2014-0036) for financial support. MH was supported by the Academy of Finland (Contracts 1260204 and 1259599). We thank A. Al-Zein, C. Henriquet, and A. Poulain for support during the experiments at ESRF and M. Paulus and G. Grübel for helpful discussions.References
- P. G. Debenedetti, J. Phys.: Condens. Matter, 2003, 15, R1669 CrossRef CAS.
- A. Nilsson and L. Pettersson, Chem. Phys., 2011, 389, 1–34 CrossRef CAS.
- L. G. Pettersson and A. Nilsson, J. Non-Cryst. Solids, 2015, 407, 399–417 CrossRef CAS.
- A. Nilsson and L. Pettersson, Nat. Commun., 2015, 6, 8998 CrossRef CAS PubMed.
- C. A. Angell, W. J. Sichina and M. Oguni, J. Phys. Chem., 1982, 86, 998–1002 CrossRef CAS.
- E. Tombari, C. Ferrari and G. Salvetti, Chem. Phys. Lett., 1999, 300, 749–751 CrossRef CAS.
- D. G. Archer and R. W. Carter, J. Phys. Chem. B, 2000, 104, 8563–8584 CrossRef CAS.
- M. Singh, D. Dhabal, A. H. Nguyen, V. Molinero and C. Chakravarty, Phys. Rev. Lett., 2014, 112, 147801 CrossRef PubMed.
- R. J. Speedy and C. A. Angell, J. Chem. Phys., 1976, 65, 851–858 CrossRef CAS.
- V. Holten, C. E. Bertrand, M. A. Anisimov and J. V. Sengers, J. Chem. Phys., 2012, 136, 094507 CrossRef CAS PubMed.
- J. A. Sellberg, C. Huang, T. A. McQueen, N. D. Loh, H. Laksmono, D. Schlesinger, R. G. Sierra, D. Nordlund, C. Y. Hampton, D. Starodub, D. P. DePonte, M. Beye, C. Chen, A. V. Martin, A. Barty, K. T. Wikfeldt, T. M. Weiss, C. Caronna, J. Feldkamp, L. B. Skinner, M. M. Seibert, M. Messerschmidt, G. J. Williams, S. Boutet, L. G. M. Pettersson, M. J. Bogan and A. Nilsson, Nature, 2014, 510, 381–384 CrossRef CAS PubMed.
- J. A. Sellberg, T. A. McQueen, H. Laksmono, S. Schreck, M. Beye, D. P. DePonte, B. Kennedy, D. Nordlund, R. G. Sierra, D. Schlesinger, T. Tokushima, I. Zhovtobriukh, S. Eckert, V. H. Segtnan, H. Ogasawara, K. Kubicek, S. Techert, U. Bergmann, G. L. Dakovski, W. F. Schlotter, Y. Harada, M. J. Bogan, P. Wernet, A. Föhlisch, L. G. M. Pettersson and A. Nilsson, J. Chem. Phys., 2015, 142, 044505 CrossRef PubMed.
- A. Taschin, P. Bartolini, R. Eramo, R. Righini and R. Torre, Nat. Commun., 2013, 4, 2401 CAS.
- M. A. Ricci, F. Bruni and A. Giuliani, Faraday Discuss., 2009, 141, 347–358 RSC.
- R. Bansil, J. Wiafe-Akenten and J. L. Taaffe, J. Chem. Phys., 1982, 76, 2221–2226 CrossRef CAS.
- G. D'Arrigo, G. Maisano, F. Mallamace, P. Migliardo and F. Wanderlingh, J. Chem. Phys., 1981, 75, 4264–4270 CrossRef.
- D. E. Hare and C. M. Sorensen, J. Chem. Phys., 1990, 93, 25–33 CrossRef CAS.
- H. J. Bakker and H.-K. Nienhuys, Science, 2002, 297, 587–590 CrossRef CAS PubMed.
- F. Perakis and P. Hamm, J. Phys. Chem. B, 2011, 115, 5289–5293 CrossRef CAS PubMed.
- A. Pietropaolo, R. Senesi, C. Andreani, A. Botti, M. A. Ricci and F. Bruni, Phys. Rev. Lett., 2008, 100, 127802 CrossRef CAS PubMed.
- A. Giuliani, F. Bruni, M. A. Ricci and M. A. Adams, Phys. Rev. Lett., 2011, 106, 255502 CrossRef CAS PubMed.
- R. Senesi, D. Flammini, A. I. Kolesnikov, E. D. Murray, G. Galli and C. Andreani, J. Chem. Phys., 2013, 139, 074504 CrossRef PubMed.
- Y. Finkelstein and R. Moreh, Chem. Phys., 2014, 431–432, 58–63 CrossRef CAS.
- X.-Z. Li, B. Walker and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6369–6373 CrossRef CAS.
- M. Ceriotti, J. Cuny, M. Parrinello and D. E. Manolopoulos, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15591–15596 CrossRef CAS PubMed.
- W. Schülke, Electron Dynamics by Inelastic X-ray Scattering, Oxford University Press, Oxford, 2007 Search PubMed.
- P. Wernet, D. Nordlund, U. Bergmann, M. Cavalleri, M. Odelius, H. Ogasawara, L. A. Näslund, T. K. Hirsch, L. Ojamäe, P. Glatzel, L. G. M. Pettersson and A. Nilsson, Science, 2004, 304, 995–999 CrossRef CAS PubMed.
- J. D. Smith, C. D. Cappa, K. R. Wilson, B. M. Messer, R. C. Cohen and R. J. Saykally, Science, 2004, 306, 851–853 CrossRef CAS PubMed.
- A. Nilsson, D. Nordlund, I. Waluyo, N. Huang, H. Ogasawara, S. Kaya, U. Bergmann, L.-Å. Nåslund, H. Öström, P. Wernet, K. Andersson, T. Schiros and L. Pettersson, J. Electron Spectrosc. Relat. Phenom., 2010, 177, 99–129 CrossRef CAS.
- T. Pylkkänen, A. Sakko, M. Hakala, K. Hämäläinen, G. Monaco and S. Huotari, J. Phys. Chem. B, 2011, 115, 14544–14550 CrossRef PubMed.
- C. J. Sahle, C. Sternemann, C. Schmidt, S. Lehtola, S. Jahn, L. Simonelli, S. Huotari, M. Hakala, T. Pylkkänen, A. Nyrow, K. Mende, M. Tolan, K. Hämäläinen and M. Wilke, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6301–6306 CrossRef CAS PubMed.
- J. A. Sellberg, S. Kaya, V. H. Segtnan, C. Chen, T. Tyliszczak, H. Ogasawara, D. Nordlund, L. G. M. Pettersson and A. Nilsson, J. Chem. Phys., 2014, 141, 034507 CrossRef PubMed.
- Y. Q. Cai, H.-K. Mao, P. C. Chow, J. S. Tse, Y. Ma, S. Patchkovskii, J. F. Shu, V. Struzhkin, R. J. Hemley, H. Ishii, C. C. Chen, I. Jarrige, C. T. Chen, S. R. Shieh, E. P. Huang and C. C. Kao, Phys. Rev. Lett., 2005, 94, 025502 CrossRef CAS PubMed.
- J. S. Tse, D. M. Shaw, D. D. Klug, S. Patchkovskii, G. Vankó, G. Monaco and M. Krisch, Phys. Rev. Lett., 2008, 100, 095502 CrossRef PubMed.
- T. T. Fister, K. P. Nagle, F. D. Vila, G. T. Seidler, C. Hamner, J. O. Cross and J. J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 174117 CrossRef.
- H. Conrad, F. Lehmkühler, C. Sternemann, A. Sakko, D. Paschek, L. Simonelli, S. Huotari, O. Feroughi, M. Tolan and K. Hämäläinen, Phys. Rev. Lett., 2009, 103, 218301 CrossRef PubMed.
- F. Lehmkühler, A. Sakko, I. Steinke, C. Sternemann, M. Hakala, C. J. Sahle, T. Buslaps, L. Simonelli, S. Galambosi, M. Paulus, T. Pylkkänen, M. Tolan and K. Hämäläinen, J. Phys. Chem. C, 2011, 115, 21009–21015 Search PubMed.
- I. Juurinen, T. Pylkkänen, K. O. Ruotsalainen, C. J. Sahle, G. Monaco, K. Hämäläinen, S. Huotari and M. Hakala, J. Phys. Chem. B, 2013, 117, 16506–16511 CrossRef CAS PubMed.
- I. Juurinen, T. Pylkkänen, C. J. Sahle, L. Simonelli, K. Hämäläinen, S. Huotari and M. Hakala, J. Phys. Chem. B, 2014, 118, 8750–8755 CrossRef CAS PubMed.
- I. Juurinen, S. Galambosi, A. G. Anghelescu-Hakala, J. Koskelo, V. Honkimäki, K. Hämäläinen, S. Huotari and M. Hakala, J. Phys. Chem. B, 2014, 118, 5518–5523 CrossRef CAS PubMed.
- M. Hakala, K. Nygård, S. Manninen, S. Huotari, T. Buslaps, A. Nilsson, L. G. M. Pettersson and K. Hämäläinen, J. Chem. Phys., 2006, 125, 084504 CrossRef CAS PubMed.
- M. Hakala, K. Nygård, S. Manninen, L. G. M. Pettersson and K. Hämäläinen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 035432 CrossRef.
- K. Nygård, M. Hakala, T. Pylkkänen, S. Manninen, T. Buslaps, M. Itou, A. Andrejczuk, Y. Sakurai, M. Odelius and K. Hämäläinen, J. Chem. Phys., 2007, 126, 154508 CrossRef PubMed.
- P. H.-L. Sit, C. Bellin, B. Barbiellini, D. Testemale, J.-L. Hazemann, T. Buslaps, N. Marzari and A. Shukla, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 245413 CrossRef.
- G. F. Reiter, A. Deb, Y. Sakurai, M. Itou, V. G. Krishnan and S. J. Paddison, Phys. Rev. Lett., 2013, 111, 036803 CrossRef CAS PubMed.
- E. D. Isaacs, A. Shukla, P. M. Platzman, D. R. Hamann, B. Barbiellini and C. A. Tulk, Phys. Rev. Lett., 1999, 82, 600–603 CrossRef CAS.
- S. Ragot, J.-M. Gillet and P. J. Becker, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 235115 CrossRef.
- K. Nygård, M. Hakala, S. Manninen, M. Itou, Y. Sakurai and K. Hämäläinen, Phys. Rev. Lett., 2007, 99, 197401 CrossRef PubMed.
- C. Bellin, B. Barbiellini, S. Klotz, T. Buslaps, G. Rousse, T. Strässle and A. Shukla, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 094117 CrossRef.
- C. Sternemann, S. Huotari, M. Hakala, M. Paulus, M. Volmer, C. Gutt, T. Buslaps, N. Hiraoka, D. D. Klug, K. Hämäläinen, M. Tolan and J. S. Tse, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195104 CrossRef.
- M. Hakala, K. Nygård, J. Vaara, M. Itou, Y. Sakurai and K. Hämäläinen, J. Chem. Phys., 2009, 130, 034506 CrossRef CAS PubMed.
- F. Lehmkühler, A. Sakko, C. Sternemann, M. Hakala, K. Nygård, C. J. Sahle, S. Galambosi, I. Steinke, S. Tiemeyer, A. Nyrow, T. Buslaps, D. Pontoni, M. Tolan and K. Hämäläinen, J. Phys. Chem. Lett., 2010, 1, 2832–2836 CrossRef.
- I. Juurinen, K. Nakahara, N. Ando, T. Nishiumi, H. Seta, N. Yoshida, T. Morinaga, M. Itou, T. Ninomiya, Y. Sakurai, E. Salonen, K. Nordlund, K. Hämäläinen and M. Hakala, Phys. Rev. Lett., 2011, 107, 197401 CrossRef CAS PubMed.
- C. J. Sahle, A. Mirone, J. Niskanen, J. Inkinen, M. Krisch and S. Huotari, J. Synchrotron Radiat., 2015, 22, 400–409 CrossRef CAS PubMed.
- N. Hiraoka, T. Buslaps, V. Honkimäki and P. Suortti, J. Synchrotron Radiat., 2005, 12, 670–674 CrossRef CAS PubMed.
- T. Pylkkänen, V. M. Giordano, J.-C. Chervin, A. Sakko, M. Hakala, J. A. Soininen, K. Hämäläinen, G. Monaco and S. Huotari, J. Phys. Chem. B, 2010, 114, 3804–3808 CrossRef PubMed.
- W. Chen, X. Wu and R. Car, Phys. Rev. Lett., 2010, 105, 017802 CrossRef PubMed.
- A. A. Zavitsas, J. Phys. Chem. A, 2003, 107, 897–898 CrossRef CAS.
- J. A. Morrone and R. Car, Phys. Rev. Lett., 2008, 101, 017801 CrossRef PubMed.
- S. Habershon, T. E. Markland and D. E. Manolopoulos, J. Chem. Phys., 2009, 131, 024501 CrossRef PubMed.
- A. L. Agapov, A. I. Kolesnikov, V. N. Novikov, R. Richert and A. P. Sokolov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 022312 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2016 |
