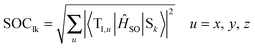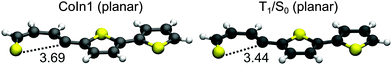Deactivation pathways of thiophene and oligothiophenes: internal conversion versus intersystem crossing

Abstract

Oligothiophenes and polythiophenes are building blocks of organic-based energy conversion materials. Therefore the lifetime of the excited states plays a central role. As a first step to understand the factors influencing the performance, we investigated the deactivation processes from the first excited state S₁ of thiophene and small oligothiophenes containing up to four rings using quantum chemical calculations. For thiophene a low-lying S₁/S₀ conical intersection seam is easily accessible and drives the fast internal conversion. In oligothiophenes barriers inhibit this passage while deactivation pathways via intersystem crossing channels open. The first one is responsible for the high triplet quantum yields and takes place shortly after the Franck–Condon region. The second one occurs in the vicinity of a local S₁ minimum. The calculated spin–orbit coupling strength together with the singlet–triplet energy gaps can explain the decreasing triplet and increasing fluorescence quantum yields for growing chain length. From the triplets the ground state is reachable by inter-ring torsions and T₁/S₀ intersections. The present results allow a deeper understanding of the deactivation pathways of thiophene and small oligothiophenes and are of potential interest for the photophysics of longer oligothiophenes and polythiophenes used in optical devices.

---

1 Introduction

In the last few decades polythiophenes and oligothiophenes have been shown to be some of the most promising candidates of organic materials for technological applications.^1,2 In particular, they have been used in solar cells,^3,4 light emitting diodes,^5,6 photoswitches⁷ and as biological labels.^8–10 Gaining detailed knowledge of the radiative and nonradiative mechanisms and the factors tuning these processes in the isolated oligomers should be the first step in improving the performance of oligothiophene-based devices.

Static absorption measurements and time-resolved spectroscopic studies have been reported for thiophene (1T) and oligothiophenes containing up to seven thiophene rings.^11–40 In our nomenclature nT is an oligothiophene with n thiophene units. The monomer 1T was shown to be non-fluorescent and non-phosphorescent.³⁷ With the aid of static quantum chemical^41–43 and nonadiabatic molecular dynamics calculations^44–46 it was revealed that 1T decays ultrafast primarily via its singlet states and conical intersections to the ground state without the involvement of triplet states. In contrast the rates of internal conversion (IC) of the oligothiophenes are very small and the relaxation processes are dominated by triplet formation and fluorescence.^13,21,22,25 It was shown that the fluorescence quantum yields increase while the triplet quantum yields decrease when extending the chain length of the oligomer. These trends are mainly attributed to changes in the nonradiative decay processes, which are dominated by effective intersystem crossing (ISC) from the singlet to the triplet manifold. Photodetachment photoelectron spectroscopy (PD-PES) measurements^32,47 explained this dependence of the triplet quantum yield as a function of the oligomer size mainly by the growing energy differences between the singlet S₁ state and the triplet T₂ state. It is important to note that the triplet energies determined by PD-PES are based on radical anions. The anion equilibrium structure of the oligothiophenes is mostly planar and thus closer to the minimum structure of the S₁ states than to the non-planar minimum of the neutral ground states.⁴⁷ Therefore the triplet energies and the state order deduced from PD-PES are also not related to the Franck–Condon (FC) region but to the structure of the S₁ minimum. For bithiophene (2T) it was shown by quantum chemical calculations that the triplet T₄ and T₃ states are below the S₁ state in the non-planar S₀ minimum geometry but above the S₁ state in its planar equilibrium geometry.⁴⁸ Furthermore femtosecond time-resolved spectroscopy measurements suggested that for 2T and 3T ultrafast ISC takes place from a twisted S₁ state responsible for the highly effective triplet generation.^28,33,34 In addition oligothiophenes are considered to be quite flexible molecules with respect to the rotation around the inter-ring bonds. Nevertheless the T₄ and T₃ states were regarded until now to play only a minor role in the efficient ISC pathways of the oligothiophenes.

In this work, we will demonstrate the crucial role of the T₃ state for the effective triplet formation and elucidate the details of the ISC processes and relaxation pathways of bithiophene (2T), terthiophene (3T) and quaterthiophene (4T). By quantum chemical calculations of the low-lying excited states and the spin–orbit coupling between the S₁ and the triplet states we will show that efficient and ultrafast ISC occurs along the geometry relaxation of the S₁ state leading to the high triplet quantum yields of the oligothiophenes. In addition we will reveal why the relaxation pathway of thiophene is dominated by its singlet states and conical intersections (CoIns) and why these CoIns are not active anymore in the oligothiophenes. The current results in conjunction with previous work offer quite a complete picture of the photophysical properties of the molecules and may be linked to the application of the oligothiophenes in optical devices.

2 Computational details

The ground state optimizations of 1T–4T have been carried out using the B3LYP functional^49–52 and the 6-311G** basis set.⁵³ In a theoretical study of 2T it was demonstrated that the optimized geometries at the B3LYP/6-311G** level of theory exhibit the best agreement with the experiments and that the torsional angle between the adjacent thiophene rings is very sensitive to both the basis set and the method used.⁵⁴

The electronic states of 1T, 2T and 3T were computed with the complete active space second-order perturbation theory method (CASPT2),⁵⁵ the equation of motion coupled cluster singles and doubles method (CCSD)⁵⁶ and the time-dependent density functional theory method (TDDFT) using the CAM-B3LYP functional.⁵⁷ The electronic states of the larger system 4T were calculated using the CCSD and the TDDFT methods. For the CCSD calculations the 6-311+G** (1T–3T) and 6-31G* (4T) basis sets⁵⁸ were used. The TDDFT calculations were carried out using the 6-311+G** basis set, while for the more demanding CASPT2 method the 6-31G* basis set was used throughout.

The reference wave function and the molecular orbitals for the CASPT2 calculation were determined using the state-averaged complete active space self-consistent field method (SA-CASSCF). For 1T and 3T five singlet and four triplet states were included in the state-averaging procedure while for 2T six singlet and four triplet states were incorporated. The CASPT2 calculations were performed using a shift of 0.3 a.u. For 1T the active space was composed of eight electrons and seven orbitals (CAS(8/7)). In addition to the π-orbitals one pair of σ-orbitals (σ/σ*) was included in the active space. The geometry optimizations of the excited states of 1T have been carried out at the CASPT2 level of theory. The Hessian matrix for the optimization of the transition state of the S₁ state was calculated numerically.

The active space of 2T contained one σ*-orbital in addition to the π-space (12 electrons/10 orbitals) in all calculations to describe the πσ* singlet state (CAS(12/11)). For the calculation of the S₁/S₀ conical intersections, the T₁/S₀ intersection and the S₁(πσ*) minima either one (CAS(14/12)) or two pairs (CAS(16/14)) of σ-orbitals were included in the active space depending on whether one or two C–S bond cleavages should be described. For the calculation of the spin–orbit coupling matrix elements (SOMEs) along the relaxation path from the FC point to the local S₁(ππ*) minimum the CAS(12/11) active space was used. The SOME computations along the ring-opening path leading to one broken C–S bond were performed with the CAS(14/12) active space. The optimizations of the excited states, conical intersections and the T₁/S₀ intersection of 2T have been carried out using the CASSCF method.

For the energy calculations of 3T the complete π-valence active space was used (CAS(18/15)). Like in a previous study of 3T⁵⁹ the CASSCF optimizations of the excited states were performed with a smaller active space, 12 electrons/12 orbitals, where the three deepest π-orbitals were kept inactive. For the optimization of the S₁/S₀ conical intersection and the T₁/S₀ intersection of 3T this active space was extended by one pair of σ-orbitals (σ/σ*). For the SOME calculations along the relaxation path from the FC point to the local S₁(ππ*) minimum the smaller π-active space (CAS(12/12)) was extended by three σ*-orbitals (CAS(12/15)) to keep the active space stable. For 4T the optimizations of the excited states have been carried at the TDDFT/6-31G* level.

The spin–orbit coupling (SOC) strength between selected singlet (S_l) and triplet (T_k) states was computed as

which can be considered as the length of the spin–orbit coupling vector SOC_lk.⁶⁰ Its component 〈T_l,u|Ĥ_SO|S_k〉 corresponds to the calculated SOME. The SOMEs were calculated by an efficient method using the Breit–Pauli spin–orbit operator⁶¹ implemented in the Molpro software package.^62,63

The CASSCF method has been employed to compute the transition dipole moments. Energy differences corrected by the CASPT2 method were used in the oscillator strength formula. The program package MOLPRO^62,63 was used for the CASSCF and CASPT2 calculations, while the DFT, TDDFT and CCSD calculations were carried out using the Gaussian 09 software package.⁶⁴

3 Results and discussion

3.1 Vertical excited states of thiophene (1T) and oligothiophenes (2T–4T)

The optimized structures for the ground state minima of 1T–4T are shown in Fig. 1. The 1T geometry is planar and has C_2v symmetry, while all others are non-planar. The trans conformation of 2T exhibits C₂ symmetry and is characterized by a torsional angle α of 150.4° between the rings. This conformation has been shown to be the global minimum of the internal rotational potential surface.⁵⁴ For 3T two nearly isoenergetic minima exist among the total number of ten already reported in previous theoretical studies.^59,65–67 The global minimum is the twisted trans–trans–syn conformation with C_s symmetry (α = 153.8°) and the trans–trans–anti conformation with C₂ symmetry (α = 154.6°) is only 0.02 eV (ΔG) above. Also the transition state between both conformers lies only 0.05 eV (ΔG) above the global minimum (Fig. S13 and Table S10 in the ESI†). The flatness of the torsional potential is in agreement with the experimental observation that more than one twisted conformation is present in solution.⁶⁸ The all-trans conformation found as a minimum structure with C₂ symmetry for 4T is characterized by an α value of 157.1° between the central rings. Like a previous study⁴⁷ our calculations show that the degree of planarity increases from 2T (α = 150°) to 4T (α = 157°).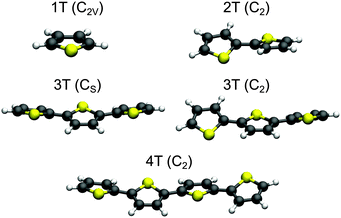

Fig. 1 Optimized B3LYP/6-311G** ground state geometries of 1T–4T. For 3T both nearly isoenergetic minima are shown. The point groups of the structures are given in parentheses.

At these geometries the low-lying ππ* and the πσ* singlet states plus the first four triplet states of 1T–4T were computed. The excitation energies, the electronic characters and oscillator strengths are listed in Table 1 together with the corresponding experimental data. To facilitate the comparison of the electronic states of the different systems, the HOMO of all molecules is denoted π₁ and the LUMO π₁* orbital (for details, see ESI†). When possible the calculations were performed on the CASPT2, CCSD and TDDFT levels of theory for comparison and we found a good agreement for all molecules studied. A complete list with the results of all methods used is given in Tables S1–S5 in the ESI.† Our focus is on the bright S₁ state and its relaxation paths after optical excitation as this state is discussed to be crucial for the use of oligothiophenes in organic devices. The πσ* singlet state is responsible for a nonradiative relaxation via a ring opening path and the triplet states induce the ISC. The results in Table 1 are discussed from these aspects. In the FC region the S₁ state has ππ* character and is completely delocalized for all investigated systems. The excitation energy of the S₁ state decreases from 1T to 4T and its corresponding oscillator strength increases. The calculated vertical excitation energy of the S₁ state agrees very well for 1T and 2T with the experimental values while for 3T and 4T larger deviations are observed. The use of larger basis sets reduces these deviations (see Tables S12, S13 and S16, ESI†). But the combination with the large active spaces required for 3T and 4T (see Section 3.2.4) cannot be handled within a reasonable computation time. The state order of the πσ* singlet state increases systematically from the S₃ state in 1T to the S₇ state in 4T as more and more ππ* states intrude (see Tables S1–S5 in the ESI†). The πσ* state is due to the σ* character more localized and does not profit as much as the ππ* states from the elongation of the π-system.

Table 1 Calculated vertical singlet and triplet excitation energies (eV) for the low-lying valence excited states plus the πσ* singlet state of 1T–4T at their ground-state minima compared with experimental data. For 3T the excitation energies are shown for both isoenergetic conformers (C_s and C₂ symmetry). Oscillator strengths are given in parentheses. The HOMO of all molecules is denoted π₁ and the LUMO π₁* orbital (for details, see ESI)

1T (C2v)				2T (C2)				3T (Cs)				3T (C2)				4T (C2)
State	Char.	CASPT2	Exp.	State	Char.	CASPT2	Exp.	State	Char.	CASPT2	CCSD	State	CASPT2	CCSD	Exp.	State	Char.	CCSD	Exp.
a Magnetic circular dichroism.^11 b Electron energy loss spectroscopy.^36 c Gas-phase absorption spectrum at room temperature.^19 d Photodetachment photoelectron spectrum in the gas phase.^47 e At the CASPT2 level of theory the S2 state of both the 3T conformers is described by an π2π1* excitation, while with the CCSD method the S2 state has π1π2* character and A′ and A symmetry, respectively, (see Tables S3 and S4 in the ESI). f Absorption spectrum in solution at room temperature.^22,25,30 g Absorption spectrum in solution at room temperature.^13,22,25
S1(A1)	π2π1*	5.58 (0.06)	5.26^a	S1(B)	π1π1*	4.51 (0.45)	4.29^c	S1(A′′)	π1π1*	4.03 (0.55)	4.15 (0.79)	S1(B)	4.08 (0.52)	4.14 (0.77)	3.5^f	S1(B)	π1π1*	4.00 (1.30)	3.2^g
S2(B2)	π1π1*	5.92 (0.11)	5.64^a	S2(B)	π4π1*	4.85 (0.14)	5.08^c	S2(A′′)^e	π2π1*	4.42 (0.06)	4.97 (0.00)	S2(B)	4.39 (0.08)	4.98 (0.00)	—	S2(A)	π1π2*	4.89 (0.00)
S3(B1)	π1σ1*	6.37 (0.00)	—	S5(A)	π1σ1*	5.40 (0.00)	—	S6(A′)	π1σ1*	—	5.46 (0.00)	S6(B)	—	5.49 (0.00)	—	S7(B)	π1σ1*	5.62 (0.00)
T1(B2)	π1π1*	3.76	3.74^b	T1(B)	π1π1*	2.86	2.32^d	T1(A′′)	π1π1*	2.40	2.56	T1(B)	2.42	2.56	1.90^d	T1(B)	π1π1*	2.36	1.75^d
T2(A1)	π2π1*	4.75	4.50^b	T2(A)	π1π2*	3.82	—	T2(A′)	π1π2*	3.19	3.38	T2(A)	3.17	3.36	2.99^d	T2(A)	π1π2*	3.00	2.56^d
T3(B1)	π1σ1*	6.11	—	T3(A)	π3π1*	4.41	—	T3(A′′)	π1π3*	3.85	4.07	T3(B)	3.87	4.08	—	T3(B)	π1π3*	3.64
T4(A2)	π2σ1*	6.13	—	T4(B)	π4π1*	4.48	—	T4(A′)	π3π1*	4.30	4.41	T4(A)	4.29	4.39	—	T4(A)	π2π1*	4.16

---

In 1T the T₃ and T₄ states have πσ* character and lie substantially above the S₁ state. The energy gap to the T₂ state with ππ* character is also large (0.83 eV). In 2T more ππ* states exist due to the extension of the system. T₂ and T₃ are such additional ππ* states and lie below the S₁ state with a small S₁–T₃ energy gap of only 0.10 eV (see Table 1). The T₄ state has comparable character to the T₂ state of 1T and is nearly isoenergetic with the S₁ state in agreement with a previous study.⁴⁸ Also in the larger oligothiophenes the four lowest triplet states are characterized by ππ* excitations, whereby the T₄ state becomes more localized for 3T and 4T and therewith shifts slightly above the S₁ state. In 3T the S₁ state is energetically close to the T₃ state. At the CASPT2 level of theory only the inclusion of all π-orbitals in the active space results in the correct electronic state order consistent with the CCSD results. The use of a smaller active space leads to artificial stabilization of the S₁ state with respect to the triplet states shifting it below the T₃ state⁵⁹ (see Table S11 in the ESI†). Also in 4T the S₁ state is only slightly above the T₃ state at the CCSD level of theory.

Of the studied molecules only 1T exhibits large singlet–triplet energy gaps at the FC point. In combination with the low-lying πσ* singlet state S₃ this gives a first hint why photoexcited 1T decays primarily via singlet states and no intersystem crossing occurs.^37,41–43 In contrast thereto, the oligothiophenes 2T–4T show small singlet–triplet energy gaps, which however increase with the chain length (0.03 eV for 2T, 0.18 eV (C_s) and 0.21 eV (C₂) for 3T and 0.36 eV for 4T). This is consistent with the experimental observation of extremely high triplet quantum yields for the oligothiophenes, which however decrease again with size (0.99 for 2T, 0.95 for 3T and 0.73 for 4T).²⁵ The details of the relaxation pathways of the different systems will be discussed in the next sections.

3.2 Deactivation pathways

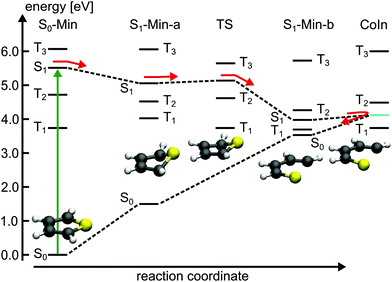
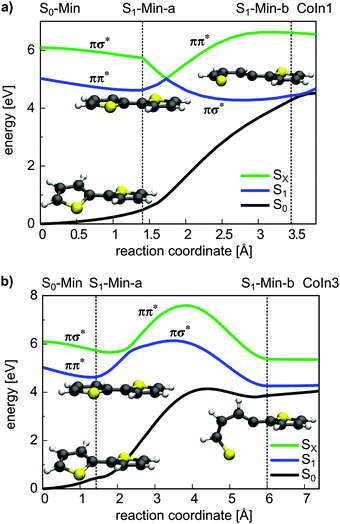
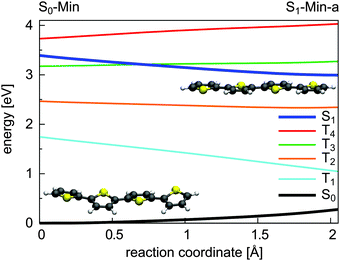
For 1T–3T all results are at the CASPT2 level of theory and when possible confirmed by CCSD calculations. For the larger 4T system the CCSD and TDDFT methods were used.

3.2.1 Thiophene (1T). For thiophene it was demonstrated by theory^41–44 and experiment³⁷ that after excitation to the S₁(ππ*) state, it quickly relaxes to the local S₁ minimum (S₁-Min-a, Fig. 2). This process is described by a time constant of 80 fs.³⁷ Thereafter the main part of the population overcomes a barrier to reach the global minimum of the S₁ state (S₁-Min-b). This relaxation is characterized by a ring-opening via the dissociative πσ* character and a time constant of 25 fs leading to C–S bond cleavage. In the vicinity of S₁-Min-b, a conical intersection (CoIn) with the ground state, associated with a small barrier of 0.06 eV,⁴³ completes the ultrafast internal conversion.

Fig. 2 Schematic illustration of the proposed deactivation mechanism of 1T after excitation to the S₁ state. The deactivation pathway is represented by red arrows. The S₁/S₀ CoIn is indicated by cyan line. The relevant optimized geometries are shown as well.

So far the barrier height for the ring-opening from S₁-Min-a to S₁-Min-b was estimated by linear interpolation at the CCSD level of theory to be 0.26 eV and understood as a consequence of an avoided crossing.⁴³ We were able to locate the transition state (TS) separating the two S₁ minima at the CASPT2 level of theory (Fig. 2, for details, see Fig. S2 and Table S6 in the ESI†). Therewith the barrier height is reduced to 0.07 eV. We also found that the CoIn is part of a low lying and thus very efficient seam along the d_SCCC dihedral angle (see Fig. S3 and S4 in the ESI†).

Salzmann et al.⁴¹ argued that due to vanishing spin–orbit coupling (SOC) and large S₁–triplet energy gaps at the FC point and at S₁-Min-a (see Fig. 2) a notable probability for ISC may only exist along the ring-opening path. However the ISC has to compete with the highly effective irreversible ring-opening path through the CoIn seam. Thus our additional results further support the interpretation that thiophene after excitation to the S₁ state decays mainly via its singlet electronic states, which is consistent with the observed dynamics and the absence of fluorescence and phosphorescence.³⁷

3.2.2 Bithiophene (2T).
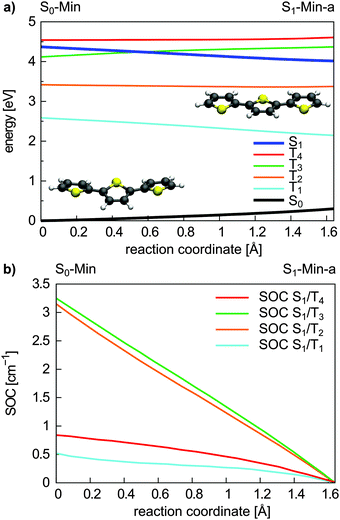
Triplet states and intersystem crossing. In 2T the triplet states T₄ and T₃ are below and close to the S₁ state at the FC point. Optimization of the S₁ state leads to the conversion of the non-planar structure to a planar minimum with C_2h symmetry (S₁-Min-a) and lowers its energy below the T₄ and T₃ states (see Table 2). We constructed a simplified reaction path RC_S by linear interpolation between the optimized S₀-Min and S₁-Min-a geometries. The calculated energies along the RC_S reveal the intersection of the S₁ state with the T₄ and T₃ states (Fig. 3a).

Table 2 Calculated CASPT2 vertical singlet and triplet excitation energies (eV) for the low-lying valence excited states of 2T at the ground-state (S₀-Min) and S₁ state (S₁-Min-a) minima. In addition the lowest excited singlet state with πσ* character is given (S₅). Oscillator strengths are shown in parentheses

State	Character	S0-Min (C2)		S1-Min-a (C2h)
		Sym.	CASPT2	Sym.	CASPT2	Exp.
a Maximum of the fluorescence spectrum in dioxane at room temperature.^25 b Photodetachment photoelectron spectrum in the gas phase.^47
S1	π1 → π1*	B	4.51 (0.45)	B u	3.71 (0.43)	3.43^a
S2	π4 → π1*	B	4.85 (0.14)	A g	4.22 (0.00)	—
S5	π1 → σ1*	A	5.40 (0.00)	A u	4.74 (0.00)	—
T1	π1 → π1*	B	2.86	B u	1.99	2.32^b
T2	π1 → π2*	A	3.82	A g	3.57	—
T3	π3 → π1*	A	4.41	A g	4.11	—
T4	π4 → π1*	B	4.48	B u	4.26	—

---

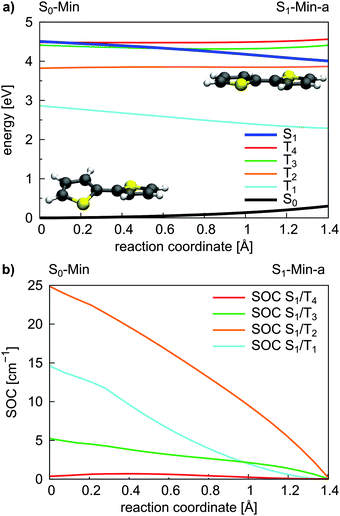Fig. 3 Energy profile of the S₀, the S₁ and the four lowest lying triplet states (a) and the SOC between the S₁ and triplet states (b) along the S₁ relaxation coordinate of 2T. The energy calculations were performed at the CASPT2/6-31G* level of theory and confirmed at the CCSD level (Fig. S9 in the ESI†). The SOCs were calculated using the CASSCF method. The reaction coordinate was generated by linear interpolation between the optimized S₀-Min and S₁-Min-a geometries.

For an effective ISC between singlet and triplet states, the spin–orbit coupling (SOC) should be reasonably strong and the states involved should be close in energy. First semiempirical calculations using the INDO/SCI approach showed for 2T, 3T and 6T that the SOC values decay with decreasing torsion angle α.⁶⁹ Since we are interested in the relaxation pathways from the S₁ state, we calculated the SOC between the S₁ and the four lowest lying triplet states along the reaction coordinate RC_S at the CASSCF level (Fig. 3b).

All SOC values also decrease along this coordinate and vanish at S₁-Min-a. Between S₁ and T₂/T₃ the SOC is zero for symmetry reasons, between S₁ and T₁/T₄ it vanishes, although the coupling is symmetry allowed. In general, for strong SOC, contributions from orbitals of heavy atoms have to be involved in the electronic configuration of the mixing states. The σ* orbital is localized on the S-atom and occurs via small πσ* contributions in the S₁ state of 2T. This πσ* contribution systematically decays along the RC_S as the planarization reduces the σ/π mixing. Correspondingly, all SOCs, also the symmetry allowed ones, decrease and vanish along this coordinate.

In view of the calculated SOC and the S₁–triplet energy gaps, the highest ISC probability along the relaxation coordinate RC_S exists with the T₃ state. The intermediate degeneracy of the S₁ and the T₃ states should compensate for their moderate spin–orbit interaction and allow a fast ISC. An example for such a scenario has been shown recently for uracil by Richter et al.⁷⁰ and has been discussed for benzene by Worth and co-workers.^71,72

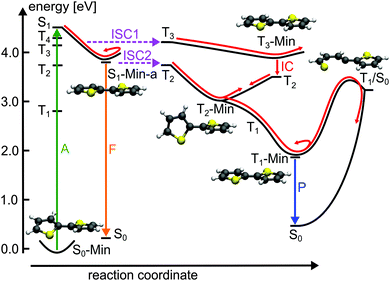
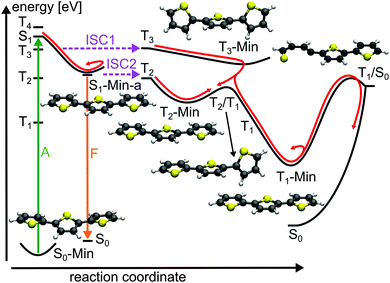
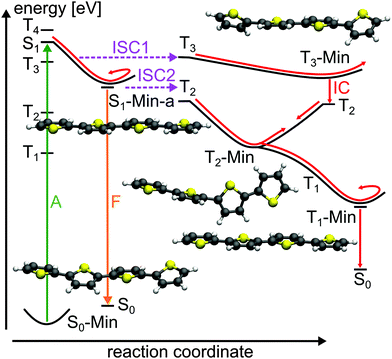
For the population that reaches S₁-Min-a a second ISC path opens between the S₁ and the T₂ states (ISC2, see Fig. 4). Here both states are close in energy and although the SOC vanishes at the minimum geometry, the torsional out-of-plane motion can induce moderate coupling. Such motions have been shown to be highly active during the S₁ dynamics of 2T–4T.^45,46

Fig. 4 Schematic illustration of the proposed deactivation mechanism of 2T after excitation to the S₁ state (A: absorption; F: fluorescence; ISC: intersystem crossing; IC: internal conversion; P: phosphorescence). The deactivation pathway is represented by red arrows. The relevant optimized geometries are shown as well.

The possibility of two ISC channels is consistent with the experimental observations of Paa et al.³⁴ using femtosecond time-resolved spectroscopy. They obtained a biexponential decay for the transient S₁ → S_n absorption (ESA) bands, with a fast (τ = 1.4 ps) and slow (τ = 29.6 ps) component. In addition the rise of the triplet–triplet absorption (TTA) is characterized by a fast time constant of 1.4 ps and a slower one of 58 ps. Therefore the authors proposed an ISC mechanism with two channels: the fast one starting from a twisted S₁ state geometry and taking place during the initial geometry relaxation. The second slower ISC channel starts from the relaxed S₁ state and competes with fluorescence from S₁-Min-a. Although the oscillator strength is reasonable at S₁-Min-a (see Table 2), the fluorescence quantum yield is reported to be small (ϕ_F = 0.014).²⁵ Thus we suggest that the major part of the S₁ population decays via the two ISC paths. The quantum yield ϕ_F of 2T is increased when the temperature is lowered from 298 to 77 K.²⁵ Under these conditions the first ISC path is less populated as the lower temperature enhances the planarity of the ground state.²⁵

Next we discuss the relaxation from T₃ and T₂ back to the ground state. The T₃ relaxation leads to the planar T₃ state minimum where the T₃ and T₂ states are close in energy (ΔE = 0.28 eV, see Table S8 in the ESI†). Therewith the T₂ state can also be populated by a fast internal conversion from T₃ (Fig. 4). T₂ is the only state considered which is described by an excitation to the π₂* orbital (see Table 2). This orbital is characterized by an antibonding π-interaction between the thiophene rings (see Fig. S5 in the ESI†), therefore the T₂ minimum is a twisted structure with orthogonal thiophene rings (T₂-Min, Fig. 4). At this minimum the T₂ state is degenerate with the T₁ state⁴⁷ (see Table S8 in the ESI†) suggesting the existence of a T₂/T₁ CoIn from where relaxation into the global excited state minimum T₁-Min (Fig. 4) can take place. The calculated vertical emission energy at this planar minimum is 1.77 eV and corresponds to the maximum of the phosphorescence spectrum (2.06 eV).³² Since the phosphorescence is weak (ϕ_P = 10⁻⁵),³² we conclude that by far most of the population return back to the ground state by a nonradiative process.²⁵ This process will be discussed in combination with a possible decay via CoIns in the next section.

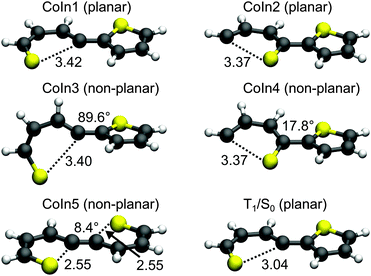
Conical intersections. A remaining question is why for 2T the deactivation path is dominated by ISC not by the ring-opening path via the S₁/S₀ CoIns which is the major path for 1T. We therefore optimized the S₁/S₀ CoIns and the S₁-Min-b minima for 2T. For 1T only one open-chain structure with a broken C–S bond is distinguishable. For the trans conformation of 2T several open-chain structures are possible. First of all four singly and six doubly opened geometries can be discriminated. The singly opened structures can be planar or non-planar and the inner or the outer C–S bond can be broken. The four optimized CoIns are shown in Fig. 5 (CoIn1–4) and are as in 1T in the vicinity of the S₁-Min-b minima. In all these structures the S₁ state has πσ* character while the S₀ state is the closed shell electronic configuration. The geometries of the CoIns1–4 and the S₁-Min-b minima are quite similar to the corresponding ones of 1T, e.g. the distances of the broken C–S bonds are nearly identical (1T CoIn: 3.41 Å). Also the barrier from the S₁-Min-b minima to the CoIns is at most 0.1 eV (Table 3) and mainly associated with a small elongation of the C–S bond (see Fig. S10 in the ESI†). CoIn1 and CoIn3 lie below and CoIn2 and CoIn4 above S₁-Min-a (see Table 3). The cleavage of an outer C–S bond leads to steric repulsion between the sulfur atom and the adjacent thiophene ring (see Fig. 5) resulting in the destabilization of CoIn2 and CoIn4. The cleavage of the inner C–S bonds leads to a lower steric repulsion and explains the stabilization of CoIn1 (0.2 eV) and CoIn3 (0.4 eV), whereby CoIn3 is the lowest intersection due to the orthogonal position of the thiophene rings.

Fig. 5 Optimized geometries of the conical intersections (CoIns) and the T₁/S₀ intersection of 2T obtained at the CASSCF/6-31G* level of theory. The distance of the broken C–S bonds are given in Angstrom (Å). For the non-planar geometries the torsional angle between the thiophene rings is also shown (defined by the S–C–C–S dihedral angle).

Table 3 Adiabatic CASPT2 excitation energies (eV) to the S₁-Min-b minima and the optimized CoIns. The stabilization energies of the CoIns relative to the S₁-Min-a are given. Negative values indicate destabilization. The barriers between S₁-Min-a and S₁-Min-b were obtained by linear interpolation between the optimized geometries and calculated at the CCSD/6-31G* level of theory

	CoIn1	CoIn2	CoIn3	CoIn4	CoIn5
S1-Min-b	3.75	4.13	3.58	4.12	—
Conical intersection	3.85	4.22	3.60	4.20	4.09
Stabilization energy	0.16	−0.21	0.41	−0.19	−0.08
Barrier	0.40	0.87	1.04	0.92	—

---

Based on these results we identified the most promising one of the six doubly opened geometries. The optimized non-planar structure CoIn5 (Fig. 5) shows that when two C–S bonds are broken the S₁/S₀ degeneracy is achieved already for smaller elongations of the C–S distance to 2.55 Å. Nevertheless CoIn5 lies above S₁-Min-a (Table 3) and is further neglected.

From the energetics at least CoIn1 and CoIn3 could be reached from S₁-Min-a. But the possible barriers in between have to be considered. This was investigated again by using simplified reaction paths RC_S2 constructed by linear interpolation between S₁-Min-a, S₁-Min-b and the respective CoIn. Based on the good agreement between CASPT2 and CCSD results obtained for the energy profile along the RC_S (see Fig. 3a and Fig. S9 in the ESI†), we calculated the four continuing ring-opening paths RC_S2 using the faster CCSD method. The single-reference method CCSD has previously been used to study the deactivation paths of thiophene⁴³ and furan⁷³ and was found to give energies of good quality even in the vicinity of CoIns. This is also found for the paths towards CoIn1/CoIn3 (Fig. 6) and CoIn2/CoIn4 (Fig. S11 in ESI†). The positions of the CoIns at the CCSD level are only slightly shifted with respect to the CASSCF results and thus the CCSD results are sufficiently accurate to estimate the barriers. The reported values for the barriers in Table 3 are an upper limit for the real ones. Optimization of the corresponding transition states would lower these barriers as shown for 1T (see Section 3.2.1). Nevertheless from the barrier heights one can see that CoIn1 is associated with the smallest barrier of 0.4 eV and the lowest CoIn (CoIn3) with a barrier of 1.0 eV. This can be understood as the geometrical distortion necessary to reach the non-planar CoIn3 from the planar S₁-Min-a is significantly larger than from the planar CoIn1. This is also reflected in the larger RC_S2 values for CoIn3 (Fig. 6b).

Fig. 6 Energetic course of the ground, ππ* and πσ* singlet states along the reaction path leading to CoIn1 (a) and CoIn3 (b). The energy calculations were performed at the CCSD/6-31G* level of theory. The reaction coordinates were generated by linear interpolation between the CASSCF optimized geometries. The positions of the minima and CoIns are indicated by vertical lines. The electronic character and the minimum structures are shown as well along each path.

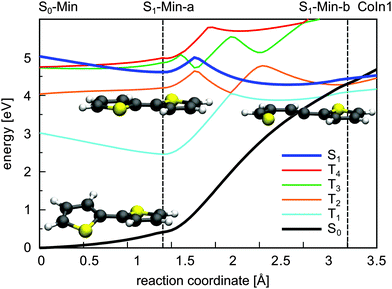
In summary, CoIn1 is the most favorable intersection of 2T and should be reachable due to an accumulated relaxation energy of 0.5 eV from the FC point to S₁-Min-a. Thus some of the excited molecules should decay to the ground state through this passage. This is, however, in contrast to the measured near-unity triplet quantum yield of 2T. A possible explanation is that also along the ring-opening path to CoIn1 the S₁ state can couple to the triplet states. We calculated the four lowest lying triplet states along this path and, indeed found several intersections between the S₁ and the triplet states (Fig. 7). In addition near and after the barrier strong SOC of the S₁ state with the triplet states occur (≈20–100 cm⁻¹, Table S9 in the ESI†) due to the rising πσ* character of the S₁ state.

Fig. 7 Adiabatic course of the S₀, the S₁ and the four lowest lying triplet states along the reaction path leading to CoIn1. The energy calculations were performed at the CCSD/6-31G* level of theory. The reaction coordinate was generated by linear interpolation between the CASSCF optimized geometries. The positions of the minima and CoIns are indicated by vertical lines. The minimum structures are shown as well along the path.

The results clearly elucidate why the deactivation path of 2T is dominated by ISC and the relaxation path of 1T by S₁/S₀ CoIns. First of all after excitation to the S₁ state only for 2T effective ISC possibilities exist during the initial motion (compare Fig. 2 and 3). Secondly the barrier to reach a CoIn is higher for 2T (0.40 eV) than for 1T (0.26 eV). And finally even if the barrier to the S₁/S₀ CoIn is overcome, the ISC to several triplet states is probable in 2T and depopulates the S₁ state.

The calculations along the ring-opening path RC_S2 (Fig. 7) also reveal the existence of a low lying intersection between the T₁ and the S₀ state. The optimized T₁/S₀ intersection is a planar structure with a broken C–S bond of 3.04 Å (Fig. 5) where the T₁ state has πσ* character and accordingly large SOC values with the S₀ state (≈100 cm⁻¹). This intersection found along the ring-opening path could also be responsible for the overall relaxation from the triplets back to the ground state. We therefore estimated the barrier from the endpoint of the triplet cascade, T₁-Min, to the T₁/S₀ intersection by linear interpolation at the CASPT2 level of theory (Fig. S12 in the ESI†). The calculated barrier height of 1.39 eV should account for the long triplet lifetime of 100 μs of 2T.²⁵ The reaction coordinate of this path is mainly characterized by an elongation of the C–S distance. As the gradient difference vector at the T₁/S₀ intersection is nearly orthogonal to this reaction coordinate (Fig. S10, ESI†), the probability for intersystem crossing is quite high after the system has crossed the barrier (for details, see ESI†). All in all the T₁/S₀ intersection completes the deactivation pathway of 2T.

3.2.3 Terthiophene (3T). In 3T for both nearly isoenergetic ground state minima (Section 3.1) the T₄ state is now above and the T₃ state is slightly below the bright S₁ state (see Table 4). Relaxation of the S₁ state again leads to a planar minimum (S₁-Min-a) with C_2v symmetry. The energy profiles are calculated at the CCSD/6-31G* level along the linear interpolated reaction coordinate RC_S between the isoenergetic ground state minima and S₁-Min-a. As in 2T the S₁ state intersects with the T₃ state (Fig. 8a and Fig. S19a, ESI†) and the SOC between the S₁ and the triplet states decrease along the RC_S and vanishes at the planar S₁-Min-a (Fig. 8b and Fig. S19b, ESI†). Analogous to 2T this can be understood by symmetry selection rules and varying πσ* contribution in the S₁ state. In the planar C_2v geometry the spin–orbit coupling between the S₁(B₁) and the T₁/T₃(B₁) is again symmetry forbidden. Overall the πσ* contribution in the S₁ state is smaller for 3T than for 2T resulting in generally lower SOC values. The intermediate degeneracy of the S₁ state and the T₃ state should again compensate their moderate spin–orbit interaction making T₃ the most probable candidate for an efficient ISC along the initial relaxation (ISC1, see Fig. 9). Like in 2T the T₂ and the S₁ state come closer during geometry relaxation to S₁-Min-a.⁵⁹ At the CCSD/6-31G* level the S₁–T₂ energy gap is still 0.64 eV (see Table S12 in the ESI†). But the gap reduces to 0.46 eV using the larger basis set 6-311+G** and approaches the value of 0.21 eV obtained at the CASPT2/6-31G* level (Table 4). Analogous to 2T for the second ISC process (ISC2, see Fig. 9) out of the S₁-Min-a some torsional vibrational activity is needed.

Table 4 Calculated CASPT2 vertical singlet and triplet excitation energies (eV) for the low-lying valence excited states of 3T at the ground-state (S₀-Min) and the S₁ state (S₁-Min-a) minima. Oscillator strengths are shown in parentheses

State	Character	S0-Min (Cs)		S1-Min-a (C2v)
		Sym.	CASPT2	Sym.	CASPT2	Exp.
a Maximum of the fluorescence spectrum in dioxane at room temperature.^25 b At S1-Min-a the S2 state is described by an double excitation (π1 ⇉ π1*). c Photodetachment photoelectron spectrum in the gas phase.^47
S1	π1 → π1*	A′′	4.03 (0.55)	B 1	3.08 (0.68)	2.91^a
S2	π2 → π1*	A′′	4.42 (0.06)	A 1	3.56 (0.00)	—
T1	π1 → π1*	A′′	2.40	B 1	1.75	1.90^c
T2	π1 → π2*	A′	3.19	A 1	2.87	2.99^c
T3	π1 → π3*	A′′	3.85	B 1	3.81	—
T4	π3 → π1*	A′	4.30	A 1	4.19	—

---

Fig. 8 Energy profile of the S₀, the S₁ and the four lowest lying triplet states (a) and SOC between the S₁ and triplet states (b) along the S₁ relaxation coordinate of 3T. The energy calculations were performed at the CCSD/6-31G* level of theory and the SOCs were calculated with the CASSCF method. The reaction coordinate was generated by linear interpolation between the optimized S₀-Min (C_s symmetry) and S₁-Min-a (C_2v symmetry) geometries.

Fig. 9 Schematic illustration of the proposed deactivation mechanism of 3T after optical excitation to the S₁ state (A: absorption; F: fluorescence; ISC: intersystem crossing). The deactivation pathway is represented by red arrows. The relevant optimized geometries are shown as well.

Also for 3T both ISC channels are confirmed by experimental results. Beyond that the experimental observations can now be understood more deeply. Rentsch and co-workers carried out femtosecond time-resolved spectroscopy with dependence on the excitation wavelength.^28,33,34 They observed a biexponential decay for the S₁ state with a fast and slow component occurring in parallel with the triplet formation. Both processes and the triplet quantum yield were found to depend on the excitation energy. At a wavelength of 400 nm (low-energy side of the S₀ → S₁ absorption band) the S₁ decay and the rise of the TTA are determined by the fluorescence lifetime of the S₁ state (165 ps).³⁴ With increasing excitation energies an additional fast channel for triplet formation with a time constant of about 2 ps occurs. The triplet quantum yield reaches a maximum value at 381 nm and remains constant up to 370 nm. Rentsch and co-workers suggested that the fast ISC channel is populated by excitation of non-planar molecules and opens while the planar S₁-Min-a is approached. With the low energy pulse mainly planar molecules are excited among the ensemble as the planar conformation has the lowest excitation energy.⁷⁴ The fast ISC channel is considered to be responsible for the highly effective triplet formation and has been quantified by temperature dependent measurements of the fluorescence quantum yield by Rossi et al.⁷⁵ They estimated that more than half of the T₁ population of 3T arises from this channel. The details of the two ISC channels are clearly elucidated by the results of the present work. Only if non-planar conformations are excited the fast ISC from the S₁ state to the T₃ state can happen. If planar conformations are excited thermal torsional vibrational activity can induce the second ISC from the S₁ to the T₂ state.

Like in 2T a remaining question is the possible role of S₁/S₀ CoIns as deactivation path. Based on the results of 2T we focused on the most promising one and optimized a planar S₁/S₀ conical intersection with a singly broken C–S bond. We also located the corresponding S₁ minimum (S₁-Min-b), which was found again in the vicinity of the CoIn. The barrier between S₁-Min-a and S₁-Min-b was estimated by linear interpolation at the CCSD/6-31G* level of theory (see Fig. S20 in the ESI†). The optimized CoIn geometry (Fig. 10) is similar to the ones of the smaller systems, only the C–S distance (3.69 Å) is slightly larger than in 2T (3.42 Å) and 1T (3.41 Å).

Fig. 10 Optimized geometries of the conical intersection (CoIn) and the T₁/S₀ intersection of 3T obtained at the CASSCF/6-31G* level of theory. The distance of the broken C–S bonds are given in Angstrom (Å).

In Table 5 the relevant points of the pathway to the CoIns are compared for 1T–3T. The adiabatic energy difference in the CoIns stays in the same range while the S₁ (ππ*) state is significantly stabilized at the FC point and at S₁-Min-a due to the increased π system. At the CoIns the S₁ state has πσ* character and is thus more localized and does not profit to the same extent from the elongation of the π-system. The significant lowering of the ππ* relative to the πσ* character in the S₁ state is also reflected by the increased barrier between S₁-Min-a and S₁-Min-b from 1T to 3T inhibiting the passage to the S₁/S₀ CoIn for the oligothiophenes. The higher barrier for 3T relative to 2T is confirmed by the even smaller rate constant for internal conversion.²⁵ The low barrier for 1T can be further understood comparing the structures of the S₁-Min-a minima. Only in 1T it is non-planar (Fig. 2) and the C–S bond is already slightly elongated in comparison to S₀-Min. Thus in 1T the initial relaxation is directed towards the ring-opening while the initial relaxation of 2T and 3T is characterized by inter-ring rotation leading to planar geometries.

Table 5 Adiabatic excitation energies (eV) of the S₁ state at the FC point, S₁ minima (S₁-Min-a and S₁-Min-b) and at the CoIn of 1T, 2T (CoIn1) and 3T at the CASPT2/6-31G* level of theory. The barriers between S₁-Min-a and S₁-Min-b were obtained by linear interpolation between the optimized geometries and calculated using the CCSD method. The value for the barrier of 1T is taken from ref. 17

	1T	2T	3T
FC point	5.58	4.51	4.03
S1-Min-a	5.07	4.01	3.27
S1-Min-b	4.00	3.75	4.16
Conical intersection	4.08	3.85	4.32
Barrier	0.26	0.40	0.81

---

From the planar S₁-Min-a the ring-opening path is thus highly unlikely for 3T. Even if the high barrier is overcome, several intersections of the S₁ state with the triplet states (see Fig. S20 in the ESI†) with strong SOC (≈20–100 cm⁻¹, Table S15 in the ESI†) exist and would again induce ISC. Another deactivation possibility out of S₁-Min-a is fluorescence. The S₁ state has a reasonable oscillator strength and the calculated vertical energy compares well with the maximum of the fluorescence spectrum (see Table 4). The higher fluorescence quantum yield of 3T (ϕ_F = 0.054) in comparison to 2T (ϕ_F = 0.024)²⁵ can be explained by the lower SOC values along the initial relaxation towards S₁-Min-a and the higher barrier for the ring-opening path. Still the major part of the S₁ population decays via ISC.

The depopulation pathways of the triplet states proceeds again via a cascade. Relaxation of the T₃ state leads to its minimum. Like the T₂ state of 2T the T₃ state of 3T is described by an excitation to an antibonding π-orbital (π₃*, Table 4) with nodal planes between the thiophene rings (see Fig. S14 in the ESI†). Accordingly, the T₃ minimum is a twisted structure with orthogonal thiophene rings (T₃-Min, Fig. 9). At this minimum the first three triplet states are close in energy (see Table S14 in the ESI†) and a fast internal conversion from T₃ to T₂ or T₁ can happen. The T₂ minimum is planar (T₂-Min, Fig. 9) and in contrast to the non-planar T₂-Min of 2T now an energy gap of 0.76 exists between T₂ and T₁ and a barrier of 0.32 eV has to be overcome to reach the T₂/T₁ conical intersection. The T₂/T₁ conical intersection is characterized by one terminal thiophene ring being orthogonal to two planar thiophene rings (Fig. 9). In T₁ the global excited state minimum is reached, which is again planar (Fig. 9). As no phosphorescence was detected,²⁵ a possible relaxation back to the ground state is again via the T₁/S₀ intersection with one broken C–S bond (Fig. 10). We estimated again the barrier between T₁-Min and T₁/S₀ by interpolation at the CCSD level of theory. The high value of 2.17 eV to reach this intersection could account for the long triplet lifetime of 3T.²⁵ But after crossing this barrier, the probability for intersystem crossing is quite high like in 2T (for details, see ESI†).

3.2.4 Quaterthiophene (4T). For 3T we showed that only the inclusion of all π-orbitals in the active space of the CASPT2 calculations results in the correct electronic state order of the S₁ and the triplet states. This order, especially T₃ below S₁ at the FC point, proved to be crucial to understand and explain the ISC processes resulting in high triplet quantum yields of 2T and 3T. For 4T such an active space means 24 electrons in 20 orbitals. In spite of symmetry restrictions, this active space is too large to be handled within a reasonable computation time. Due to the good agreement of the CCSD and TDDFT results with the CASPT2 results for 1T–3T (see Tables S1–S4 in the ESI†), we studied 4T using the faster CCSD and TDDFT methods. The choice of these methods allows no calculation of the SOC and we can only extrapolate from our knowledge of 2T and 3T. The depopulation of the S₁ state occurs via ISC as in the smaller oligothiophenes. The initial relaxation leads to the planar S₁-Min-a, the T₃ state intersects with the S₁ state (see Table 6 and Table S16 (ESI†) and Fig. 11) and should allow for the fast ISC channel (ISC1, Fig. 12). For the second ISC channel (ISC2) out of S₁-Min-a to the T₂ state torsional vibrational activity is again necessary to induce SOC between T₂ and S₁. For symmetry reasons the SOC between the S₁(B_u) and the T₃(B_u) is allowed at both the twisted S₀-Min and the planar S₁-Min-a geometries, while the SOC between the S₁(B_u) and the T₂(A_g) is allowed only for the twisted S₀-Min.

Table 6 Calculated CCSD vertical singlet and triplet excitation energies (eV) for the low-lying valence excited states of 4T at the ground-state (S₀-Min) and the S₁ state (S₁-Min-a) minima. Oscillator strengths are shown in parentheses

State	Character	S0-Min (C2)		S1-Min-a (C2h)
		Sym.	CCSD	Sym.	CCSD	Exp.
a Maximum of the fluorescence spectrum in dioxane at room temperature.^25 b Photodetachment photoelectron spectrum in the gas phase.^47
S1	π1 → π1*	B	4.00 (1.30)	B u	3.30 (1.40)	2.59^a
S2	π1 → π2*	A	4.89 (0.00)	A g	4.40 (0.00)	—
T1	π1 → π1*	B	2.36	B u	1.59	1.75^b
T2	π1 → π2*	A	3.00	A g	2.58	2.56^b
T3	π1 → π3*	B	3.64	B u	3.44	—
T4	π2 → π1*	A	4.16	A g	4.14	—

---

Fig. 11 Energy profile of the S₀, the S₁ and the four lowest lying triplet states along the S₁ relaxation coordinate of 4T. The energy calculations were performed at the TDDFT/6-31G* level of theory. The reaction coordinate was generated by linear interpolation between the optimized S₀-Min (C₂ symmetry) and S₁-Min-a (C_2h symmetry) geometries.

Fig. 12 Schematic illustration of the proposed deactivation mechanism of 4T after excitation to the S₁ state (A: absorption; F: fluorescence; ISC: intersystem crossing; IC: internal conversion). The deactivation pathway is represented by red arrows. The relevant optimized geometries are shown as well.

Our conclusions are supported by the slow (390 ps) and fast (36 ps) time constants measured for the decay of the fluorescence of 4T.²⁷ For comparison the fast time constant for this signal is found to be 16 ps for 3T while for the fast ESA decay and TTA rise it was 2 ps. The 390 ps time constant coincides well with the recently determined time constant for the TTA rise of 398 ps of 4T.⁴⁰ In addition a biexponential triplet formation was mentioned for 4T.³¹ We assume that the fast ISC channel of 4T has not been observed until now as no femtosecond time-resolved measurements with dependence on the excitation wavelength were performed similar to 3T. Based on the presented results we suggest that also in 4T the fast ISC to the T₃ state accounts for the high triplet quantum yield of 0.73.²⁵ Reasons for the decreasing triplet quantum yield from 2T to 4T are the diminishing SOC values along the initial relaxation (ISC1) and the increasing S₁–T₂ energy gap at S₁-Min-a (ISC2) (see Table S18 in the ESI†), also shown by photodetachment photoelectron spectroscopy.⁴⁷

The return from the triplets back to the ground state involves similar steps as in 2T. T₃ relaxation leads to its minimum where the outer thiophene rings are twisted versus the two planar inner rings (Fig. 12) due to the π₃*-orbital (Table 6) characterizing nonbonding and bonding interactions between the thiophene rings (see Fig. S23 in the ESI†). The moderate T₃–T₂ energy gap of 0.41 eV at T₃-Min suggests the possibility of an internal conversion to T₂. From there the T₂ minimum can be reached characterized by an orthogonal arrangement of the thiophene rings with respect to the central bond (Fig. 12) due to the π₂* orbital (see Fig. S23 in the ESI†). At T₂-Min the T₂ and T₁ states are degenerated like in 2T (see Table S17 in ESI†), leading to fast internal conversion to T₁. In T₁ the global excited state minimum is reached, which is again planar (see Fig. 12). As no phosphorescence was detected,²⁵ an ISC like in 2T and 3T should lead the molecule back to the ground state. The smaller T₁–S₀ energy gap of 1.0 eV (CCSD/6-31G* level) at the T₁-Min in comparison to 3T (1.42 eV) and 2T (1.77) could account for the decreasing triplet lifetime from 2T to 4T.²⁵ Although the fluorescence from S₁ is increased compared to 2T and 3T,²⁵ the major part of the 4T population still relaxes to the ground state via ISC and triplet states.

4 Conclusions

For thiophene 1T and the oligothiophenes 2T–4T the relaxation processes from the first excited singlet state were investigated using quantum chemical calculations. We demonstrated that 1T decays primarily via its singlet states. Due to large singlet–triplet energy gaps intersystem crossing (ISC) is ineffective, while internal conversion via a low lying S₁/S₀ conical intersection (CoIn) seam is associated with a very small barrier and thus highly efficient. In contrast the deactivation paths of the oligothiophenes are dominated by ISC. The S₁/S₀ CoIns are inactive although their energetic position with respect to the ground state minimum is similar for all systems. However, the excited S₁ state is significantly stabilized with increasing chain length due to its ππ* character in the Franck–Condon (FC) region and at the S₁ minimum (S₁-Min-a). At the S₁/S₀ CoIns the S₁ state character has changed to πσ* which is more localized and does not profit to the same extent from the elongation of the π-system. Thus in the oligothiophenes the barriers towards the CoIns are increased and inhibit the passage through them. Furthermore the extension of the π-system induces more ππ* states and shifts the triplet state T₃ below and close to the S₁ state at the FC point for all investigated oligothiophenes. During the initial relaxation from the non-planar conformation to the planar S₁-Min-a the T₃ state intersects with the S₁ state opening the first ISC path. Around S₁-Min-a thermal torsional fluctuations can induce the second, less effective ISC channel with the T₂ state. In view of the experimental findings and our results, we conclude that the first ISC channel is responsible for the high triplet quantum yields. Hereby we can say that the correlation between the planarization and the ISC is the key property. The overall diminishing SOC from 2T to 4T and the increasing S₁–T₂ energy gaps at S₁-Min-a should account for the slightly decreasing triplet and increasing fluorescence quantum yields.²⁵ A quantitative determination of the rate constants and branching ratios of the two ISC channels would require dynamical studies but these are clearly beyond the scope of the present work. The return from the triplets back to the ground state is made possible by inter-ring torsions and T₁/S₀ intersections, the latter are characterized by open-ring structures similar to the S₁/S₀ CoIns of 1T. We found two different kinds of triplet relaxation. For the even-numbered oligothiophenes we found a T₃ → T₂ → T₁ cascade, while for the odd oligothiophene an additional direct T₃ → T₁ path exists.

The present results in combination with previous theoretical and experimental observations offer a quite complete picture of the photophysics of 1T–4T and allow making predictions for the longer oligothiophenes. Also for the longer oligothiophenes and polythiophenes triplet formation has been observed.^25,76–79 From our results for 2T–4T we extrapolate that the first ISC path should be present as well and non-planarity should enhance its efficiency. Preliminary calculations for 5T–10T show, with the exception of 6T, an intersection of the S₁ state with a triplet state along the planarization to S₁-Min-a (see Tables S19 and S20 in the ESI†). The special behavior of 6T is consistent with its highest fluorescence quantum yield (ϕ_F) in the row from 2T to 7T.²⁵ Furthermore for polythiophenes in solution and films it was shown that ϕ_F decreases due to more efficient nonradiative decay channels when the non-planarity of the thiophene backbone is increased by substitution.⁸⁰ The higher degree of non-planarity should enhance the SOC and prolong the interaction time for the ISC. As triplet states are also present in polythiophene-based solar cells^81,82 a deeper understanding of the relaxation processes and the factors influencing the efficiency of these processes should be a first step in improving the performance of the thiophene-based devices.

Acknowledgements

Financial support of this work from the Deutsche Forschungsgemeinschaft through the SFB749 and the excellence cluster ‘Munich-Centre for Advanced Photonics’ (MAP) is gratefully acknowledged. We thank Alexander André and Moritz Hönig for their contribution to the initial calculations of 1T and 2T.

References

1. Handbook of Conducting Polymers, ed. T. A. Skotheim and J. R. Reynolds, CRC Press, Boca Raton, FL, 3rd edn, 2007.
2. Handbook of Thiophene-Based Materials: Applications in Organic Electronics and Photonics, ed. I. F. Perepichka and D. F. Perepichka, John Wiley & Sons Ltd, Chichester, UK, 2007.
3. B. L. Rupert, W. J. Mitchell, A. J. Ferguson, M. E. Köse, W. L. Rance, G. Rumbles, D. S. Ginley, S. E. Shaheen and N. Kopidakis, J. Mater. Chem., 2009, 19, 5311–5324.
4. F. Zhang, D. Wu, Y. Xu and X. Feng, J. Mater. Chem., 2011, 21, 17590–17600.
5. G. Gigli, O. InganKäs, M. Anni, M. De Vittorio, R. Cingolani, G. Barbarella and L. Favaretto, Appl. Phys. Lett., 2001, 78, 1493–1495.
6. M. Mazzeo, D. Pisignano, L. Favaretto, G. Barbarella, R. Cingolani and G. Gigli, Synth. Met., 2003, 139, 671–673.
7. M. Irie, T. Fukaminato, K. Matsuda and S. Kobatake, Chem. Rev., 2014, 114, 12174–12277.
8. G. Barbarella, M. Zambianchi, A. Ventola, E. Fabiano, F. Della Sala, G. Gigli, M. Anni, A. Bolognesi, L. Polito, M. Naldi and M. Capobianco, Bioconjugate Chem., 2006, 17, 58–67.
9. H.-A. Ho, A. Najari and M. Leclerc, Acc. Chem. Res., 2008, 41, 168–178.
10. M. Zambianchi, F. D. Maria, A. Cazzato, G. Gigli, M. Piacenza, F. D. Sala and G. Barbarella, J. Am. Chem. Soc., 2009, 131, 10892–10900.
11. R. Håkansson, B. Nordén and E. W. Thulstrup, Chem. Phys. Lett., 1977, 50, 306–308.
12. D. Birnbaum and B. E. Kohler, J. Chem. Phys., 1989, 90, 3506–3510.
13. H. Chosrovian, S. Rentsch, D. Grebner, D. Dahm, E. Birckner and H. Naarmann, Synth. Met., 1993, 60, 23–26.
14. D. Lap, D. Grebner, S. Rentsch and H. Naarmann, Chem. Phys. Lett., 1993, 211, 135–139.
15. R. Rossi, M. Ciofalo and P. Glauco, J. Photochem. Photobiol., A, 1993, 70, 59–67.
16. S. Yamaguchi and H.-o. Hamaguchi, Chem. Phys. Lett., 1994, 227, 255–260.
17. J. E. Chadwick and B. E. Kohler, J. Phys. Chem., 1994, 98, 3631–3637.
18. W. J. Buma, B. E. Kohler and T. A. Shaler, J. Phys. Chem., 1994, 98, 4990–4992.
19. M. Belletête, M. Leclerc and G. Durocher, J. Phys. Chem., 1994, 98, 9450–9456.
20. R. Colditz, D. Grebner, M. Helbig and S. Rentsch, Chem. Phys., 1995, 201, 309–320.
21. R. S. Becker, J. Seixas de Melo, A. L. Maçanita and F. Elisei, Pure Appl. Chem., 1995, 67, 9–16.
22. D. Grebner, M. Helbig and S. Rentsch, J. Phys. Chem., 1995, 99, 16991–16998.
23. G. Lanzani, M. Nisoli, S. De Silvestri and R. Tubino, Chem. Phys. Lett., 1996, 251, 339–345.
24. P. Landwehr, H. Port and H. Wolf, Chem. Phys. Lett., 1996, 260, 125–129.
25. R. S. Becker, J. Seixas de Melo, A. L. Maçanita and F. Elisei, J. Phys. Chem., 1996, 100, 18683–18695.
26. D. V. Lap, D. Grebner and S. Rentsch, J. Phys. Chem. A, 1997, 101, 107–112.
27. A. Yang, M. Kuroda, Y. Shiraishi and T. Kobayashi, J. Phys. Chem. B, 1998, 102, 3706–3711.
28. W. Paa, J.-P. Yang, M. Helbig, J. Hein and S. Rentsch, Chem. Phys. Lett., 1998, 292, 607–614.
29. N. DiCésare, M. Belletête, M. Leclerc and G. Durocher, Chem. Phys. Lett., 1998, 291, 487–495.
30. N. DiCésare, M. Belletête, C. Marrano, M. Leclerc and G. Durocher, J. Phys. Chem. A, 1999, 103, 795–802.
31. J. Yang, W. Paa and S. Rentsch, Synth. Met., 1999, 101, 624–625.
32. S. Rentsch, J. P. Yang, W. Paa, E. Birckner, J. Schiedt and R. Weinkauf, Phys. Chem. Chem. Phys., 1999, 1, 1707–1714.
33. J.-P. Yang, W. Paa and S. Rentsch, Chem. Phys. Lett., 2000, 320, 665–672.
34. W. Paa, J.-P. Yang and S. Rentsch, Appl. Phys. B: Lasers Opt., 2000, 71, 443–449.
35. W. Paa, J.-P. Yang and S. Rentsch, Synth. Met., 2001, 119, 525–526.
36. H. Haberkern, K. R. Asmis, M. Allan and P. Swiderek, Phys. Chem. Chem. Phys., 2003, 5, 827–833.
37. R. Weinkauf, L. Lehr, E. W. Schlag, S. Salzmann and C. M. Marian, Phys. Chem. Chem. Phys., 2008, 10, 393–404.
38. D. M. P. Holland, A. B. Trofimov, E. A. Seddon, E. V. Gromov, T. Korona, N. de Oliveira, L. E. Archer, D. Joyeux and L. Nahon, Phys. Chem. Chem. Phys., 2014, 16, 21629–21644.
39. J. Zhou, W. Yu and A. E. Bragg, J. Phys. Chem. Lett., 2015, 6, 3496–3502.
40. S.-m. Sun, S. Zhang, K. Liu, Y.-p. Wang and B. Zhang, Photochem. Photobiol. Sci., 2015, 14, 853–858.
41. S. Salzmann, M. Kleinschmidt, J. Tatchen, R. Weinkauf and C. M. Marian, Phys. Chem. Chem. Phys., 2008, 10, 380–392.
42. X.-F. Wu, X. Zheng, H.-G. Wang, Y.-Y. Zhao, X. Guan, D. L. Phillips, X. Chen and W. Fang, J. Chem. Phys., 2010, 133, 134507.
43. M. Stenrup, Chem. Phys., 2012, 397, 18–25.
44. G. Cui and W. Fang, J. Phys. Chem. A, 2011, 115, 11544–11550.
45. D. Fazzi, M. Barbatti and W. Thiel, Phys. Chem. Chem. Phys., 2015, 17, 7787–7799.
46. A. Prlj, B. F. E. Curchod and C. Corminboeuf, Phys. Chem. Chem. Phys., 2015, 17, 14719–14730.
47. S. Siegert, F. Vogeler, C. M. Marian and R. Weinkauf, Phys. Chem. Chem. Phys., 2011, 13, 10350–10363.
48. M. Rubio, M. Merchán, R. Pou-Amérigo and E. Ortí, ChemPhysChem, 2003, 4, 1308–1315.
49. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
50. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
51. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
52. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
53. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
54. H. A. Duarte, H. F. Dos Santos, W. R. Rocha and W. B. De Almeida, J. Chem. Phys., 2000, 113, 4206–4215.
55. P. Celani and H.-J. Werner, J. Chem. Phys., 2000, 112, 5546–5557.
56. J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039.
57. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
58. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665.
59. M. Rubio, M. Merchán and E. Ortí, ChemPhysChem, 2005, 6, 1357–1368.
60. M. Merchán, L. Serrano-Andrés, M. A. Robb and L. Blancafort, J. Am. Chem. Soc., 2005, 127, 1820–1825.
61. A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823–1833.
62. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
63. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2012.1, a package of ab initio programs, 2012, see http://www.molpro.net/.
64. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian Inc., Wallingford, CT, 2009.
65. M. Ciofalo and G. L. Manna, Chem. Phys. Lett., 1996, 263, 73–78.
66. S. Millefiori, A. Alparone and A. Millefiori, J. Heterocycl. Chem., 2000, 37, 847–853.
67. F. Liu, P. Zuo, L. Meng and S. J. Zheng, THEOCHEM, 2005, 726, 161–169.
68. G. Zerbi, B. Chierichetti and O. Ingänas, J. Chem. Phys., 1991, 94, 4637–4645.
69. D. Beljonne, Z. Shuai, G. Pourtois and J. L. Bredas, J. Phys. Chem. A, 2001, 105, 3899–3907.
70. M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Phys. Chem. Lett., 2012, 3, 3090–3095.
71. D. Parker, R. Minns, T. Penfold, G. Worth and H. Fielding, Chem. Phys. Lett., 2009, 469, 43–47.
72. T. Penfold and G. Worth, Chem. Phys., 2010, 375, 58–66.
73. M. Stenrup and A. Larson, Chem. Phys., 2011, 379, 6–12.
74. M. Breza, V. Lukeš and I. Vrábel, THEOCHEM, 2001, 572, 151–160.
75. W. Porzio, S. Destri, M. Mascherpa, S. Rossini and S. Brückner, Synth. Met., 1993, 55, 408–413.
76. B. Kraabel, D. Moses and A. J. Heeger, J. Chem. Phys., 1995, 103, 5102.
77. H. Burrows, J. Seixas de Melo, C. Serpa, L. Arnaut, M. G. Miguel, A. Monkman, I. Hamblett and S. Navaratnam, Chem. Phys., 2002, 285, 3–11.
78. S. Cook, A. Furube and R. Katoh, Energy Environ. Sci., 2008, 1, 294.
79. D. Sahoo, Y. Tian, G. Sforazzini, H. L. Anderson and I. G. Scheblykin, J. Mater. Chem. C, 2014, 2, 6601.
80. M. Theander, O. Inganäs, W. Mammo, T. Olinga, M. Svensson and M. R. Andersson, J. Phys. Chem. B, 1999, 103, 7771–7780.
81. Z. Xu and B. Hu, Adv. Funct. Mater., 2008, 18, 2611–2617.
82. M. Liedtke, A. Sperlich, H. Kraus, A. Baumann, C. Deibel, M. J. M. Wirix, J. Loos, C. M. Cardona and V. Dyakonov, J. Am. Chem. Soc., 2011, 133, 9088–9094.

---

Footnote

† Electronic supplementary information (ESI) available: Complete computational results and optimized geometries: Tables S1–S20 and Fig. S1–S23. See DOI: 10.1039/c5cp07634j

---