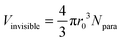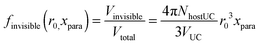Homogeneity of doping with paramagnetic ions by NMR

Abstract

In NMR, paramagnetic dopants change the relaxation behavior and the chemical shift of the nuclei in their immediate environment. Based on the concept that the “immediate environment” in a diamagnetic host material can be described as a sphere with radius r₀, we developed a function for the fraction of unperturbed nuclei (the fraction of nuclei outside the sphere) which gives a link between the effective radius and the doping concentration. In the case of a homogeneous doping scenario a characteristic dependence is observed in both theory and experiment. We validated the model on a sample series where paramagnetic Eu(II) ions are doped into crystalline SrH₂. The fraction of unperturbed nuclei was determined from the ¹H NMR signal and follows the predicted curve for a homogeneous doping scenario where the radius r₀ is 17 Å.

---

Introduction

Doping by paramagnetic ions enables the functionalization of inorganic materials such as phosphors^1–5 and semiconductors.^6–8 For example, one type of phosphor-converted white-light LED is realized with a diamagnetic SrSi₂O₂N₂ host doped with only 2% of Eu which yields quantum efficiencies as high as 91%.⁹ In the case of long lasting phosphors (LLPs), it has been observed that only a small fraction of the dopants participate in the process of phosphorescence.^10,11 Many long lasting phosphors are based on paramagnetic doping with rare-earth elements. Clearly, the distribution of paramagnetic dopant ions in the host lattice could affect the brightness,^12,13 the emission wavelength,¹⁴ the efficiency¹³ and the afterglow duration^15–17 of phosphors. One reason is the concentration quenching effect^10,18 which refers to the phenomenon that the luminescence yield decreases with increasing activator concentration at high concentrations. According to the statistical trap mechanism,^18–21 for the inorganic phosphors, the energy transfer probability increases dramatically if the activator ions are close to each other, due to the D⁻⁶ dependence (D is the distance between two activator centers) which relates to the electric dipole–dipole interaction nature of this energy transfer.

Therefore, homogeneous doping is often demanded in order to achieve optimal optical properties, and in fact methods such as the sol–gel method²² and the homogeneous precipitation²³ are often applied in phosphor synthesis to improve doping homogeneity.

What does “homogeneous doping” mean? According to the IUPAC gold book,²⁴ “homogeneous” refers to “the degree to which a property or a constituent is uniformly distributed throughout a quantity of material”. By this definition, a specific scale for the material's quantity is required over which a property is homogeneous. While glass appears homogeneous to the human eye at the wavelength of several hundred nanometers, its refractive index gives evidence of the inner disorder when going to shorter wavelengths, for example, under a scanning electron microscope (SEM) by the electron beam with wavelengths of few nm or Å.²⁵

The investigation of doping homogeneity can be achieved by different analytical techniques depending on the required length scale of homogeneity. Homogeneous doping is often assumed if the lattice parameters determined by X-ray diffraction follow Vegard's empirical law.^26,27 While neutron diffraction and some X-ray diffraction devices can be used to determine pair-distribution functions to study doping inhomogeneity,^28–30 this is hardly possible on standard laboratory X-ray diffractometers;³¹ optical spectroscopy techniques such as X-ray photoelectron spectroscopy (XPS)³² can provide the distribution of paramagnetic dopant ions on the surface but not in the bulk; another surface technique to study homogeneity is electron microscopy^33,34 which offers a direct image on spots of the surface of the sample down to the atomic scale. In addition, atomic probe tomography³⁵ can provide 3D pictures on the distribution of dopants down to nm and atomic scale.

Here we want to focus on magnetic resonance spectroscopy to study doping homogeneity. By electron spin resonance spectroscopy (ESR) information about the homogeneity of doping with paramagnetic atoms can be extracted via lineshape analysis^36,37 or by multipulse spectroscopy.³⁸ In this contribution we use nuclear magnetic resonance spectroscopy (NMR) to analyze the environment of the doped paramagnetic atoms to obtain information about their distribution in the diamagnetic host material. The advantage of this inverse approach as compared to ESR is that non-doped areas which are not visible in the ESR experiment are not overlooked. So far NMR studies of sample homogeneity^37,39–53 have focused on the variation of magnetization with the spin lattice relaxation time T₁. Often combined models are suggested which try to derive the observed relaxation time distribution from models taking into account spin-diffusion between nuclear spins and paramagnetic relaxation pathways of nuclear spin-systems. Models suggest that spin-diffusion only becomes efficient for nuclei outside a certain radius (the so called wipe-out radius^54–56) around the paramagnetic ion. Owing to the extremely fast relaxation mechanism near typical paramagnetic ions, the detection of the nuclei in their direct environment is technically quite difficult due to significant distortions in the measured relaxation distribution function. In addition, the paramagnetic shift due to Fermi-contact and pseudo-contact interactions might shift the resonance line out of the spectral window thereby rendering it non-observable.

Interestingly, although the effects induced by paramagnetic ions^53,57–59 regarding the paramagnetic shift, relaxation and lineshape (Fig. 1) are well understood, for example, ⁶Li MAS NMR spinning side band manifolds⁶⁰ and shifts⁶¹ are shown to be very sensitive to the nearest coordination sphere of Mn ions, to the best of our knowledge, the approach to simply quantify the signal intensity of the nuclei outside the wipe-out radius to study the doping homogeneity has not been used so far.

Fig. 1 A schematic sketch of a paramagnetic ion doped inorganic crystal structure and the possible corresponding paramagnetic ion induced effects (paramagnetic shift and broadening) in the solid state NMR spectra of X nuclei. M stands for the paramagnetic dopant ion, A is the to-be-substituted host ion while X refers to the NMR nuclei; d is the distance between the paramagnetic ion and the NMR nuclei, and r₀ is the wipe-out radius. The resonances of X nuclei become apparently non-observable or they “vanish” if d < r₀.

Based on the above considerations, the working hypothesis here is that the doping homogeneity on the atomic scale can be accessed by quantitative solid state NMR via the peak area measurements.

Experimental

Synthesis of Sr_1−xEu_xH₂ doping series

Eu is incorporated in the Sr metal before contacting with H₂ to make sure that the doping is as homogeneous as possible within the limit of the lab work. The starting materials and the metal hydride products are very sensitive to air and were therefore handled in an argon filled glove box. Strontium and europium were melted together in order to achieve optimal homogeneity as described in the earlier work.⁶² The resulting alloys were hydrogenated in an autoclave made from hydrogen resistant Nicrofer® 5219 alloy (Inconel 718) at 650 K and 100 bar hydrogen pressure. The europium content was determined by ICP-MS analysis. Further details of preparation, X-ray diffraction and chemical analysis can be found in earlier work.⁶²

Solid state NMR

The solid state NMR experiments were performed at 11.75 T on a Bruker Avance III NMR spectrometer equipped with a commercial 1.3 mm MAS probe at a ¹H frequency of 500 MHz under ambient conditions. The sample spinning frequency was 40 kHz.

The chemical shifts of ¹H are reported using the δ scale, relative to 1% tetramethylsilane (TMS) in CDCl₃.⁶³ The peak area quantification is based on the analysis of back-extrapolated spin-echo experiments.⁶⁴

The side bands were taken into consideration when calculating the peak area. An estimated error of 10% for the quantification against the external reference adamantane was taken into account subsequently. Peak areas were obtained by deconvolution with several Gaussian and Lorentzian functions using a home-written program.

Results and discussion

In order to test the hypothesis, we present a case study where we use crystalline SrH₂ as the host material doped with the paramagnetic ions of Eu(II). Strontium hydride and europium hydride form a solid solution Sr_1−xEu_xH₂ and show a Vegard²⁷ like behaviour,⁶⁵ which can be expected considering the crystal chemical similarities of strontium and europium hydrides.⁶⁶ The unit cell volume shows an approximate linear dependence on x for the full substitution range 0 ≤ x ≤ 1 (Fig. 2).

Fig. 2 Unit cell volumes as a function of the substitution degree x in Sr_1−xEu_xH₂ as determined by Rietveld refinement based on X-ray powder diffraction data. The dotted line represents a linear fit resulting in V(Sr_1−xEu_xH₂) = 1.8067(7)·10⁸ pm³ − 8.8(1)·10⁶ pm³·x.

The mole fraction of the paramagnetic dopant is defined as , where N_para and N_host refer to the number of dopant ions and the corresponding host sites that can be occupied by the dopant ions (for simplicity, they are written as the host ions in the rest of the paper). In this case, the dopant ion is Eu²⁺ and the host ion is Sr²⁺, therefore we specify the doping mole fraction of Eu as x_Eu in the figures.

In order to test our hypothesis, the correlation between x_para and the visible peak areas is first set up, and the experimentally visible H fraction f_visible was introduced. In the ideal case, with a suitable internal reference, the observed peak area fraction is a quantitative reflection of the visible H percentage. On the other hand, in the following sub-chapters, in all theoretical models, the visible H percentage is calculated as the ratio of the number of NMR “visible” ¹H nuclei, which are located outside of the Eu influencing spheres, to the total number of H atoms.

The presented analysis is organized in the following way. In the first part we present the experimental data obtained by quantitative ¹H NMR measurements and an empirical function for describing the observed findings. In the second part we discuss the assumptions made for deriving analytical functions for the fraction of visible ¹H atoms as a function of the doping concentration. In part three analytical functions are derived for describing the obtained NMR data for the statistical doping scenario.

We obtained quantitative ¹H NMR spectra of a doping series of Sr_1−xEu_xH₂. The NMR spectra (see ESI†) qualitatively show a decay of signal intensity for the ¹H peak found in the sample with the lowest doping mole fraction x = 10⁻⁸, and a broadening of the resonance with higher doping concentration x.

From the observed peak area per mole of sample (A/n) of Sr_1−xEu_xH₂ we define the ratio f_visible as . Here visible refers to nuclei whose ¹H NMR peaks remain approximately at the same position in the spectrum as a non-doped sample. For the following treatment we assume that the paramagnetic shift of atoms is the dominant reason why a nucleus becomes “invisible” in the above sense and we neglect the relaxation effects which can make the signal of a nucleus vanish in the dead-time delay of the probehead.

The ratio f_visible is experimentally accessible and plotted against x_Eu on a logarithmic scale, which, as expected, shows a simple behavior following a monotonous decay (see ESI†). Empirically the following function was found which can describe the experimental data (see ESI†):

The coefficients k₁ and k₂ were used as fitting parameters which took the values k₁ = 425 ± 113 and k₂ = 1.00 ± 0.04, respectively.

In order to derive analytical functions for f_visible = f_visible (x_para) we make a number of assumptions. We assume that all atoms inside a radial sphere of influence (called wipe-out radius r₀) around a paramagnetic atom (Fig. 3) will be shifted to an extreme spectral range which makes them virtually invisible to NMR experiments. The concept of a radial sphere of influence is well established (shell-of-influence model^43,67) and still questionable if one takes into account (1) the angular dependence of the hyperfine interaction, (2) the unrealistic, discontinuous consideration at the border between visible and invisible H atoms and (3) the possibility of multiple interactions with different Eu atoms, which could mutually cancel each other. On the other hand, the pseudo-contact shift carries a term with an inverse cubic distance dependence which corresponds to a strong radial dependence.

Fig. 3 A schematic drawing of the influence sphere model. M is the paramagnetic center while X represents the NMR nuclei. According to the influence sphere model, if the distance d_M−X between an X nucleus and the paramagnetic ion M is smaller than the wipe-out radius r₀, the X nucleus is not visible by NMR. On the other hand, the X nuclei with d_M−X > r₀ are visible by NMR.

In order to calculate the visible fraction f_visible as the visible volume divided by the total volume, the assumption about the number density of H ions has to be made first. Only in the condition that the number density is already approximately a constant at a distance smaller than the wipe-out radius, the oscillating error induced by the number density variation of the lattice at small distance can be neglected. The following is to show that the calculation system of 5 Å is enough for obtaining a fairly good (<20% error) number density approximation.

To evaluate the number density of H atoms, a discrete point-model based on the crystal structure may serve as a reference. Such models were implemented in Fortran90 (ESI†) to analyze different doping scenarios, however their analysis always requires full information about the unit cell which is hardly feasible in a general case. A more practical approach is to follow a continuous model, namely to calculate the expected number of observed nuclei around a dopant with the help of the average number density and the volume of a sphere. The difference between these two approaches becomes apparent from the normalized integral of the radial pair distribution function of Sr_1−xEu_xH₂ (Fig. 4). The better the continuous approximation the smaller the difference from 1.0. From the G_SrH(r) it becomes obvious that for spheres with a size bigger than 4.7 Å the errors in the number of atoms in the sphere deviates by less than 20% from the value expected from the number density. We conclude that the continuous approximation is acceptable given that the radius r₀ below which the ¹H nuclei become invisible is of the order of 10 to 20 Å.

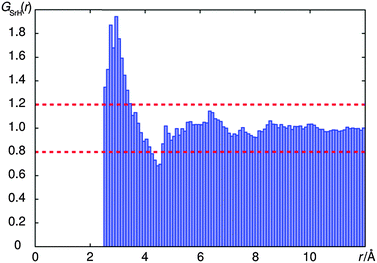Fig. 4 The integrated pair distribution function G_SrH(r) of SrH₂ calculated from the crystal structure by counting atoms on a grid of 0.1 Å.

The visible H fraction is easily counted for a statistical doping scenario for a given wipe-out radius r₀ with the help of a small computer program. By comparing the experimental plot with the calculated data for different assumed radii, the wipe-out radius can be estimated at around 17 Å with a convergence criterion of 3% for the lowest doping level (see ESI†).

An interesting question is how the empirical fitting function can be given a physical meaning in the sense that becomes a function of the wipe-out radius f_visible = f_visible(r₀,x_para) and the average number densities according to the crystal structure.

The approach we took is to calculate the regime of extreme low doping concentrations. For those the function f_visible = f_visible(r₀,x_para) should approach values calculated from the total volume V_invisible of all wipe-out spheres from the volume of an individual sphere multiplied by the number of dopants. These spheres are not likely to be superimposed at low concentration, which justifies the approach.

Here N_para is the number of dopant ions in the total volume of the crystal V_total. The doping mole fraction x_para helps relate N_para and the unit cell volume V_UC to the total volume of the crystal V_total. The term N_host UC refers to the number of “dopable” sites in the unit cell, in this example, the number of Sr atoms per unit cell.

Assuming equal ¹H number densities in each volume unit, the invisible fraction is proportional to the invisible volume ratio, which can be described as a function of the wipe-out radius r₀.

The pre-factor a in the empirical exponential fitting function f_visible(r₀,x_para) = exp(−ar₀³x_para) is fitted to be a = 0.0863 ± 0.0016, which shows a resemblance with the theoretical value , which can be explained mathematically by the Taylor expansion in the small x_para range:

By asymptotic analysis, as x_para approaches zero, the higher order terms can be neglected, and the following equation holds

f_visible(r₀,x_para) ∼ 1 −ar₀³x_para as x_para → 0

or written as , which shows a resemblance to the formula
with .

Due to the fact that the experimental data fit the calculated curve based on the statistical distribution model (see Fig. 5), we conclude that the SrH₂:Eu samples are homogeneously doped on the Å scale and this homogeneity refers to a statistical distribution of Eu²⁺ ions.

Fig. 5 The comparison of the visible H fraction f_visible calculated from the ¹H MAS NMR back extrapolated full echo series experiments⁶³ with error bars, calculated according to the statistical distribution model and the fitted function f_visible = exp(−ar₀³x_Eu) with a = 0.0863 ± 0.0016, plotted against the Eu doping mole fraction x_Eu in the log scale. The wipe-out radius r₀ is taken as 17 Å. The hollow circle, the hollow triangle and the dashed line represent the experimental data, the calculated data and the function plot, respectively. The dotted line at x_Eu ≈ 0.0163 is the cut-off concentration x₀ line, at which the f_visible approaches zero (f_visible < 0.1%).

A remaining question is if the wipe-out radius r₀ for a paramagnetic dopant ion is a constant or within a certain limit. If so, testing the homogeneity by a single NMR experiment could be feasible and promising. Here we provide an embryo idea for further NMR investigation by introducing a parameter, namely the cut-off mole fraction x₀. Based on the statistical distribution model, x₀ is defined that if a sample is statistically doped at the doping level x_para > x₀, then the macroscopic signal in the MAS NMR measurement is very weak or non-observable (f_visible < 0.1%), see Fig. 5.

To the best of our knowledge, the numeric value for the wipe-out radius r₀ has not been published before, and for the first time, we calculated the r₀ for Eu²⁺ to be around 17 Å. If the wipe-out radius r₀ would be approximately a calculable constant for Eu²⁺ in different host lattices, and if the empirical fitting function could be applied, then the doping homogeneity could be accessible by only one NMR experiment at the cut-off mole fraction x₀ together with a measurement of the non-doped sample.

Conclusions

The main question of this work is whether the paramagnetic doping homogeneity can be quantitatively investigated by solid state NMR. Based on the comparison of the experimental and the calculated data, we conclude that by applying a simple function f_visible(r₀,x_para) = exp(−ar₀³x_para) with which connects the wipe-out radius r₀ and the doping mole fraction x_para with the NMR visible signal fraction f_visible, the statistical doping scenario can be described adequately.

The above-mentioned method may serve as an efficient tool for quantitative analysis of the doping homogeneity of an arbitrary paramagnetic dopant in different host lattices, especially for the rare earth and transition metal elements. This may be helpful for applications such as the design of quantum dots and phosphors. The approach is hardly limited by the choice of the isotope as long as a signal can be obtained in 1D NMR spectroscopy. Thus studies even with less common NMR nuclei such as ⁷¹Ga, ⁷⁵As or ³⁷Cl are possible. This method is also applicable to homogeneity analysis of nano-scale materials on an Å scale.

Acknowledgements

The author would like to acknowledge Prof. Dr. Wolfgang Schnick and Dr. Thomas Bräuniger for providing access to the lab instrument and Christian Minke for technical support and maintenance of the NMR spectrometer.

References

1. R.-J. Xie, N. Hirosaki, Y. Li and T. Takeda, Materials, 2010, 3, 3777–3793.
2. K. Van den Eeckhout, P. F. Smet and D. Poelman, Materials, 2010, 3, 2536–2566.
3. W. Schnick, Phys. Status Solidi RRL, 2009, 3, A113–A114.
4. R. Mueller-Mach, G. Mueller, M. R. Krames, H. A. Höppe, F. Stadler, W. Schnick, T. Juestel and P. Schmidt, Phys. Status Solidi A, 2005, 202, 1727.
5. C. C. Lin and R.-S. Liu, J. Phys. Chem. Lett., 2011, 2, 1268–1277.
6. A. Bonanni, Semicond. Sci. Technol., 2007, 22, R41.
7. R. I. Epstein and M. Sheik-Bahae, Optical Refrigeration, Science and Applications of Laser Cooling of Solids, Wiley-VCH, 2009, pp. 1–32.
8. R. Jones, Opt. Mater., 2006, 28, 718–722.
9. V. Bachmann, C. Ronda, O. Oeckler, W. Schnick and A. Meijerink, Chem. Mater., 2008, 21, 316–325.
10. G. Blasse and B. C. Grabmaier, Luminescent Materials, Springer Berlin Heidelberg, Berlin, Heidelberg, 1994.
11. F. Clabau, X. Rocquefelte, T. Le Mercier, P. Deniard, S. Jobic and M.-H. Whangbo, Chem. Mater., 2006, 18, 3212–3220.
12. I. Yu and M. Senna, Appl. Phys. Lett., 1995, 66, 424–426.
13. W. Park, T. C. Jones, W. Tong, S. Schön, M. Chaichimansour, B. K. Wagner and C. J. Summers, J. Appl. Phys., 1998, 84, 6852–6858.
14. N. C. George, K. A. Denault and R. Seshadri, Annu. Rev. Mater. Res., 2013, 43, 481–501.
15. D. Poelman, N. Avci and P. F. Smet, Opt. Express, 2009, 17, 358–364.
16. F. Clabau, X. Rocquefelte, S. Jobic, P. Deniard, M.-H. Whangbo, A. Garcia and T. Le Mercier, Chem. Mater., 2005, 17, 3904–3912.
17. K. Van den Eeckhout, P. F. Smet and D. Poelman, Materials, 2011, 4, 980–990.
18. D. L. Dexter and J. H. Schulman, J. Chem. Phys., 1954, 22, 1063–1070.
19. T. Förster, Ann. Phys., 1948, 437, 55–75.
20. D. L. Dexter, J. Chem. Phys., 1953, 21, 836–850.
21. J. Knoester and J. E. V. Himbergen, J. Chem. Phys., 1987, 86, 3571–3576.
22. M. L. Pang, J. Lin, J. Fu, R. B. Xing, C. X. Luo and Y. C. Han, Opt. Mater., 2003, 23, 547–558.
23. Y. Kawahara, V. Petrykin, T. Ichihara, N. Kijima and M. Kakihana, Chem. Mater., 2006, 18, 6303–6307.
24. W. Horwitz, Pure Appl. Chem., 2009, 62, 1193–1208.
25. A. Ben-Yakar, R. L. Byer, A. Harkin, J. Ashmore, H. A. Stone, M. Shen and E. Mazur, Appl. Phys. Lett., 2003, 83, 3030.
26. L. Vegard, Z. Phys., 1921, 5, 17–26.
27. L. Vegard and H. Dale, Z. Kristallogr., Kristallgeom., Kristallphys., Kristallchem, 1928, 67, 148–162.
28. E. S. Božin, G. H. Kwei, H. Takagi and S. J. L. Billinge, Phys. Rev. Lett., 2000, 84, 5856–5859.
29. S. J. L. Billinge, T. Proffen, V. Petkov, J. L. Sarrao and S. Kycia, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 1203–1211.
30. J. Huang, J. Xu, H. Luo, X. Yu and Y. Li, Inorg. Chem., 2011, 50, 11487–11492.
31. C. Michaelsen, Philos. Mag. A, 1995, 72, 813–828.
32. C. Dong, J. Pichaandi, T. Regier and F. C. J. M. van Veggel, J. Phys. Chem. C, 2011, 115, 15950–15958.
33. J. Liu, J. Electron Microsc., 2005, 54, 251–278.
34. R. Pantel and G. Servanton, in Transmission Electron Microscopy in Micro-Nanoelectronics, ed. A. Claverie and M. Mouis, John Wiley & Sons, Inc., 2012, pp. 37–64.
35. G. Scappucci, W. M. Klesse, L. A. Yeoh, D. J. Carter, O. Warschkow, N. A. Marks, D. L. Jaeger, G. Capellini, M. Y. Simmons and A. R. Hamilton, Sci. Rep., 2015, 5, 12948.
36. C. P. Poole and H. A. Farach, Bull. Magn. Reson., 1979, 1, 162–194.
37. S. Sen and J. F. Stebbins, J. Non-Cryst. Solids, 1995, 188, 54–62.
38. R.-A. Eichel, J. Am. Ceram. Soc., 2008, 91, 691–701.
39. N. Bloembergen, Physica, 1949, 15, 386–426.
40. P.-G. de Gennes, J. Phys. Chem. Solids, 1958, 7, 345–350.
41. W. W. Simmons, W. J. O'Sullivan and W. A. Robinson, Phys. Rev., 1962, 127, 1168–1178.
42. H. E. Rorschach Jr., Physica, 1964, 30, 38–48.
43. C. D. Jeffries, Proc. Phys. Soc., 1966, 88, 257–258.
44. G. R. Khutsishvili, Phys.-Usp., 1966, 8, 743–769.
45. I. J. Lowe and S. Gade, Phys. Rev., 1967, 156, 817–825.
46. I. J. Lowe and D. Tse, Phys. Rev., 1968, 166, 279–291.
47. G. R. Khutsishvili, Phys.-Usp., 1969, 11, 802–815.
48. M. Punkkinen, Phys. Kondens. Mater., 1971, 13, 79–88.
49. E. F. W. Seymour and C. A. Sholl, J. Phys. C: Solid State Phys., 1985, 18, 4521–4537.
50. G. B. Furman, E. M. Kunoff, S. D. Goren, V. Pasquier and D. Tinet, Solid State Nucl. Magn. Reson., 1995, 4, 255–258.
51. G. B. Furman, E. M. Kunoff, S. D. Goren, V. Pasquier and D. Tinet, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 10182–10187.
52. G. B. Furman, A. M. Panich, A. Yochelis, E. M. Kunoff and S. D. Goren, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 439–444.
53. S. Maron, G. Dantelle, T. Gacoin and F. Devreux, Phys. Chem. Chem. Phys., 2014, 16, 18788–18798.
54. M. Punkkinen, Phys. Kondens. Mater., 1971, 13, 79–88.
55. P. Bernier, H. Launois and H. Alloul, J. Phys., Colloq., 1971, 32, C1-513–C1-515.
56. B. Giovannini, P. Pincus, G. Gladstone and A. J. Heeger, J. Phys., Colloq., 1971, 32, C1-163–C1-171.
57. H. Eckert, J. P. Yesinowski, L. A. Silver and E. M. Stolper, J. Phys. Chem., 1988, 92, 2055–2064.
58. G. Aromí, M. J. Knapp, J.-P. Claude, J. C. Huffman, D. N. Hendrickson and G. Christou, J. Am. Chem. Soc., 1999, 121, 5489–5499.
59. S. E. Butcher, F. H.-T. Allain and J. Feigon, Biochemistry, 2000, 39, 2174–2182.
60. Y. J. Lee and C. P. Grey, J. Phys. Chem. B, 2002, 106, 3576–3582.
61. Y. J. Lee, S.-H. Park, C. Eng, J. B. Parise and C. P. Grey, Chem. Mater., 2002, 14, 194–205.
62. R. Hahn, N. Kunkel, C. Hein, R. Kautenburger and H. Kohlmann, RSC Adv., 2015, 5, 9722–9726.
63. R. K. Harris and E. D. Becker, J. Magn. Reson., 2002, 156, 323–326.
64. Y. S. Avadhut, D. Schneider and J. Schmedt auf der Günne, J. Magn. Reson., 2009, 201, 1–6.
65. N. Kunkel, H. Kohlmann, A. Sayede and M. Springborg, Inorg. Chem., 2011, 50, 5873–5875.
66. K. Yvon, H. Kohlmann and B. Bertheville, Chim. Int. J. Chem., 2001, 55, 505–509.
67. T. J. Schmugge and C. D. Jeffries, Phys. Rev., 1965, 138, A1785–A1801.

---

Footnote

† Electronic supplementary information (ESI) available: Error propagation; a comparison of different wipe-out radii with the experimental data; and details of the Fortran program. See DOI: 10.1039/c5cp07606d

---