Polarization effects on the interfacial conductivity in LaAlO₃/SrTiO₃ heterostructures: a first-principles study

Abstract

We studied the influence of uniaxial [100] strain (−1% to +1%) on the electron transport properties of a two-dimensional electron gas (2DEG) at the n-type interface of the LaAlO₃/SrTiO₃(LAO/STO) heterostructure (HS)-based slab system from the perspective of polarization effects via first-principles density functional theory calculations. We first analyzed the unstrained system, and found that the induced polarization toward the vacuum in the LAO film leads to a small charge carrier density on the order of 10¹³ cm⁻² (less than the theoretical value of 3.3 × 10¹⁴ cm⁻² from the superlattice-model-based polar catastrophe mechanism), which is in excellent agreement with the experimental values of oxygen-annealed LAO/STO HS samples. Upon applying [100] tensile strain on the STO substrate, we found a significant reduction of the induced polarization in the LAO film. This reduction weakens the driving force against charge transfer from LAO to STO, causing an increase in the interfacial charge carrier density. The uniaxial strain also leads to a decrease of the effective mass of interfacial mobile electrons, resulting in a higher electron mobility. These findings suggest that applying uniaxial [100] tensile strain on the STO substrate can significantly enhance the interfacial conductivity of the LAO/STO HS system, which gives a comprehensive explanation for experimental observations. In contrast, compressively strained LAO/STO systems show stronger LAO film polarization than the unstrained system, which reduces the interfacial charge carrier density and increases the electron effective mass, thus suppressing the interfacial conductivity.

---

1 Introduction

In the past decade, the two-dimensional electron gas (2DEG) at the n-type (LaO)¹⁺/(TiO₂)⁰ interface in LaAlO₃/SrTiO₃ (LAO/STO) heterostructures (HS) has attracted considerable attention because of its unique electronic properties and potential applications in nanoelectronic devices.^1–4 When a LAO film is deposited on an STO substrate, the polar discontinuity at the (LaO)¹⁺/(TiO₂)⁰ interface leads to the divergence of the electrostatic potential. To compensate this divergence, according to the polar catastrophe mechanism,^1,5 0.5e⁻ is transferred from the polar (LaO)¹⁺ layer of LAO to the nonpolar (TiO₂)⁰ layer of the STO substrate. These electrons partially occupy Ti 3d orbitals near the interfacial region, producing a 2DEG with a theoretical charge carrier density of 3.3 × 10¹⁴ cm⁻². However, systematic experiments on oxygen-annealed samples show a sheet carrier density of about 1–2 × 10¹³ cm⁻²,^6–11 one order of magnitude smaller than the theoretical value. Some research efforts are still being made to explore a comprehensive model that can account for all the experimental phenomena in the LAO/STO HS.^12,13 Several possible explanations for this discrepancy have been proposed from various viewpoints.^12–17 For example, from density functional theory (DFT) calculations, Popović et al. suggested that the transferred electrons are not only confined to the interfacial TiO₂ layer but also extend over several deeper TiO₂ layers, which dilutes the sheet carrier density.¹⁴ Using first-principles electronic structure calculations, Krishnaswamy et al. proposed that the sheet carrier density of 3.3 × 10¹⁴ cm⁻² is intrinsic to the LaO/TiO₂ interface in the LAO/STO system, while the AlO₂-terminated surface may transfer electrons from the 2DEG to the surface states, leading to a smaller sheet carrier density at the interface.¹³ Pentcheva et al., for the first time, have proposed that the polar distortion in the LAO overlayers on the STO substrate can neutralize the polar catastrophe, leading to the insulating behavior up to five monolayers of LAO.¹⁵ As a result, one may speculate that the polarization, i.e., the polar distortion, in the LAO film may be weak enough when the LAO film is more than five monolayers thick so that the polar distortion is not capable of fully neutralizing the polar catastrophe. Consequently, a charge transfer less than 0.5e⁻ may occur from the LAO to the STO, producing a 2DEG at the interface which exhibits lower than expected sheet carrier density. This hypothesis may reconcile the discrepancy between the experimental and theoretical sheet charge carrier densities in the LAO/STO system if it is true, and thus a systematic computational study on the correlation among the LAO film thickness, LAO film polarization, and the sheet carrier density in the LAO/STO HS system is essential. This partially motivates the work presented in this paper.

Despite the discrepancy between experimental and theoretical sheet charge carrier densities, substantial efforts continue to be expended for optimizing the interfacial electron transport properties in the LAO/STO system, in order to realize its potential applications in high-performance nanoelectronics. For example, it has been shown that transition metal and rare earth metal layer doping can significantly enhance the 2DEG charge carrier density in the LAO/STO HS.^18–25 Another potential method to tailor 2DEG properties in LAO/STO HS systems is to apply a strain on the STO substrate. Experimentally, various degrees of strain in the LAO/STO HS can be achieved by growing STO on single-crystal substrates with a lattice mismatch; a LAO film can then be deposited on the strained STO to form the HS. For example, Eom et al. grew STO on a variety of substrates before depositing LAO films, demonstrating substantial differences in 2DEG properties with respect to strain.²⁶ They found that the sheet charge carrier density increases as the STO substrate undergoes a strain from −1.5% to 0.5%, which is consistent with recent first-principles electronic structure calculations.²⁷ Eom's team also found the required critical thickness of LAO films to produce 2DEG changes with biaxial compressive strain; specifically, compressive strain requires more than the 4 unit cells of LAO which are normally sufficient in the unstrained case.

Recently Moler et al.²⁸ found that uniaxial tensile strain in either [100]_p or [010]_p direction substantially enhances the local conductivity in LAO/STO HS-based slab systems, but a simultaneous elongation in both directions (i.e. biaxial tensile strain) yields no such increase. The higher conductivity is attributed to an increase in either mobility or charge carrier density in the tetragonal domain structure in the STO substrate. The authors speculated that strain-induced changes in the polarization perpendicular to the interface could lead to changes in interfacial conductivity, but more details are necessary to clarify the origin of this behavior. A subsequent first-principles study revealed the role of uniaxial strain in tailoring the interfacial electronic properties using an LAO/STO superlattice model (without vacuum). It was found that uniaxial tensile strain can considerably increase the interfacial charge carrier density, which can partially explain the enhanced conductivity observed in the tetragonal domain structure of the LAO/STO system.²⁹ Although the periodic superlattice model can reproduce the polar catastrophe effects well,^14,16,27 it might not be able to exactly model the LAO/STO interface in reality.³⁰ This is mainly because, experimentally, the LAO film is grown on the STO substrate and has a surface polar discontinuity that significantly influences the material properties.¹⁵ Thus periodic LAO/STO superlattice models cannot accurately model the polarization effects induced by the surface polar discontinuity, i.e., the relative displacement between the cations and anions in the LAO film. In fact, the interfacial conductivity is strongly linked to the polarization in both the film and the substrate,^31,32 and particularly, recent first-principles calculations suggest that strain-induced polarization is responsible for the interfacial conductivity in the CaZrO₃/SrTiO₃ HS system.³³ Despite widespread agreement regarding the potential of strain as an optimization tool for the 2DEG in HS systems, fundamental and predictive knowledge of its effects, particularly the strain-induced polarization effects, remains elusive. A more systematic study of the influence of strain on the polarization of LAO/STO HS, and the consequent changes in the interfacial conductivity, is therefore essential.

In this work, we employed first-principles electronic structure calculations to investigate the effects of uniaxial [100] strain on the electron transport properties of the 2DEG at the n-type (LaO)¹⁺/(TiO₂)⁰ interface in LAO/STO HS slab systems from the perspective of the polarization effects. Here, our main motivation is to examine the effects of uniaxial [100] compressive and tensile strains on the charge carrier density, electron mobility, and conductivity of the 2DEG in the LAO/STO system. We suspect that these effects are mediated in large part by strain-induced changes in the LAO film polarization. Therefore, first we study the unstrained LAO/STO system to establish a clear point of reference, then explore the influence of uniaxial [100] strain on the electronic properties of 2DEG in the LAO/STO HS slab system. To the best of our knowledge, this is the first theoretical work which clearly explains the polarization mechanisms influencing the enhanced charge carrier density, mobility, and conductivity of the 2DEG in the uniaxially tensile strained LAO/STO system. This conclusion is in excellent agreement with recent experimental findings, where higher local conductivity is observed in the uniaxial tensile strained system. In contrast, the compressively strained systems show less favorable electron transport properties than the unstrained LAO/STO HS system.

2 Calculation methods and structural details

Spin-polarized DFT calculations were carried out using the Vienna ab initio Simulation Package (VASP).^34,35 The projector augmented wave (PAW)³⁶ pseudopotentials were employed for electron–ion interactions. The generalized gradient approximation (GGA) parameterized by Perdew–Burke–Ernzerhof (PBE)³⁷ was used in combination with appropriate on-site Coulomb interactions (GGA+U) to describe the electron exchange and correlation potentials. The respective U values for Ti 3d and La 4f orbitals were set to 5.8 eV and 7.5 eV, as it is well established that such values are appropriate to describe these strongly-correlated states.^27,38–41 A 450 eV cut-off energy for the plane wave basis set was used, and a 10 × 10 × 1 Γ-centered k-point mesh was found to be well-converged for self-consistent calculations. The convergence threshold for the self-consistent-field iteration was set to 10⁻⁵ eV. The densities of states (DOSs) were calculated using the tetrahedron method with Blöchl corrections.⁴² Atomic positions were relaxed along the c-direction until all components of the residual forces were smaller than 0.02 eV Å⁻¹. In the calculations of Born effective charges for bulk LAO and STO, identical parameters were used, with the exception of a 8 × 8 × 8 Γ-centered k-point mesh instead of the 10 × 10 × 1 Γ-centered k-point mesh used in HS calculations.

A supercell approach was used to model the LAO/STO HS slab system by depositing a LAO film on an STO substrate of eight unit cell thickness. A vacuum layer of approximately 14 Å along the [001] direction was added to resemble the actual epitaxial growth process of the HS system. Hence, one n-type interface and two distinct polar discontinuities are present in this study. The first polar discontinuity occurs at the LAO/STO interface, and the other at the LAO surface/vacuum interface, see Fig. S1 of the ESI.† The experimental lattice constant of STO, 3.905 Å, was fixed in the ab-plane to construct the unstrained HS system. The lattice parameter along the [100] axis was adjusted to simulate various applied uniaxial strains from −1% to 1%. Interfacial charge carrier densities were calculated by integrating the occupation number of the interfacial Ti 3d orbitals from the conduction band minimum to the Fermi level, and then dividing by the interfacial area. This is because the interfacial conducting states are mainly contributed by the Ti 3d orbital at the interfacial TiO₂ layer.⁴³

3 Results and discussion

3.1 Unstrained systems

3.1.1 Polarization strength and critical thickness. We first explored the origin of the required critical thickness to form the 2DEG in the unstrained LAO/STO HS system from the viewpoint of the polarization in the LAO film; specifically, the polarization strength versus the LAO film thickness. To do this, we modeled LAO/STO HS slab systems by depositing LAO films of various thicknesses on the TiO₂-terminated STO substrate along the [001] direction. Hereafter, these interface systems are referred to as (LAO)_n/STO, in which n (n = 1–6) denotes the number of LAO unit cells. The analysis of these relaxed HS indicates that the La/Al cations in the LAO film move towards the vacuum,³⁰ producing relative displacements between the cations and anions (oxygen atoms) and a resulting polarization towards the vacuum. This polarization produces an internal electric field in the LAO film, which inhibits the polar-discontinuity-driven charge transfer from LAO to STO. As a result, one may speculate that the interfacial polar discontinuity in the LAO/STO system can be partially or entirely counteracted by the polarization in the LAO film, and the degree of the counteraction depends on the polarization strength.

To quantify the relationship between the polarization strength and the LAO film thickness, we calculated the average polarization P of the LAO unit cells in LAO/STO HS slab systems using the following formula:^44,45

where Ω is the total volume of the LAO film, N is the number of atoms in the unit cell, Z_i* is the Born effective charge of each atom, and δz_i is the relative displacement of the ith atom in the HS. The relative displacement (δz) of La(Al) cations with respect to the oxygen ions within the same LaO and AlO₂ planes is calculated as δz_La/Al = z_La/Al − z_O. Our calculated Born effective charges Z_i* are 4.45, 2.92, −2.48, and −2.44 for La, Al, and O in the LaO, and O in the AlO₂ layers for the tetragonal bulk LAO, respectively.

The estimated average polarization P_LAO of the LAO layers in the LAO/STO HS systems is plotted with respect to the number of LAO unit cells in Fig. 1a. As an additional comparison, the band gap with respect to the LAO film thickness is shown in Fig. 1b, in which the band gap is defined as the energy gap between the O 2p states in the valence band and the Ti 3d states near the conduction band bottom, and is calculated from the DOS. The DOSs of the (LAO)_n/STO (n = 1–6) HS slab systems are provided in Fig. S2 of the ESI.† One can clearly see from Fig. 1a and b that as the LAO film thickness is increased from 1 to 6 unit cells the polarization strength in the LAO film decreases, and the band gap also decreases. This implies that the barrier to charge transfer from the LAO film to the STO substrate weakens as the LAO film thickness increases. In other words, as the LAO film thickness increases, the tendency for electron transfer from the LAO film to the STO substrate increases, which leads to the insulator-to-metal transition in the LAO/STO HS system.

Fig. 1 Calculated (a) average polarization (P) in the LAO film, (b) band gap values, (c) interfacial charge carrier density (n), and (d) polarization in the first (blue), second (red), and third (green) STO unit cells (u.c.) with respect to the LAO film thickness in unstrained (LAO)_n/STO (n = 1–6) HS slab systems. The dashed blue lines indicate the polarization strength in the LAO film and the band gap value at the critical thickness of the LAO unit cell.

At the critical thickness (i.e., 5 unit cells) the polarization in the LAO film becomes sufficiently diminished to permit charge transfer from the interfacial (LaO)¹⁺ to the (TiO₂)⁰ layer, leading to a zero band gap and the formation of the 2DEG. The determination of the critical thickness, 5 unit cells of LAO, is consistent with prior theoretical studies.^15,30,46 Consequently, we can infer that the critical LAO polarization, above which the 2DEG formation is strongly hindered, is ≈38–40 μC cm⁻². This value is quite consistent with that in prior theoretical work.¹⁷ Below 5 unit cells, the polarization of the LAO film is strong enough to counteract the polar-discontinuity-induced charge transfer from the LAO film to the STO substrate, and thus the LAO/STO HS system exhibits insulating behavior. At and above 5 unit cells, the polarization is weakened such that it can only partially counteract the polar-catastrophe-induced charge transfer, and the remaining electrons (much less than 0.5e) are transferred to the STO substrate, forming the 2DEG at the interface.

It is noted that, unlike in experimental studies, the DFT-calculated interfacial charge carrier density tends to increase with the number of LAO unit cells after the LAO critical thickness has been reached.⁴⁷ Our present calculations show the same trend, as do those in our prior work.^27,30 As demonstrated in Fig. 1c, below 5 unit cells the strong LAO film polarization prevents any polar-discontinuity-driven charge transfer, leading to zero interfacial charge carrier density. Above 5 unit cells, the interfacial charge carrier density increases as the LAO film thickness increases. However, it is interesting to note that the calculated interfacial charge carrier density for the unstrained (LAO)₅/STO system is about 1.6 × 10¹³ cm⁻², which is in excellent agreement with the experimental value in the range of 1–2 × 10¹³ cm⁻².^6–11 In contrast, the superlattice model produces an interfacial charge carrier density about five to ten times greater than this value,^14,27 indicating that the slab model is more appropriate in describing the interfacial electronic states than the superlattice model. This is mainly attributed to the fact that the slab model can appropriately reproduce the polarization behavior in the LAO film while the superlattice model cannot.

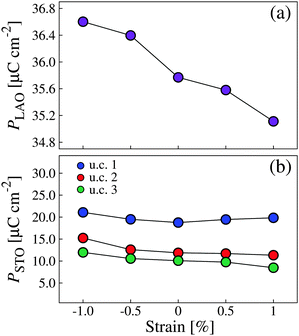
We also examined the polarization strength in the first three STO unit cells near the interface as a comparison with the LAO film, in which the vast majority of transferred charge is confined. After structural relaxation, the STO substrate exhibits polarization in the opposite direction from that in the LAO film, though its magnitude is much smaller. The calculated Born effective charges using the bulk cubic STO, Z_i*, are 2.56, 7.42, −5.89, and −2.03 for Sr, Ti, O in the SrO, and O in the TiO₂ layers, respectively, which were used in the polarization calculation. Fig. 1d shows the polarization in the first three STO unit cells nearest the interface with respect to the LAO film thickness, demonstrating several facts. First, the polarization in all three STO cells tends to increase with the LAO film thickness. At the critical thickness of 5 LAO unit cells, there is a significant degree of polarization in the first STO unit cell (≈20 [μC cm⁻²]). It is worth mentioning that the great majority of this polarization is contributed by the relative displacement between Sr and O ions in the SrO layers of the STO substrate, while that between the Ti and O ions in the TiO₂ layers have negligible contributions. This is consistent with prior work in which Ti and O ions were found to have only a slight polar distortion.¹⁵

3.1.2 Electronic properties. Next we considered the unstrained (LAO)₅/STO HS slab system to provide a frame of reference for the strained systems. The calculated spin-polarized total DOSs, projected DOSs for Ti 3d orbitals from the first three (i.e., IF-I/III/V) interfacial TiO₂ layers in the STO substrate (b), and the projected DOSs for O 2p orbitals from the surface (AlO₂)⁻¹ layer are depicted in Fig. 2. The total DOSs (Fig. 2a) clearly show that the system exhibits conductivity, indicating that 5 unit cells of LAO film is sufficient to produce a 2DEG in the STO substrate. This result is consistent with previous GGA+U and hybrid functional calculations.^15,30,46 Three consecutive (TiO₂)⁰ layers, extending from the interface into the STO substrate, were denoted IF-I, IF-III, and IF-V. Fig. 2b demonstrates that the Ti 3d orbitals at the IF-I (TiO₂)⁰ layer have the majority contribution to the interfacial conductivity, while the contribution from IF-III and IF-V layers is substantially less. Nevertheless, this small contribution from the IF-III and IF-V (TiO₂)⁰ layers indicates that the 2DEG in the unstrained LAO/STO HS slab system extends three unit cells into the STO substrate, having a c-direction width of approximately 10 Å. All deeper (TiO₂)⁰ layers show insulating character, which confirms the formation of a 2DEG.

Fig. 2 Calculated spin-polarized total (a), partial DOS projected on the Ti 3d orbitals from the first three successive TiO₂ layers near the interfacial region (b), and partial DOS projected on the O 2p orbitals from the surface (AlO₂)⁻¹ layer and (c) in the unstrained (LAO)₅/STO HS slab system. IF-I, IF-III, and IF-V represent the first, third, and fifth TiO₂ layers of the STO substrate, respectively. The vertical dashed line indicates the Fermi level at 0 eV.

Moreover, O 2p surface states (Fig. 2c) from the (AlO₂)⁻¹ surface layer also have a significant contribution to the conductivity and the hole states occur at the surface (AlO₂)⁻¹ layer, which can be compensated by oxygen vacancies² or passivated with H atoms.⁴⁸ In this case, the only metallic states would be present at the n-type interface. Finally, the calculated orbital-resolved DOS (see Fig. S3 of the ESI†) of the unstrained system shows that Ti 3d_xy and O 2p_x/p_y orbitals from interfacial (TiO₂)⁰ and surface (AlO₂)⁻¹ layers are mainly responsible for the interfacial and surface conductivities, respectively. These results are also consistent with prior theoretical and experimental studies.^30,49,50

3.2 [100] Uniaxially strained systems

3.2.1 Polarization strength and critical thickness. Herein, we examined the effect of uniaxial strain on the polarization strength in the LAO film and the STO substrate. To do this, the experimental lattice parameter a of the STO substrate, 3.905 Å, was used as a reference point and then varied in a range from −1% to +1% to simulate the applied uniaxial [100] strain. Negative values indicate compressive strain, while positive values signal tensile strain. The average polarization in the LAO film (P_LAO) is depicted in Fig. 3a with respect to uniaxial [100] strain. It can be clearly seen that P_LAO decreases under tensile strain and increases under compressive strain. Thus, the interfacial polarization discontinuity is weakened by uniaxial tensile strain, weakening the driving force opposing the charge transfer from LAO to STO. Uniaxial compressive strain, by contrast, strengthens P_LAO and discourages charge transfer from LAO to STO relative to the unstrained system. We also plotted the polarization in the first (blue), second (red), and third (green) unit cells of the STO substrate with respect to uniaxial strain in Fig. 3b. While no clear trend can be established for the polarization in the first STO unit cell, the polarization in the second and third cells appears to decrease with tensile strain and increase with compressive strain. However, the overall polarization in the STO substrate is minor compared to the LAO film. Even in the STO unit cell nearest the interface, the polarization value is far less than P_LAO.

Fig. 3 Calculated average polarization (P_LAO) in the LAO film (a), and in the first (blue), second (red), and third (green) STO unit cells (b) with respect to [100] uniaxial strain from −1% to +1% on the STO substrate in (LAO)₅/STO HS slab systems.

Given that [100] uniaxial strain affects P_LAO, one may consider whether the critical LAO film thickness (d_crit) to form the 2DEG is affected as well. In fact, biaxial strains have been shown to significantly affect d_crit in experimental²⁶ and theoretical³⁰ studies. To investigate the situation in the uniaxial strain case, we calculated the total DOS for each of our strained systems (−1%, −0.5%, +0.5%, and +1%). The total DOSs for −1% and +1% [100] uniaxially strained LAO/STO HS slab systems are shown in Fig. 4a and b, clearly demonstrating that uniaxial strain in this range has no effect on d_crit. This result can be easily understood in the context of the earlier polarization discussion: none of the applied strains increase P_LAO beyond the critical threshold (≈40 [μC cm⁻²]), and thus 5 unit cells are sufficient to achieve n-type interfacial conductivity in each system.

Fig. 4 Calculated spin-polarized total DOS for n-type (LAO)₅/STO HS slab systems under −1% (a) and +1% (b) [100] uniaxial strain. Calculated partial DOS of Ti 3d orbitals from IF-I, IF-III, and IF-V TiO₂ layers in the STO substrate of the same systems under −1% (c) and +1% (d) [100] uniaxial strain.

3.2.2 Electronic properties. Here we studied the effects of uniaxial strain on the 2DEG electron transport properties of the LAO/STO HS slab system. As mentioned previously, the free electrons transferred from LAO—which comprises the interfacial 2DEG—reside primarily in Ti 3d orbitals of the first (IF-I), third (IF-III), and fifth (IF-V) TiO₂ layers of the STO substrate. Thus, Fig. 4c and d depict the calculated PDOS of Ti 3d orbitals at IF-I, IF-III, and IF-V TiO₂ layers for −1% and +1% uniaxially strained systems. Our results indicate that in the compressively strained system (Fig. 4c), the contribution to the 2DEG from all three TiO₂ layers is comparable. In other words, the 2DEG in the compressively strained system is almost equally dispersed among IF-I, IF-III, and IF-V TiO₂ layers. In the tensile strained system (Fig. 4d), by contrast, IF-I Ti 3d orbitals have a dominant contribution to the 2DEG. This indicates a 2DEG with a greater interfacial charge carrier density, and a greater degree of concentration in the IF-I layer, relative to that in the compressively strained system.

To provide a quantitative comparison between the unstrained and strained systems, we calculated the partial occupation number and the charge carrier density of the interfacial (IF-I) Ti 3d orbitals in each case by integrating the partial DOS near the Fermi level. The calculated IF-I Ti 3d partial occupation numbers and the respective charge carrier densities n for the unstrained and [100] uniaxially strained systems are shown in Fig. 5. Our results indicate that the charge carrier density increases as strain is adjusted from −1% to +1%. This increase is due to two factors. First, the LAO film polarization is consistently reduced by increasing the tensile strain (see Fig. 3a), weakening the driving force opposing charge transfer from LAO to STO, and ultimately promoting more charge transfer to STO. Second, strain changes the distribution of charge among the first three TiO₂ layers near the interface, resulting in a superior concentration of charge at the IF-I TiO₂ layer in the tensile strained system relative to that in the compressively strained system (see Fig. 4c, d, and Fig. S4, ESI†). It is particularly worth mentioning that the calculated interfacial charge carrier density for the unstrained (LAO)₅/STO system is about 1.6 × 10¹³ cm⁻², which is in excellent agreement with the experimental value in the range of 1–2 × 10¹³ cm⁻².^6–11 In contrast, the superlattice model produces an interfacial charge carrier density about five to ten times greater than this value,^14,27 indicating that the slab model is more appropriate in describing the interfacial electronic states than the superlattice model. This is mainly attributed to the fact that the slab model can appropriately reproduce the polarization behavior in the LAO film while the superlattice model cannot.

Fig. 5 Calculated orbital occupation numbers and the respective charge carrier densities (n) of Ti 3d orbitals at the interfacial TiO₂ layer in the STO substrate with respect to [100] uniaxial strain in the (LAO)₅/STO HS slab system.

Here, we would like to mention that our earlier work on the [100] uniaxially strained periodic (i.e. without vacuum) LAO/STO superlattice system showed that compressive strains substantially increased the interfacial electron carrier density relative to the unstrained and tensile strained systems.²⁹ The enhanced charge carrier density in the compressive strained systems was attributed to interfacial Ti 3d_yz orbitals instead of d_xy. In LAO/STO HS-based vacuum slab models, however, 2DEG originates only from Ti 3d_xy orbitals for all the strained systems and the charge carrier density decreases for compressively strained systems, which is in excellent agreement with experiment.²⁸ The orbital-resolved Ti 3d DOSs from the IF-I TiO₂ layers for −1% (a), 0% (b), and +1% (c) uniaxially strained LAO/STO HS slab systems are plotted in Fig. S3 of the ESI.† One can clearly see that in each case, only d_xy orbitals cross the Fermi level, and are thus singularly responsible for the formation of the 2DEG. The d_yz and d_xz orbitals remain unoccupied and stay at higher energies in the conduction band. Fig. S3 (ESI†) also indicates that the partial occupation number of IF-I Ti 3d_xy orbitals increases when strain is applied on the STO substrate from −1% to +1%, resulting in enhanced carrier density. In each case, O 2p_x/p_y states give rise to the surface conductivity. We also plotted the charge density projected on the bands forming the metallic states in −1%, 0%, and +1% uniaxially strained systems (see Fig. S4 of the ESI†), which supports the conclusion that IF-I charge carrier density is enhanced by tensile strain and diminished by compressive strain.

The effect of strain on the orbital occupation number can also be analysed from the band structure. Fig. 6 shows the band structure near the Γ point for −1%, 0%, and +1% strained systems, with the red band indicating the IF-I Ti 3d band. It can be clearly seen that compressive strain reduces the partial occupation of Ti 3d orbitals, while tensile strain increases it. The band structure of these strained systems thus corroborates our DOS analysis of Fig. 4c and d. Some hole states can also be easily discerned at the M point. These hole states are due to the dangling bonds at the surface layers, which can be typically compensated by oxygen vacancies² or passivated with H atoms.⁴⁸

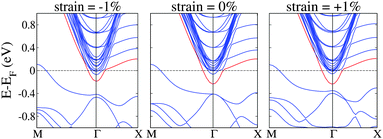Fig. 6 Calculated band structure for −1%, 0%, and +1% uniaxially strained (LAO)₅/STO HS slab systems. The red lines indicate the Ti 3d bands in the interfacial layer.

The conductivity of the LAO/STO HS system is not only determined by the interfacial charge carrier density but also by the electron mobility, a quantity closely related to the electron effective mass. Hence, to evaluate the influence of the uniaxial strain on the mobility, we calculated the effective mass (m*/m_e) of free electrons at IF-I Ti 3d bands (colored red in Fig. 6), which are mainly responsible for 2DEG in the strained and unstrained LAO/STO HS slab systems. We then normalized these effective masses to that of the unstrained system (m₀/m_e), yielding a series of normalized values m*/m₀. Electron mobility can be related to m* using the following equation: 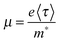,⁵¹ where e is the fundamental charge and 〈τ〉 is the average scattering time. Using the fact that the electron mobility (μ) is inversely proportional to the electron effective mass, along with the assumption that 〈τ〉 is a constant in these systems, we also generated a series of normalized mobility values μ/μ₀ for the strained systems. The normalized electron effective masses and the corresponding electron mobilities of all the systems are plotted in Fig. 7a. It can be clearly seen that tensile strains reduce the electron effective mass and increase the electron mobility. This comes in addition to the improvement in the charge carrier density discussed earlier. Compressive strains, by contrast, increase the effective mass and suppress the electron mobility, in addition to its negative effect on charge carrier density. However, it is noted that the effect of strain on charge carrier density is more pronounced than on electron mobility.

Fig. 7 (a) Calculated normalized electron effective masses (m*/m₀) and the corresponding mobilities (μ/μ₀), and (b) normalized electrical conductivities (σ/σ₀) for Ti 3d electrons in the interfacial TiO₂ layer with respect to [100] uniaxial strain in (LAO)₅/STO HS slab systems.

It can thus be concluded that tensile strains increase the interfacial charge carrier density (see Fig. 5) and electron mobility (see Fig. 7), while compressive strains have the opposite effect on both of these quantities. This trend is mostly attributed to the induced ferroelectric polarization in the LAO film with respect to the applied uniaxial [100] strain. Given these facts, an examination of interfacial conductivity itself is also appropriate. Electron conductivity can be calculated as σ = neμ, where n is the charge carrier density, and μ the electron mobility. The calculated conductivity (σ), normalized by the conductivity of the unstrained system (σ₀), is plotted with respect to strain in Fig. 7b. As demonstrated in Fig. 7b, there is an ≈9% increase in interfacial conductivity under +1% tensile strain. Compressive (−1%) strain causes a large drop in the interfacial conductivity, mostly due to the sharp reduction in interfacial charge carrier density (Fig. 5). In short, our calculations show that when uniaxial [100] strain on the STO substrate is adjusted from −1% to +1%, the interfacial electron carrier density and mobility are both increased, resulting in enhanced interfacial conductivity. These results are in excellent agreement with Moler et al.'s experimental findings,²⁸ in which the local conductivity is significantly enhanced under uniaxial tensile strain. Our results provide a convincing explanation for such a phenomenon.

4 Conclusions

The polarization characters and electronic properties of unstrained and uniaxially [100] strained LAO/STO HS slab systems were examined using first-principles density functional theory calculations. We first systematically revealed the correlation among the LAO film thickness, polarization, and the interfacial sheet carrier density, which can explain the discrepancy between experimental and theoretical values of the 2DEG carrier density. When the HS system undergoes a compressive uniaxial strain, we found that the polarization magnitude in the LAO film increases with respect to that of the unstrained system, which has a negative impact on the electron transport properties of the LAO/STO HS system. Tensile strain, however, was found to reduce the polarization strength in the LAO film, which weakens the driving force against charge transfer from the LAO to the STO substrate, thus improving the interfacial 2DEG charge carrier density and mobility. This improvement results in an enhanced interfacial conductivity, which is in excellent agreement with experimental findings. Hence, we propose that uniaxial tensile strain could be an effective route to improve the interfacial conductivity in the LAO/STO system.

Acknowledgements

This work was partially supported by a Department of Defense National Security Science and Engineering Faculty Fellowship (under the ONR contract no. N000141510030). KY acknowledges support from start-up funds from the University of California, San Diego.

References

1. A. Ohtomo and H. Y. Hwang, Nature, 2004, 427, 423–426.
2. C. Cen, S. Thiel, G. Hammerl, C. W. Schneider, K. E. Andersen, C. S. Hellberg, J. Mannhart and J. Levy, Nat. Mater., 2008, 7, 298.
3. C. Cen, S. Thiel, J. Mannhart and J. Levy, Science, 2009, 323, 1026–1030.
4. D. Stornaiuolo, S. Gariglio, A. Fête, M. Gabay, D. Li, D. Massarotti and J.-M. Triscone, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 235426.
5. N. Nakagawa, H. Y. Hwang and D. A. Muller, Nat. Mater., 2006, 5, 204–209.
6. M. Huijben, G. Rijnders, D. H. A. Blank, S. Bals, S. V. Aert, J. Verbeeck, G. V. Tendeloo, A. Brinkman and H. Hilgenkamp, Nat. Mater., 2006, 5, 556–560.
7. S. Thiel, G. Hammerl, A. Schmehl, C. W. Schneider and J. Mannhart, Science, 2006, 313, 1942–1945.
8. W. Siemons, G. Koster, H. Yamamoto, W. A. Harrison, G. Lucovsky, T. H. Geballe, D. H. A. Blank and M. R. Beasley, Phys. Rev. Lett., 2007, 98, 196802.
9. A. Annadi, A. Putra, Z. Q. Liu, X. Wang, K. Gopinadhan, Z. Huang, S. Dhar, T. Venkatesan and Ariando, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 085450.
10. Z. Liu, C. Li, W. Lü, X. Huang, Z. Huang, S. Zeng, X. Qiu, L. Huang, A. Annadi, J. Chen, J. Coey, T. Venkatesan and Ariando, Phys. Rev. X, 2013, 3, 021010.
11. A. Kalabukhov, R. Gunnarsson, J. Börjesson, E. Olsson, T. Claeson and D. Winkler, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 121404.
12. L. Yu and A. Zunger, Nat. Commun., 2014, 5, 5118.
13. K. Krishnaswamy, C. E. Dreyer, A. Janotti and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 085420.
14. Z. S. Popović, S. Satpathy and R. M. Martin, Phys. Rev. Lett., 2008, 101, 256801.
15. R. Pentcheva and W. E. Pickett, Phys. Rev. Lett., 2009, 102, 107602.
16. H. Chen, A. M. Kolpak and S. Ismail-Beigi, Adv. Mater., 2010, 22, 2881–2899.
17. Y. Li and J. Yu, J. Appl. Phys., 2010, 108, 013701.
18. T. Fix, J. L. MacManus-Driscoll and M. G. Blamire, Appl. Phys. Lett., 2009, 94, 172101.
19. T. Fix, F. Schoofs, J. L. MacManus-Driscoll and M. G. Blamire, Appl. Phys. Lett., 2010, 97, 072110.
20. W. S. Choi, S. Lee, V. R. Cooper and H. N. Lee, Nano Lett., 2012, 12, 4590–4594.
21. F. Schoofs, M. Egilmez, T. Fix, J. L. MacManus-Driscoll and M. G. Blamire, Solid State Commun., 2013, 156, 35–37.
22. A. S. Disa, D. P. Kumah, A. Malashevich, H. Chen, D. A. Arena, E. D. Specht, S. Ismail-Beigi, F. J. Walker and C. H. Ahn, Phys. Rev. Lett., 2015, 114, 026801.
23. M. Hosoda, C. Bell, Y. Hikita and H. Y. Hwang, Appl. Phys. Lett., 2013, 102, 091601.
24. S. Nazir, C. Bernal and K. Yang, ACS Appl. Mater. Interfaces, 2015, 7, 5305–5311.
25. S. Nazir, J. Cheng, M. Behtash, J. Luo and K. Yang, ACS Appl. Mater. Interfaces, 2015, 7, 14294–14302.
26. C. W. Bark, D. A. Felker, Y. Wang, Y. Zhang, H. W. Jang, C. M. Folkman, J. W. Park, S. H. Baek, H. Zhou, D. D. Fong, X. Q. Pan, E. Y. Tsymbal, M. S. Rzchowski and C. B. Eom, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4720–4724.
27. S. Nazir, M. Behtash and K. Yang, Appl. Phys. Lett., 2014, 105, 141602.
28. B. Kalisky, E. M. Spanton, H. Noad, J. R. Kirtley, K. C. Nowack, C. Bell, H. K. Sato, M. Hosoda, Y. Xie, Y. Hikita, C. Woltmann, G. Pfanzelt, R. Jany, C. Richter, H. Y. Hwang, J. Mannhart and K. A. Moler, Nat. Mater., 2013, 12, 1091–1095.
29. S. Nazir, M. Behtash and K. Yang, RSC Adv., 2015, 5, 15682–15689.
30. S. Nazir and K. Yang, ACS Appl. Mater. Interfaces, 2014, 6, 22351–22358.
31. J. Seidel, L. W. Martin, Q. He, Q. Zhan, Y.-H. Chu, A. Rother, M. E. Hawkridge, P. Maksymovych, P. Yu, M. Gajek, N. Balke, S. V. Kalinin, S. Gemming, F. Wang, G. Catalan, J. F. Scott, N. A. S. J. Orenstein and R. Ramesh, Nat. Mater., 2009, 8, 229–234.
32. J. Guyonnet, I. Gaponenko, S. Gariglio and P. Paruch, Adv. Mater., 2011, 23, 5377–5382.
33. S. Nazir, J. Cheng and K. Yang, ACS Appl. Mater. Interfaces, 2016, 8, 390–399.
34. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
35. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
36. P. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
38. K. Yang, Y. Dai, B. Huang and Y. P. Feng, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 033202.
39. K. Yang, Y. Dai, B. Huang and Y. P. Feng, J. Phys. D: Appl. Phys., 2014, 47, 275101.
40. R. Arras, V. G. Ruiz, W. E. Pickett and R. Pentcheva, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125404.
41. R. Pentcheva and W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 205106.
42. P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233.
43. S. Nazir and K. Yang, ACS Appl. Mater. Interfaces, 2014, 6, 22351–22358.
44. W. Zhong, R. D. King-Smith and D. Vanderbilt, Phys. Rev. Lett., 1994, 72, 3618–3621.
45. X. Liu, Y. Wang, P. V. Lukashev, J. D. Burton and E. Y. Tsymbal, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125407.
46. F. Cossu, U. Schwingenschlögl and V. Eyert, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 045119.
47. W.-J. Son, E. Cho, B. Lee, J. Lee and S. Han, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 245411.
48. W. Joon Son, E. Cho, J. Lee and S. Han, J. Phys.: Condens. Matter, 2010, 22, 315501.
49. E. Lesne, N. Reyren, D. Doennig, R. Mattana, H. Jaffrés, F. P. V. Cros, F. Choueikani, P. Ohresser, R. Pentcheva, A. Barthélémy and M. Bibes, Nat. Commun., 2012, 5, 4291.
50. J. H. You and J. H. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 155111.
51. Y. U. Peter and M. Cardona, Fundamentals of Semiconductors: Physics and Materials Properties, Springer Science & Business Media, 2010.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp07581e

---