 Open Access Article
Open Access ArticleTwo-dimensional interlocked pentagonal bilayer ice: how do water molecules form a hydrogen bonding network?
Weiduo
Zhu
a,
Wen-Hui
Zhao
a,
Lu
Wang
a,
Di
Yin
a,
Min
Jia
a,
Jinlong
Yang
a,
Xiao Cheng
Zeng
*ab and
Lan-Feng
Yuan
*a
aHefei National Laboratory for Physical Sciences at Microscale, Department of Chemical Physics, University of Science and Technology of China, Hefei, Anhui 230026, China. E-mail: yuanlf@ustc.edu.cn
bDepartment of Chemistry, University of Nebraska-Lincoln, Lincoln, NE 68588, USA. E-mail: xzeng1@unl.edu
First published on 24th March 2016
Abstract
The plethora of ice structures observed both in bulk and under nanoscale confinement reflects the extraordinary ability of water molecules to form diverse forms of hydrogen bonding networks. An ideal hydrogen bonding network of water should satisfy three requirements: (1) four hydrogen bonds connected with every water molecule, (2) nearly linear hydrogen bonds, and (3) tetrahedral configuration for the four hydrogen bonds around an O atom. However, under nanoscale confinement, some of the three requirements have to be unmet, and the selection of the specific requirement(s) leads to different types of hydrogen bonding structures. According to molecular dynamics (MD) simulations for water confined between two smooth hydrophobic walls, we obtain a phase diagram of three two-dimensional (2D) crystalline structures and a bilayer liquid. A new 2D bilayer ice is found and named the interlocked pentagonal bilayer ice (IPBI), because its side view comprises interlocked pentagonal channels. The basic motif in the top view of IPBI is a large hexagon composed of four small pentagons, resembling the top view of a previously reported “coffin” bilayer ice [Johnston, et al., J. Chem. Phys., 2010, 133, 154516]. First-principles optimizations suggest that both bilayer ices are stable. However, there are fundamental differences between the two bilayer structures due to the difference in the selection among the three requirements. The IPBI sacrifices the linearity of hydrogen bonds to retain locally tetrahedral configurations of the hydrogen bonds, whereas the coffin structure does the opposite. The tradeoff between the conditions of an ideal hydrogen bonding network can serve as a generic guidance to understand the rich phase behaviors of nanoconfined water.
Introduction
Water is one of the most ubiquitous molecules on earth, and remains to be a subject of intense interest. The phase diagram of bulk water is amazingly complicated: at least seventeen bulk crystalline ice phases have been found.1,2 Nanoscopic confinement of water can disrupt and rearrange the hydrogen bonding networks, resulting in even more complex phase behavior.3–13 For instance, water confined in carbon nanotubes can form square, pentagonal, hexagonal, and octagonal single-walled ice nanotubes.4 In their simulations, Bai et al.14 observed high-density nanoice exhibiting helical structures. Water confined between two parallel plates can form many 2D ice polymorphs, such as monolayer and bilayer square ice,15 distorted bilayer hexagonal ice,16,17 bilayer hexagonal and rhombic ices,18–21 monolayer rhombic ices,22,23 trilayer ice,24 and trilayer heterogeneous fluid.25,26The multiplicity of the low-dimensional ice phases reflects the extraordinary ability of water molecules to form diverse forms of hydrogen bonding networks. To understand this multiplicity of ices in low-dimensions, we look into the selection among three requirements for an ideal hydrogen bonding network of water: (1) four hydrogen bonds for every water molecule to maximize the number of hydrogen bonds, (2) nearly linear hydrogen bonds to minimize the electrostatic repulsion between the donor and acceptor O atoms, and (3) tetrahedral orientation for the four hydrogen bonds around an O atom to match the four lobes of sp3 hybridization. For bulk ice, there exist many ways to fulfill the three requirements, leading to the multiplicity of bulk ice phases. Indeed, only in bulk ice, the hydrogen bonding network can simultaneously satisfy the three requirements. The combination of the three conditions means that the hydrogen bonding network is extended infinitely in all the three directions, therefore, under nanoscale confinements, some of them must be unmet. This leads to various possible selections on which condition to be sacrificed and which to be kept. For example, monolayer ices15,27 with in-plane hydrogen bonds sacrifice the tetrahedral orientation of the O atom to retain the linear hydrogen bonds, whereas another monolayer ice28 with out-of-plane O atoms sacrifices the linear hydrogen bonds to retain tetrahedrality. In addition to various basic motifs, different ways of compromise also lead to diverse forms of low-dimensional ice phases.
In this work, we perform MD simulations for water confined between two hydrophobic parallel walls with the TIP5P water model. In particular, we find a new bilayer ice structure not reported in the literature, namely, the interlocked pentagonal bilayer ice (IPBI). The “coffin” structure in the literature,29 obtained based on the TIP4P water model, is similar to the IPBI in the top views, but exhibits fundamental structural differences due to different selection among the three requirements. The IPBI sacrifices linear hydrogen bonds to retain the tetrahedral orientation, while the coffin structure does the opposite.
Simulation and analysis methods
The simulation system is composed of 400 water molecules confined between two smooth walls. The wall separation D (the difference between the heights of the two plates in the z direction) is set within the range of 0.8 nm to 1.0 nm. The water molecules interact with each other via the TIP5P pair potential30 and with the wall via the 9–3 Lennard-Jones (L-J) potential:31–35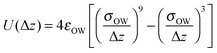 | (1) |
Here Δz is the distance from the oxygen atom of a water molecule to the wall, and the potential parameters are σOW = 0.25 nm and εOW = 1.25 kJ mol−1.19,36,37 Simulations were performed in the isothermal–isostress NPLT ensemble with periodic boundary conditions in the parallel (x and y) directions, where PL is the lateral pressure, set as 1 GPa. Temperature (T) and the lateral pressure are controlled using a Nosé–Hoover thermostat38,39 and a Parrinello–Rahman barostat,40 respectively. A cutoff of 1 nm is adopted for the L-J interactions, and the long-range electrostatic interactions are treated by the slab-adapted Ewald sum method.41 Depending on T and D, the simulations last for 10–100 ns, with a MD step of 2 fs.
Results and discussion
During the cooling of the system, three different crystalline structures can be obtained, depending on the wall separation D. A semi-quantitative wall-separation-temperature (D–T) phase diagram is plotted in Fig. 1. The phase boundaries are determined through independent two-phase coexistence simulations. For 0.80 nm ≤ D ≤ 0.87 nm, liquid water transforms into flat rhombic bilayer ice (fRBI), analogous to a system demonstrated by Han et al.19 For 0.88 nm ≤ D ≤ 0.94 nm, the new phase IPBI is obtained. And for 0.95 nm ≤ D ≤ 1.00 nm, the flat hexagonal-rhombic trilayer ice (fHRTI) is obtained, as from our previous study.24 | ||
| Fig. 1 A semi-quantitative D–T phase diagram of bilayer water confined between two hydrophobic walls. | ||
For each D, the temperature T is lowered from 350 K to 230 K in a step of 10 K. First-order phase transitions between liquid and solid are indicated by abrupt changes of various properties. For instance, at T = 250 K and D = 0.9 nm, the potential energy U drops by 3 kJ mol−1 (Fig. 2b), and the lateral diffusion coefficient DL changes from 1.0 × 10−6 cm2 s−1 to 2.0 × 10−9 cm2 s−1.
The transverse density profile (TDP) is defined as the density distribution of oxygen atoms in the z direction (i.e., normal to the walls). Fig. 3a is the TDP of fRBI, with two peaks. When the wall separation D increases to 0.95 nm, the TDP splits into three peaks (Fig. 3c), indicating that the structure becomes a trilayer.
When D is in the range between the bilayer and trilayer regions, as Fig. 3b shows, the TDP appears to be fourfold. Nevertheless, the O atoms in the outer layers (I and II of Fig. 3b) are not in register with those in the inner layers (I′ and II′), as can be seen from the top view (Fig. 4a, shown in below). Therefore, we view the ice as a bilayer, and name each peak in the TDP as a “sublayer”, while an outer layer plus an inner layer (i.e., I + I′ or II + II′) as a “macrolayer”.
As Fig. 4a shows, the atoms in the two macrolayers of IPBI are not in register. If only from the top view of one macrolayer (Fig. 4b), we can see that the water molecules form pentagonal rings, and four pentagons constitute a larger hexagon. Fig. 4c and d show the side views of the whole IPBI along the y-direction and the x-direction, respectively. The side view along the x-direction shows pentagons and hexagons, and is not easy to be described in a simple way. Hereafter we will focus on the side view along the y-direction (Fig. 4c). It shows only pentagons which are linked one by one along the y-direction, resulting in two types of channels with different sizes. So it can be understood as interlocked pentagonal nanotubes.
In a unit cell of IPBI, there are six pentagons (including those sharing vertices) along the x-direction and two pentagons (without shared vertices) along the y-direction. To observe these pentagons in more detail, we draw six rectangle boxes in a unit cell of IPBI (Fig. 5a). Each box contains two pentagons linked by two hydrogen bonds along the y-direction, and the overlapping parts between adjacent boxes represent the shared oxygen atoms of adjacent pentagons. All these pentagons can be divided into two classes according to whether they have hydrogen bonds between the inner sublayers I′ and II′ (marked as blue), named A (no) and B (yes). The heights (i.e., the distance between the highest and lowest oxygen atoms in the z-direction) of pentagons are 3.66 ± 0.08 Å for the A class and 2.92 ± 0.03 Å for the B class, respectively. The maximum and minimum O–O–O angles for A and B are: θmax-A = 128.9° ± 1.1°, θmin-A = 89.9° ± 1.3°; θmax-B = 154.7° ± 1.7°, and θmin-B = 68.2° ± 1.2°. So the B-type pentagons are more oblate than the A-type ones. And according to the distributions of O atoms among the sublayers, there are also two types of pentagons, so we furthermore classify A and B as A1, A2, B1 and B2. As Fig. 5b shows, in A1 and B1 there are two oxygen atoms in the upper macrolayer and three in the lower macrolayer, and in A2 and B2 the distribution is opposite. The arrangement pattern of pentagons in a unit cell is given in the red part of Fig. 5c. The pentagons sharing oxygen atoms connect sequentially along the x-direction as B1A2B1B2A1B2, in a unit cell. Along the y-direction, the pentagons are aligned as A1A2A1A2… or B1B2B1B2…, making two types of channels. Because the B-type pentagons are more oblate than the A-type ones, the channels made of A-type pentagons give larger radius.
In the literature, there is a bilayer ice whose top view is similar to that of a macrolayer of the IPBI, i.e., also consists hexagons made of four pentagons. This structure was named29 the “coffins”, and obtained with the condition of D = 0.85 nm, PL = 0.5 GPa and T = 200 K by the TIP4P water model. We repeat this simulation, and as Fig. 3d shows, the TDP of the coffins is similar to that of the IPBI (both at the same temperature 200 K). The oxygen atoms in the outer layers also are not in register with those in the inner layers, so we will also use the concepts of sublayers and macrolayers for the coffin structure. However, the oxygen atoms in the two macrolayers of the coffins are in register, so the top views of a macrolayer and of the whole system are the same. The coffins has fourfold rotational symmetry, hence its side view along the x-direction is identical to that along the y-direction. This side view is made up of tetragons and hexagons (Fig. 5d), with no pentagon, totally different from that of the IPBI. It can be seen that one third of water molecules are involved in tetragons. In such different ways, the IPBI and the coffins both satisfy the ice rules, i.e., every molecule participates in four hydrogen bonds.
To examine the stability of the two structures, we perform density functional theory (DFT) calculations using the QUICKSTEP42 program implemented in the CP2K package. The optimized structures of IPBI and coffins, based on the BLYP43,44 exchange–correlation functional with the dispersion correction (D3) proposed by Grimme,45 are presented in Fig. 6. The DFT optimizations indicate the stability of both 2D ices, consistent with the classical MD simulations. The vibrational frequency analyses show no imaginary frequencies, suggesting that both structures are locally stable. Additionally, the vdW-DF246 functional is used for further check, and the two structures are also stable under optimizations.
The abundance of tetragons in the coffin structure is quite noteworthy, indicating significant deviation from tetrahedral orientation of H-bonds. This implies that the coffin structure sacrifices the third condition (tetrahedral orientation). What does it gain by doing this? The answer should be to keep the second condition (nearly linear H-bonds). The opposite choice seems to be taken by the IPBI: sacrifice the linearity of H-bonds to retain the tetrahedrality of H-bond networks. With this in mind, we find more structural differences between them.
First, the IPBI has 36 water molecules in a unit cell, and the numbers of water molecules in the four sublayers are 10, 8, 8, and 10 (I, I′, II′, and II), respectively. On the other hand, the coffins have 24 water molecules in a unit cell, and the numbers of water molecules in the four sublayers are 8, 4, 4, and 8, respectively. Second, in a unit cell, the IPBI has three larger hexagonal rings while the coffins have only one, because the oxygen atoms shared by adjacent larger hexagonal rings are located in both outer and inner sublayers in the IPBI (i.e., some in red and some in blue in Fig. 4b), while only in the outer sublayers in the coffins. Third, the rotational symmetry of the coffins is fourfold, while that of the IPBI is twofold.
As stated above, we speculate that the structural differences between the two phases originate from their different choices: the coffins sacrifice the tetrahedral orientation to retain the linearity of H-bonds, and the IPBI does the opposite. To further check this key hypothesis, we design a series of structural indices to compare the two phases.
First, if the hypothesis is true, then the average H-bond strength of IPBI should be weaker than that of the coffins, or the proportion of weak H-bonds among all the H-bonds should be higher in the IPBI than in the coffins. So we do the statistics of the O–H⋯O angles and O⋯H distances of the hydrogen bonds in the two unit cells optimized by DFT (Fig. 7a and b), and in all the MD snapshots within 50 ns of sampling after equilibration (Fig. 7c and d). The discrete distributions for the former and the smooth curves for the latter share the same trends. As Fig. 7c shows, the peaks of the O–H⋯O angle distributions of both structures are around 170°, but the probability for the angle to be “too small” is much higher for the IPBI than for the coffins. Similar situation is met for the O⋯H distance index: the probability of the O⋯H distance to be “too long” is also much higher for the IPBI than for the coffins. The two curves in Fig. 7c (Fig. 7d) intersect at 152° (2.06 Å), and we take these values as the thresholds between strong and weak H-bonds. A hydrogen bond is marked as “weak” if its O–H⋯O angle is smaller than 152° or its O⋯H length is longer than 2.06 Å. Under this definition, the IPBI has 18 weak hydrogen bonds, accounting for 1/4 of its 72 hydrogen bonds, while the 6 weak hydrogen bonds in the coffins account for only 1/8 of its 48 hydrogen bonds, indeed supporting our hypothesis.
Second, how to measure the tetrahedrality? It can be reflected in the distribution of the H⋯O⋯H angles (i.e., between two hydrogen bonds around an O atom) and the H⋯O–H angles (i.e., between a hydrogen bond and a covalent bond around an O atom). For regular tetrahedra, these angles are 109.5°. According the VSEPR (valence shell electron pair repulsion) model, the repulsion due to a lone pair is stronger than that due to a covalent bond, which makes the H–O–H covalent bond angle smaller than 109.5° (actually 104.5°), so the H⋯O⋯H and H⋯O–H angles should be larger than 109.5° (by several degrees). With these in mind, we calculate the distributions of these angles for the two phases in their DFT optimized unit cells and in all the snapshots within the 50 ns sampling time, respectively (Fig. 8). As Fig. 8b shows, the peak value of IPBI is about 114°, indeed in the range of 109.5° plus several degrees, while the peak value of the coffins is about 101°, which is significantly too small. Besides, the full width at half maximum (FWHM) of the curve for the coffins in Fig. 8b is 42°, much greater than that for the IPBI (25°). This also indicates that the proportion of “bad” HOH angles in the hydrogen bonding network of the coffins is much higher than that for the IPBI.
Based on the above analyses, our key hypothesis is validated. Furthermore, we can use the information on the distribution of weak H-bonds to explain the different distributions of molecules among the sublayers for the two phases. Most of the weak hydrogen bonds involve the outer sublayers, because the environments of their molecules are further away from bulk than the molecules in the inner sublayers. Since the IPBI has higher proportion of weak H-bonds, it would like to adjust its structure so that the proportion of molecules in the outer sublayers becomes smaller, to reduce the energy penalty. This rationalizes the (10, 8, 8, 10) vs. (8, 4, 4, 8) distributions for the IPBI and the coffins.
The two structures are both stable structures in DFT optimizations, but are found by different water models in MD simulations. Here we propose an explanation. Different potential fields could give different weights for the three conditions. The TIP5P model places two dummy atoms with negative charges in the directions of the two lone pairs of the oxygen atom, mimicking the sp3 hybridization much better than the TIP4P model. Therefore, TIP4P tends to predict a structure retaining linearity and sacrificing tetrahedrality, while TIP5P has the opposite tendency. This is exactly what we see in this work. A similar story also occurs in our previous work,23 where TIP5P predicts a rhombic monolayer ice in which all the O atoms are in a plane while no one H atom is in the same plane (stable under DFT optimization), while TIP4P predicts a rhombic monolayer ice in which all the H and O atoms are in the same plane (unstable under DFT optimization).
Finally, we note that both the TIP4P and TIP5P water models used in this study are empirical potentials developed from fitting experimental data, such as density, self-diffusion constant, and radial distribution functions of bulk liquid water.30,47 Recently, several new water models (e.g., MB-pol,48 CC-pol49 and WHBB50) have been developed based on fitting results from ab initio computations. Thus far, applications of these new models have been limited to water clusters and bulk liquid water. Apparently, the models can give markedly better descriptions in properties such as the dimer spectra,51 virial coefficients,48,52 cluster structures and cluster energies.53–55 It would be of high interest to examine whether these new models can generate accurate bulk ice phase diagrams, before their applications to nanoconfined water/ice systems.
Conclusions
Based on extensive MD simulations, a semi-quantitative phase diagram of water confined between two hydrophobic parallel walls is obtained, showing three crystalline phases and a bilayer liquid phase. A novel structure IPBI is obtained during the cooling of the liquid at 1 GPa within a range of the separation D between hydrophobic parallel walls (0.88 nm ≤ D ≤ 0.94 nm). In the top view of the IPBI, the O atoms form pentagons, and four pentagons constitute a larger hexagonal ring. In the side view, four kinds of pentagons are aligned as interlocked rows, resulting in channels of two sizes.The “coffin” structure29 is similar to the IPBI in their top views. Both the two structures are locally stable based on DFT optimizations, but still exhibit fundamental differences. The most pronounced one is that 1/3 of the water molecules in the coffin structure are involved in tetragons. This leads us to speculate that the IPBI structure sacrifices the linear H-bond requirement to retain the tetrahedral orientation requirement, while the coffin structure does the opposite. This hypothesis is confirmed by a series of indices designed to show the linearity and tetrahedrality of their hydrogen bonding networks. The most important insight obtained from this study is that under the nanoscale confinement, the hydrogen bonding networks of water can be understood in terms of tradeoff between the conditions for an ideal network. This generic notion may be extended to other hydrogen bonding-network systems.
Acknowledgements
We are grateful to Prof. Francesco Paesani, Dr Andrea Zonca and Sandeep Kumar Reddy for participating in the discussions. This work is supported by the National Natural Science Foundation of China (21503205, 21121003, 91021004, 20933006, and 51172223), by the Anhui Provincial Natural Science Foundation (1608085QB30), by CNPC and CAS (2015A-4812), by the National Key Basic Research Program (2011CB707305, 2011CB921404, and 2012CB922001), by Fundamental Research Funds for the Central Universities (WK2060140014 and WK2060190025), by CAS Strategic Priority Research Program (XDB01020300, XDB10030402), and by USTCSCC. XCZ is supported by grants from the University of Nebraska Center for Energy Sciences Research and a grant from USTC for (1000plan) Qianren-B summer research. WDZ, WHZ and XCZ are also supported by a grant (1401042004) from Bureau of Science & Technology of Anhui Province.References
- O. Mishima and H. E. Stanley, Nature, 1998, 396, 329–335 CrossRef CAS.
- G. Malenkov, J. Phys.: Condens. Matter, 2009, 21, 283101 CrossRef PubMed.
- K. Koga, H. Tanaka and X. C. Zeng, Nature, 2000, 408, 564–567 CrossRef CAS PubMed.
- K. Koga, G. T. Gao, H. Tanaka and X. C. Zeng, Nature, 2001, 412, 802–805 CrossRef CAS PubMed.
- P. Kumar, S. V. Buldyrev, F. W. Starr, N. Giovambattista and H. E. Stanley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 051503 CrossRef PubMed.
- N. Giovambattista, P. J. Rossky and P. G. Debenedetti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 041604 CrossRef PubMed.
- D. Takaiwa, I. Hatano, K. Koga and H. Tanaka, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 39–43 CrossRef CAS PubMed.
- C. Guse and R. Hentschke, J. Phys. Chem. B, 2011, 116, 751–762 CrossRef PubMed.
- W.-H. Zhao, L. Wang, J. Bai, J. S. Francisco and X. C. Zeng, J. Am. Chem. Soc., 2014, 136, 10661–10668 CrossRef CAS PubMed.
- W.-H. Zhao, L. Wang, J. Bai, L.-F. Yuan, J. Yang and X. C. Zeng, Acc. Chem. Res., 2014, 47, 2505–2513 CrossRef CAS PubMed.
- H. Qiu, X. C. Zeng and W. Guo, ACS Nano, 2015, 9, 9877–9884 CrossRef CAS PubMed.
- Y. Zhu, F. Wang, J. Bai, X. C. Zeng and H. Wu, ACS Nano, 2015, 9, 12197–12204 CrossRef CAS PubMed.
- W. H. Zhao, J. Bai, L. Wang, L. F. Yuan, J. L. Yang, J. S. Francisco and X. C. Zeng, J. Mater. Chem. A, 2015, 3, 5547–5555 CAS.
- J. Bai, J. Wang and X. C. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19664–19667 CrossRef CAS PubMed.
- G. Algara-Siller, O. Lehtinen, F. Wang, R. Nair, U. Kaiser, H. Wu, I. Grigorieva and A. Geim, Nature, 2015, 519, 443–445 CrossRef CAS PubMed.
- K. Koga, X. C. Zeng and H. Tanaka, Phys. Rev. Lett., 1997, 79, 5262–5265 CrossRef CAS.
- J. Slovák, H. Tanaka, K. Koga and X. C. Zeng, Physica A, 2003, 319, 163–174 CrossRef.
- R. Zangi and A. E. Mark, J. Chem. Phys., 2003, 119, 1694–1700 CrossRef CAS.
- S. Han, M. Y. Choi, P. Kumar and H. E. Stanley, Nat. Phys., 2010, 6, 685–689 CrossRef CAS.
- N. Kastelowitz, J. C. Johnston and V. Molinero, J. Chem. Phys., 2010, 132, 124511 CrossRef PubMed.
- J. Bai and X. C. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 21240–21245 CrossRef CAS PubMed.
- R. Zangi and A. E. Mark, Phys. Rev. Lett., 2003, 91, 025502 CrossRef PubMed.
- W.-H. Zhao, J. Bai, L.-F. Yuan, J. Yang and X. C. Zeng, Chem. Sci., 2014, 5, 1757–1764 RSC.
- M. Jia, W.-H. Zhao and L.-F. Yuan, Chin. J. Chem. Phys., 2014, 27, 15–19 CrossRef CAS.
- A. L. Ferguson, N. Giovambattista, P. J. Rossky, A. Z. Panagiotopoulos and P. G. Debenedetti, J. Chem. Phys., 2012, 137, 144501 CrossRef PubMed.
- N. Giovambattista, P. J. Rossky and P. G. Debenedetti, Phys. Rev. Lett., 2009, 102, 050603 CrossRef PubMed.
- T. Kaneko, J. Bai, K. Yasuoka, A. Mitsutake and X. C. Zeng, J. Chem. Phys., 2014, 140, 184507 CrossRef PubMed.
- R. Zangi and A. E. Mark, Phys. Rev. Lett., 2003, 91, 025502 CrossRef PubMed.
- J. C. Johnston, N. Kastelowitz and V. Molinero, J. Chem. Phys., 2010, 133, 154516 CrossRef PubMed.
- M. W. Mahoney and W. L. Jorgensen, J. Chem. Phys., 2000, 112, 8910–8922 CrossRef CAS.
- P. Kumar, S. V. Buldyrev, F. W. Starr, N. Giovambattista and H. E. Stanley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 051503 CrossRef PubMed.
- K. Koga and H. Tanaka, J. Chem. Phys., 2005, 122, 104711 CrossRef PubMed.
- S. Han, P. Kumar and H. E. Stanley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 041202 CrossRef PubMed.
- J. Bai, C. A. Angell and X. C. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 5718–5722 CrossRef PubMed.
- D. Bratko, C. D. Daub and A. Luzar, Phys. Chem. Chem. Phys., 2008, 10, 6807–6813 RSC.
- C. Y. Lee, J. A. McCammon and P. J. Rossky, J. Chem. Phys., 1984, 80, 4448–4455 CrossRef CAS.
- S. H. Lee and P. J. Rossky, J. Chem. Phys., 1994, 100, 3334–3345 CrossRef CAS.
- S. Nosé and M. L. Klein, Mol. Phys., 1983, 50, 1055–1076 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- I.-C. Yeh and M. L. Berkowitz, J. Chem. Phys., 1999, 111, 3155–3162 CrossRef CAS.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- K. Lee, E. D. Murray, L. Z. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101 CrossRef.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- V. Babin, C. Leforestier and F. Paesani, J. Chem. Theory Comput., 2013, 9, 5395–5403 CrossRef CAS PubMed.
- R. Bukowski, K. Szalewicz, G. C. Groenenboom and A. Van der Avoird, Science, 2007, 315, 1249–1252 CrossRef CAS PubMed.
- Y. Wang, X. Huang, B. C. Shepler, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2011, 134, 094509 CrossRef PubMed.
- R. Bukowski, K. Szalewicz, G. C. Groenenboom and A. van der Avoird, J. Chem. Phys., 2008, 128, 094314 CrossRef PubMed.
- V. Babin, G. R. Medders and F. Paesani, J. Chem. Theory Comput., 2014, 10, 1599–1607 CrossRef CAS PubMed.
- G. R. Medders, V. Babin and F. Paesani, J. Chem. Theory Comput., 2014, 10, 2906–2910 CrossRef CAS PubMed.
- H. Liu, Y. Wang and J. M. Bowman, J. Phys. Chem. B, 2014, 118, 14124–14131 CrossRef CAS PubMed.
- Y. Wang, V. Babin, J. M. Bowman and F. Paesani, J. Am. Chem. Soc., 2012, 134, 11116–11119 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2016 |







