Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Charging and aggregation of latex particles in aqueous solutions of ionic liquids: towards an extended Hofmeister series
Tamas
Oncsik
,
Anthony
Desert†
,
Gregor
Trefalt
,
Michal
Borkovec
and
Istvan
Szilagyi
*
Department of Inorganic and Analytical Chemistry, University of Geneva, 30 Quai Ernest-Ansermet, CH-1205 Geneva, Switzerland. E-mail: istvan.szilagyi@unige.ch; Tel: +41 22 3796031
First published on 9th February 2016
Abstract
The effect of ionic liquid (IL) constituents and other monovalent salts on the stability of polystyrene latex particles was studied by electrophoresis and light scattering in dilute aqueous suspensions. The surface charge and the aggregation rate were both sensitive to the type of ion leading to different critical coagulation concentration (CCC) values. Systematic variation of the type of IL cation and anion allows us to place these ions within the Hofmeister series. We find that the dicyanoamide anion should be placed between iodide and thiocyanate, while all 1-alkyl-3-methylimidazolium cations can be positioned to the left of the tetramethylammonium and ammonium ions. The hydrophobicity of the 1-butyl-1-methylpyrrolidinium (BMPL+) ion is intermediate between 1-ethyl-3-methylimidazolium (EMIM+) and 1-butyl-3-methylimidazolium (BMIM+). With increasing alkyl chain length, the 1-alkyl-3-methylimidazolium cations adsorb on the latex particles very strongly, and 1-hexyl-3-methylimidazolium (HMIM+) and 1-octyl-3-methylimidazolium (OMIM+) lead to pronounced charge reversal and to an intermediate restabilization region.
1. Introduction
Ionic liquids (ILs) consist entirely of cations and anions, and these systems became the focus of intense research recently, mainly due to their uncommon properties, such as low vapour pressure or wide electrochemical window.1–3 These aspects make ILs promising media in material science applications, including energy storage, extraction of minerals or biomolecules and electrodeposition.2–8 An important class of materials in these applications are particle suspensions in ILs, as they are relevant in nanoparticle synthesis, catalysis, solar cells, or printing inks.9–13 For example, numerous researchers have synthesized novel metal nanoparticles in ILs and they could relate the stability of these suspensions to their catalytic activity.11,14–17 In this context, the stability of these suspensions plays a key role, and therefore particle aggregation in ILs was investigated recently.18–23Such particle aggregation studies also focused on IL–water mixtures, and it was quickly realized that on the water-rich side the IL fully dissociates into ions, and that aqueous solutions of ILs closely resemble simple electrolytes.19,20,24 A good understanding of the influence of the presence of water in ILs is further important, since most ILs contain water to a certain extent.
Studies of colloidal particle aggregation in simple electrolyte solutions have a long history, including the landmark development of the Derjaguin, Landau, Verwey, and Overbeek (DLVO) theory.25 This theory predicts, in agreement with experiment, that the aggregation of charged colloidal particles is slow at low salt concentrations, while at higher concentrations it becomes rapid. The sharp transition between these two regimes occurs at the so-called critical coagulation concentration (CCC). The CCC represents an important characteristic concerning the destabilization power of a given salt, or more precisely of the constituent ions. A major achievement of the DLVO theory was to rationalize the Schulze–Hardy rule, which states that multivalent counterions strongly lower the CCC.25–27
However, the CCC can be also influenced by other ionic properties than their valence. A well-studied aspect represents the Hofmeister series, which orders ions according to their hydrophobicity.28 This series was originally developed to account for the stabilization power of protein solutions, namely
| CO32− < SO42− < H2PO4− < F− < Cl− < Br− < NO3− < I− < ClO4− < SCN− |
| N(CH3)4+ < NH4+ < Cs+ < Rb+ < K+ < Na+ < Li+ < Mg2+ < Ca2+ |
The series indicates that negatively charged proteins form stable solutions even in the presence of high concentration of ions located on the right hand side, while the ions of the left hand side induce their precipitation already at low concentrations. Typically, particle aggregation follows the same series.29–33 In particular, negatively charged particles follow the (above) direct Hofmeister series, whereby the ions on the left induce lower CCCs, while the ones on the right, higher ones. On the other hand, positively charged particles follow the (reversed) indirect Hofmeister series. Thereby, the ions on the left lead to higher CCCs, while the ones on the right, to lower ones. The role of divalent ions is more complicated, since their effect on particle aggregation is greatly influenced by the increased valence as described by the Schulze–Hardy rule.25–27 Therefore, divalent ions are not considered here.
The position of an ion in the Hofmeister series can be qualitatively correlated with its hydrophobicity or its degree of solvation.34,35 Hydrophilic and well-solvated anions, such as F− or Cl−, appear on the left, while hydrophobic and poorly hydrated anions, such as I− or SCN−, on the right. The cations are arranged in the opposite way. The hydrophilic cations, such as Li+ or Na+, appear on the right, while the hydrophobic ones, such as N(CH3)4+ or NH4+, on the left. Many colloidal particles have a hydrophobic surface (e.g., polystyrene latex) and the hydrophobic ions will adsorb more strongly to these surfaces than the hydrophilic ones. Therefore, CCC will be lower in the presence of hydrophobic counterions than in the presence of hydrophilic ones. Conversely, the CCC will be higher in the presence of hydrophobic coions than in the presence of hydrophilic ones. In the latter situation, however, electrostatic repulsion between the coions and the charged particle may lead to very weak adsorption, and these effects may not be noticeable. In general, the CCCs will decrease with increasing hydrophobicity of cations for negatively charged hydrophobic particles (direct Hofmeister series), while they will also decrease with decreasing hydrophobicity of cations for positively charged particles (indirect Hofmeister series). The reverse argumentation applies to hydrophilic particles (e.g., silica). These trends have been confirmed by CCC measurements in numerous systems experimentally.29,31,32,36–38
In the present study, we investigate charging and aggregation of polystyrene latex particles in aqueous solutions of ILs. From the concentration dependence of the aggregation rate, one can extract the CCC, and the observed sequences in these quantities can be used to place the IL constituents into the Hofmeister series. The present investigation is related to an earlier study published by us, which focused on simple monovalent ions only.29 That study used the same particles as the present one, thus facilitating a direct comparison of both. While ion specific effects on protein solubilisation and enzymatic activity in aqueous solutions of ILs were studied with a similar aim,39–43 we believe that the determination of the CCC for uniform particles provides a reliable measure concerning the position of IL constituents within the Hofmeister series.
2. Experimental
2.1 Materials
Sulfate and amidine functionalized polystyrene latex particles were purchased from Invitrogen Corporation. The size and polydispersity of the particles were determined by interpreting static light scattering (SLS) data in stable suspensions using Mie theory.44 Very good agreement was found with the values obtained in transmission electron microscopy (TEM) measurements by the manufacturer (Table 1). Dynamic light scattering (DLS) yielded slightly higher hydrodynamic radii, probably due to sample polydispersity. The same particles were used in our previous study,29 where further properties of these particles are given. Prior to the experiments, the particles were dialyzed against ultrapure water until the conductivity remained constant and below 0.8 μS cm−1. For the dialysis, cellulose ester and polyvinylidene fluoride membranes (Spectrum Rancho) were used for the sulfate and amidine modified latex suspensions, respectively. The particle concentrations in the dialyzed stock suspensions were determined by SLS, whereby a calibration curve of the scattering intensity obtained with the original particle suspensions of known concentration was used. Typical concentrations in these stock suspensions were 65 and 7 g L−1 for sulfate and amidine particles, respectively. Ultrapure Milli-Q water (Millipore) was used throughout.ILs used in this study were purchased from IoLiTech and they include 1-butyl-3-methylimidazolium as a cation with chloride (BMIM–Cl), bromide (BMIM–Br), dicyanoamide (BMIM–N(CN)2) and thiocyanate (BMIM–SCN) ions, 1-butyl-1-methylpyrrolidinium ILs as the same anions (BMPL–Cl, BMPL–Br, BMPL–N(CN)2 and BMPL–SCN) and the chloride salts of 3-methylimidazolium (MIM–Cl), 1-ethyl-3-methylimidazolium (EMIM–Cl), 1-hexyl-3-methylimidazolium (HMIM–Cl) and 1-octyl-3-methylimidazolium cations (OMIM–Cl) (Fig. 1). The ILs were dried under vacuum at 50 °C for one day and Karl-Fischer titration (Metrohm) was performed to determine their final water content, which was always below 1 g L−1. The dried ILs were handled in a glove box. In some cases, mixing the ILs with water resulted in the formation of precipitates due to the presence of impurities, which could be detected by light scattering. These precipitates were removed by allowing the aqueous solutions to stand overnight and filtering with a 0.1 μm syringe filter (Millipore). Inorganic salts of analytical grade were purchased from Sigma Aldrich (NaCl, NaN(CN)2 and NaSCN) and Fluka (NaBr). Their solutions were prepared by mixing the calculated amount of solid salt with ultrapure water. All stock solutions and water were adjusted to pH 4.0 with HCl and filtered prior to sample preparation. The measurements were carried out at a temperature of 25.0 ± 0.2 °C.
2.2 Electrophoresis
A ZetaSizer Nano ZS (Malvern) instrument was used to determine the electrophoretic mobility of the particles. During sample preparation, water was mixed with the appropriate volume of stock electrolyte or IL solutions to reach the desired concentration. The particles were then added from the concentrated stock suspension to get final particle concentrations of 5 mg L−1 in the case of amidine and 50 mg L−1 for the sulfate latex. The samples were equilibrated for one minute in the instrument prior to the measurements. Five repetitions were performed and averaged.2.3 Particle aggregation
Time-resolved DLS was used to follow the aggregation process in aqueous particle suspensions. This technique has proved to be most suitable to determine aggregation rates of colloidal particles.45–47 The instrument used was an ALV/CGS-3 goniometer (ALV) system, equipped with a He/Ne laser of a wavelength of 633 nm and an avalanche photodiode as a detector. Samples were prepared in borosilicate glass cuvettes (Kimble Chase). Before the measurements, the cuvettes were cleaned in piranha solution, which is a mixture of concentrated H2SO4 (Carlo Erba) and 30% H2O2 (Reactolab) in a volume ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Subsequently, they were washed with water and dried in a dust-free oven at 60 °C. The particle concentrations were varied in the range of 2–10 mg L−1 for the amidine latex and 50–200 mg L−1 for the sulfate latex, which corresponds to the number concentration range of (0.3–2.0) × 1015 m−3. To start the aggregation experiment, the particle stock suspension was injected into a cuvette containing the respective salt solution, and the sample was mixed and inserted in the light scattering system. The correlation function was recorded for 20 seconds at a scattering angle of 90° and the second-order cumulant fit was used to determine the hydrodynamic radius. The change in this quantity was followed in 50–100 subsequent runs. To probe the early stages of the aggregation, the hydrodynamic radius values never increased more than 40% in these experiments. This increase is an adequate compromise between good measurement accuracy and minor interferences of higher aggregates.45,48 The apparent dynamic aggregation rate coefficient Δ was determined from the initial rate of increase
1. Subsequently, they were washed with water and dried in a dust-free oven at 60 °C. The particle concentrations were varied in the range of 2–10 mg L−1 for the amidine latex and 50–200 mg L−1 for the sulfate latex, which corresponds to the number concentration range of (0.3–2.0) × 1015 m−3. To start the aggregation experiment, the particle stock suspension was injected into a cuvette containing the respective salt solution, and the sample was mixed and inserted in the light scattering system. The correlation function was recorded for 20 seconds at a scattering angle of 90° and the second-order cumulant fit was used to determine the hydrodynamic radius. The change in this quantity was followed in 50–100 subsequent runs. To probe the early stages of the aggregation, the hydrodynamic radius values never increased more than 40% in these experiments. This increase is an adequate compromise between good measurement accuracy and minor interferences of higher aggregates.45,48 The apparent dynamic aggregation rate coefficient Δ was determined from the initial rate of increase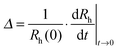 | (1) |
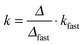 | (2) |
2.4 Viscosity
A DV-II Pro viscometer (Brookfield) was used to measure the dynamic viscosities of the IL solutions. The concentration ranges of the monovalent electrolytes were chosen according to the concentrations investigated in the mobility and aggregation measurements, usually up to 1.0 M. In this range, the viscosities varied linearly with the concentration, and the values for the individual samples were obtained from a linear fit of the data.3. Results and discussion
Surface charge and aggregation rates of sulfate and amidine modified polystyrene latex particles were investigated in the presence of ILs and monovalent electrolytes by electrophoresis and DLS. The principal aim of these experiments was to place some common IL constituents (Fig. 1) into the Hofmeister series. In addition, the influence of the alkyl chain length within the 1-alkyl-3-methylimidazolium series was investigated.3.1 General trends
Electrophoretic mobilities and aggregation rates of sulfate and amidine latex particles were measured in different ionic environments. Initially, we investigated the effect of anions, namely Cl−, Br−, N(CN)2− and SCN−, in the presence of Na+ as the cation (Fig. 2). Subsequently, the same anions were investigated in the presence of BMIM+ (Fig. 3) and BMPL+ (Fig. 4) as cations. In all systems, the electrophoretic mobility increases with the salt concentration for the sulfate particles and decreases for the amidine particles, sometimes resulting in an isoelectric point (IEP) and a subsequent weak charge reversal. These trends are mainly caused by the progressive screening through the electrolyte and simultaneous adsorption of the counterions. The particle aggregation rates increase rapidly with increasing salt concentration in the slow aggregation regime, and reach a constant value at higher concentrations in the fast aggregation regime. The CCC is located in the narrow transition zone between these two regimes. This behaviour is typical for charged colloidal particles dispersed in electrolyte solutions and can be predicted by the DLVO theory,25 in some situations even quantitatively.49,50 The characteristic influence of the type of ion present on the CCCs will be detailed below. No clear trends were observed in the dependencies of the aggregation rates on the salt concentration in the slow aggregation regimes.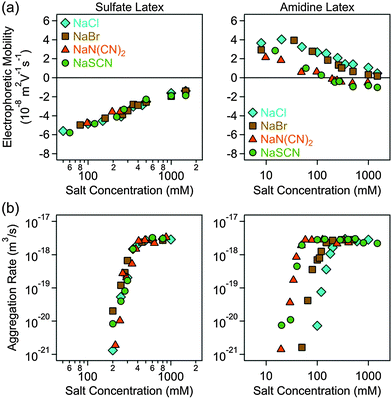 | ||
| Fig. 2 Electrophoretic mobility (a) and absolute aggregation rate (b) for sulfate (left column) and amidine (right column) latex particles as a function of the salt concentration for different monovalent electrolytes of the sodium cation. The results with the Cl−, Br− and SCN− ions have been already published earlier.29 | ||
3.2 Fast aggregation regime
The possible influence of the ion type on the fast aggregation rate coefficients measured above the CCCs was addressed. The ions investigated include Cl−, Br−, N(CN)2− and SCN− anions, and Na+, BMIM+ and BMPL+ cations. As one must consider viscosity effects, the absolute rate coefficients in the fast aggregation regime were normalized by Smoluchowski’s rate coefficient for diffusion controlled aggregation51 | (3) |
3.3 Ion specific effects
For negatively charged sulfate latex particles, there were no specific effects of the coions, provided Na+ was used as the counterion. All the anions used, namely Cl−, Br−, N(CN)2− and SCN−, adsorb to the particle surface only weakly, and therefore the electrophoretic mobility (Fig. 2a), aggregation rates (Fig. 2b) and CCCs (Fig. 5b) remain the same within the experimental error. With the exception of the N(CN)2− anion, the same observation was already reported earlier.29 For the amidine latexes, the electrophoretic mobilities decrease with the salt level and their values at the same concentration decrease within the series Cl−, Br−, N(CN)2−, and SCN− (Fig. 2a). The adsorption of N(CN)2− and SCN− ions results in an IEP and a charge reversal, suggesting that these ions are rather hydrophobic and that they adsorb on these particles strongly. Similar charge reversal has been observed with other less solvated monovalent ions.29,34,52 The trend in the mobilities is also reflected in the CCCs (Fig. 2b and 5c). One observes that the CCC decreases in the same sequence as stated above, namely for Cl− being the highest and for N(CN)2− and SCN− the lowest. This order can be explained as follows. The hydrophobic counterions, such as N(CN)2− and SCN−, adsorb strongly on the hydrophobic particle surface, leading to a decrease of the surface charge and to lower CCCs. On the other hand, the hydrophilic Cl− counterion adsorbs weakly leading to highly charged particles, which also have higher CCCs. The observed sequence Cl− > Br− > SCN− reflects the expected indirect Hofmeister series, as reported before.29 The new finding here is that N(CN)2− behaves similar to SCN−. This observation agrees with earlier protein precipitation experiments.42When the BMIM+ counterion was used, electrophoretic mobilities and aggregation rates of the negatively charged sulfate latex particles were strongly influenced by the type of coion (Fig. 3a and b). The magnitude of the mobility and of the CCCs (Fig. 5b) was significantly lower in the presence of BMIM+ than for Na+, confirming the considerable adsorption of the BMIM+ counterions to the oppositely charged surface. In these systems, the mobilities and CCCs were sensitive to the type of coion, whereby the CCCs increase in the sequence Br− < N(CN)2− < SCN−. With the exception of the Cl− ion, this trend reflects the expected direct Hofmeister series for negatively charged hydrophobic surfaces.33 This finding is in line with recent colloidal probe experiments with hydrophilic silica particles in the presence of the BMIM+ counterions, which reports the strength of the short-range attraction to increase in the sequence Cl− < N(CN)2− < SCN−.24 Such attraction was significant at salt levels close to the CCCs, and therefore the CCC is expected to decrease in the same sequence as stated above in agreement with the indirect Hofmeister series for negatively charged hydrophilic particles.
A similar sequence of counterions was observed for the amidine particles as in the presence of Na+. The mobilities (Fig. 3a) and the CCCs (Fig. 5c) decreased again in the sequence Cl− > Br− > N(CN)2− > SCN− in agreement with the indirect Hofmeister series for positively charged hydrophobic surfaces.33 The electrophoretic mobilities remain positive for weakly adsorbing Cl− and Br− counterions, while the strongly adsorbing SCN− ions induce a charge reversal. However, the IEP is situated at much lower concentration than for the Na+ ions, which suggests that the hydrophobic BMIM+ coion adsorbs to the particle surface, which in turn induces a stronger co-adsorption of SCN− ions due to ion pair formation on the surface. The formation of ion pairs between cations and anions has been reported in various ILs.53–57 The IL constituent ions adsorbed on the particle surface may also form ion pairs with the oppositely charged ions. The formation of such surface ion pairs will then influence the surface charge and also the CCC. For the N(CN)2− anion, charge neutralization occurs as well, but the adsorption is not strong enough to reverse the particle charge.
For the BMPL+ counterion, specific effects of coions were equally observed for sulfate latex particles. Similar electrophoretic mobilities were measured for Cl− and Br−, however, the presence of N(CN)2− and SCN− ions led to higher mobilities (Fig. 4a) and lower CCCs (Fig. 4b and 5b). This trend is opposite to the one observed for BMIM+, and does not follow the anticipated direct Hofmeister series. This reversal of the Hofmeister series could be related to the counterion affinity to the oppositely charged particles and the extent of ion pairing on the surface. The observed trends in the CCCs indicate stronger ion pairing in the BMIM–SCN system than for BMPL–SCN. For the amidine particles, a weak charge reversal is again observed for the SCN− ions, but the electrophoretic mobilities remain positive for the other counterions (Fig. 4a). The charge reversal occurred at higher concentration than in the BMIM+ system, which may indicate either weaker BMPL+ adsorption on the particle surface or weaker ion pair interactions between BMPL+ and SCN− ions. Nevertheless, the trends in both the charging and aggregation properties of the amidine particles in the presence of BMPL+ and BMIM+ counterions are similar. Accordingly, the mobilities at the same concentration as well as the CCCs follow Cl− > Br− > N(CN)2− > SCN− (Fig. 4a and 5c). This order is in agreement with the indirect Hofmeister series expected for positively charged hydrophobic particles.31,33
The observed trends for the cation dependence are summarized in Fig. 5b and c. For the sulfate latex, the presence of the BMIM+ counterion leads to lower CCCs than BMPL+ in the presence of simple anions, while the trend is reversed in the presence of hydrophobic N(CN)2− and SCN− anions. This reversal is probably related to the variable extent of ion pair formation in these systems. No trend with CCCs was observed for amidine latex particles when the coions were varied.
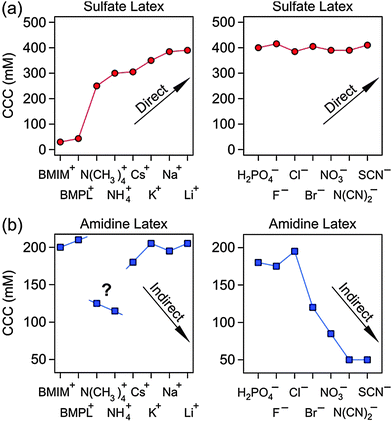
Let us now compare the present results with the ones of an earlier study, which investigated the CCCs of exactly the same particles.29 In particular, various anions in the presence of Na+ and various cations in the presence of Cl− were investigated. Combining the present results with the ones from that study29 enables us to place the IL constituents into the established Hofmeister series (Fig. 6). For sulfate latex particles, the extended Hofmeister series becomes
| BMIM+ < BMPL+ < N(CH3)4+ < NH4+ < Cs+ < K+ < Na+ < Li+ |
| H2PO4− > F− > Cl− > Br− > NO3− > N(CN)2− > SCN− |
The N(CN)2− counterion has to be placed between NO3− and SCN−. The BMIM+ and BMPL+ coions have again no influence on the CCC of the amidine particles. However, the N(CH3)4+ and NH4+ coions lead to systematically lower CCCs, probably, due to specific interactions with the amidine groups.
3.4 Effect of the alkyl chain length
As shown in the previous section, the hydrophobic BMIM+ counterions strongly adsorb on the negatively charged sulfate latex particles and thus modify the particle charge and their CCCs (Fig. 3a and 5b). To further investigate the effects of cation hydrophobicity on charging and aggregation of these particles, we have studied electrophoretic mobilities and aggregation rates of sulfate latex particles in the presence of 1-alkyl-3-methylimidazolium counterions, namely for MIM+, EMIM+, BMIM+, HMIM+ and OMIM+. Their hydrophobicity increases from the left to the right due to the increasing length of the alkyl chains (Fig. 1). In all cases, the Cl− coion was used.At sufficiently low concentrations, the electrophoretic mobilities increase with the concentration (Fig. 7a). In the presence of MIM+ and EMIM+, the particles remained negatively charged within the entire range investigated. This increase is primarily due to screening by the increasing salt level, but the adsorption of these ions to the particle surface also contributes to this trend. However, adsorption of these counterions becomes more pronounced for longer aliphatic chains and leads to slight charge reversal for BMIM+. The adsorption of HMIM+ and OMIM+ counterions becomes even more important and induces charge neutralization and a significant charge reversal. At higher concentrations, the mobilities decrease due to screening, as particularly evident in the presence of the OMIM+ cation. A similar charge reversal was already reported for negatively charged kaolinite particles in OMIM–Cl solutions.58
The charging behaviour is well-reflected in the respective aggregation rates. For the BMIM+, EMIM+ and MIM+ cations with short alkyl chains, the aggregation rates (Fig. 7b) show the classical behaviour of slow aggregation at low concentrations and rapid aggregation at high concentrations, with a CCC in between these two regimes. This situation is similar to the systems discussed above. The CCCs decrease systematically with increasing alkyl chain length, which is caused by the increasing adsorption strength due to increasing length of the alkyl chain.
However, the dependence of the aggregation rate on the IL concentration is notably different in the presence of the OMIM+ counterion (Fig. 7c). The aggregation rates are small at low IL concentrations, and they go through a maximum near the IEP. The rate constant at the maximum corresponds to its value in the fast aggregation regime. Upon increasing the IL concentration further, one observes a decrease of the aggregation rate. The rate passes through a minimum and increases again to reach the value in the fast aggregation regime. A similar dependence is observed for the HMIM+ counterion, albeit the intermediate minimum is much less pronounced. This shallower minimum is due to the weaker charge reversal of HMIM+ as revealed by the electrophoresis. Clearly, OMIM+ adsorbs most strongly, and the adsorption strength decreases with decreasing chain length.
One might suspect that the formation of micelles could be relevant in these systems, especially for the cations with a longer apolar alkyl chain. The CMC of OMIM–Cl was reported to be 220 mM and for HMIM–Cl 900 mM.59,60 The latter value is at the end of the concentration range used in the present study. Therefore, the formation of micelles does not play any role in the adsorption and particle aggregation mechanism in the HMIM–Cl system. For the OMIM–Cl system, the CMC falls into the upper range of the destabilization due to charge screening by the chloride counterions. Again, micellization plays a minor role.
The observed dependence of the aggregation rate on the concentration of 1-alkyl-3-methylimidazolium can be interpreted in terms of a succession of three CCCs. The first CCC occurs at low concentration during the transition from the slow to fast regime. The second CCC is located after the maximum in the IL concentration, whereby the system undergoes a transition from the fast to slow regime. The third CCC is situated at the highest concentrations after the minimum in the aggregation rate, when the aggregation becomes fast again. Comparing the location of the CCCs with the electrophoretic mobilities in the same concentration ranges, one can realize that the first CCC is caused by charge neutralization, the second is connected with the charge reversal process, while the third CCC is due to the screening effect of the counterions on the surface charge.
A stability map of the CCCs versus the type of counterion of different chain lengths summarizes this characteristic behaviour well (Fig. 8). Three CCCs are observed for HMIM+ and OMIM+ counterions, while only one CCC is found for MIM+, EMIM+ and BMIM+. Therefore, this map shows two regions where the dispersions are stable, meaning that the particle aggregation is significantly slower than that in the case of fast aggregation. That region is indicated as unstable. The first stability region in the lower left corner corresponds to the regular stabilization due to the negative charge of the latex particles. The second region on the right hand side corresponds to the positively charged particles after charge reversal, which is induced by the strong adsorption of the less solvated IL cations. The unstable region in the upper part of the map is due to destabilization and screening at high salt concentrations. The narrow unstable channel in the lower right part of the map is due to the destabilization and charge neutralization at the IEP. The first CCC values at low IL concentration in the presence of 1-alkyl-3-methylimidazolium counterions reflect the decreasing chain length and increasing hydrophilicity within the series
| OMIM+ < HMIM+ < BMIM+ < EMIM+ < MIM+ |
On the left hand side of the series, one finds the hydrophobic cations with a longer alkyl chain. They adsorb more strongly to the particle surface, and induce lower CCCs. Those on the right hand side are more hydrophilic and feature a shorter alkyl chain. The latter counterions adsorb more weakly, and lead to higher CCCs. This trend is reminiscent to previous findings for oxide and silver halide particles in the presence of ionic surfactants of variable chain lengths, whereby the IEP or the first CCC shifts towards smaller concentrations with increasing alkyl chain length.61–64 In addition, the restabilization occurred in all systems containing surfactants with an octyl chain or longer. A subsequent destabilization at high concentrations was also observed, quite in analogy to OMIM+.64 Enzymatic activity reflects the same order, namely, the proteins lose their activity in the presence of HMIM+ at lower concentration than for EMIM+.39,40
Similar stability behaviour was reported for the aggregation of latex particles in the presence of multivalent ions or short-chain oligoamines.65,66 In particular, the similarity to the system with the oligoamines is striking, and deservers further discussion.66 These authors have studied electrophoresis and particle aggregation rates for negatively charged sulfate latex particles in the presence of aliphatic oligoamines with the structural formula H2NCH2CH2(NHCH2CH2)nNH2 for n = 0, 1, 2, and 4. Under the mildly acidic conditions used, these oligoamines form multivalent cations. The concentration dependence of electrophoretic mobilities and of the aggregation rate was very similar to the one shown in Fig. 7, and shows an analogous trend with the increasing chain length. Moreover, the stability map of the CCCs versus the chain length looks surprisingly similar to Fig. 8. Due to these analogies, one might suspect in these two systems that the underlying mechanisms leading to charge reversal and destabilization are similar. The hydrophobic interaction will become more important with increasing chain length and this aspect might be responsible in both systems for the increased extent of adsorption, which would then induce similar patterns in the charging behaviour and aggregation rates. Moreover, these oligoamines are only partially ionized and their charge could be further reduced by complexation of counterions and ion condensation effects. The interesting consequence of this hypothesis is that the multivalent nature of the longer-chain oligoamines becomes secondary and their increasing hydrophobicity determines the adsorption of these molecules and as a consequence, the aggregation of these particles.
4. Conclusions
The effect of simple monovalent ions and water-miscible ILs on the surface charge and aggregation of polystyrene latex particles was investigated by electrophoresis and time-resolved light scattering in dilute aqueous solutions. From studies performed on negatively charged sulfate latex particles, the Hofmeister series for the cations may be extended as| OMIM+ < HMIM+ < BMIM+ < BMPL+ < EMIM+ < MIM+ < N(CH3)4+ < NH4+ < Cs+ < K+ < Na+ < Li+ |
The hydrophobic ions shown on the left hand side lead to the lowest CCCs. The most hydrophobic ones, such as OMIM+ and HMIM+, show more pronounced charge reversal and a subsequent restabilization. The left hand side of the series reflects the known trend of decreasing hydrophilicity with increasing chain length in surfactant solutions. For amidine latex particles, we conclude that the Hofmeister series for the anions should be extended as
| Cl− > Br− > N(CN)2− > SCN− |
Acknowledgements
The present research was supported by the Swiss National Science Foundation, the University of Geneva and the COST Action CM1206.References
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS PubMed.
- A. P. Abbott and K. J. McKenzie, Phys. Chem. Chem. Phys., 2006, 8, 4265–4279 RSC.
- M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629 CrossRef CAS PubMed.
- A. Izgorodin, R. Hocking, O. Winther-Jensen, M. Hilder, B. Winther-Jensen and D. R. MacFarlane, Catal. Today, 2013, 200, 36–40 CrossRef CAS.
- N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123–150 RSC.
- E. G. Garcia, A. K. Ressmann, P. Gaertner, R. Zirbs, R. L. Mach, R. Krska, K. Bica and K. Brunner, Anal. Bioanal. Chem., 2014, 406, 7773–7784 CrossRef PubMed.
- R. Zirbs, K. Strassl, P. Gaertner, C. Schroder and K. Bica, RSC Adv., 2013, 3, 26010–26016 RSC.
- R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS PubMed.
- A. Podgorsek, A. S. Pensado, C. C. Santini, M. F. C. Gomes and A. A. H. Padua, J. Phys. Chem. C, 2013, 117, 3537–3547 CAS.
- P. S. Campbell, C. C. Santini, D. Bouchu, B. Fenet, K. Philippot, B. Chaudret, A. A. H. Padua and Y. Chauvin, Phys. Chem. Chem. Phys., 2010, 12, 4217–4223 RSC.
- M. Anouti and J. Jacquemin, Colloids Surf., A, 2014, 445, 1–11 CrossRef CAS.
- P. Wang, S. M. Zakeeruddin, P. Comte, I. Exnar and M. Gratzel, J. Am. Chem. Soc., 2003, 125, 1166–1167 CrossRef CAS PubMed.
- Z. Zolek-Tryznowska, J. Izdebska and M. Golazbek, Color. Technol., 2014, 130, 314–318 CAS.
- E. Vanecht, K. Binnemans, S. Patskovsky, M. Meunier, J. W. Seo, L. Stappers and J. Fransaer, Phys. Chem. Chem. Phys., 2012, 14, 5662–5671 RSC.
- K. Richter, A. Birkner and A. V. Mudring, Phys. Chem. Chem. Phys., 2011, 13, 7136–7141 RSC.
- L. L. Lazarus, C. T. Riche, N. Malmstadt and R. L. Brutchey, Langmuir, 2012, 28, 15987–15993 CrossRef CAS PubMed.
- G. Salas, A. Podgorsek, P. S. Campbell, C. C. Santini, A. A. H. Padua, M. F. C. Gomes, K. Philippot, B. Chaudret and M. Turmine, Phys. Chem. Chem. Phys., 2011, 13, 13527–13536 RSC.
- C. Guibert, V. Dupuis, J. Fresnais and V. Peyre, J. Colloid Interface Sci., 2015, 454, 105–111 CrossRef CAS PubMed.
- J. A. Smith, O. Werzer, G. B. Webber, G. G. Warr and R. Atkin, J. Phys. Chem. Lett., 2010, 1, 64–68 CrossRef CAS.
- I. Szilagyi, T. Szabo, A. Desert, G. Trefalt, T. Oncsik and M. Borkovec, Phys. Chem. Chem. Phys., 2014, 16, 9515–9524 RSC.
- K. Ueno, A. Inaba, M. Kondoh and M. Watanabe, Langmuir, 2008, 24, 5253–5259 CrossRef CAS PubMed.
- J. Nordstrom, L. Aguilera and A. Matic, Langmuir, 2012, 28, 4080–4085 CrossRef PubMed.
- M. Mamusa, J. Siriex-Plenet, F. Cousin, E. Dubois and V. Peyrea, Soft Matter, 2014, 10, 1097–1101 RSC.
- V. Valmacco, G. Trefalt, P. Maroni and M. Borkovec, Phys. Chem. Chem. Phys., 2015, 17, 16553–16559 RSC.
- D. F. Evans and H. Wennerstrom, The Colloidal Domain, John Wiley, New York, 1999 Search PubMed.
- T. Oncsik, G. Trefalt, Z. Csendes, I. Szilagyi and M. Borkovec, Langmuir, 2014, 30, 733–741 CrossRef CAS PubMed.
- C. Schneider, M. Hanisch, B. Wedel, A. Jusufi and M. Ballauff, J. Colloid Interface Sci., 2011, 358, 62–67 CrossRef CAS PubMed.
- P. Lo Nostro and B. W. Ninham, Chem. Rev., 2012, 112, 2286–2322 CrossRef CAS PubMed.
- T. Oncsik, G. Trefalt, M. Borkovec and I. Szilagyi, Langmuir, 2015, 31, 3799–3807 CrossRef CAS PubMed.
- D. F. Parsons, M. Bostrom, P. Lo Nostro and B. W. Ninham, Phys. Chem. Chem. Phys., 2011, 13, 12352–12367 RSC.
- T. Lopez-Leon, M. J. Santander-Ortega, J. L. Ortega-Vinuesa and D. Bastos-Gonzalez, J. Phys. Chem. C, 2008, 112, 16060–16069 CAS.
- J. M. Peula-Garcia, J. L. Ortega-Vinuesa and D. Bastos-Gonzalez, J. Phys. Chem. C, 2010, 114, 11133–11139 CAS.
- N. Schwierz, D. Horinek and R. R. Netz, Langmuir, 2010, 26, 7370–7379 CrossRef CAS PubMed.
- C. Calero, J. Faraudo and D. Bastos-Gonzalez, J. Am. Chem. Soc., 2011, 133, 15025–15035 CrossRef CAS PubMed.
- M. Lund, R. Vacha and P. Jungwirth, Langmuir, 2008, 24, 3387–3391 CrossRef CAS PubMed.
- F. J. M. Ruiz-Cabello, G. Trefalt, T. Oncsik, I. Szilagyi, P. Maroni and M. Borkovec, J. Phys. Chem. B, 2015, 119, 8184–8193 CrossRef PubMed.
- F. Dumont, J. Warlus and A. Watillon, J. Colloid Interface Sci., 1990, 138, 543–554 CrossRef CAS.
- R. Tian, G. Yang, H. Li, X. D. Gao, X. M. Liu, H. L. Zhu and Y. Tang, Phys. Chem. Chem. Phys., 2014, 16, 8828–8836 RSC.
- C. Lange, G. Patil and R. Rudolph, Protein Sci., 2005, 14, 2693–2701 CrossRef CAS PubMed.
- Z. Yang, J. Biotechnol., 2009, 144, 12–22 CrossRef CAS PubMed.
- C. Sanfilippo, N. D’Antona and G. Nicolosi, Biotechnol. Lett., 2004, 26, 1815–1819 CrossRef CAS PubMed.
- D. Constantinescu, H. Weingartner and C. Herrmann, Angew. Chem., Int. Ed., 2007, 46, 8887–8889 CrossRef CAS PubMed.
- K. Fujita, D. R. MacFarlane and M. Forsyth, Chem. Commun., 2005, 4804–4806 RSC.
- M. I. Mishchenko, L. D. Travis and A. A. Lacis, Scattering, Absorption, and Emission of Light by Small Particles, University Press, Cambridge, 2002 Search PubMed.
- H. Holthoff, S. U. Egelhaaf, M. Borkovec, P. Schurtenberger and H. Sticher, Langmuir, 1996, 12, 5541–5549 CrossRef CAS.
- K. L. Chen, S. E. Mylon and M. Elimelech, Langmuir, 2007, 23, 5920–5928 CrossRef CAS PubMed.
- A. Zaccone, H. Wu, M. Lattuada and M. Morbidelli, J. Phys. Chem. B, 2008, 112, 1976–1986 CrossRef CAS PubMed.
- M. Schudel, S. H. Behrens, H. Holthoff, R. Kretzschmar and M. Borkovec, J. Colloid Interface Sci., 1997, 196, 241–253 CrossRef CAS PubMed.
- S. H. Behrens, M. Borkovec and P. Schurtenberger, Langmuir, 1998, 14, 1951–1954 CrossRef CAS.
- M. Kobayashi, M. Skarba, P. Galletto, D. Cakara and M. Borkovec, J. Colloid Interface Sci., 2005, 292, 139–147 CrossRef CAS PubMed.
- M. Elimelech, J. Gregory, X. Jia and R. A. Williams, Particle Deposition and Aggregation: Measurement, Modeling, and Simulation, Butterworth-Heinemann Ltd., Oxford, 1995 Search PubMed.
- T. Lopez-Leon, J. L. Ortega-Vinuesa and D. Bastos-Gonzalez, ChemPhysChem, 2012, 13, 2382–2391 CrossRef CAS PubMed.
- A. Stoppa, J. Hunger, G. Hefter and R. Buchner, J. Phys. Chem. B, 2012, 116, 7509–7521 CrossRef CAS PubMed.
- R. Sadeghi and N. Ebrahimi, J. Phys. Chem. B, 2011, 115, 13227–13240 CrossRef CAS PubMed.
- M. Bester-Rogac, A. Stoppa, J. Hunger, G. Hefter and R. Buchner, Phys. Chem. Chem. Phys., 2011, 13, 17588–17598 RSC.
- M. Bester-Rogac, J. Hunger, A. Stoppa and R. Buchner, J. Chem. Eng. Data, 2011, 56, 1261–1267 CrossRef CAS.
- H. K. Stassen, R. Ludwig, A. Wulf and J. Dupont, Chem. – Eur. J., 2015, 21, 8324–8335 CrossRef CAS PubMed.
- M. Markiewicz, W. Mrozik, K. Rezwan, J. Thoming, J. Hupka and C. Jungnickel, Chemosphere, 2013, 90, 706–712 CrossRef CAS PubMed.
- U. Preiss, C. Jungnickel, J. Thoming, I. Krossing, J. Luczak, M. Diedenhofen and A. Klamt, Chem. – Eur. J., 2009, 15, 8880–8885 CrossRef CAS PubMed.
- J. Luczak, J. Hupka, J. Thoming and C. Jungnickel, Colloids Surf., A, 2008, 329, 125–133 CrossRef CAS.
- D. W. Fuerstenau and M. Colic, Colloids Surf., A, 1999, 146, 33–47 CrossRef CAS.
- A. Watanabe, Bull. Inst. Chem. Res., Kyoto Univ., 1960, 38, 179–215 CAS.
- L. Liang and J. J. Morgan, Aquat. Sci., 1990, 52, 32–55 CrossRef.
- R. H. Ottewill and M. C. Rastogi, Trans. Faraday Soc., 1960, 56, 866 RSC.
- P. Sinha, I. Szilagyi, F. J. M. Ruiz-Cabello, P. Maroni and M. Borkovec, J. Phys. Chem. Lett., 2013, 4, 648–652 CrossRef CAS PubMed.
- I. Szilagyi, A. Polomska, D. Citherlet, A. Sadeghpour and M. Borkovec, J. Colloid Interface Sci., 2013, 392, 34–41 CrossRef CAS PubMed.
Footnote |
| † Present address: École normale supérieure de Lyon, CNRS, Université de Lyon 1, Laboratoire de Chimie (UMR 5182), 46 Allée d’Italie, F-69364 Lyon, France. |
| This journal is © the Owner Societies 2016 |