Cage effects on conformational preference and photophysics in the host–guest complex of benzenediols with 18-Crown-6

Abstract

The conformational preference and modification of photophysics of benzenediols, namely hydroquinone (HQ), resorcinol (RE) and catechol (CA), upon host–guest complex formation with 18-Crown-6 (18C6) have been investigated, under supersonically jet-cooled conditions. Laser induced fluorescence (LIF) and UV–UV hole-burning spectra indicate the presence of two conformers for HQ and RE and one conformer for CA. On the other hand, the number of isomers is reduced to one in the 18C6·HQ and 18C6·RE complexes, while the 18C6·CA complex has three stable isomers. The IR spectra of the OH stretching vibration reveal that the two OH groups are H-bonded in 18C6·CA and 18C6·RE. In 18C6·RE, RE adopts the highest energy conformation in the bare form. In 18C6·HQ, the H-bonding of one OH group affects the orientation of the other OH group. The complex formation changes the photophysics of the S₁ state of the benzenediols in a different manner. In our previous work, we reported a remarkable S₁ lifetime elongation in 18C6·CA complexes; the S₁ lifetime of CA is elongated more than 1000 times longer (8 ps → 10.3 ns) in 18C6·CA (F. Morishima et al., J. Phys. Chem. B, 2015, 119, 2557–2565), which we called the “cage effect”. In 18C6·RE, the increase of S₁ lifetime is moderate: 4.0 ns (monomer) → 10.5 ns (complex). On the other hand, the S₁ lifetime of HQ is shortened in 18C6·HQ: 2.6 ns (monomer) → 0.54 ns (complex). Density functional theory (DFT) calculations suggest that these behaviors are related to the S₁ (¹ππ*)–¹πσ* energy gap, the character of the S₂ state and the symmetry of benzenediol. These experimental results clearly show the potential ability of 18C6 to control the conformation and modification of the electronic structure of guest species.

---

1. Introduction

Crown ethers (CEs) have been widely known as functional molecules, especially as inclusion compounds in host–guest chemistry. CEs can hold cations in their cavity and are soluble in organic solvents as well as protic solvents. Owing to these characteristics, they are used as phase transfer catalysts. It is also known that CEs exhibit a preference to encapsulate cations in bulk, depending on the size matching between the cation and the CE cavity. Applications of CEs as molecular receptors, metal cation extraction agents, fluoroionophores and phase transfer catalytic media have been described in a number of studies.^1–24 CEs can include not only metal ions but also various ionic and neutral species through non-covalent interactions.^25–31 In our previous study, we investigated the structure of a cold 3n-Crown-n·phenol neutral complex (n = 5–8)²⁹ and found that 18-crown-6 (18C6) and phenol form a single substantially stable 18C6·phenol 1 : 1 host–guest complex. 18C6 modifies its shape to be nicely matched to phenol showing “induced fit”. The structure is strongly stabilized by collective intermolecular interactions, such as OH⋯O H-bonding and CH⋯π bonding. Furthermore, we recently studied the 18C6·catechol (CA) host–guest complex and found that 18C6 modifies not only the geometrical but also the excited state electronic structures of the guest species,³¹ that is the S₁ lifetime of the CA monomer, 8 ps, becomes 10.3 ns in the 18C6·CA complex. This remarkable elongation of the S₁ lifetime was interpreted to be due to the destruction of the πσ* character of the S₂ state by 18C6, which is generally responsible for the nonradiative decay of the S₁ state.³¹

In the present work, we extend our study to the host–guest complexes of all the benzenediols, hydroquinone (HQ), resorcinol (RE) and CA, with 18C6. We investigate their structures and the effect of complex formation on the S₁ dynamics of benzenediols. Particularly, CA has only one stable conformation, while HQ has two and RE has three possible conformations arising from the orientation of two OH groups. We first investigate how the conformations of benzenediols and 18C6 are modified for forming the stable host–guest complex through “induced-fitting”. We then investigate how the complex formation changes the electronic structure of benzenediols by measuring their S₁ lifetime. We apply various laser spectroscopic methods for the supersonically cooled molecules and complexes to measure the electronic and IR spectra. The number of conformers and isomers is determined by UV–UV hole-burning spectroscopy, and the structure of the specific isomer is investigated by IR–UV double resonance spectroscopy and quantum chemical calculations at density functional theory. The S₁ state lifetime is obtained by deconvoluting the fluorescence decay profiles or the picosecond pump–probe time profiles. We will discuss how the induced-fit model can be applied for forming the most stable complex structures and how the complex formation affects the excited state electronic structure of guest benzenediols.

2. Experimental and computational

2.1 Experimental

Details of the experimental setup have been described elsewhere.³² The supersonic free jet of benzenediol and 18C6·benzenediol complexes was generated by the supersonic expansion of a gaseous mixture of 18C6 and benzenediols diluted in He carrier gas (4 bar). The solid 18C6 and benzenediol samples were separately heated at different sample housings (340–370 K for 18C6, and 348, 363 and 473 K for CA, RE and HQ respectively) to be vaporized. The gas mixture was expanded into a vacuum chamber through a 1 mm orifice of a pulsed nozzle. The S₁–S₀ electronic spectra were observed by laser induced fluorescence (LIF) spectroscopy. A tunable UV light obtained by frequency doubling the output of Nd³⁺:YAG laser pumped dye laser (Lambda Physik Scanmate/Continuum Surelite II) was introduced into the vacuum chamber to be crossed with the supersonic jet at ∼30 mm downstream (x/D = 30) of the orifice. The LIF spectra were obtained by detecting the total fluorescence as a function of UV frequency. The vibronic bands belonging to different isomers were discriminated by UV–UV hole-burning (HB) spectroscopy;³³ the frequency of the probe UV laser was fixed to a certain vibronic band of a specific species and its fluorescence intensity was monitored. Under these conditions, another tunable UV laser (hole burning (HB) laser) pulse obtained by SHG of the Nd³⁺:YAG laser pumped dye laser (Continuum ND6000/Surelite II) was introduced at 10 mm upstream of the crossing point between the jet and the probe laser with a timing of ∼4 μs prior to the probe laser pulse. Then the depletion of the fluorescence intensity induced by the HB laser was monitored by scanning the frequency of the UV HB laser. The UV–UV HB spectra were thus obtained as dip spectra. For IR–UV double resonance (DR) spectroscopy, the output of a pulsed tunable OPO IR laser (LaserVision pumped by Quanta-Ray GCR250) was employed as a HB laser. The IR laser was introduced coaxially to the probe UV pulse with an interval of 80 ns prior to the UV pulse. The UV probe laser frequency was fixed to a certain vibronic band and the IR laser frequency was scanned. The depletion of the fluorescence induced by the IR pump laser was detected, giving fluorescence-dip IR spectra for the UV monitored species.

The S₁ lifetimes of 18C6·CA and 18C6·RE complexes were obtained by deconvoluting the time profiles of the fluorescence decay curves by assuming the laser pulse shape as a Gaussian function with a 4.5 ns pulse width. The S₁ lifetimes of benzenediol monomers and H₂O·HQ and 18C6·HQ complexes were too short to be determined from the fluorescence decay, so that they were obtained by pump–probe experiments using a picosecond laser system. In this experiment, the molecules or complexes in the molecular beam were ionized by stepwise two-photon ionization with two picosecond lasers. The setup of the picosecond laser system has also been described in detail elsewhere.^34,35 The first picosecond pump pulse excites the molecules or complexes to the S₁ origin, and the second probe laser pulse ionizes the S₁ state species. The ions are mass-analyzed with a 50 cm time-of-flight tube and are detected using a channeltron (Burle 4900). The ion signals were processed by using a boxcar integrator (Par model 4401/4420) connected with a PC. By changing the delay time between the pump and probe lasers, the decay time profile of the S₁ state was obtained. The decay time constants were determined by deconvoluting the time profiles with the 12 ps laser pulses. All the decay curves were fitted as a single exponential decay. 18C6 and all benzenediols were purchased from Sigma-Aldrich and Nacalai Tesque, respectively, and used without further purification.

2.2 Computational

The initial structures of 18C6·benzenediol complexes were obtained by Monte Carlo simulation by mixed torsional search with low-mode sampling³⁶ in MacroModel V.9.1³⁷ with the MMFF94s force field.³⁸ The geometries were optimized by the PRCG algorithm with a convergence threshold of 0.05 kJ mol⁻¹. From this calculation, 165 isomers for 18C6·HQ, 46 isomers for 18C6·RE and 193 isomers for 18C6·CA were obtained, within 20 kJ mol⁻¹ of the most stable one. All of these isomers were geometry-optimized by density functional theory (DFT) calculations at the M05-2X/6-31+G* level with loose optimization criteria. This calculation yielded 5, 19, and 61 isomers for 18C6·HQ, 18C6·RE and 18C6·CA, respectively, within 20 kJ mol⁻¹. These loose-optimized isomers were further optimized at the ωB97X-D/6-31++G** level with tight optimization criteria and ultrafine grid. The total energies were corrected by nonscaled zero-point vibrational energy (ZPE). The interaction energy (E_int) of 18C6·benzenediol complexes was computed with counterpoise correction to remove the basis set superposition error (BSSE),

E_int(18C6⋯benzenediol) = E(18C6⋯benzenediol) − E(18C6) − E_int(benzenediol) + E_BSSE(18C6⋯benzenediol), (1)

where conformations of 18C6 and benzenediol fragments were the same as those in the 18C6·benzenediol complex. The IR spectra were obtained by vibrational analysis, and the vertical electronic transition energies were obtained by TD-DFT calculations at the ωB97X-D/6-31++G** level. All the DFT calculations were performed using the Gaussian 09 package, revision D.01.³⁹ The OH stretching frequencies were scaled by 0.9346, 0.9325 and 0.9325 for HQ, RE, and CA, respectively, to reproduce the observed OH stretching vibration of each monomer. Though the calculated electronic energies are the vertical excitation energies, they are scaled by 0.8645, 0.8603 and 0.8598, for HQ, RE and CA, respectively, to reproduce the observed S₁–S₀ band origin energy of each monomer.

3. Results

3.1 S₁–S₀ spectra of benzenediols and their complexes

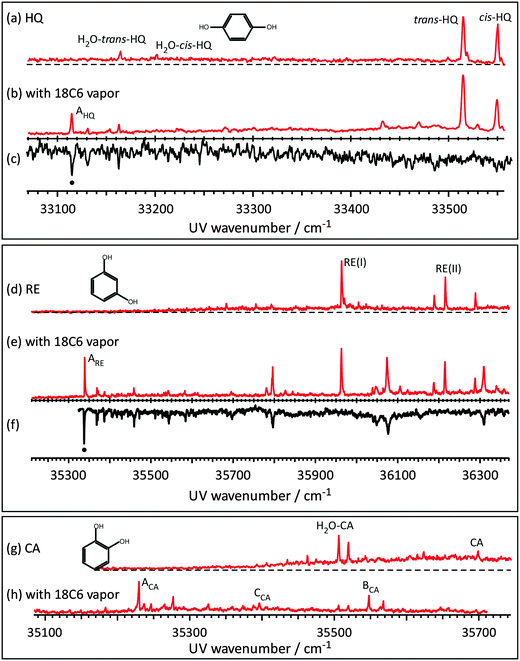
Fig. 1 shows the LIF and UV–UV HB spectra of the S₁–S₀ transition of jet cooled HQ, RE, and CA and their complexes with 18C6. Fig. 1(a) shows the LIF spectrum of HQ in the S₁–S₀ band origin region. Two strong bands at 33 515 and 33 550 cm⁻¹ are already assigned to the 0,0 band of two conformers of HQ, namely trans- and cis-HQ, respectively⁴⁰ (see Scheme 1). Weak bands at 33 164 and 33 201 cm⁻¹ are the band origins of the H₂O·HQ 1 : 1 complex⁴¹ due to the residual water in the sample. Fig. 1(b) shows the LIF spectrum measured by adding 18C6 vapor to the gas mixture. New bands appearing around 33 100–33 200 cm⁻¹ can be assigned to the 18C6·HQ 1 : 1 complex. The UV–UV HB spectrum obtained by monitoring band A_HQ is shown in Fig. 1(c). This result clearly shows that the 18C6·HQ 1 : 1 complex has a single isomer in spite of the fact that the HQ monomer has two conformers with almost equal abundance. The ratio of the band intensity for cis-HQ/trans-HQ is 0.86 without 18C6 vapor, while it becomes 0.57 with 18C6 vapor, indicating that the relative abundance of cis-HQ is reduced by the addition of 18C6 and that the cis-HQ conformer prefers the complex formation with 18C6 more than trans-HQ.

Fig. 1 The S₁–S₀ LIF spectra of jet-cooled (a) HQ, (b) 18C6·HQ complex, (d) RE, (e) 18C6·RE complex, (g) CA and (h) 18C6·CA complex in the band origin region. (c) and (f) The UV–UV hole-burning spectra of 18C6·HQ and18C6·RE, respectively.

Scheme 1

Fig. 1(d) and (e) exhibit the LIF spectra of RE without and with 18C6 vapor, respectively. The RE monomer has three possible conformations (see Scheme 1, conformers I, II and III). Hereafter we call these conformers RE(I), RE(II) and RE(III), respectively. The bands at 35 965 and 36 217 cm⁻¹ are assigned to the 0,0 band of RE(I) and RE(II), respectively.⁴² Thus, under the present jet-cooled conditions, only RE(I) and RE(II) are observed in the LIF spectrum. The total energy of RE(III) is 8.86 kJ mol⁻¹ higher than that of RE(I) at the present level of the calculation, and the electronic transition of RE(III) appears only under warmer jet conditions.⁴³ By the addition of 18C6 vapor, many bands due to the 18C6·RE 1 : 1 complex appear as seen in Fig. 1(e). The UV–UV HB spectrum in Fig. 1(f) indicates that they belong to the same isomer showing the band A_RE (35 339 cm⁻¹) as the 0,0 band. Thus, the 18C6·RE 1 : 1 complex has only one isomer although the RE monomer has three possible conformations.

Fig. 1(g) and 1(h) show the LIF spectra of CA without and with 18C6 vapor, respectively. The spectra are essentially the same as those reported in our previous paper.³¹ The band labeled CA in Fig. 1(g) at 35 695 cm⁻¹ is the 0,0 band of the CA monomer. In the spectrum, the bands of the H₂O·CA complex also appeared. This is due to the presence of residual water in the sample. In CA, two adjacent OH groups form an intramolecular H-bond, so that it has a stable single conformer as seen in Scheme 1. The intensity of band CA in Fig. 1(g) is very weak due to the fast internal conversion (IC) to the ¹πσ* state. On the other hand, the band intensities of the 18C6·CA 1 : 1 complex in Fig. 1(h) are much stronger. The UV–UV HB spectra, not shown here, indicate that the new bands in Fig. 1(h) are attributed to vibronic bands belonging to either of three species labeled A_CA–C_CA.³¹ Thus, the 18C6·CA complex has three stable isomers, although bare CA has only one conformation. This is in contrast to the other two benzenediols, HQ and RE. The structures of the 18C6·benzenediol 1 : 1 complexes will be described in a later section. The frequencies of the 0,0 bands of the S₁–S₀ transition for the observed species are listed in Table 1.

Table 1 Observed and calculated frequencies of the OH stretching vibrations, observed S₁–S₀ transition energy, calculated vertical S₁–S₀ and S₂–S₀ transition energies and oscillator strengths, S₂–S₁ energy gap (ΔE_2–1), observed S₁ lifetime and molecular symmetry of each species. The calculations are performed at the ωB97X-D/6-31++G** level

	Band labeling	OH stretching freq. [cm^−1]			Excitation energy [eV] and oscillator strength^a		ΔE2−1 [eV]	S1 lifetime [ns]	Symmetry in S0	Symmetry in S1^b
		Obs.	Calc.	S1–S0 transition energy [cm^−1 (eV)]	S1	S2
a Calculated energies are scaled by 0.8645, 0.8603 and 0.8598 for HQ, RE and CA, respectively, so as to reproduce the observed S1–S0 transition of each benzenediol monomer. b Ref. 53.
cis-HQ	—	3663	3662, 3663	33 550 (4.160)	4.161(0.0706)	4.649(0.0000)	0.488	2.6	C 2h	C 2h
trans-HQ	—	3662	3663	33 515 (4.156)	4.155(0.0715)	4.726(0.0000)	0.571		C 2v	C 2v
H2O·cis-HQ	—	—	—	33 201 (4.117)	4.112(0.0726)	4.455(0.0000)	0.343	1.2	C s	—
H2O·trans-HQ	—	—	—	33 164 (4.106)	4.108(0.0727)	4.510(0.0000)	0.402
18C6·cis-HQ-I	AHQ	3444, 3657	3420, 3653	33 115 (4.106)	4.092(0.0740)	4.588(0.0005)	0.496	0.54	C 1	—
18C6·cis-HQ-II	—	—	3410, 3628	—	4.104(0.0729)	4.758(0.0045)	0.654	—
RE(I)	—	3658	3656, 3658	35 965 (4.460)	4.465(0.0363)	4.936(0.0007)	0.471	4	C s	C s
RE(II)	—	3658	3659	36 217 (4.491)	4.484(0.0257)	4.923(0.0000)	0.439		C 2h	C 2h
RE(III)	—	—	—	—	4.425(0.0482)	4.894(0.0000)	0.469	—	C 2h	—
18C6·RE(III)-I	ARE	3465	3371, 3396	35 339 (4.382)	4.368(0.0316)	4.880(0.0008)	0.512	10.5	C 1	—
18C6·RE(III)-II	—	—	3359, 3401	—	4.343(0.0381)	4.968(0.0008)	0.625	—
18C6·RE(III)-III	—	—	3391, 3429	—	4.371(0.0365)	4.843(0.0000)	0.472	—
18C6·RE(III)-IV	—	—	3358, 3369	—	4.359(0.0417)	4.838(0.0000)	0.479	—
18C6·RE(III)-V	—	—	3412, 3462	—	4.398(0.0376)	4.939(0.0001)	0.541	—
CA	—	3611, 3673	3612, 3672	35 695 (4.426)	4.426(0.0507)	4.682(0.0004)	0.256	0.008	C s	C 1
18C6·CA-A1	CCA	3281, 3507	3311, 3584	35 397 (4.389)	4.347(0.0422)	4.895(0.0020)	0.548
18C6·CA-E1	ACA	3385, 3407	3372, 3429	35 230 (4.369)	4.320(0.0513)	5.041(0.0241)	0.721	10.3	C 1	—
18C6·CA-E4	BCA	3424	3386, 3396	35 548 (4.408)	4.354(0.0554)	4.993(0.0181)	0.639	10.3

---

3.2 IR spectra of benzenediols and 18C6·benzenediol complexes in the S₀ state

Fig. 2(a)–(i) display the IR–UV DR spectra of HQ, RE, CA and their complexes with 18C6 in the OH stretching frequency region obtained by monitoring their 0,0 bands. For the CA monomer, the position of the IR bands reported in a previous study is shown as arrows.⁴⁴Table 1 also lists the observed frequencies of the OH stretching vibrations. The OH bands of trans- and cis-HQ appear at 3662 and 3663 cm⁻¹, respectively.⁴⁵ In HQ, the two OH groups are symmetrically equivalent in the two conformers. So, the observed IR band is assigned to the antisymmetric OH stretching vibration in trans-HQ, while the symmetric and antisymmetric OH stretching vibrations are thought to be overlapped in cis-HQ. The IR spectrum of the 18C6·HQ complex (A_HQ) is shown in Fig. 2(c). The bands at 3444 and 3657 cm⁻¹ are assigned to the H-bonded OH stretch and the free OH stretch, respectively. Several bands appearing at the higher frequency side of the H-bonded OH are assigned to the combination bands with low frequency vibrations, probably intermolecular vibrations. Thus, in the 18C6·HQ complex, one OH group is H-bonded and the other is free from the H-bond.

Fig. 2 (a)–(i) The IR–UV DR spectra of benzenediol monomers and their complexes with 18C6. (j) and (k) The calculated IR spectra of HQ and RE and the complexes with 18C6 at the level of ωB97X-D/6-31++G**. In the IR spectra of 18C6·CA complexes, the calculated spectra are shown for comparison. Arrows represent the positions of the OH stretching vibrations of the CA monomer. The calculated IR frequencies are scaled by 0.9346 for CA and its complex, 0.9325 for RE and its complex, and 0.9325 for CA and its complex, in order to reproduce the observed OH stretching vibration of each monomer.

Fig. 2(d) and (e) show the IR spectra of the RE(I) and RE(II) monomers, respectively. In RE(II), the antisymmetric OH stretch band has a stronger IR intensity, while in RE(I) two OH bands may have similar intensity because of the lower molecular symmetry. Actually, in both RE(I) and RE(II), only one OH band appeared at the same frequency at 3658 cm⁻¹ in the observed spectra.⁴⁵ This result indicates that the coupling between the two OH groups is very weak, which is also supported in the calculated spectra of Fig. 2(k). In the IR–UV spectrum of the 18C6·RE complex (A_RE) (Fig. 2(f)), no free OH band is seen at ∼3650 cm⁻¹ and three bands appear in the 3460–3500 cm⁻¹ region, which are assigned to the H-bonded OH. Among them, the intensity of the lowest frequency band at 3465 cm⁻¹ is the strongest. Since RE has only two OH groups, the appearance of three bands means that one of the two higher frequency bands is the combination band with a low frequency intermolecular vibration.

Fig. 2(g)–(i) display the IR–UV spectra (red curves) of 18C6·CA by monitoring the intensity of bands C_CA, A_CA and B_CA, and the calculated IR spectra (black curves) of the corresponding structures. Since the IR spectrum of monomer CA could not be obtained because of its weak fluorescence intensity, we adopted the reported values of the frequencies of IR bands.⁴⁴ The IR spectrum of species C_CA shows a broad OH band centered at 3281 cm⁻¹ and a sharp one at 3507 cm⁻¹. The former band is assigned to the H-bonded OH with 18C6 and the latter to the intramolecular H-bonded OH band. The IR spectra of species A_CA and B_CA exhibit the OH bands at the 3350–3450 cm⁻¹ region, indicating that the two OH groups are H-bonded with 18C6 with almost equal strength. The assignments of the OH vibrations by comparison with the calculated ones will be given in a later section.

3.3 S₁ lifetimes of the benzenediol monomers and their complexes

We then measured the S₁ lifetime of each monomer and complexes. Fig. 3 shows the picosecond pump–probe decay profiles of (a) cis-HQ, (d) RE(I), (e) RE(II) and (g) CA monomers, respectively. They are observed by exciting at the 0,0 band of S₁, giving the lifetime of 2.6 ± 0.2 ns, 4.2 ± 0.3 ns, 4.5 ± 0.5 ns, and 8.0 ps, respectively. The very short S₁ lifetime of CA was investigated by Livingstone et al.⁴⁶ and Chatterley et al.,⁴⁷ and is attributed to the fast IC to the nearby ¹πσ* state, leading to an atomic hydrogen elimination of the acceptor OH (^bOH in Scheme 1). Fig. 3(c), (f), (h) and (i) display the decay profiles of the 18C6 complexes. The change of the S₁ lifetime upon complexation is quite different for different benzenediols; in the case of HQ, the S₁ lifetime of the 18C6·HQ complex (0.54 ns, Fig. 3(c)) is shorter by a factor of 5 than that of the monomer. In contrast, the lifetime of the 18C6·RE complex (10.5 ns) is 2.5 times longer than that of the RE monomer, and the lifetime of the 18C6·CA complex (10.3 ns) is 1280 times longer than that of the CA monomer.

Fig. 3 Picosecond pump–probe decay profiles of (a)–(c) HQ monomers and the 18C6·HQ complex, (d and e) RE monomers and (g) CA monomer. Fluorescence decay curves of (f) the 18C6·RE complex and (h) and (i) 18C6·CA complexes, obtained using nanosecond laser excitation. The inset of (g) is the expanded view of the time profile of CA.

4. Discussion

4.1 Structure of 18C6·benzenediol 1 : 1 complexes

4.1.1 18C6·HQ complex. As shown in Fig. 1(c), only one isomer appears for the 18C6·HQ complex. The fact that the reduction of the band intensity of cis-HQ upon complex formation is greater than that of trans-HQ in the LIF spectrum suggests that the conformation of HQ in the 18C6·HQ complex can be the cis-form. Fig. 4(a) and (b) show the calculated most stable structures of the 18C6·HQ complex within the energy of 10 kJ mol⁻¹. The relative energies of the isomers are also listed in Table 2. The dashed lines in Fig. 4 represent the OH⋯O (r_H⋯O < 2.7 Å) and CH⋯π (r_H⋯π < 3.0 Å) H-bonding between HQ (guest) and 18C6 (host) molecules. In these structures, one OH group is H-bonded to the oxygen atom in the ether ring and the opposite OH is free from an intermolecular H-bond. These structures well describe the observed IR spectra of the OH stretching vibrations, that is one OH is H-bonded and the other is free. An interesting point is that HQ adopts the cis-form in these conformers. This result is consistent with the experimental results that cis-HQ forms the complex more easily than trans-HQ. Of course, the trans-HQ may change to the cis-HQ upon complex formation. Anyway, the conformation preference of HQ, cis-HQ, in 18C6·HQ becomes clear when we examine higher energy isomers. Fig. 4(c) shows the most stable 18C6·trans-HQ complex. This complex is 23.2 kJ mol⁻¹ higher than the most stable 18C6·cis-HQ-I (Fig. 4(a)) so that the complex does not exist under jet-cooled conditions. The reason why HQ prefers the cis-form in the complex can be explained by the fact that the complex is largely stabilized by the dipole–dipole interaction between cis-HQ and 18C6; cis-HQ has a dipole moment of 2.789 D, while that of trans-HQ is almost zero. In addition, though the most stable 18C6 has a planar structure (C_i symmetry) in the bare form,^48–51 it changes the structure so that it has a dipole moment to include HQ. Thus, both the molecules cooperatively change the conformation to have dipole moments and stabilize during the process of the host–guest complex formation. Thus, the complex formation mechanism can be called as “induced-fitting”.

Fig. 4 (a) and (b) Structures of the lowest energy isomers of 18C6·cis-HQ within the energy of 10 kJ mol⁻¹ at the level of ωB97X-D/6-31++G** calculation. (c) Structure of the 18C6·trans-HQ complex, which is ∼23 kJ mol⁻¹ higher than 18C6·cis-HQ-I.

Table 2 Relative total energies (ΔE [kJ mol⁻¹]) of the complexes, interaction energies (E_int [kJ mol⁻¹]), relative energies of the conformers of the 18C6 part (ΔE_CE [kJ mol⁻¹]) and the benzenediol part (ΔE_{HQ, RE or CA} [kJ mol⁻¹]) in the complexes, and dihedral angles of the OH groups of benzenediol in the complexes. The species with bold letters are those experimentally observed. The calculations are performed at the ωB97X-D/6-31++G** level

18C6-cis-HQ							18C6-RE(III)							18C6-CA
	ΔE	E int	ΔECE^a	ΔEHQ^b	Dihedral angle^c			ΔE	E int	ΔECE	ΔERE	Dihedral angle^c			ΔE	E int	ΔECE	ΔECA	Dihedral angle^c
					^aOH	^bOH						^aOH	^bOH						^aOH	^bOH
a ΔECE are relative values to that of the most stable 18C6 conformer in the monomer. b ΔEHQ, RE or CA are relative values to that of the most stable conformer in each benzenediol monomer. c Dihedral angles of ^aOH and ^bOH are defined in Scheme 1.
I	0.00	94.3	9.00	1.64	178	178	I	0.00	113	20.0	11.4	178	171	A1	0.00	92.1	10.2	2.28	179	179
II	9.10	88.7	9.26	2.11	168	178	II	1.86	113	17.7	12.2	165	180	E1	3.94	93.2	9.34	7.98	151	160
	—	—	—	—			III	1.97	112	19.1	12.6	167	163	E4	8.66	93.9	7.01	16.2	170	140
	—	—	—	—			IV	3.34	93.7	2.83	10.6	179	179
	—	—	—	—			V	8.75	91.3	4.13	12.9	158	174		—	—	—	—	—	—

---

Fig. 2(j) shows the calculated IR spectra of bare HQ and the 18C6·cis-HQ-I complex of Fig. 4(a). Both trans- and cis-HQ in the bare form show the free OH stretching bands at 3663 cm⁻¹. In the complex, the calculated IR spectrum of 18C6·cis-HQ-I shows the H-bonded (3420 cm⁻¹) and free (3653 cm⁻¹) OH stretching vibrations, which nicely reproduces the observed spectrum of species A_HQ (Fig. 2(c)). It should be noted that 18C6·cis-HQ-I, -II and 18C6·trans-HQ show very similar calculated IR spectra with each other (see Fig. S1, ESI†). Based on the relative energies and IR spectra, it is concluded that the structure of species A_HQ is 18C6·cis-HQ-I. This complex is stabilized through multiple interactions such as the OH⋯O H-bond, CH⋯π, and dipole–dipole interactions. This synergetic effect is very important for the stabilization and conformer preference of this host–guest complex.

4.1.2 18C6·RE complex. Fig. 5(a)–(e) show the stable isomers of the 18C6·RE complex within the energy of 10 kJ mol⁻¹. As shown in Fig. 5, RE takes the RE(III) conformation in all isomers, which did not appear in the monomer form. Actually, the calculated energies of R(II) and R(III) are 0.40 and 8. 86 kJ mol⁻¹ higher than R(I) in the monomer. In the complex, however, the lowest energy isomer having RE(I) conformation (18C6·RE(I)) is 27.1 kJ mol⁻¹ higher than 18C6·RE(III)-I (see Fig. S2(a), ESI†), and the 18C6·RE(II) isomer is not obtained as a stable structure even up to 40 kJ mol⁻¹. The stability of the 18C6·RE(III) isomer mostly comes from the formation of two OH⋯O H-bonds as seen in Fig. 5. Fig. 2(k) shows the calculated IR spectra of RE(I), RE(II), 18C6·RE(III)-I and 18C6·RE(I). Similar to HQ, bare RE shows only a free OH stretch band. RE(I) and RE(II) have C_s and C_2v symmetry, respectively. The two free OH bands are overlapped with each other with equal intensity in RE(I), but in RE(II) the anti-symmetric OH stretch band appears much stronger than the symmetric OH stretch. In any case, both the symmetric and anti-symmetric OH stretches have almost the same frequency. The IR spectrum of 18C6·RE(III)-I shows two H-bonded OH stretching vibrations at 3371 and 3396 cm⁻¹, which reproduces the observed IR spectra of A_RE. The IR spectrum of the 18C6·RE(I) isomer exhibits a free OH stretching vibration at ∼3655 cm⁻¹, which does not reproduce the observed IR spectrum of A_RE. Thus, the observed species A_RE is assigned to the 18C6·RE(III) isomer.

Fig. 5 (a)–(e) Structures of the lowest energy isomers of 18C6·RE(III) within the energy of 10 kJ mol⁻¹ at the level of ωB97X-D/6-31++G** calculation.

Similar to the case of HQ, multiple conformers coexist in the bare form in RE, but the complexation with 18C6 controls the conformation of RE to the highest energy one (RE(III)) to form the most stable complex. In addition, 18C6 also changes its conformation so as to fit the guest species in its cavity. The complex is finally stabilized by two OH⋯O H-bonds and CH⋯π interactions, and this synergetic effect is also essential for the stabilization of the host–guest complex of crown ether.

4.1.3 18C6·CA complex. The difference between CA and the other benzenediols (HQ and RE) is the presence of intramolecular H-bonding in bare CA, which leads to a unique feature of CA, such as the very short S₁ lifetime compared to HQ or RE. Complexation with 18C6 largely affects this intramolecular H-bonding. Fig. 6 shows the calculated structures of 18C6·CA assignable to the observed three species, A_CA, B_CA and C_CA, in our previous study.³¹ In that paper, species A_CA and B_CA were assigned to 18C6·CA-E1 (Fig. 6(b)) and 18C6·CA-E4 (Fig. 6(c)), respectively, in which the intramolecular H-bonding of CA is broken and the two OH groups are independently H-bonded to the oxygen atoms of 18C6 (we call it Type-E). On the other hand, in species C_CA (structure 18C6·CA-A1), CA retains its intramolecular H-bonding and its acceptor OH is H-bonded to the oxygen of 18C6 (we call it Type-A). Other possible isomers of the18C6·CA complex are shown in Fig. S2b (ESI†). The calculated IR spectra (black curves) of the three isomers of 18C6·CA are shown below the observed ones. The calculated IR spectrum of 18C6·CA-E1 shows H-bonded OH stretches at 3372 and 3429 cm⁻¹, and that of 18C6·CA-E4 at 3386 and 3396 cm⁻¹. In the IR spectrum of 18C6·CA-A1, an intermolecular H-bonded OH appears at 3325 cm⁻¹ and intramolecular H-bonded OH at 3584 cm⁻¹. Though isomer 18C6·CA-A1, assigned to species C_CA, is the most stable structure, the fluorescence intensity of species C_CA is rather weak compared to A_CA or B_CA. One of the possibilities of the weakness of this band is a smaller fluorescence quantum yield of this species than that of A_CA and B_CA. A measurement of the fluorescence lifetime of band C_CA was unsuccessful because of its weakness, so that it is difficult to discuss the relative abundance of the complexes.

Fig. 6 (a)–(c) Structures of the observed three isomers of the 18C6·CA complexes determined at the level of ωB97X-D/6-31++G** calculation.

Based on the results of IR measurements, it is concluded that the 18C6·CA complex has two types of isomers having different H-bonding structures. An important point is that 18C6 has an ability to break the intramolecular H-bond of CA, which is connected to the drastic changes of the excited state electronic structure of guest CA, as will be discussed later.

4.2 Energetics of 18C6·benzenediol 1 : 1 complexes

As described above, 18C6 and benzenediols form the most stable host–guest complexes at the expense of changing each structure to higher energy ones. In this section, we compare the energies of the bare form in the most stable conformations, and those of the distorted one for forming the complex, and that of the complex. Fig. 7(a) and (b) show the schematic energy diagram of the 18C6·HQ and 18C6·RE systems: the most stable structures of benzenediols and 18C6 (left), distorted structures (middle), and the stable 18C6·benzenediol complexes (right). It should be noted that in the figures the horizontal axis does not mean the complex formation coordinate. In Fig. 7, ΔE_CE is the energy difference of 18C6 between the most stable structure in the bare form and that in the complex. ΔE_{HQ, RE or CA} is also the energy difference of the benzenediol part. E_int is the interaction energy of the complex,²⁹ which is obtained by using eqn (1) described in the Computational section. In the 18C6·HQ-I complex, E_int is obtained to be 94.3 kJ mol⁻¹. In the case of HQ (Fig. 7(a)), the most stable structure of bare HQ has the trans form. The energy difference between “most stable trans-HQ monomer + most stable 18C6” and 18C6·HQ-I complex corresponds to the binding energy of the 18C6·HQ-I complex. In the complex, the 18C6 and HQ components take higher energy structures, (18C6)^≠ and (HQ)^≠ (middle in Fig. 7(a)), to form the stable complex (right in Fig. 7(a)). The energy necessary for this distortion, (ΔE_CE + ΔE_HQ), is 10.6 kJ mol⁻¹. Hence, the interaction energy E_int is represented by using the binding energy and (ΔE_CE + ΔE_HQ), as follows:

E_int = Binding energy + (ΔE_CE + ΔE_{HQ or RE or CA}) (2)

The BSSE corrected binding energy of the complex is obtained to be 83.7 kJ mol⁻¹. This value leads E_int to be 94.3 kJ mol⁻¹ by using eqn (2), which is equal to that obtained by using eqn (1). Fig. 7(b) shows the schematic energy diagram for the 18C6·RE complex. The energy difference between the most stable monomers and distorted ones, (ΔE_CE + ΔE_RE), is 31.4 kJ mol⁻¹, the binding energy of the complex is 81.6 kJ mol⁻¹, and the interaction energy E_int is 113 kJ mol⁻¹.

Fig. 7 Energy level of 18C6 and benzenediol in the most stable conformation in bare forms, that of the distorted ones for forming the complex, and that of the complexes; (a) 18C6·HQ and (b) 18C6·RE. ΔE_CE, ΔE_HQ and ΔE_RE represent the destabilization energies due to the distortion of conformation to form the stable complex. E_int represents the interaction energy described in the Computational section (see text).

Fig. 8 shows a similar energy diagram for the 18C6·CA complex system. In this case, two different types of stable complexes are formed, 18C6·CA-A1 and 18C6·E1, as described previously. The value of (ΔE_CE + ΔE_CA) is 12.5 kJ mol⁻¹ for 18C6·CA-A1 and 17.3 kJ mol⁻¹ for 18C6·CA-E1. The binding energy of the complex is 79.7 for 18C6·CA-A1 and 75.8 kJ mol⁻¹ for 18C6·CA-E1, and E_int is 92.1 kJ mol⁻¹ for 18C6·CA-A1 and 93.2 kJ mol⁻¹ for 18C6·CA-E1. Table 2 lists the relative energies of the complexes (ΔE), E_int, ΔE_CE, ΔE_HQ, ΔE_RE and ΔE_CA and the dihedral angles of OH groups (^aOH, ^bOH) with respect to the benzene plane. For the benzenediol part, ΔE_HQ is 1.64–2.11 kJ mol⁻¹, ΔE_RE is 10.6–12.9 kJ mol⁻¹, and ΔE_CA is 2.28–16.2 kJ mol⁻¹. These values are quite different for different species and conformations. As seen in Fig. 7 and 8 and Table 2, all the necessary energies for forming the higher energy conformations are easily compensated by the large interaction energy of 90–110 kJ mol⁻¹ or the binding energies of 83.7 kJ mol⁻¹ for 18C6·cis-HQ-I, 81.6 kJ mol⁻¹ for 18C6·RE(III)-I and 70.7–79.6 kJ mol⁻¹ for 18C6·CA complexes. These binding energies are roughly 4 times larger than the normal OH⋯O H-bond energy (for example the H-bond energy of the water dimer is 19–20 kJ mol⁻¹).⁵² Such a large binding energy comes from the multiple interactions between benzenediols and 18C6, such as the OH⋯O H-bond, CH⋯π and dipole–dipole interactions. These interactions are actually seen in the calculated structures in Fig. 4–6. In these figures, the number of OH⋯O and CH⋯π bonding are also shown; the most stable isomers have the largest number of intermolecular bonding between the host and guest molecules. These results strongly indicate that the 18C6·benzenediol host–guest complex formation is not described as a simple rigid “lock-and-key” model, but as a flexible “induced-fit” model, like an enzyme–substrate fitting.

Fig. 8 Energy level of 18C6 and CA in the most stable conformation in bare forms and that of the distorted ones for forming the complex. ΔE_CE and ΔE_CA represent the destabilization energy due to the distortion to form the stable host–guest complex. E_int represents the interaction energy described in the Computational section (see text).

4.3 The S₁ lifetime of 18C6·benzenediol complexes

The observed S₁ lifetimes of benzenediols and 18C6·benzenediol complexes are also listed in Table 1. As described in the Introduction section, the major non-radiative pathway of the S₁ state of benzenediols is thought to be IC to S₂ (πσ*) via the conical intersection, followed by the O–H bond fission along the repulsive S₂ potential curve or the further IC to S₀via the S₂–S₀ conical intersection. Anomalous short lifetime of bare CA (8 ps) is described by the low barrier height of the S₁–S₂ conical intersection due to the small S₁/S₂ energy gap (ΔE_2–1) and low symmetry (C₁) in the S₁ state.^53,54 So, we calculated the vertical excitation energies to the S₁ and S₂ states with the fixed S₀ geometry and obtained the S₁–S₂ energy gap ΔE_2–1, which is also listed in Table 1. Since we do not calculate the potential energy curves along the O⋯H coordinate, ΔE_2–1 is not equal to the barrier height at the S₁–S₂(πσ*) conical intersection. Even if it is so, we consider that this value is roughly proportional to the barrier height. The calculated ΔE_2–1 of bare HQ and RE is 0.439–0.571 eV, while that of CA is much smaller, 0.256 eV. This difference is in good agreement with the shorter S₁ lifetime of CA than HQ or RE. The complex formation with 18C6 greatly affects the nonradiative process of each benzenediol in a different manner. First, in the case of HQ, the S₁ lifetime is shortened by a factor of five (2.6 ns → 0.54 ns) in the complex, while the lifetime is 2.5 times lengthened in the RE complex (4.0 ns → 10.5 ns) and 1280 times in the Type-E complex of CA (8.0 ps → 10.3 ns). Thus, the 18C6·HQ complex shows an opposite trend of the S₁ lifetime behavior compared to that of 18C6·RE and 18C6·CA. This difference is attributed to the presence of free OH in 18C6·HQ but not in 18C6·RE and 18C6·CA. As seen in Table 1, the presence of free OH does not affect strongly the ΔE_2–1 value: 0.471 eV for RE(I) changes to 0.512 eV for 18C6·RE(III)-I and 0.488 eV for cis-HQ changes to 0.496 eV for 18C6·HQ-II. Only CA shows a large change in the ΔE_2–1 value upon complex formation: 0.256 eV for CA → 0.721 eV for 18C6·CA-E1. However, the difference can be seen clearly in the molecular orbitals of the electronic states between 18C6·HQ, 18C6·RE and 18C6·CA. The molecular orbitals responsible for the S₁ and S₂ electronic sates are shown in Fig. S3 (ESI†). In the figure, it is clear that the σ* character dominates in the S₂ state in all the monomer species. On the other hand, for the 18C6 complexes, the σ* character can be seen only at the free OH site of 18C6·HQ (Fig. S3(c), ESI†). In addition, the dihedral angle defined in Scheme 1 of cis-HQ becomes 168–178 degree, indicating that the molecular symmetry of cis-HQ becomes lower from C_2h to C₁ by complexation. Hence, this lower molecular symmetry causes the shorter S₁ lifetime of HQ upon complexation. In the case of 18C6·RE and 18C6·CA, the cage of 18C6 diminishes the σ* character in the S₂ state, leading to the suppression of the OH cleavage. Rizzo and co-workers observed a similar lifetime elongation in a protonated tryptophan–(H₂O)₂ complex.⁵⁵ The protonation to tryptophan lowers the energy of the πσ* (σ* of N–H) state, facilitating a mixing between the πσ* and indole ππ* states. Thus, the protonated tryptophan monomer exhibits a very broad electronic spectrum. In contrast, the hydration to the NH₃⁺ group by two water molecules shifts the σ* of N–H to higher energy, resulting in the decoupling of πσ* from ππ*. In other words, two water molecules “block” the N–H bond fission of protonated tryptophan in the excited state, resulting in the sharp electronic spectrum. In the case of 18C6·HQ, the πσ* character is still retained in the free OH group in the S₂ sate as seen in Fig. S3(e) (ESI†).

5. Conclusion

In the present study, we investigated the formation of host–guest complexes between 18C6 and benzenediols in the gas phase under supersonically jet-cooled conditions. We found that 18C6 and benzenediols cooperatively change their conformations from the stable bare forms to higher energy ones for the best-fitted stable complexes. The complexes are stabilized synergistically through multiple interactions. Especially, the RE part in 18C6·RE takes the characteristic conformation (RE(III)), which is the highest energy one in the monomer form. In the 18C6·CA Type-E complex, CA breaks its intramolecular H-bond to form two intermolecular H-bonds with 18C6. It is also found that complex formation controls the direction of the OH group remote from the direct contact. All the complexes are stabilized by synergetic intermolecular interactions, which are produced by the geometry changes of the host and guest species via a typical “induced-fit” mechanism.

It was also found that the host–guest complexation with crown ethers drastically changes the electronic excited state of guest species. In the case of RE and CA, the S₁ lifetime is lengthened by a factor of 2.5 and 1280, respectively. This drastic change is described partly by an increase of the S₁/S₂ energy gap and mostly by the destruction of the πσ* character of the S₂ state. In contrast, in HQ, the complexation shortens the S₁ lifetime of HQ by a factor of five, thus accelerating the nonradiative decay rate. The present study has shown that 18C6, a simple crown ether, can exert isomeric preference and modify the excited state dynamics of guest species through multiple interactions. In future work, we will extend this work to more flexible molecules as guest molecules and elucidate the potential ability of crown ether to control the conformer preference as well as the excited state dynamics of the guest.

Acknowledgements

T. E. acknowledges the Japan Society for the Promotion of Science (JSPS) for the support through a Grant-in-Aid project (No. 25410017).

References

1. C. J. Pedersen, J. Am. Chem. Soc., 1967, 89, 7017–7036.
2. C. J. Pedersen and H. K. Frensdorff, Angew. Chem., Int. Ed. Engl., 1972, 11, 16–25.
3. C. J. Pedersen, Science, 1988, 241, 536–540.
4. R. M. Izatt, J. H. Rytting, D. P. Nelson, B. L. Hayamore and J. J. Christensen, Science, 1969, 164, 443–444.
5. R. M. Izatt, D. P. Nelson, J. H. Rytting and J. J. Christensen, J. Am. Chem. Soc., 1971, 93, 1619–1623.
6. R. M. Izatt, R. E. Terry, B. L. Haymore, L. D. Hansen, N. K. Dalley, A. G. Avondet and J. J. Christensen, J. Am. Chem. Soc., 1976, 98, 7620–7626.
7. R. M. Izatt, R. E. Terry, D. P. Nelson, Y. Chan, D. J. Eatough, J. S. Bradshaw, L. D. Hansen and J. J. Christensen, J. Am. Chem. Soc., 1976, 98, 7626–7630.
8. J. D. Lamb, R. M. Izatt, C. S. Swain and J. J. Christensen, J. Am. Chem. Soc., 1980, 102, 475–479.
9. H. Zhang, J. H. Chu, S. Leming and D. V. Dearden, J. Am. Chem. Soc., 1991, 113, 7415–7417.
10. H. Zhang and D. V. Dearden, J. Am. Chem. Soc., 1992, 114, 2754–2755.
11. S. Maleknia and J. Brodbelt, J. Am. Chem. Soc., 1992, 114, 4295–4298.
12. I. H. Chu, H. Zhang and D. V. Dearden, J. Am. Chem. Soc., 1993, 115, 5736–5744.
13. L. X. Dang, J. Am. Chem. Soc., 1995, 117, 6954–6960.
14. P. D. J. Grootenhuis and P. A. Kollman, J. Am. Chem. Soc., 1989, 111, 2152–2158.
15. D. Ray, D. Feller, M. B. More, E. D. Glendening and P. B. Armentrout, J. Phys. Chem., 1996, 100, 16116–16125.
16. F. Sobott, W. Kleinekofort and B. Brutschy, Anal. Chem., 1997, 69, 3587–3594.
17. M. B. More, D. Ray and P. B. Armentrout, J. Phys. Chem. A, 1997, 101, 4254–4262.
18. M. B. More, D. Ray and P. B. Armentrout, J. Phys. Chem. A, 1997, 101, 7007–7017.
19. M. B. More, D. Ray and P. B. Armentrout, J. Am. Chem. Soc., 1999, 121, 417–423.
20. Y. Inokuchi, O. V. Boyarkin, R. Kusaka, T. Haino, T. Ebata and T. R. Rizzo, J. Am. Chem. Soc., 2011, 133, 12256–12263.
21. Y. Inokuchi, O. V. Boyarkin, R. Kusaka, T. Haino, T. Ebata and T. R. Rizzo, J. Phys. Chem. A, 2012, 116, 4057–4068.
22. Y. Inokuchi, R. Kusaka, T. Ebata, O. V. Boyarkin and T. R. Rizzo, ChemPhysChem, 2013, 14, 649–660.
23. Y. Inokuchi, T. Mizuuchi, T. Ebata, T. Ikeda, T. Haino, T. Kimura, H. Guo and Y. Furutani, J. Am. Chem. Soc., 2014, 592, 90–95.
24. Y. Inokuchi, T. Ebata, T. R. Rizzo and O. V. Boyarkin, Chem. Phys. Lett., 2014, 136, 1815–1824.
25. R. Kusaka, Y. Inokuchi and T. Ebata, Phys. Chem. Chem. Phys., 2007, 9, 4452–4459.
26. R. Kusaka, Y. Inokuchi and T. Ebata, Phys. Chem. Chem. Phys., 2008, 10, 6238–6244.
27. R. Kusaka, Y. Inokuchi and T. Ebata, Phys. Chem. Chem. Phys., 2009, 11, 9132–9140.
28. S. Kokubu, R. Kusaka, Y. Inokuchi, T. Haino and T. Ebata, Phys. Chem. Chem. Phys., 2010, 12, 3559–3565.
29. R. Kusaka, Y. Inokuchi, T. Haino and T. Ebata, J. Phys. Chem. Lett., 2012, 3, 1414–1420.
30. Y. Inokuchi, O. V. Boyarkin, T. Ebata and T. R. Rizzo, Phys. Chem. Chem. Phys., 2012, 14, 4457–4462.
31. F. Morishima, R. Kusaka, Y. Inokuchi, T. Haino and T. Ebata, J. Phys. Chem. B, 2015, 119, 2557–2565.
32. Y. Inokuchi, Y. Kobayashi, T. Ito and T. Ebata, J. Phys. Chem. A, 2007, 111, 3209–3215.
33. R. J. Lipert and S. D. Colson, J. Phys. Chem., 1989, 93, 3894–3896.
34. Y. Yamada, N. Mikami and T. Ebata, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12690–12695.
35. R. Kusaka and T. Ebata, Angew. Chem., Int. Ed., 2010, 49, 6989–6992.
36. I. Kolossváry and W. C. Guida, J. Am. Chem. Soc., 1996, 118, 5011–5019.
37. MacroModel, version 9.1, Schrödinger, LLC, New York, 2005.
38. T. A. Halgren, J. Comput. Chem., 1999, 20, 730–748.
39. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
40. S. J. Humphrey and D. W. Pratt, J. Chem. Phys., 1993, 99, 5078 ( J. Chem. Phys. , 1996 , 104 , 2752 ).
41. P. S. Meenakshi, N. Biswasa and S. Wategaonkar, Phys. Chem. Chem. Phys., 2003, 5, 294–299.
42. M. Gerhards, W. Perl and K. Kleinermanns, Chem. Phys. Lett., 1995, 240, 506–512.
43. S. Melandri, G. Maccaferri, W. Caminati and P. G. Favero, Chem. Phys. Lett., 1996, 256, 513–517.
44. M. Gerhards, C. Unterberg and K. Kleinermanns, Phys. Chem. Chem. Phys., 2000, 2, 5538–5544.
45. K. Hattori and S. Ishiuchi, J. Phys. Chem. A, 2007, 111, 6028–6033.
46. R. A. Livingstone, J. O. F. Thompson, M. Iljina, R. J. Donaldson, B. J. Sussman, M. J. Paterson and D. Townsend, J. Chem. Phys., 2012, 137, 184304.
47. A. S. Chatterley, J. D. Young, D. Townsend, J. M. Żurek, M. J. Paterson, G. M. Roberts and V. G. Stavros, Phys. Chem. Chem. Phys., 2013, 15, 6879–6892.
48. G. Wipff, P. Weiner and P. Kollman, J. Am. Chem. Soc., 1982, 104, 3249–3258.
49. Y. Sun and P. A. Kollman, J. Chem. Phys., 1992, 97, 5108.
50. E. D. Glendening, D. Feller and M. A. Thompson, J. Am. Chem. Soc., 1994, 116, 10657–10669.
51. M. J. Bovill, D. J. Chadwick, I. O. Sutherland and D. Watkin, J. Chem. Soc., Perkin Trans. 2, 1980, 1529–1543.
52. M. W. Feyereisen, D. Feller and D. A. Dixon, J. Phys. Chem., 1996, 100, 2993–2997.
53. (a) M. Gerhards, C. Unterberg and S. Schumm, J. Chem. Phys., 1999, 111, 7966; (b) W. B. Tzeng, K. Narayanan, C. Y. Hsieh and C. C. Tung, Spectrochim. Acta, Part A, 1997, 53, 2595–2604; (c) S. J. Humphrey and D. W. Pratt, J. Chem. Phys., 1993, 99, 5078; (d) G. A. King, T. A. A. Oliver, R. N. Dixon and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2012, 14, 3338–3345.
54. M. Weiler, M. Miyazaki, G. Féraud, S. Ishiuchi, C. Dedonder, C. Jouvet and M. Fujii, J. Phys. Chem. Lett., 2013, 4, 3819–3823.
55. S. R. Mercier, O. V. Boyarkin, A. Kamariotis, M. Guglielmi, I. Tavernelli, M. Cascella, U. Rothlisberger and T. R. Rizzo, J. Am. Chem. Soc., 2006, 128, 16938–16943.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp07171b

---