Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effect of cation structure on the oxygen solubility and diffusivity in a range of bis{(trifluoromethyl)sulfonyl}imide anion based ionic liquids for lithium–air battery electrolytes†
Alex R.
Neale
 a,
Peilin
Li
b,
Johan
Jacquemin
*a,
Peter
Goodrich
a,
Sarah C.
Ball
c,
Richard G.
Compton
*b and
Christopher
Hardacre
*a
a,
Peilin
Li
b,
Johan
Jacquemin
*a,
Peter
Goodrich
a,
Sarah C.
Ball
c,
Richard G.
Compton
*b and
Christopher
Hardacre
*a
aThe School of Chemistry and Chemical Engineering, Queen's University of Belfast, Stranmillis Road, Belfast BT9 5AG, UK. E-mail: johan.jacquemin@qub.ac.uk; c.hardacre@qub.ac.uk
bDepartment of Chemistry, Physical and Theoretical Chemistry Laboratory, Oxford University, South Parks Road, Oxford OX1 3QZ, UK. E-mail: richard.compton@chem.ox.ac.uk
cJohnson Matthey Technology Centre, Blounts Court, Sonning Common, Reading, RG4 9NH, UK
First published on 17th March 2016
Abstract
This paper reports on the solubility and diffusivity of dissolved oxygen in a series of ionic liquids (ILs) based on the bis{(trifluoromethyl)sulfonyl}imide anion with a range of related alkyl and ether functionalised cyclic alkylammonium cations. Cyclic voltammetry has been used to observe the reduction of oxygen in ILs at a microdisk electrode and chronoamperometric measurements have then been applied to simultaneously determine both the concentration and the diffusion coefficient of oxygen in different ILs. The viscosity of the ILs and the calculated molar volume and free volume are also reported. It is found that, within this class of ILs, the oxygen diffusivity generally increases with decreasing viscosity of the neat IL. An inverse relationship between oxygen solubility and IL free volume is reported for the two IL families implying that oxygen is not simply occupying the available empty space. In addition, it is reported that the introduction of an ether-group into the IL cation structure promotes the diffusivity of dissolved oxygen but reduces the solubility of the gas.
1 Introduction
In parallel with the development of new and, more importantly, sustainable technologies for energy production, significant research interest is also being paid towards the advancement of electrical energy storage systems. In addition to improving electrical energy storage systems in portable electronics, where lithium-ion (Li-ion) secondary batteries dominate at present, this aspiration also arises from the goal of developing the next generation of high energy capacity systems for electric vehicles (EVs) and hybrid-electric vehicles (HEVs).Of all of the prospective secondary battery technologies, lithium–oxygen (Li–O2) [or lithium–air (Li–air)] batteries have received significant interest in recent years. This attention, in both the academic and industrial fields, can be attributed to the remarkable theoretical specific energy of this particular chemistry, which is close to 3,458 W h kg−1 based on the mass of the discharge product, lithium peroxide, Li2O2 (calculation based on the nominal voltage of 2.96 V).1 However, many investigations have revealed important practical challenges associated with this electrochemistry, including high overpotentials during charging and discharging, and undesirable decomposition reactions of the electrolyte or electrode materials.2,3 These factors dramatically reduce the efficiency and cyclability of such systems. As such, the primary focus of research into this field concerns investigations in search of stable electrolytes and cathode materials.
During the ideal discharge of Li–O2 batteries, the oxygen reduction reaction (ORR) at the cathode generates a superoxide radical (O2˙−) (1a) which, in turn, rapidly reacts with Li+ ions (1b) to form lithium-oxide discharge products; lithium superoxide (LiO2) (1c) and, by disproportionation of LiO2, lithium peroxide (Li2O2) (1d).2,4
| O2 + e− ⇌ O2˙− | (1a) |
| Li ⇌ Li+ + e− | (1b) |
| O2˙− + Li+ ⇌ LiO2 | (1c) |
| 2LiO2 ⇌ Li2O2 + O2 | (1d) |
Ionic liquids (ILs) have received growing attention due to their potential use as electrolytes for electrochemical energy storage devices and numerous advantages including non-flammability, negligible vapour pressure, hydrophobicity and good thermal and electrochemical stability. Perhaps most interestingly, the selection of ionic liquid structures, most notably utilising non-aromatic alkylammonium cations, is considered to exhibit good stability towards the superoxide radical.10–12 Indeed, the electrochemical generation of O2˙− (ORR) has been studied in ionic liquids for over two decades and was first observed irreversibly in a 1-ethyl-3-methylimidazolium chloride–aluminium chloride IL.13 The first reported instance of the reversible electroreduction of O2 (i.e. without significant and rapid side-reactions between O2˙− and the IL) was observed at a glassy carbon macroelectrode in 1-butyl-3-methylimidazolium hexafluorophosphate ([C4mim][PF6])14 and has since been reported in numerous other studies concerning imidazolium, tetraalkylammonium and tetraalkylphosphonium based ILs.10,11,15–22 Nevertheless, while the long-term stability of aromatic imidazolium-based ILs towards O2˙− is understood to be insufficient for battery application,23 several recent reports have highlighted that ILs based on non-aromatic cyclic alkylammonium cations may not be as stable as previously proposed.24,25 Furthermore, it has been reported that the stability of the IL is, as expected, dependant on both cation and anion species.26
Among several contributing factors affecting the rate capability and power output of Li–air batteries, the supply of reactants to the cathode surface is very significant. The other factors include, but are not limited to, cathode porosity,27 electrolyte and gas penetration into the porous cathode,28,29 and cathode surface passivation with insoluble discharge products.30 The question of transporting and supplying the reactants brings to light the major drawback of using IL-based electrolytes. ILs are typically quite viscous and, although this class of liquids are completely ionic in form, they generally exhibit relatively low conductivity. Crucially, since the diffusivity of components within the electrolyte (Li+ and O2) is inversely proportional to the viscosity of the system, it is not surprising that the sluggish transport of these reactants in viscous ILs impedes the rate capability of IL-based Li–air batteries; this observation has been reported.31–33
The properties of ionic liquids are determined by the structure of both the cation and the anion, of which there are a virtually unlimited number of combinations. With this in mind, ILs may be considered tuneable solvents and the structures can be modified with the goal of optimising certain properties including the solubility and diffusivity of oxygen.
To date, in addition to electrochemical techniques, oxygen solubility has been measured using isochoric34–36 and gravimetric techniques.37 Therein, oxygen solubilities and diffusion coefficients have been observed in the order of 10−3–10−4 mol dm−3 and 10−10 m2 s−1, respectively, for a range of imidazolium, pyridinium and ammonium-based ionic liquids. In this work, electrochemical methods have been used to determine the solubility and diffusivity of oxygen in the selection of pure ILs based on the bis{(trifluoromethyl)sulfonyl}imide anion paired with a selection of cyclic alkylammonium based cations. These observations are compared with the measured viscosity and the calculated free volume of the ILs. Exploring the relationship between the IL structure and the measured transport capabilities is necessary in the future design of novel ionic liquid structures with improved characteristics.
2 Experimental methodology
2.1 Materials and synthesis
The materials used for synthesis were sourced as follows: azepane (99%) (INVISTA); pyrrolidine (99%), N-methylpyrrolidine (99%), piperidine (99%), N-methylpiperidine (99%), 2-chloromethylethyl ether (98%), 1-bromobutane (98%), iodomethane (98%), dimethylsulfate (99%) (Sigma-Aldrich); and lithium bis{(trifluoromethyl)sulfonyl}imide (battery grade) (3 M). All reagents for synthesis were used as received. Additionally, the commercial 1-butyl-1-methylpyrrolidinium bis{(trifluoromethyl)sulfonyl}imide, [Pyrr14][TFSI], (98%) was purchased from Merck. Microanalysis and lithium content analysis were performed by Analytical Services (ASEP and QUB). 1H and 13C NMR spectra were recorded at 20 °C on a Bruker Advance DPX spectrometer at 300 MHz and 75 MHz, respectively.1-Butylazepane was obtained as a colourless liquid after distillation in vacuo (68–71 °C, 10 mbar), 9.48 g, 61% yield. 1H NMR (300 MHz, CDCl3): δ 2.70–2.55 (m, 4H), 2.52–2.37 (m, 2H), 1.60 (s, 8H), 1.52–1.37 (m, 2H), 1.30 (dq, J = 14.5, 7.1 Hz, 2H), 0.91 (t, J = 7.2 Hz, 3H).
1-(2-Methoxyethyl)pyrrolidine was obtained as a colourless liquid after distillation in vacuo (47–49 °C, 9.8 mbar), 8.64 g, 67% yield. 1H NMR (300 MHz, CDCl3): δ 2.70–2.55 (m, 4H), 2.52–2.37 (m, 2H), 1.60 (s, 8H), 1.52–1.37 (m, 2H), 1.30 (dq, J = 14.5, 7.1 Hz, 2H), 0.91 (t, J = 7.2 Hz, 3H).
1-(2-Methoxyethyl)piperidine was obtained as a colourless liquid after distillation in vacuo (58–60 °C, 10 mbar), 9.15 g, 64% yield. 1H NMR (300 MHz, CDCl3): δ 3.50 (dd, J = 11.9, 6.1 Hz, 2H), 3.35 (s, 3H), 2.52 (dd, J = 13.2, 7.4 Hz, 2H), 2.41 (s, 4H), 1.60 (dt, J = 10.5, 5.3 Hz, 4H), 1.43 (d, J = 5.0 Hz, 2H).
1-Butyl-1-methylpyrrolidinium bromide, ([Pyrr14]Br). Under an inert atmosphere 1-bromobutane (27.4 g, 0.2 mol) was added dropwise to a stirred solution of N-methylpyrrolidine (17.01 g, 0.2 mol) in acetonitrile (50 cm3) cooled in an ice-water bath. The mixture was left to reach room temperature and stirred vigorously overnight under reflux conditions. Volatiles were removed and the resulting yellowish solid was washed with a mixture of acetone and diethyl ether. After filtration and drying, the product was obtained as a white solid, 43.48 g, 98%. The product was characterized using 1H NMR spectroscopy (300 MHz, DMSO): δ 3.50 (m, 4H), 3.38 (m, 2H), 3.02 (s, 3H), 2.08 (s, 4H), 1.68 (m, 2H), 1.31 (m, 2H), 0.92 (t, J = 7.1 Hz, 3H).
1-Butyl-1-methylpiperidinium bromide, ([Pip14]Br). Under an inert atmosphere 1-bromobutane (27.4 g, 0.2 mol) was added dropwise to a stirred solution of N-methylpiperidine (19.80 g, 0.2 mol) in acetonitrile (50 cm3) cooled in an ice-water bath. The mixture was left to reach room temperature and stirred vigorously overnight under reflux conditions. Volatiles were removed and the resulting yellowish solid was washed with a mixture of acetone and diethyl ether. After filtration and drying, the product was obtained as a white solid, 45.78 g, 97%. The product was characterized using 1H NMR spectroscopy: (300 MHz, CDCl3): δ 3.73 (ddd, J = 22.3, 14.7, 8.3 Hz, 6H), 3.34 (s, 3H), 1.91 (t, J = 11.5 Hz, 4H), 1.87–1.66 (m, 4H), 1.57–1.37 (m, 2H), 1.01 (t, J = 7.3 Hz, 3H).
1-Butyl-1-methylazepinium iodide, ([Aze14]I). Under an inert atmosphere, iodomethane (28.4 g, 0.2 mol) was added dropwise to a stirred solution of 1-butylazepane (15.50 g, 0.1 mol) in diethylether (50 cm3) cooled in an ice-water bath. The mixture was left to reach room temperature and stirred vigorously overnight. The resulting yellowish solid was washed with a mixture of hexane/diethyl ether. After filtration and drying the product was obtained as an off-white white solid 29.19 g, 98%. The product was characterized using 1H NMR spectroscopy (300 MHz, CDCl3): δ 3.68 (m, 4H), 3.59 (m, 2H), 3.26 (s, 3H), 1.99 (m, 4H), 1.80 (m, 6H), 1.48–1.30 (m, 2H), 0.98 (t, J = 7.3 Hz, 3H).
1-Butyl-1-methylpyrrolidinium bis{(trifluoromethyl)sulfonyl}imide, [Pyrr14][TFSI]. (20.5 g, 98%) 1H NMR (300 MHz, DMSO): δ1H NMR 3.62 (m, 4H), 3.40 (m, 2H), 3.13 (s, 3H), 1.78 (d, 4H), 1.54 (m, 4H), 1.34 (m, 2H), 0.91 (t, 3H). 13C NMR (75 MHz, DMSO): δ 126.26 (s), 122.00 (s), 117.73 (s), 113.46 (s), 63.78 (s), 63.28 (s), 47.85 (s), 40.46 (t, J = 19.3 Hz), 40.17 (s), 40.12–40.05 (m), 39.77 (d, J = 18.8 Hz), 39.65 (s), 39.48 (d, J = 20.9 Hz), 39.06 (s), 25.29 (s), 21.43 (s), 19.67 (s), 13.81 (s). CHNS theoretical: C, 31.28; H, 4.77; N, 6.63; S, 15.18; found: C, 31.69; H, 5.15; N, 6.28; S, 15.01. Li content 23 ppm.
1-Butyl-1-methylpiperidinium bis{(trifluoromethyl)sulfonyl}imide, [Pip14][TFSI]. (20.72 g, 97%) 1H NMR (300 MHz, DMSO): δ 3.13 (d, J = 8.7 Hz, 1H), 3.07 (dd, J = 11.0, 5.5 Hz, 6H), 2.76 (s, 3H), 2.31–2.26 (m, 1H), 1.56 (d, J = 4.9 Hz, 4H), 1.50–1.22 (m, 4H), 1.18–1.04 (m, 2H), 0.73 (t, J = 7.3 Hz, 3H). 13C NMR (75 MHz, DMSO): δ 126.58–125.96 (m), 121.99 (s), 117.73 (s), 62.65 (s), 60.36 (s), 47.33 (s), 23.31 (s), 21.04 (s), 19.61 (s), 13.77 (s). CHNS theoretical: C, 33.02; H, 5.08; N, 6.42; S, 14.69; found: C, 33.01; H, 4.93; N, 6.42; S, 14.69. Li content 36 ppm.
1-Butyl-1-methylazepanium bis{(trifluoromethyl)sulfonyl}imide, [Aze14][TFSI]. (21.37 g, 98%) 1H NMR (300 MHz, DMSO): δ 3.52–3.29 (m, 4H), 3.29–3.17 (m, 2H), 3.00 (s, 3H), 1.88 (s, J = 24.5 Hz, 4H), 1.80–1.61 (m, 6H), 1.48–1.30 (m, 2H), 0.98 (t, J = 7.3 Hz, 3H). 13C NMR (75 MHz, DMSO): δ 122.38 (s), 118.12 (s), 65.90 (s), 65.17 (s), 50.85 (s), 27.85 (s), 24.83 (s), 22.13 (s), 19.90 (s), 13.74 (s). CHNS theoretical: C, 34.68; H, 5.37; N, 6.22; S, 14.20; found: C, 34.28; H, 5.18; N, 6.17; S, 13.70. Li content 14 ppm.
1-(2-Methoxyethyl)-1-methylpyrrolidinium methylsulfate, [Pyrr1(2o1)][MeSO4]. 1H NMR (300 MHz, DMSO): δ 3.64–3.55 (m, 2H), 3.44–3.37 (m, 2H), 3.38–3.28 (m, 4H), 3.21 (d, J = 5.2 Hz, 3H), 3.14 (d, J = 5.5 Hz, 3H), 2.87 (s, 3H), 2.35 (dt, J = 3.4, 1.7 Hz, 2H), 1.92 (s, 4H).
1-(2-Methoxyethyl)-1-methylpiperidinium methylsulfate, [Pip1(2o1)][MeSO4]. 1H NMR (300 MHz, DMSO): δ 3.75 (s, 2H), 3.57 (dd, J = 12.6, 7.9 Hz, 2H), 3.38 (s, 3H), 3.35 (m, 4H), 3.30 (s, 3H), 3.05 (s, 3H), 1.78 (s, 4H), 1.63–1.41 (m, 2H).
1-(2-Methoxyethyl)-1-methylpyrrolidinium bis{(trifluoromethyl)sulfonyl}imide, [Pyrr1(2o1)][TFSI]. 1H NMR (300 MHz, DMSO): δ 3.95 (m, 2H), 3.78 (m, 6H), 3.40 (s, 3H), 3.30 (s, 3H), 2.32 (m, 4H). 13C NMR (75 MHz, DMSO): δ 126.26 (s), 122.00 (s), 117.73 (s), 113.46 (s), 66.36 (s), 64.53 (s), 62.43 (s), 58.42 (s), 48.37 (s), 21.20 (s). CHNS theoretical: C, 28.30; H, 4.27; N, 6.60; S, 15.11; found: C, 27.99; H, 5.15; N, 6.48; S, 15.03. Li content 33 ppm.
1-(2-Methoxyethyl)-1-methylpiperidinium bis{(trifluoromethyl)sulfonyl}imide, [Pip1(2o1)][TFSI]. 1H NMR (300 MHz, DMSO): δ 3.75 (d, J = 4.2 Hz, 4H), 3.59–3.52 (m, 4H), 3.40–3.31 (m, 9H), 3.30 (s, 6H), 3.05 (s, 6H), 1.78 (d, J = 5.3 Hz, 8H), 1.59–1.45 (m, 4H). 13C NMR (75 MHz, DMSO): δ 126.16 (s), 121.89 (s), 117.48 (s), 113.26 (s) 65.39 (s), 62.07 (s), 61.20 (s), 58.48 (s), 48.33 (s), 20.93 (s), 19.66 (s). CHNS theoretical; C, 30.14; H, 4.60; N, 6.39; S, 14.63; found: C, 30.62; H, 5.01; N, 6.38; S, 14.31. Li content 44 ppm.
The chemical structure of the 5 cations and the bis{(trifluoromethyl)sulfonyl}imide anion, and their respective abbreviations, are shown in Fig. 1.
2.2. Physical and electrochemical measurements
Prior to any electrochemical or physical measurements, the synthesised ILs and the commercial [Pyrr14][TFSI] sample were dried by completing several freeze/thaw cycles under high vacuum (10−3 mbar). Following the freeze/thaw process, the ILs were kept under high vacuum at elevated temperature (90 °C) with stirring overnight. The resulting moisture content of the ILs did not exceed 40 ppm water, as measured by Karl Fischer titration using an 899 Coulometer (Metrohm). ILs were immediately stored and sealed under an Ar atmosphere inside an Ar filled glovebox before further use. The viscosity of the ILs was measured using a Gemini Rotonetic Drive 2 cone and a plate rheometer (Bohlin).Electrochemical measurements were performed using a μ-Autolab III potentiostat (Metrohm). A three-electrode arrangement was utilised for all electrochemical measurements. A platinum microdisk electrode (10 μm diameter, Model G0225, Princeton Applied Research) was employed as the working electrode and two silver wires (0.5 mm diameter, Goodfellow Cambridge Ltd) were used as a counter electrode and a pseudo-reference electrode. The platinum microelectrode was polished using alumina slurries of decreasing grain size (1.0 μm, 0.3 μm, and 0.05 μm, Buehler) in distilled water on microcloth soft lapping pads (Kemet Ltd). After polishing, the microelectrode was sonicated in distilled water for 2 min to remove any residual alumina. The diameter of the microelectrode was calibrated by measuring the steady-state current of the single-electron oxidation of 2 mmol dm−3 ferrocene in acetonitrile containing 0.1 mol dm−3 of tetrabutylammonium perchlorate (TBAP). The known diffusion coefficient of ferrocene in this solution, 2.3 × 10−9 m2 s−1 at 293.15 K,38 (2.43 × 10−9 m2 s−1 at 298.15 K)39 was used to calibrate the radius, re, of the microelectrode using eqn (2):
| iss = 4nFDCbre | (2) |
Electrochemical experiments were conducted in a T-cell (described previously)22 designed to permit the study of very small amounts of electrolyte under a controlled atmosphere, enabling the introduction of oxygen by means of a continuous gas-flow through the cell (see Fig. 2). The 3-electrode T-cell was constructed, and all subsequent electrochemical measurements were conducted, inside an Ar filled glovebox. A section of a plastic disposable pipette tip was securely placed around the end of the working electrode to create a cavity within which 10 μL of the IL sample was placed.
 | ||
| Fig. 2 Schematic of the T-cell arrangement used to measure O2 electrochemistry in small volumes of ILs. | ||
The cell was placed inside a Faraday cage inside the glove box and then connected to a gas line. Externally to the glove box, the gas line (Ar or O2) was fitted to a Dreschel bottle containing CaCl2 to remove the residual water from the gas stream. The outlet of the gas line terminated inside a fume hood, via a connection through the glove box wall, to prevent the leakage of gas into the glove box atmosphere. The cell was initially purged with Ar for at least 30 min.
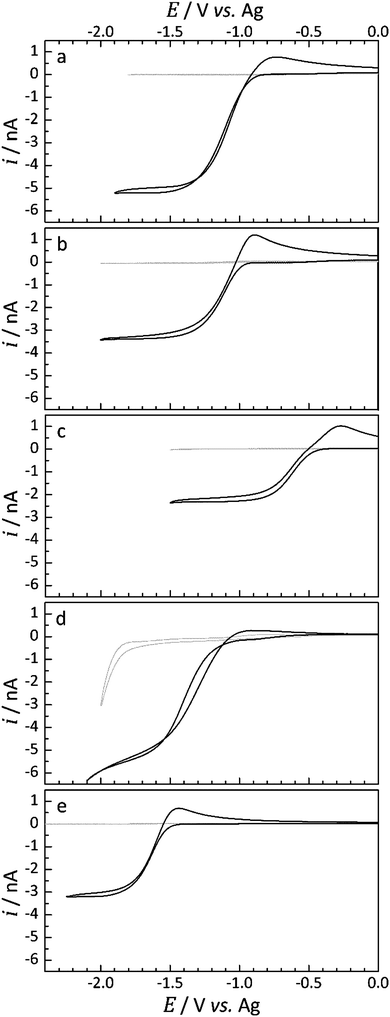
Under an Ar atmosphere, cyclic voltammetry was performed to observe any processes occurring in the absence of dissolved O2. These scans were performed at 100 mV s−1 and between ca. 0 V vs. Ag and −2.5 V vs. Ag. The cell was then exposed to a flow of pure O2 gas at a pressure of 1 barg to allow diffusion of O2 into the liquid sample. After 45 min, voltammograms for the reduction of O2 are recorded. This was performed periodically until the resulting voltammograms were consistent, ensuring that O2 saturation in the IL had occurred. Once saturation was reached, typically within a period of 1.5 to 2.5 h (see voltammograms presented in Fig. 3 and the Results and discussion section), the concentration and diffusion coefficients of dissolved O2 were determined by chronoamperometric measurements.
In chronoamperometry, the potential of the working electrode is stepped from a potential at which the flow of Faradaic current is negligible (0 V vs. Ag) to a potential where the reduction of O2 at the electrolyte/electrode interface is diffusion controlled. Since a silver pseudo-reference electrode was used, the exact reference potential is dependent on surface treatment and composition of the silver wire and, as such, the reference potential can vary between experiments.40 Consequently, the actual step potential used for each chronoamperometry experiment is determined by a point after the peak for O2 reduction on the measured voltammogram. The potential was held at the reduction potential and the current response is recorded over a period of several seconds. The chronoamperometry measurements were repeated several times while the system was still in O2 with a period of at least 15 min between individual measurements. This period was utilised to allow the dissolved O2 to equilibrate after the perturbation caused by the potential step, such that the concentration of O2 local to the electrode surface relaxes to equal the concentration of O2 in the bulk electrolyte. It was found that allowing the system to relax for periods of time longer than 15 min had no effect on the chronoamperometric measurements.
The potential step transients obtained were then analysed, between 20 ms and 2 s using the Shoup and Szabo eqn (3).41 The measured current response (i) is fitted as a function of time (t), the analyte concentration (C), the analyte diffusion coefficient (D) and the radius of the microelectrode (re),
| i = 4nFCDf(t) | (3) |
 | (4) |
 | (5) |
2.3. Computational methods for calculating free volume
The method for calculating the free volume of ILs was completed using the COSMOthermX software (version C30 15.01) with COSMO files computed using the DFT/B3LYP/TZVP level of theory as reported by our group previously.42 Classically, the free volume is calculated by the difference between the molar volume and the van der Waals volume (VvdW), wherein the VvdW values are generally calculated using group contribution methods like Bondi's method, for example.43 It has been shown previously that the estimation of the IL free volume can be made relatively straightforwardly using the COSMO-RS (Conductor-like Screening Model for Real Solvents) computational method.44 In summary, the molar volume of each IL was calculated based on the IL molecular weight divided by the computed density for each of the 5 anion–cation combinations reported in this work. The total COSMO volume of each IL (i.e. the volume enclosed by the calculated COSMO surface) was calculated by the sum of the COSMO volumes of the anion and the cation. An estimation of the IL free volume is then calculated by taking the difference between the calculated molar volume and the COSMO volume of the IL using the COSMOthermX software.3 Results and discussion
Several ionic liquids were selected as electrolytes to study the electrochemical reduction of dissolved oxygen and a microdisk electrode. It has been shown previously that the specific nature of both the anion and the cation will play a role in the solubility and transport of oxygen in the ionic liquid.17 For this particular study, the anion species, [TFSI]−, is kept constant and the effect of modified cation structures is considered to investigate the interplay between the fine-tuning of cation structure, modification of physical properties and the oxygen electrochemistry. The exploration of these properties will, hopefully, be useful for the future design of improved IL-based electrolytes for Li–air batteries.3.1. Cyclic voltammetry of oxygen in ILs
Cyclic voltammetry of the platinum microdisk electrode was initially used to probe the electroreduction of O2 dissolved in the IL electrolyte. For all voltammograms presented, the potential was swept initially in the negative direction from a starting voltage of 0 V vs. Ag at a scan rate of 100 mV s−1. The background voltammograms, collected under an Ar-atmosphere (labelled: blank), and the voltammograms obtained once O2 saturation in each selected IL had occurred are presented in Fig. 3.Under an Ar atmosphere, the current response was found to be very low and completely negligible within the potential region of interest for the ILs, with the exception of [Pyrr1(2o1)][TFSI]. The blank CV obtained for [Pyrr1(2o1)][TFSI], Fig. 3d, shows the onset of reduction of an unknown species at ca. −1.8 V vs. Ag. Under different conditions, dissolved gases could be more effectively removed by bubbling with Ar directly into the liquid, an option not possible for the 10 μL used in T-cells, or by exposing the IL to vacuum.
For the three ionic liquids functionalised with the butyl group, [Pyrr14][TFSI], [Pip14][TFSI] and [Aze14][TFSI] (Fig. 3a–c) and for the ether functionalised piperidinium-based IL, [Pip1(2o1)][TFSI] (Fig. 3e), no measurable reduction current was observed prior to the onset potential of O2 reduction. In contrast, the ether functionalised pyrrolidinium-based IL, [Pyrr1(2o1)][TFSI] (Fig. 3d), exhibited a small pre-peak feature in the O2 saturated CV. The current magnitude of this feature corresponds to approximately 2% of the O2 reduction peak-current in [Pyrr1(2o1)][TFSI]. These pre-peak processes indicate the possibility of the O2 reduction reaction being coupled with an immediate chemical reaction of the superoxide product with either solvent molecules or impurities within the solvent, known as an EC mechanism.45 The direct chemical reaction of the superoxide radical leads to a depletion of the concentration of the reduced species local to the electrode surface. This, in turn, causes a shift of the reduction wave towards more positive potentials provided the wave is electrochemically reversible. The magnitude of this pre-peak indicates the likelihood that the chemical reaction of the O2˙− is occurring with impurities in the electrolyte, where the concentration of these unknown impurities does not exceed the bulk concentration of O2. This can be inferred due to the presence of two reduction peaks (i.e. the pre-peak peak and the main O2 reduction peak). Once the impurity species is completely consumed via the chemical reaction with O2˙−, the remaining O2 undergoes reduction at the electrode by a mechanism more representative of the heterogeneous process: an electrochemical reduction in the absence of a coupled chemical reaction. This observation has been made previously in a study into Li2O2 formation by reduction of O2 in the presence of known concentrations of Li+ ions in the solvent.4
Considering the reductive peak for this set of ILs, the peak shape appears to resemble steady-state characteristics. This behaviour is typical of oxygen reduction at microdisk electrodes where the convergent diffusion of the reactants is expected at slow-to-mid scan rates.18 The shape of the overall voltammograms is Asymmetric and a clear transient peak, associated with more planar diffusion, is observed for the reverse oxidation process. This observation is quite typical for the oxygen systems due to the asymmetry exhibited by the diffusion coefficients of the neutral and reduced species; the diffusion coefficient of the superoxide radical has been found to be over one order of magnitude lower than the neutral oxygen in many media.11,15,46 Significant interactions between the charged superoxide species and the charged species of the IL are likely to contribute to the very low mobility of the anion. Additionally, the magnitude of the oxidative peak relative to the reduction peak increases in the order [Pyrr14][TFSI] < [Pip14][TFSI] < [Aze14][TFSI] which correlates with an increase in the viscosity in the same order (see later for viscosity data), as expected.
For the ILs containing the ether-functional group, Fig. 3d and e, the relative magnitude of the current response on the reverse oxidation sweep is smaller. For [Pip1(2o1)][TFSI], this relative difference is minimal but appears to be quite significant for [Pyrr1(2o1)][TFSI]; where the shape of the reverse oxidation sweep is more representative of a system under convergent hemispherical type diffusion.
Based on these observations alone, it is implausible to associate the lack of a transient peak on the reverse scan with a much greater mobility of the superoxide radical in this IL. Nevertheless, the presence of oxygen in the ether-functional group of the cation could certainly be expected to alter the cation charge distribution and, in turn, alter the strength or the manner of interaction between the IL cation and the radical superoxide anion. The types of transient oxidation peaks observed in Fig. 3a–c and e are typically observed for the electrochemical oxidation of the superoxide radical at microelectrodes in more viscous media.18 This absence of a reverse transient peak upon oxidation in [Pyrr1(2o1)][TFSI] could also potentially be the result of a direct chemical reaction and consumption of the superoxide with the IL, but this is worth further investigation.
3.2. Chronoamperometric measurements
Chronoamperometry was performed on each of the O2-saturated IL electrolytes to determine the solubility and diffusivity of the dissolved oxygen. As described in the experimental methodology section, the potential was stepped from 0 V vs. Ag (where the Faradaic current is negligible) to a potential where the reduction of the dissolved oxygen is diffusion controlled. As shown in the voltammograms presented in Fig. 3, this potential varied between each sample as a result of using a silver pseudo-reference electrode. As such, the step potential for a given IL (given in brackets in the legend of Fig. 4) is determined from the associated voltammogram of that particular IL. The potential was held at the steady state reducing potential over a period of a few seconds and the resulting transients were analysed using the Shoup and Szabo equation (eqn (3)) to extract the diffusion coefficient of oxygen, D(O2), and the concentration of oxygen dissolved in the bulk electrolyte, c(O2). The number of electrons, n, involved in the oxygen reduction reaction is reasonably presumed to be 1 across the full range of studied ILs. This single-electron mechanism has been reported on several occasions for [Pyrr14][TFSI] and several closely related [TFSI]− anion-based ILs.11,20,47 The resulting experimental chronoamperometric transients and the associated simulated transients are presented in Fig. 4. Excellent agreement between the experimental and the Shoup and Szabo computed transients is observed. The solubility, c(O2), and the diffusion coefficient, D(O2), of oxygen derived from the Shoup and Szabo analysis are presented in Table 1 along with the viscosity, molar volume and calculated free volume of each IL.| Ionic liquid | c(O2)/mmol dm−3 | D(O2)/×10−10 m2 s−1 | η/mPa s | V m/cm3 mol−1 | V f/cm3 mol−1 |
|---|---|---|---|---|---|
| a Ref. 48; solubility and diffusion coefficient data for O2 in DMSO was measured electrochemically at 298 K with 0.1 mol dm−3 tetrabutylammonium hexafluorophosphate as the supporting electrolyte. b Ref. 49; viscosity of pure DMSO given at 298 K. | |||||
| [Pyrr14][TFSI] | 9.15 ± 0.15 | 2.67 ± 0.05 | 80.02 | 300.86 | 39.81 |
| [Pip14][TFSI] | 8.48 ± 0.09 | 1.82 ± 0.02 | 177.93 | 317.14 | 43.01 |
| [Aze14][TFSI] | 7.98 ± 0.20 | 1.50 ± 0.04 | 323.27 | 328.42 | 47.31 |
| [Pyrr1(2o1)][TFSI] | 6.67 ± 0.13 | 3.76 ± 0.14 | 55.49 | 291.74 | 36.81 |
| [Pip1(2o1)][TFSI] | 6.00 ± 0.08 | 2.55 ± 0.06 | 108.56 | 301.47 | 40.23 |
| DMSO | 1.8a | 18a | 1.99b | ||
Multiple chronoamperometric experiments were performed for each IL, as described in the experimental methodology section, and, as such, the solubility and diffusion coefficient values in Table 1 represent the average values of these experiments and the calculated standard error is shown for each sample.
The mobility of the dissolved oxygen in this selection of ILs appears to approximately follow an inverse trend with respect to the viscosity, as expected. Similarly, within the two families of ILs (i.e. the two ethereal ILs and the three alkyl ILs), the observed solubility of O2 appears to increase with decreasing free volume and decreasing viscosity of the IL. These relationships are discussed in more depth in the following sections.
Also presented in Table 1 is the equivalent data for DMSO with 0.1 mol dm−3 tetrabutylammonium hexafluorophosphate as the supporting electrolyte.48 DMSO is a commonly used electrolyte solvent for Li–air battery studies. The measured oxygen solubility across the full range of studied ILs is several times greater than that reported in the DMSO-based electrolyte. However, as is expected for relatively viscous systems like ILs, the observed range for mobility of the dissolved oxygen in these ILs (from 1.39 × 10−10 to 3.76 × 10−10 m2 s−1) is significantly lower than that for the lower viscosity molecular solvent. It should be noted that the data for c(O2) and D(O2) in DMSO provided were referenced from a study concerning the properties of a DMSO/[Pyrr14][TFSI] blended electrolyte.48 It was reported in this study that a reduction in the viscosity upon the addition of DMSO to the IL improved the mobility of the dissolved oxygen relative to the pure IL system.48 Furthermore, the same authors recently reported on the effects of the introduction of a Li-salt to DMSO/IL blended electrolytes on the mobility of dissolved oxygen.50 At low levels of the Li[TFSI] salt (i.e. 0.05 mol dm−3), the authors demonstrated the variation of D(O2) with the use of digital simulation of CV experiments. However, the c(O2) at saturation, initially determined by the Shoup and Szabo analysis of chronoamperometric measurements in the absence of a Li-salt, was then assumed to be unchanged after the addition of the Li-salt.50
3.3. The relationship between diffusivity and viscosity
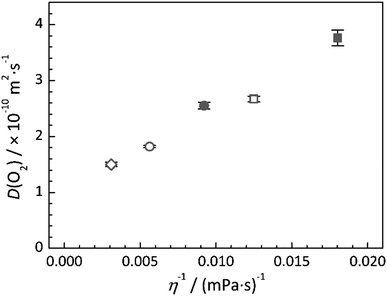
As previously stated, the diffusion coefficient of dissolved species is generally found to be inversely proportional to the viscosity of the solvent medium. For the ILs presented herin, the change in viscosity associated with different cation structures is well known. For example, the largest observed differences is associated with the observed increase in viscosity as the size of the alkyl ring of the cation is increased, from the 5 membered ring of [Pyrr14][TFSI] to the 6 and 7 membered rings of [Pip14][TFSI] and [Aze14][TFSI], respectively. Additionally, the measured reduction in viscosity as a result of substituting the butyl functional group of the cation with the 2-methoxyethyl group has been documented previously.51 This reduction in viscosity for the ether-functionalised cation analogue (i.e. compared [Pyrr14][TFSI] to [Pyrr1(2o1)][TFSI] and [Pip14][TFSI] to [Pip1(2o1)][TFSI]) has been previously related to the additional conformational flexibility of the ethereal chain.51 The relationship between the measured viscosity of the IL and the diffusion coefficient of a species can be quite well described, for certain systems provided that the molecule is sufficiently large, using the Stokes–Einstein equation,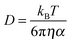 | (6) |
Across the full range of ILs studied, the measured diffusion coefficients of oxygen appear to correlate reasonably well with a decrease in IL viscosity. There have been previous studies concerning the applicability of the standard Stokes–Einstein equation for ILs which have shown that for small molecules, such as H2, H2S and O2, the expected relationship does not directly apply and suggests that analyte–IL interactions may play a more significant role in the movement, or lack thereof, of the analyte.17 However, the structure of different ILs used in this particular study varied significantly whereas the structures of the [TFSI]−-based ILs reported in this work are more closely related. As such, the nature of the analyte–IL interactions would be expected to be relatively consistent across the range of 5 ILs studied in this work and the mobility of the dissolved oxygen is found to show a degree of linear dependence of the fluidity (η−1) of the neat IL. However, it is clear that there is not a direct dependence of D on η−1 since an approximate linear fit of the data would have a large intercept. Furthermore, a significant deviation away from the observed relationship is obvious if the diffusion coefficient of O2 in DMSO and the viscosity of this solvent (Table 1) are considered. Extrapolation of an approximate linear fit of the data presented in Fig. 5 would indicate that the mobility of the oxygen in the lower viscosity solvent, DMSO, should approach 70–80 × 10−10 m2 s−1, indicating that a different diffusivity–viscosity relationship exists in IL systems.
3.4. Relationships affecting oxygen solubility in the ILs
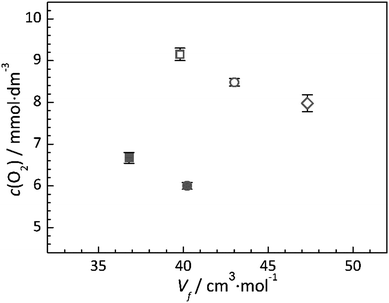
In general, IL–gas systems where only physical absorption of a gas occurs (i.e. where no chemical absorption occurs by chemical reaction between the IL and solute), the free volume of the IL is considered to be one of the primary factors contributing to solubility.44 Comparing all ILs studied, a direct relationship between their oxygen solubility and their calculated molar volume or free volume is not immediately apparent. However, a graphical representation of the solubility and free volume data (Fig. 6) provides potential insight into the existence of two relationships. Firstly, simply comparing the ILs with the same functional groups (i.e. the alkyl chain or the ether chain) shows that the solubility of oxygen within the IL decreases as the calculated IL free volume increases. This observation clearly shows that the oxygen is not simply occupying empty space between the ions. Secondly, the data presented in Fig. 6 highlight the effect of introducing the ether group to the cation; for both the pyrrolidinium and piperidinium based ILs, substitution of the butyl group with the 2-methoxyethyl group reduces the measured oxygen solubility.Additionally, when comparing the two families of ILs studied, there appears to be a general trend that the oxygen solubility increases with decreasing viscosity. Since the viscosity of an IL is a property which is closely linked to the molecular cohesive interactions within the liquid, this observation may be associated with the ability of O2 to restructure the liquid upon dissolving, as it is very well known that solvation properties between O2 and IL are mainly entropy driven. In general, the anion–cation structure does not change upon the addition of solutes whereas the structures of the cation–cation environments are affected.53–56 In the higher viscosity liquids, the strength of the cation–cation interactions often dominate the viscosity as these have to move relative to each other under shear stress. Therefore, within the given family of ILs, the trend that the O2 solubility increases with decreasing cation–cation interaction energy is expected.
3.5. Comparison with reported literature values and a commercial IL
The oxygen solubility and diffusivity data as measured in this work are compared, in Table 2, with other reported literature values for two of the ILs where electrochemical methods were used. [Pyrr14][TFSI] is very commonly used IL for Li–air electrolytes owing to its good apparent electrochemical stability with superoxide chemistry and its moderately good transport properties. As such, the solubility and the diffusion coefficient have been measured a number of times previously.| Ionic liquid cation | c(O2)/mmol dm−3 | D(O2)/×10−10 m2 s−1 | Ref. | Method |
|---|---|---|---|---|
| a Shoup and Szabo analysis of chronoamperometric transients measured at a 25 μm Pt-microdisk electrode. b Shoup and Szabo analysis of chronoamperometric transients measured at a 10 μm Au-microdisk electrode. c Combination of Cottrellian analysis of chronoamperometric transients at a 3 mm glassy carbon macroelectrode and steady-state current analysis at 5–11 μm carbon fibre microdisk electrode. | ||||
| [Pyrr14]+ | 9.15 ± 0.15 | 2.67 ± 0.05 | This work | |
| [Pyrr14]+ | 12.78 ± 0.64 | 2.54 ± 0.03 | 48 | |
| [Pyrr14]+ | 3.6 | 5.49 | 17 | |
| [Pyrr14]+ | 3.9 | 6.3 | 57 | |
| [Pip1(2o1)]+ | 6.00 ± 0.08 | 2.55 ± 0.06 | This work | |
| [Pip1(2o1)]+ | 4.4 | 5.1 | 57 | |
The data shown in Table 2 for [Pyrr14][TFSI] show that there is a significant amount of variation between the measured values for both c(O2) (3.6–12.78 mmol dm−3) and D(O2) (2.54 × 10−10–6.3 × 10−10 m2 s−1) in this IL. A similar, yet smaller, degree of variation can also been seen for the O2 data for the lesser studied piperidinium-based IL, [Pip1(2o1)][TFSI]. However, the measured values all lie within the same approximate order of magnitude and, since the concentration and diffusion coefficients are small, a higher relative degree of variation may be expected.
The measurement of the O2 solubility and diffusivity was also conducted using a commercial sample of [Pyrr14][TFSI] (Merck) to investigate potential variations in the measurements between synthesised and purchased IL batches. As described in the Experimental section, the commercial IL was dried using the same freeze–pump–thaw vacuum process as for the synthesised ILs but was, otherwise, used as received (i.e. with no further purification). The water content of the dried commercial IL was 50 ppm, slightly higher than that for the synthesised ILs (all below 40 ppm). The cyclic voltammograms (O2 saturated and under Ar-atmosphere) and the associated chronoamperometric transient for the commercial IL are presented in Fig. S1 and S2, respectively, in the ESI.†
The c(O2) and D(O2) values for the commercial IL were found to be 8.21(±0.05) mmol dm−3 and 2.80 × 10−10 (±0.01 × 10−10) m2 s−1, respectively, as determined by the average values attained by Shoup and Szabo analysis of several chronoamperometric transients. These values are in reasonable agreement with the values attained for the in-house synthesised [Pyrr14][TFSI] (9.15 mmol dm−3 and 2.67 × 10−10 m2 s−1) and, in further agreement with these observations, the magnitude and nature of the reduction and oxidation peaks observed in the CV experiments are very much congruent. Nevertheless, the CV for O2 reduction in the commercial IL (Fig. S1, ESI†) does display a small pre-peak reductive current response (−0.6 V vs. Ag) before the main O2 reduction peak. This feature is absent in the O2 saturated CV of the synthesised [Pyrr14][TFSI] (Fig. 3a). As discussed in Section 3.1., the presence of these pre-peak reduction features implies that the reduced O2 may undergo a coupled chemical reaction with a reactive species in the liquid (either solvent molecules or impurities). This was observed and discussed for the synthesised IL, [Pyrr1(2o1)][TFSI] (Fig. 3d). Since this feature is not observed in the CV of the synthesised [Pyrr14][TFSI], it can be inferred that the pre-reduction peak is caused by the presence of reactive impurities within the commercial IL and this may account for the small differences found between commercial and synthesised ILs. However, the quantity and nature of the impurity species found in commercial ILs could be expected to vary by the supplier and also with the specific batch of ILs.
4 Conclusions
Five ionic liquids made up of the bis{(trifluoromethyl)sulfonyl}imide anion and a selection of alkyl- and ether functionalised cyclic alkylammonium based cations were synthesised, purified and dried in preparation for viscosity and electrochemical measurements. The electrochemical reduction of dissolved oxygen in the ionic liquids was studied at a platinum microdisk electrode. Clear oxygen reduction peaks were observed by cyclic voltammetry in all five dry IL samples. The concentrations and diffusion coefficients of the dissolved oxygen in the different ILs were analysed by chronoamperometric measurements and the diffusivity of dissolved oxygen is compared with the measured viscosity of the neat IL. As is typically expected, it is seen that the diffusivity of oxygen generally increases as the viscosity of the IL decreases. Additionally, the free volume of the ILs was estimated using computational methods. A comparison of the IL free volume with oxygen solubility showed inverse relationships within the two IL families showing clearly that oxygen is not simply occupying free space within the IL.While this study propagates the understanding of ILs as useful solvents for studying the electrochemistry of dissolved oxygen and as potential tuneable IL electrolyte components, it can be assumed that the observed transport capabilities reported herein can be considered too low for practical application. To improve the transport properties of IL-based electrolytes for Li–air batteries, there exist two primary options worth further consideration. Firstly, the design and synthesis of ILs with considerably lower viscosity and, secondly, the investigation of blended electrolytes with ILs and molecular solvents.
Acknowledgements
The authors would like to gratefully acknowledge the funding from EPSRC (EP/L505262/1) and Innovate UK for the Practical Lithium–Air Batteries project (project number: 101577). Additionally, the authors would like thank Keith Whiston and INVISTA intermediates for supplying the azepane sample for this work. Supporting data are openly available on Queen's University Research Portal http://pure.qub.ac.uk/portal/en/datasets.References
- G. Girishkumar, B. McCloskey, C. Luntz, S. Swanson and W. Wilcke, J. Phys. Chem. Lett., 2010, 1, 2193–2203 CrossRef CAS.
- P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Nat. Mater., 2012, 11, 19–29 CrossRef CAS PubMed.
- M. Balaish, A. Kraytsberg and Y. Ein-Eli, Phys. Chem. Chem. Phys., 2013, 16, 2801–2822 RSC.
- Z. Peng, S. A. Freunberger, L. J. Hardwick, Y. Chen, V. Giordani, F. Bardé, P. Novák, D. Graham, J.-M. Tarascon and P. G. Bruce, Angew. Chem., Int. Ed., 2011, 50, 6351–6355 CrossRef CAS PubMed.
- W. Xu, K. Xu, V. V. Viswanathan, S. A. Towne, J. S. Hardy, J. Xiao, Z. Nie, D. Hu, D. Wang and J.-G. Zhang, J. Power Sources, 2011, 196, 9631–9639 CrossRef CAS.
- S. A. Freunberger, Y. Chen, N. E. Drewett, L. J. Hardwick, F. Barde and P. G. Bruce, Angew. Chem., Int. Ed., 2011, 50, 8609–8613 CrossRef CAS PubMed.
- S.-M. Han, J.-H. Kim and D.-W. Kim, J. Electrochem. Soc., 2014, 161, A856–A862 CrossRef CAS.
- M. J. Trahan, S. Mukerjee, E. J. Plichta, M. A. Hendrickson and K. M. Abraham, J. Electrochem. Soc., 2013, 160, A259–A267 CrossRef CAS.
- D. G. Kwabi, T. P. Batcho, C. V. Amanchukwu, N. Ortiz-Vitoriano, P. Hammond, C. V. Thompson and Y. Shao-Horn, J. Phys. Chem. Lett., 2014, 5, 2850–2856 CrossRef CAS PubMed.
- M. Hayyan, F. S. Mjalli, M. A. Hashim, I. M. AlNashef, S. M. Al-Zahrani and K. L. Chooi, J. Electroanal. Chem., 2012, 664, 26–32 CrossRef CAS.
- J. Herranz, A. Garsuch and H. A. Gasteiger, J. Phys. Chem. C, 2012, 116, 19084–19094 CAS.
- K. Takechi, S. Higashi, F. Mizuno, H. Nishikoori, H. Iba and T. Shiga, ECS Electrochem. Lett., 2012, 1, A27–A29 CrossRef CAS.
- M. T. Carter, C. L. Hussey, S. K. D. Strubinger and R. A. Osteryoung, Inorg. Chem., 1991, 30, 1149–1151 CrossRef CAS.
- I. M. AlNashef, M. L. Leonard, M. C. Kittle, M. A. Matthews and J. W. Weidner, Electrochem. Solid-State Lett., 2001, 4, D16–D18 CrossRef CAS.
- M. C. Buzzeo, O. V. Klymenko, J. D. Wadhawan, C. Hardacre, K. R. Seddon and R. G. Compton, J. Phys. Chem. A, 2003, 107, 8872–8878 CrossRef CAS.
- A. S. Barnes, E. I. Rogers, I. Streeter, L. Aldous, C. Hardacre, G. G. Wildgoose and R. G. Compton, J. Phys. Chem. C, 2008, 112, 13709–13715 CAS.
- X.-J. Huang, E. I. Rogers, C. Hardacre and R. G. Compton, J. Phys. Chem. B, 2009, 113, 8953–8959 CrossRef CAS PubMed.
- E. I. Rogers, X.-J. Huang, E. J. F. Dickinson, C. Hardacre and R. G. Compton, J. Phys. Chem. C, 2009, 113, 17811–17823 CAS.
- C. J. Allen, S. Mkurjee, E. J. Plichta, M. A. Hendrickson and K. M. Abraham, J. Phys. Chem. Lett., 2011, 2, 2420–2424 CAS.
- C. J. Allen, J. Hwang, R. Kautz, S. Mukerjee, E. J. Plichta, M. A. Hendrickson and K. M. Abraham, J. Phys. Chem. C, 2012, 116, 20755–20764 CAS.
- M. Hayyan, F. S. Mjalli, I. M. AlNashef and M. A. Hashim, J. Fluorine Chem., 2012, 142, 83–89 CrossRef CAS.
- P. Li, E. O. Barnes, C. Hardacre and R. G. Compton, J. Phys. Chem. C, 2015, 119, 2716–2726 CAS.
- M. Hayyan, F. S. Mjalli, M. A. Hashim and I. M. AlNashef, J. Mol. Liq., 2013, 181, 44–50 CrossRef CAS.
- K. U. Schwenke, J. Herranz, H. A. Gasteiger and M. Piana, J. Electrochem. Soc., 2015, 162, A905–A914 CrossRef CAS.
- M. Piana, J. Wandt, S. Meini, I. Buchberger, N. Tsiouvaras and H. A. Gasteiger, J. Electrochem. Soc., 2014, 161, A1992–A2001 CrossRef CAS.
- S. Das, J. Højberg, K. B. Knudsen, R. Younesi, P. Johansson, P. Norby and T. Vegge, J. Phys. Chem. C, 2015, 119, 18084–18090 CAS.
- S. B. Ma, D. J. Lee, V. Roev, D. Im and S.-G. Doo, J. Power Sources, 2013, 244, 494–498 CrossRef CAS.
- C. Tran, X.-Q. Yang and D. Qu, J. Power Sources, 2010, 195, 2057–2063 CrossRef CAS.
- M. Balaish, A. Kraytsberg and Y. Ein-Eli, ChemElectroChem, 2014, 1, 90–94 CrossRef.
- B. D. McCloskey, A. Speidel, R. Scheffler, D. C. Miller, V. Viswanathan, J. S. Hummelshøj, J. K. Nørskov and A. C. Luntz, J. Phys. Chem. Lett., 2012, 3, 997–1001 CrossRef CAS PubMed.
- S. Higashi, Y. Kato, K. Takechi, H. Nakamoto, F. Mizuno, H. Nishikoori, H. Iba and T. Asaoka, J. Power Sources, 2013, 240, 14–17 CrossRef CAS.
- F. Soavi, S. Monaco and M. Mastragostino, J. Power Sources, 2013, 224, 115–119 CrossRef CAS.
- W. Xu, J. Hu, M. H. Engelhard, S. A. Towne, J. S. Hardy, J. Xiao, J. Feng, M. Y. Hu, J. Zhang, F. Ding, M. E. Gross and J.-G. Zhang, J. Power Sources, 2012, 215, 240–247 CrossRef CAS.
- J. Jacquemin, P. Husson, V. Majer and M. F. C. Gomes, Fluid Phase Equilib., 2006, 240, 87–95 CrossRef CAS.
- Y. Zhao, X. Zhang, H. Dong, Y. Zhen, G. Li, S. Zeng and S. Zhang, Fluid Phase Equilib., 2011, 302, 60–64 CrossRef CAS.
- J. Kumełan, Á. P.-S. Kamps, D. Tuma and G. Maurer, J. Chem. Eng. Data, 2009, 54, 966–971 CrossRef.
- J. L. Anderson, J. K. Dixon and J. F. Brennecke, Acc. Chem. Res., 2007, 40, 1208–1216 CrossRef CAS PubMed.
- M. Sharp, Electrochim. Acta, 1983, 28, 301–308 CrossRef CAS.
- Y. Wang, E. I. Rogers and R. G. Compton, J. Electroanal. Chem., 2010, 648, 15–19 CrossRef CAS.
- G. A. Snook, A. S. Best, A. G. Pandolfo and A. F. Hollenkamp, Electrochem. Commun., 2006, 8, 1405–1411 CrossRef CAS.
- D. Shoup and A. Szabo, J. Electroanal. Chem. Interfacial Electrochem., 1982, 140, 237–245 CrossRef CAS.
- N. Ab Manan, C. Hardacre, J. Jacquemin, D. W. Rooney and T. G. A. Youngs, J. Chem. Eng. Data, 2009, 54, 2005–2022 CrossRef CAS.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- M. S. Shannon, J. M. Tedstone, S. P. O. Danielsen, M. S. Hindman, A. C. Irvin and J. E. Bara, Ind. Eng. Chem. Res., 2012, 51, 5565–5576 CrossRef CAS.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley, New York, 2nd edn, 2001, ch. 12, pp. 471–533 Search PubMed.
- R. G. Evans, O. V. Klymenko, S. A. Saddoughi, C. Hardacre and R. G. Compton, J. Phys. Chem. B, 2004, 108, 7878–7886 CrossRef CAS.
- S. Monaco, A. M. Arangio, F. Soavi, M. Mastragostino, E. Paillard and S. Passerini, Electrochim. Acta, 2012, 83, 94–104 CrossRef CAS.
- A. Khan and C. Zhao, Electrochem. Commun., 2014, 49, 1–4 CrossRef CAS.
- R. G. LeBel and D. A. I. Goring, J. Chem. Eng. Data, 1962, 7, 100–101 CrossRef CAS.
- A. Khan and C. Zhao, ACS Sustainable Chem. Eng., 2016, 4, 506–513 CrossRef CAS.
- Z. J. Chen, T. Xue and J.-M. Lee, RSC Adv., 2012, 2, 10564–10574 RSC.
- M. A. Vorotyntsev, V. A. Zinovyeva and M. Picquet, Electrochim. Acta, 2010, 55, 5063–5070 CrossRef CAS.
- M. Deetlefs, C. Hardacre, M. Nieuwenhuyzen, O. Sheppard and A. K. Soper, J. Phys. Chem. B, 2005, 109, 1593–1598 CrossRef CAS PubMed.
- T. G. A. Youngs, C. Hardacre and J. D. Holbrey, J. Phys. Chem. B, 2007, 111, 13765–13774 CrossRef CAS PubMed.
- C. Hardacre, J. D. Holbrey, C. L. Mullan, M. Nieuwenhuyzen, T. G. A. Youngs, D. T. Bowron and S. J. Teat, Phys. Chem. Chem. Phys., 2010, 12, 1842–1853 RSC.
- C. Hardacre, C. Mullan and T. G. A. Youngs, in Ionic Liquids Completely UnCOILed: Critical Expert Overviews, ed. N. V. Plechkova and K. R. Seddon, Wiley & Sons, Inc., New Jersey, USA, 2016, ch. 4, pp. 55–82 Search PubMed.
- H. Nakamoto, Y. Suzuki, T. Shiotsuki, F. Mizuno, S. Higashi, K. Takechi, T. Asaoka, H. Nishikoori and H. Iba, J. Power Sources, 2013, 243, 19–23 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp07160g |
| This journal is © the Owner Societies 2016 |