Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical analysis of NMR shieldings in XSe and XTe (X = Si, Ge, Sn and Pb): the spin-rotation constant saga†
Taye Beyene
Demissie
Centre for Theoretical and Computational Chemistry, Department of Chemistry, UiT The Arctic University of Norway, N-9037 Tromsø, Norway. E-mail: taye.b.demissie@uit.no
First published on 21st December 2015
Abstract
The nuclear spin-rotation (NSR) and absolute nuclear magnetic resonance (NMR) shielding tensors of the nuclei in the series of X77Se and X125Te (X = 29Si, 73Ge, 119Sn and 207Pb) are calculated using four-component relativistic density functional theory (DFT) and coupled-cluster singles-doubles with a perturbative triples correction (CCSD(T)). The results for the NSR constants are compared to available experimental data. The best theoretical estimates are obtained when relativistic corrections from DFT are added to the accurate non-relativistic CCSD(T) results. All the calculated NSR constants are in excellent agreement with the corresponding experimental values. Even though there are previously estimated absolute shielding constants and spans from experimental NSR tensors, new accurate values are reported following the same approach used to calculate the NSR constants in this study. The main reasons for the discrepancy between the previously reported NMR properties and the accurate results obtained in this study are also discussed.
1. Introduction
Until recently,1–3 it has been assumed that the absolute nuclear magnetic resonance (NMR) shielding constant can be estimated indirectly from the nuclear spin-rotation (NSR) constant, an approach experimentalists have been using for many years. The assumption was that the electronic contribution to the NSR constant CelK,iso could be directly related to the paramagnetic contribution to the absolute shielding constant σparaK,iso and then added to a calculated diamagnetic contribution σdiaK,iso4–7 to estimate σK,iso, as shown for example in eqn (1) for diatomic molecules: | (1) |
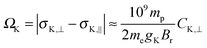 | (2) |
These approaches have shortcomings due to missing relativistic corrections.1,3,8–12 Nevertheless, absolute shielding constants and spans for many nuclei have been reported using these approaches. As have already been noted,3,10–12 the approach may give reasonable results only for very light nuclei (in a molecule composed of very light atoms) where relativistic effects are small (see for instance ref. 13–15 and references therein). The results for heavy nuclei estimated using eqn (1) and (2) are inaccurate due to the neglected relativistic corrections.10–12,16 Besides the approaches discussed above, the most popular computational methodologies are also based on the Schrödinger equation where relativistic corrections are missing, which really are important for both the heavy atoms as well as light atoms in the vicinity of the heavy ones.17,18
The theoretical calculations of NMR properties of heavy nuclei are demanding because one has to use the full four-component relativistic Dirac–Kohn–Sham (DKS) Hamiltonian (as implemented, for example, in the ReSpect19 and DIRAC20 program packages) and in some cases the two-component spin–orbit zeroth-order regular approximation (SO-ZORA) (as implemented in the Amsterdam density functional, ADF21) in order to obtain reasonable results. Approaches employing the relativistic Hamiltonian are currently based on density functional theory (DFT). Although DFT is a powerful and elegant method of calculation, it has shortcomings since approximations are required for the exchange–correlation energy functional. The lack of relativistic corrections in most of the currently available quantum chemical packages is also another limitation. One can reduce these shortcomings only by combining the relativistic corrections obtained from non-relativistic and four-component relativistic DFT calculations with those obtained from highly accurate non-relativistic coupled-cluster calculations. For instance, good agreement between the NSR constants obtained using this scheme and the experimental values for various molecules have been reported.10–12,22,23
In this paper, the NSR and NMR absolute shielding tensors of the monoselenides and monotellurides of silicon, germanium, tin and lead (X77Se and X125Te where X = 29Si, 73Ge, 119Sn and 207Pb) with the ambition that the results will be used for future benchmarking of theoretical methods. These molecules are also interesting since their bulk materials are narrow band-gap semiconductors used in opto-electronic and semiconductor applications24–26 and hence the results presented in this study are useful for improving our understanding of their molecular properties. As such, attention was given to obtain good agreement between the gas-phase experimental and the calculated NSR tensors and thereby determine the absolute shielding tensors of all nuclei using the same computational approach. The full four-component relativistic and coupled-cluster singles-doubles with perturbative triples corrections (CCSD(T)) approaches were used to determine these highly accurate results. Experimental gas-phase studies showed that all molecules are closed-shell linear molecules with 1Σ+ ground states. However, the CCSD(T) calculations in this study predicted closed-shell 1π singlet ground states.
For all the molecules, experimental gas-phase NSR constants were reported by Grabow and co-workers.27–30 Following the same approach as in previous studies,11,12,16 the nonzero component (not the trace) of the NSR tensors are reported. In addition, the signs of the experimental NSR constants were changed either to (+) or (−) based on the signs of the calculated values in this work to be consistent with the sign convention used by Flygare.7
2. Computational details
The highly accurate non-relativistic coupled-cluster singles-doubles with perturbative triples corrections CCSD(T) results for the NSR and NMR absolute shielding tensors were obtained using the coupled-cluster analytic linear response methods, developed by Gauss and Stanton31,32 and implemented in the CFOUR program package.33 The code has been modified locally to include the g factors for the heavy nuclei. Fully uncontracted double-ζ polarized Douglas–Kroll–Hess (denoted as unc-DZP-DKH) basis sets34–36 were used in one set of calculations, and the uncontracted atomic natural orbital-relativistic correlation-consistent basis sets (denoted as unc-ANO-RCC)37 were used in another set of calculations. It is important to note that the CCSD(T) calculations for the molecules involving heavy atoms are very expensive. For example CCSD(T)/unc-DZP-DKH for SnSe took a walltime of only 46 hours, whereas CCSD(T)/unc-ANO-RCC for the same molecule needed 1328 hours. The results obtained from these two basis sets do not show big differences (vide infra).The four-component Dirac–Kohn–Sham (DKS) relativistic DFT results were obtained using a development version of the program package ReSpect19 employing the BP8638,39 and B3LYP40–42 functionals. The modules using the restricted magnetic balance scheme43,44 and the restricted kinetic balance scheme45 were used for the NMR absolute shielding and NSR tensor calculations, respectively. DFT basis set dependence studies for both NMR absolute shielding and NSR tensors were performed using Dyall's relativistically optimized all-electron valence double-ζ (v2z);46,47 core-valence double-ζ (cv2z);46,47 valence triple-ζ (v3z);47,48 core-valence triple-ζ (cv3z);47,48 valence quadruple-ζ (v4z)47 and core-valence quadruple-ζ (cv4z)47 basis sets. The corresponding non-relativistic DFT results, used for the analysis of relativistic effects, were obtained using BP86 and B3LYP functionals and the cv4z basis sets.
The gauge-including atomic orbitals (GIAOs49,50) were employed to ensure origin independence for the absolute shielding constant calculations, while the common gauge-origin (CGO) approach45 was used for the NSR constant calculations using the ReSpect program. It is important to note that rotational London orbitals (RLOs) facilitate the basis set convergence for the calculation of NSR constants. However, these have not yet been implemented in ReSpect and hence large uncontracted all-electron basis sets were used to determine the relativistic corrections to the NSR constants. The basis set convergence study (vide infra) also shows well-converged CGO results. Relativistic and non-relativistic shielding calculations using the CGO approach were also performed for the purpose of analysis.
The scalar relativistic effects in the four-component calculations of NMR absolute shielding and NSR constants were calculated following the procedures used in ref. 16, 51 and 52. The scalar relativistic corrections were calculated as differences between the results obtained from calculations performed by removing the spin–orbit (SO) effects and the corresponding non-relativistic results. Similarly, the SO contributions to the NMR absolute shielding and NSR tensors were calculated as differences between the full four-component results and those with SO effects removed.16,51,52
Calculations of NMR absolute shielding constants were also performed using the two-component spin–orbit zeroth-order-regular approximation (SO-ZORA)53,54 using the Amsterdam Density Functional (ADF, version 2014.01) program package21 employing the BP86 and B3LYP functionals together with the all-electron quadruple-ζ quadruple polarized (QZ4P) Slater-type basis sets optimized for ZORA computations.55
Experimental geometries were reported for different isotopes of all the molecules. However, for the purpose of consistence and direct comparison, the isotopically independent Born–Oppenheimer experimental equilibrium bond lengths (rBOe) of re(Si–Se) = 2.05828249 Å, re(Si–Te) = 2.27354785 Å, re(Ge–Se) = 2.13460287 Å, re(Ge–Te) = 2.34014248 Å, re(Sn–Se) = 2.32559945 Å, re(Sn–Te) = 2.52281737 Å, re(Pb–Se) = 2.402308 Å and re(Pb–Te) = 2.595065 Å were used for all calculations, all taken from the studies of Grabow and co-workers.27–30 All nuclear g-factors are taken from ref. 56.
3. Results and discussion
3.1. Nuclear spin-rotation constants
The basis set dependence of the NSR constants of all nuclei in the X77Se and X125Te (X = 29Si, 73Ge, 119Sn and 207Pb) molecules are presented in Table 1. For all molecules, basis set dependence is found to be very small and converged results are obtained using cv3z basis sets. However, the larger cv4z basis set was used in all the other calculations to obtain accurate NSR constants. In the same table, the results obtained with the B3LYP functional and the cv4z basis set are also compared to the BP86 results. The largest difference between the BP86 and B3LYP results is for C(Pb) in PbSe (6%) and C(Pb) in PbTe (5%).| GeSe | GeTe | SnSe | SnTe | PbSe | PbTe | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ge | Se | Ge | Te | Sn | Se | Sn | Te | Pb | Se | Pb | Te | |
| a Calculated using BP86 unless stated otherwise. b Calculated using PBE. c Calculated using B3LYP. | ||||||||||||
| v2z | 2.624 | −15.596 | 2.120 | 29.136 | 35.947 | −11.116 | 27.496 | 18.952 | −52.115 | −9.064 | −36.495 | 13.636 |
| cv2z | 2.676 | −15.823 | 2.160 | 29.433 | 36.387 | −11.255 | 27.886 | 19.142 | −52.603 | −9.152 | −36.859 | 13.751 |
| v3z | 2.700 | −15.763 | 2.190 | 29.317 | 36.878 | −11.298 | 28.373 | 19.260 | −52.883 | −9.172 | −37.111 | 13.812 |
| cv3z | 2.732 | −15.913 | 2.211 | 29.484 | 37.073 | −11.357 | 28.517 | 19.319 | −52.946 | −9.175 | −37.166 | 13.809 |
| v4z | 2.711 | −15.819 | 2.199 | 29.370 | 36.998 | −11.341 | 28.493 | 19.325 | −52.935 | −9.191 | −37.194 | 13.848 |
| cv4z | 2.734 | −15.931 | 2.214 | 29.485 | 37.110 | −11.380 | 28.575 | 19.356 | −52.981 | −9.193 | −37.236 | 13.842 |
| cv4zb | 2.688 | −15.652 | 2.165 | 29.015 | 36.238 | −11.122 | 27.691 | 18.961 | −51.286 | −8.955 | −35.790 | 13.511 |
| cv4zc | 2.799 | −16.226 | 2.288 | 29.996 | 38.100 | −11.593 | 29.484 | 19.582 | −56.132 | −9.453 | −39.089 | 14.027 |
In Table 2, non-relativistic results from HF, CCSD(T) and DFT calculations together with the four-component relativistic DFT results are presented. As the atoms become heavier, the non-relativistic methods underestimate the magnitude of the NSR constants. This is most pronounced for the lead nuclei. For instance, C(Pb) in PbSe calculated using NR/BP86 and CCSD(T)/unc-DZP-DKH are respectively −21.565 kHz and −18.312 kHz, whereas that calculated using DKS/BP86 is −52.981 kHz (≈146% change with respect to NR/BP86). For the Se and Te nuclei, with the exception of C(Te) in SiTe and GeTe (which show a 9% change between NR/BP86 and DKS/BP86), such big changes are not observed. When we compare the HF and CCSD(T) results, we also see that HF overestimates the NSR constants compared to the other NR approaches. In other words, the CCSD(T) results always lie in the bottom line of all the HF results. From Table 2, one can also see that correlation effects [CCSD(T)-HF] are important. For instance, the correlation effect for C(Ge) in GeTe is −0.509 kHz (a 30% change), whereas it is 0.417 kHz for C(Se) in PbSe (a 5% change), see Tables 2 and 3. The differences between the CCSD(T) results using the unc-DZP-DKH and unc-ANO-RCC basis sets show very small basis set dependence. However, considering the size of the basis sets, the CCSD(T) results obtained using the latter basis set should be more accurate.
| NR | DKS | |||||||
|---|---|---|---|---|---|---|---|---|
| HFa | BP86b | B3LYPb | CCSD(T)a | CCSD(T)c | BP86b | B3LYPb | ||
| a The unc-DZP-DKH basis set was used. b The Dyall-cv4z basis set was used. c The unc-ANO-RCC basis set was used; not calculated for PbTe due to a large number of electrons. | ||||||||
| SiSe | Si | 11.156 | 10.440 | 10.799 | 9.155 | 9.571 | 10.709 | 11.045 |
| Se | −25.980 | −26.771 | −26.897 | −25.191 | −23.686 | −27.813 | −27.886 | |
| SiTe | Si | 10.143 | 8.952 | 9.405 | 7.808 | 8.242 | 9.481 | 9.892 |
| Te | 51.706 | 52.892 | 53.576 | 48.012 | 47.536 | 57.562 | 57.857 | |
| GeSe | Ge | 2.716 | 2.477 | 2.543 | 2.198 | 2.223 | 2.734 | 2.799 |
| Se | −16.598 | −15.219 | −15.536 | −14.834 | −13.515 | −15.931 | −16.226 | |
| GeTe | Ge | 2.191 | 1.918 | 1.996 | 1.682 | 1.724 | 2.214 | 2.288 |
| Te | 29.388 | 27.111 | 27.865 | 25.210 | 24.420 | 29.485 | 29.996 | |
| SnSe | Sn | 30.811 | 28.624 | 29.360 | 25.161 | 25.718 | 37.110 | 38.100 |
| Se | −11.397 | −10.796 | −11.017 | −10.597 | −9.608 | −11.380 | −11.593 | |
| SnTe | Sn | 23.006 | 20.890 | 21.630 | 18.189 | 19.942 | 28.575 | 29.484 |
| Te | 18.493 | 18.025 | 18.453 | 16.889 | 15.831 | 19.356 | 19.582 | |
| PbSe | Pb | −23.104 | −21.565 | −22.082 | −18.312 | −17.996 | −52.981 | −56.132 |
| Se | −9.246 | −8.645 | −8.829 | −8.526 | −8.058 | −9.193 | −9.453 | |
| PbTe | Pb | −15.972 | −14.787 | −15.259 | −12.440 | — | −37.236 | −39.089 |
| Te | 13.849 | 13.517 | 13.830 | 12.681 | — | 13.842 | 14.027 | |
| Δ(correl)a | ΔC(rel 1)b | ΔC(rel 2)c | CCSD(T)d | Total 1e | Total 2f | Exp.g | ||
|---|---|---|---|---|---|---|---|---|
| a Δ(correl) is an estimated electron correlation effect [CCSD(T)-HF] (see Table 2). b ΔC(rel 1) is the difference between DKS and NR results using BP86/cv4z (see Table 2). c ΔC(rel 2) is the difference between DKS and NR results using B3LYP/cv4z (see Table 2). d unc-ANO-RCC (unc-DZP-DKH for PbTe) basis sets (see Table 2). e Total 1 is the sum of ΔC(rel 1) and the CCSD(T) calculated values. f Total 2 is the sum of ΔC(rel 2) and the CCSD(T) calculated values. g Experimental values for different isotopes are given in the corresponding references. h Taken from ref. 27. i Taken from ref. 28. j Taken from ref. 29. k Taken from ref. 30. | ||||||||
| SiSe | Si | −2.001 | 0.269 | 0.246 | 9.571 | 9.840 | 9.817 | (+)10.20h |
| Se | 0.789 | −1.042 | −0.989 | −23.686 | −24.728 | −24.675 | (−)25.46h | |
| SiTe | Si | −2.335 | 0.529 | 0.487 | 8.242 | 8.771 | 8.729 | (+)9.22h |
| Te | −3.694 | 4.670 | 4.281 | 47.536 | 52.206 | 51.817 | (+)53.75h | |
| GeSe | Ge | −0.518 | 0.257 | 0.256 | 2.223 | 2.480 | 2.479 | (+)2.330(27)i |
| Se | 1.764 | −0.712 | −0.690 | −13.515 | −14.227 | −14.205 | (−)13.70(19)i | |
| GeTe | Ge | −0.509 | 0.296 | 0.292 | 1.724 | 2.020 | 2.016 | (+)1.847(45)i |
| Te | −4.178 | 2.374 | 2.131 | 24.420 | 26.794 | 26.551 | (+)26.130(97)i | |
| SnSe | Sn | −5.650 | 8.486 | 8.740 | 25.718 | 34.204 | 34.458 | (+)32.34(83)j |
| Se | 0.800 | −0.584 | −0.576 | −9.608 | −10.192 | −10.184 | (−)10.11(82)j | |
| SnTe | Sn | −4.817 | 7.685 | 7.854 | 19.942 | 27.627 | 27.796 | (+)25.48(17)j |
| Te | −1.604 | 1.331 | 1.129 | 15.831 | 17.162 | 16.960 | (+)16.53(16)j | |
| PbSe | Pb | 4.792 | −31.416 | −34.050 | −17.996 | −49.412 | −52.046 | (−)47.04(32)k |
| Se | 0.417 | −0.548 | −0.624 | −8.058 | −8.606 | −8.682 | (−)9.35(23)k | |
| PbTe | Pb | 3.532 | −22.449 | −23.830 | −12.440 | −34.889 | −36.270 | (−)30.91(44)k |
| Te | −1.168 | 0.325 | 0.510 | 12.681 | 13.006 | 13.191 | (+)13.58(44)k | |
The relativistic corrections obtained from the two DFT functionals are listed in Table 3. Large relativistic corrections to the NSR constants are observed for lead in PbSe and PbTe compared to the other molecules. For instance, the relativistic correction calculated using the BP86 functional contributes to 15% of the total NSR constant of Ge in GeTe, but 28% for C(Sn) in SnTe and 64% for C(Pb) in PbTe. The B3LYP calculated results also show similar trends for the relativistic effects. For the C(Sn) and C(Pb) NSR tensors in all molecules, relativistic effects are more important than electron correlation effects. For example, the electron correlation effect on C(Sn) in SnSe is −5.650 kHz, whereas the BP86 relativistic correction is 8.486 kHz (see Table 3).
The results listed in Table 3 also show that CCSD(T) gives NSR constants of Ge in GeSe and GeTe with an approximate errors of 6% and 9% compared to the corresponding experimental values, whereas the error increases to 22% and 29% for C(Sn) in SnSe and SnTe, respectively. For C(Pb) in PbSe and PbTe, CCSD(T) underestimates these results by approximately 61% and 60%, respectively, compared to the experimental values as well as the final NSR results determined by adding the relativistic corrections (ΔC(rel)), obtained from DFT calculations, to the CCSD(T) calculated values. These analyses show the importance of combining the CCSD(T) and four-component relativistic DFT methodologies to obtain reasonably good results that can be compared to experimental values. With the exception of C(Pb) in PbTe (which show an error of 13%), all the final calculated NSR constants are in quite good agreement with the corresponding gas-phase experimental NSR constants. The most impressive final results are those of tin and lead where the errors of these final results are significantly reduced compared to the errors of the results obtained from the pure CCSD(T) and DFT calculations, indicating that the scheme followed in this study is a powerful remedy for these kinds of calculations. We have previously also employed this scheme to determine the NSR constants of 47 nuclei in 22 molecules.10–12,16,22 All these studies point to the need for relativistic coupled-cluster methods for the calculation of magnetic properties.
3.2. NMR shielding constants
A basis set dependence study of the absolute shielding constants are presented in Table 4. For all nuclei, with the exception of σ(Te), there are considerable differences between the double-ζ results and those obtained using other basis sets. As the size of the basis sets increase, the results become more stable showing convergence to the basis set limit. Hence, the larger cv4z basis set was used for the remaining calculations of the absolute shielding tensors. This is important especially for the results calculated using B3LYP employing the CGO approach. Similarly, the all-electron QZ4P basis set was also used for the calculations performed in ADF.| GeSe | GeTe | SnSe | SnTe | PbSe | PbTe | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ge | Se | Ge | Te | Sn | Se | Sn | Te | Pb | Se | Pb | Te | |
| a Calculated using BP86 employing the GIAO approach unless stated otherwise. b Calculated using BP86 employing the CGO approach. | ||||||||||||
| v2z | 181.0 | 207.0 | −356.5 | 1516.9 | 857.9 | −14.3 | −47.5 | 1424.6 | −264.2 | −209.4 | −2496.1 | 1509.7 |
| cv2z | 168.3 | 198.5 | −379.3 | 1503.7 | 833.3 | −26.5 | −91.7 | 1408.0 | −398.2 | −227.0 | −2637.8 | 1492.6 |
| v3z | 111.9 | 205.2 | −449.1 | 1483.7 | 717.4 | −1.6 | −228.9 | 1405.5 | −659.0 | −163.5 | −2900.3 | 1550.0 |
| cv3z | 110.2 | 204.9 | −455.6 | 1485.1 | 722.0 | 1.4 | −232.8 | 1410.2 | −637.2 | −158.8 | −2897.1 | 1556.0 |
| v4z | 107.2 | 204.8 | −456.8 | 1479.8 | 704.8 | 1.2 | −249.4 | 1404.2 | −701.7 | −152.9 | −2968.9 | 1557.1 |
| cv4z | 107.8 | 207.5 | −457.9 | 1485.6 | 715.7 | 8.9 | −241.4 | 1415.7 | −672.5 | −147.7 | −2943.3 | 1564.3 |
| cv4zb | 104.0 | 212.5 | −456.8 | 1499.1 | 705.2 | 31.0 | −252.3 | 1450.8 | −770.0 | −119.5 | −3077.0 | 1601.2 |
The absolute shielding constants obtained using different methods are listed in Table 5. Comparing the NR results obtained from both the coupled-cluster and DFT calculations shows that none of the NR methods give close results among each other for most of the molecules. The results obtained using the BP86 and B3LYP functionals show that the dependence of σ(Te) in all molecules is small compared to the other nuclei, whereas considerable dependence on the functional as well as the Hamiltonian is observed for the other nuclei. This dependence is most pronounced for σ(Pb). For example, σ(Sn) in SnTe calculated using DKS/BP86 −241.4 ppm and using DKS/B3LYP is −486.8 ppm, and σ(Pb) in PbTe using DKS/BP86 is −2943.3 ppm and using DKS/B3LYP is −4173.0 ppm. Test calculations for these two nuclei using DKS/PBE also show considerable differences from the above results. One may suspect slower basis set convergence (since the B3LYP results are obtained employing CGOs), however, the results listed in Table 4 (compare the last two rows) show that the results obtained employing the CGO and GIAO approaches do not show big differences. Moreover, additional calculations using DKS/B3LYP were also performed by putting the gauge-origin on tin and lead atoms. The results obtained in this case for Pb in both PbSe and PbTe do not show considerable differences, for instance σ(Pb) and σ(Te) in PbTe when the gauge-origin is on Pb are −4171.1 and 1474.5 ppm, respectively (to be compared with −4173.0 and 1491.8 ppm, respectively, when the gauge-origin is at the center of mass). Similarly, σ(Sn) and σ(Te) in SnTe calculated by putting the gauge on Sn are −473.3 and 1390.3 ppm, whereas those calculated by putting the gauge-origin at the center of mass are −486.8 and 1399.2 ppm, respectively.
| NR | SO-ZORA | DKS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HFa | BP86b | B3LYPc | CCSD(T)a | CCSD(T)d | BP86e | B3LYPe | BP86b | B3LYPc | ||
| a The unc-DZP-DKH basis set was used. b The Dyall-cv4z basis set was used together with the GIAO approach. c The Dyall-cv4z basis set was used together with the CGO approach. d The unc-ANO-RCC basis set was used; not calculated for PbTe due to a large number of electrons. e The all-electron QZ4P basis set was used together with the GIAO approach. | ||||||||||
| SiSe | Si | −211.4 | −140.8 | −175.9 | −16.1 | −56.9 | −144.7 | −181.1 | −149.8 | −183.1 |
| Se | 377.3 | 297.6 | 284.8 | 456.6 | 608.5 | 341.0 | 371.5 | 481.7 | 474.5 | |
| SiTe | Si | −471.5 | −312.5 | −372.8 | −161.1 | −218.9 | −346.5 | −412.9 | −371.9 | −423.0 |
| Te | 1078.3 | 980.4 | 923.4 | 1384.1 | 1423.8 | 1178.1 | 1324.2 | 1798.1 | 1778.9 | |
| GeSe | Ge | −114.4 | 139.2 | 69.0 | 433.1 | 407.3 | 75.4 | −10.8 | 107.8 | 33.4 |
| Se | −205.0 | 61.4 | 0.1 | 135.3 | 389.8 | 90.0 | 45.2 | 207.5 | 155.8 | |
| GeTe | Ge | −666.6 | −239.4 | −361.3 | 129.0 | 63.5 | −421.2 | −583.1 | −457.9 | −582.4 |
| Te | 312.5 | 704.1 | 574.3 | 1030.2 | 1166.2 | 967.4 | 956.8 | 1485.6 | 1420.0 | |
| SnSe | Sn | 584.7 | 905.2 | 797.3 | 1410.2 | 1328.9 | 579.4 | 364.6 | 715.8 | 553.3 |
| Se | −258.7 | −87.0 | −150.3 | −30.3 | 252.3 | −122.4 | −164.9 | 8.9 | −30.9 | |
| SnTe | Sn | −72.4 | 403.0 | 236.7 | 1007.5 | 966.4 | −196.7 | −549.6 | −241.4 | −486.8 |
| Te | 476.3 | 600.4 | 486.9 | 899.9 | 930.7 | 857.8 | 894.5 | 1415.7 | 1399.2 | |
| PbSe | Pb | 2419.3 | 2927.4 | 2756.3 | 4004.3 | 3876.7 | 142.6 | −1389.0 | −672.5 | −1862.1 |
| Se | −387.1 | −167.0 | −234.4 | −123.5 | −196.9 | −260.4 | 246.0 | −147.7 | −240.9 | |
| PbTe | Pb | 1497.9 | 2133.0 | 1879.1 | 3392.0 | — | −1206.2 | −3034.5 | −2943.3 | −4173.0 |
| Te | 411.5 | 530.6 | 418.3 | 828.8 | — | 981.4 | 1048.7 | 1564.3 | 1491.8 | |
The two- and four-component results listed in Table 5 show that the two Hamiltonians give very different results, especially for the heavier atoms. For instance, σ(Te) in SnTe using SO-ZORA/BP86 is 857.8 ppm and using SO-ZORA/B3LYP is 894.5 ppm, whereas those calculated using DKS/BP86 and DKS/B3LYP are 1415.7 ppm and 1399.2 ppm, respectively. It is important to note that one may improve (but not always) the SO-ZORA results by introducing dispersion correction57 to the functional. For instance, σ(Sn) and σ(Te) calculated using SO-ZORA/BP86-D3/QZ4P are −283.9 ppm and 757.5 ppm, respectively. If we take the DKS/BP86 results as benchmarks, we see that the former shows improvement and that of Te gets worse compared to those obtained using SO-ZORA/BP86.
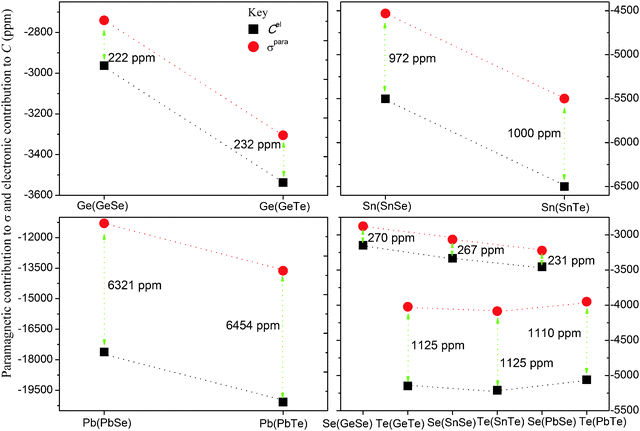
In Table 6, the paramagnetic and diamagnetic contributions to the shielding tensors are presented together with the corresponding values of the paramagnetic contributions determined from the electronic contribution to the NSR tensors. From the results we see that the paramagnetic contribution to all nuclear shielding tensors obtained from the direct calculations of the absolute shielding tensors are the same as to those derived from the electronic contribution to the NSR tensors in the non-relativistic theory. For example, Cel,iso(Pb) in PbTe calculated using NR/BP86 is −8043.7 ppm, and σpara,iso(Pb) in the same molecule obtained using NR/BP86 is −8043.7 ppm. This is because the magnetic and angular momentum operators have the same form in the non-relativistic theory.1,2 On the other hand, there is no agreement between Cel,iso and σpara,iso in the four-component relativistic calculations. In the four-component relativistic theory, the magnetic and angular momentum operators are different since the magnetic momentum operator couples the large and small components of the wave function, whereas the total angular momentum operator does not.1,2,16 This makes the paramagnetic contribution obtained from the four-component relativistic calculations to be different from the one derived from the electronic contribution to the NSR tensors. The difference becomes large as the nuclei become heavier. For instance, the values of Cel,iso(Ge) and σpara,iso(Ge) in GeSe calculated using DKS/BP86 are −2962.9 ppm and −2740.5 ppm, respectively (a difference of 222.4 ppm), but for Pb in PbTe these values are −20078.0 ppm and −13624.0 ppm, respectively (a difference of 6454 ppm).
| NRa | DKS b | Previousc | NR a | DKS b | Previousc | |
|---|---|---|---|---|---|---|
| a NR stands for non-relativistically calculated results using BP86/cv4z. b DKS stands for full four-component relativistically calculated results using BP86/cv4z. c C el,iso and C⊥ are converted (kHz to ppm) values, σpara,iso is estimated from Cel,iso and Ω is estimated from C⊥. d Taken from ref. 27. e Calculated diamagnetic contribution reported in the corresponding references. f Taken from ref. 28. g Taken from ref. 29. h Taken from ref. 30. | ||||||
| SiSe | Si | Se | ||||
| C el,iso | −1057.7 | −1083.8 | −1147.0d | −2748.1 | −2853.2 | −2644.9d |
| σ para,iso | −1057.7 | −1067.6 | −1167d | −2748.1 | −2582.4 | −2573d |
| σ dia,iso | 916.9 | 917.7 | 1061e | 3045.7 | 3064.2 | 3362e |
| Ω | 1535.8 | 1605.0 | 1518d | 4064.0 | 4284.1 | 3764d |
| C ⊥ | −1522.8 | −1562.0 | −1487.8d | −4052.6 | −4210.2 | −3854.1d |
| SiTe | Si | Te | ||||
| C el,iso | −1227.4 | −1297.4 | −1435.1d | −4429.7 | −4816.6 | −4511.5d |
| σ para,iso | −1227.4 | −1281.6 | −1445d | −4429.7 | −3692.1 | −4394d |
| σ dia,iso | 914.9 | 915.6 | 1121e | 5410.0 | 5487.8 | 6623e |
| Ω | 1796.5 | 1996.3 | 1845d | 6582.8 | 7404.1 | 6505d |
| C ⊥ | −1780.3 | −1885.4 | −1833.6d | −6574.1 | −7154.5 | −6680.7d |
| GeSe | Ge | Se | ||||
| C el,iso | −2690.6 | −2962.9 | −2608.7f | −3010.3 | −3147.8 | −2783.3f |
| σ para,iso | −2690.6 | −2740.5 | −2662f | −3010.3 | −2877.4 | −2808f |
| σ dia,iso | 2829.8 | 2844.5 | 3134e | 3071.6 | 3089.9 | 3439e |
| Ω | 3938.4 | 4482.9 | 3768f | 4421.4 | 4743.5 | 4001f |
| C ⊥ | −3926.6 | −4335.2 | −3694f | −4406.9 | −4613.2 | −3967f |
| GeTe | Ge | Te | ||||
| C el,iso | −3073.3 | −3536.9 | −3090.7f | −4740.1 | −5147.9 | −4669.3f |
| σ para,iso | −3073.3 | −3305.3 | −3140f | −4740.1 | −4022.7 | −4635.3f |
| σ dia,iso | 2833.9 | 2848.5 | 3194e | 5444.2 | 5521.8 | 6693e |
| Ω | 4509.5 | 5531.3 | 4397f | 6999.7 | 7948.1 | 6760f |
| C ⊥ | −4494.4 | −5189.8 | −4329f | −6988.6 | −7600.4 | −6811f |
| SnSe | Sn | Se | ||||
| C el,iso | −4264.0 | −5503.4 | −4800.7g | −3165.8 | −3332.7 | −3304.7g |
| σ para,iso | −4264.0 | −4531.6 | −4912g | −3165.8 | −3065.9 | −3317.3g |
| σ dia,iso | 5169.2 | 5236.8 | 6203e | 3078.9 | 3096.9 | 3327e |
| Ω | 6279.6 | 8695.6 | 7163g | 4647.4 | 5165.3 | 4672g |
| C ⊥ | −6271.0 | −8130.2 | −7000g | −4629.7 | −4880.0 | −4674g |
| SnTe | Sn | Te | ||||
| C el,iso | −4777.3 | −6499.9 | −5167.3g | −4858.2 | −5209.9 | −4869.3g |
| σ para,iso | −4777.3 | −5499.8 | −5263.3g | −4858.2 | −4085.1 | −4886g |
| σ dia,iso | 5180.2 | 5247.5 | 6203e | 5458.6 | 5535.9 | 6639e |
| Ω | 7036.0 | 10670.4 | 7604g | 7158.3 | 8282.9 | 7049g |
| C ⊥ | −7024.3 | −9608.4 | −7461g | −7144.3 | −7672.0 | −7020g |
| PbSe | Pb | Se | ||||
| C el,iso | −7228.8 | −17618.0 | 15620.7h | −3253.5 | −3454.2 | 3747.33h |
| σ para,iso | −7228.8 | −11297.0 | −15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 976h 976h |
−3253.5 | −3223.4 | −3749.3h |
| σ dia,iso | 10156.2 | 10527.0 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688e 688e |
3086.5 | 3104.0 | 3619e |
| Ω | 10705.4 | 31678.3 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 765h 765h |
4770.4 | 6130.5 | 5143h |
| C ⊥ | −10697.9 | −26282.0 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335h 335h |
−4749.8 | −5051.0 | 5137h |
| PbTe | Pb | Te | ||||
| C el,iso | −8043.7 | −20078.0 | 16778.7h | −4944.5 | −5060.7 | 5156h |
| σ para,iso | −8043.7 | −13624.0 | −17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 059h 059h |
−4944.5 | −3950.3 | −5157.3h |
| σ dia,iso | 10176.6 | 10546.8 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 743e 743e |
5475.0 | 5551.5 | 6862e |
| Ω | 11900.0 | 37812.2 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306h 306h |
7265.6 | 9319.6 | 7172h |
| C ⊥ | −11889.4 | −29941.0 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 854h 854h |
−7249.2 | −7423.5 | 7283h |
The correlations between the paramagnetic contributions from direct calculations of the absolute shielding tensors and the electronic contributions to the NSR tensors are shown in Fig. 1. Surprisingly, the trends show a periodic behavior. For example, the difference between Cel,iso and σpara,iso of Ge and Se (which are both in period 4 of the periodic table) in all the molecules lie within the 222–270 ppm range. Similarly, these differences for Sn and Te (both in period 5) are within a range of 972–1125 ppm (see Table 6 and Fig. 1 for details). Additional test calculations were also done for SnPo and PbPo. The results show that these differences for Pb and Po lie within the range of 6320–7500 ppm. From Fig. 1, one can also see that the differences between Cel,iso and σpara,iso (also they refer to the relativistic corrections to the shielding tensor) are atomic in nature. For instance, the difference between Cel,iso and σpara,iso of Te in all molecules is 1125 ppm (1110 ppm in PbTe), indicating that the difference is independent of the nature of the atom bonded to tellurium. These differences also indicate that the absolute shielding scales determined indirectly from experimental NSR constants are off by the above numbers for the respective nuclei, keeping in mind that the diamagnetic contributions are obtained using appropriate shielding calculations. Further studies using perturbation analysis are underway in our group to investigate the validity of these differences.58
The relativistic corrections, electron correlation effects and final calculated absolute shielding constants are presented in Table 7, together with the previously determined values from experimental NSR tensors. The relativistic correction, the differences between the DKS and NR results, that is obtained from both functionals increase as the atoms become heavier. The effect of the heavy atom on the neighboring nucleus can also be seen from Table 7. For instance, the relativistic correction for σ(Sn) in SnSe calculated using BP86 is −189.4 ppm, whereas that in SnTe is −644.4 ppm. Similarly, the relativistic correction calculated using BP86 for σ(Te) is 781.5 ppm in GeTe, 815.3 ppm in SnTe and 1033.7 ppm in PbTe, showing the effect of the neighboring atoms on the absolute shielding constant of tellurium.
| Δ(correl)a | Δσ(rel 1)b | Δσ(rel 2)c | CCSD(T)d | Total 1e | Total 2f | Previous | Best estimatek | ||
|---|---|---|---|---|---|---|---|---|---|
| a Δ(correl) is an estimated electron correlation effect [CCSD(T)-HF] (see Table 5). b Δσ(rel 1) is the difference between DKS and NR results using BP86/cv4z (see Table 5). c Δσ(rel 2) is the difference between DKS and NR results using B3LYP/cv4z (see Table 5). d unc-ANO-RCC (unc-DZP-DKH for PbTe) basis sets (see Table 5). e Total 1 is the sum of Δσ(rel 1) and the CCSD(T) calculated values. f Total 2 is the sum of Δσ(rel 2) and the CCSD(T) calculated values. g Taken from ref. 27. h Taken from ref. 28. i Taken from ref. 29. j Taken from ref. 30. k Error bars are estimated based on calculations performed using different functionals. | |||||||||
| SiSe | Si | 195.3 | −9.0 | −7.2 | −56.9 | −65.9 | −64.1 | −106g | −65 ± 5 |
| Se | 79.3 | 184.1 | 189.7 | 608.5 | 792.6 | 798.2 | 789g | 790 ± 10 | |
| SiTe | Si | 310.4 | −59.4 | −50.2 | −218.9 | −278.3 | −269.1 | −324g | −270 ± 16 |
| Te | 305.8 | 817.7 | 855.5 | 1423.8 | 2241.5 | 2279.3 | 2229g | 2200 ± 123 | |
| GeSe | Ge | 547.5 | −31.4 | −35.6 | 407.3 | 375.9 | 371.7 | 472h | 380 ± 25 |
| Se | 340.3 | 146.1 | 155.7 | 389.8 | 535.9 | 545.5 | 612h | 540 ± 38 | |
| GeTe | Ge | 795.6 | −218.5 | −221.1 | 63.5 | −155.0 | −157.6 | −24h | −150 ± 16 |
| Te | 717.7 | 781.5 | 845.7 | 1166.2 | 1947.7 | 2011.9 | 2058h | 1900 ± 105 | |
| SnSe | Sn | 825.5 | −189.4 | −244.0 | 1328.9 | 1139.5 | 1084.9 | 1291i | 1150 ± 57 |
| Se | 228.4 | 95.9 | 119.4 | 252.3 | 348.2 | 371.7 | 10i | 360 ± 18 | |
| SnTe | Sn | 1079.9 | −644.4 | −723.5 | 966.4 | 322.0 | 242.9 | 940i | 330 ± 15 |
| Te | 423.6 | 815.3 | 912.3 | 930.7 | 1746.0 | 1843 | 1753i | 1700 ± 95 | |
| PbSe | Pb | 1585.0 | −3599.9 | −4618.4 | 3876.7 | 276.8 | −741.7 | 4712j | — |
| Se | 263.6 | 19.3 | −6.5 | −196.9 | −177.6 | −203.4 | −130j | −185 ± 10 | |
| PbTe | Pb | 1894.1 | −5076.3 | −6052.1 | 3392.0 | −1684.3 | −2660.1 | 3684j | −2000 ± 280 |
| Te | 417.3 | 1033.7 | 1073.5 | 828.8 | 1862.5 | 1902.3 | 1705j | 1800 ± 80 | |
With the exception of the nuclei in PbSe and PbTe, the final absolute shielding constants obtained by adding the CCSD(T) calculated results to the Δσ(rel) values obtained from BP86 and B3LYP are in good agreement with each other (see Table 7). On the other hand, with the exception of a very few nuclei, the previously reported absolute shielding constants obtained indirectly from NSR constants are in disagreement with the values determined in this work. As already pointed out in earlier studies,3,10–12,45,59 the indirect determination of absolute shielding constants from NSR tensors leads to inaccurate results due to the missing relativistic corrections to the shielding tensors (see Tables 5 and 7). The difference is most pronounced for the heavy nuclei, see for instance σ(Pb) in Table 7 and Table S1 of the ESI.† In addition, the diamagnetic contribution used in ref. 27–30 are not accurate enough to estimate the absolute shielding constants. For example, σdia(Sn) in SnSe in ref. 29 is 6203 ppm, whereas 5236.8 ppm at the DKS/BP86/cv4z level in this work (see Table 6). Test calculations using DKS/BP86/cv4z for the free Sn atom gives a σdia,FA(Sn) of 5154.2 ppm. Adding the nuclear contribution Cnuc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 of 83.4 ppm (σdia,FA + Cnuc) gives 5236.8 ppm, which is in good agreement with the one obtained from direct shielding calculations. In ref. 30, a calculated value of 20
5 of 83.4 ppm (σdia,FA + Cnuc) gives 5236.8 ppm, which is in good agreement with the one obtained from direct shielding calculations. In ref. 30, a calculated value of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688 ppm was used for σdia(Pb), which is twice greater than that obtained in this work (10527.0 ppm). Similar test calculations for the free Pb atom give 10431.8 ppm, which becomes 10528.7 ppm together with Cnuc (86.9 ppm). Taylor et al.60 also reported 9950 ppm for σdia(Pb) and 5311 ppm for σdia(Te) in [PbTe6H6]4− and [TePb6F18]8− calculated using SO-ZORA/BP86/TZ2P. The CCSD(T)/unc-DZP-DKH calculated values for σdia(Pb) in this study are 10193.3 ppm in PbSe and 10248.4 ppm in PbTe.
688 ppm was used for σdia(Pb), which is twice greater than that obtained in this work (10527.0 ppm). Similar test calculations for the free Pb atom give 10431.8 ppm, which becomes 10528.7 ppm together with Cnuc (86.9 ppm). Taylor et al.60 also reported 9950 ppm for σdia(Pb) and 5311 ppm for σdia(Te) in [PbTe6H6]4− and [TePb6F18]8− calculated using SO-ZORA/BP86/TZ2P. The CCSD(T)/unc-DZP-DKH calculated values for σdia(Pb) in this study are 10193.3 ppm in PbSe and 10248.4 ppm in PbTe.
In some molecules there appears to be good agreement between the results calculated in this work and previously estimated values (see Table 7). This is mainly due to error cancellations between σdia and σpara as there are errors in σdia used in the earlier studies due to method inaccuracies and the missing relativistic corrections from σpara determined from the experimental Cel. For example, in Table 6 it is shown that σpara(Sn) in SnSe determined from the experimental Cel is −4912 ppm, whereas σpara(Sn) calculated using DKS/BP86 is −4531.6 ppm (Δσpara of −380.4 ppm), and σdia(Sn) used in ref. 29 is 6203 ppm and that obtained in this work is 5236.8 ppm (Δσdia of 966.2 ppm), causing a net error cancellation of the two contributions. Considering the levels of calculations used, the final absolute shielding constants of all nuclei reported in this study should be accurate. Based on the results obtained from different functionals and basis sets, accuracy ranges are also estimated for all the studied nuclei (see Table 7).
3.3. NMR shielding spans
Calculated shielding spans are presented in Table 8, Tables S1 and S2 of the ESI.† The relativistic effects on the shielding spans increase as the nuclei become heavier, compare for example ΔΩ(rel1) of Ge, Sn and Pb in the corresponding selenide molecules. Relativistic effects are the largest contributions to the span for the lead nuclei in both PbSe and PbTe. For instance, it contributes 18% to the total DKS/BP86 calculated Ω(Ge) in GeTe, 34% to Ω(Sn) in SnTe and 68% to Ω(Pb) in PbTe. The relativistic effects obtained from the two functionals show the largest difference for the span of lead in PbSe and PbTe (11% and 10%, respectively). The effect of the heavy atoms on light atoms (HALA) is another interesting observation from the table. For example, tellurium affects stronger than selenium when we compare the germanium molecules; Ω(Ge) in GeSe calculated using DKS/BP86 is 4477 ppm, while that in GeTe is 5533 ppm. The same is also true for the span of Te when comparing GeTe, SnTe and PbTe, of which lead causes the strongest HALA effect (a difference of 932 ppm between the relativistic correction for the span of Te in SnTe and PbTe at the DKS/BP86/cv4z level).| NR | SO-ZORA | DKS | ΔΩ(rel 1)c | ΔΩ(rel 2)d | CCSD(T)e | Total 1f | Total 2g | Previous | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BP86a | B3LYPa | BP86b | B3LYPb | BP86a | B3LYPa | ||||||||
| a Using cv4z basis sets (all using GIAO, except B3LYP where CGO was used). b Using ZORA optimized all-electron QZ4P basis sets. c ΔΩ(rel 1) is the difference between DKS and NR results using BP86/cv4z (relativistic corrections). d ΔΩ(rel 2) is the difference between DKS and NR results using B3LYP/cv4z (relativistic corrections). e unc-ANO-RCC (unc-DZP-DKH for PbTe) basis sets. f Total 1 is the sum of the CCSD(T) results and ΔΩ(rel 1) from BP86/cv4z, absolute values. g Total 2 is the sum of the CCSD(T) results and ΔΩ(rel 2) from B3LYP/cv4z, absolute values. h Taken from ref. 27. i Taken from ref. 28. j Taken from ref. 29. k Taken from ref. 30. | |||||||||||||
| SiSe | Si | 1536 | 1588 | 1574 | 1633 | 1605 | 1655 | 69 | 67 | 1409 | 1478 | 1476 | 1518h |
| Se | 4064 | 4083 | 4286 | 4280 | 4284 | 4294 | 220 | 211 | 3597 | 3817 | 3808 | 3764h | |
| SiTe | Si | 1797 | 1886 | 1918 | 2031 | 2005 | 2083 | 208 | 197 | 1655 | 1863 | 1852 | 1845h |
| Te | 6583 | 6668 | 7526 | 7478 | 7401 | 7428 | 818 | 760 | 5917 | 6735 | 6677 | 6505h | |
| GeSe | Ge | 3938 | 4043 | 4358 | 4504 | 4477 | 4594 | 539 | 551 | 3536 | 4075 | 4087 | 3768i |
| Se | 4421 | 4513 | 4739 | 4818 | 4751 | 4831 | 330 | 318 | 3928 | 4258 | 4246 | 4028i | |
| GeTe | Ge | 4510 | 4692 | 5228 | 5520 | 5533 | 5732 | 1023 | 1040 | 4055 | 5078 | 5095 | 4514i |
| Te | 7000 | 7194 | 8076 | 8125 | 7968 | 8076 | 968 | 882 | 6306 | 7274 | 7188 | 6760i | |
| SnSe | Sn | 6280 | 6441 | 8221 | 8627 | 8680 | 8960 | 2400 | 2519 | 5643 | 8043 | 8162 | 7163j |
| Se | 4647 | 4742 | 5163 | 5256 | 5198 | 5264 | 551 | 522 | 4138 | 4689 | 4660 | 4672j | |
| SnTe | Sn | 7036 | 7285 | 9693 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 406 406 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 654 654 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 076 076 |
3618 | 3791 | 6129 | 9747 | 9920 | 7604j |
| Te | 7158 | 7328 | 8424 | 8433 | 8335 | 8369 | 1177 | 1041 | 6708 | 7885 | 7749 | 7049j | |
| PbSe | Pb | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705 705 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 961 961 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 385 385 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 767 767 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 532 532 |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 109 109 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 827 827 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148 148 |
9092 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 919 919 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 240 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 765k 765k |
| Se | 4770 | 4872 | 5868 | 6092 | 6173 | 6339 | 1403 | 1467 | 4705 | 6108 | 6172 | 5143k | |
| PbTe | Pb | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280 280 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 639 639 |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 092 092 |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 612 612 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 480 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 712 712 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 014 014 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 726 726 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 214 214 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306k 306k |
| Te | 7266 | 7434 | 9059 | 9189 | 9375 | 9482 | 2109 | 2048 | 6818 | 8927 | 8866 | 7172k | |
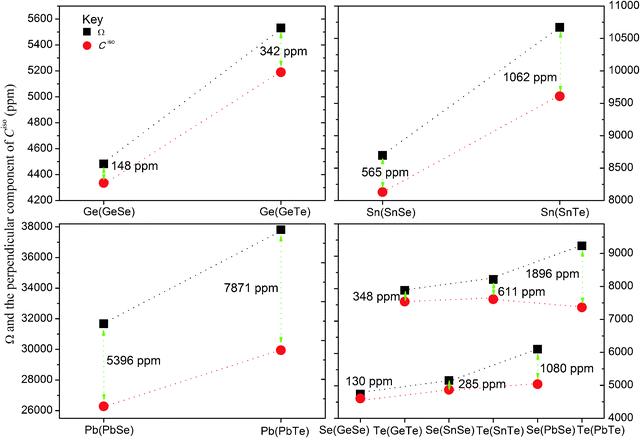
With the exception of PbSe and PbTe, the shielding spans obtained using the SO-ZORA and DKS methods do not show considerable differences (the maximum difference is 10% for Ω(Sn) in SnTe). SO-ZORA/BP86 underestimates Ω(Pb) by 20% in PbSe and by 27% in PbTe compared to DKS/BP86. In Table 6, the shielding spans determined from the calculated NSR constants and those derived from direct absolute shielding constant calculations are reported. The results show that in the non-relativistic domain, the spans are in perfect agreement with each other. However, there are considerable differences between those obtained in the four-component relativistic calculations. For instance, the NR/BP86 results of Ω(Sn) in SnSe are 6279.6 ppm and −6271.0 ppm, for the value obtained from the direct calculation of the shielding constant and that determined from the calculated NSR constant, respectively. The values obtained from the DKS/BP86 calculations for the same nucleus are 8695.6 ppm and −8130.2 ppm, respectively (see Table 6). Such differences are huge for Ω(Pb) in PbSe and PbTe, indicating that using the equation relating the shielding span and NSR constant (eqn (2)) leads to unrecoverable errors for heavy atoms where spin–orbit coupling is prominent. The correlation diagram between the span obtained from these two approaches is shown in Fig. 2. The correlations shows that the error becomes larger as the nuclei become heavier, see for instance the plot for Se in GeSe and in PbSe where the difference is smaller compared to the other nuclei, whereas it is large when we compare Ge, Sn and Pb.
The previously reported shielding spans collected in Table 8 are determined from the experimental NSR constants.28–30 The equation relating the span and NSR tensors (eqn (2)) works perfectly in the non-relativistic and scalar relativistic domains, whereas for very heavy nuclei, the relation breaks down due to the considerable spin–orbit coupling. We also see these effects in Table 8 where the non-relativistic spans are in relatively good agreement with those derived from the experimental NSR constants for the light atoms. For instance, the NR/BP86 values for Ge in GeTe is 4510 ppm and the previously determined value is 4514 ppm. Also for Te in PbTe, the NR/BP86 value is 7266 ppm which is in fair agreement with the previously reported value of 7172 ppm (see Table 8). However, the differences become large as the nuclei become heavier. For instance, the NR/BP86 calculated value of Ω(Pb) in PbTe is 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 ppm, whereas that derived from the experimental NSR constant is 25
900 ppm, whereas that derived from the experimental NSR constant is 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306 ppm and the DKS/BP86 result is 37612 ppm. This difference is mainly due to the large spin–orbit coupling in PbTe.
306 ppm and the DKS/BP86 result is 37612 ppm. This difference is mainly due to the large spin–orbit coupling in PbTe.
In Table S1 of the ESI,† a comparison of the scalar and SO contributions to the span of all nuclei are presented. In the NR theory, the span derived from the perpendicular and parallel components of the shielding tensors and those derived from the electronic contribution to the calculated NSR constants are identical. This is in line with our expectation since eqn (2) does not consider relativistic effects. However, surprisingly, the values calculated in the presence of only scalar relativistic effects are also similar, indicating that eqn (2) is also valid in the absence of SO effects. The situation is completely different when SO effects are included, making eqn (2) invalid (see Ω and Ciso⊥ of all nuclei calculated using the different methods in Table 6 and Table S1 of the ESI†). For instance, Ω and Ciso⊥ of Pb in PbTe calculated using NR/BP86 are 11900.0 and −11889.4 ppm, and those using SC/BP86 are 16640.1 ppm and −16618.0 ppm, whereas those calculated using DKS/BP86 are 37812.2 ppm and −29940.5 ppm, respectively. These analyses indicate that the previously estimated shielding spans from the experimental NSR (C⊥) constants do not represent the nuclei studied (especially the heavy ones) due to the missing relativistic corrections. This can be explained using the modified version of eqn (2) by including the corresponding relativistic corrections:
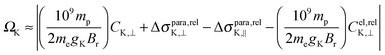 | (3) |
The final shielding spans are determined by adding ΔΩ(rel), the difference between the DKS and NR results, to the accurate non-relativistic CCSD(T) results. Unlike the absolute shielding constants, the final results for the spans using the two functionals do not show considerable differences for most of the molecules, with the exception of Ω(Pb) in PbSe and PbTe which show a very large difference in the results obtained with the two functionals. There is good agreement between the calculated spans and those derived from the experimental NSR constants for the light atoms, whereas the agreement deteriorates as the atoms become heavier. For example, the differences between the final calculated and the experimental results for Ω(Si) and Ω(Se) in SiSe are only 2.6% and 1.4%, respectively; whereas the errors for Ω(Pb) and Ω(Te) in PbTe are 41% and 24%, respectively. Considering the levels of the calculations and the shortcomings of eqn (2), the final shielding spans presented in Table 8 should be accurate.
4. Conclusions
In this contribution, the nuclear spin-rotation and absolute shielding tensors of all nuclei in the XSe and XTe (X = Si, Ge, Sn and Pb) molecules, calculated at the non-relativistic (CCSD(T) and DFT) and four-component relativistic DFT levels of theory, are presented. The final calculated results are obtained by adding the difference between DKS and NR results obtained using either BP86/cv4z or B3LYP/cv4z, Δ(rel), to the non-relativistic CCSD(T) results. The electron correlation effects are more reliably described by coupled-cluster methods than by DFT. Hence, this scheme is used to account for the electron correlation and relativistic effects, giving NSR constants in quite good agreement with the corresponding experimental values.The relativistic effects on the shielding constants are large compared to the effects on the nuclear spin-rotation constants and shielding spans. The final absolute shielding constants obtained by adding the CCSD(T) calculated results to the Δσ(rel) values obtained from BP86 and B3LYP are in good agreement with each other, showing small effects of the functional used to determine Δσ(rel). There is good agreement between the calculated spans and those derived from experiment for the light atoms, whereas the agreement deteriorates as the atoms become heavier. In addition, the relativistic effects in Ω of the light atoms is small, whereas it becomes huge as the atoms become heavier, see Table 6. For most of the molecules studied, including relativistic effects in the calculations leads to a very significant change of the magnetic properties studied. The difference between the electronic contribution to the spin-rotation constant and the paramagnetic contribution to the shielding shows a periodic trend (see Fig. 1). Overall, the shielding constants and spans of all nuclei reported in this study should be more accurate than the previously reported values determined from the experimental NSR constants due to the lack of relativistic corrections when employing eqn (1) and (2). Even though the scheme used in this study is an immediate remedy for these kinds of calculations, the study points to the need for relativistic coupled-cluster methods for the calculation of magnetic properties.
Acknowledgements
This work has received support from the Research Council of Norway through a Centre of Excellence Grant (Grant No. 179568/V30). This work has also received support from the Norwegian Supercomputing program NOTUR (Grant No. NN4654K). I would also like to thank Prof. Kenneth Ruud and the anonymous reviewers for the constructive comments.References
- I. A. Aucar, S. S. Gómez, M. C. Ruiz de Azúa and C. G. Giribet, J. Chem. Phys., 2012, 136, 204119 CrossRef PubMed.
- I. A. Aucar, S. S. Gómez, J. I. Melo, C. C. Giribet and M. C. Ruiz de Azúa, J. Chem. Phys., 2013, 138, 134107 CrossRef PubMed.
- E. Malkin, S. Komorovsky, M. Repisky, T. B. Demissie and K. Ruud, J. Phys. Chem. Lett., 2013, 4, 459–463 CrossRef CAS PubMed.
- N. F. Ramsey, Phys. Rev., 1950, 78, 699–703 CrossRef CAS.
- W. H. Flygare and J. Goodisman, J. Chem. Phys., 1968, 49, 3122–3125 CrossRef CAS.
- W. H. Flygare, J. Chem. Phys., 1964, 41, 793–800 CrossRef CAS.
- W. H. Flygare, Chem. Rev., 1974, 74, 653–687 CrossRef CAS.
- Y. Xiao and W. Liu, J. Chem. Phys., 2013, 138, 134104 CrossRef PubMed.
- Y. Xiao and W. Liu, J. Chem. Phys., 2013, 139, 034113 CrossRef PubMed.
- K. Ruud, T. B. Demissie and M. Jaszuński, J. Chem. Phys., 2014, 140, 194308 CrossRef PubMed.
- M. Jaszuński, T. B. Demissie and K. Ruud, J. Phys. Chem. A, 2014, 118, 9588–9595 CrossRef PubMed.
- T. B. Demissie, M. Jaszuński, E. Malkin, S. Komorovský and K. Ruud, Mol. Phys., 2015, 113, 1576–1584 CrossRef CAS.
- A. M. Teale, O. B. Lutnæs, T. Helgaker, D. J. Tozer and J. Gauss, J. Chem. Phys., 2013, 138, 024111 CrossRef.
- T. Helgaker, J. Gauss, G. Cazzoli and C. Puzzarini, J. Chem. Phys., 2013, 139, 244308 CrossRef PubMed.
- C. Puzzarini, G. Cazzoli, M. E. Harding, J. Vázquez and J. Gauss, J. Chem. Phys., 2009, 131, 234304 CrossRef PubMed.
- T. B. Demissie, M. Jaszuński, S. Komorovsky, M. Repisky and K. Ruud, J. Chem. Phys., 2015, 143, 164311 CrossRef PubMed.
- P. Pyykkö, Annu. Rev. Phys. Chem., 2012, 63, 45–64 CrossRef.
- U. Edlund, T. Lejon, P. Pyykkö, T. K. Venkatachalam and E. Buncel, J. Am. Chem. Soc., 1987, 109, 5982–5985 CrossRef CAS.
- Relativistic Spectroscopy DFT program of authors S. Komorovsky, M. Repisky, V. G. Malkin, O. L. Malkina, M. Kaupp, K. Ruud, with contributions from R. Bast, U. Ekström, M. Kadek, S. Knecht, I. Malkin Ondik, E. Malkin, ReSpect, version 3.3.0, 2014, see http://www.respectprogram.org.
- DIRAC, a relativistic ab initio electronic structure program, Release DIRAC13 (2013), written by L. Visscher, H. J. Aa. Jensen, R. Bast, and T. Saue, with contributions from V. Bakken, K. G. Dyall, S. Dubillard, U. Ekström, E. Eliav, T. Enevoldsen, E. Faßhauer, T. Fleig, O. Fossgaard, A. S. P. Gomes, T. Helgaker, J. K. Lærdahl, Y. S. Lee, J. Henriksson, M. Iliaš, Ch. R. Jacob, S. Knecht, S. Komorovský, O. Kullie, C. V. Larsen, H. S. Nataraj, P. Norman, G. Olejniczak, J. Olsen, Y. C. Park, J. K. Pedersen, M. Pernpointner, K. Ruud, P. Sałek, B. Schimmelpfennig, J. Sikkema, A. J. Thorvaldsen, J. Thyssen, J. van Stralen, S. Villaume, O. Visser, T. Winther and S. Yamamoto, see http://www.diracprogram.org.
- E. J. Baerends, J. Autschbach, A. Berces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, L. Cavallo, D. P. Chong, L. Deng, R. M. Dickson, D. E. Ellis, M. van Faassen, L. Fischer, T. H. Fan, C. Fonseca Guerra, S. J. A. van Gisbergen, J. A. Groeneveld, O. V. Gritsenko, M. Gruning, F. E. Harris, P. van den Hoek, C. R. Jacob, H. Jacobsen, L. Jensen, G. van Kessel, F. Kootstra, E. van Lenthe, D. A. McCormack, A. Michalak, J. Neugebauer, V. P. Osinga, S. Patchkovskii, P. H. T. Philipsen, D. Post, C. C. Pye, W. Ravenek, P. Ros, P. R. T. Schipper, G. Schreckenbach, J. G. Snijders, M. Sola, M. Swart, D. Swerhone, G. teVelde, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. van Wezenbeek, G. Wiesenekker, S. Wolff, T. Woo, A. Yakovlev and T. Ziegler, ADF2014.01, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2014, http://www.scm.com Search PubMed.
- M. Jaszuński, M. Repisky, T. B. Demissie, S. Komorovsky, E. Malkin, K. Ruud, P. Garbacz, K. Jackowski and W. Makulski, J. Chem. Phys., 2013, 139, 234302 CrossRef PubMed.
- S. Komorovsky, M. Repisky, E. Malkin, K. Ruud and J. Gauss, J. Chem. Phys., 2015, 142, 091102 CrossRef PubMed.
- K. Hummer, A. Gruneis and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 195211 CrossRef.
- D. Yu, J. Wu, Q. Gu and H. Park, J. Am. Chem. Soc., 2006, 128, 8148–8149 CrossRef CAS PubMed.
- X. Sun, B. Yu, G. Ng and M. Meyyappan, J. Phys. Chem. C, 2007, 111, 2421–2425 CAS.
- B. M. Giuliano, L. Bizzocchi and J.-U. Grabow, J. Mol. Spectrosc., 2008, 251, 261–267 CrossRef CAS.
- B. M. Giuliano, L. Bizzocchi, R. Sanchez, P. Villanueva, V. Cortijo, M. E. Sanz and J.-U. Grabow, J. Chem. Phys., 2011, 135, 084303 CrossRef PubMed.
- L. Bizzocchi, B. M. Giuliano, M. Hess and J.-U. Grabow, J. Chem. Phys., 2007, 126, 114305 CrossRef PubMed.
- B. M. Giuliano, L. Bizzocchi, S. Cooke, D. Banser, M. Hess, J. Fritzschec and J.-U. Grabow, Phys. Chem. Chem. Phys., 2008, 10, 2078–2088 RSC.
- J. Gauss and J. F. Stanton, J. Chem. Phys., 1995, 102, 251–253 CrossRef CAS.
- J. Gauss and J. F. Stanton, J. Chem. Phys., 1996, 104, 2574–2583 CrossRef CAS.
- CFOUR, a quantum chemical program package written by J. F. Stanton, J. Gauss, M. E. Harding, P. G. Szalay with contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, J. Bomble, L. Cheng, O. Christiansen, M. Heckert, O. Heun, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, D. A. Matthews, T. Metzroth, L. A. Mück, D. P. O'Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen. For the current version, see http://www.cfour.de.
- G. G. Camiletti, A. Canal Neto, F. E. Jorge and S. F. Machado, THEOCHEM, 2009, 910, 122–125 CrossRef CAS.
- P. J. P. de Oliveira, C. L. Barros, F. E. Jorge, A. Canal Neto and M. Campos, THEOCHEM, 2010, 948, 43–46 CrossRef CAS.
- A. Canal Neto and F. E. Jorge, Chem. Phys. Lett., 2013, 582, 158–162 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef , erratum, ibid. 1986, 34, 7406.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- S. Komorovsky, M. Repisky, O. L. Malkina, V. G. Malkin, I. Malkin Ondik and M. Kaupp, J. Chem. Phys., 2008, 128, 104101 CrossRef PubMed.
- S. Komorovsky, M. Repisky, O. L. Malkina and V. G. Malkin, J. Chem. Phys., 2010, 132, 154101 CrossRef PubMed.
- S. Komorovsky, M. Repisky, E. Malkin, T. B. Demissie and K. Ruud, J. Chem. Theory Comput., 2015, 11, 3729–3739 CrossRef CAS PubMed.
- K. G. Dyall, Theor. Chem. Acc., 1998, 99, 366–371 CAS.
- K. G. Dyall, Theor. Chem. Acc., 2006, 115, 441–447 CrossRef CAS , basis sets available from the Dirac web site, http://dirac.chem.sdu.dk.
- K. G. Dyall, Theor. Chem. Acc., 2002, 108, 335–340 CrossRef CAS , erratum, ibid. 2003, 109, 284.
- F. London, J. Phys. Radium, 1937, 8, 397–409 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- P. Manninen, P. Lantto, J. Vaara and K. Ruud, J. Chem. Phys., 2003, 119, 2623–2637 CrossRef CAS.
- J. I. Melo, M. C. Ruiz de Azúa, C. G. Giribet, G. A. Aucar and R. H. Romero, J. Chem. Phys., 2003, 118, 471 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- E. van Lenthe, A. Ehlers and E. J. Baerends, J. Chem. Phys., 1999, 110, 8943–8953 CrossRef CAS.
- E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- E. R. Cohen, T. Cvitaš, J. G. Frey, B. Holmström, K. Kuchitsu, R. Marquardt, I. Mills, F. Pavese, M. Quack, J. Stohner, H. L. Strauss, M. Takami and A. J. Thor, Quantities, Units and Symbols in Physical Chemistry, IUPAC Green Book, 3rd Edition, 2nd Printing, IUPAC & RSC Publishing, Cambridge, 2008 Search PubMed.
- S. Grimme, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Komorovsky, M. Repisky, T. B. Demissie, E. Malkin and K. Ruud, Understanding the atomic nature of the difference between relativistic spin-rotation and NMR shielding constants of the tin atom, unpublished.
- S. Komorovsky, M. Repisky, E. Malkin, K. Ruud and J. Gauss, J. Chem. Phys., 2015, 142, 091102 CrossRef PubMed.
- R. E. Taylor, F. Alkan, D. Koumoulis, M. P. Lake, D. King, C. Dybowski and L. S. Bouchard, J. Phys. Chem. C, 2013, 117(17), 8959–8967 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp07025b |
| This journal is © the Owner Societies 2016 |