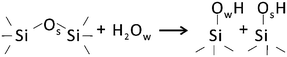Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electron stimulated hydroxylation of a metal supported silicate film†
Xin
Yu
a,
Emre
Emmez
a,
Qiushi
Pan
a,
Bing
Yang
a,
Sascha
Pomp
ab,
William E.
Kaden
a,
Martin
Sterrer
ab,
Shamil
Shaikhutdinov
*a,
Hans-Joachim
Freund
a,
Itziar
Goikoetxea
c,
Radoslaw
Wlodarczyk
c and
Joachim
Sauer
*c
aAbteilung Chemische Physik, Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany. E-mail: shaikhutdinov@fhi-berlin.mpg.de
bInstitut für Physik, Universität Graz, Universitätsplatz 5, 8010 Graz, Austria
cInstitut für Chemie, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. E-mail: js@chemie.hu-berlin.de
First published on 6th January 2016
Abstract
Water adsorption on a double-layer silicate film was studied by using infrared reflection–absorption spectroscopy, thermal desorption spectroscopy and scanning tunneling microscopy. Under vacuum conditions, small amounts of silanols (Si–OH) could only be formed upon deposition of an ice-like (amorphous solid water, ASW) film and subsequent heating to room temperature. Silanol coverage is considerably enhanced by low-energy electron irradiation of an ASW pre-covered silicate film. The degree of hydroxylation can be tuned by the irradiation parameters (beam energy, exposure) and the ASW film thickness. The results are consistent with a generally accepted picture that hydroxylation occurs through hydrolysis of siloxane (Si–O–Si) bonds in the silica network. Calculations using density functional theory show that this may happen on Si–O–Si bonds, which are either parallel (i.e., in the topmost silicate layer) or vertical to the film surface (i.e., connecting two silicate layers). In the latter case, the mechanism may additionally involve the reaction with a metal support underneath. The observed vibrational spectra are dominated by terminal silanol groups (ν(OD) band at 2763 cm−1) formed by hydrolysis of vertical Si–O–Si linkages. Film dehydroxylation fully occurs only upon heating to very high temperatures (∼1200 K) and is accompanied by substantial film restructuring, and even film dewetting upon cycling hydroxylation/dehydroxylation treatment.
1. Introduction
The interaction of silica (SiO2) with water plays an important role in natural processes such as weathering and dissolution. In addition, it is generally accepted that the catalytic performance of silica either as a support or an active phase is primarily determined by surface hydroxo species, which are commonly discussed in terms of isolated silanols (i.e. single silanols, Si–OH, and geminal silanols, Si–(OH)2), and groups of hydrogen-bonded silanols.1,2Because of the structural complexity and diversity of silica, thin silica films supported on metal substrates have been used as suitable model systems.3,4 Using this model approach, well-ordered silica structures have been prepared as monolayer5 and bilayer6 films, with a hexagonal layer of corner-sharing SiO4 tetrahedra as a structural motif. Our previous infrared reflection–absorption spectroscopy (IRAS) and temperature programmed desorption (TPD) studies showed that these silicate films, which are terminated by siloxane bridges (Si–O–Si), are essentially hydrophobic, as the amount of silanol species, that could be formed by water adsorption, accounted for a few percent of the Si atoms available at the surface.7 It therefore appears that the hydroxylation primarily occurs at structural defects. Direct visualization of surface hydroxyls on silica by scanning tunneling microscopy (STM) was achieved so far only on single-layer silicates (silicatenes).8,9 In particular, it was found that preferential adsorption sites for the surface hydroxyls involved Si at the junction nodes of three non-equivalent silica polygons, for example, 5-,6-, and 7-membered rings. This suggests that the coverage of silanols and its spatial distribution could, in principle, be tuned by controllable creation of surface defects.
Driven by technological applications of silica in electronics, defect formation on silica films has been subject of numerous studies focusing on ion implantation and irradiation effects. Basically, irradiation induced damage may consist of vacancies, interstitials, dangling bonds, etc. It was shown, for example, that neutral beam irradiation does not cause preferential sputtering of oxygen from SiO2, whereas an ion beam with the same energy (i.e. 300–500 eV) causes significant preferential sputtering.10 In the case of silica irradiated by high energy (150 keV) Ar+ ions, X-ray photoelectron spectroscopy measurements suggested that a sub-oxide is formed.11
In continuation of our studies of water interaction with silica surfaces, we employ an electron irradiation at low energies (∼200 eV) as a means to enhance and control the degree of hydroxylation of hydrophobic silica surfaces. In principle, two different approaches could be envisioned: (i) irradiation of a silica surface followed by exposure to water, and (ii) irradiation of silica precovered by a thin water film. The second approach is thought to be more efficient if the mechanism were due to the creation of short-living surface defects, which could immediately react with water molecules in proximity, or electron-stimulated activation (dissociation) of the water molecules adsorbed on silica.
Certainly, in a conventional ultra-high vacuum (UHV) setup, water cannot be put onto a solid support as a liquid. Water adsorption at low temperatures results in amorphous solid water (ASW) films.12 A few studies of electron-stimulated reactions on thin ASW films adsorbed on Pt(111) have recently been reported.12–14 It was concluded, that the final reactions leading to the production of molecular oxygen and hydrogen occur at or near the ASW/vacuum interface. However, dissociation of water molecules at the ASW/Pt interface may also contribute to the reactions at the ASW/vacuum interface. The results suggested that mobile electronic excitations are responsible for the reactions at the interfaces, although the mechanisms remain speculative.12 Electron bombardment of physisorbed water may also cause metal oxidation as shown for hydrogenated Si(111) surfaces upon irradiation with low energy electrons (<20 eV). The results suggested that the initial step of the chemisorption process involves the resonant formation of the transient (H2O)˙− species.15 In another example, a disordered aluminum oxide film was formed by 100 eV electrons. It has been suggested that the excitation proceeds via direct electron attachment, leading to dissociative production of an OH radical species, which is very effective for surface oxidation.16 It is noteworthy that chemical reactions on the surface of cosmic ice dust play an important role in chemical evolution in space.17 Also, some reactions resulting in significant amounts of H2O are believed to occur on dust grains, mainly composed of silicates.18
In this work, we show that electron bombardment of a silicate surface covered by an ASW film considerably enhances the surface hydroxylation. The degree of hydroxylation can be tuned by the electron irradiation parameters (e-beam energy, exposure) and the ASW film thickness. We focus in this study on the structural aspects of hydroxyl formation. Density functional theory (DFT) was employed to explain the experimental results and to identify the atomic structure of the hydroxylated silicate films. The precise mechanism of hydroxylation under electron irradiation remains to be established. Nonetheless, the resulting hydroxylated silica surfaces may further be used for studying chemical reactions on silica, in particular, anchoring of catalytically active species.
2. Materials and methods
The experiments were carried out in several ultrahigh vacuum (UHV) chambers. One chamber is equipped with low-energy electron diffraction (LEED, from Omicron), an IRA-spectrometer (Bruker IFS 66v), and an STM (Omicron). The Ru(0001) crystal (8 mm in diameter, 99.99% from MaTeck GmbH) was mounted on an Omicron sample holder, with the temperature measured by a type K (chromel–alumel) thermocouple spot-welded to the edge of the crystal.The second UHV chamber is equipped with LEED (Omicron), IRAS (Bruker IFS 66v), and a differentially pumped quadrupole mass spectrometer (QMS, Hiden 301) for TPD measurements. In this setup, the temperature was measured by a type K thermocouple spot-welded to the back side of the crystal, which was, in turn, spot-welded to a pair of parallel Ta wires used for resistive heating to ∼1300 K as well as cooling to ∼90 K by filling the manipulator rod with liquid nitrogen.
The clean Ru(0001) surface was obtained following several ion sputtering and vacuum annealing cycles. A bilayer silicate film (henceforth, “silicate” film, for brevity) was prepared by vapor deposition of calibrated amounts of Si (99.99% from Goodfellow) onto the 3O(2 × 2)–Ru(0001) surface at ∼100 K in 2 × 10−7 mbar O2 using an e-beam assisted evaporator (EMT3, Omicron). The film was then oxidized in 3 × 10−6 mbar O2 at ∼1200 K.
For electron irradiation, we used a resistively-heated tungsten filament placed ∼1 cm away from the silicate surface. The crystal was biased to the voltage in the range 100–600 V that accelerates electrons from the filament towards the sample. In addition, we used the e-gun of LEED having a beam spot about 1 mm in diameter. To ensure surface homogeneity, the e-beam had to scan the entire surface by moving the sample. Comparison of resulted silica surfaces, irradiated either by a LEED gun or a W filament, showed basically the same effects.
The IRA-spectra were recorded using p-polarized light at an 84° grazing angle of incidence (spectral resolution 4 cm−1). TPD spectra were obtained with a heating rate 3 K s−1.
DFT calculations were performed using the Vienna ab initio simulation package (VASP).19 The calculations have been carried out using a 4 × 4 × 1 Monkhorst–Pack k-point grid. The projector augmented wave method is adopted with a kinetic energy cutoff of 400 eV for the plane-wave basis set. In the case of the bilayer, the Si16O32 unit cell has been used with the following cell parameters a = 1079.22, b = 934.64, c = 2700 pm, α = β = γ = 90°. The Ru(0001) substrate was modeled with five Ru layers. The Perdew–Burke–Ernzerhof (PBE) exchange correlation functional is employed.20
For the hydrated silica bilayer, low energy minimum structures have been obtained in the following way. First, a genetic algorithm (GA)21 has been used. Two hydrogen atoms and one oxygen atom have been added to the bilayer with the atoms of the bottom layer kept frozen. A function has been implemented in the algorithm that penalizes the existence of water molecules. Each time GA identifies a water molecule it will add a huge constant value to the energy associated to this structure, so that this candidate will be removed from the next population presented to the algorithm. The GA run generated 1000 structures, of which only 30 corresponded to dissociated water molecules. Afterwards, the most stable hydroxylated structures were fully optimized including the atoms of the bottom layer. Additional starting structures for local optimization have been manually generated assuming hydroxylation of vertical Si–O–Si bonds.
Harmonic vibrational frequencies have been calculated using a finite difference method with 0.02 Å displacements of the atoms in each Cartesian direction. The intensities were obtained from the derivatives of the dipole moment component perpendicular to the surface. Simulations for different isotopes were performed using the in-house THERMO code.
To compensate for systematic errors of DFT and neglected anharmonicities the calculated harmonic frequencies have been scaled by a factor f derived for the arithmetic mean of the symmetric (s) and antisymmetric (a) OH stretching frequencies as ratio of experimental (ν), and calculated values (ω), i.e. f = ½(νs + νa)/½(ωs + ωa). Table S1 in the ESI† shows the scaling factors for H16O (0.9814), D16O (0.9951) and D18O bonds (0.9952), together with the calculated and experimental results from which they are derived. The scaling factor for the Si–O stretching vibrations (1.0341) has been derived from experimental and calculated frequencies for α-quartz as described in ref. 6.
3. Results and discussion
3.1. Experimental results
Water (D2O) adsorption at ∼100 K on the “as grown” silicate film and subsequent heating to 300 K only results in a small signal at 2763 cm−1 assigned to ν(OD) vibrations of silanol (Si–OD) species (Fig. 1, black line). The phonon bands at 1300 and 693 cm−1, which are associated with vibrations of the siloxane (Si–O–Si) bonds oriented normal and parallel to the film surface, respectively,6 remain practically unaltered. For direct comparison, the same sample was again covered by the ASW film and then bombarded by 150 eV electrons. As in previous studies of ASW/Pt(111),14 we found that electrons efficiently sputter the ASW film. The ASW related bands attenuate with increasing beam exposure time and almost disappear. After we flashed the sample to 300 K to desorb remaining water, the IRA spectra revealed a much stronger ν(OD) signal (Fig. 1, red line). Using a hydroxylated single layer silicate film for calibration9 we roughly estimated the OD coverage in this sample to be ∼15% with respect to the Si atoms in the top layer. (Note that such an estimate based on the IR band intensity gives the low limit, as some hydroxyls become “invisible” in IRA-spectroscopy if oriented parallel to the surface). The considerable surface hydroxylation is also reflected by strong attenuation of the silica phonon bands and their shift to lower frequencies, in this case to 1271 and 668 cm−1, respectively. In addition, a new band at ∼960 cm−1 appears upon hydroxylation. Such a band is typical for vibrations including Si–O bonds in silanols.1 It is also instructive to recall that a monolayer silicate film on Ru(0001) exhibits a principal phonon band at ∼1135 cm−1, while three-dimensional silica particles and “thick” silica films are characterized by an asymmetrical broad band centered at ∼1250 cm−1.22 Therefore, the IRAS results indicate that the bilayer structure of the silicate film is maintained upon electron stimulated hydroxylation.Fig. 2 compares room temperature STM images of the “as grown” silicate film and the film after e-beam assisted hydroxylation. Although atomic resolution could not yet be achieved, the irradiated film displays a planar morphology and does not dewet under these conditions (otherwise it would result in three-dimensional particles and clusters), in full agreement with the IRAS results. Not surprisingly, the corrugation amplitude on the hydroxylated film terraces is much larger when compared to the pristine film (i.e. 0.7 Å vs. 0.2 Å), measured by STM at similar tunneling conditions. Therefore, we conclude that irradiation of an ASW/silicate surface with low energy electrons promotes surface hydroxylation without destroying the principal (bilayer) structure of a silicate film.
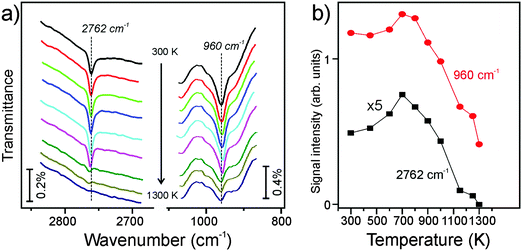
In the next set of experiments, we examined the thermal stability of the silanol species by measuring IRA spectra after the hydroxylated film was flashed to stepwise increasing temperatures. The spectra in the 2760 and 960 cm−1 regions are shown in Fig. 3a, and the integral intensities of the two bands as a function of annealing temperature are shown in Fig. 3b. Clearly, both bands behave very similarly with temperature: the signals first gain some intensity on heating to 700 K before they strongly attenuate above 1100 K and ultimately disappear after heating to temperatures as high as 1300 K. Concomitantly, the principal silica phonons gradually shift back, but never to the same intensity and frequency as observed for the “as prepared” film (Fig. S1 in the ESI†). The effect depends on the degree of hydroxylation: the higher the density of silanols, the less recoverable was the structure. This finding indicates that dehydroxylation of an OD-containing silicate film by UHV annealing considerably alters the original structure of the film in that the number of Si–O–Si bonds linking top and bottom silicate layers was reduced. Also, it is worth mentioning that the 960 cm−1 band partially remains, although at a lower intensity, after final annealing at 1300 K for 5 min, whereas the OD species completely disappeared (see Fig. 3a). Therefore, this band may have another origin beside the Si–O bond vibrations in silanols.
The experiments at various exposure conditions on different samples revealed that the amount of silanol species, as judged by IRAS, considerably depends on the e-beam energy and exposure time as well as the nominal thickness of the bombarded ASW film. Therefore, one may tune, in principle, the degree of surface hydroxylation of the otherwise hydrophobic silicate surface by using low energy electrons. Certainly, the precise mechanism of hydroxylation under electron irradiation needs further investigations. In the following, we focus on establishing the atomic structure of the hydroxylated films.
It is generally accepted that hydroxylation of silica proceeds via “opening” of siloxane bonds2 as shown schematically below:
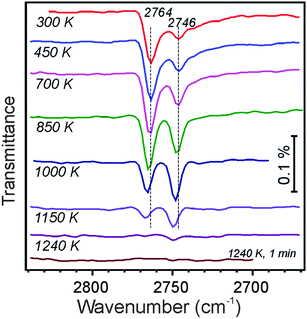
Following these ideas, we carried out water adsorption experiments on silicate films prepared with 18O2. The Si18O2 film was exposed to D216O at ∼100 K, then irradiated with 150 eV electrons, and heated in UHV to 300 K. The top spectrum in Fig. 4 reveals two bands in the ν(OD) region, i.e. at 2764 and 2746 cm−1, which may be assigned to 16OD and 18OD species, respectively, on the basis of a reduced mass analysis. Although the presence of two OD species nicely agrees with the above-shown scheme, the intensity of the 16OD signal (i.e., with oxygen from adsorbed water) is considerably higher than of 18OD (i.e., with oxygen in silicate). Also upon heating, the two bands behave differently (Fig. 4). Up to ∼700 K, the integral intensities of the bands stay fairly constant, although the widths of the bands decrease. Upon further heating, the 2764 cm−1 signal attenuates, whereas the 2746 cm−1 band gains intensity, so that it becomes even larger than the peak at 2764 cm−1. Both bands attenuate at T > 1000 K, and ultimately disappear upon heating to 1240 K. One has to bear in mind, however, that the intensity of IRA bands on metal supported films depends not only on the total amount of IR absorbing oscillators, but also on their orientation with respect to the metal surface normal.31 Therefore, spectral changes may also be affected by structural relaxations (transformations).
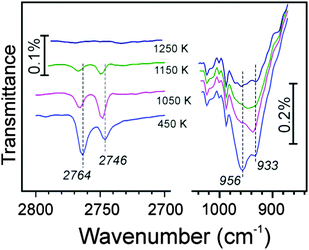
Again, as in the previous experiments with 16O-prepared films, we took a closer look at the ∼960 cm−1 band. Although this spectral region somewhat suffered from baseline instabilities, and the signals are much broader than in the ν(OD) region, Fig. 5 shows that the phonon frequency follows the oxygen isotope that is involved in O-D vibrations: the 2764 cm−1 band basically correlates with the one at 956 cm−1, and the 2746 cm−1 band – with the one at 933 cm−1. A linear correlation, observed between intensities of the ν(OD) and corresponding phonon bands, provides strong evidence that the ∼960 cm−1 band originates from Si–O bond vibrations in respective silanols.
To complement the IRAS results, we performed TPD measurements. Dehydroxylation of oxide surfaces usually proceeds through desorption of water via recombination of hydroxo species, although it is case sensitive.32Fig. 6 compares desorption traces for selected masses (20 amu (D2O) and 4 amu (D2)) obtained on two samples. The red curves show signals from the ASW/silica surface irradiated with 150 eV electrons and then annealed at 200 K for 5 min prior to the TPD run. The black curves correspond to the sample that was not irradiated.
Firstly, we note a large amount of D2 desorbing at 200–450 K, which turned out to be only ∼20% smaller than observed in the blank experiment on the silica-free, clean Ru sample under the same conditions (not shown here). As D2 has only been observed on the irradiated samples, this suggests that electron bombardment of an ASW film produces D (or D2) which may react with the support. Secondly, the comparison shows that irradiated silicate samples exhibit desorption of considerably larger amounts of water (D2O). Although desorption traces at low temperatures may, to some extent, be affected by well-known low pumping speed for water resulting in long desorption tails, there is definitely an additional desorption signal between 500 and 700 K, which is missing on the non-irradiated sample. Note that this is the temperature region where in the corresponding IRA spectra the ν(OD) band becomes sharper and the low-frequency tail disappears and (Fig. 3–5). Finally, at temperatures above 900 K, both D2O and D2 desorption peaks are observed, which cannot be assigned to cracking (fragmentation) patterns of the two molecules in the mass-spectrometer. The shared high-temperature desorption thresholds for D2 and D2O (∼1020 K) suggest that both processes are directly limited by the energy needed to overcome the silica-bound D diffusion barrier. Since, as mentioned above, one expects the silica dehydroxylation to occur through water desorption, the simultaneous D2 formation is indicative of the D spillover onto the Ru surface and subsequent recombinative desorption.
3.2. Computational results
In principle, two types of Si–O–Si bonds are present in a double-layer silicate film, the hydrolysis of which results in silanol species: those lying almost parallel to the film surface, and those linking the top and bottom silicate layers. In the case of breaking “in-plane” Si–O–Si bonds, the resulting two silanol species are at the surface (structure Ia in Fig. 7). Another scenario includes breaking of the Si–O–Si linkage between the silicate layers and a vertical distortion of the upper Si out of the surface plane upon forming an OD bond (structure Ib in Fig. 7). The hydroxylated Si–O–Si bond of structure Ia is part of a six-membered ring (parallel to the surface) and a four-membered ring (normal to the surface), whereas it is part of three four-membered rings in structure Ib. In addition to this mechanism I, which is basically the same as assumed for bulk silica surfaces and all-silica zeolites, another mechanism II is possible for a metal supported silicate film, which additionally involves a redox step: hydrogen is produced, and the Ru surface is partially oxidized. The structure involves an inverted SiO4 tetrahedron in the bottom layer with one O atom forming a bond to the Ru substrate (structure II, Fig. 7).| Mechanism I H2O + [Si–O–Si]SiO2/Ru → [SiOH,SiOH]SiO2/Ru | (1) |
| Mechanism II H2O + [Si–O–Si]SiO2/Ru → [SiORu,SiOH]SiO2/Ru + ½H2 | (2) |
 | ||
| Fig. 7 Top (a) and side (b) views of the pristine silica bilayer. Top (c) and side (d) views of the hydroxylation structure Ia. (e) Side view of the hydroxylated structure Ib. (f) Side view of the structure II that forms a Si–O–Ru bridge to the Ru surface. Si, O and Ru atoms are shown in yellow, red, and gray, respectively. The O (or H for a H-precovered model, see Table 1) atoms only adsorbed on the Ru(0001) surface are shown in blue. | ||
We use the term “mechanism” here, but this does not imply a simulation of the formation process. We use the term to stress the formation of different final structures. While structure Ia has been found using a genetic algorithm (see Materials and methods), starting structures for Ib and II have been generated by chemical consideration and then locally optimized.
It is well established that the “as prepared” silicate films always contain some oxygen atoms adsorbed directly onto a Ru substrate.33 On the other hand, the above-presented TPD results suggest that the Ru surface becomes partly covered by H(D) atoms upon electron stimulated hydroxylation. Since it is still unclear whether the intercalation occurs before, after, or simultaneously with silica hydroxylation, we performed calculations for different oxygen and hydrogen coverage on Ru, that is with 2 and 6 oxygen (hydrogen) atoms per orthogonal (2 × 2) unit cell, corresponding to O(H)(2 × 2)- and 3O(H)(2 × 2)-Ru(0001) surfaces, respectively.
Fig. 7 depicts the DFT-optimized hydroxylated structures Ia, Ib, and II. Table 1 shows the reaction energies computed for these models. Mechanism II, involving hydrolysis of a vertical siloxane bond, followed by the interlayer oxygen flipping and binding to the Ru surface, is the most favorable structure for an initially clean Ru surface underneath the silicate film. The reaction is exothermic by ∼30 kJ mol−1. Structure II remains favorable for Ru with low coverage of oxygen or hydrogen. However, at higher O(H) coverages, structure II becomes less stable than structures Ia and Ib, because adatoms on Ru suppress binding of the Si–O fragment.
Note that for the O pre-covered Ru surface, there is an additional driving force for the formation of type II structures: the hydrogen atoms produced in the reaction (2) may further react with O atoms on Ru to form water:
 | (3) |
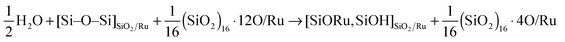 | (4) |
Table 2 shows the computed interatomic distances and stretching frequencies of the different hydroxyl groups present in the respective structures for the hydroxylated silica film on the clean and O(2 × 2)-covered Ru surfaces. In the following, we will refer to numbers for the clean interface only, because the differences in the calculated values for the various models are such that a comparison with experiment would not affect the conclusions drawn. For comparison, Table 2 also shows the results for isolated terminal OH groups obtained within a periodic edingtonite (EDI)-derived surface model previously suggested in ref. 34 (see Fig. S3, ESI†).
| d OH | ν OH | ν OD | ΔνODc | 〈μz〉2 | |
|---|---|---|---|---|---|
| a Scaled (0.9814). b Scaled (0.9951). c With respect to ν(OD) on EDI. | |||||
| Ia: O1D1 |
97.10
97.13 |
3707
3702 |
2736
2733 |
−31
−34 |
0.36
0.41 |
| Ia: O2D2 |
97.45
97.61 |
3637
3617 |
2683
2668 |
−84
−99 |
0.45
0.43 |
| Ib: OhDh |
97.56
97.63 |
3589
3579 |
2647
2640 |
−120
−127 |
3.15
3.19 |
| Ib: OtDt |
96.98
96.82 |
3737
3757 |
2757
2772 |
−10
+5 |
3.03
3.19 |
| II: OtDt |
97.00
96.77 |
3733
3764 |
2755
2778 |
−12
+11 |
2.98
3.18 |
| EDI: OtDt | 96.91 | 3749 | 2767 | — | — |
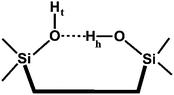
Before we proceed to an analysis of the DFT results presented in Table 2, it is instructive to recall that isolated silanol groups with an IR band around 3750 cm−1 are always present on amorphous silica as well as at crystalline surfaces, e.g. on the outer surfaces of zeolite crystallites. For example, for the high-silica (Si/Al = 25) zeolite H-ZSM-5, such a band is observed at 3745 cm−1 (2759 cm−1 for the D-ZSM-5 counterpart).35 Unclosed Si–O–Si bonds in zeolite frameworks give rise to “internal silanols”36 which most likely exist as vicinal silanol groups with a terminal (OHt) and a hydrogen bonded (OHh) species as shown below:37,38
The results in Table 2 show that both hydroxyl groups belonging to structure Ia are engaged as donor groups in hydrogen bonds, which are weak for O1D1 and stronger for O2D2. Their computed frequencies (2733 and 2668 cm−1, respectively) deviate significantly from the experimentally observed one at 2762 cm−1 (Fig. 3). Note, however, that due to their bond orientation, which is almost parallel to the surface, the IRA signal intensity (which is proportional to the dipole moment change along the surface normal, 〈μz〉 in Table 2) is one order of magnitude lower than for silanols which are oriented perpendicular to the surface. Those are the terminal SiOtHt groups in structures Ib and II with calculated frequencies, 2772 and 2778 cm−1, respectively, which are also close to the calculated value for terminal silanols in the edingtonite model (2767 cm−1) and to the experimentally observed value (2759 cm−1) in H-ZSM-5.35 The agreement is slightly better for model Ib. Structure Ib features another silanol group, Si–OhDh, for which we predict a sizable intensity at 2640 cm−1, and which is definitely missing in the IRA-spectra. However, this band may escape detection because hydroxyl groups engaged in hydrogen bonds are well-known for band broadening40 (Fig. S2, ESI†). Accordingly, the bands around 960 cm−1 (Fig. 3) can be assigned to stretching vibrations of the Si–O bond in the terminal silanols. Transitions with significant intensity are calculated at 937 cm−1 for model Ib and at 933 and 950 cm−1 for model II (Table 3, and Tables S5 and S6 in ESI†). Note that in the normal modes, the Sit–Ot bond stretching vibrations of structures II and Ib are coupled with antiphase (Sia–O3Ru)as and in-phase Sia–Oh stretching vibrations, respectively.
| II: OtDt | (Sit–Ot) + (Sia–O3Ru)asb | Ib: OtDt | OhDh | (Sit–Ot) + (Sia–Oh)b | |
|---|---|---|---|---|---|
| a Scaling factor for OD vibrations – 0.995, for Si–O vibrations – 1.0341. (O16D = 0.9951 and O18D = 0.9952). b Shown in parenthesis is 〈μz〉2 (in Debye2 Å−2 amu−1). | |||||
| 16OtDt/Si16O2 |
2755
2778 |
1012 (141) + 934 (65)
950 (48) + 933 (69) |
2757
2772 |
2647
2640 |
931 (85)
937 (85) |
| 16OtDt/Si18O2 |
2755
2778 |
970 (128) + 932(64)
948 (48) + 898 (60) |
2757
2772 |
2631
2624 |
941 (14) + 923 (66)
945 (31) + 923 (47) |
| 18OtDt/Si18O2 |
2738
2761 |
970 (131) + 907 (64)
923 (46) + 898 (66) |
2741
2755 |
2631
2624 |
905 (81)
910 (81) |
A DFT-based interpretation on the IRA spectra obtained in experiments with mixed isotopes (D216O adsorption on Si18O2, Fig. 4) is more difficult. Table 3 shows the results of calculations for 16OtDt/Si18O2 and 18OtDt/Si18O2 models to be compared with the above-presented results on 16OtDt/Si16O2 models. As expected, the OD stretching frequency in the terminal, Si–OtDt silanol is determined solely by the oxygen isotope involved in the hydroxyl group. The corresponding isotopic shift obtained for structures II and Ib is 17 cm−1, which nicely agrees with the experimentally observed band splitting (∼18 cm−1, Fig. 4). Substitution by 18O isotope in the silicate film causes a red-shift of the ν(OhDh) band as well (by 16 cm−1 as computed), independent of the oxygen isotope in terminal OtDt. However, as discussed above, this band may escape detection due to spectral broadening caused by hydrogen bonding.
The calculations for the IRAS active vibrations of Si–O bonds involved in silanols also revealed band splitting for the mixed O isotopes (see Table 3, full results are summarized in Tables S4–S9 in the ESI†). For example, for the structure II, in-phase and antiphase coupling of the Sit–16Ot stretching mode with the (Sia–18O3–Ru)as stretching mode results in two bands with nearly equal intensity at 948 and 898 cm−1, respectively. The band splitting (50 and 22 cm−1, for models II and Ib, respectively) is of the same order as the one observed experimentally (∼23 cm−1, i.e. 956 and 933 cm−1, Fig. 5). Note, however, that the experimental signals in this spectral region are much broader than in the ν(OD) one and that the spectra additionally suffer from baseline instability. As a conclusion, the results for the ν(Si–O) vibrations can hardly be used to decide which model fits best, but the observations do not contradict the assignment based on the ν(OD) bands.
3.3. Discussion
According to the hydroxylation energies presented in Table 1, the relative stabilities of the three considered structures depend on the amount of O(H) atoms adsorbed directly onto the Ru surface. The TPD results (Fig. 6) show that a considerable amount of hydrogen (deuterium) is produced during electron-assisted hydroxylation, which could in part be chemisorbed on the Ru surface below the hydroxylated silica film. The fact, that D2 desorption is observed only on irradiated samples, agrees well with electron stimulated hydrogen formation reported for the ASW/Pt(111) interface,14 although the mechanism remains unclear. Apparently, electron bombardment produces D (or D2) which may reach the Ru surface, although covered by a silicate film, as small molecules may penetrate the silicate layer and intercalate the interface.41 The formation of silanols solely by atomic D, if the latter is produced by electrons, can be excluded as this would result in OD involving only silica lattice oxygen, which is not observed in isotopic experiments (Fig. 4). If the Ru surface is covered with H(D), structure Ia appears to be the most stable one. In favor of structure Ia is the experimental fact that the phonon band at ∼693 cm−1, which involves bending vibrations of in plane O–Si–O bonds, is affected to a much larger extent as compared to the high-frequency band at 1300 cm−1 (Fig. 1) associated solely with vertical Si–O–Si linkages involved in structures Ib and II. However, according to the DFT calculations, IRAS cannot precisely identify the structure Ia, because the corresponding hydroxyls (O1D1 and O2D2) are oriented nearly parallel to the surface. Nonetheless, SiO1D1 species, which are only involved in weak H bonding and thus exhibit a moderate red-shift (to 2733 cm−1 as computed), are to be detected, if they are present in a considerably large amount. A long tail (down to ∼2720 cm−1) at the low-frequency side of the principal peak, which is always present in spectra of “as prepared” hydroxylated films at 300 K, could tentatively be assigned to such SiO1D1 silanols. Additional support for the presence of structure Ia comes from the TPD results, which showed that the disappearance of the low-frequency tail in IRAS is accompanied by water desorption between 500 and 700 K. The process leading to water desorption may, therefore, be attributed to the recombination of O1D1 and O2D2 silanols upon heating.On the basis of DFT results, a principal IRA band at 2763 cm−1 can be assigned to the terminal OtDt groups formed on top of the silicate layer in the models Ib and II, for which the calculations for the silicate film on the pure Ru surface predict wavenumbers of 2772 and 2778 cm−1, respectively. Another silanol group, SiOhDh, formed in structure Ib is strongly red-shifted (2640 cm−1) and most likely escapes detection because hydroxyl groups engaged in hydrogen bonds are well-known for their band broadening (see Fig. S2 in ESI† for a quantitative estimate).40 The above assignment is further supported by the agreement between the isotopic shift of 17 cm−1 calculated for 16OtDt/Si18O2 and 16OtDt/Si16O2 models of structures Ib and II, respectively, with the experimentally observed band splitting of ∼18 cm−1 (Fig. 4). To explain the isotopic experiments based on models Ib or II, i.e. the observation of two species, 16OtDt and 18OtDt, we have to consider that 16O oxygen in the water readily exchanges with 18O oxygen in the silicate film upon water D216O dissociation under electron bombardment.
Although Si–OhDh silanol, formed in structure Ib, is predicted to be invisible in IRAS, it seems to manifest itself in TPD experiments. Indeed, upon heating to high temperatures, this silanol may react with Ru to form structure II and D atoms, with the latter immediately desorbing as D2 at ∼1020 K (Fig. 6). The progressive formation of Si–O–Ru linkages also explains why dehydroxylation by UHV annealing at high temperatures never recovers the original phonon spectrum of the silica film. Also, the vibrations of the formed Si–O–Ru linkage fall into the same range as the band at 960 cm−1 which does not completely disappear from the spectra upon dehydroxylation (Fig. 3). Certainly, recombination of different types of hydroxyls at very high temperatures may be a stochastic process, accompanied by structural transformations, which results in a complex spectral evolution of the related OD bands on heating (Fig. 6). It appears, however, that dehydroxylation of silicate films is not the reverse process of hydroxyl formation. Repeated hydroxylation over the once dehydroxylated film leads to a further red-shift of the principal phonon, and ultimate disintegration (de-wetting) of the silica film after few cycles.
4. Conclusions
Electron bombardment of a double-layer silicate film covered by ice (amorphous solid water) greatly enhances the degree of hydroxylation of this otherwise hydrophobic silica surface. The results are consistent with the generally accepted picture that hydroxylation occurs through siloxane bond breaking in the silica network. Hydroxyls formed by hydrolysis of “in plane” Si–O–Si bonds are hardly visible in IRAS, but give rise to water desorption at lower temperatures (500–700 K). In the case of “vertical” Si–O–Si bond cleavage, the terminal silanol is standing upright at the surface, whereas the second hydroxyl is “buried” in the silica film and is invisible in IRAS, but may react with a metal substrate underneath to form a Si–O–Ru linkage.Our preliminary experiments with Ar+ irradiation at ∼500 eV (using a sputter gun) instead of electron irradiation also lead to an enhanced hydroxylation of the silica film, but very mild conditions have to be chosen in order to avoid sputtering of the entire silica film.42
Besides the fundamental understanding of irradiation effects on ice covered substances in troposphere and space, in general, electron (and ion) irradiation of ice covered silica surfaces provides a well-suited tool to create surface hydroxyls randomly distributed over the silica surface and to control their abundance. These hydroxylated films may be used further for studying anchoring of active species on silica surfaces and subsequent reactions.
Acknowledgements
The work was supported by Deutsche Forschungsgemeinschaft through SFB 1109 and German Israeli Foundation (Grant No. 1236) as well as by grants for computing time at the high-performance computer centers HLRN (North-German Supercomputing Alliance in Berlin and Hannover). MS acknowledges funding from the European Research Council (FP7), ERC Grant agreement no. 280070, STRUBOLI. WK thanks the Alexander von Humboldt Foundation for the fellowship.References
- L. T. Zhuravlev, Colloids Surf., A, 2000, 173, 1 CrossRef.
- A. Rimola, D. Costa, M. Sodupe, J.-F. Lambert and P. Ugliengo, Chem. Rev., 2013, 113, 4216 CrossRef PubMed.
- S. Shaikhutdinov and H.-J. Freund, Adv. Mater., 2013, 25, 49 CrossRef PubMed.
- C. Büchner, L. Lichtenstein, X. Yu, J. A. Boscoboinik, B. Yang, W. E. Kaden, M. Heyde, S. K. Shaikhutdinov, R. Włodarczyk, M. Sierka, J. Sauer and H.-J. Freund, Chem. – Eur. J., 2014, 20, 9176 CrossRef PubMed.
- J. Weissenrieder, S. Kaya, J. L. Lu, H. J. Gao, S. Shaikhutdinov, H. J. Freund, M. Sierka, T. K. Todorova and J. Sauer, Phys. Rev. Lett., 2005, 95, 076103 CrossRef PubMed.
- D. Löffler, J. J. Uhlrich, M. Baron, B. Yang, X. Yu, L. Lichtenstein, L. Heinke, C. Büchner, M. Heyde, S. Shaikhutdinov, H. J. Freund, R. Włodarczyk, M. Sierka and J. Sauer, Phys. Rev. Lett., 2010, 105, 146104 CrossRef PubMed.
- B. Yang, E. Emmez, W. E. Kaden, X. Yu, J. A. Boscoboinik, M. Sterrer, S. Shaikhutdinov and H. J. Freund, J. Phys. Chem. C, 2013, 117, 8336 CAS.
- B. Yang, J. A. Boscoboinik, X. Yu, S. Shaikhutdinov and H.-J. Freund, Nano Lett., 2013, 13, 4422 CrossRef CAS PubMed.
- B. Yang, S. Shaikhutdinov and H.-J. Freund, J. Phys. Chem. Lett., 2014, 5, 1701 CrossRef CAS PubMed.
- T. Mizutani, J. Non-Cryst. Solids, 1995, 181, 123 CrossRef CAS.
- B. Garrido, J. Samitier, S. Bota, C. Domínguez, J. Montserrat and J. R. Morante, J. Non-Cryst. Solids, 1995, 187, 101 CrossRef CAS.
- R. S. Smith, N. G. Petrik, G. A. Kimmel and B. D. Kay, Acc. Chem. Res., 2011, 45, 33 CrossRef PubMed.
- N. G. Petrik, A. G. Kavetsky and G. A. Kimmel, J. Phys. Chem. C, 2006, 125, 124702 CrossRef PubMed.
- N. G. Petrik and G. A. Kimmel, J. Chem. Phys., 2005, 123, 054702 CrossRef PubMed.
- D. Klyachko, P. Rowntree and L. Sanche, Surf. Sci., 1996, 346, L49 CrossRef CAS.
- H. D. Ebinger and J. T. Yates Jr, Surf. Sci., 1998, 412–413, 1 CrossRef.
- N. Watanabe and A. Kouchi, Prog. Surf. Sci., 2008, 83, 439 CrossRef CAS.
- D. Jing, J. He, M. Bonini, J. R. Brucato and G. Vidali, J. Phys. Chem. A, 2013, 117, 3009 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- R. Włodarczyk, M. Sierka, K. Kwapień, J. Sauer, E. Carrasco, A. Aumer, J. F. Gomes, M. Sterrer and H.-J. Freund, J. Phys. Chem. C, 2011, 115, 6764 Search PubMed.
- B. Yang, W. E. Kaden, X. Yu, J. A. Boscoboinik, Y. Martynova, L. Lichtenstein, M. Heyde, M. Sterrer, R. Wlodarczyk, M. Sierka, J. Sauer, S. Shaikhutdinov and H.-J. Freund, Phys. Chem. Chem. Phys., 2012, 8336 Search PubMed.
- S. Bordiga, P. Ugliengo, A. Damin, C. Lamberti, G. Spoto, A. Zecchina, G. Spanò, R. Buzzoni, L. Dalloro and F. Rivetti, Top. Catal., 2001, 15, 43 CrossRef CAS.
- B. A. Morrow and I. A. Cody, J. Phys. Chem., 1976, 80, 1995 CrossRef CAS.
- B. A. Morrow, I. A. Cody and L. S. M. Lee, J. Phys. Chem., 1976, 80, 2761 CrossRef CAS.
- B. C. Bunker, D. M. Haaland, T. A. Michalske and W. L. Smith, Surf. Sci., 1989, 222, 95 CrossRef CAS.
- B. C. Bunker, D. M. Haaland, K. J. Ward, T. A. Michalske, W. L. Smith, J. S. Binkley, C. F. Melius and C. A. Balfe, Surf. Sci., 1989, 210, 406 CrossRef CAS.
- A. M. Ferrari, E. Garrone, G. Spoto, P. Ugliengo and A. Zecchina, Surf. Sci., 1995, 323, 151 CrossRef CAS.
- V. Bolis, C. Busco, S. Bordiga, P. Ugliengo, C. Lamberti and A. Zecchina, Appl. Surf. Sci., 2002, 196, 56 CrossRef CAS.
- J. Sauer, P. Ugliengo, E. Garrone and V. R. Saunders, Chem. Rev., 1994, 94, 2095 CrossRef CAS.
- F. M. Hoffmann, Surf. Sci. Rep., 1983, 3, 107 CrossRef CAS.
- M. A. Henderson, Surf. Sci. Rep., 2002, 46, 1 CrossRef CAS.
- R. Włodarczyk, M. Sierka, J. Sauer, D. Löffler, J. J. Uhlrich, X. Yu, B. Yang, I. M. N. Groot, S. Shaikhutdinov and H. J. Freund, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 085403 CrossRef.
- B. Civalleri, S. Casassa, E. Garrone, C. Pisani and P. Ugliengo, J. Phys. Chem. B, 1999, 103, 2165 CrossRef CAS.
- K. Chakarova and K. Hadjiivanov, J. Phys. Chem. C, 2011, 115, 4806 CAS.
- G. L. Woolery, L. B. Alemany, R. M. Dessau and A. W. Chester, Zeolites, 1986, 6, 14 CrossRef CAS.
- A. J. Van Roosmalen and J. C. Mol, J. Phys. Chem., 1979, 83, 2485 CrossRef CAS.
- J. Sauer and A. Bleiber, Catal. Today, 1988, 3, 485 CrossRef CAS.
- S. Bordiga, L. Regli, D. Cocina, C. Lamberti, M. Bjørgen and K. P. Lillerud, J. Phys. Chem. B, 2005, 109, 2779 CrossRef CAS PubMed.
- C. M. Huggins and G. C. Pimentel, J. Phys. Chem., 1956, 60, 1615 CrossRef CAS.
- E. Emmez, B. Yang, S. Shaikhutdinov and H.-J. Freund, J. Phys. Chem. C, 2014, 118, 29034 CAS.
- B. Yang, S. Shaikhutdinov, H.J. Freund, unpublished.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp06852e |
| This journal is © the Owner Societies 2016 |