Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Atomic scale insights into urea–peptide interactions in solution†
Nicola
Steinke
a,
Richard J.
Gillams
a,
Luis Carlos
Pardo
b,
Christian D.
Lorenz
*c and
Sylvia E.
McLain
 *a
*a
aDepartment of Biochemistry, University of Oxford, Oxford OX1 3QU, UK. E-mail: sylvia.mclain@bioch.ox.ac.uk
bDepartament de Física i Enginyeria Nuclear, Escola Tècnica Superior d'Enginyeria Industrial de Barcelona (ETSEIB), Universitat Politècnica de Catalunya, 08028 Barcelona, Catalonia, Spain
cDepartment of Physics, King's College London, London WC2R 2LS, UK. E-mail: c.lorenz@kcl.ac.uk
First published on 7th January 2016
Abstract
The mechanism by which proteins are denatured by urea is still not well understood, especially on the atomic scale where these interactions occur in vivo. In this study, the structure of the peptide GPG has been investigated in aqueous urea solutions in order to understand the combination of roles that both urea and water play in protein unfolding. Using a combination of neutron diffraction enhanced by isotopic substitution and computer simulations, it was found, in opposition with previous simulations studies, that urea is preferred over water around polar and charged portions of the peptides. Further, it appears that while urea directly replaces water around the nitrogen groups on GPG that urea and water occupy different positions around the peptide bond carbonyl groups. This suggests that urea may in fact weaken the peptide bond, disrupting the peptide backbone, thus ultimately causing denaturation.
1 Introduction
It has long been known that proteins unfold in the presence of urea in vitro.1 There are a multiplicity of theories as to how the presence of this small molecule denatures these relatively large macromolecules, yet there is no consensus on the mechanism by which this occurs. There are two broad categories of current theories concerning this process on an atomistic level – “direct” and “indirect” denaturation. The so-called “indirect” model suggests that urea disrupts or interferes with the water structure surrounding the protein which indirectly leads to a loss in its stability. One proposed mechanism for this is that urea indirectly “dries” the protein thus lowering the protein hydration and weakening the hydrophobic effect.2Compared with theories which support an “indirect” mechanism, there are a much larger number of “direct” theories, investigations which support the direct denaturation of proteins by urea propose a variety of preferred urea–protein interactions sites – the protein backbone,3 the side chains,4 hydrophobic5 or polar and charged residues6 have all been suggested as the sites where denaturation is initialized. Stepwise denaturation processes of proteins by urea have also been proposed, where Hua et al. have suggested that once urea has expelled the first hydration layer around the protein, the hydrophobic core is penetrated by urea as opposed to water.7,8 This is contrary to other investigations which found that the hydrophobic core was preferentially solvated by water in the first instance.9
Despite this relatively wide range of computational studies, there is little experimental information concerning how urea molecules interact with different components of proteins on the atomic scale as these interactions can only be probed via techniques which measure on the order of angstroms (10−10 m Å). While NMR does provide some experimental evidence of folded and unfolded protein structure in aqueous solution upon the addition of urea, the timescale of NMR makes it difficult to assess the process of unfolding, direct urea–protein interactions and more importantly how urea and water molecules might or might not interact with each other to affect a structural change in the protein. Moreover, as the unfolded state of proteins is conformationally highly flexible it is difficult to employ structural experimental techniques to address the conflicting explanations on protein folding and unfolding.
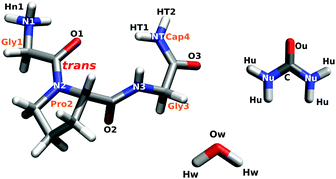
In the current work, the structure of the short glycine–proline–glycine peptide (GPG–NH2; Fig. 1) in the presence of urea in water has been determined using a combination of neutron scattering and computational techniques. This small peptide, which contains a sequence common in β-turns found in many proteins,10–14 presents an ideal model for understanding how urea interacts with different components of a peptide in order to nucleate the unfolding process. The atomic-scale hydration and conformation of this short chain peptide have been previously measured,15,16 thus allowing for a direct understanding of how urea and water interact with this molecule in solution. This peptide is also small enough to be investigated experimentally using neutron diffraction techniques which directly address molecular structure and, importantly, structural interactions between water and biomolecules in solution. Using this experimental technique in concert with computation, the interplay between water and urea and how, on a site-specific basis, this relates to how proteins unfold in the presence of urea can be assessed.
2 Methods
2.1 Sample preparation
Glycyl-L-prolyl-glycinamide·HCl (GPG·HCl) was purchased from Bachem (Bubendorf, Switzerland), urea from Sigma Aldrich and both were used without further purification. For the samples which required deuterium labeling, GPG·HCl and urea were dissolved in 99.8% D2O and then subsequently freeze-dried to remove the heavy water solvent. This process was repeated three times to ensure an adequate level of deuteration of the exchangeable hydrogens on GPG. The same procedure was followed to deuterate the hydrogen atoms on urea. Isotopomeric NDIS samples were prepared by weight under a N2 atmosphere with degased H2O and/or D2O (99.994%) to ensure sample purity, where the final molecular ratio of GPG![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) urea
urea![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water was 1
water was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 for each sample. The measured pH of GPG in water with urea (3.3 M) for the samples measured here is 6.0 at ≈1 M concentrations.
58 for each sample. The measured pH of GPG in water with urea (3.3 M) for the samples measured here is 6.0 at ≈1 M concentrations.
2.2 Neutron diffraction with isotopic substitution
NDIS is a well established experimental technique which can be used to determine the atomic structure of molecules in solution.15,17–28 This is largely due to the fact that the neutron scattering length b for hydrogen (−3.74 fm) is very different to that of deuterium (6.67 fm).29 This difference can be exploited by measuring a set of isotopically different yet chemically equivalent solutions, resulting in a number of unique diffraction patterns. The diffraction pattern (or static structure factor) for a liquid or solution is F(Q),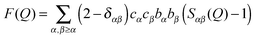 | (1) |
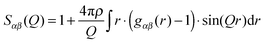 | (2) |
Neutron diffraction measurements were performed at 298 K on the SANDALS instrument located at the ISIS Facility (STFC, UK) on GPG–NH3+Cl− in aqueous urea solutions (see Fig. 1) using five isotopically substituted water solvents and appropriately labelled peptides and urea molecules to match these solvents (see ESI†). The samples were contained in SiO2 cells which had a sample thickness of 1 mm and a wall thickness of 1 mm. Diffraction data were collected for between 8 and 9.5 hours per sample. Data were also collected for the empty cells, the empty instrument and a vanadium standard for background subtraction and normalization. The data for samples, cells, empty instrument and vanadium were corrected for absorption, multiple scattering and inelasticity effects and then subsequently converted to F(Q) using the GUDRUN program.30,31
2.3 Empirical potential structure refinement
Empirical potential structure refinement (EPSR) is a reverse Monte Carlo technique which can be used to determine local interactions present in disordered materials, where the EPSR model is constrained by a set of diffraction data. EPSR uses a box of molecules at the concentration, density and temperature of the diffraction samples. In addition, ‘seed’ or starting potentials are given to each unique atom, where these starting potentials consist of a Lennard-Jones potential, defined by σ (the distance at which the potential is zero) and ε (the well depth) as well as appropriate atomic charges (qe). During the EPSR fitting process, these potentials are iteratively refined until a good ‘fit’ to the diffraction data is obtained.32,33In the current EPSR simulation, the modeling box contained 20 GPG molecules (Fig. 1), 20 Cl− ions, 80 urea molecules and 1160 water molecules at the measured density (ρ = 0.101 atoms Å−3) at 298 K. Parameters for water molecules were taken from the SPC/E water model34 and parameters for the GPG molecules, urea molecules and Cl− ion were from the CHARMM forcefield (see Section 2.4) and modified in order to adjust for different atomic labelling in EPSR compared with MD while ensuring electroneutrality of the simulation box. The full list of the parameters used for the starting potentials are shown in the ESI.† Similar to previous studies,15,16 the EPSR simulation contained a mixture of cis and trans GPG molecules (with respect to the Gly1–Pro2 bond) in ratios which correspond with that measured by 1H NMR (10% cis; 90% trans).†
Among other things, such as the ANGULA analysis described below, the individual site–site g(r)s (eqn (2)) can be extracted from the EPSR model. Coordination numbers (nβα(r)), which give the average number of β atoms around a central α atom at a distance between rmin and rmax, can then be calculated by integration of these g(r) functions via
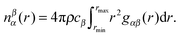 | (3) |
2.4 Molecular dynamics
Two MD simulations at the same molecular ratios as the neutron measurements, were also performed; one consisted of GPG molecules in the trans conformation and one with all the molecules in a cis conformation, however here only the trans simulation results are shown in the main text as this is the dominant species in solution and no appreciable difference between cis and trans conformations were evident in the simulations.Each system contained 64 GPG–NH3+–molecules, 64 Cl− counter ions, 256 urea molecules and 3712 water molecules. The GPG–NH3+–molecules and the Cl− ions were modelled using the CHARMM force field,35,36 and the water molecules were modeled using TIP3P37 modified for the CHARMM force field.38 All of the bonds and angles for the water molecules were constrained using the SHAKE algorithm39 and both simulations were conducted using GROMACS 4.40 The same simulation protocol was used for both of the simulations carried out as part of this study. Initially, an energy minimisation simulation was used to eliminate any atomic overlaps that resulted from the construction of the initial configurations. Then a 2 ns simulation utilising the NVT ensemble with a target temperature of 300 K was performed in order to equilibrate the temperature of the system. Then a 2 ns NPT simulation was performed with a target temperature of 300 K and a target pressure of 1 atm, in order to equilibrate the pressure and volume of the simulated systems. Finally, a NPT production simulation was performed at 300 K and 1 atm for 50 ns with a timestep of 2 fs. The Nose–Hoover thermostat41,42 was used in all simulations to control the temperature, while the Martyna–Tuckerman–Tobias–Klein (MTTK) barostat43 was used in the NPT simulations to control the pressure. A cut-off of 14 Å was used for the van der Waals interactions, and the long range Coulomb interactions were calculated using the particle mesh Ewald (PME) algorithm.44,45
2.5 ANGULA analysis
In addition to the g(r)s, the three-dimensional arrangements of molecules relative to one another can also be extracted from the EPSR simulation box using the program ANGULA.46 Orthonormal coordinate systems were assigned to different fragments of the GPG molecule, to the water and urea molecules (see ESI†). Using these coordinate systems, the distribution of the neighbouring water or urea molecules can be plotted relative to specific sites on the GPG molecule.47,48 Using 5000 snapshots of the simulation boxes (both for EPSR and MD, vide infra), the first interaction shells of water/urea, within a specific distance range, can be depicted via a spatial density map (SDM).16,48 Whole molecule analysis (WMA) was also performed using ANGULA.49 In this analysis, any molecule within a chosen distance range from any atom on a central molecule (in this case GPG) can be extracted. WMA was performed over a specific distance range (Section 3.5) for water and urea around the most probable GPG conformations, enabling the aggregate distribution of water and urea around GPG to be plotted with reference to the whole molecule.3 Results and discussion
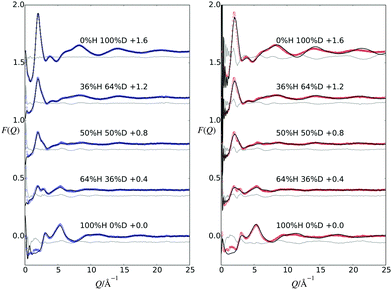
Fig. 2 shows the measured F(Q) data along with the EPSR fits to these data and a difference between the two. Additionally, this figure shows a comparison between the measured data and F(Q) functions which have been derived from the MD trajectory. From this figure, the EPSR fits are good, with only small differences occurring at low Q values, due to the fact that the inelastic background in this region is difficult to correct.50 The MD derived data does not provide as good a comparison to the measured data compared with the EPSR fits. The corresponding Fourier transformations which show the data in real space are shown in the ESI,† along with the EPSR fits and the MD comparison.3.1 Water structure
Fig. 3 shows the water oxygen RDFs (gOwOw(r)) for the current GPG:urea:water system compared with the same function for pure water,33 gpg:water in the absence of urea,16 and for urea![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water solutions at a ratio of 1
water solutions at a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16, approximately the same concentration as urea
16, approximately the same concentration as urea![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water here (1
water here (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14.5).51 The other water–water RDFs (gOwHw(r) & gHwHw(r)) are shown in the ESI.† The gOwOw(r) function, is considered a ‘signature’ for the tetrahedral water structure,52,53 as it is sensitive to changes in this structure. From this figure, the first neighbour water distances are similar, with all of the RDFs showing first peaks at around 2.8 Å, while the second nearest neighbour water shells are different in each. For GPG in both solutions, the water–water shells show two second neighbour distances compared to pure water.33 In GPG, the closer of these two second shells most likely occurs from both the Cl− ion–water interactions and GPG–water interactions (GPG is cationic), as ions have been observed to have a constricting effect on the second nearest neighbour distance in the Ow–Ow RDF in solutions.52 Interestingly, in the present GPG:urea:water solutions, the further second neighbour peak has shifted to slightly higher r values relative to GPG in the absence of urea. This shift to higher values has also been observed for higher concentrations of urea in solution,54 while in contrast mixtures of trimethylamine N-oxide (TMAO) and urea in solution showed a more limited perturbation to this second hydration shell in solution.25
14.5).51 The other water–water RDFs (gOwHw(r) & gHwHw(r)) are shown in the ESI.† The gOwOw(r) function, is considered a ‘signature’ for the tetrahedral water structure,52,53 as it is sensitive to changes in this structure. From this figure, the first neighbour water distances are similar, with all of the RDFs showing first peaks at around 2.8 Å, while the second nearest neighbour water shells are different in each. For GPG in both solutions, the water–water shells show two second neighbour distances compared to pure water.33 In GPG, the closer of these two second shells most likely occurs from both the Cl− ion–water interactions and GPG–water interactions (GPG is cationic), as ions have been observed to have a constricting effect on the second nearest neighbour distance in the Ow–Ow RDF in solutions.52 Interestingly, in the present GPG:urea:water solutions, the further second neighbour peak has shifted to slightly higher r values relative to GPG in the absence of urea. This shift to higher values has also been observed for higher concentrations of urea in solution,54 while in contrast mixtures of trimethylamine N-oxide (TMAO) and urea in solution showed a more limited perturbation to this second hydration shell in solution.25
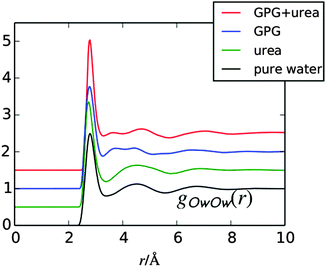 | ||
| Fig. 3 RDF for water oxygens (Ow) from the GPG:urea:water EPSR fits to the neutron data compared with the same function in pure water,33 gpg:water,16 and urea:water51 solutions. Plots have been shifted for clarity. | ||
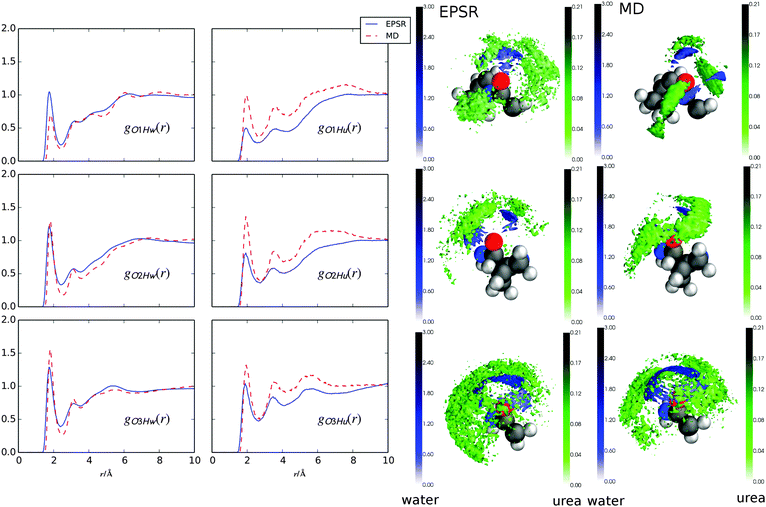
3.2 Urea and water interactions with peptide bond oxygens
Fig. 4 shows the RDFs for water and urea around the peptide bond carbonyl oxygens in GPG (Fig. 1) from both EPSR fits to the neutron data and the MD simluations. It is immediately evident that all of the hydrogen bonds from either water or urea to the GPG oxygens occur at the same distances (∼1.9 Å). There are also fewer hydrogen bonds from urea to the GPG oxygens compared with water (the coordination numbers (nβα; eqn (3)) for the RDFs in Fig. 4 are listed in Table 1). What is also clear from Fig. 4 and Table 1 is that the GPG oxygens interact with water to varying degrees, specifically the hydration increases from O1 to O3 in both simulations. This same trend is observed for urea–GPG interactions, with O3 showing the highest number of urea–hydrogen bonds and the O1 oxygen the least. In general, the water coordination numbers from the EPSR fits to the neutron data are larger than from the MD trajectories, and MD shows comparatively more Ox–urea contacts.| g(r) | EPSR | MD |
|---|---|---|
| O1–Hw | 1.30 | 0.88 |
| O2–Hw | 1.61 | 1.37 |
| O3–Hw | 1.76 | 1.77 |
| O1–Hu | 0.12 | 0.22 |
| O2–Hu | 0.21 | 0.27 |
| O3–Hu | 0.26 | 0.29 |
Fig. 4 also shows spatial density maps (SDMs)48 which depict the most probable location of water and urea molecules in 3-dimensions around each of the GPG oxygens within a specific distance range. In both simulations, the SDMs are similar, where for each oxygen there is much broader distribution of urea molecules compared with water molecules in the surrounding shells. For instance, for the Gly1–Pro2 peptide bond oxygen (O1; Fig. 1) the urea molecules have a high probability of not only being located behind the oxygen atom (in the −x direction towards the proline ring) but also on either side of the O1 atom. Water molecules, on the other hand, show a more narrow distribution of locations with a high probability of being located behind the O1 atom. To varying degrees this is true for all of the oxygen sites; urea preferentially occupies spaces where the waters have a low probability of being located.
3.3 Urea and water interactions with backbone nitrogens
Fig. 5 shows g(r)s between urea and water oxygens (Ou and Ow, respectively) and the GPG nitrogens (Fig. 1) and the coordination numbers for these functions are listed in Table 2. In both EPSR fits to the neutron data and MD simulations, both the water and urea interactions with the GPG nitrogens are broadly similar although MD shows significantly more urea interactions compared with EPSR (Table 2). This is especially evident in the N2 and N3 g(r)s and in the comparison of coordination numbers for these functions. The –NH3+–nitrogen clearly shows the most prominent peaks for the water–nitrogen and urea–nitrogen interactions, which are a result of hydrogen bonding from the N-terminal hydrogens to the Ow and Ou oxygens (the gHOu/Ow(r)s are shown in the ESI†). The Pro2–Gly3 peptide bond nitrogen (N3) also shows sharp peaks for both water and urea molecules at relatively low r values, which again are a result of hydrogen bonding between the Hn3 hydrogen (Fig. 1) and the Ow and Ou atoms. Interestingly, while the N1 and N3 (Fig. 5) first peaks are sharp and well defined, both the proline ring nitrogen (N2) and Gly3–Ncap (NT) nitrogen–water g(r)s show broader and less well defined first peaks, indicating a more disordered distribution of water molecules around the Pro2 ring and Ncap portions of GPG. For N2, this is unsurprising given the lack of a hydrogen on the proline ring to which water or urea molecules could potentially form hydrogen bonds. For the Ncap (NT), the relatively broad peak in the gNTOw(r) function is rather unexpected given that hydrogen bonds are formed between the both HT1 and HT2 atoms and water oxygens. In comparison the terminal amide nitrogen–urea nearest neighbour g(r) is much more well defined.| g(r) | r 1/Å | EPSR | MD |
|---|---|---|---|
| N1–Ow | 3.60 | 3.38 | 4.04 |
| N2–Ow | 6.75 | 27.13 | 26.37 |
| N3–Ow | 3.42 | 0.95 | 1.06 |
| NT–Ow | 4.26 | 6.24 | 5.80 |
| N1–Ou | 3.60 | 0.30 | 0.36 |
| N2–Ou | 6.75 | 1.79 | 2.34 |
| N3–Ou | 3.42 | 0.11 | 0.13 |
| NT–Ou | 4.26 | 0.42 | 0.41 |
Fig. 5 also shows the SDMs for water and urea around the nitrogen atoms in GPG. As opposed to the SDMs in Fig. 4 where water and urea are in different places around the oxygen atoms, both water and urea occupy similar locations around each nitrogen for both EPSR fits to the neutron data and the MD simulations. This indicates that urea is likely to directly replace the waters around the peptide-bond nitrogen groups, rather than coordinating in a different location. The only slight exception to this is the EPSR for the proline (N2) nitrogen which shows a more diffuse shell of urea molecules around the proline nitrogen compared with the MD. This is, in part, likely a result of these closest urea molecules being spread over a much larger distance range as evidenced by the gN2Ou(r) function.
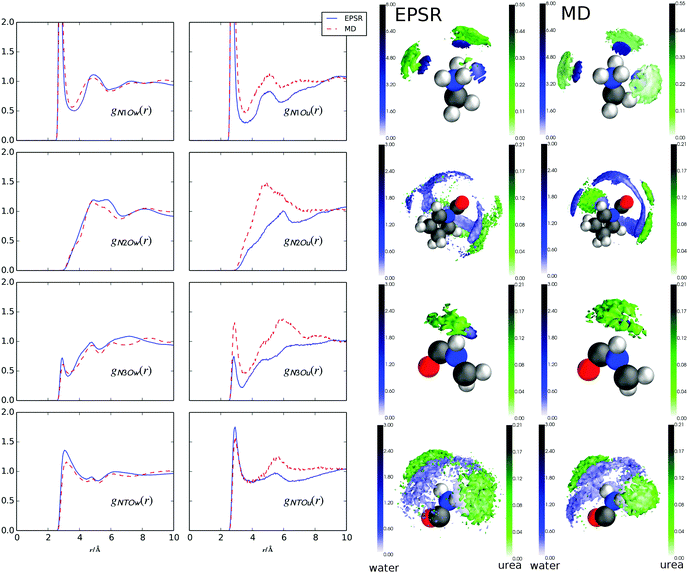 | ||
| Fig. 5 Radial distribution function (g(r)) for GPG peptide bond nitrogens and N terminal nitrogen and Ow/Ou atoms from water and urea, respectively, from MD and EPSR. Spatial density maps (SDMs) of Ow (blue) and Ou (green) around N1, N2, N3, NT from EPSR (left column) and MD (right column). In each case, the 3D shells show the top 20% of nearest neighbour molecules in a distance range from 0 Å to the distance shown in Table 2 for each atom. | ||
3.4 Urea preferred over water for most peptide bond atoms
In order to quantify the preference of water or urea around specific sites on GPG, a contact coefficient analysis was performed. Previously, a similar analysis was used for MD simulations for small peptides in aqueous urea solutions,55 where in that investigation the contact was defined as any atom on a water or urea molecule being within 3.5 Å of a particular atom on the amino acid. Given the variety of first peak positions in the RDFs in Fig. 4 and 5, here the relative preference of urea or water around a specific site was determined using distances that correspond to the first minimum in the g(r) as a criteria. This relative preference can be defined by a preference ratio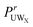 where
where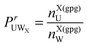 | (4) |
This relative preference was quantified by taking the ratio of the coordination numbers (eqn (1)) of GPG atoms (X) around water and urea.
It should be noted that in eqn (4) the “inverse” coordination numbers (see ESI†) to those shown in Tables 1 and 2 were used to determine this ratio – giving, for instance the number of N1 atoms around Ow atoms rather than the number of Ow atoms around O1 atoms – as this automatically corrects for the fact that there are more waters than urea in the present solutions (the inverse coordination numbers are shown in the ESI†). The 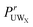 has been determined for all of the GPG nitrogens and are tabulated in Table 3. Similar to previous investigations,55 a contact coefficient greater than 1 indicates that urea is preferred over water and less than 1 indicates that water is preferred over urea.
has been determined for all of the GPG nitrogens and are tabulated in Table 3. Similar to previous investigations,55 a contact coefficient greater than 1 indicates that urea is preferred over water and less than 1 indicates that water is preferred over urea.
| g(r) | r 1/Å | EPSR | MD |
|---|---|---|---|
| Hu/w–O1 | 2.52 | 0.68 | 1.78 |
| Hu/w–O2 | 2.52 | 1.11 | 1.45 |
| Hu/w–O3 | 2.52 | 1.06 | 1.22 |
| Ou/w–N1 | 3.60 | 1.30 | 1.30 |
| Ou/w–N2 | 6.75 | 0.96 | 1.29 |
| Ou/w–N3 | 3.42 | 1.61 | 1.74 |
| Ou/w–NT | 4.26 | 0.98 | 1.02 |
| Ou/w–Hn1 | 2.25 | 1.57 | 1.51 |
| Ou/w–Hn3 | 2.58 | 2.02 | 2.11 |
| Ou/w–HT1 | 2.49 | 1.21 | 1.52 |
| Ou/w–HT2 | 2.40 | 2.05 | 1.93 |
From Table 3, both GPG nitrogens and oxygens preferentially interact with urea over water, this is especially clear for the Pro2–Gly3 peptide bond and N-terminal hydrogens where urea shows a relatively large preference for these polar/charged portions of the peptide. The Gly1–Pro2 (N2) and Ncap (NT) nitrogen atoms on the other hand, show a less marked preference for urea and for the EPSR fits to the neutron data these nitrogens prefer water over urea, if only marginally. Interestingly, although the hydration and urea contacts around the oxygen atoms showed the same trend in coordination for both MD and EPSR, the contact coefficients reveal that in MD all of the oxygens preferentially interact with urea over water, while in EPSR only O2 and O3 show this preference. These two methods also show a large difference in the relative contact coefficients for O1 with MD showing a large preference of urea while in EPSR this atom shows a marked preference to be hydrated.
This may be a result of how ‘folded’ the peptides are in solution. The MD simulation has more folded peptides, as a comparison between the O1–HT1/2 intra-peptide contacts, which is indicative of beta-turn formation (see ESI†),15 shows a larger number of folded GPG molecules in the MD simulation (∼24%) compared with EPSR (∼4%) and oddly here there are slightly more folded GPG peptides in the presence of urea than without in the MD simulations.15 More unfolded peptides would be more solvent accessible and therefore somewhat higher solvation might be expected around the O1 atom. To test this, the O1–Hw coordination numbers were taken for folded vs. unfolded peptides in the MD simulation, where GPG was considered to be ‘folded’ when the HT1–O1 distance was less than 4.5 Å. The coordination numbers do show that the O1 atom is slightly less hydrated when folded 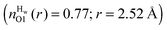 compared with unfolded
compared with unfolded 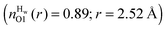 , however O1 also showed more urea interactions when GPG was unfolded
, however O1 also showed more urea interactions when GPG was unfolded 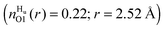 and as such the O1 atom still shows a preference for urea when the GPG molecules are unfolded (
and as such the O1 atom still shows a preference for urea when the GPG molecules are unfolded (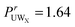 for unfolded molecules in MD). Despite these differences in coordination numbers between the two methods, the urea–O1 SDMs in Fig. 4 for both MD and EPSR are similar, with both showing urea in different locations to the surrounding water shell.
for unfolded molecules in MD). Despite these differences in coordination numbers between the two methods, the urea–O1 SDMs in Fig. 4 for both MD and EPSR are similar, with both showing urea in different locations to the surrounding water shell.
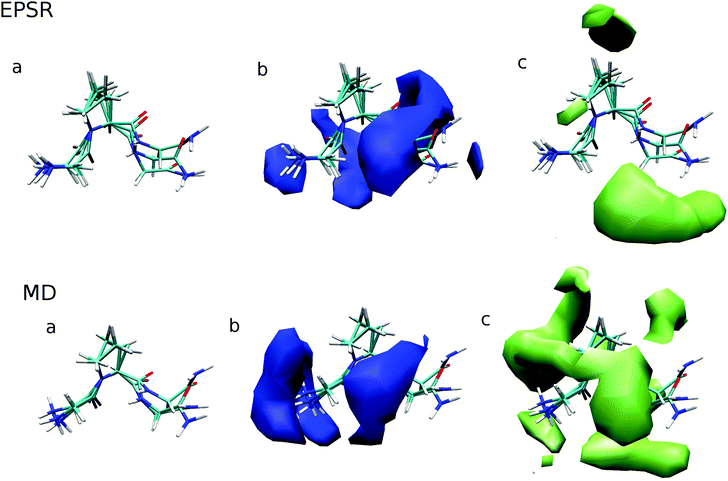
3.5 Whole molecule analysis
In addition to site-specific analysis of urea and water around GPG in aqueous urea solution, whole molecule analysis (WMA) has also been performed using ANGULA.49 This analysis allows for the most probable location of solvent molecules – water or urea – around the entire GPG molecule to be determined. In the WMA in Fig. 6, the GPG molecules at the center of these plots are representative of the distribution of the GPG conformations in each of the simulations.The probability distribution of water molecules around GPG are shown in the b panels of Fig. 6 within a distance range of 0–3.5 Å. In both MD and EPSR there is a marked preference for water to be located around the polar regions of the peptides with MD showing a higher propensity for waters being either around the –NH3– terminus or around the Pro2–Gly3 peptide bond in a fairly broad distribution. EPSR on the other hand shows a similar hydration shell but also shows density ‘behind’ the GPG peptide and overall a broader distribution of hydration compared with MD. In each of these hydration WMA plots, there is an absence of water around the proline ring portions of the peptide.
The c panels in Fig. 6 shows the most probable locations of urea molecules around GPG, with EPSR and MD showing fairly different density distributions. For EPSR, urea preferentially occupies spaces where water is absent, while MD shows a broader distribution of urea, where water and urea have a similar propensity to occupy many the same spaces around the GPG peptide; this is most clear for the band of urea density around the Pro2–Gly3 portion of the molecule in Fig. 6. As opposed to the hydration density, the GPG–urea WMA shows density around the proline ring, with both MD and EPSR showing some density near this ring, although not in the same places.
4 Conclusions
In the current investigation, the bulk water structure in the GPG:water:urea system does not appear to be significantly perturbed by the presence of urea in solution over and above the slight perturbation to second neighbour shell in the gOwOw(r) for GPG in the absence of urea in Fig. 3.16 This is consistent with previous investigations on TMAO/urea in aqueous solution where it was found that large increases in the amount of urea in solution did not significantly perturb the bulk water structure.25 This lack of perturbation suggests that an ‘indirect’ mechanism of protein denaturation by urea altering the bulk water structure is unlikely, in agreement with previous investigations.54,56As opposed to previous simulations which found that water was preferred over urea for the charged and polar portions of the peptides,55 here the charged groups of the GPG peptide in almost all cases showed a preference to form hydrogen bonds with urea rather than water (Table 3). The only exception to this preference is the Gly1–Pro2 peptide bond carbonyl oxygen (O1) from the EPSR fits to the neutron data which show a clear preference to be hydrated rather than to form hydrogen bonds with urea, which may be due to the fact that MD is more ‘folded’ or just due to a difference between the two simulation methods.
In general, MD also showed a slightly higher level of urea–GPG contacts compared to EPSR where this preference was most notable for the Gly1–Pro2 (N2) nitrogen (Fig. 5). This preference for urea in the MD simulations is accentuated by the WMA shown in Fig. 6 where there is a much broader distribution of GPG–urea interactions compared with the WMA for the EPSR fits to the neutron data. Even though the distribution of urea is quite different for each simulation, they both show a fairly significant probability of urea–proline ring interactions while there is an absence of water–proline contacts in GPG WMAs. This observation indicates that urea preferentially associates with the hydrophobic core of proteins rather than water as proposed by Hua et al.7 What is perhaps most striking about the urea WMAs for both MD and EPSR fits to the neutron data is that a large portion of the density in both cases is located around different parts of the GPG backbone. This observation supports simulation studies on group transfer free energies which suggest that urea denatures proteins due to largely favourable interactions with the protein backbone.3
That urea is preferred over water around the peptide bonds indicates that urea can easily replace water along the GPG backbone, thus lowering the overall hydration of the peptide. This is what seems to occur for the amide nitrogens in the backbone, with the SDMs Fig. 5 suggesting that waters are simply replaced by urea in the same locations around these nitrogen containing groups, this is especially evident for the Pro2–Gly3 peptide bond. For the peptide bond carbonyl oxygens however, the SDMs in Fig. 4 indicate that while there is some replacement of water by urea, that urea also has a high probability to bind to the backbone oxygens at different locations in space. Taken together, these two phenomenon suggest that the amide hydrogens in the protein backbone are the initial site of water replacement by urea forming strong hydrogen bonds with –NH– groups in a peptide or, perhaps, by extension proteins. Although in the current work only a small model peptide has been used, it may be that when initiating denaturation of a peptide or protein backbone, urea first attacks the backbone by displacing the waters around the amide groups and then as a secondary step bridges from the –NH– group to the peptide bond oxygens – which eventually will ‘unzip’ the backbone, exposing the hydrophobic core to the surrounding solvent molecules.
Acknowledgements
We thank the ISIS Facility (Rutherford Appleton Laboratories, STFC, UK) for the allocation of neutron beam time, the UK Engineering and Physical Sciences Research Council for (EP/J002615/1), the Ministerio de Ciencia y Tecnología (FIS2014-54734-P) and the Catalonia Government (2014SGR-0581) for funding and Sebastian Busch (Helmholz) for providing the initial input files for the SDM analysis. Through CDL's membership within the UK HPC Materials Chemistry Consortium, which is funded by the Office of Science and Technology through the EPSRC High End Computing Programme (EP/L000202), the facilities of ARCHER – the UK national high performance computing service – were used for the MD aspects of this work.References
- C. B. Anfinsen, Science, 1973, 181, 223–230 CAS.
- Y. Rezus and H. Bakker, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 18417–18420 CrossRef CAS PubMed.
- M. Auton, L. M. F. Holthauzen and D. W. Bolen, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 15317–15322 CrossRef CAS PubMed.
- D. R. Canchi and A. E. Garca, Biophys. J., 2011, 100, 1526–1533 CrossRef CAS PubMed.
- M. C. Stumpe and H. Grubmüller, Biophys. J., 2009, 96, 3744–3752 CrossRef CAS PubMed.
- E. P. O'Brien, R. I. Dima, B. Brooks and D. Thirumalai, J. Am. Chem. Soc., 2007, 129, 7346–7353 CrossRef PubMed.
- L. Hua, R. Zhou, D. Thirumalai and B. Berne, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 16928–16933 CrossRef CAS PubMed.
- P. J. Rossky, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 16825–16826 CrossRef CAS PubMed.
- B. Bennion and V. Daggett, Proc. Natl. Acad. Sci. U. S. A., 2003, 101, 6433–6438 CrossRef PubMed.
- P. N. Lewis, F. A. Momany and H. A. Scheraga, Proc. Natl. Acad. Sci. U. S. A., 1971, 68, 2293–2297 CrossRef CAS.
- P. Y. Chou and G. D. Fasman, Biochemistry, 1974, 13, 222–245 CrossRef CAS PubMed.
- C. M. Wilmot and J. M. Thornton, J. Mol. Biol., 1988, 203, 221–232 CrossRef CAS PubMed.
- E. G. Hutchinson and J. M. Thornton, Protein Sci., 1994, 3, 2207–2216 CrossRef CAS PubMed.
- K. Guruprasad and S. Rajkumar, J. Biosci., 2000, 25, 143–156 CAS.
- S. Busch, C. D. Bruce, C. Redfield, C. D. Lorenz and S. E. McLain, Angew. Chem., Int. Ed., 2013, 49, 13091–13095 CrossRef PubMed.
- S. Busch, L. C. Pardo, W. B. O'Dell, C. D. Bruce, C. D. Lorenz and S. E. McLain, Phys. Chem. Chem. Phys., 2013, 15, 21023–21033 RSC.
- O. Sobolev, G. J. Cuello, G. Román-Ross, N. T. Skipper and L. Charlet, J. Phys. Chem. A, 2007, 111, 5123–5125 CrossRef CAS PubMed.
- S. E. McLain, C. J. Benmore, J. E. Siewenie, J. Urquidi and J. F. C. Turner, Angew. Chem., Int. Ed., 2004, 43, 1952–1955 CrossRef CAS PubMed.
- F. Foglia, M. J. Lawrence, C. D. Lorenz and S. E. McLain, J. Chem. Phys., 2010, 133, 145103 CrossRef PubMed.
- J. Hladílková, H. E. Fischer, P. Jungwirth and P. E. Mason, J. Phys. Chem. B, 2015, 119, 6357–6365 CrossRef PubMed.
- S. K. Callear, A. Johnston, S. E. McLain and S. Imberti, J. Chem. Phys., 2015, 142, 014502 CrossRef PubMed.
- E. Scoppola, A. Sodo, S. McLain, M. Ricci and F. Bruni, Biophys. J., 2014, 106, 1701–1709 CrossRef CAS PubMed.
- M. Vazdar, P. Jungwirth and P. E. Mason, J. Phys. Chem. B, 2013, 117, 1844–1848 CrossRef CAS PubMed.
- N. H. Rhys, A. K. Soper and L. Dougan, J. Phys. Chem. B, 2012, 116, 13308–13319 CrossRef CAS PubMed.
- F. Meersman, D. Bowron, A. K. Soper and M. H. J. Koch, Phys. Chem. Chem. Phys., 2011, 13, 13765–13771 RSC.
- L. Tavagnacco, J. W. Brady, F. Bruni, S. Callear, M. A. Ricci, M. L. Saboungi and A. Cesáro, J. Phys. Chem. B, 2015, 119, 13294–13301 CrossRef CAS PubMed.
- T. G. A. Youngs, J. D. Holbrey, C. L. Mullan, S. E. Norman, M. C. Lagunas, C. D'Agostino, M. D. Mantle, L. F. Gladden, D. T. Bowron and C. Hardacre, Chem. Sci., 2011, 2, 1594–1605 RSC.
- A. J. Johnston, Y. Zhang, S. Busch, L. C. Pardo, S. Imberti and S. E. McLain, J. Phys. Chem. B, 2015, 119, 5979–5987 CrossRef CAS PubMed.
- V. F. Sears, Neutron News, 1992, 3, 26–37 CrossRef.
- A. K. Soper, GudrunN and GudrunX: Programs for correcting raw neutron and x-ray total scattering data to differential cross section, Rutherford Appleton Laboratory, STFC, UK, 2011 Search PubMed.
- http://https://www.facebook.com/disord.matt .
- A. K. Soper, Mol. Simul., 2012, 38, 1171–1185 CrossRef CAS.
- A. K. Soper, ISRN Phys. Chem., 2013, 2013, 1–67 CrossRef.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- A. D. MacKerell, J. Comput. Chem., 2004, 25, 1584–1604 CrossRef CAS PubMed.
- J. A. D. MacKerell, D. Bashford, M. Bellott, J. R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, I. W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926 CrossRef CAS.
- W. I. Reiher, PhD thesis, Harvard University, 1985.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- W. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- G. J. Martyna, M. E. Tuckerman, D. J. Tobias and M. L. Klein, Mol. Phys., 1996, 87, 1117–1157 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577 CrossRef CAS.
- http://https://gcm.upc.edu/en/members/luis-carlos/angula/ANGULA .
- L. C. Pardo, M. Rovira-Esteva, J. L. Tamarit, N. Veglio, J. F. Bermejo and G. J. Cuello, in Metastable Systems under Pressure, ed. R. Sylwester, D. Aleksandra and M. Victor, Springer, Netherlands, 2010, pp. 79–91 Search PubMed.
- S. Busch, C. D. Lorenz, J. Taylor, L. C. Pardo and S. E. McLain, J. Phys. Chem. B, 2014, 118, 14267–14277 CrossRef CAS PubMed.
- A. J. Johnston, S. Busch, L. C. Pardo, S. K. Callear, P. C. Biggin and S. E. McLain, Phys. Chem. Chem. Phys., 2016, 18, 991–999 RSC.
- A. K. Soper, Mol. Phys., 2009, 107, 1667–1684 CrossRef CAS.
- A. Soper, Unpublished data courtesy of AK Soper.
- R. Mancinelli, A. Botti, F. Bruni, M. A. Ricci and A. K. Soper, Phys. Chem. Chem. Phys., 2007, 9, 2959–2967 RSC.
- A. H. Narten and H. A. Levy, Science, 1969, 165, 447–454 CAS.
- A. Soper, E. Castner Jr and A. Luzar, Biophys. Chem., 2003, 105, 649–666 CrossRef CAS PubMed.
- M. C. Stumpe and H. Grubmüller, J. Am. Chem. Soc., 2007, 129, 16126–16131 CrossRef CAS PubMed.
- P. O. Åstrand, A. Wallqvist, G. Karlström and P. Linse, J. Chem. Phys., 1991, 95, 8419–8429 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp06646h |
| This journal is © the Owner Societies 2016 |