Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electric dipole moments and chemical bonding of diatomic alkali–alkaline earth molecules†
Johann V.
Pototschnig
*,
Andreas W.
Hauser
and
Wolfgang E.
Ernst
Graz University of Technology, Institute of Experimental Physics, Petersgasse 16, 8010 Graz, Austria. E-mail: johann.pototschnig@tugraz.at; wolfgang.ernst@tugraz.at; Tel: +43 316 873-8152
First published on 27th January 2016
Abstract
We investigate the properties of alkali–alkaline earth diatomic molecules in the lowest Σ+ states of the doublet and quartet multiplicity by ab initio calculations. In all sixteen cases studied, the permanent electric dipole moment points in opposite directions for the two spin states. This peculiarity can be explained by molecular orbital theory. We further discuss dissociation energies and bond distances. We analyze trends and provide an empirically motivated model for the prediction of the permanent electric dipole moment for combinations of alkali and alkaline earth atoms not studied in this work.
1 Introduction
In the last years ultracold molecules have attracted a lot of attention due to their outstanding properties.1–6 The low temperature reduces the decoherence, and ensembles of ultracold molecules can be used to simulate quantum systems7–12 or perform quantum computations.13 Most degrees of freedom are frozen out at these temperatures, which allows precise control of chemical reactions.14–16 Another advantage is the reduction of the linewidth and noise in measurements of fundamental physical properties and constants17 such as the proton to electron mass ratio,18–20 the electron electric dipole moment21,22 or the fine structure constant.23,24The first molecules produced in the ultracold temperature regime were homonuclear alkali-dimers,25–28 which do not have a permanent electric dipole moment. A few years later, ultracold heteronuclear alkali-dimers were produced.29–34 Their permanent electric dipole moment gives experimentalists an additional handle for manipulation via electric fields. In this sense, the next logical step is the production of ultracold molecules with a dipole moment plus an additional magnetic moment, originating from an unpaired electron spin. This magnetic moment causes additional interactions and enables control of these molecules via magnetic fields. Currently, the most promising candidates are alkali (AK)–alkaline earth (AKE) and AK–Yb diatomic molecules because the involved atoms are well under control in ultracold atomic physics. Bose–Einstein condensation, for example, has been achieved for most AK atoms,35 Ca,36 Sr37 and Yb.38 In a series of recent studies combining experimental and computational efforts39–43 we found permanent electric dipole moments (PEDM) with opposite signs in the lowest Σ+ states of the doublet and the quartet multiplicity for AK–AKE molecules. In this work we analyze this behavior and discuss the trends in greater detail. The magnitude of the permanent electric dipole moment (PEDM) is of special importance for future applications. A significant value is necessary to align molecules in an optical lattice,44,45 to control interactions with an external microwave field,4,11,46 and it might even be useful to reach low vibrational levels.47
Early on, there has been interest in the prediction of dipole moments for alkali halides and alkaline earth halides. These two groups of molecules with predominantly ionic bonding could successfully be described by electrostatic interaction models.48–50 The Rittner model48 for alkali halides assumes a complete charge transfer of one electron and considers the polarizabilities of the ions. Törring et al.51,52 applied a similar model to AKE halides. More sophisticated computations using ligand field theory were performed for AKE halides53 and lanthanum containing diatomics.54,55 A model taking orbital mixing into account was applied to SrBr in ref. 56. However, these techniques assume a transfer of at least one electron and can therefore not be applied to AK–AKE molecules. Recently, an empirical model for the relation between dipole moment and vibrational frequencies was presented.57
There are a few theoretical and experimental studies concerned with the properties of AK–AKE molecules. Bauschlicher et al.58 performed one of the first calculations. Two theoretical studies examined the ground state of Li–AKE molecules by coupled cluster calculations.59,60 The ground states of neutral AK–Sr molecules and several states of the molecular ions have been investigated by a configuration interaction method.61,62 In ref. 63, the ground states of AK–Mg diatomic molecules were calculated at the coupled cluster level of theory. Using the same approach, Gopakumar et al.45 recently investigated the AK–AKE molecules (Na, K, Rb)–(Ca, Sr). The combination of barium with an alkali atom has also been considered in the ground state.64 Some older studies analyzed the ground and several excited states of LiBa65,66 and NaBa.67 The most thoroughly studied representative of these diatomic molecules is LiCa, with experimental,68–70 theoretical71,72 and combined investigations.39,73 The first realization of a combined quantum degenerate mixture of Rb and Sr74 was followed by a series theoretical and experimental publications.40–42,75–77 The excited states of LiSr,72 RbBa,78 LiMg,79 and RbCa43 were calculated recently.
In this study, we investigate the energetically lowest electronic states of neutral AK (Li, Na, K, Rb)–AKE (Be, Mg, Ca, Sr) molecules in the doublet and quartet manifold. Throughout the article, the coordinate system is defined such that the AKE atom is on the negative side of the axis and the AK atom on the positive side. Therefore, a positive value of the PEDM corresponds to a dipole moment pointing in axis direction from the AKE to the AK atom (i.e., the center of the negative charge lies closer to the AKE atom).
This manuscript is structured as follows: in the next section details of the computational method are given, then an overview of the results and a comparison to previous results. After discussing trends for AK–AKE molecules we give a qualitative description of the situation for the lowest Σ+ states in AK–AKE molecules. Finally, we present an empirical model in Section 3.4.
2 Computational details
All ab initio calculations were carried out with the MOLPRO80 software package. A multiconfigurational self consistent field calculation (MCSCF81,82) was performed, followed by multireference configuration interaction including Davidson correction (MRCI83,84). The quintuple-zeta basis set family of Peterson et al. covers most atoms of our study and was used where possible. All electrons basis sets85 were applied for Li, Na, Be and Mg. For the heavier atoms the corresponding effective core potential basis sets86 of Peterson were combined with the recommended effective core potentials87,88 of Lim et al. For K and Rb, however, no Peterson basis sets were available. In these cases, we fell back on the basis sets provided by Lim,87,88 decontracted them, and added several diffuse functions to obtain a description of similar accuracy.‡ The same strategy has recently been applied to RbCa,43 yielding excitation energies in good agreement with experimental measurements.We further applied core polarization potentials (CPPs) as introduced by Müller and Meyer89 due to their importance for correct magnitudes of the permanent electric dipole moments90,91 (see Fig. 1). The parameters of the core polarization potential are given (see Table 1) and were optimized for our effective core potentials and basis sets. This approach only allows basis functions with an angular quantum number below 5. Therefore, basis functions with higher quantum numbers were neglected. No core polarization was added for Li and Be due to their small cores and large energy difference between the core orbitals and valence orbitals compared to the other elements. With this approach the energy difference between the first excited state (2PAK/3PAKE) and the ground state agrees within 150 cm−1 (1%) with the atomic values92 in the asymptotic limit.
| AK | α core/a.u. | ρ/Å−2 | AKE | α core/a.u. | ρ/Å−2 |
|---|---|---|---|---|---|
| Na | 1.00 | 1.27 | Mg | 1.20 | 0.60 |
| K | 5.61 | 0.46 | Ca | 7.16 | 0.25 |
| Rb | 9.74 | 0.35 | Sr | 9.28 | 0.28 |
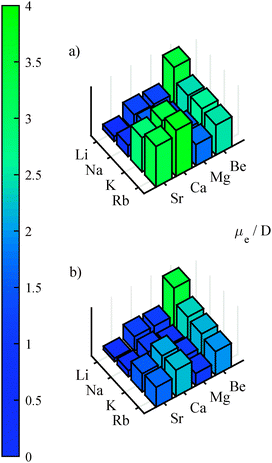
It is known that the correlation or polarization of the core electrons has a significant influence on the dipole moment.90,91 The importance of this contribution can be estimated by looking at Fig. 1, where the results without (a) and with (b) core polarization potentials are compared. Typically, the PEDM is overestimated if the polarization of the core is neglected, which agrees well with the observations of ref. 90. This error increases with atomic mass. The largest deviation was found for RbSr, where the dipole moment is reduced by 1.65 D to about half its value after inclusion of core polarization. The PEDMs for the computations including core polarization potentials (see plot b of Fig. 1) were obtained by finite field calculations,§ which we carried out for different field strengths varying from 10−5 to 5 × 10−3 a.u. for all 16 molecules. For each field strength the PEDMs and polarizabilities were computed by three point and five point finite field approximations and compared to each other to estimate the size of numerical error. The values were then taken where the smallest deviation was observed. (The values and the field strengths for their calculation are listed in the ESI.†)
The PEDMs for the lowest Σ+ state of the quartet multiplicity were also changed significantly by the core polarization potential, especially for heavy molecules, but without a clear trend. An improvement of the potential depth of LiCa was achieved by a new set of recently adjusted core polarization parameters. The potential depth for LiCa obtained in this work (2613 cm−1) now agrees better with the experimental value (2605 cm−1)69 than our previous calculation.39 However, part of the improvement might originate also from the slightly different basis set. On average, the equilibrium distance was reduced by the core polarization potential, although some minor deviations occurred, especially for the quartet states.
In the MCSCF and MRCI calculation the same active space was applied, but it was necessary to adapt it to the different basis sets and effective core potentials. Details on the size and definition of the active space for the various diatomics can be found in the ESI.† Note that the lowest Σ+ state in the quartet multiplicity is an electronically excited state accompanied by several excited states of the doublet manifold. Therefore, several excited states were calculated in both spin configurations to obtain a meaningful description of this state. In a combined MCSCF calculation 16 to 32 states of doublet multiplicity and 3 or 8 states of quartet multiplicity were optimized. The number of states was kept the same in the MRCI calculation for the quartet multiplicity, but the number of doublet states was reduced to 12–17 states. With this setup for the state-averaged calculations we obtained smooth potential energy curves up to an internuclear separation of 10 Å. At this distance, the deviation for the ground state from the asymptotic value is only 10 cm−1 for light atoms and about 25 cm−1 for heavy atoms (ESI†).
3 Results
3.1 Overview
The properties of 16 AK–AKE molecules have been calculated by MCSCF + MRCI and the values for the ground state are listed in Table 2. Results for the lowest Σ+ state in the quartet multiplicity are given in Table 3. Besides the ab initio calculations performed in this work, several other theoretical predictions as well as three experimental studies are listed in Table 2. Overall agreement between the various studies is good except for significant differences in dissociation energies. LiCa, the best studied molecule in the literature, with data available from 8 different sources, shows a large variation of the dissociation energy. Our value and the value of ref. 60 agree best with recent experimental findings.69 Two older experimental results93,94 are also listed in Table 2. A recent experiment of our group40 yielded a vibrational constant (ωe) of (42 ± 5) cm−1 for RbSr, which is in good agreement with the theoretical results in Table 2. The calculated PEDMs are all positive and differ on average by 0.16 D (13%) from previous computations, with the largest difference observed for the PEDM of KCa in ref. 45. Note that the PEDM values listed in Table 2 were evaluated for the respective equilibrium distance. When zero-point motion is considered, the PEDM is on average reduced by 0.03 D for the doublet states and by 0.06 D for the quartet states (details are provided in the ESI†). The difference to other equilibrium distances is on average 0.05 Å (1%) with the largest deviations occurring for RbSr and RbCa when compared to ref. 45. This deviation in the latter cases also explains the slight difference in the PEDM as the listed values are taken at the equilibrium separation. A small disagreement can also be found between the parallel polarizabilities (along the internuclear axis) listed in Table 2. Note that only the polarizabilities (α∥) at the equilibrium distances along the internuclear axis are given here. A more detailed treatment of polarizabilities and their experimental significance is provided in ref. 45 for AK–AKE molecules or in ref. 44 for AK–AK molecules.| Mol. | Ref. | μ e/D | r e/Å | D e/cm−1 | ω e/cm−1 | α ∥ /a.u. |
|---|---|---|---|---|---|---|
| a Polarizabilities along the internuclear axis for the diatomic molecules. b Experimental results. c d 0 values are given. | ||||||
| LiBe | This work | 3.47 | 2.60 | 2427 | 313 | 365 |
| 60 | 3.58 | 2.58 | 2406 | 300 | ||
| 58 | 2.61 | 2339 | 300 | |||
| 93 | 2.59 | 295 | ||||
| LiMg | This work | 1.18 | 3.10 | 1538 | 181 | 470 |
| 79 | 1.22 | 3.10 | 1395 | 174 | ||
| 63 | 1.02 | 3.10 | 1445 | 180 | ||
| 59 | 0.86c | 3.12 | 1332 | 187 | 482 | |
| 60 | 1.12 | 3.11 | 1432 | 206 | ||
| 58 | 3.11 | 1613 | 183 | |||
| 94 | 1331 | 190 | ||||
| LiCa | This work | 1.19 | 3.39 | 2613 | 200 | 588 |
| 39 | 3.34 | 2883 | 203 | |||
| 72 | 3.40 | 2131 | 206 | |||
| 59 | 1.10c | 3.40 | 2260 | 210 | 599 | |
| 60 | 1.12 | 3.36 | 2607 | 207 | ||
| 73 | 3.40 | 2178 | 204 | |||
| 71 | 3.30 | 2355 | 196 | |||
| 69 | 3.36 | 2605 | 202 | |||
| LiSr | This work | 0.28 | 3.57 | 2471 | 181 | 653 |
| 72 | 3.58 | 2074 | 181 | |||
| 59 | 0.31c | 3.53 | 2223 | 196 | 640 | |
| 60 | 0.24 | 3.55 | 2401 | 184 | ||
| 61 | 0.34 | 3.48 | 2587 | 185 | ||
| NaBe | This work | 2.33 | 2.97 | 1291 | 173 | 397 |
| 58 | 3.05 | 1129 | 164 | |||
| NaMg | This work | 0.86 | 3.47 | 946 | 90 | 432 |
| 63 | 0.72 | 3.53 | 825 | 83 | ||
| 58 | 3.56 | 887 | 85 | |||
| NaCa | This work | 1.18 | 3.67 | 1792 | 103 | 577 |
| 45 | 1.01 | 3.72 | 1453 | 97 | 594 | |
| NaSr | This work | 0.51 | 3.84 | 1728 | 87 | 636 |
| 45 | 0.49 | 3.89 | 1441 | 82 | 633 | |
| 61 | 0.62 | 3.82 | 1597 | 85 | ||
| KBe | This work | 2.22 | 3.51 | 920 | 122 | 628 |
| KMg | This work | 1.08 | 3.99 | 779 | 64 | 656 |
| 63 | 0.83 | 4.09 | 647 | 58 | ||
| KCa | This work | 2.12 | 4.20 | 1455 | 71 | 869 |
| 45 | 1.67 | 4.32 | 974 | 61 | 892 | |
| KSr | This work | 1.52 | 4.39 | 1358 | 57 | 925 |
| 45 | 1.27 | 4.53 | 964 | 48 | 942 | |
| 61 | 1.52 | 4.41 | 1166 | 52 | ||
| RbBe | This work | 1.97 | 3.70 | 816 | 104 | 631 |
| RbMg | This work | 1.04 | 4.17 | 744 | 54 | 664 |
| 63 | 0.79 | 4.29 | 586 | 47 | ||
| RbCa | This work | 2.19 | 4.37 | 1337 | 57 | 922 |
| 43 | 2.54 | 4.37 | 1406 | 58 | ||
| 45 | 1.75 | 4.53 | 921 | 49 | 961 | |
| RbSr | This work | 1.64 | 4.56 | 1279 | 43 | 972 |
| 42 | 1.80 | 4.59 | 1274 | 42 | ||
| 77 | 4.67 | 1041 | 38 | |||
| 76 | 4.67 | 1018 | 36 | |||
| 45 | 1.41 | 4.72 | 916 | 36 | 1009 | |
| 61 | 1.54 | 4.60 | 1073 | 32 | ||
| Mol. | Ref. | μ e/D | r e/Å | D e/cm−1 | ω e/cm−1 | α ∥ /a.u. |
|---|---|---|---|---|---|---|
| a Polarizabilities along the internuclear axis for the diatomic molecules. | ||||||
| LiBe | This work | −0.61 | 5.51 | 59 | 25 | 223 |
| LiMg | This work | −2.52 | 4.72 | 222 | 32 | 423 |
| LiCa | This work | −4.58 | 4.59 | 522 | 55 | 1031 |
| 39 | 4.33 | 608 | 67 | |||
| 72 | 5.01 | 265 | 30 | |||
| LiSr | This work | −6.61 | 4.59 | 692 | 61 | 1340 |
| 72 | 4.60 | 401 | 47 | |||
| NaBe | This work | −0.45 | 5.84 | 50 | 18 | 229 |
| NaMg | This work | −0.99 | 5.71 | 131 | 21 | 326 |
| NaCa | This work | −1.62 | 5.74 | 237 | 24 | 686 |
| NaSr | This work | −2.00 | 5.81 | 287 | 23 | 1200 |
| KBe | This work | −0.72 | 5.99 | 48 | 16 | 300 |
| KMg | This work | −1.58 | 5.73 | 157 | 20 | 338 |
| KCa | This work | −2.50 | 5.73 | 343 | 26 | 950 |
| KSr | This work | −2.99 | 5.95 | 376 | 22 | 1523 |
| RbBe | This work | −0.79 | 6.03 | 47 | 15 | 363 |
| RbMg | This work | −1.66 | 5.84 | 170 | 18 | 645 |
| RbCa | This work | −2.13 | 6.05 | 316 | 19 | 922 |
| 43 | 5.98 | 336 | 19 | |||
| RbSr | This work | −2.66 | 6.15 | 343 | 16 | 1491 |
| 42 | 6.17 | 390 | 16 | |||
| 77 | 6.25 | 329 | 15 | |||
| 77 | 6.15 | 336 | 15 | |||
A similar compilation of data for the lowest 4Σ+ state is given in Table 3, although fewer theoretical and experimental values are available.¶ In general, the equilibrium radius is larger and the potential depth and vibrational constant are smaller than corresponding quantities for the ground state. For the polarizability no clear trend can be observed.
3.2 Trends for AK–AKE molecules
A diatomic molecule formed by a single alkali atom and a single alkaline earth atom comprises three valence electrons. If excitations of core electrons and ionizations are neglected, these three electrons can only form a doublet or a quartet state. The AK atom, providing one unpaired electron, is always in a doublet state in the asymptotic limit of separated atoms. In contrast, the AKE atom can be either in a singlet or in a triplet state. A doublet state of the molecule is therefore either realized by the combination of a singlet AKE atom with the doublet AK atom, or by the combination of a triplet AKE atom with an anti-aligned electron from the AK atom. Quartet multiplicity can only arise if a triplet state of the AKE atom is combined with an aligned electron on the AK atom. The ground state of the molecule must be a doublet state, since the lowest state of the AKE atom is of singlet character. Only an excited triplet state of the AKE can result in a quartet state. For the AKE atoms considered in this study (Be–Sr), this is a 3P state with excitation energies between 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and 14
000 cm−1 and 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1. For Ba and Ra the lowest excitation has 3D character. The lowest excitation of the AK atom is a 2P state with energies ranging from 12
500 cm−1. For Ba and Ra the lowest excitation has 3D character. The lowest excitation of the AK atom is a 2P state with energies ranging from 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 to 17
500 cm−1 to 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. The energy difference between the lowest excitation of the AKE (3P) and the AK atom (2P) is plotted in graphics (a) of Fig. 2. Note that there are negative values for combinations of light alkali atoms and heavy alkaline earth atoms. Rather than the 3D-excitations, which are the lowest ones, the 3P-excitations were used in Fig. 2 for Ba and Ra. In plot (b) of Fig. 2 the difference in electronegativities (ENs) is shown with a behavior similar to the differences in excitation energies. A positive value of the electronegativity difference indicates that the electron density is pulled towards the AKE atom. Only combinations of light AK atoms with heavy AKE atoms have negative differences. Within our test set only LiSr has a negative EN difference. The difference in excitation energy or electronegativities characterizes the direction and magnitude of the pull at the electron density. Additionally, the polarizability is important as it measures the flexibility of the electron density. The atomic values for the polarizability range from 37 to 248 a.u. for AKE atoms and from 164 to 313 a.u. for AK atoms,95 with an increasing value for heavier atoms. The change in the orbital of the AK atom can be expected to be larger than the change for the AKE atom if atoms of similar mass are combined. Such a behavior was observed and is discussed in Section 3.3.
000 cm−1. The energy difference between the lowest excitation of the AKE (3P) and the AK atom (2P) is plotted in graphics (a) of Fig. 2. Note that there are negative values for combinations of light alkali atoms and heavy alkaline earth atoms. Rather than the 3D-excitations, which are the lowest ones, the 3P-excitations were used in Fig. 2 for Ba and Ra. In plot (b) of Fig. 2 the difference in electronegativities (ENs) is shown with a behavior similar to the differences in excitation energies. A positive value of the electronegativity difference indicates that the electron density is pulled towards the AKE atom. Only combinations of light AK atoms with heavy AKE atoms have negative differences. Within our test set only LiSr has a negative EN difference. The difference in excitation energy or electronegativities characterizes the direction and magnitude of the pull at the electron density. Additionally, the polarizability is important as it measures the flexibility of the electron density. The atomic values for the polarizability range from 37 to 248 a.u. for AKE atoms and from 164 to 313 a.u. for AK atoms,95 with an increasing value for heavier atoms. The change in the orbital of the AK atom can be expected to be larger than the change for the AKE atom if atoms of similar mass are combined. Such a behavior was observed and is discussed in Section 3.3.
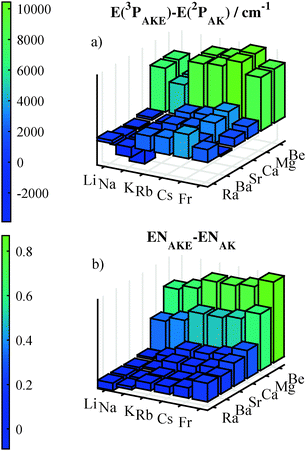 | ||
| Fig. 2 Differences between AK and AKE atoms for two atomic properties are shown in the figure, in the upper plot energy differences of the first P-excitations92 and in the lower plot the differences in the electronegativities according to Pauling's scale.96 | ||
Fig. 3 shows the PEDMs (a) and dissociation energies (b) for the ground state of the 16 AK–AKE molecules within our test set. The smallest PEDM was obtained for LiSr, but unlike the difference in ENs, it still is positive. The largest EN difference for the calculated molecules is found for the RbBe molecule, but LiBe shows the largest dipole moment. The increase by going from light to heavy AK atoms and AKE atoms as seen in the difference of ENs in plot (b) of Fig. 2 is not seen for the PEDMs. For KMg and RbMg small PEDMs are observable in Fig. 3. The small PEDMs for Mg containing molecules are probably related to the significantly smaller electronegativity difference for Mg than for Be, although they have similar differences in excitation energies (Fig. 2). Also, the potential depths are different. In plot (b) of Fig. 3 the potential depths are shown and the values for molecules containing Mg are noticeably smaller than for the other AKE atoms, with no other trend being obvious for AKE atoms. However, there is a trend for AK atoms. The potential depth decreases seemingly exponentially in going from light to heavy AK atoms. The largest potential depth was determined for LiCa (2613 cm−1), the smallest one for RbMg (744 cm−1). In contrast to the PEDM and the equilibrium radii, the core polarization potential changes the potential depth in both directions. In cases where the AK atom is significantly lighter than the AKE atom the potential depth is reduced. However, if the AKE atom is lighter, the potential depth is increased. The equilibrium radii increase with inclusion of core polarization potentials. This effect is larger for heavier AK atoms, but shows no recognizable dependence on the AKE atom (ESI†).
 | ||
| Fig. 3 The permanent electric dipole moment (a) and the potential depth (b) for several AK–AKE molecules in their ground state (2Σ+) are shown. | ||
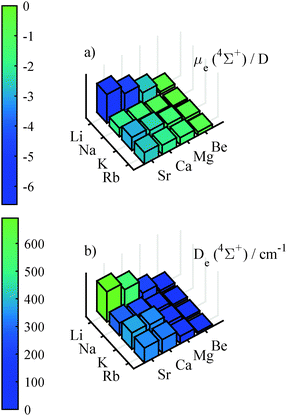
In contrast to the strictly positive PEDM for the doublet ground states the PEDMs for the lowest Σ+ state in the quartet manifold are negative, as can be seen in Fig. 4. The PEDMs for the quartet states show a correlation with the difference in ENs (b) in Fig. 2. The most negative PEDM is found for the only molecule with a negative EN difference (LiSr), while small PEDMs are obtained for strongly positive EN differences. Small PEDMs of the 4Σ+ state are observable in plot (a) in Fig. 4 for Na containing diatomic molecules including NaBe with the smallest value. This seems to be related to the first excitation energy of Na, which is the largest of all AK atoms. The large excitation energy leads to the small – and for some combinations with Na even negative – differences in the excitation energy, as can be seen in graphics (a) of Fig. 2. The potential depth turns out to be a reliable descriptor for the magnitude of the PEDM, as is evident by comparing plot (a) and (b) of Fig. 4, but is less useful for the estimation of PEDMs in the doublet manifold. For the 4Σ+ state the dissociation energy and the PEDM have a correlation coefficient of R = −0.97.
The equilibrium internuclear distances of the lowest Σ+ states in the two multiplicities are given in the Tables 2 and 3. The re values for the doublet state are all below 4.57 Å, those for the quartet states lie above this value. The equilibrium distances can be compared to the tabulated covalent97 and van der Waals98 radii (ESI†). The internuclear distances for the ground state minimum lie in between the covalent and van der Waals values. On average, they are off by 0.4 Å from the covalent radii and by 1.4 Å from the van der Waals radii. Them being closer to the covalent radii indicates a covalent or ionic bond in the lowest state of the doublet manifold. The lowest 4Σ+ states have equilibrium internuclear separations that are on average 0.5 Å larger than predicted by the tabulated van der Waals values, which indicates a weak bond.
The fraction of ionic character48 can be estimated by dividing the determined dipole moment by the dipole moment obtained by shifting one electron by the equilibrium distance: 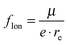 . For the ground state, this fraction lies below 21%, except for molecules containing Be, where the values are always above 21%. As is obvious from the method of calculation, this quantity is correlated with the determined dipole moment and should be interpreted with caution. For the quartet states, particularly high values are observed for Li containing molecules.
. For the ground state, this fraction lies below 21%, except for molecules containing Be, where the values are always above 21%. As is obvious from the method of calculation, this quantity is correlated with the determined dipole moment and should be interpreted with caution. For the quartet states, particularly high values are observed for Li containing molecules.
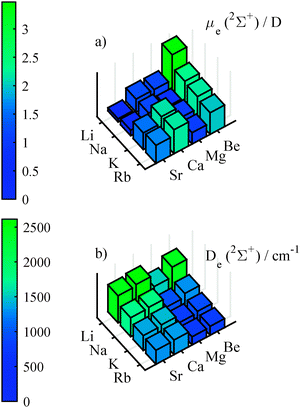
With finite field calculations, which we performed in order to determine the dipole moment, we could also determine the polarizabilities of the molecules along the internuclear axis. Graphics (a) of Fig. 5 shows the polarizabilities for the ground state, which increase with atomic mass. These values are about 3.7 (with an variation from 3.4 to 4.0) times larger than the mean of the polarizability of the atoms involved. The polarizabilities for the quartet states show stronger variations (from 1.8 to 7.7 of the mean of the atomic pol.) than for the doublet states, as can be seen in graphics (b) of Fig. 5. Furthermore, there is a pronounced increase of polarizability for heavy AKE atoms, but no clear trend for the AK atoms. This dependence is probably related to the lowering of the first excitation energy when going from light to heavy AKE atoms. An increased mixing of the s-orbital of the AK atom and the p-orbital of the AKE atom facilitates a change in the electron density distribution.
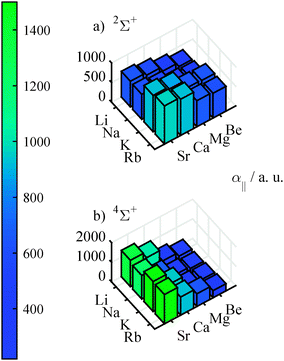 | ||
| Fig. 5 Finite-field polarizabilities in the doublet ground state (upper graphics) and the lowest 4Σ+ state (lower graphics), calculated at the corresponding equilibrium geometry. | ||
3.3 Qualitative picture
Typical potential energy curves and PEDM curves for the lowest Σ+ states in the two multiplicities are shown in Fig. 6. The lowest 2Σ+ is strongly bound with a positive PEDM. The PEDM approaches zero for large internuclear distances as expected for neutral molecules. In contrast, the lowest 4Σ+ state is weakly bound with a negative PEDM. In general, the maximum (2Σ+) or minimum (4Σ+) of the PEDM curve is found for internuclear distances smaller than the equilibrium distance. The results displayed in Fig. 6 refer to LiBe, but the same behavior was previously observed for LiCa,39 RbCa,42 and RbSr.43 In the current study, all 16 AK–AKE molecules confirm this trend. However, this behavior is not very pronounced for LiSr, and a different sign of the dipole moment can be expected in the ground state if Ba or Ra atoms are combined with Li. In fact, this has been observed by Gou et al.64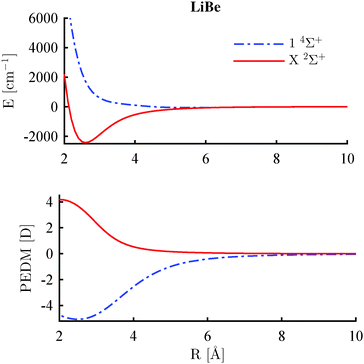 | ||
| Fig. 6 Potentials and PEDMs of the lowest Σ+ state in the doublet and quartet multiplicity for the LiBe molecule. | ||
Our findings are summarized in Fig. 7. The ground state, displayed in graphics (a), shows a smaller bond distance. The dipole moment is positive, the vector of the dipole moment points from the AKE atom (++) to the AK atom (+). This is the result of the center of charge of the electrons being closer to the AKE atom than the center of positive charge. The quartet state has a larger bond distance and a negative dipole moment. The center of electron charge is now closer to the AK atom than the center of positive charge. We explain this behavior by the orbital occupation indicated on the right side of Fig. 7. In the ground state (a) the 1st orbital, mainly an s-orbital around the AKE atom,|| is doubly occupied. The 2nd orbital, mainly a mixture of s-orbitals from the AK atom and p-orbitals from the AKE atom, is singly occupied. Because the AKE orbital mixes into it, it is not centered at the AK atom. Therefore, the center of negative charge is closer to the AKE atom, and a positive PEDM is obtained in our coordinate system. This agrees with the situation indicated by the atomic polarizabilities. In general, the AK atoms have larger polarizabilities than AKE atoms. In the ground state, the highest occupied AK orbital should deform more easily and mix with AKE orbitals. The situation is different for the lowest Σ+ state in the quartet multiplicity (b) in Fig. 7. Since all spins need to be aligned, the Pauli principle does not allow for a double occupation of the 1st orbital. Therefore, one electron is transferred from this orbital into the 3rd orbital, which is a mixture of s-orbitals from the AK atom and p-orbitals from the AKE atom. For this reason, it has a probability density close to the AK atom, which changes the direction of the PEDM compared to the ground state. The 3rd orbital also mixes s- and p-orbital contributions in a similar way as the 2nd orbital does. However, unlike the 2nd orbital, it has an additional node between the atoms, not only at the center of the AKE core.|| It corresponds, at least approximately, to the antibonding counterpart of the 2nd orbital, which explains the small dissociation energy of the lowest 4Σ+ state.
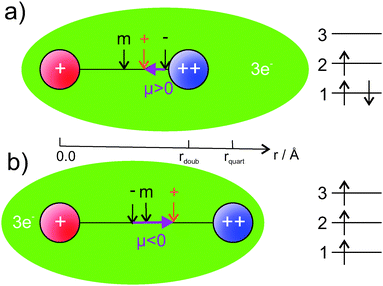 | ||
| Fig. 7 A visualization of the charge distribution in our set of 16 AK–AKE molecules (no absolute scale). The AK (+) atom is shown in red, the AKE (++) atom in blue. Center of mass, positive and negative charge are indicated by arrows. On the right side the orbital occupation discussed in the text is depicted. Calculated isosurfaces of the corresponding orbitals can be found in the ESI.† | ||
3.4 Dipole moment predictions
In this section we attempt to describe and predict the behavior of the dipole moment in the ground state due to its experimental importance for several applications mentioned in the introduction. The PEDMs of the lowest Σ+ state of the quartet multiplicity are well correlated with the dissociation energy, which is not the case for the ground state. However, we find the following empirical equation to reproduce the dipole moments surprisingly well for all species under investigation: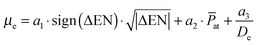 | (1) |
![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) at, and the dissociation energy De as input for the evaluation of the dipole moment. We note that it does not have yet a clear theoretical justification, as it was derived from an analysis of correlations between the dipole moment and atomic properties by a simple trial and error approach. However, it agrees very well with the available ab initio data, as can be seen from Fig. 8, although it only requires three fitting parameters a1, a2 and a3. At least the occurrence of the atomic descriptors in the formula can be readily justified. The difference in ENs accounts for the pull on the electron density, and the corresponding contribution to the dipole moment must therefore be related to a charge transfer. We do not have an explanation for the square root dependence, which made it necessary to also introduce the sign function in order to have the sign of the EN difference correlate with the direction of dipole moment. Because the value of the EN difference covers only a region from −0.1 to 0.9 other functions might also be suitable to capture the behavior. Slightly worse results are obtained for functions like
at, and the dissociation energy De as input for the evaluation of the dipole moment. We note that it does not have yet a clear theoretical justification, as it was derived from an analysis of correlations between the dipole moment and atomic properties by a simple trial and error approach. However, it agrees very well with the available ab initio data, as can be seen from Fig. 8, although it only requires three fitting parameters a1, a2 and a3. At least the occurrence of the atomic descriptors in the formula can be readily justified. The difference in ENs accounts for the pull on the electron density, and the corresponding contribution to the dipole moment must therefore be related to a charge transfer. We do not have an explanation for the square root dependence, which made it necessary to also introduce the sign function in order to have the sign of the EN difference correlate with the direction of dipole moment. Because the value of the EN difference covers only a region from −0.1 to 0.9 other functions might also be suitable to capture the behavior. Slightly worse results are obtained for functions like 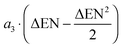 or the bounded a3·tanh(ΔEN). The increase of the PEDM with increasing mean polarizability is easily understood by the greater spatial flexibility of the electron distribution. However, an explanation for the third term in eqn (1) is less straight-forward. The corresponding fitting parameter a3 takes a negative value in the model, therefore reducing the dipole moment proportional to the inverse of the corresponding dissociation energy. In other words, the weaker the bond, the more effectively this term reduces the dipole moment. This last contribution is not fully understood, but both properties are related to the spatial distribution of the orbitals.
or the bounded a3·tanh(ΔEN). The increase of the PEDM with increasing mean polarizability is easily understood by the greater spatial flexibility of the electron distribution. However, an explanation for the third term in eqn (1) is less straight-forward. The corresponding fitting parameter a3 takes a negative value in the model, therefore reducing the dipole moment proportional to the inverse of the corresponding dissociation energy. In other words, the weaker the bond, the more effectively this term reduces the dipole moment. This last contribution is not fully understood, but both properties are related to the spatial distribution of the orbitals.
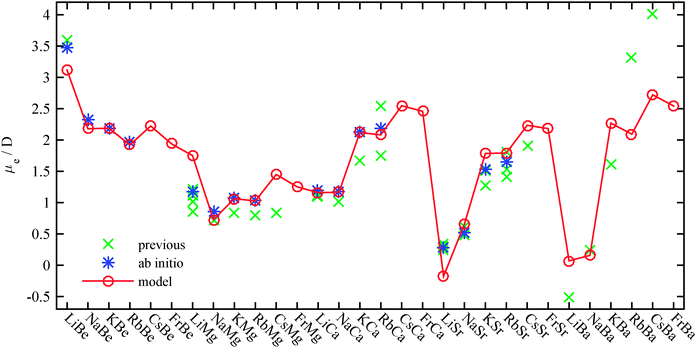 | ||
| Fig. 8 Dipole moment predictions as described in the text (○). The three parameters of the model were determined by fitting to the ab initio results of this work (*). The resulting model shows good agreement with results from previous theoretical treatments (×) listed in Table 2. Additional values have been added for the CsMg (ref. 61), CsSr (ref. 63) and AK–Ba molecules (ref. 64). | ||
This empirical model allows us to predict the dipole moments for other AK–AKE molecules. However, while the required ENs and the atomic polarizabilities can be found in ref. 95 and 96, the dissociation energies need to be estimated. For Ba, the values from ref. 64 have been used. The potential depth of molecules including Cs or Fr were extrapolated with an exponential function from values for smaller AK atoms, since an exponential dependence was observed for the dissociation energy in Fig. 3. These results, together with previous theoretical results for AK–AKE molecules beyond our test set,61,63,64 are shown in Fig. 8. We note that Gou et al.64 neglected the polarization of the cores, which might explain their larger amplitudes, similar to what we observed without core polarization potentials (Fig. 1). A detailed comparison between predicted and previous values is given in the ESI.†
4 Conclusion
The lowest Σ+ states in the doublet and quartet manifold for a selection of 16 AK–AKE molecules were analyzed at the MCSCF + MRCI level of theory. Trends for the PEDMs, equilibrium internuclear separations, dissociation energies, and polarizabilities along the internuclear axis were discussed. We find that the PEDMs of the lowest Σ+ state in the doublet and quartet multiplicity are pointing in opposite directions for all molecules under investigation, which is in line with previous calculations. This behavior was explained in a molecular orbital picture. We further presented an empirical formula which describes the PEDM in the 2Σ+ state as a function of two atomic descriptors (electronegativity, polarizability) and the dissociation energy. After fitting three parameters of the formula to our test set, we used this model to successfully predict the PEDM of several AK–AKE molecules beyond our initial test set.The PEDM is important for applications of ultracold molecules, since it is the essential parameter for the interaction with microwaves, and, in combination with the polarizability, for the alignment in electric fields and optical lattices. A high PEDM is favorable because lower intensities and field strengths are sufficient to manipulate the molecules. In our study we find the highest PEDM for combinations with Be. However, handling these molecules might be a problem in the experiment due to the toxicity of beryllium. Good alternatives with high PEDM are RbCa, KCa, and RbSr, with the latter being the most promising candidate at present.74 Our extrapolation formula indicates that CsCa might also be a promising choice.
Acknowledgements
The authors gratefully acknowledge support from NAWI Graz. This research was supported by the Austrian Science Fund (FWF) under Grant No. 22962-N20.References
- J. Ulmanis, J. Deiglmayr, M. Repp, R. Wester and M. Weidemuller, Chem. Rev., 2012, 112, 4890–4927 CrossRef CAS PubMed.
- G. Quéméner and P. S. Julienne, Chem. Rev., 2012, 112, 4949–5011 CrossRef PubMed.
- I. Bloch and P. Zoller, in Ultracold Bosonic and Fermionic Gases, ed. A. L. F. Kathryn Levin and D. M. Stamper-Kurn, Elsevier, 2012, vol. 5, pp. 121–156 Search PubMed.
- L. D. Carr, D. DeMille, R. V. Krems and J. Ye, New J. Phys., 2009, 11, 055049 CrossRef.
- J. Doyle, B. Friedrich, R. Krems and F. Masnou-Seeuws, Eur. Phys. J. D, 2004, 31, 149–164 CrossRef CAS.
- M. Baranov, L. Dobrek, K. Goral, L. Santos and M. Lewenstein, Phys. Scr., 2002, T102, 74–81 CrossRef CAS.
- L. Santos, G. V. Shlyapnikov, P. Zoller and M. Lewenstein, Phys. Rev. Lett., 2000, 85, 1791–1794 CrossRef CAS PubMed.
- K. Goral, L. Santos and M. Lewenstein, Phys. Rev. Lett., 2002, 88, 170406 CrossRef CAS PubMed.
- L. D. Carr, G. V. Shlyapnikov and Y. Castin, Phys. Rev. Lett., 2004, 92, 150404 CrossRef CAS PubMed.
- M. A. Baranov, L. Dobrek and M. Lewenstein, Phys. Rev. Lett., 2004, 92, 250403 CrossRef CAS PubMed.
- H. P. Buchler, E. Demler, M. Lukin, A. Micheli, N. Prokof'ev, G. Pupillo and P. Zoller, Phys. Rev. Lett., 2007, 98, 060404 CrossRef CAS PubMed.
- M. A. Baranov, M. Dalmonte, G. Pupillo and P. Zoller, Chem. Rev., 2012, 112, 5012–5061 CrossRef CAS PubMed.
- D. DeMille, Phys. Rev. Lett., 2002, 88, 067901 CrossRef CAS PubMed.
- B. K. Stuhl, M. T. Hummon and J. Ye, Annu. Rev. Phys. Chem., 2014, 65, 501–518 CrossRef CAS PubMed.
- R. V. Krems, Phys. Chem. Chem. Phys., 2008, 10, 4079–4092 RSC.
- E. R. Hudson, C. Ticknor, B. C. Sawyer, C. A. Taatjes, H. J. Lewandowski, J. R. Bochinski, J. L. Bohn and J. Ye, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 73, 063404 CrossRef.
- C. Chin, V. V. Flambaum and M. G. Kozlov, New J. Phys., 2009, 11, 055048 CrossRef.
- M. Kajita, G. Gopakumar, M. Abe and M. Hada, J. Phys. B: At., Mol. Opt. Phys., 2013, 46, 025001 CrossRef.
- M. Kajita, G. Gopakumar, M. Abe and M. Hada, J. Mol. Spectrosc., 2014, 300, 99–107 CrossRef CAS.
- V. V. Flambaum and M. G. Kozlov, Phys. Rev. Lett., 2007, 99, 150801 CrossRef CAS PubMed.
- E. R. Meyer and J. L. Bohn, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 80, 042508 CrossRef.
- E. R. Meyer, J. L. Bohn and M. P. Deskevich, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 73, 062108 CrossRef.
- K. Beloy, A. W. Hauser, A. Borschevsky, V. V. Flambaum and P. Schwerdtfeger, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 062114 CrossRef.
- E. R. Hudson, H. J. Lewandowski, B. C. Sawyer and J. Ye, Phys. Rev. Lett., 2006, 96, 143004 CrossRef PubMed.
- A. Fioretti, D. Comparat, A. Crubellier, O. Dulieu, F. Masnou-Seeuws and P. Pillet, Phys. Rev. Lett., 1998, 80, 4402–4405 CrossRef CAS.
- T. Takekoshi, B. M. Patterson and R. J. Knize, Phys. Rev. Lett., 1998, 81, 5105–5108 CrossRef CAS.
- T. Takekoshi, B. M. Patterson and R. J. Knize, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, R5–R7 CrossRef CAS.
- A. N. Nikolov, E. E. Eyler, X. T. Wang, J. Li, H. Wang, W. C. Stwalley and P. L. Gould, Phys. Rev. Lett., 1999, 82, 703–706 CrossRef CAS.
- A. J. Kerman, J. M. Sage, S. Sainis, T. Bergeman and D. DeMille, Phys. Rev. Lett., 2004, 92, 153001 CrossRef PubMed.
- A. J. Kerman, J. M. Sage, S. Sainis, T. Bergeman and D. DeMille, Phys. Rev. Lett., 2004, 92, 033004 CrossRef PubMed.
- J. M. Sage, S. Sainis, T. Bergeman and D. DeMille, Phys. Rev. Lett., 2005, 94, 203001 CrossRef PubMed.
- M. W. Mancini, G. D. Telles, A. R. L. Caires, V. S. Bagnato and L. G. Marcassa, Phys. Rev. Lett., 2004, 92, 133203 CrossRef CAS PubMed.
- D. Wang, J. Qi, M. F. Stone, O. Nikolayeva, H. Wang, B. Hattaway, S. D. Gensemer, P. L. Gould, E. E. Eyler and W. C. Stwalley, Phys. Rev. Lett., 2004, 93, 243005 CrossRef CAS PubMed.
- D. Wang, J. Qi, M. F. Stone, O. Nikolayeva, B. Hattaway, S. D. Gensemer, H. Wang, W. T. Zemke, P. L. Gould, E. E. Eyler and W. C. Stwalley, Eur. Phys. J. D, 2004, 31, 165–177 CrossRef CAS.
- A. J. Leggett, Rev. Mod. Phys., 2001, 73, 307–356 CrossRef CAS.
- S. Kraft, F. Vogt, O. Appel, F. Riehle and U. Sterr, Phys. Rev. Lett., 2009, 103, 130401 CrossRef PubMed.
- S. Stellmer, M. K. Tey, B. Huang, R. Grimm and F. Schreck, Phys. Rev. Lett., 2009, 103, 200401 CrossRef PubMed.
- Y. Takasu, K. Maki, K. Komori, T. Takano, K. Honda, M. Kumakura, T. Yabuzaki and Y. Takahashi, Phys. Rev. Lett., 2003, 91, 040404 CrossRef PubMed.
- G. Krois, J. V. Pototschnig, F. Lackner and W. E. Ernst, J. Phys. Chem. A, 2013, 117, 13719–13731 CrossRef CAS PubMed.
- F. Lackner, G. Krois, T. Buchsteiner, J. V. Pototschnig and W. E. Ernst, Phys. Rev. Lett., 2014, 113, 153001 CrossRef PubMed.
- G. Krois, F. Lackner, J. V. Pototschnig, T. Buchsteiner and W. Ernst, Phys. Chem. Chem. Phys., 2014, 16, 22373–22381 RSC.
- J. V. Pototschnig, G. Krois, F. Lackner and W. E. Ernst, J. Chem. Phys., 2014, 141, 234309 CrossRef PubMed.
- J. V. Pototschnig, G. Krois, F. Lackner and W. E. Ernst, J. Mol. Spectrosc., 2015, 310, 126–134 CrossRef CAS PubMed.
- J. Deiglmayr, M. Aymar, R. Wester, M. Weidemueller and O. Dulieu, J. Chem. Phys., 2008, 129, 064309 CrossRef PubMed.
- G. Gopakumar, M. Abe, M. Hada and M. Kajita, J. Chem. Phys., 2014, 140, 224303 CrossRef PubMed.
- A. Micheli, G. K. Brennen and P. Zoller, Nat. Phys., 2006, 2, 341–347 CrossRef CAS.
- S. Kotochigova, Phys. Rev. Lett., 2007, 99, 073003 CrossRef PubMed.
- E. S. Rittner, J. Chem. Phys., 1951, 19, 1030–1035 CrossRef CAS.
- P. Brumer and M. Karplus, J. Chem. Phys., 1973, 58, 3903–3918 CrossRef CAS.
- R. L. Matcha and S. C. King, J. Am. Chem. Soc., 1976, 98, 3420–3432 CrossRef CAS.
- T. Törring, W. E. Ernst and J. Kändler, J. Chem. Phys., 1989, 90, 4927–4932 CrossRef.
- T. Törring, W. E. Ernst and S. Kindt, J. Chem. Phys., 1984, 81, 4614–4619 CrossRef.
- S. F. Rice, H. Martin and R. W. Field, J. Chem. Phys., 1985, 82, 5023–5034 CrossRef CAS.
- J. Schamps, M. Bencheikh, J. C. Barthelat and R. W. Field, J. Chem. Phys., 1995, 103, 8004–8013 CrossRef CAS.
- H. Schall, M. Dulick and R. W. Field, J. Chem. Phys., 1987, 87, 2898–2912 CrossRef CAS.
- W. E. Ernst and J. O. Schröder, Z. Phys. D: At., Mol. Clusters, 1986, 1, 103–112 CrossRef CAS.
- S. Hou and P. F. Bernath, J. Phys. Chem. A, 2015, 119, 1435–1438 CrossRef CAS PubMed.
- C. W. Bauschlicher, S. R. Langhoff and H. Partridge, J. Chem. Phys., 1992, 96, 1240–1247 CrossRef CAS.
- G. Gopakumar, M. Abe, M. Kajita and M. Hada, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 062514 CrossRef.
- S. Kotochigova, A. Petrov, M. Linnik, J. Klos and P. S. Julienne, J. Chem. Phys., 2011, 135, 164108 CrossRef PubMed.
- R. Guerout, M. Aymar and O. Dulieu, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 042508 CrossRef.
- M. Aymar, R. Guerout and O. Dulieu, J. Chem. Phys., 2011, 135, 064305 CrossRef CAS PubMed.
- L. Augustovičová and P. Soldán, J. Chem. Phys., 2012, 136, 084311 CrossRef PubMed.
- D. Z. Gou, X. Y. Kuang, Y. F. Gao and D. M. Huo, J. Chem. Phys., 2015, 142, 034308 CrossRef PubMed.
- A. R. Allouche and M. Aubert-Frécon, J. Chem. Phys., 1994, 100, 938–944 CrossRef CAS.
- J. D'Incan, C. Effantin, A. Bernard, G. Fabre, R. Stringat, A. Boulezhar and J. Vérges, J. Chem. Phys., 1994, 100, 945–949 CrossRef.
- N. Boutassetta, A. R. Allouche and M. Aubert-Frécon, Chem. Phys., 1994, 189, 33–39 CrossRef CAS.
- M. Ivanova, A. Stein, A. Pashov, A. V. Stolyarov, H. Knockel and E. Tiemann, J. Chem. Phys., 2011, 135, 174303 CrossRef PubMed.
- A. Stein, M. Ivanova, A. Pashov, H. Knöckel and E. Tiemann, J. Chem. Phys., 2013, 138, 114306 CrossRef PubMed.
- C. H. Wu, H. R. Ihle and K. A. Gingerich, Int. J. Mass Spectrom., 1983, 47, 235–238 CrossRef CAS.
- A. R. Allouche and M. Aubert-Frécon, Chem. Phys. Lett., 1994, 222, 524–528 CrossRef CAS.
- G. Gopakumar, M. Abe, M. Hada and M. Kajita, J. Chem. Phys., 2013, 138, 194307 CrossRef PubMed.
- L. M. Russon, G. K. Rothschopf, M. D. Morse, A. I. Boldyrev and J. Simons, J. Chem. Phys., 1998, 109, 6655–6665 CrossRef CAS.
- B. Pasquiou, A. Bayerle, S. M. Tzanova, S. Stellmer, J. Szczepkowski, M. Parigger, R. Grimm and F. Schreck, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 023601 CrossRef.
- P. S. Zuchowski, J. Aldegunde and J. M. Hutson, Phys. Rev. Lett., 2010, 105, 153201 CrossRef PubMed.
- T. Chen, S. B. Zhu, X. L. Li, J. Qian and Y. Z. Wang, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 063402 CrossRef.
- P. S. Zuchowski, R. Guerout and O. Dulieu, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 012507 CrossRef.
- S. Knecht, L. K. Sorensen, H. J. A. Jensen, T. Fleig and C. M. Marian, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 055101 CrossRef.
- Y. F. Gao and T. Gao, Mol. Phys., 2014, 112, 3015–3023 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2012.1, a package of ab initio programs, 2012, see http://www.molpro.net Search PubMed.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Theor. Chem. Acc., 1992, 84, 95–103 CrossRef CAS.
- B. P. Prascher, D. E. Woon, K. A. Peterson, T. H. Dunning and A. K. Wilson, Theor. Chem. Acc., 2011, 128, 69–82 CrossRef CAS.
- H. D. Li, H. Feng, W. G. Sun, Y. Zhang, Q. C. Fan, K. A. Peterson, Y. M. Xie and H. F. Schaefer, Mol. Phys., 2013, 111, 2292–2298 CrossRef CAS.
- I. S. Lim, P. Schwerdtfeger, B. Metz and H. Stoll, J. Chem. Phys., 2005, 122, 104103 CrossRef PubMed.
- I. S. Lim, H. Stoll and P. Schwerdtfeger, J. Chem. Phys., 2006, 124, 034107 CrossRef PubMed.
- W. Müller, J. Flesh and W. Meyer, J. Chem. Phys., 1984, 80, 3297–3310 CrossRef.
- W. Müller and W. Meyer, J. Chem. Phys., 1984, 80, 3311–3320 CrossRef.
- D. A. Fedorov, A. Derevianko and S. A. Varganov, J. Chem. Phys., 2014, 140, 184315 CrossRef PubMed.
- Y. Ralchenko, A. Kramida, J. Reader and NIST ASD Team, National Institute of Standards and Technology, Gaithersburg, MD, 2015, available: http://physics.nist.gov/asd.
- R. Schlachta, I. Fischer, P. Rosmus and V. E. Bondybey, Chem. Phys. Lett., 1990, 170, 485–491 CrossRef CAS.
- K. R. Berry and M. A. Duncan, Chem. Phys. Lett., 1997, 279, 44–49 CrossRef CAS.
- J. Mitroy, M. S. Safronova and C. W. Clark, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 202001 CrossRef.
- CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, 85th edn, 2004 Search PubMed.
- B. Cordero, V. Gomez, A. E. Platero-Prats, M. Reves, J. Echeverria, E. Cremades, F. Barragan and S. Alvarez, Dalton Trans., 2008, 2832–2838 RSC.
- S. Alvarez, Dalton Trans., 2013, 42, 8617–8636 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Several tables regarding the calculations and their results as well as orbital pictures. See DOI: 10.1039/c5cp06598d |
| ‡ The basis sets were completely decontracted and additional basis functions were added: K[s: 0.0037, 0.0017; p: 0.0016, 0.00062; d: 4.34, 0.011; f: 0.0296]; Rb[s: 0.0036, p: 0.0042, d: 0.0116, 2.860, f: 0.0624 g: 0.33]. |
| § This was necessary because the dipole moments determined by the MRCI routine in MOLPRO do not include the dipole moment of the polarized core. However, the difference between the dipole moments determined by the routine and the finite field calculations are smaller than 0.05 D in all cases. |
| ¶ Note that this is not the lowest state in the quartet multiplicity. The 14Π state has the same asymptote but is more strongly bound than the 14Σ+ state. |
| || The isosurfaces of the three orbitals indicated on the left side in Fig. 7 can be found in the ESI.† |
| This journal is © the Owner Societies 2016 |