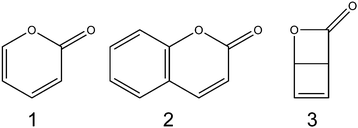
Contrasting ring-opening propensities in UV-excited α-pyrone and coumarin

Abstract

The photoisomerisation dynamics following excitation to the S₁ electronic state of two structurally related heterocyclic molecules, α-pyrone and coumarin, in acetonitrile solution have been probed by time-resolved vibrational absorption spectroscopy. Following irradiation at 310 nm, α-pyrone relaxes rapidly from its initially excited state, with a quantum yield for parent molecule reformation of 68%. Probing the antisymmetric ketene stretch region between 2100 cm⁻¹ and 2150 cm⁻¹ confirms the presence of at least two isomeric ring-opened photoproducts, which are formed highly vibrationally excited and relax on a picosecond timescale. Following vibrational cooling, a secondary, thermally driven, isomerisation is observed with a 1.8(1) ns time constant. In contrast, coumarin reforms the parent molecule with essentially 100% efficiency following excitation at 330 nm. The conical intersections driving the non-radiative relaxation of α-pyrone have been investigated using an automated search algorithm. The two lowest energy conical intersections possess remarkably similar structures to the two energetically accessible conical intersections reported previously for coumarin, suggesting that the differing photochemistry is the result of dynamical effects occurring after passage through these intersections.

---

Introduction

The rapid loss of electronic energy by conversion to heat (through vibrational energy transfer to the surrounding solvent) is an important photoprotection strategy employed by many biologically relevant molecules.¹ In order for this process to be competitive with alternative, potentially harmful, photofragmentation/photoisomerisation pathways there must be one or more low energy conical intersections linking the electronically excited state with the ground electronic manifold.² One class of conical intersections likely to be important in heterocyclic systems is those lying along a localised ring-bond extension coordinate, which have been implicated in the relaxation dynamics of a series of molecules including furan,^3–6 thiophene,^7–9 psoralen,¹⁰ β-glucose,¹¹ various substituted spiropyrans,^12–14 and DNA bases.¹⁵

Recent work from the Bristol group used transient vibrational absorption (TVA) spectroscopy to investigate the UV-induced relaxation pathways of the heterocyclic α-carbonyl molecules furanone and thiophenone.¹⁶ Following irradiation, both molecules were found to isomerise rapidly (<1 ps) to yield ring-opened photoproducts, as confirmed by the appearance of a characteristic antisymmetric ketene (C=C=O) stretching feature around 2150 cm⁻¹. Complementary ab initio calculations of potential energy cuts (PECs) along the S–C(=O) and O–C(=O) ring-extension coordinates revealed the presence of conical intersections at extended bond distances in both molecules, which offer routes to branching between fully ring-opened products and reversion to the ground state ring-closed precursor. Despite the similarities between the PECs obtained for these molecules, the quantum yields of ring-opening were markedly different (∼40% for thiophenone as compared to >90% for furanone). In order to better understand the relationship between molecular structure/conical intersection geometry and ring-opening propensity, we have studied the photoisomerisation dynamics of two structurally related heterocyclic α-carbonyl molecules, α-pyrone (2H-pyran-2-one; 1) and coumarin (1,2-benzopyrone; 2).

There have been several previous reports of the photochemistry of α-pyrone. Corey and Streith¹⁷ irradiated an ether solution at −10 °C and observed the formation of its bicyclic Dewar isomer, 2-oxa-3-oxobicyclo[2.2.0]hex-5-ene (3), while Pirkle and McKendry¹⁸ photoexcited α-pyrone in a THF–CH₂Cl₂ glass at 77 K and reported the production of a ketene containing ring-opened isomer. The UV-induced photochemistry of α-pyrone confined in cryogenic Ar matrices at 8 K was probed using high resolution infrared (IR) spectroscopy,^19,20 where careful analysis of the ketene stretch region (2100–2150 cm⁻¹) revealed four vibrational bands, indicating the presence of four ring-open rotamers. Upon heating the sample to 35 K, Chapman and coworkers²⁰ observed a thermally driven equilibration of these rotamer populations. Later investigations²¹ used a combination of Hg lamp irradiation of cryogenic Ar matrices and Fourier transform IR spectroscopy to conclude that the most efficient photoreaction was α-cleavage, resulting in the formation of no fewer than seven isomeric ring-opened ketene products. These studies also concluded that ring opening was accompanied by a slow ring-contraction reaction to form the Dewar isomer, albeit with a low quantum yield.

Arnold and coworkers²² used TVA spectroscopy to investigate the ring-opening dynamics of α-pyrone at UV pump/IR probe time delays between 200 ns and 20 μs. Following 308 nm irradiation of a solution of α-pyrone in cyclohexane, these authors probed the 1640 – 1880 cm⁻¹ wavenumber range (i.e., the carbonyl stretch region), monitoring the populations of the parent molecule and any photoproducts. 200 ns after irradiation, peaks assignable to α-pyrone and two different product molecules – a ring-opened ketene (quantum yield of formation, ϕ_ketene = 0.52) and the bicyclic Dewar isomer (ϕ_Dewar = 0.09) – were observed. Both of these molecules were deduced to be primary products of the photochemical reaction. The peak assigned to the ring-opened ketene photoproduct decayed on a 2.9 μs timescale, with a concurrent ∼95% recovery of the parent molecule. This simultaneous photoproduct decay and parent molecule recovery was concluded to be a sign of thermally induced reversion of the ring-opened ketene back to the ring-closed α-pyrone. In contrast, the Dewar isomer population remained constant over the timescale probed.

While coumarin derivatives form the well-known family of eponymous laser dyes, bare coumarin has a reported fluorescence quantum yield of just 0.03% (in cyclohexane)²³ indicating the presence of other, more competitive, relaxation pathways. The structural similarity between coumarin and α-pyrone suggests that ring-opening might be such a pathway, but the matrix isolation FTIR study of Kuş et al.²⁴ observed no photoreaction when using UV excitation wavelengths longer than 235 nm. These authors provided several possible rationales for the different photochemistry, including the higher density of electronic and vibrational states for coumarin, and the increased relative stability of the ring-open isomers in α-pyrone.^24,25 Krauter and coworkers²⁶ used ultrafast transient electronic absorption (TEA) spectroscopy to probe the 330 nm induced photochemistry of coumarin dissolved in methanol, cyclohexane, and acetonitrile. The TEA data indicated that the initially excited S₁ state decayed on the ps time scale, and again provided no evidence of any photoproduct formation. These authors performed an ab initio investigation of the potential energy landscape of coumarin by elongating the O–C(=O) bond in small steps and allowing the rest of the molecular framework to relax on the S₁ potential energy surface (PES). This procedure revealed the presence of a conical intersection linking the S₁ and S₀ PESs at extended bond distances, suggesting that the non-radiative relaxation of coumarin does indeed occur via ring-opening, but that rapid ring-closure in the ground electronic state renders this structure an intermediate only.

The prediction of a ring-open conical intersection in coumarin was subsequently confirmed by Maeda and coworkers,²⁷ who investigated the minimum energy conical intersection (MECI) structures near the Franck–Condon region. By combining the seam model function approach²⁸ with the single component artificial force induced reaction method,²⁹ 19 conical intersection structures were identified through an automated search algorithm. Of these 19 structures, only two (labeled 3-1 and 3-2 in ref. 27) were energetically accessible at the energies used in the TEA experiments of Krauter et al.;²⁶ both were found to possess highly extended O–C(=O) bonds (3.65 Å and 2.83 Å for structures 3-1 and 3-2, respectively) relative to the parent coumarin (1.40 Å).

Here we report the application of TVA spectroscopy to investigate the UV-induced photochemistry of α-pyrone and coumarin following excitation at 330 nm (coumarin) and 310 nm (α-pyrone). These pump wavelengths were chosen to excite the molecules in the red edges of their respective first electronic absorption bands (UV absorption spectra of both molecules in acetonitrile are included in the ESI†). The application of TVA spectroscopy is inherently well suited to the study of ring-opening in these systems, since the carbonyl stretch modes around 1600 cm⁻¹ allow the parent molecule population to be monitored as a function of pump/probe time delay, while any ring-opened photoproducts are readily observable through the characteristic ketene antisymmetric stretching vibration in the 2100–2150 cm⁻¹ region. Calculations of the MECI structures of α-pyrone were carried out to complement those already existing for coumarin, and ab initio predictions of the potential energy curves and intrinsic reaction coordinates (IRC) involved in the photochemical transformations of both these molecules provide insights into the decay pathways available in these heterocyclic systems.

Experimental and computational methodology

The TVA data were recorded in two locations, the University of Bristol, and the ULTRA laser facility³⁰ at the Rutherford Appleton Laboratory. Both ultrafast system are based around amplified titanium sapphire lasers generating 800 nm (band center) pulses with <50 fs pulse duration and 10 kHz (1 kHz in Bristol) repetition rates. A portion of this light was used to generate the UV pump radiation via a tunable optical parametric amplifier (OPA). The broadband mid-IR probe radiation (∼500 cm⁻¹ bandwidth) was produced by difference frequency generation in a second OPA. The pump and probe pulses were overlapped in the sample with their linear polarization vectors aligned at the magic angle, before the transmitted radiation was dispersed by a grating onto a 128-element HgCdTe array detector. Coumarin (>99% stated purity), α-pyrone (>90%) and acetonitrile (spectrophotometric grade) were obtained from Sigma-Aldrich and used without further purification. 5 mM (coumarin) and 20 mM (α-pyrone) solutions were used, thereby ensuring an absorbance A ≈ 0.5 at 330 nm for coumarin and at 310 nm for α-pyrone. Samples were flowed continuously through a Harrick cell with a 100 μm PTFE spacer between CaF₂ windows.

The S₀/S₁-MECI geometries of α-pyrone were investigated using a combination of seam model function (SMF),²⁸ single-component artificial force induced reaction (SC-AFIR),²⁹ and spin-flip time dependent density functional theory SF-TDDFT³¹ methods. The SMF/SC-AFIR/SF-TDDFT search was performed from the ground state equilibrium structure of α-pyrone and employed the BHHLYP functional and the 6-31G(d) basis set. The model collision energy parameter for the SC-AFIR search was set as 100 kJ mol⁻¹. Meta-IRC (the steepest descent path in mass weighted coordinates) calculations in the ground state were performed on coumarin and α-pyrone from the ring-open type MECIs to investigate the ring-opening/closure processes on the electronic ground state at the UB3LYP/6-31G(d) level of theory, with subsequent energy corrections performed at the MP2/def2-TZVP level. Cuts through the ab initio S₁ and S₀ PESs linking the S₀ equilibrium geometry with the low-energy MECI structures were constructed using the linearly interpolated internal coordinate (LIIC) methodology at the ADC(2)/def2-TZVP (S₁) and MP2/cc-pVTZ (S₀) levels of theory. The energies and transition state barriers linking the ring-opened isomers of α-pyrone were calculated at the MP2/cc-pVTZ level with implicit solvation using the polarisation continuum model (PCM). All of the SF-TDDFT calculations were performed using the GAMESS program,³² and the MP2 and ADC(2) calculations were carried out using Gaussian09³³ and TurboMole V5.10.³⁴ The structural deformation and optimizations under the SMF/SC-AFIR approach were performed using a developmental version of the GRRM program.³⁵

Results and discussion

(A) Transient absorption measurements

(i) α-Pyrone. Fig. 1(a) displays TVA spectra obtained by pumping a 20 mM solution of α-pyrone in CH₃CN at 310 nm and setting the broadband probe to cover the 1500–1775 cm⁻¹ range. Four negative-going (henceforth termed bleach) features are evident, centred around 1545, 1625, 1715, and 1735 cm⁻¹. As the pump/probe time delay is increased, the intensity of these features decreases, indicating a repopulation of the ground electronic state. The incomplete bleach recovery – asymptotically reaching 68% – indicates that a sizable fraction of the initially excited population is evolving to form photoproducts. In addition to the bleaches, several positive absorption features are also present in Fig. 1(a). A broad transient absorption spanning the 1650–1730 cm⁻¹ range is seen at early Δt, before decaying away and disappearing by ∼50 ps. Careful observation reveals that this peak is shifting to higher wavenumber and narrowing as Δt increases, characteristic of vibrational cooling; it is therefore assigned to vibrationally hot α-pyrone(S₀) molecules. The positive peaks at 1560, 1595, and 1665 cm⁻¹ demonstrate different behavior. They are absent at the earliest pump/probe time delays but grow in with increasing Δt and are thus attributable to photoproduct formation. In contrast to the previous experimental studies,^17,19–22 no peak ascribable to the bicyclic Dewar isomer – which should have an absorption around 1850 cm⁻¹ – is seen, casting doubt on its assignment as a primary photoproduct (in acetonitrile solution).

Fig. 1 Transient vibrational absorption spectra at various pump/probe time delays of a 20 mM solution of α-pyrone in CH₃CN following excitation at 310 nm and probing in the wavenumber range (a) 1500–1775 cm⁻¹ and (b) 1970–2170 cm⁻¹, and (c) of a 5 mM solution of coumarin in CH₃CN following excitation at 330 nm and probing the 1570–1800 cm⁻¹ region.

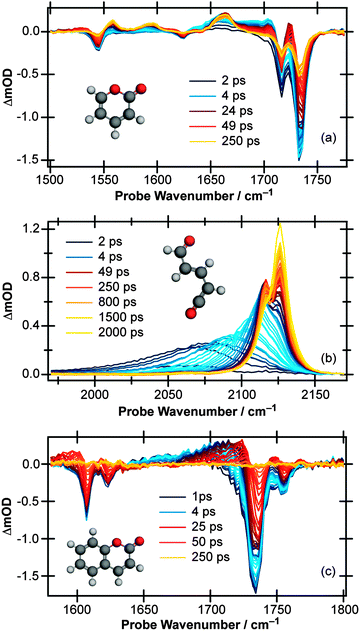
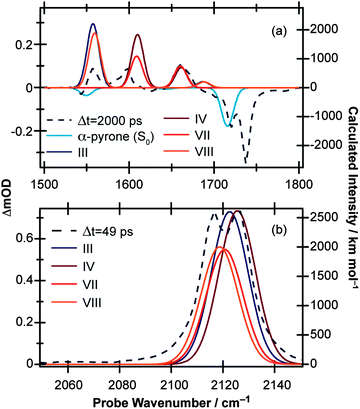
Moving the probe region to cover the 1970–2170 cm⁻¹ range (Fig. 1(b)) allows the buildup of any ketene product molecules to be monitored. At early pump/probe time delays, an extremely broad (∼125 cm⁻¹) transient feature centered around 2060 cm⁻¹ is observed which narrows and blue shifts on a ps timescale. At late times, two peaks are clearly identifiable, centered around 2115 and 2125 cm⁻¹, indicating that at least two product conformers are formed during the ring-opening process. Furthermore, the intensity of the 2115 cm⁻¹ feature decreases at late times while the 2125 cm⁻¹ peak continues to grow, an observation which suggests that there is a secondary isomerisation reaction occurring in this system.

(ii) Coumarin. Fig. 1(c) displays the TVA spectra obtained by pumping a 5 mM coumarin/CH₃CN solution at 330 nm and setting the probe to cover the 1570–1800 cm⁻¹ region. Four bleach features with peak centres at 1607, 1623, 1734, and 1755 cm⁻¹ are observed. As in α-pyrone, a transient signal attributable to vibrationally (and possibly electronically) excited molecules is seen at small Δt, being especially evident on the low wavenumber side of the 1734 cm⁻¹ bleach feature. Unlike in α-pyrone, an essentially complete bleach recovery is observed within 100 ps, indicating that there is very little photoproduct formation following excitation at 310 nm. This view is supported by the complete absence of any ketene stretching features in the 2000–2200 cm⁻¹ region (data not shown). The lack of any photoproduct formation is in agreement with the previous matrix isolation FTIR²⁴ and TEA²⁶ experimental studies.

(B) Kinetic analysis

The TVA spectra of α-pyrone and coumarin were analysed by decomposing each time slice in terms of model basis functions. More details and representative decompositions are given in the ESI.†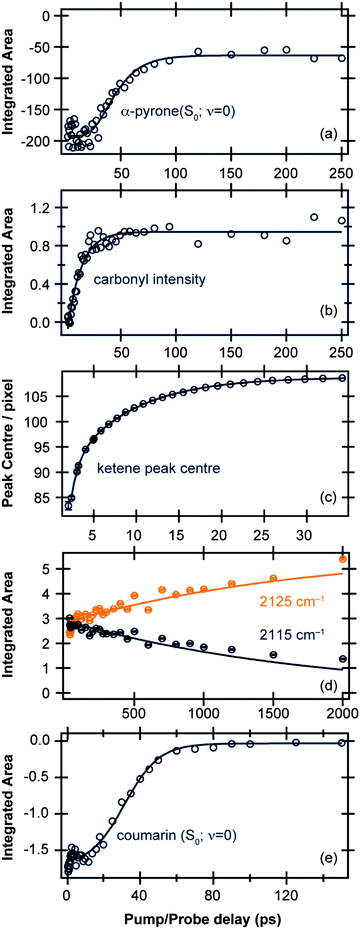

(i) α-Pyrone. Fig. 2(a) depicts the population of α-pyrone (S₀; ν = 0), which demonstrates a sigmoidal change with time. The bleach signal remains constant for ∼20 ps before beginning to recover, which can be interpreted as the time required for the photoexcited α-pyrone(S₁) molecules to internally convert to a highly vibrationally-excited region of the S₀ manifold and undergo vibrational relaxation down to levels with ν = 1, from where repopulation of the ν = 0 level (and accompanying decrease in the bleach signal) can begin. Fitting the extracted bleach amplitude to a qualitative model based upon the vibrational relaxation of a harmonic oscillator¹⁶ results in an estimated rate coefficient of 0.061 ps⁻¹ for the final ν = 1 → ν = 0 step (time constant of ∼16 ps). Our analysis also suggests that 68% of the initially excited population reforms the parent molecule, indicating that a maximum of 32% of the photoexcited pyrone molecules react to form ring-open conformers. Fig. 2(b) shows the growth of the product vibrational features located at 1560, 1595, and 1665 cm⁻¹. The extensive overlap between these features and those attributable to α-pyrone (S₀; ν > 0) necessitated that they be modeled using a single “product” basis spectrum, and consequently a single kinetic trace describes the growth of all three features. Fitting this rise time to an exponential function yields a best-fit rate coefficient of 0.082(7) ps⁻¹ (12(1) ps time coefficient), similar to the ν = 1 → ν = 0 relaxation rate extracted for the parent bleach dynamics, suggesting that the experimentally observed formation rate of the product carbonyl features is also dominated by vibrational cooling.

Fig. 2 Time-dependent band intensities of (a) α-pyrone (S₀; ν = 0) and (b) carbonyl-containing photoproducts following excitation of α-pyrone at 310 nm. (c) Evolution of the ketene peak centre for Δt < 35 ps, and (d) time-dependent band intensities of ketene peaks centered around 2115 cm⁻¹ and 2125 cm⁻¹ for Δt > 35 ps. (e) Time-dependent band intensity of coumarin (S₀; ν = 0) following excitation at 330 nm. All the kinetic traces (open circles) were obtained by the decomposition procedures detailed in the ESI,† and the solid lines are fits to functions described in the main text.

Fig. 2(c) and (d) display the vibrational cooling and subsequent isomerisation rates of the ketenes formed following UV excitation of α-pyrone. The simplifying assumption that both product conformers are initially formed simultaneously was used, and the data were fit in two different time regimes: (i) Δt < 35 ps to capture the vibrational cooling of the ketenes, and (ii) Δt > 35 ps to probe the conformer isomerisation. Fig. 2(c) depicts the evolution of the peak centre as a function of pump/probe delay (Δt < 35 ps), which provides a measure of the vibrational cooling rate. Since the rate of cooling in solution is vibrational energy level dependent,³⁶ the obtained kinetics are by their very nature multi-exponential. Consequently the fit in Fig. 2(c) has used a biexponential function, revealing a time constant of 0.83(4) ps for highly vibrationally excited levels, reducing to 7.4(1) ps for lower energy states. Fig. 2(d) shows the populations of the two ketenes as a function of pump/probe time delay (Δt > 35 ps) along with fits to a simple A → B isomerisation model. This kinetic fit yields a time constant of 1.8(1) ns, far slower than any of the other time constants observed in this system and hinting that the isomerisation process is thermally driven.

(ii) Coumarin. Fig. 2(e) shows the S₀ bleach recovery dynamics extracted from the coumarin data. Just as in α-pyrone, the parent molecule repopulation kinetics are sigmoidal in shape. However, the initial invariance of the bleach intensity with pump probe time delay now has at least some contribution from the electronically excited S₁ state of coumarin which has a lifetime of ∼20 ps in acetonitrile.²⁶ Due to the relatively long-lived nature of the initially photoprepared state, the qualitative harmonic oscillator model used for α-pyrone cannot be used here. Instead a simple sigmoidal type fit was used, resulting in a vibrational relaxation rate coefficient of 0.11(1) ps⁻¹ (time constant of 9.4(9) ps) being determined.

(C) Computational results

(i) Minimum energy conical intersections. The experimental results detailed above highlight how, despite involving a common heterocycle structure, coumarin and α-pyrone demonstrate very different ring-opening probabilities upon S₁ ← S₀ electronic excitation. It is well established that conical intersections play a key role in molecular photochemistry;^37,38 the shape of, and dynamics through, such regions of electronic degeneracy determine the product branching ratios.³⁹ Therefore, one of the goals of the computational part of this study is to see if the differing dynamics seen experimentally can be explained simply by differences in the conical intersection structures of these two molecules. We have extended previous investigations of coumarin²⁷ to probe the MECIs near the Franck–Condon region in α-pyrone. In total, nine MECIs were identified (shown in the ESI†), seven of which involve puckering of the six-membered ring. However, the geometries at the two lowest energy MECIs identified in α-pyrone (shown in Fig. 3) are strikingly similar to the energetically accessible MECIs reported previously for coumarin (also shown in Fig. 3). One pair of MECIs has a torsional angle of ∼35° between the carbonyl and ketene moieties, the other has an angle closer to 90°. Potential energy curves linking the Franck–Condon point of the S₁ surfaces with these conical intersection structures were calculated for α-pyrone and coumarin and are shown in Fig. 4(a) and (b), respectively. In order to aid interpretation, the excited-state PECs returned by the ADC(2) calculations have been approximately diabatised through inspection of the molecular orbitals involved in the electronic transitions at each point. These LIIC PECs predict there to be no potential barrier hindering access to any of the MECIs, in agreement with the relatively short excited state lifetimes exhibited by both molecules. In both coumarin and α-pyrone, the route to the 35° MECI involves a curve crossing with a state best described as having πσ* electronic character (denoted S₃ and S₄ in α-pyrone and coumarin, respectively), which subsequently goes on to form the MECI with the S₀ state. In contrast, the 90° out-of-plane MECI is accessed by remaining on the S₁(ππ*) potential, without the need for any curve crossing. Such ππ* mediated ring-opening was not implicated in any of our prior work on heterocyclic photoisomerisation reactions,^16,40 however those investigations did not include such an exhaustive search of the potential energy landscape and attendant MECIs.

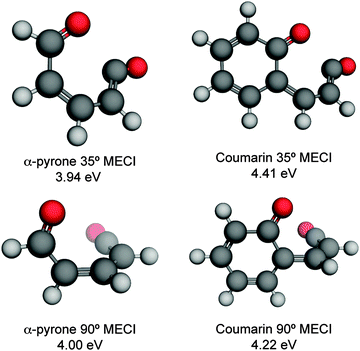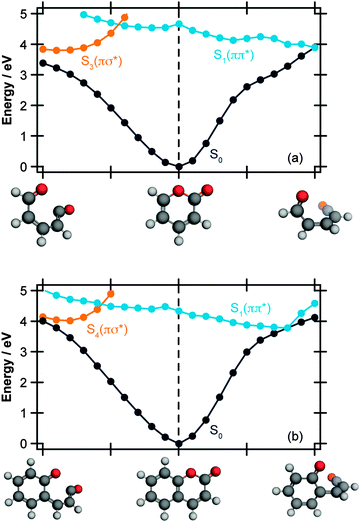
Fig. 3 Energetically accessible MECI structures for α-pyrone (left hand side) and coumarin (right hand side; structures taken from ref. 27) at the SF-TDDFT BHHLYP/6-31G(d) level of theory. The structures can be classified into two groups depending upon the torsional angle between the ketene and carbonyl moieties. The energies are quoted relative to the electronic ground state of the respective parent molecules.

Fig. 4 Potential energy curves along the LIIC reaction paths linking the Franck–Condon region of (a) α-pyrone, and (b) coumarin with the energetically accessible MECI structures. The S₀ curves were calculated at the MP2/cc-pVTZ level, and the electronically excited states calculated at the ADC(2)/def2-TZVP level. The curves have been approximately diabatised to aid in interpretation.

In addition to the ring-opened MECIs mentioned above, a third energetically accessible conical intersection was also located for α-pyrone (MECI-3 in the ESI†). This MECI is structurally similar to the transition state linking α-pyrone (S₀) with the bicyclic Dewar isomer, and thus provides a possible pathway to its photochemical generation. The absence of any Dewar isomer formation in the present experiments suggests that this is a minor pathway however.

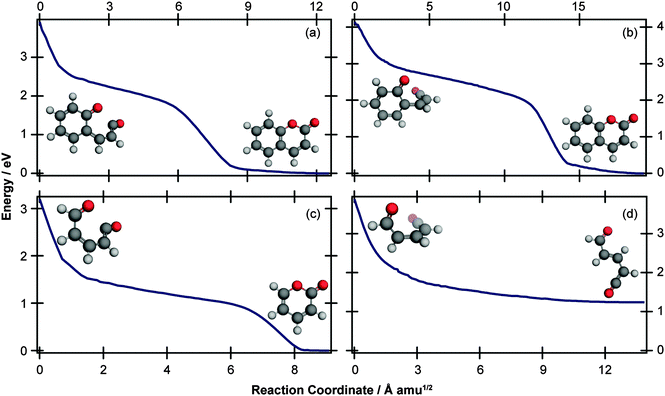
The computational results shown in Fig. 3 and 4 suggest that coumarin and α-pyrone have similar excited state potential landscapes and MECI geometries, yet the ring-opening quantum yields are starkly different. It seems reasonable to assume therefore, that these differences are a consequence of the dynamics through, and subsequent to, the low-energy conical intersections. In order to investigate possible causes for the differing ground state dynamics, we performed IRC analyses at the UB3LYP/6-31G(d) level of theory (with subsequent single point energy corrections performed at the MP2/def2-TZVP level) starting from these four MECI structures (viz. the two lowest-energy MECIs in both coumarin and α-pyrone), the results of which are displayed in Fig. 5. The IRC scans from either of the MECIs in coumarin (Fig. 5(a) and (b)) indicate that ring-closure back to the parent structure is the most likely outcome – in agreement with the experimental observation. Starting from the 35° out-of-plane conical intersection of α-pyrone (Fig. 5(c)) also results in reformation of the parent molecule. In contrast, the IRC from the 90° out-of-plane MECI of α-pyrone (Fig. 5(d)) suggests that the forces acting upon the molecule at this geometry favor formation of a ring-opened photoproduct with an energy of ∼1.2 eV relative to the ring-closed parent. Since nonadiabatic transitions will occur from points close to the conical intersection (i.e., not exactly at the MECI itself), the results obtained from such an analyses are qualitative in nature; in general, quantitative predictions of the final product branching ratios may only be obtained by running hundreds of trajectories starting from the Franck–Condon region. Further, the present calculations neglect the effect of motion through the conical intersection region and non-IRC dynamics of internally hot S₀ molecules. Despite the limitations, the predictions of these IRC calculations still provide a plausible rationale for the experimentally observed difference in ring-opening quantum yields between coumarin and α-pyrone.

Fig. 5 IRC paths starting at the (a) 35° MECI and (b) 90° MECI in coumarin, and (c) 35° MECI and (d) 90° MECI in α-pyrone. The IRC scans were performed at the UB3LYP/6-31G(d) level of theory, with subsequent single point energy corrections performed at the MP2/def2-TZVP level. In each case, the initial and final structures are shown.

The extended π electron system of coumarin relative to α-pyrone provides a possible explanation for the different behaviour exhibited following radiationless transfer via their 90° MECIs. Upon opening the pyrone ring of coumarin, the aromaticity of the neighbouring phenyl ring is reduced;²⁵ consequently its most stable ring-opened isomer (shown in the ESI†) is 1.98 eV higher in energy (at the MP2/cc-pVTZ; acetonitrile PCM level of theory) than the parent molecule – nearly double the offset between α-pyrone and its lowest-energy photoproduct (Fig. 6). A reduced potential gradient in the direction of ring opening is therefore expected in the case of coumarin, tipping the balance back towards the reformation of the parent molecule.

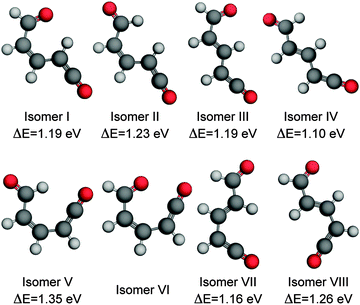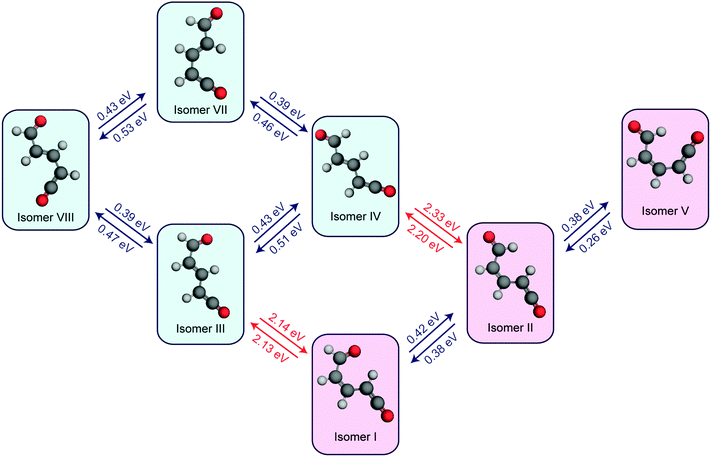
Fig. 6 Ring-open isomers of α-pyrone calculated at the MP2/cc-pVTZ level of theory with implicit solvation accounted for using the PCM method. All energies are quoted relative to the S₀ equilibrium value of the parent molecule. Isomer VI is unstable with respect to ring closure, and therefore has no reported energy. The numbering scheme used is the same as that presented in the work by Breda et al. in ref. 21.

(ii) Isomerisation pathways in ring-opened α-pyrone. In total, ring opening in α-pyrone can result in the formation of eight conformers, which are shown in Fig. 6 (labeled using the numbering scheme introduced by Breda and coworkers).²¹ These conformers can be separated into four E- and four Z-isomers, depending upon the molecular orientation around the central C=C bond. One of the Z-isomers (structure VI) is unstable with respect to ring closure and is not considered further. Previous matrix isolation IR work^19–21 concluded that only the Z-isomers were primary photoproducts, with E-isomers being formed through subsequent photochemically induced Z → E isomerisation.²¹ The results of the MECI and IRC calculations presented in Fig. 3, 5(c), and (d) lead us to propose that the opposite is true in the solution phase, i.e., that E-isomers are the primary photoproducts. Torsion around the C=C double bond is required in order to access either of the low energy MECIs of Fig. 3 and, once there, it is easy to imagine that the momentum induced by this motion will drive the system naturally towards the formation of E-isomers. The shape of the potential around the MECIs will also play a role in the photoproduct branching ratios and, while the IRC calculations suggest that the forces encountered at the 35° MECI will tend towards ring closure (Fig. 5(c)), the 90° MECI is predicted to favor the formation of conformer VIII (Fig. 5(d)) – one of the E-isomers.

Simulated IR spectra (computed at the B3LYP/6-311++G(d,p) level with acetonitrile PCM) of the E-isomers and parent molecule are shown in Fig. 7(a) for the carbonyl region (the wavenumbers have been scaled by multiplying the calculated values by 0.99) and in Fig. 7(b) for the ketene region (calculated wavenumbers multiplied by 0.975) and show generally good agreement with the experimental data. For completeness, the corresponding simulated IR spectra for the Z-isomers are included in the ESI.† While the simulated spectra presented in Fig. 7 suggest that nearly all of the observed product features can be assigned to a combination of conformers III, IV, VII, and VIII (i.e., the E-isomers) there simply are not enough experimental features to allow conclusive identification of the photoproducts. However, further support for our assignment of E-isomers as the primary photoproducts in solution comes when considering the cause of the slower secondary isomerisation clearly observed experimentally in the ketene stretch region (Fig. 1(b)). Since all electronic and vibrational relaxation processes are complete by ∼35 ps, the interconversion between ketene molecules has to be thermally driven.

Fig. 7 Simulated IR spectra for the four ring-open E-isomers of α-pyrone calculated at the B3LYP/6-311++G(d,p) level of theory with implicit solvation accounted for using the PCM method. Panels (a) and (b) cover the 1500–1800 cm⁻¹ and 2050–2150 cm⁻¹ regions, respectively. The solid lines are the computed spectra (represented by Gaussian functions with 10 cm⁻¹ FWHM), and the dashed lines are the experimental data recorded at time delays of 2000 ps and 49 ps in (a) and (b), respectively.

In order to investigate the thermal isomerisation of the product ketene molecules further, ground state potential barriers for possible interconversion pathways involving rotation around one bond (including around the central C=C bond) have been calculated at the MP2/cc-pVTZ level. In doing so, we build up a simple “connectivity map” linking the conformers, which is shown in Fig. 8. As expected, rotations about single bonds (blue arrows in Fig. 8) are hindered by far lower potential barriers than transformations involving Z ↔ E isomerisation of the C=C bond (red arrows). Immediately following passage through the MECIs, the ring-opened molecules possess enough energy to surmount any of these barriers and are therefore free to form any of the ring-opened conformers (although following on from the arguments given above, we would expect the E-isomers to dominate). Subsequent vibrational cooling will rapidly quench the photoproducts into the individual conformer wells, and after this period all isomerisation has to be thermally driven. The magnitudes of the barriers predicted for Z ↔ E isomerisation (>2 eV) suggest that this is unlikely to occur on the timescales probed experimentally here. From the arguments presented above, at short pump/probe time delays it might be expected that a mixture of all four E-isomers (III, IV, VII, and VIII) is present. If these isomers reach thermal equilibrium, a simple Boltzmann calculation suggests that the long-time population ratios should be 0.002 : 0.03 : 0.1 : 1 (VIII : III : VII : IV), which according to Fig. 7(b) would manifest as a blue shift in the ketene wavenumber – in agreement with the ∼10 cm⁻¹ blue shift seen experimentally (Fig. 1(b)). If the Z-isomers were formed, by the same arguments a red shift in the ketene peak would occur as isomers II and V convert to isomer I (shown in Fig. S8 of the ESI†). The barrier values calculated for the interconversion of the E-isomers are still far too high to account for the 1.8 ns isomerisation rate observed experimentally, but rotation around a single bond, although the most direct isomerisation route, is only a crude approximation of the true minimum energy pathway. Recent work by Maeda et al. serves to highlight the extreme complexity of a complete IRC network, even in the case of a much smaller molecule (CH₃NO).⁴¹ Further, Chapman et al. observed thermal isomerisation of the ring opened α-pyrone photoproducts over a period of five minutes in an Ar matrix at 35 K.²⁰ At 300 K the reaction would be orders of magnitude quicker.

Fig. 8 Calculated potential energy barriers linking the ring-open isomers of α-pyrone (MP2/cc-pVTZ level of theory; CH₃CN PCM). Only isomerisations involving rotation around one carbon–carbon bond were considered. Rotations around C–C single bonds are depicted with blue arrows, and rotations around C=C double bonds are represented with red arrows. The E-isomers (i.e., isomers III, IV, VII, and VIII) have blue backgrounds, while the Z-isomers have red backgrounds.

E-isomers being the primary photoproduct of α-pyrone in the solution phase also helps to reconcile some of the differences between the results described here, and those reported in the prior TVA studies of Arnold and coworkers.²² Chief among these is the quantum yield of parent molecule reformation and its associated timescale. While our results showed an apparently asymptotic 68% bleach recovery within the first 2 ns, Arnold et al. reported a 95% bleach recovery between Δt = 200 ns and 4.2 μs, with a 2.9 μs time constant (albeit in a different solvent – cyclohexane – to that used in the current investigation). In order to reform the parent α-pyrone molecule, the E-isomers need to undergo an E → Z isomerisation. Notwithstanding the apparent overestimation of barrier heights presented in Fig. 8, it is still likely that such a transformation is energetically less favorable, and hence slower, than the isomerisations driven by rotations around single bonds discussed previously. It is possible, therefore, that the 2.9 μs time constant reported by Arnold et al. is actually a measure of the mean E ↔ Z isomerisation rate.

Conclusions

TVA spectroscopy has been used to explore the UV-induced photochemistry demonstrated by two structurally related heterocyclic α-carbonyl molecules, α-pyrone and benzo-α-pyrone (coumarin), in acetonitrile at 293 K by monitoring the evolution of both the parent and potential product molecules in time. Of particular interest in the present investigation is non-radiative relaxation via ring opening, a decay channel seen previously to be active in several heterocyclic systems.^3–16 The observation of an intense antisymmetric ketene stretch vibration between 2100 cm⁻¹ and 2150 cm⁻¹ would provide strong evidence for such a reaction. Following irradiation at 310 nm, α-pyrone relaxes rapidly from its initially excited state, with a quantum yield for parent molecule reformation of 68%. Probing the ketene stretch region confirms the presence of ring-opened photoproducts, which are formed highly vibrationally excited before cooling on a ps timescale. Following vibrational cooling, a secondary isomerisation is seen to occur on a 1.8 ns timescale, as gauged by the evolving intensities of two closely spaced ketene absorption features. The slow rate of this latter isomerisation suggests strongly that it is a thermally driven process occurring on the ground electronic potential. In contrast, coumarin is found to reform the parent molecule with near 100% efficiency following UV excitation at 330 nm. In order to explain the different near-UV photochemistry exhibited by α-pyrone and coumarin, the MECI structures linking the S₁ and S₀ potential energy surfaces in α-pyrone have been explored using an automated procedure³⁵ combining the seam model function approach²⁸ with a single component artificial force induced reaction methodology and compared with similar literature data for the coumarin molecule.²⁹ In total, nine MECIs were discovered. The two lowest energy conical intersections in α-pyrone were found to display very similar structures to the energetically accessible MECIs of coumarin; one MECI where the ketene moiety exhibits an ∼35° torsional angle with respect to the carbonyl group, and the other which is closer to 90° out of plane. The differing photochemistry of α-pyrone and coumarin is instead rationalised by consideration of the forces acting upon the molecules at these MECI geometries on the S₀ states of both molecules. In particular, we find that the 90° out-of-plane MECI in α-pyrone is the only one to promote ring-opening rather than reformation of the parent molecule. We note, however, that such IRC analyses assume that the nuclei within the molecule are stationary at the MECI configuration, and calculations including the dynamical effects of passage through these intersections would surely help shed more light on the very different photochemical behaviour of these two molecules.

Acknowledgements

The Bristol group thanks the European Research Council (ERC, Advanced Grant 290966 CAPRI) for financial support. The ULTRA Laser Facility at the Rutherford Appleton Laboratory is supported by the Science and Technology Facilities Council (STFC, Facility Grant ST/501784). The Hokkaido group thanks the Japan Science and Technology Agency (JST) for financial support through a Core Research for Evolutional Science and Technology (CREST) grant in the area of “Establishment of Molecular Technology towards the Creation of New Functions”. RAI gratefully acknowledges receipt of a Japan Society for the Promotion of Science Short Term Pre/Postdoctoral Fellowship for North American and European Researchers that was invaluable in fostering the collaboration between the Bristol and Hokkaido groups.

References

1. C. E. Crespo-Hernández, B. Cohen, P. M. Hare and B. Kohler, Chem. Rev., 2004, 104, 1977–2019.
2. A. Rosspeintner, B. Lang and E. Vauthey, Annu. Rev. Phys. Chem., 2013, 64, 247–271.
3. M. Stenrup and Å. Larson, Chem. Phys., 2011, 379, 6–12.
4. E. V. Gromov, C. Léveque, F. Gatti, I. Burghardt and H. Köppel, J. Chem. Phys., 2011, 135, 164305.
5. E. V. Gromov, A. B. Trofimov, F. Gatti and H. Köppel, J. Chem. Phys., 2010, 133, 164309.
6. N. Gavrilov, S. Salzmann and C. M. Marian, Chem. Phys., 2008, 349, 269–277.
7. M. Stenrup, Chem. Phys., 2012, 397, 18–25.
8. G. Cui and W. Fang, J. Phys. Chem. A, 2011, 115, 11544–11550.
9. S. Salzmann, M. Kleinschmidt, J. Tatchen, R. Weinkauf and C. M. Marian, Phys. Chem. Chem. Phys., 2008, 10, 380–392.
10. J. Tatchen and C. M. Marian, Phys. Chem. Chem. Phys., 2006, 8, 2133–2144.
11. D. Tuna, A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2014, 16, 38–47.
12. M. Rini, A.-K. Holm, E. T. J. Nibbering and H. Fidder, J. Am. Chem. Soc., 2003, 125, 3028–3034.
13. F. Liu and K. Morokuma, J. Am. Chem. Soc., 2013, 135, 10693–10702.
14. S. Prager, I. Burghardt and A. Dreuw, J. Phys. Chem. A, 2014, 118, 1339–1349.
15. S. Perun, A. L. Sobolewski and W. Domcke, Chem. Phys., 2005, 313, 107–112.
16. D. Murdock, S. J. Harris, J. Luke, M. P. Grubb, A. J. Orr-Ewing and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2014, 16, 21271–21279.
17. E. J. Corey and J. Streith, J. Am. Chem. Soc., 1964, 86, 950–951.
18. W. H. Pirkle and L. H. McKendry, J. Am. Chem. Soc., 1969, 91, 1179–1186.
19. R. G. S. Pong and J. S. Shirk, J. Am. Chem. Soc., 1973, 95, 248–249.
20. O. L. Chapman, C. L. McIntosh and J. Pacansky, J. Am. Chem. Soc., 1973, 95, 244–246.
21. S. Breda, I. Reva, L. Lapinski and R. Fausto, Phys. Chem. Chem. Phys., 2004, 6, 929–937.
22. B. R. Arnold, C. E. Brown and J. Lusztyk, J. Am. Chem. Soc., 1993, 115, 1576–1577.
23. J. Sérgio Seixas de Melo, R. S. Becker and A. L. Maçanita, J. Lumin., 1994, 98, 6054–6058.
24. N. Kuş, S. Breda, I. Reva, E. Tasal, C. Ogretir and R. Fausto, Photochem. Photobiol., 2007, 83, 1237–1253.
25. R. Fausto, S. Breda and N. Kuş, J. Phys. Org. Chem., 2008, 21, 644–651.
26. C. M. Krauter, J. Möhring, T. Buckup, M. Pernpointner and M. Motzkus, Phys. Chem. Chem. Phys., 2013, 15, 17846–17861.
27. S. Maeda, Y. Harabuchi, T. Taketsugu and K. Morokuma, J. Phys. Chem. A, 2014, 118, 12050–12058.
28. S. Maeda, T. Taketsugu, K. Ohno and K. Morokuma, J. Am. Chem. Soc., 2015, 137, 3433–3445.
29. S. Maeda, T. Taketsugu and K. Morokuma, J. Comput. Chem., 2014, 35, 166–173.
30. G. M. Greetham, P. Burgos, Q. Cao, I. P. Clark, P. S. Codd, R. C. Farrow, M. W. George, M. Kogimtzis, P. Matousek, A. W. Parker, M. R. Pollard, D. A. Robinson, Z.-J. Xin and M. Towrie, Appl. Spectrosc., 2010, 64, 1311–1319.
31. Y. Shao, M. Head-Gordon and A. I. Krylov, J. Chem. Phys., 2003, 118, 4807–4813.
32. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363.
33. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013.
34. TURBOMOLE V5.10 2008, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
35. S. Maeda, Y. Osada, Y. Harabuchi, T. Taketsugu, K. Morokuma and K. Ohno, GRRM, a developmental version, Hokkaido university, Sapporo, 2015.
36. J. C. Owrutsky, D. Raftery and R. M. Hochstrasser, Annu. Rev. Phys. Chem., 1994, 45, 519–555.
37. W. Domcke and D. R. Yarkony, Annu. Rev. Phys. Chem., 2012, 63, 325–352.
38. S. Matsika and P. Krause, Annu. Rev. Phys. Chem., 2011, 62, 621–643.
39. T. J. Martinez, Nature, 2010, 467, 412–413.
40. D. Murdock, S. J. Harris, I. P. Clark, G. M. Greetham, M. Towrie, A. J. Orr-Ewing and M. N. R. Ashfold, J. Phys. Chem. A, 2015, 119, 88–94.
41. S. Maeda, Y. Harabuchi, Y. Ono, T. Taketsugu and K. Morokuma, Int. J. Quantum Chem., 2015, 115, 258–269.

---

Footnote

† Electronic supplementary information (ESI) available: UV absorption spectra of α-pyrone and coumarin dissolved in CH₃CN. Details and example fits from the decomposition procedures used in the extraction of the kinetic traces shown in Fig. 2. Complete list of MECI structures identified for α-pyrone. Ring-open isomers of coumarin. Simulated IR spectra for the three ring-open Z-isomers of α-pyrone. See DOI: 10.1039/c5cp06597f

---