Excited state structural evolution during charge-transfer reactions in betaine-30

Abstract

Ultrafast photo-induced charge-transfer reactions are fundamental to a number of photovoltaic and photocatalytic devices, yet the multidimensional nature of the reaction coordinate makes these processes difficult to model theoretically. Here we use femtosecond stimulated Raman spectroscopy to probe experimentally the structural changes occurring following photoexcitation in betaine-30, a canonical intramolecular charge-transfer complex. We observe changes in vibrational mode frequencies and amplitudes on the femtosecond timescale, which for some modes results in frequency shifts of over 20 cm⁻¹ during the first 200 fs following photoexcitation. These rapid mode-specific frequency changes track the planarization of the molecule on the 400 ± 100 fs timescale. Oscillatory amplitude modulations of the observed high frequency Raman modes indicate coupling between specific high frequency and low frequency vibrational motions, which we quantify for 6 low frequency modes and 4 high frequency modes. Analysis of the mode-specific kinetics is suggestive of the existence of a newly discovered electronic state involved in a relaxation pathway, which may be a low-lying triplet state. These results directly track the multiple nuclear coordinates involved in betaine-30's reactive pathway, and should be of use in rationally designing molecular systems with rapid electron transfer processes.

---

Introduction

Electron transfer reactions are of paramount importance in a variety of photo-driven processes, including photovoltaic and photocatalytic systems.^1,2 Many of these devices rely on ultrafast electron transfer reactions, in which the system does not have time to thermalize and intramolecular vibrational motions are thought to play a critical role in driving the reaction.³ In these systems, condensing the highly multidimensional potential energy surface down to a single reorganization parameter comes at the cost of understanding how exactly the reaction proceeds. In highly reactive systems undergoing electron transfer, an understanding of the multidimensional potential energy surface is required in order to accurately predict rates and yields of electron transfer reactions.

Betaine-30 is a highly solvatochromatic molecule which undergoes photoinduced charge transfer.⁴ Its ground state geometry, which is sensitive to the solvent environment,^5,6 is stabilized as a charge separated state. The molecule undergoes ultrafast intermolecular charge transfer upon photoexcitation. The charge-transferred S₁ excited state decays rapidly via a back electron transfer (bET) process.^5–8 The solvent dependent rate constant has been reported to range from 1.2 ps in acetonitrile to 9.7 ps in ethylene glycol.⁹ The back electron transfer process has been the subject of a number of studies, as it is several orders of magnitude faster than would be predicted by conventional Marcus theory.^10,11 The assumption is that in addition to solvent reorganization and thermal fluctuations, high frequency vibrational modes must couple to the charge transfer coordinate to drive the back electron transfer process.^3,12–16

Despite excellent experimental and theoretical efforts, the identity of the high frequency modes driving bET is currently unknown. Additionally, it is unclear how these high frequency modes couple to low frequency modes to create a highly reactive potential energy landscape, and at which points along the reaction coordinate they come into play. Ultrafast transient absorption measurements in different solvents were used to estimate values for reorganization energies by considering the effects of low and high frequency vibrational motions, but these electronic measurements cannot identify the contribution of specific vibrational modes to the total reorganization energy.^7,17 Resonance Raman intensity analysis has been used to probe initial Franck–Condon dynamics including solvent isotope effects, suggesting that methyl group motions play a larger role than hydroxyl group motion in the dephasing of the electronic state.^18,19 Picosecond time-resolved Raman spectroscopy was used to follow cooling and intramolecular vibrational redistribution on the electronic ground state following the back electron transfer reaction, but unfortunately the time resolution was insufficient to directly monitor structural changes on the electronic excited state.^20,21 Theoretical approaches have included density matrix formulations²² and time-dependent quantum mechanical calculations.^23–25 Recent transient fluorescence data of similar pyridinium phenoxides indicate that there is an inverse relationship between the lifetime of the Franck–Condon state and the dihedral angle between the pyridinium and phenoxide rings.²⁶ Theory points to the strong role of high frequency modes in driving the electronic coupling during back electron transfer, as well as the role of torsional dynamics.^27,28 However to date these results have not been verified experimentally.

Based on the solid foundation of results obtained through studies on solvation, transient absorption, and resonance Raman intensity analysis, we set out to probe the rapid high frequency vibrational response on betaine-30's excited electronic state. Probing the structural evolution on a femtosecond time scale is critical to understanding the multidimensional reaction coordinate of betaine-30 during bET. Here we use femtosecond stimulated Raman spectroscopy (FSRS),^29,30 which has the capability of probing excited state vibrational features on a femtosecond time resolution, to probe the instantaneous structural changes following photoexcitation of betaine-30. Frequency changes can be used to identify structural changes after initial charge transfer, and amplitude kinetics and oscillatory features are used to map out the potential energy surfaces which play a role in betaine-30's photochemistry.

Experimental

Femtosecond stimulated Raman spectroscopy

We performed FSRS experiments on our newly built optical table as described previously.³¹ The 4.4 W fundamental output of a femtosecond amplifier (Coherent Libra-F-1K-HE) generated the three pulses needed for FSRS. The Raman pump beam was generated by passing 480 mW of the fundamental beam through a home-built grating filter,³² creating a 2.1 ps pulse with 9 mW maximum power. We used a 2 : 1 collimation telescope to precompensate the focusing of the Raman pump at the sample, and a variable neutral density filter to attenuate the power. We generated the continuum probe by focusing 2.5 mW of the 800 nm pulse on the back edge of a 2 mm sapphire crystal, followed by compression in a fused silica prism compressor. To generate the actinic pulse, we used a home-built non-collinear parametric amplifier. This amplifier was seeded by a continuum generated in 2 mm thick sapphire and pumped by a 400 nm pump beam. The beams were focused onto a 1 mm thick BBO crystal at an approximately 5° spatial angle. An SF10 prism pair was used to compress the linear chirp of the resultant visible beam. In these experiments, the actinic pump beam was tuned to a central wavelength of 532 nm, and had a full-width at half maximum bandwidth of 14 nm with a Gaussian spectral profile. We varied the time delay of the actinic pump relative to Raman pump–probe overlap using a piezoelectric delay stage (Physik Instrumente, M683).

A 2′′ diameter, 100 mm focal length lens focused all three beams to the sample non-collinearly. The 700 μW Raman pump beam had a diameter of 160 μm, the 300 μW actinic pump beam had a diameter of 170 μm, and the probe beam had a diameter of 35 μm. We used the optical Kerr effect to obtain the cross correlation time (117 ± 2 fs) of the photoexcitation beam and the probe beam in the sample cell. After passing through the sample, a 100 mm focal length lens collimated the FSR signal along with the probe beam and directed the beams into a 1/3 meter spectrograph (Princeton Instruments 2300i). A thermoelectrically cooled CCD (Princeton Instruments PIXIS 100F) collected the single shot spectra at a 1 kHz repetition rate.¹⁹ An RG1000 filter compensated for the low detection efficiency of the silicon detector at the high wavelength region. A home built flip-flop initiated the CCD triggering when the phase of the Raman pump chopper (Thorlabs MC2000) and laser are synchronized. We collected each FSR spectrum at 1 kHz repetition rate by using a home-built Labview program and obtained the Raman gain by dividing Raman-pump-on spectrum by the following Raman-pump-off spectrum. We collected data for 30–90 seconds per spectrum depending on signal level.

Sample preparation

We used betaine-30 and HPLC grade methanol (Sigma-Aldrich) as received, which were flowed in a 2 mm thick glass flow cuvette at an optical density (OD) of 1.0 at 532 nm. There was no observable sample degradation as determined by absorption spectroscopy using an Ocean Optics 4000+.

Theoretical calculations

We calculated the molecular geometries and vibrational frequencies of solvated betaine-30 using restricted and unrestricted density functional theory. We used a triple-split-valence basis set 6-311++G(d,p) with the B3LYP functional for all atoms. We included the conductor-like polarizable continuum model (CPCM) with methanol as a solvent for each calculation to mimic the solvent environment around this highly solvatochromatic molecule. The calculated ground state Raman spectrum of betaine-30 is in agreement with experimental values after scaling by 0.967.³³ To probe mode specific anharmonic couplings, we performed a scan of frequency calculations for optimized geometries at several points along the central dihedral torsional coordinate. For facile comparison to our optimized geometry frequencies, we used the same basis set and solvation model for these calculations.

Results and discussion

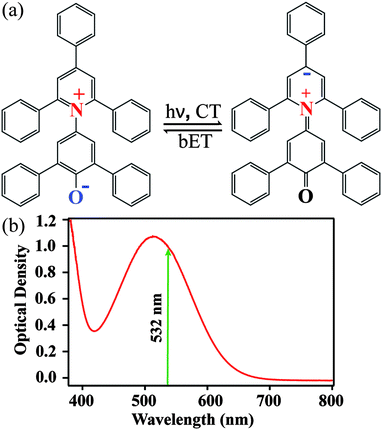
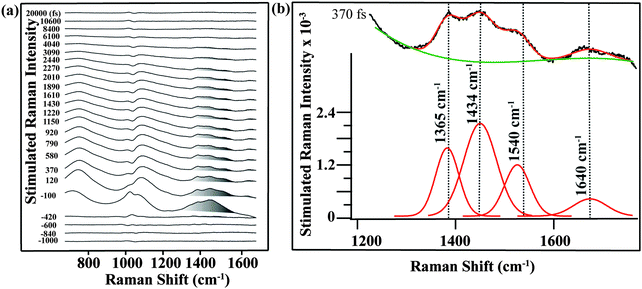
The structures of ground-state betaine-30 and its charge-transferred state are depicted in Fig. 1a. Photoexcitation results in the transfer of electron density from the O atom of the phenoxide ring to the pyridine ring. In methanol, betaine-30 absorbs at 514 nm with a 142 nm full width at half maximum (Fig. 1b). The excitation pulse used for these studies was located at 532 nm and is indicated in the figure.

Fig. 1 (a) Structures indicating photoinduced charge transfer (CT) and back electron transfer (bET) in betaine-30. (b) Absorption spectrum of betaine-30 in methanol, with the FSRS photoexcitation wavelength indicated.

We used FSRS to probe the excited state vibrations of betaine-30 after photoinduced charge transfer and before the rapid back electron transfer process. In Fig. 2a, we display the FSR spectra of betaine-30 in methanol following photoexcitation at 532 nm. These spectra are presented as offset difference spectra, with a one-to-one subtraction of the non-resonant ground state spectrum. The time-resolved spectra contain transient absorption and transient Raman features. Near time zero, we see a large absorption feature resulting from excited state absorption in the charge-transferred state, and rapid evolution of the vibrational features. The amplitude of the femtosecond Raman peaks are initially quite large due to resonant enhancement of the charge-transferred state, and decrease in intensity as the population of the excited state decay. In this work, we will focus on the four vibrational features in the 1350 to 1680 cm⁻¹ spectral region, which are highlighted in grey (Fig. 2a).

Fig. 2 (a) Femtosecond stimulated Raman spectra of betaine-30 from −1 ps to 20 ps. The main Raman modes of betaine-30 are highlighted in gray. There is a methanol subtraction artifact at 1040 cm⁻¹, and a broad oscillatory feature due to transient probe beam absorption in the excited state. (b) Fitting procedure of FSR spectrum at 370 fs. We fit the selected spectral range of the spectrum to four Gaussian peaks (red color) and a third order polynomial baseline (green color) to extract the main Raman modes of betaine-30. Spectra were taken with a 700 μW Raman pump power and 300 μW actinic pump power.

Analysis of the mode-specific frequency and amplitude evolutions can be determined after fitting the peaks and baseline. In Fig. 2b, we show the fitting procedure for the 370 fs spectrum. The 1350 to 1680 cm⁻¹ region is fit to four Gaussian peaks (red), with a third order polynomial baseline (green) to account for the electronic transient absorption. As a result of the strong Raman amplitudes, the error in the fitting is quite low, and the frequencies and amplitudes obtained from the fits are extremely reproducible across multiple data sets.

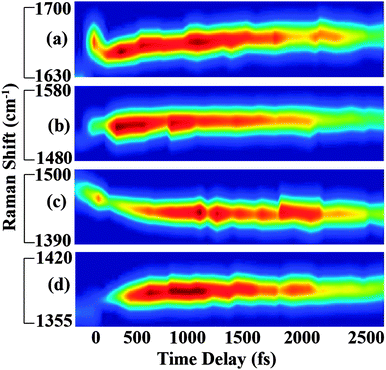
In Fig. 3, we show the structural evolution of the individual vibrational mode components, as extracted from the fitting. Oscillations in the mode specific amplitudes are clearly visible, and are different for each of the high frequency modes observed. Additionally, we observe clear changes in the vibrational frequencies on the femtosecond and few picosecond time scales. Assigning these observed vibrational frequencies to specific modes is challenging due to the lack of accurate frequency calculations on this highly reactive and solvent-dependent excited state potential energy surface. The excited state frequencies are significantly shifted from the previously observed and assigned ground state vibrational modes.³⁴ Therefore it is not straightforward to assign these excited state modes, although all must involve some degree of CC and CN stretching. For this reason, we will refer to each excited state vibrational mode by its frequency value at time t = 120 fs.

Fig. 3 Transient vibrational response of betaine-30 following photoexcitation. (a), (b), (c) and (d) correspond to 1640 cm⁻¹, 1540 cm⁻¹, 1434 cm⁻¹, and 1365 cm⁻¹ Raman modes of betaine-30, respectively. Mode-specific frequency shifts and amplitude oscillations are clearly visible in the spectra.

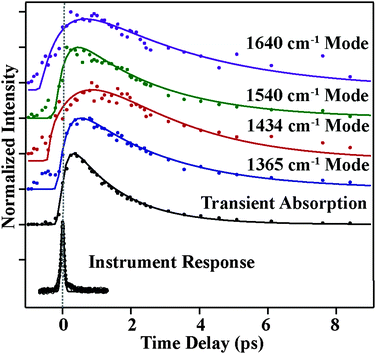
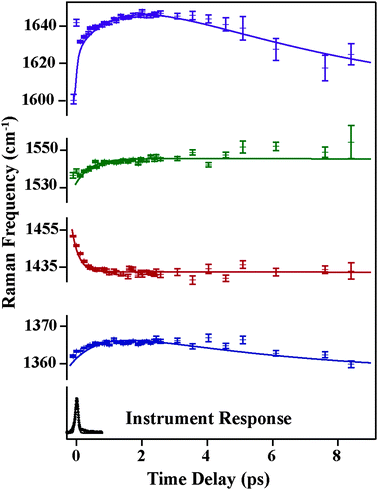
Fig. 4 and 5 plot the mode-specific amplitude and frequency changes, respectively. In both, the black trace at the bottom displays the instrument response of our measurement, as determined by a cross correlation of the actinic pump and Raman probe. The dots represent experimental data, as extracted from our fits, and the solid lines represent exponential fits to the data. For all data the error bars, as determined from the fitting, are contained within the markers.

Fig. 4 Transient Raman amplitudes of vibrational modes of betaine-30 from −0.5 ps to 9 ps. Experimental data points are represented by dots, and the lines are exponential fits. The bottom trace shows the instrument response obtained via the optical Kerr effect. Deviations from the fitted exponentials represent oscillatory components in the amplitude.

Fig. 5 Transient Raman frequencies of betaine-30 from −0.5 ps to 9 ps. Solid dots correspond to extracted data and lines indicate the exponential fits. The bottom trace is the instrument response obtained via the optical Kerr effect.

The amplitude kinetics are shown in Fig. 4. The bottom trace shows the transient absorption response, as determined by averaging the 850 cm⁻¹, 1175 cm⁻¹ and 2030 cm⁻¹ spectral regions. These values are taken with the Raman pump present on the sample, and Fig. S4 (ESI†) compares the dynamics with and without the Raman pump. This trace is fit to two exponentials, with time constants of 200 ± 50 (fs) and 1800 ± 50 (fs), in agreement with previously published work.⁷ The other traces in this figure show the amplitudes of the various Raman peaks seen in the FSR spectra. It is clear that the Raman amplitudes persist for timescales longer than the lifetime of the initially excited electronic state. We believe this is a result of a newly identified electronic state, as described below. Additionally, we see that the rise and decay of each mode occurs on slightly different timescales, which is likely due to mode specific overlap resonance conditions. Interestingly, the Raman amplitudes show oscillatory features, which will be discussed later.

The mode specific frequencies provide information about structural evolution on the charge-transferred potential energy surface. This information can be used to describe how the structure of the molecule evolves after the charge transfer process, or can probe vibrational energy redistribution following the electronic change. Fig. 5 shows the frequency evolution in the four modes observed in FSRS. All four modes experience a rapid frequency change in the first 500 fs, with the 1365, 1540, and 1640 cm⁻¹ modes rapidly increasing in frequency, and the 1434 cm⁻¹ mode decreasing in frequency. Following this rapid change, we see a slow drop in frequency in the 1365 and 1640 cm⁻¹ modes on the several picosecond timescale. Again, frequency changes occur on different time scales than the transient absorption kinetics. Table 1 summarizes the mode specific frequency and amplitude dynamics during charge-transfer processes in betaine-30 in methanol.

Table 1 Time constants extracted from exponential fitting of mode-specific femtosecond stimulated Raman amplitudes and frequencies. We extracted transient absorption kinetics by averaging the 850 cm⁻¹, 1175 cm⁻¹ and 2030 cm⁻¹ spectral regions, which are free from Raman features. The last column displays the low frequency oscillatory values observed in the data in Fig. 7, indicating the mode-specific couplings

Raman mode (cm^−1)	Amplitude		Raman frequency shifts			Fourier transform components (cm^−1)
	τ 1 (fs)	τ 2 (fs)	τ 1 (fs)	τ 2 (fs)	τ 3 (fs)
1365	300 ± 200	2700 ± 300	900 ± 100	6200 ± 800	N/A	73, 110, 159
1434	900 ± 300	2600 ± 600	200 ± 30	N/A	N/A	12, 37, 98, 159
1540	300 ± 100	2600 ± 200	500 ± 100	N/A	N/A	24, 73,122
1640	600 ± 100	3600 ± 300	100 ± 50	1500 ± 100	6700 ± 600	12, 37
Transient absorption	200 ± 50	1800 ± 50	N/A	N/A	N/A	N/A

---

Frequency changes can result from vibrational cooling or structural reorganization on a reactive potential energy surface. Cooling is manifested as an increase in vibrational frequency and concurrent decrease in vibrational linewidth as wavepackets drop along an anharmonic potential energy surface. Given the excess energy added by photoexcitation, cooling is likely contributing to the rapid frequency increases in the 1365, 1540, and 1640 cm⁻¹ modes. However, rapid decreases in vibrational frequency, such as that seen for the 1434 cm⁻¹ mode, cannot be explained by cooling. Two plausible explanations for this rapid drop in vibrational frequency are either heating or structural reorganization of the molecule. Rapid intramolecular vibrational relaxation (IVR) on the electronic excited state surface could lead to an increase in energy deposited in this mode and concurrent frequency decrease. However, previous picosecond time-resolved Raman and transient acoustic grating studies on betaine-30's ground state indicate that IVR is relatively slow due to the molecule's size.^21,35 Additionally, we do not see a significant increase in the Raman linewidth of the mode, making IVR an unlikely source of the frequency shift. Thus, given the number of normal modes and the magnitude of frequency decrease, a structural reorganization argument seems more plausible, particularly given the significant and rapid change in charge density in betaine-30 following photoexcitation. Further support for the effects of structural reorganization on specific mode frequencies can be provided by calculations of molecular frequencies at different nuclear coordinates.

To identify possible structural changes causing shifting of Raman frequencies in the first several picoseconds, we compared the experimentally observed vibrational frequencies to DFT calculations. The geometry of the charge-transferred state of betaine-30 has a more planar central dihedral angle compared to that of the ground state geometry.^23,36 Charge transfer (CT) from the phenoxide ring to the pyridinium ring results in planarization of the main dihedral angle, which facilitates delocalization of the electron cloud on the two main moieties of betaine-30. Thus one practical way of modeling the structural changes during the rapid CT and bET processes is to obtain the optimized geometries and vibrational frequencies of betaine-30 at various values of this central dihedral angle. A change in this central dihedral angle between the phenoxide and pyridinium rings is primarily assigned to the 112 cm⁻¹ mode, in which 21% of the nuclear motion arises from rotation around the central dihedral angle, out of 396 total internal coordinates. If higher frequency vibrational modes change frequency as this angle is varied, they are anharmonically coupled to the 112 cm⁻¹ torsional mode. Comparing the frequency shifts of various modes as a function of torsion angle enable us to determine which modes observed in FSRS are coupled to the charge transfer process. However, as excited state calculations in this highly reactive and solvatochromatic molecular are beyond the computation feasibility of this work, we used ground state calculations to mimic the charge-transfer process. We scanned the ground state potential energy surface along one coordinate by changing the central dihedral angle from 100° through the equilibrium geometry of 66° to a more planar geometry of 6°. All other 3N-7 coordinates were optimized. We see a 20 fold increase in electron density on the para carbon atom in pyridine ring while scanning from the ground state geometry to the more planar geometry as determined by natural bond orbital analysis. Thus it is clear that this single nuclear coordinate plays a significant role in the charge transfer process.

Fig. 6a shows the relative energy of the betaine-30 molecule with respect to the change in the main dihedral angle. If the two main moieties of betaine-30 could rotate freely along the main dihedral angle, we could expect a very small energy change during this torsional motion. However, we observe an energy rise of more than 5100 cm⁻¹ during dihedral rotation. This large energy rise is evidence for coupling of the torsional motion to higher frequency vibrational modes, likely in part as a result of steric hindrance. In Fig. 6b, we examine the effects of dihedral rotation on the vibrational frequency of the modes in the region probed experimentally with FSRS. Here it is difficult to correlate each calculated frequency with experimentally observed values. Therefore we plot all of the prominent frequency modes in the 1350 cm⁻¹ to 1700 cm⁻¹ spectral region. Planarization along the torsional coordinate strongly affects some frequency modes (type i), down-shifting them by about 12 cm⁻¹ as the molecule is perturbed from the ground state equilibrium at dihedral angle value of 66°. In contrast, other modes (type ii) are less sensitive to main dihedral torsion, downshifting by less than 1 cm⁻¹. Interestingly, all Raman active modes fit into these two categories, with no modes showing frequency increases as the dihedral angle decreases.

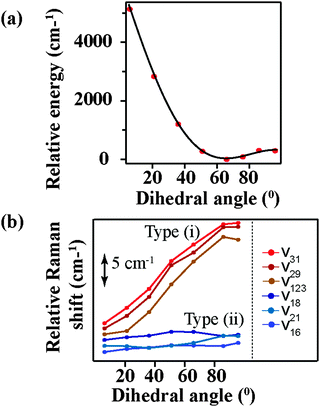Fig. 6 Calculated values for (a) total energy, as normalized to equilibrium geometry and (b) select Raman frequencies as a function of central dihedral rotation.

The change in the frequency of the 1434 cm⁻¹ mode observed by FSRS follows a similar trend as observed for the type (i) modes. There is a drop in frequency of over 30 cm⁻¹ in the first 200 fs following photoexcitation, resulting from the structural reorganization of the molecule. Based on the theoretical calculations shown in Fig. 6b, this indicates that the molecule is becoming more planar on a rapid time scale. Although quantitative comparisons are hindered by the ground state nature of our calculations, it seems as though the central dihedral angle drops significantly within several hundred femtoseconds after excitation.

A surprising feature of our excited-state FSR spectra is that mode frequencies do not recover to the ground state frequencies even after 8 picoseconds. The predominant ground state vibrational frequencies, as measured previously and shown in Fig. S3 (ESI†), are 1320, 1360, 1586, 1602 and 1622 cm⁻¹. At 8 ps, our FSR spectra show frequencies of 1374, 1439, 1545, and 1644 cm⁻¹, which are quite shifted from the ground state values. Given that the excited state lifetime as measured by transient absorption studies and observed here indicates that the population of the charge-transferred state decays with a time constant of 2 ps, these long-lived frequencies are unlikely to arise from molecules in the charge-transferred state. Additionally, we see that the Raman amplitudes decay with time constants much longer than the electronic state lifetimes as obtained from transient absorption measurements. One possible explanation for these observations is that the charge-transferred surface might open a different channel to populate a lower-lying electronic state, in addition to the main pathway to the hot ground state. This newly discovered state must be off-resonant with previous transient absorption measurements, indicating that it must have absorption and emission features in the near infrared region. This would also enable some pre-resonance enhancement with our 800 nm Raman pump pulse, giving rise to intense Raman features which persist beyond the transient absorption lifetime. Thus, we think the most plausible explanation for the spectra obtained by FSRS is the existence of a lower-lying electronic state in the betaine-30 molecule.

This new state is most likely to be a low-lying triplet state, as there are no signatures of additional optically allowed transition as measured by absorption spectroscopy. Dark triplet states exist in similar aromatic compounds such as rubrene, and are attractive for singlet fission applications.³⁷ We attempted to measure the phosphorescence spectrum of betaine-30, which would provide additional confirmation of this assignment. However, intereference from known impurities which have hindered previous resonance Raman studies³⁸ prevented definitive assignment of any phosphorescence signal.

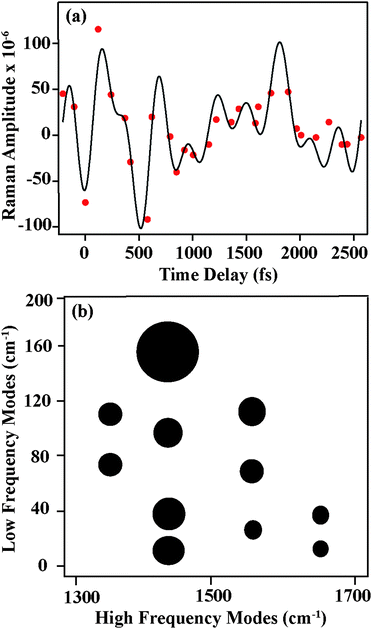
Having identified the origin of frequency and amplitude dynamics observed in betaine-30 with FSRS, we can return to the oscillatory components observed in the amplitudes as displayed in Fig. 4. As compared to the frequency shifts, the amplitudes show significantly more deviation from the exponential fits, indicating that oscillatory components are much more readily seen as amplitude modulation. In Fig. 7a, we show the amplitude modulations of the 1434 cm⁻¹ peak, after subtracting the exponential fit. The modulation depth is significantly above the noise level. These oscillatory features can be fit to a minimum of four sinusoidal functions, and a representative fit is shown in black. After Fourier transformation of the fit, we obtain the component frequencies, which correspond to several low frequency vibrations in betaine-30. Similar analysis on a different data set is shown in Fig. S5 (ESI†), indicating the reproducibility of these features. A similar procedure on the three other high frequency peaks provides a coupling map, shown in Fig. 7b. This map depicts the mode-specific couplings following the initial charge-transfer process in betaine-30. The size of the dots corresponds to the amplitude coefficient for a particular low frequency mode in the high frequency fit function, and indicates the strength of the coupling. These low frequency components agree well with calculated ground state vibrational frequencies for various phenyl ring torsions. As these are excited state vibrational modes, specific assignments await accurate excited state frequency calculations, but these low frequency modes clearly result from various torsional motions. All of these modes clearly contribute to shaping the potential energy landscape of the excited state of betaine-30, and are coupled to the higher frequency modes observed in our spectra.

Fig. 7 (a) Amplitude modulations in FSR spectra (red solid dots) of the 1434 cm⁻¹ mode after subtracting the fitted exponential decay. The black line shows the fit to four sinusoidal functions. (b) Depiction of oscillatory components as extracted from amplitude fitting. The size of each circle represents the low frequency mode amplitude as obtained from Fourier transformation, and is representative of the magnitude of mode-specific couplings.

The amplitude modulations of the FSR features clearly seen in Fig. 7 are unexpected, as previous transient absorption measurements show no oscillatory features.⁷ Indeed, our transient absorption measurements, as shown in Fig. 4, confirm these previous results. Due to coupling between low frequency vibrational torsional motions and the high frequency vibrational modes, each oscillatory cycle of a low frequency mode can significantly oscillate the high frequency nuclear wave packet from a more on-resonance geometry to a more off-resonance geometry. Within the potential well for a given high frequency mode, low frequency mode oscillations drive the wavepacket in and out of pre-resonance with the next excited electronic state. This causes a modulation in the Raman amplitude, in that the system experiences more resonance enhancement on one side of the potential energy surface compared to the other.

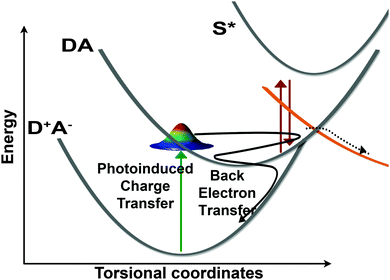
The oscillatory features in the Raman spectra provide an insight into the reactive potential energy surfaces which play a role in the photocycle of betaine-30. These amplitude oscillatory features become prominent at ∼100 fs and remain until 2.5 ps, meaning that they arise from the excited charge-transferred state. The oscillations only arise between coupled modes,³⁹ appearing as amplitude modulations due to transient changes in the resonance condition. The anharmonic coupling information provided by our FSRS data can be used to determine the multidimensional potential energy landscape during this rapid electron transfer process, which provide new insight into vibrationally-mediated bET process of betaine-30 (Fig. 8).

Fig. 8 Schematic depiction of the betaine-30 photocycle as determined by FSRS probing. Photoexcitation promotes the system from the D⁺A⁻ state into the DA state. A large fraction of the population oscillates along torsional coordinates in this state, and is transiently pre-resonantly enhanced to the S* state. This population undergoes back electron transfer in the Marcus inverted region in ∼2 ps. Based on analysis of the Raman kinetics, we conclude a fraction of the initially excited population is transferred to another state, undergoing relaxation on a different pathway.

Conclusions

Determining the mechanism of rapid photoinduced electron transfer processes is crucial for the design of efficient photovoltaic systems. We have used the structurally sensitive FSRS technique to probe electron transfer in betaine-30, a well-studied model system for vibrationally assisted charge transfer. Our transient Raman spectra track the structural evolution on the charge-transferred state's potential energy surface, following the distribution of energy as the molecule planarizes. We observe mode-specific vibrational cooling, as well as structural changes resulting from ring planarization. These experimental results, coupled with ground state DFT calculations, indicate that the planarization process is quite fast, with structural changes complete on the 200 fs timescale. Surprisingly, we find large amplitude modulations of the high frequency vibrational modes, indicating strong coupling of these high frequency stretching modes to a number of low frequency torsional modes. Additionally, an analysis of the frequency and amplitude kinetics obtained by the FSRS experiment suggest a new relaxation pathway through a low-lying electronic excited state. This work provides key insights into vibrational coupling which can be used to describe the multidimensional potential energy landscape during the rapid photo-induced electron transfer processes.

Acknowledgements

This work was funded by University of Minnesota start-up funds. We thank Dr Dong-sheng Yang from the University of Kentucky for providing access to the University of Kentucky High Performance Computer Center, which was used for dihedral-angle dependent frequency calculations. We thank Dr Nathaniel C. Brandt for valuable discussions.

References

1. A. Hagfeldt and M. Gratzel, Acc. Chem. Res., 2000, 33, 269–277.
2. A. E. Jailaubekov, A. P. Willard, J. R. Tritsch, W.-L. Chan, N. Sai, R. Gearba, L. G. Kaake, K. J. Williams, K. Leung, P. J. Rossky and X. Y. Zhu, Nat. Mater., 2013, 12, 66–73.
3. J. Jortner and M. Bixon, J. Chem. Phys., 1988, 88, 167–170.
4. C. Reichardt, Chem. Rev., 1994, 94, 2319–2358.
5. I. Renge, J. Lumin., 2009, 129, 469–473.
6. X. H. Zhao, F. J. Knorr and J. L. McHale, Chem. Phys. Lett., 2002, 356, 214–220.
7. S. A. Kovalenko, N. Eilers-Konig, T. A. Senyushkina and N. P. Ernsting, J. Phys. Chem. A, 2001, 105, 4834–4843.
8. M. C. Beard, G. M. Turner and C. A. Schmuttenmaer, J. Phys. Chem. A, 2002, 106, 878–883.
9. S. A. Kovalenko, N. Eilers-Konig, T. A. Senyushkina and N. P. Ernsting, J. Phys. Chem. A, 2001, 105, 4834–4843.
10. E. Akesson, G. C. Walker and P. F. Barbara, J. Chem. Phys., 1991, 95, 4188–4194.
11. E. Akesson, A. E. Johnson, N. E. Levinger, G. C. Walker, T. P. Dubruil and P. F. Barbara, J. Chem. Phys., 1992, 96, 7859–7862.
12. H. Sumi and R. A. Marcus, J. Chem. Phys., 1986, 84, 4894–4914.
13. G. C. Walker, E. Akesson, A. E. Johnson, N. E. Levinger and P. F. Barbara, J. Phys. Chem., 1992, 96, 3728–3736.
14. G. C. Walker, E. Akesson, A. E. Johnson, N. E. Levinger and P. F. Barbara, J. Phys. Chem., 1992, 96, 3728–3736.
15. P. J. Reid, S. Alex, W. Jarzeba, R. E. Schlief, A. E. Johnson and P. F. Barbara, Chem. Phys. Lett., 1994, 229, 93–100.
16. P. J. Reid and P. F. Barbara, J. Phys. Chem., 1995, 99, 3554–3565.
17. X. H. Zhao, J. A. Burt and J. L. McHale, J. Chem. Phys., 2004, 121, 11195–11201.
18. Y. P. Zong and J. L. McHale, J. Chem. Phys., 1997, 107, 2920–2929.
19. X. H. Zhao and J. L. McHale, Chem. Phys. Lett., 2003, 378, 582–588.
20. S. Hogiu, W. Werncke, M. Pfeiffer and T. Elsaesser, Chem. Phys. Lett., 1999, 312, 407–414.
21. S. Hogiu, W. Werncke, M. Pfeiffer, J. Dreyer and T. Elsaesser, J. Chem. Phys., 2000, 113, 1587–1594.
22. C. Fuchs and M. Schreiber, J. Chem. Phys., 1996, 105, 1023–1028.
23. J. Lobaugh and P. J. Rossky, J. Phys. Chem. A, 2000, 104, 899–907.
24. T. Ishida and P. J. Rossky, J. Phys. Chem. A, 2001, 105, 558–565.
25. H. Kim, H. Hwang and P. J. Rossky, J. Phys. Chem. A, 2006, 110, 11223–11229.
26. G. Duvanel, J. Grilj, H. Chaumeil, P. Jacques and E. Vauthey, Photochem. Photobiol. Sci., 2010, 9, 908–915.
27. M. Caricato, B. Mennucci and J. Tomasi, Mol. Phys., 2006, 104, 875–887.
28. V. Kharlanov and W. Rettig, J. Phys. Chem. A, 2009, 113, 10693–10703.
29. R. R. Frontiera and R. A. Mathies, Laser Photonics Rev., 2011, 5, 102–113.
30. R. R. Frontiera, C. Fang, J. Dasgupta and R. A. Mathies, Phys. Chem. Chem. Phys., 2012, 14, 405–414.
31. W. R. Silva, E. L. Keller and R. R. Frontiera, Anal. Chem., 2014, 86, 7782–7787.
32. S. Shim and R. A. Mathies, Appl. Phys. Lett., 2006, 89, 121124.
33. NIST, http://cccbdb.nist.gov/vibscalejust.asp.
34. Y. P. Zong and J. L. McHale, J. Chem. Phys., 1997, 106, 4963–4972.
35. M. Terazima, Chem. Phys. Lett., 1999, 305, 189–196.
36. S. R. Mente and M. Maroncelli, J. Phys. Chem. B, 1999, 103, 7704–7719.
37. M. B. Smith and J. Michl, in Annu. Rev. Phys. Chem., ed. M. A. Johnson and T. J. Martinez, Annual Reviews, Palo Alto, 2013, vol. 64, pp. 361–386.
38. Y. P. Zong and J. L. McHale, J. Chem. Phys., 2004, 120, 11333.
39. D. P. Hoffman, S. R. Ellis and R. A. Mathies, J. Phys. Chem. A, 2014, 118, 4955–4965.

---

Footnote

† Electronic supplementary information (ESI) available: Optimized geometries for betaine-30 in ground state geometry and along dihedral angle scan. Comparison of transient absorption spectra and FSR spectra. Raman pump power dependence on excited state lifetime and dynamics. Validation of the amplitude modulations in FSRS data. Ground state spontaneous Raman spectrum of betaine-30 in methanol with 785 nm excitation. See DOI: 10.1039/c5cp06195d

---