 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploiting orientation-selective DEER: determining molecular structure in systems containing Cu(II) centres†
Alice M.
Bowen‡
ab,
Michael W.
Jones‡
a,
Janet E.
Lovett
ac,
Thembanikosi G.
Gaule
d,
Michael J.
McPherson
d,
Jonathan R.
Dilworth
a,
Christiane R.
Timmel
*a and
Jeffrey R.
Harmer
*ae
aCentre for Advanced Electron Spin Resonance, University of Oxford, South Parks Road, Oxford, OX1 3QR, UK. E-mail: Christiane.timmel@chem.ox.ac.uk
bInstitute of Physical and Theoretical Chemistry, Goethe University Frankfurt, Max-von-Laue-Str. 7, 60438, Frankfurt am Main, Germany
cSUPA, School of Physics and Astronomy, University of St Andrews, North Haugh, St Andrews, KY16 9SS, UK
dAstbury Centre for Structural Molecular Biology, Institute of Molecular and Cellular Biology, Faculty of Biological Sciences, University of Leeds, Leeds LS2 9JT, UK
eCentre for Advanced Imaging, University of Queensland, St Lucia, QLD 4072, Australia. E-mail: Jeffrey.harmer@cai.uq.edu.au
First published on 3rd February 2016
Abstract
Orientation-selective DEER (Double Electron-Electron Resonance) measurements were conducted on a series of rigid and flexible molecules containing Cu(II) ions. A system with two rigidly held Cu(II) ions was afforded by the protein homo-dimer of copper amine oxidase from Arthrobacter globiformis. This system provided experimental DEER data between two Cu(II) ions with a well-defined distance and relative orientation to assess the accuracy of the methodology. Evaluation of orientation-selective DEER (os DEER) on systems with limited flexibility was probed using a series of porphyrin-based Cu(II)–nitroxide and Cu(II)–Cu(II) model systems of well-defined lengths synthesized for this project. Density functional theory was employed to generate molecular models of the conformers for each porphyrin-based Cu(II) dimer studied. Excellent agreement was found between DEER traces simulated using these computed conformers and the experimental data. The performance of different parameterised structural models in simulating the experimental DEER data was also investigated. The results of this analysis demonstrate the degree to which the DEER data define the relative orientation of the two Cu(II) ions and highlight the need to choose a parameterised model that captures the essential features of the flexibility (rotational freedom) of the system being studied.
Introduction
Pulse dipolar spectroscopy (PDS) is a powerful technique providing structural information in biological and materials sciences applications by measurement of the distance (from ca. 1.5 to 8 nm for protonated systems and ≥10 nm in deuterated systems)1,2 and, in favourable cases, orientations between two paramagnetic spin probes. As the majority of biomolecules are naturally diamagnetic, PDS studies on such systems typically employ spin labels, for example the nitroxide MTSL (S-(2,2,5,5-tetramethyl-2,5-dihydro-1H-pyrrol-3-yl)methylmethanesulfonothioate) which can be attached selectively to the protein of interest through site directed spin labelling of a targeted cysteine residue and formation of a covalent disulfide linkage.3The results of PDS report directly on the inter-spin dipolar interaction, from which a distance distribution can be easily computed for experiments without orientational selection using Tikhonov regularization.4 The distance distribution obtained can yield information on the flexibility of the spin label tether and/or any structural disorder in the molecule.5,6 However, at the typically employed X- and Q-band frequencies, the inherent flexibility of the MTSL tethers often results in a loss of all inter-spin orientation information.7 Although orientation selection may complicate the analysis, its presence can provide a wealth of additional information about the molecular system if it can be successfully measured and modelled.8–10
Intrinsic paramagnetic centres in biomolecules are, in principle, ideal spin probes to be exploited in a PDS experiment.11,12 They are usually fixed rigidly within their parent biomolecule resulting in very accurate and narrow inter-spin distance distributions. Conversely, significant flexibility and/or disorder of the protein structure (e.g. unfolded proteins or different conformations) will dominate the distance distribution profile allowing assessment and quantification of these factors. Intrinsic Cu(II) centres constitute important spin probes for PDS as they occur widely in biology; for example in hemocyanin, laccases, superoxide dismutases and ceruloplasmin. Many biomolecules contain other naturally occurring metal cations, e.g. zinc (found in the zinc finger domains of many DNA binding proteins), iron (present in the plethora of heme containing proteins) or manganese (occurring in Arginase, a member of the ureohydrolase family of enzymes). Whilst many of these metal cations are paramagnetic themselves, their replacement by Cu(II),13 if chemically feasible, would be advantageous as its relatively long relaxation times and low g-value anisotropy make it a suitable candidate for PDS studies. Biologically copper is important, for example the binding of Cu(II) to amyloid-beta fibrils of Alzheimer's disease has also been observed.14 Copper centres have recently been incorporated into the helix of DNA using tailored metal mediated base pairs, providing a rigid spin probe for potential PDS spectroscopy studies.15–18 Furthermore, copper has been incorporated into a protein structure in the form of a copper binding loop and distances between this centre and a nitroxide spin label probed using both DEER (Double Electron Electron Resonance), synonymously PELDOR (Pulsed Electron Double Resonance), and relaxation measurements.19 It has also been shown that in some proteins copper can associate selectively with histidine residues, allowing the inter-residue distance to be used to identify the site of interaction.20 Based upon this, a bis-histidine moiety has been designed as a selective binding site for copper and been shown to provide a stable copper based spin label for DEER experiments.21 Alternatively a cysteine specific copper tag has been synthesised, that can be attached to the protein via a disulfide linkage in a similar manner to the nitroxide MTSL mentioned previously.22
Here we study molecules containing Cu(II) centres with orientation selective PDS experiments using three and four-pulse DEER. The orientation selectivity is a result of the microwave pulses exciting only a small part of the Cu(II) EPR spectrum: at X-band (∼9.5 GHz), the Cu(II) spectrum extends over some 500 MHz due to g-anisotropy and the copper hyperfine couplings whilst the bandwidth of a typical π/2 pulse (e.g., 16 ns) does not exceed 50 MHz. This selectivity of the microwave (mw) pulse results in a particular DEER experiment only exciting a relatively small set of molecular orientations of the pair of Cu(II) spins (inter-spin vectors) with respect to the magnetic field vector, B0.
To date there have been several DEER reports using Cu(II) ions. The first such study was carried out on a homo-dimer of the protein Azurin by van Amsterdam et al.11 who extracted an approximate distance but no orientation information. Cu(II)–Cu(II) distances were also measured in a protein (multi-copper nitrate reductase) by van Wonderen et al.23 who applied a relaxation filter to distinguish between different copper centres, however their study did not account for orientation effects. More recently, Merz et al.24 measured inter-copper distances in Superoxide Dismutase (SOD1) using both DEER and 6-pulse Double Quantum Coherence (DQC) at Ku-band (17 GHz). Although orientation selection was considered, the effect was determined to be small due to the relative orientation of the two copper centres and no account was made of this in the analysis. Orientation selection was also observed although not analysed by Narr et al.25 on a copper bisnitroxide model system. The first orientation-selective DEER analysis study on Cu(II)–NO˙ model systems was presented by Bode et al.26,27 who used a geometric model, based on a 15° bend of the linker and rotation of the nitroxide moiety around this linker, as the basis for their simulations. The use of the nitroxide moiety significantly simplified the orientational analysis as only the Cu(II) orientational selection needed to be considered. The orientation selection between a Cu(II)–nitroxide spin pair was also considered by Abdullin et al.28 who used this information to allow for the trilateration of the position of the bound copper ion within a monomer of Azurin that had been labelled with MTSL nitroxide at known positions.
Saxena et al.29–32 studied two Cu(II) centres each coordinated by the hexapeptide sequence PHGGGW which is implicated in a number of prion diseases,33–35 with each copper moiety linked by a number of proline amino acids (PHGGGW(P)nHGGGW, with variable n). The initial system, PHGGGWPPPHGGGW with Cu(II) coordinated, did not show any orientation selectivity due to the system geometry.29 Using a chemically similar but geometrically different model system (PHGGGWPPPPPHGGGW) the same authors were able to perform an orientational analysis of two copper centres using a generic molecular model,20,30,31 which may not be applicable in all circumstances, as discussed below. Marko et al.36,37 discussed a model free approach using data from rigid bisnitroxide systems fitted using a simulated DEER trace library to reconstruct the experimental data. However, the symmetry of the spin system prevented determination of a unique solution. Currently no universal single method exists for the analysis of orientation-selective DEER with a distribution of spin–spin distances and orientations and consequently best results rely on some prior structure knowledge to reduce the number of possible solution sets.
The aim of this study is to explore the limits and capabilities of orientation-selective DEER in extracting distance and orientation information from systems containing two Cu(II) spins. Firstly, we investigated the homo-dimer of copper amine oxidase from Arthrobacter globiformis, a protein system embedding two tightly coordinated Cu(II) centres well characterized by high quality X-ray data. Next we examined a series of porphyrin-based Cu(II)–Cu(II) rod-like molecules of differing lengths with a reasonably large degree of conformational flexibility and, in addition, the corresponding Cu(II)–NO˙ and NO˙–NO˙ systems. Different models were analysed with regard to their capability of describing the conformational flexibility and the resulting orientation-selective DEER traces.
Experimental
Experimental synthesis
The model compounds were designed to be semi-rigid rods holding the two radical labels a fixed distance apart. Cu(II)–Cu(II) (1–5), Cu(II)–NO˙ (6 and 7) and bisnitroxide, NO˙–NO˙ (8), derivatives were prepared by multi-step synthesis to provide benchmark measurements against which the accuracy of the modelling could be reliably ascertained. The stability and convenient synthesis and purification routes of the tetraphenyl porphyrin template made it the obvious choice of copper-chelating moiety for this study. Attempts to use several other well-known Cu(II) ligands were not successful due to the formation of polymeric material during coordination to Cu(II) under a range of conditions. The amide functionality acts as a type of ‘circuit breaker’ diminishing the through-bond electronic exchange that could occur between the two paramagnetic centres impeding the determination of accurate distances. To minimize the level of uncertainty in the spin–spin distances and orientations, the central spacers were designed to be as stable and rigid as possible. However, the DFT calculations (below) show that the molecules still exhibit a significant angular flexibility.The target molecules were prepared by the peptide coupling of 5-(4-aminophenyl)-10,15,20-triphenylporphyrin (TPPNH2)38,39 or 4-amino-TEMPO with the requisite 1,4-phenyl dicarboxylic acids, and subsequent metallation with Cu(II). With the exception of terephthalic acid which was commercially available and 1,1-biphenyl-4,4′-dicarboxylic acid (available as the diester), the diacids containing 3–5 phenyl groups in the central linkers were prepared with Suzuki coupling reactions and subsequent ester hydrolysis. Polyaromatic molecules often suffer from solubility problems which can be circumvented by the attachment of aliphatic sidegroups, as for instance employed by Godt et al.40 in the synthesis of model bisnitroxides for use in their DEER methodology work. For compounds with three or more phenyl groups in the central linker it was necessary to employ this strategy. The two smaller compounds, with 1- and 2-phenyl groups as the central spacer, did not suffer from significant solubility problems. BOP (benzotriazol-1-yloxytris(dimethylamino)-phosphonium hexafluorophosphate) coupling with an excess of the TPPNH2 congener in all cases afforded the diporphyrin proligands in moderate yields after flash chromatography. Metallation of the diporphyrin species was relatively trivial; a methanolic solution of Cu(II) acetate was introduced to a stirred solution of diporphyrin in chloroform and the subsequent mixture heated at reflux to afford the model compounds 1–5 cleanly.
The Cu(II)–NO˙ species 6 and 7 were prepared via the BOP coupling of one equivalent of TPPNH2 to the requisite acid, followed by attachment of the TEMPO motif also using a BOP mediated coupling procedure. This order of addition was employed to aid purification processes as the porphyrin derivative is clearly visible (dark purple) on silica gel. Finally, the insertion of metal was achieved in the same way as for the symmetrical Cu(II)–Cu(II) species. The NO˙–NO˙ compound 8 was prepared simply, again by BOP mediated coupling of the TEMPO–NH2 motif to the 3-phenyl acid. The compounds were characterized (where appropriate) by thin layer chromatography and MALDI analysis, UV-vis and IR spectroscopy, 1H and 13C NMR, mass spectrometry and CW-EPR at X-band.
Detailed synthetic schemes and relevant characterization data for all of the compounds prepared and the intermediates are given in the ESI.†
Sample preparation
Samples of Cu(II)–Cu(II), Cu(II)–NO˙ and NO˙–NO˙ model systems (compounds 1–8) were prepared to a concentration of 0.1 mM in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of chloroform
1 mixture of chloroform![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) toluene
toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) THF. Toluene was included to prevent π-stacking of aromatic rings of the compounds and a chloroform/THF mixture was found to form a suitable frozen glass. To account for the different relaxation properties of Cu(II) and nitroxides, EPR measurements on the Cu(II)–Cu(II) systems (1–5) were conducted at 15 K, those on the Cu(II)–NO˙ systems (6 and 7) at 25 K and those on the NO˙–NO˙ (8) system at 50 K. These temperatures were chosen as they provided the most favourable combinations of T1 and T2.
THF. Toluene was included to prevent π-stacking of aromatic rings of the compounds and a chloroform/THF mixture was found to form a suitable frozen glass. To account for the different relaxation properties of Cu(II) and nitroxides, EPR measurements on the Cu(II)–Cu(II) systems (1–5) were conducted at 15 K, those on the Cu(II)–NO˙ systems (6 and 7) at 25 K and those on the NO˙–NO˙ (8) system at 50 K. These temperatures were chosen as they provided the most favourable combinations of T1 and T2.
Recombinant copper amine oxidase from A. globiformis (AGAO) with a C-terminal Strep-tag II, was prepared in E. coli according to the method of Juda et al.41 A stock solution of strep-tagged copper amine oxidase was prepared using 120 mg ml−1 (1.7 mM concentration of the protein monomer) in 50 mM HEPES buffer at pH 7.2. This stock solution was diluted, adding 30% glycerol by volume to produce the EPR sample containing ca. 1.2 mM concentration of the protein monomer. EPR measurements on this system were also conducted at 15 K.
DEER spectroscopy
Experiments were recorded at X-band on a Bruker Elexsys E680 pulsed spectrometer equipped with an Oxford Instruments cryostat using a 3 mm split-ring Bruker resonator (EN 4118X-MS3). DEER experiments with Cu(II)–NO˙ and NO˙–NO˙ centres used a four-pulse (4P) DEER sequence1,42 with τ2 times of 1 μs and 2 μs for the 1-phenyl (6) and 3-phenyl (7) Cu(II)–NO˙ systems, respectively and 0.8 μs for NO˙–NO˙ (8). The short phase memory times of the Cu(II)–Cu(II) and AGAO samples necessitated the use of the simpler three-pulse (3P) DEER sequence43,44 to collect traces of sufficient length such that oscillations could be observed. 3P DEER traces have a dead-time resulting from pulse overlap which obscures the zero-time. Therefore 3P DEER was collected with a τ time of 1500 ns (Cu(II)–Cu(II) systems, compounds 1–5) and 2000 ns (AGAO), and 4P DEER with a τ2 = 200 ns. The 3P and 4P traces were then combined using DEER-Stitch.45 For all experiments the π/2 and π observer pulses were 32 ns with a 12 ns pump pulse.Analysis methods
Orientation selective DEER
Our DEER trace simulation algorithm is described in detail elsewhere.10 Briefly, the time-domain trace for intra-molecular interaction between pairs of spins is described by| F(t) = 1 − Δ(1 − f(t)) | (1) |
| Δ = cΔsim | (2) |
| D(t) = F(t)B(t) | (3) |
Modelling the conformations of the porphyrin-based rod-like model systems
To compute the reduced form factor f(t) starting from first principles requires knowledge of the molecular conformations and their corresponding relative populations. Our approach to determine the conformation ensemble of each molecule used density functional theory (DFT) calculations. For this we employed the Amsterdam Density Functional (ADF)47,48 software package with a BLYP functional and a TZ2P basis set.The molecules (Fig. 1) are relatively large for DFT geometry optimizations and exhibit a large number of torsional angles resulting in slow convergence of the geometry optimization. To overcome this and reduce calculation time we assumed that rotation about each flexible bond is independent of rotation about all other flexible bonds within the molecule. This allowed each molecule to be broken down into smaller molecular fragments (see ESI† for details for the fragments used). By calculating a linear transit for the rotation of each flexible bond within a fragment and optimizing the geometry at 10° intervals an energy profile for the rotation about the bond was computed. All angles found within kBT at the freezing point of the solvent (kB = 8.6173 × 10−5 eV K−1, Boltzmann constant, T = 134.15 K, kBT = 0.11547 eV) were assumed to be thermally accessible and equally populated, thus providing an allowed range of torsion angles for each bond type. A Monte Carlo approach to determine a set of molecular configurations was then obtained by rotating each of the flexible bonds of each fragment by a randomly selected angle that lies within the calculated allowed range of torsion angles for that bond type. Plots of the energy profiles for each of the bonds and the distribution profiles of the two Cu(II) ions with respect to each other for each molecule are given in the ESI† (Fig. S2).
Spin density distribution
An important parameter required for the simulation of DEER time traces is the location of the spin density, ρ. The DFT calculation for the Cu(II)–porphyrin molecular fragment yielded a spin density distribution with ρ(Cu) = 51%, and on each nitrogen ρ(N) = 11%. This result is similar to that calculated by Bode et al. (ρ(Cu) = 56%, ρ(N) = 10.6%).27 However, it is known that DFT calculations frequently overestimate covalent bonding for the Cu(II) ion, resulting in too much spin transfer onto the ligands.49 A previously employed model for the copper porphyrin moiety used ρ(Cu) = 84% and ρ(N) = 4%,10 which is consistent with typical porphyrin nitrogen hyperfine couplings. Given this uncertainty, it was therefore decided to test the sensitivity of the DEER simulations to changes in the spin density distribution between the Cu(II) ion and the coordinating nitrogens (see below).A. globiformis Amine Oxidase (AGAO) contains a copper centre ligated by three histidine ligands and two water molecules, one equatorial and the other axial, as shown in Fig. 2b. DFT studies on the isolated reaction centre from Hansenula polymorpha copper amine oxidase, which is structurally very similar to AGAO have been published previously.50 In these calculations ρ(Cu) ≅ 62% and ρ(N) = 11% (the remainder of the spin density was delocalised over the rest of the porphyrin). These results are comparable to the DFT data calculated for the copper–porphyrin systems where again the degree of covalent bonding is likely to be overestimated. In the DEER simulations for AGAO we tested three distributions with ρ(N) = 0%, 5% and 10% with the remaining spin density on the Cu(II) ion, ρ(Cu) = 100%, 85% and 70%, respectively. A different DEER response is theoretically expected with a change in the spin density distribution because the dipolar frequency scales as 1/r3. Comparing the results from all three trials no significant difference was observed in the DEER traces calculated, which results from the small region over which the spin density is distributed as compared to the relatively large inter-copper distance.
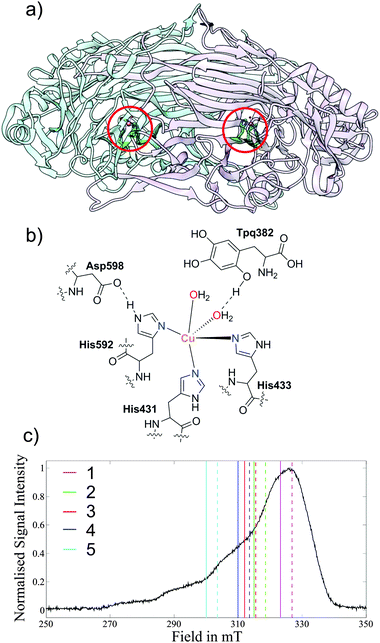 | ||
| Fig. 2 (a) X-ray structure of the Copper Amine Oxidase (AGAO) homodimer (pdb code: 1IU7)52 from A. globiformis with the Cu(II) centres highlighted in red circles. (b) Cu(II) coordination sphere showing the histidine residues and water molecules. (c) Field-sweep X-band EPR spectrum depicting the DEER pulse positions; experiments are grouped in coloured pairs with dashed lines representing pump positions and solid lines detection positions. The numeric key corresponds to the traces in Fig. 3. | ||
For the nitroxide, the spin density is essentially split between the nitrogen and the oxygen, with the larger portion localised on the oxygen.51 In all the following calculations the ρ was positioned wholly on the oxygen, ρ(O) = 100%.
Results and discussion
Cu(II) centres with a single fixed orientation
The two Cu(II) centres in the protein homodimer of AGAO (Fig. 2a) are separated by a well-defined distance and related by one single relative orientation as characterized by a number of X-ray studies. The protein therefore serves as an ideal model system to test the accuracy of orientation-selective DEER on Cu(II) containing molecules. Fig. 2c shows the observer positions for the five orientation-selective DEER measurements which were carried out.The crystal structure (pdb code: 1IU7)52 provides the relative orientations of the two Cu(II) centres with respect to one another. However, it does not provide direct information on the g-tensor orientations of the two centres with respect to the molecular frame.
Experimental single-crystal studies for a copper tetraphenyl porphyrin centre, in which the copper centre is ligated by four nitrogens, have shown that the g-tensor is aligned such that the gz axis is perpendicular to the plane of the porphyrin ring.53 In comparison the distorted geometry of the AGAO copper centre (Fig. 2b), in which the copper is ligated by three histidines and two water molecules in our aerobic preparation52 (in anaerobic preparations the oxygen of tyrosine 382 replaces the water)54 makes predicting the g-tensor orientation more complex. A DFT study performed on a phenolate Cu(II) compound,55 which bears some resemblance to the AGAO copper centre when the protein is prepared under anaerobic conditions, calculated a g-tensor orientation where the gz axis lies in the plane of the three coordinating nitrogens. This orientation is orthogonal to that which could be predicted in analogy with a copper–porphyrin where the gz axis is perpendicular to the plane of the ligating nitrogens. The AGAO sample used in this study was prepared aerobically and therefore tyrosine 382 will have already reacted to form TPQ so there is no longer a direct interaction between this residue and the copper centre.52 Considering the above, a reasonable initial guess of the g-tensor orientation for AGAO is to place the gz axis perpendicular to the plane of the three ligating histidine residue nitrogens, in analogy to a copper–porphyrin complex. The DEER simulations using this orientation are shown in Fig. S5 (ESI†) and provide a fair fit to the experiment.
However, to determine how accurately the DEER data defines the g-tensor orientation we fixed the distance according to the crystal structure and trailed different axial g-tensor orientations with respect to the protein structure. This was carried out by changing the gz axes of both centres under the constraint that the g-tensor orientation in one protein is mirrored in the second (Fig. 3).
 | ||
| Fig. 3 X-band DEER data from the Copper Amine Oxidase (AGAO) homodimer from A. globiformis. Top: Arrows representing the orientation of the gz vectors for the 10 best fitting DEER traces, assessed by the least-squares residuals of the simulated to experimental traces, from a total of 161 simulated orientations. The least-squares residuals for all 161 orientations are plotted in Fig. S8 (ESI†). The best fitting orientation is depicted by a red arrow and the 10th best fit by a black arrow. Due to the symmetry of the g-tensor it is not possible to define an absolute gz direction and thus each orientation is shown as a double-headed arrows projecting through the central copper ions. The relative position in space of the two copper centres was taken from the crystal structure (pdb code: 1IU7), with an inter-spin distance of 3.60 nm.52 Bottom: The 1st (red) and 10th (black) best-fitting DEER traces along with the experimental form factors (blue) computed by removal of the background B(t). The numbers to the right of each trace identify the DEER positions within the EPR spectrum in Fig. 2. In order to demonstrate the differences due to orientation selection between the traces the position of the first minimum of each trace is marked with a * and the position of the first maximum with a #. In trace 4 the (*) gives the position of the 2nd minimum which is more intense than the first minimum due to convolution of the trace with a proton ESEEM modulation that could not be completely suppressed using τ-averaging. | ||
The results of this analysis (calculated with ρ(N) = 5%, ρ(Cu) = 85%) show that the best fits to the DEER traces occur in one open conical-like distribution that contains orientations where the gz axis is approximately normal to the plane formed by the three nitrogens (Fig. 3). As the g-matrix has inversion symmetry, the distribution of gz vectors in Fig. 3 is plotted using double headed arrows and thus appears to take the form of an hourglass. The best fitting traces from this analysis provide a better fit to the experimental data than the traces calculated from the initial guess of the g-tensor orientation. Note that the two water molecules in the active site move the Cu(II) ion out of the plane of the nitrogens and therefore, on symmetry grounds, it is likely that the gz axis does not lie exactly normal to the nitrogen plane.
Considering the (almost) axial nature of the g-matrix it is to be expected that a range of different g-tensor orientations produce a good fit to the experimental DEER data, even though the system is rigid (as demonstrated by the presence of several oscillations in the DEER traces, Fig. 3) and will have just one dominant g-tensor orientation (small deviations occur due to strain in the protein structure surrounding the copper centre). The relative angle of the gz axis with respect to the inter-spin vector is determined from the experimental data, but as the gx and gy principal values are not well resolved neither are the orientations of the axes gx and gy. As noted above, further restrictions on a unique solution are imposed by the symmetry of the spin Hamiltonian. In principle, measurements at higher frequencies would allow gx and gy values to be resolved and thus orientation information relative to the gx and gy axes to be obtained.
The above analysis was repeated with 0% and 10% spin density on each nitrogen and no significant change in the distribution of the most favourable gz orientations was observed. The analysis was performed with both an axial g-tensor (gx/y = 2.065, gz = 2.29) and a slightly rhombic g-tensor (gx = 2.035, gy = 2.1 and gz = 2.29) and the results again showed no significant differences.
The modulation depth, Δ, for the set of 5 orientation-selective DEER traces was fitted with a single constant c (eqn (2)) for each g-matrix orientation trialled. This very useful fitting restraint uses the property that the percentage error in the simulated modulation depth, Δsim, is constant for a data set measured under identical conditions (i.e. resonator tuning, pulse length, pulse strength, frequency difference, etc.). In each case Δsim for the trace recorded at position 1 was fitted with c to the experimental data and the other field positions utilised the same c value. Trace 1 was chosen for calibration of Δ as it has the largest modulation depth and consequently the best signal-to-noise ratio.
The inter-spin distance can also be optimized in the simulation; the different crystal structures published for AGAO show a variation in the inter-copper distance of 3.559 nm to 3.615 nm. Using the best fitting orientation of the two g-tensors and ρ(N) = 5%, ρ(Cu) = 85%, it was found that a distance range of r = 3.62 ± 0.05 nm provided good fits (Fig. S7, ESI†).
Even though there is ambiguity in determining orientation, the clear oscillations in the DEER traces (Fig. 3) enables a tight range of inter-copper distances to be determined, a result that will be expanded upon in the next section.
Limitations of a model free approach and symmetry
For two centres with rhombic g-tensors, five angles are needed to define the absolute configuration of the two centres with respect to one another; polar angles (χ, ψ) define the relative position and Euler angles (α, β, γ) define the g-frame orientation of centre 2 with respect to centre 1.5 In the case of two axially symmetric g-tensors this can be reduced to three angles as demonstrated by Yang et al.30 In their reduced axial notation, centre 1 is fixed with x∥gx1, y∥gy1 and z∥gz1, and centre 2 is defined by the angle χ between the inter-spin vector with respect to z (gz1) of centre 1, and two Euler angles, γ (tilt of gz2 away from z axis) and η (rotation of gz2 in the x/y plane), see Fig. 4.Examining the simulation results using this reduced axial notation shows the favourable orientations would correspond to an angle of γ ≅ 90° and a poorly defined η angle. The favourable and unfavourable relative positions of the two centres in space are shown in Fig. S8 (ESI†), the favourable positions show an open conical distribution and thus χ is poorly defined.
This analysis demonstrates the limitations of using a model free fitting approach for two copper centres as the DEER data is not sufficient to define a unique structure and thus many possible solutions exist, and any fitting algorithm will be biased by the starting point chosen and will find false minima in terms of the underlying molecular structure even if an exhaustive search is undertaken.
Cu(II) centres with a conformational distribution
For systems where the two spin centres are not held in a rigid orientation with respect to one another a conformational distribution must be considered when analysing orientation selective DEER data. Examples of this type of system are the Cu(II)–Cu(II) (1–5), Cu(II)–NO˙ (6 and 7) and NO˙–NO˙ (8) model systems investigated here.The DEER trace analysis of the AGAO exhibiting two axial Cu(II) centres with a single rigid relative orientation demonstrates clearly that the lack of information on the g-tensor orientations of the paramagnetic sites may, even under such stringent conditions, lead to a large variation in the obtained angles χ, γ and η defining the orientation.
No X-ray structures of the model molecules 1–8 were available, however their chemical structures are known and this allowed distributions of molecular geometries to be built using DFT as described in the Methods section. Each molecular geometry determined by DFT defines the relative orientations of the two paramagnetic centres and the corresponding g-matrices and copper hyperfine interactions needed as input for the orientation-selective DEER trace simulation.10 Summing the simulated traces over the set of molecular orientations provides the DEER simulation of the DFT conformation distribution. To test the accuracy of this approach, we compared the DEER experimental data with simulations computed using DFT derived models for the NO˙–NO˙, NO˙–Cu(II) and Cu(II)–Cu(II) systems. The conformation distributions for each molecule are depicted in Fig. S3 (ESI†). For the NO˙–NO˙ system good agreement was found between the distance distributions computed from the experimental data using DeerAnalysis4 and those obtained using the DFT model. Data for the NO˙–NO˙ system is provided in the ESI† (Fig. S9).
Fig. 5 and 6 show the DEER data and corresponding simulations for the NO˙–Cu(II) and the Cu(II)–Cu(II) model systems, respectively. The excellent prediction of the simulated DEER traces as compared to the experimental traces for all systems demonstrates the accuracy of our DFT approach in modelling the set of molecular conformations.
 | ||
| Fig. 5 Top: Field-sweep EPR spectrum depicting the DEER pump (dashed red arrow) and detection (solid red arrow) positions used for the experiments on the 1-phenyl Cu(II)–NO˙ and 3-phenyl Cu(II)–NO˙ systems (compounds 6 and 7). Bottom: DEER traces (blue) with corresponding simulations (red) for molecules 1-phenyl Cu(II)–NO˙ (compound 6, upper traces) and 3-phenyl Cu(II)–NO˙ (compound 7, lower traces). Left: Raw experimental data and simulations. Right: Experimental form factors obtained after background correction and corresponding simulations. Simulations are based on the molecular conformations determined by DFT modelling to compute f(t) and the related S(t), as defined by eqn (D) of the ESI,† before c and k of eqn (2) and eqn (B) of the ESI† are optimized to fit the traces. | ||
 | ||
| Fig. 6 (a) Field-sweep EPR spectrum depicting experimental DEER pump (dashed arrows) and detection (solid arrows) positions for all five Cu(II)–Cu(II) compounds. The cyan arrows correspond to the lower DEER traces (observer field 316.5 mT) and the magenta arrows the upper DEER traces (observer field 323.5 mT) for each compound in (b). (b) Experimental data for the 1- to 5-phenyl Cu(II)–Cu(II) compounds (molecules 1–5) (blue) with corresponding simulations (red) that are based on the molecular conformers determined by DFT modelling. Labels on the right refer to both (b) plots. Left: Raw experimental DEER data. Right: Experimental form factors f(t) after background removal. The experimental f(t) amplitudes have been scaled using c to match the simulated modulation depth. The high frequency oscillations at the end of the traces are nuclear modulation artefacts due to overlap of the pump and probe pulse excitation bandwidths.61 | ||
As can be seen in Fig. 6b, there is significant variation in the modulation depths, Δ, of the traces recorded on the different Cu(II)–Cu(II) molecules, and thus the modulation depth scaling factors, c, were different (see eqn (2)). The c value was, however, consistent within all measurements taken for each sample since they used the same experimental tuning conditions and detection/pump frequency difference of Δν = 200 MHz, with only the B0 field position changed. The variation in modulation depths is due to slightly different labelling efficiencies of the systems and different pump pulse inversion efficiencies.6
DEER simulations with approximate conformation modelling
As shown above, the first principles DEER simulations computed from conformers with a defined molecular structure provide an accurate description of the experimental data. However, producing the structural conformers is a complex task and knowledge of the chemical structure is required. As typically DEER is used to determine structure, we therefore now explore the utility of parameterised structural models that are generated from a minimum of structural information.A number of models of varying sophistication have been described in the literature for systems including one or more Cu(II) centres.26,30,31 Here we discuss six models (Fig. 7 upper part), some of which are based upon the different types of models trialled in the literature, and the corresponding DEER simulations (Fig. 7 lower part) for the case of the 3-phenyl Cu(II)–Cu(II) molecule (compound 3). A seventh model (Fig. 8) is also employed to investigate the limits of angular flexibility for the 3-phenyl Cu(II)–Cu(II) system.
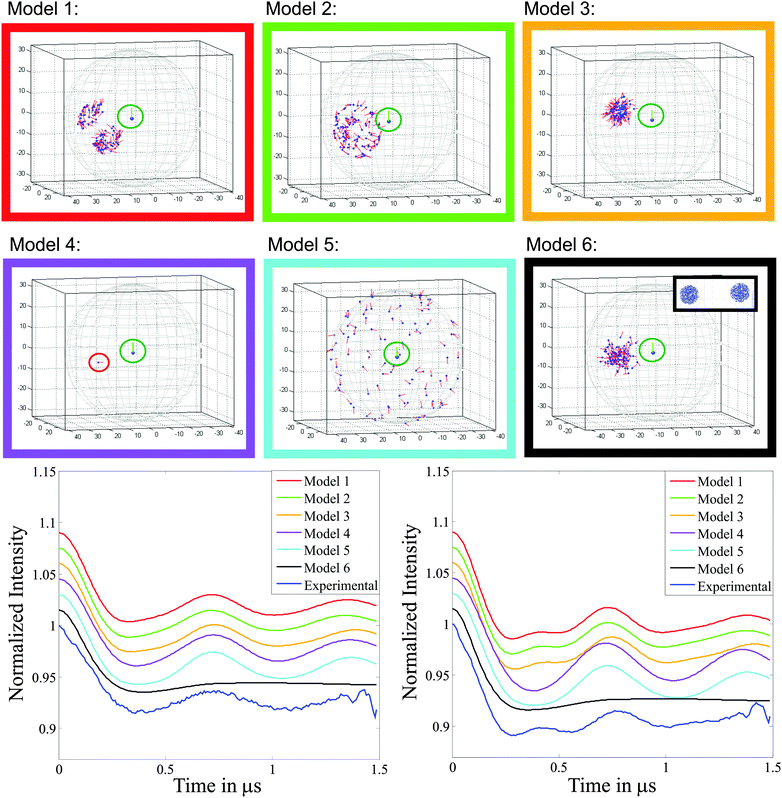 | ||
| Fig. 7 Top: Schematic representation of the six models trialled for the 3-phenyl Cu(II)–Cu(II) system (compound 3), the axes correspond to x, y and z in Å, the radius of the sphere in each case is 33.5 Å, the average inter-spin separation. The surrounding box colour corresponds to the simulated DEER traces in the lower part of the figure. All models have gz perpendicular to the plane formed by the four nitrogens. The gz axis of the detection centre is highlighted by a red line and the pump centre by a green line. Bottom: Simulated and experimental form factors f(t) (i.e. background corrected experimental data). Left and right panels correspond to the DEER measurement positions cyan (observer field 316.5 mT) and magenta (observer field 323.5 mT), respectively, shown in Fig. 6a. | ||
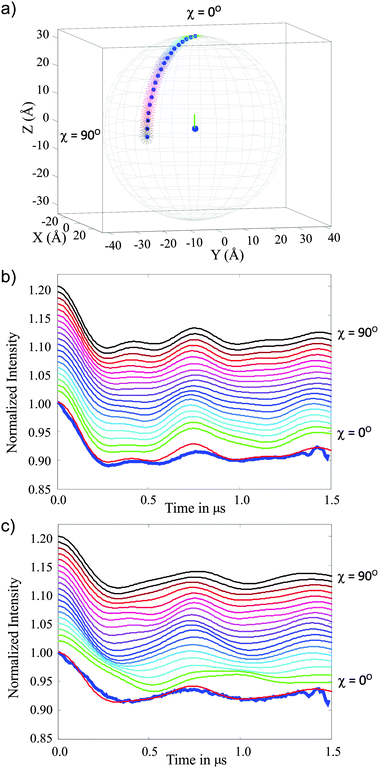 | ||
| Fig. 8 Simulation for the 3-phenyl Cu(II)–Cu(II) molecule (compound 3) using model 7 that is parameterised by polar angle χ and a uniform distribution of gz vectors perpendicular to the spin–spin vector. (a) Shows the χ range (0° to 90° in 5° intervals). (b) and (c) show the corresponding simulated DEER traces. Data collected at the magenta pulse positions (observer field 323.5 mT) in Fig. 6a is shown in (b) and data from the cyan pulse positions (observer field 316.5 mT) in Fig. 6a is plotted in (c). The colour code is consistent between the panels and the experimental data is shown as a thick blue line and is overlaid by the best fit where χ = 75°. | ||
Here our model uses two spherical distributions of Cu(II) centres, each sphere has a radius of ΔR = 0.5 nm and is centred at the weighted average (x, y, z) coordinate derived from model 1, giving a mean inter-spin distance, R = 3.32 nm. In our model the radius of the spheres ΔR was chosen so that it would encompass both the maximum and minimum distances and relative spatial positions (angle) found in the DFT derived model 1. The centre of the second sphere was positioned at an angle χ = 87°, corresponding to the centre of one of the distributions in model 1. In our model σχ = 0° as the variation in χ observed in model 1 is included within the radius of the spheres. The g-tensors of the second centre with respect to the first have the same range of orientations as those determined from the DFT conformers of model 1 (further details are given in Fig. S11, ESI†). The large degree of positional freedom provided in this model is seen to ‘wash out’ much of the structure in the DEER trace.
It is clear that a model using two spheres of fixed position and relatively large radius is a poor choice for these rod-like systems where the distance between the centres is well defined. In the model used by Yang et al. when studying copper centres attached to polypeptide chains, it is likely that a more even flexibility of the relative copper positions in all directions in their systems required the use of a relative large radius with respect to the inter-sphere separation in their ball-like model. It should also be noted that in their model a variation in χ was also included.30,31 However, for both their systems and the rod like model systems studied here, it is not possible to completely describe the conformer distribution with a spherical distribution for each centre.
Fig. 8 presents results for this model in one quadrant (χ = 0° to 90°) which is sufficient due to the axial symmetry of the g-tensor (four-fold symmetry). These data show good agreement between the simulated and experimental DEER traces in the range χ = 65–90°, establishing a structural restriction on the distribution of the two centres. This result is consistent with the DFT derived model 1 and the conical geometric model 4 where similar limitations on the angular distributions are found.
Computation of a distance distribution
Computation and validation of models to determine the orientation and spatial distribution of two centres can be complicated and, as shown above, several different models can adequately describe the experiment. In many cases the most important single piece of information is the inter-spin distance. Here we examine methods to extract this information independently of the relative orientation of the two centres.The most commonly used method for extracting distance distribution information from DEER traces is Tikhonov regularization using kernel functions appropriate for nitroxide spin centres. These kernel functions depend only upon the inter-spin distance (defining a complete dipolar Pake pattern) and use an average nitroxide g-value (2.0023 in the DeerAnalysis software used here)56 to compute the dipolar frequencies (ωdd):
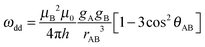 | (4) |
Initial processing of the two experimental traces for the 3-phenyl Cu(II)–Cu(II) model system (compound 3) using DeerAnalysis yielded distance distributions (red and blue traces, top panel Fig. 9) with an average distance for the main peak which deviated from the DFT model by ca. 0.1 nm (green trace, top panel Fig. 9). However, if the experimental distance distributions are corrected with the average Cu(II)–Cu(II) 3-phenyl (compound 3) g-values excited by the pump and detection pulses (magenta and cyan traces, top panel Fig. 9), then the agreement of the experimental and DFT distance distributions improves significantly. The g-value correction used is (g = 2.0023 is used for nitroxides in DEER analysis):
 | (5) |
Within the restrictions of the deviations which occur due to differing g-values the main peak of the distance distribution can be obtained via Tikhonov regularization from measurements obtained around the gx/gy value positions since both detection and pump pulses excite the gx/gy plane of orientations,10 leading to a strong representation of frequencies around ν⊥ (θ = π/2, 3π/2 in eqn (4)), which is independent of the relative spin centre orientations. This dominant representation of the ν⊥ turning point enables an approximate estimate of the mean sample distance. To remove orientation effects it is necessary to excite all orientations of the centres with respect to one another. Theoretically this could be achieved using isotropic excitation of the whole spectrum (trace shown in the bottom panel of Fig. 9).
It has been shown experimentally for bisnitroxide molecules that orientation effects in DEER traces can be strongly suppressed by averaging multiple DEER traces recorded at different fields with a constant frequency offset.57,58 A more accurate approach is to additionally vary the pump–probe offset,59 but this requires retuning the pulses between experiments which is not easy to automate. One thing that limits the accuracy of a summed trace approach is dealing with the distribution of orientations and corresponding g-values contributing to each trace which is difficult to include precisely in the analysis.59 Although these trace summing approaches require the measurement of a number of experimental data sets, they simplify the analysis considerably by allowing a reliable mean distance and an estimate of the distance distribution to be extracted, typically via Tikhonov regularization, using for example DeerAnalysis.4 A similar approach can be applied to copper centres and is trialled here for the 3-phenyl Cu(II)–Cu(II) model system (compound 3). DEER data was simulated using a constant offset of Δν = 100 MHz, and the field was shifted by steps of 10 mT (8 steps in total) so as to sample the whole Cu(II) field-sweep EPR spectrum. The simulated DEER traces were summed and a g-value corrected distance distribution computed using DeerAnalysis and eqn (5) (trace shown in the bottom panel of Fig. 9).
Note that this method does not simultaneously sample all relative g-matrix orientations of the Cu(II) pairs. For example with the detection pulses positioned at gz (which corresponds to the lowest field position in the EPR spectrum) and a pulse offset of Δν = 100 MHz between the detection and pump pulses, it is not possible to excite the gx and gy positions (ca. 400 MHz off-resonance from gz). Nevertheless, both the distance distribution from the theoretical isotropic excitation and from the sum of the traces simulated across the Cu(II) spectrum agree well with the DFT distribution (Fig. 9, bottom panel). In addition, the agreement of the distance distributions for the 8 summed traces and the theoretical simulation for full isotropic excitation is very good and therefore we can conclude that by measuring several traces across the Cu(II) spectrum we can adequately suppress orientation selection effects in the summed trace.
As a comparison the distance distribution from the sum of the two experimental traces (trace shown in the bottom panel of Fig. 9) still has a strong contribution from the peak centred at 2.75 nm. Therefore, in this case summing two single traces, one of which primarily samples gx/gy values (323.5 mT trace) and the other of which includes a strong gz value component (316.5 mT trace) is not sufficient to satisfactorily suppress orientation selection effects. The time traces for the simulated theoretical isotropic excitation and the 8 summed DEER traces collected across the copper spectrum with constant pump–probe frequency offset are shown in Fig. S13 (ESI†).
Conclusions
To examine the utility of orientation-selective DEER spectroscopy as applied to systems containing Cu(II) centres we chose a protein homo-dimer with a single relative orientation between two Cu(II) centres. Furthermore, a set of model compounds with different distances between the two Cu(II) centres that exhibit a range of conformers in frozen solution has been investigated.X-band orientation-selective DEER on the rigidly held Cu(II) centres of a homodimer of AGAO provided an accurate distance distribution measurement. However, in this case of a single molecular orientation the DEER data provided only a broad range of possible orientations all of which satisfactorily described the experimental DEER data. This uncertainty in the orientation of the two copper centres is due to the intrinsic limitations resulting from the spin Hamiltonian symmetry, and also the uncertainty in orientating the g-matrix, which is required to compute the DEER orientation selectivity. However, the orientation-selective DEER data can still be exploited to limit the relative orientations of the two paramagnetic centres to a reasonably small range. In cases where the g-tensor orientation is not known it could be determined experimentally through a detailed analysis of orientation-selective ENDOR and/or HYSCORE data in conjunction with the structure of the paramagnetic centre if it is known.60
A series of model systems; NO˙–NO˙, NO˙–Cu(II) and Cu(II)–Cu(II) (1–8), were employed to determine how accurately the conformation ensemble could be defined from the DEER data alone. Firstly the conformers for each model molecule (1–8) in frozen-solution were accurately determined using DFT calculations employing a fragment approach. These computed conformer distributions yielded DEER simulations for the NO˙–Cu(II) and Cu(II)–Cu(II) systems that provided an excellent description of the experiments with all detailed oscillation features in the DEER traces being accurately modelled.
A satisfactory mean distance and distance distribution estimate with orientation artefacts strongly suppressed can be obtained from a Tikhonov regularization analysis from measurements on Cu(II) centres by summing a set of traces that select different orientations and using effective Cu(II) g-values (geff,pump and geff,det).
Moreover, various models were employed to ascertain the structural information, in particular orientation information, derivable from the DEER traces themselves. The utility and reliability of these various models was compared to the DFT computed conformer distribution. This analysis was carried out on the Cu(II)–Cu(II) compound 3.
As revealed by DFT computations (model 1) compound 3 has a conformation distribution with a relatively narrow distance distribution but a complicated conformation distribution that defines two separate populations (Fig. 7). The gz axis of the g-matrix is approximately perpendicular to the axis joining the two Cu(II) centres but approximately randomly orientated around this axis.
The structural models 2, 3 and 7 provided satisfactory simulations of the DEER data. Model 2 represents a full set of conformers based on the known structure but, unlike model 1, without any population cut-off. This model maintained both a suitable distance distribution to describe the DEER data and the gz axis approximately perpendicular to the Cu–Cu axis. Model 3 employs structural parameters (angles and distances) which approximate well the DFT derived conformer distribution; the linker length and amount of bend provide useful parameters to define the distance distribution between the Cu(II) centres. Furthermore, in model 3 the gz axis is also maintained approximately perpendicular to the linker axis and randomly orientated around it. This model thus provides DEER simulations that match well the experimental data. Model 7 essentially is a statement of the orientation information that can be uniquely extracted from the DEER data: the gz axis is fixed perpendicular to the Cu–Cu axis, although allowed to freely rotate about this axis, and the polar angle χ between the Cu(II) centres was varied. It was found that χ = 75° provided the best fit to the experimental data.
Models using a single average structure (model 4) or a single distance and random g-matrix orientation (model 5) failed. Likewise models with a large distance distribution (model 6) failed, even if the gz axis orientation was restricted.
This analysis of various models demonstrates that useful structural information can be extracted from orientation-selective DEER. Distance information can be determined and restrictions can be placed on the possible relative orientations of the two Cu(II) paramagnetic centres that can be used to support/constrain structural models. Particularly in cases where there is very limited structural information available to guide the DEER trace analysis, we recommend firstly to obtain an estimate of the distance distribution from a summed trace approach to strongly suppress orientation artefacts, then building the structural model to simulate the orientation-selective DEER traces constrained by this distance distribution.
Acknowledgements
We gratefully acknowledge financial support from the EPSRC, BBSRC and Royal Society. JRH thanks the ARC (FT120100421) for financial support. JEL and AMB would like to thank University College, Oxford for financial support. JEL would also like to thank The Royal Society for a University Research Fellowship. TGG and AMB were supported by a BBSRC studentships. We are grateful to the Department of Chemistry's Research Services (University of Oxford) for their support and advice (Mass Spectrometry, NMR, CAESR and X-ray Crystallography). We thank Prof. David Dooley (Rhode Island) for providing an Arthrobacter globiformis amine oxide clone and Prof. Thomas Prisner (Goethe University Frankfurt) for useful discussions. Molecular graphics images were produced using the UCSF Chimera package from the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco (supported by NIH P41 RR-01081). We acknowledge the Oxford Supercomputing Centre for the computing power used for the ADF calculations.Notes and references
- M. Pannier, S. Veit, A. Godt, G. Jeschke and H. W. Spiess, J. Magn. Reson., 2000, 142, 331–340 CrossRef CAS PubMed.
- R. Ward, A. Bowman, E. Sozudogru, H. El-Mkami, T. Owen-Hughes and D. G. Norman, J. Magn. Reson., 2010, 207, 164–167 CrossRef CAS PubMed.
- A. P. Todd, J. Cong, F. Levinthal, C. Levinthal and W. L. Hubbell, Proteins, 1989, 6, 294–305 CrossRef CAS PubMed.
- G. Jeschke, V. Chechik, P. Ionita, A. Godt, H. Zimmermann, J. Banham, C. R. Timmel, D. Hilger and H. Jung, Appl. Magn. Reson., 2006, 30, 473–498 CrossRef CAS.
- A. M. Bowen, C. E. Tait, C. R. Timmel and J. R. Harmer, in Structure and bonding: spin-labels and intrinsic paramagnetic centres in the biosciences: structural information from distance measurements, ed. C. R. Timmel and J. R. Harmer, SpringerLink, 2013, vol. 152 Search PubMed.
- D. Margraf, B. E. Bode, A. Marko, O. Schiemann and T. F. Prisner, Mol. Phys., 2007, 105, 2153–2160 CrossRef CAS.
- Y. Polyhach, E. Bordignon, R. Tschaggelar, S. Gandra, A. Godt and G. Jeschke, Phys. Chem. Chem. Phys., 2012, 14, 10762–10773 RSC.
- R. G. Larsen and D. J. Singel, J. Chem. Phys., 1993, 98, 5134–5146 CrossRef CAS.
- S. Milikisyants, E. J. J. Groenen and M. Huber, J. Magn. Reson., 2008, 192, 275–279 CrossRef CAS PubMed.
- J. E. Lovett, A. M. Bowen, C. R. Timmel, M. W. Jones, J. R. Dilworth, D. Caprotti, S. G. Bell, L. L. Wong and J. Harmer, Phys. Chem. Chem. Phys., 2009, 11, 6840–6848 RSC.
- I. M. C. van Amsterdam, M. Ubbink, G. W. Canters and M. Huber, Angew. Chem., Int. Ed., 2003, 42, 62–64 CrossRef CAS.
- M. Ubbink, J. A. R. Worrall, G. W. Canters, E. J. J. Groenen and M. Huber, Annu. Rev. Biophys. Biomol. Struct., 2002, 31, 393–422 CrossRef CAS PubMed.
- X. Zheng, L. Wu, D. Gao, N. Chi, Q. Lin and J. Hu, Spectrochim. Acta, Part A, 2003, 59, 1751–1755 CrossRef.
- C. J. Sarell, C. D. Syme, S. E. J. Rigby and J. H. Viles, Biochemistry, 2009, 48, 4388–4402 CrossRef CAS PubMed.
- S. Atwell, E. Meggers, G. Spraggon and P. G. Schultz, J. Am. Chem. Soc., 2001, 123, 12364–12367 CrossRef CAS PubMed.
- E. Meggers, P. L. Holland, W. B. Tolman, F. E. Romesberg and P. G. Schultz, J. Am. Chem. Soc., 2000, 122, 10714–10715 CrossRef CAS.
- M. K. Schlegel, L. Essen and E. Meggers, J. Am. Chem. Soc., 2008, 130, 8158–8159 CrossRef CAS PubMed.
- N. Zimmermann, E. Meggers and P. G. Schultz, Bioorg. Chem., 2004, 32, 13–25 CrossRef CAS PubMed.
- Z. Yang, G. Jiménez-Osés, C. J. López, M. D. Bridges, K. N. Houk and W. L. Hubbell, J. Am. Chem. Soc., 2014, 136, 15356–15365 CrossRef CAS PubMed.
- Z. Yang, M. R. Kurpiewski, M. Ji, J. E. Townsend, P. Mehta, L. Jen-Jacobson and S. Saxena, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E993–E1000 CrossRef CAS PubMed.
- T. F. Cunningham, M. R. Putterman, A. Desai, W. S. Horne and S. Saxena, Angew. Chem., Int. Ed., 2015, 54, 6330–6334 CrossRef CAS PubMed.
- T. F. Cunningham, M. D. Shannon, M. R. Putterman, R. J. Arachchige, I. Sengupta, M. Gao, C. P. Jaroniec and S. Saxena, J. Phys. Chem. B, 2015, 119, 2839–2843 CrossRef CAS PubMed.
- J. H. van Wonderen, D. N. Kostrz, C. Dennison and F. MacMillan, Angew. Chem., Int. Ed., 2013, 52, 1990–1993 CrossRef CAS PubMed.
- G. E. Merz, P. P. Borbat, A. J. Pratt, E. D. Getzoff, J. H. Freed and B. R. Crane, Biophys. J., 2014, 107, 1669–1674 CrossRef CAS PubMed.
- E. Narr, A. Godt and G. Jeschke, Angew. Chem., Int. Ed., 2002, 41, 3907–3910 CrossRef CAS.
- B. E. Bode, J. Plackmeyer, M. Bolte, T. F. Prisner and O. Schiemann, J. Organomet. Chem., 2009, 694, 1172–1179 CrossRef CAS.
- B. E. Bode, J. Plackmeyer, T. F. Prisner and O. Schiemann, J. Phys. Chem. A, 2008, 112, 5064–5073 CrossRef CAS PubMed.
- D. Abdullin, N. Florin, G. Hagelueken and O. Schiemann, Angew. Chem., Int. Ed., 2015, 54, 1827–1831 CrossRef CAS PubMed.
- Z. Yang, J. Becker and S. Saxena, J. Magn. Reson., 2007, 188, 337–343 CrossRef CAS PubMed.
- Z. Yang, D. Kise and S. Saxena, J. Phys. Chem. B, 2010, 114, 6165–6174 CrossRef CAS PubMed.
- Z. Yang, M. Ji and S. Saxena, Appl. Magn. Reson., 2010, 39, 487–500 CrossRef CAS.
- J. S. Becker and S. Saxena, Chem. Phys. Lett., 2005, 414, 248–252 CrossRef CAS.
- E. Aronoff-Spencer, C. S. Burns, N. I. Avdievich, G. J. Gerfen, J. Peisach, W. E. Antholine, H. L. Ball, F. E. Cohen, S. B. Prusiner and G. L. Millhauser, Biochemistry, 2000, 39, 13760–13771 CrossRef CAS PubMed.
- C. S. Burns, E. Aronoff-Spencer, G. Legname, S. B. Prusiner, W. E. Antholine, G. J. Gerfen, J. Peisach and G. L. Millhauser, Biochemistry, 2003, 42, 6794–6803 CrossRef CAS PubMed.
- G. L. Millhauser, Acc. Chem. Res., 2004, 37, 79–85 CrossRef CAS PubMed.
- A. Marko, D. Margraf, P. Cekan, S. T. Sigurdsson, O. Schiemann and T. F. Prisner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 1–9 CrossRef PubMed.
- A. Marko and T. F. Prisner, Phys. Chem. Chem. Phys., 2013, 15, 619–627 RSC.
- R. Luguya, L. Jaquinod, F. R. Fronczek, A. G. H. Vicente and K. M. Smith, Tetrahedron, 2004, 60, 2757–2763 CrossRef CAS.
- A. D. Adler, F. R. Longo, J. D. Finarell, J. Goldmach, J. Assour and L. Korsakof, J. Org. Chem., 1967, 32, 476 CrossRef CAS.
- A. Godt, C. Franzen, S. Veit, V. Enkelmann, M. Pannier and G. Jeschke, J. Org. Chem., 2000, 65, 7575–7582 CrossRef CAS PubMed.
- G. A. Juda, J. A. Bollinger and D. M. Dooley, Protein Expression Purif., 2001, 22, 455–461 CrossRef CAS PubMed.
- R. E. Martin, M. Pannier, F. Diederich, V. Gramlich, M. Hubrich and H. W. Spiess, Angew. Chem., Int. Ed., 1998, 37, 2834–2837 CAS.
- A. D. Milov, K. M. Salikhov and M. D. Shchirov, Sov. Phys., Solid State, 1981, 23, 565–569 Search PubMed.
- A. D. Milov, A. B. Ponomarev and Y. D. Tsvetkov, Chem. Phys. Lett., 1984, 110, 67–72 CrossRef CAS.
- J. E. Lovett, B. W. Lovett and J. Harmer, J. Magn. Reson., 2012, 223, 98–106 CrossRef CAS PubMed.
- G. Jeschke, in Structure and bonding: spin-labels and intrinsic paramagnetic centres in the biosciences: structural information from distance measurements, ed. C. R. Timmel and J. Harmer, SpringerLink, 2012, vol. 152 Search PubMed.
- SCM, http://www.scm.com/.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- F. Neese, Magn. Reson. Chem., 2004, 42, S187–S198 CrossRef CAS PubMed.
- R. Prabhakar, P. E. M. Siegbahn, B. F. Minaev and H. Ågren, J. Phys. Chem. B, 2004, 108, 13882–13892 CrossRef CAS.
- Y. Pontillon, A. Grand, T. Ishida, E. Lelièvre-Berna, T. Nogami, E. Ressouche and J. Schweizer, J. Mater. Chem., 2000, 10, 1539–1546 RSC.
- S. Kishishita, T. Okajima, M. Kim, H. Yamaguchi, S. Hirota, S. Suzuki, S. Kuroda, K. Tanizawa and M. Mure, J. Am. Chem. Soc., 2003, 125, 1041–1055 CrossRef CAS PubMed.
- T. G. Brown and B. M. Hoffman, Mol. Phys., 2006, 39, 1073–1109 CrossRef.
- M. Kim, T. Okajima, S. Kishishita, M. Yoshimura, A. Kawamori, K. Tanizawa and H. Yamaguchi, Nat. Struct. Biol., 2002, 9, 591–596 CAS.
- S. Ghosh, J. Cirera, M. A. Vance, T. Ono, K. Fujisawa and E. I. Solomon, J. Struct. Biol., 2008, 130, 16262–16273 CAS.
- G. Jeschke, 2012, http://www.epr.ethz.ch/software/index.
- A. Godt, M. Schulte, H. Zimmermann and G. Jeschke, Angew. Chem., Int. Ed., 2006, 45, 7560–7564 CrossRef CAS PubMed.
- G. Jeschke, M. Sajid, M. Schulte, N. Ramezanian, A. Volkov, H. Zimmermann and A. Godt, J. Am. Chem. Soc., 2010, 132, 10107–10117 CrossRef CAS PubMed.
- A. Marko, V. Denysenkov, D. Margraf, P. Cekan, O. Schiemann, S. T. Sigurdsson and T. F. Prisner, J. Am. Chem. Soc., 2011, 133, 13375–13379 CrossRef CAS PubMed.
- J. A. B. Abdalla, A. M. Bowen, S. G. Bell, L. L. Wong, C. R. Timmel and J. Harmer, Phys. Chem. Chem. Phys., 2012, 14, 6526–6537 RSC.
- G. Jeschke, Annu. Rev. Phys. Chem., 2012, 63, 419–446 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Detailed synthetic schemes, procedures and characterization data for the compounds studied. CCDC 1040894. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5cp06096f |
| ‡ A. M. B. (ESR measurements and analysis) and M. W. J. (Model system synthesis) contributed equally. |
| This journal is © the Owner Societies 2016 |



