Self-interaction error in DFT-based modelling of ionic liquids

Abstract

The modern computer simulations of potential green solvents of the future, involving the room temperature ionic liquids, heavily rely on density functional theory (DFT). In order to verify the appropriateness of the common DFT methods, we have investigated the effect of the self-interaction error (SIE) on the results of DFT calculations for 24 ionic pairs and 48 ionic associates. The magnitude of the SIE is up to 40 kJ mol⁻¹ depending on the anion choice. Most strongly the SIE influences the calculation results of ionic associates that contain halide anions. For these associates, the range-separated density functionals suppress the SIE; for other cases, the revPBE density functional with dispersion correction and triple-ζ Slater-type basis is suitable for computationally inexpensive and reasonably accurate DFT calculations.

---

1 Introduction

Ionic liquids (ILs) – salts with low melting point – attract considerable research interest in the fields of surface science and physical chemistry, due to combinations of physicochemical properties that make them excellent candidates for a wide range of applications.^1,2 These properties include negligible vapour pressure at room and elevated temperatures, high thermal and (electro)chemical stability, a broad liquid range, ionic conductivity, catalytic activity, and also good solvent and miscibility properties for chemical compounds. A particular combination of properties results from a subtle balance of Coulomb and van der Waals interactions, donor–acceptor bonds, conformational flexibility, and steric effects. Therefore, a task-specific set of properties can be achieved by structural variations and selection of the right combination of ions.

Molecular physics and computational chemistry are playing a significant role in the exploration of the IL properties-landscape depending on the chemical composition.³ In particular, because of the continuous increase in computing power, the use of quantum chemical methods becomes more and more attractive for studying the electronic structure and reactivity of ILs. Due to the favourable accuracy-to-computational cost ratio, density functional theory (DFT) methods are most actively used for the electronic structure calculations of ILs as well as for parametrization of molecular dynamics (MD) force fields.^4,5 However, common density functionals, mostly in the generalized-gradient approximation (GGA), suffer from a known set of intrinsic errors, which for certain systems could lead to a wrong description of the electronic structure and the interactions between the ions. Such functionals are often employed without verification of the reliability of results.^6–16 Only in a few studies of ILs, DFT methods were examined in comparison to the more accurate post Hartree–Fock (HF) methods, such as the Møller–Plesset perturbation method, e.g. MP2, and the couple cluster technique, e.g. CCSD(T).^17–20 The authors of these studies emphasized the importance of the dispersion correction which considerably improves the results of DFT calculations in comparison to CCSD(T) and MP2 results of anion–cation interaction energies.^19–23

The interaction energies along with ionic charges were evaluated in numerous studies, using DFT methods.^24–36 In these kinds of calculations, the self-interaction error (SIE) plays a central role in electronic polarization. The SIE is the spurious interaction of an electron with itself, and it is related to Coulomb energy of the Kohn–Sham Hamiltonian. It is an intrinsic error of the DFT approach, in contrast to the HF approach where self-interaction is explicitly and totally cancelled by the exchange contribution.³⁷ This well-known problem leads to over-stabilization. To the best of our knowledge, only in two studies the effect of SIE on the IL calculations was investigated. Grimme et al. estimated the impact of the SIE for three ionic pairs showing how this error is responsible for the artificial charge transfer and inaccurate interaction energies.²⁰ Weber et al. demonstrated the SIE effect on calculated interaction energies and structural properties of an adsorption process of two ionic pairs at the anatase surface.³⁸

The use of the hybrid functionals, including a portion of the HF exchange, is known to suppress the SIE and thereby reaches the accuracy of SIE-free post-HF methods.³⁹ For example, the ionic charges obtained with the B3LYP hybrid density functional and the MP2 method are almost identical for [BMIm]Cl.⁴⁰ In contrast, charge analyses confirm that the value of the Cl⁻ ionic charge in [MMIm]Cl is lower by 0.05–0.10e in MP2-level calculations than in pure GGA DFT calculations.^41,42 Accordingly, as the ionic charge is sensitive to the inclusion of the HF exchange, a range of ionic charge values varying from −0.6e to −0.8e was obtained for chloride in ILs using similar charge analysis methods, but with different GGA density functionals.^{5,6,26,29,32,43}

The ionic charges are important parameters in MD simulations of ILs. Their values are usually estimated using quantum chemical calculations and are known to have a strong effect on the modelled structural and dynamic parameters of ILs.²⁷ Particularly, an application of a range of chloride ionic charge values obtained with DFT leads to markedly different MD simulation results. Simulations of [MMIm]Cl performed using force fields with ionic charges of ±1e give good results for the static properties, but too low conductivity in comparison to the experimental data.^44,45 Better dynamics can be obtained with ionic charges of ±0.8e.⁴⁶ Note that on the absolute scale the ionic charge is lower from the discrete value due to polarization, and charge analysis of DFT results provides a value of ±0.8e for ionic charges in most ionic pairs.^26,32 However, according to the pure GGA DFT results it may be concluded that the ionic charge for chloride is −0.6e,^32,33,46 which implies a significant partial charge transfer between the ions of opposite charge.

The question then arises: “Is the polarization between the cation and the (halide) anion in an ionic liquid (pair) so strong that can be treated as partial charge transfer, or is it artificially induced by the SIE?” Previous studies of the SIE effect on the DFT calculations revealed that the error is common for both molecular and ionic substances, like halides.^47–49 Grimme and co-workers demonstrated how the SIE influences the potential energy curves and molecular orbitals for three ionic pairs, hence, indicating the need for a detailed study of the SIE in DFT-based modelling of ILs.²⁰ In this work, we qualitatively evaluate the magnitude of the SIE for 24 ionic pairs and 48 ionic associates by applying the counterpoise method to the basis set superposition error (BSSE),⁵⁰ Perdew–Zunger (PZ) SIE correction,^51–54 and Grimme's dispersion correction,⁵⁵ as well as the global hybrid and range-separated functionals.

2 Computational methods

All DFT calculations were run using the ADF 2013 program.^56–58 MP2 calculations were performed using the ORCA program.⁵⁹ Figures for orbitals and structures were prepared using Avogadro software.⁶⁰

The computations were divided into three case studies:

(1) We investigated the effect of HF exchange inclusion on the dipole moment in the [BMIm]Cl ionic pair by using GGA and meta-GGA (BLYP,^61,62 PBE,⁶³ revPBE,⁶⁴ and TPSS⁶⁵), global hybrid (B3LYP,⁶⁶ revPBE38,²⁰ PBE0,⁶⁷ and TPSSh⁶⁵) functionals, the family of Minnesota functionals (M06⁶⁸) as well as the range-separated functional LCY-revPBE and its variations.⁶⁹

(2) In order to determine the relationship between the chemical composition and the SIE, we studied a set of 24 ionic pairs formed by a combination of three cations (1-butyl-3-methylimidazolium = [BMIm]⁺, N-butylpyridinium = [BPy]⁺ or N-methyl-N-butylpyrrolidinium = [BMPyr]⁺) with eight anions (tetrafluoroborate = [BF₄]⁻, chloride = Cl⁻, tris(pentafluoroethyl)trifluorophosphate = [FEP]⁻, iodide = I⁻, dicyanamide = [N(CN)₂]⁻, hexafluorophosphate = [PF₆]⁻, thiocyanate = SCN⁻‡ and bis(trifluoromethyl-sulfonyl)imide = [TFSI]⁻), see Fig. 1. For most ionic pairs, the initial configuration was taken from the work of Rigby and Izgorodina²⁶ and re-optimized using the revPBE functional in combination with a triple-ζ Slater-type basis set (TZ2P) and with Grimme's dispersion correction.⁵⁵ The core potential was only used in calculations involving iodide anions. The self-interaction corrected optimized effective potential for the TZ2P basis set was used for the sulphur atom in SCN⁻ and halogen atoms in calculations with the PZ correction. The optimized geometries were used in all consequent calculations of the ionic pair properties. The geometries are available at the NaRIBaS repository.⁷⁰

Fig. 1 The van der Waals space-filling representation of anions and cations used in this work. H – white, C – grey, N – dark blue, O – red, F – light blue, and S – yellow. All studied ionic associates were divided into sets: SET1 includes ionic associates containing [FEP]⁻, SET2 includes ionic associates containing (pseudo)halide anions (Cl⁻, Br⁻, I⁻, SCN⁻), and SET3 consists of ionic associates containing [BF₄]⁻, [B(CN)₄]⁻, [C(CN)₃]⁻, [N(CN)₂]⁻, [PF₆]⁻, [FSI]⁻, and [TFSI]⁻ anions.

Zahn et al.¹⁹ found small differences (from 2 to 6 kJ mol⁻¹) between MP2 and CCSD(T) energies for a set of 236 ionic pairs. Izgorodina et al.¹⁸ suggested the use of the triple-ζ Pople type basis set including the diffusion and polarization for comparing DFT results obtained with triple-ζ Slater-type basis sets. Therefore, the MP2/6-311+G(3df) level with the BSSE correction was used for the qualitative evaluation of the DFT calculation results. The 24 ionic pairs are divided into three groups; SET1 includes ionic pairs containing [FEP]⁻, SET2 includes ionic pairs containing Cl⁻, I⁻, and SCN⁻ anions, and SET3 consists of ionic pairs containing [BF₄]⁻, [N(CN)₂]⁻, [PF₆]⁻ and [TFSI]⁻ anions.

(3) Single point calculations for associates consisting of four anions and four cations were performed using revPBE and LCY-revPBE density functionals^64,69 in combination with the DZP basis set. The set of ions was extended with tetracyanoborate = [B(CN)₄]⁻, bromide = Br⁻, tricyanomethanide = [C(CN)₃]⁻, bis(fluorosulfonyl)imide = [FSI]⁻ anions, and the N,N,N-triethyl-N-propylammonium = [TEPA]⁺ cation. The associates were prepared using the NaRIBaS scripting framework⁷⁰ and packmol⁷¹ as follows: four cations were placed into four 7 Å × 7 Å × 7 Å boxes situated in the corners of a tetrahedron inside a cube; each anion was placed in the unoccupied space of the cube according to the Packmol algorithm so that ions of opposite charge form the distorted tetrahedron inside the cube. The cube edge length was chosen to be 10 Å for associates containing halide and CN-group anions, and 14 Å for all other associates. Fig. 2 displays the geometry of a [TEPA][B(CN)₄] associate. Smaller cubes were selected because of convergence problems that arise for the revPBE density functional when the anion–cation distance is increased (see the detailed discussion in the work by Grimme et al.²⁰). The associate geometry resembles a NaCl type unit cell; it corresponds to neither the solid nor liquid phase, yet allows us to evaluate the effect of the inclusion of HF exchange for ionic systems that are more complex than an ionic pair.

Fig. 2 The van der Waals space-filling representation of a [TEPA][B(CN)₄] associate. H – white, B – pink, C – grey, and N – dark blue. The cube borders are drawn with black lines, and the box borders are drawn with red dashed lines.

The 48 ionic associates are divided into three groups; SET1 includes ionic associates containing the [FEP]⁻ anion, SET2 includes ionic associates containing (pseudo)halide anions (Cl⁻, Br⁻, I⁻, SCN⁻), and SET3 consists of ionic associates containing [BF₄]⁻, [B(CN)₄]⁻, [C(CN)₃]⁻, [N(CN)₂]⁻, [PF₆]⁻, [FSI]⁻, and [TFSI]⁻ anions.

Interaction energy was calculated as:

ΔE_int = E_nCA − nE_A − nE_C (1)

where E_nCA is the total energy of the ionic associate consisting of n anions and n cations, and E_A and E_C are the energies of the anion and the cation in the associate geometry, respectively.

In the range-separated (RS) functionals the Coulomb operator is separated into short-range and long-range regions:⁶⁹

where α is the ratio of the global mixing of the HF exchange and α + β is the mixing ratio of the HF exchange in r₁₂ = ∞. In this work the Yukawa potential was used to express f(r₁₂) as exp(−γr₁₂) where γ is the Yukawa parameter. The amount of HF exchange was varied by changing the α parameter and keeping α + β = 1. For calculations in the set of 24 ionic pairs and 48 ionic associates we have used α = 0 and β = 1, that is the range-separated functional LCY-revPBE.⁶⁹

The dispersion contribution to the interaction energy was accounted for using the third version of Grimme's dispersion correction to the density functional used.⁵⁵ The BSSE was evaluated by application of the counterpoise method to the interaction energy.⁵⁰ The SIE was addressed (i) by applying the PZ SIE correction^51–54 and (ii) by using range-separated density functionals. In the first case, the SIE correction was applied self-consistently using the Krieger–Li–Iafrate approximation.^47–49 The scaled version of the PZ correction proposed by Vydrov et al.⁷² was also applied.

3 Results

For the set of 24 ionic pairs, the analysis of interaction energies, BSSE and dipoles at the revPBE level increasing the size of the basis set (DZ, DZP, TZP, TZ2P, and QZ4P) was carried out in order to determine the influence of the basis set on interaction energies and dipoles (see Tables S1–S3 in the ESI†). The BSSE was evaluated by application of the counterpoise method to the interaction energy. BSSE was found to be negligible for TZ2P and QZ4P, except for ionic pairs containing Cl⁻ and I⁻. For these cases the QZ₄P basis set is needed to suppress the BSSE. The addition of diffuse functions (ATZ2P) was also evaluated. According to the analysis of interaction energies and dipoles presented (see Tables S4 and S5 in the ESI†), the difference found in calculations with and without the diffuse functions is in general small. There are some ionic pairs where marked differences are seen, but still they are much smaller than those produced by the SIE.

3.1 Case study of [BMIm]Cl

As aptly noted by Perdew and co-workers, there are the “road more traveled” and the “road less traveled” towards the elimination of the SIE.⁷³ The roads correspond to the application of hybrid density functionals and PZ SIE correction, respectively.

The PZ correction of the SIE is expected to give highly accurate results at low computational cost. However, in practice the results are worse. In the case of [BMIm]Cl pair, application of the full PZ correction leads to a significant overcorrection of the dipole moment and interaction energy values (12.4 D and −247.8 kJ mol⁻¹) in comparison to the MP2 results (9.2 D and −378.2 kJ mol⁻¹). However, the agreement between PZ corrected DFT and MP2 results can be improved by scaling the PZ correction by a factor of ⅕ that gives ΔE^sPZ_int = −368.4 kJ mol⁻¹.

The application of hybrid density functionals is computationally more demanding than the pure GGA DFT methods but leads to a marked improvement in the calculated properties. As an illustration, Fig. 3 shows the dipole moment value dependence on the portion of the HF exchange that suppresses the SIE. The amount of HF exchange was varied by changing the α parameter and keeping α + β = 1 as well as by varying the Yukawa parameter γ from the default value of 0.75 to 0.50. It can be seen that the addition of HF exchange improves the agreement between the DFT and MP2 values. For GGA (BLYP) and meta-GGA (TPSS) functionals the use of the corresponding hybrid functionals (B3LYP and TPSSh) only slightly improves the results. For PBE and M06 an amount of almost 100% is needed to achieve the MP2 quality. The results obtained with the range-separated version of the revPBE functional with variable α, β and γ parameters (eqn (2)) are in much better agreement with the MP2 results even at low HF exchange addition (see Fig. 3).

Fig. 3 Dependence of the dipole moment on the amount of HF exchange for the [BMIm]Cl ionic pair and comparison with the MP2 value (red line). Calculations were performed using PBE and M06 functionals with a variable amount of the HF exchange. RS stands for the range-separated revPBE functional with variable α, β and γ parameters (see text for details).

3.2 Case study of 24 ionic pairs

Table 1 shows the interaction energy values obtained in DFT calculations with the BSSE, dispersion and SIE corrections. The correlation with MP2 results is displayed in Fig. 4. It can be seen that, in general, the dispersion correction significantly improves the agreement between the DFT and MP2 results. However, for SETS 1 and 2 the deviation from the MP2 results remains significant and is comparable to the average magnitude of the dispersion correction (37 kJ mol⁻¹) that in turn is much larger than the average BSSE (5 kJ mol⁻¹). Application of range-separated functionals and scaled PZ correction results are in reasonable agreement with the MP2 results, lowering the interaction energies by 10–40 kJ mol⁻¹ for SETS 1 and 2.

Table 1 Interaction energy (kJ mol⁻¹) calculated at the revPBE/TZ2P level of theory in combination with the dispersion, BSSE, scaled PZ SIE corrections, and range-separated HF exchange addition (denoted D, B, sPZ and LCY, respectively). MP2/6-311+G(3df) results with BSSE correction are given in the last column

Ionic pair	revPBE	revPBE + D	revPBE + DB	LCY-revPBE + DB	revPBE + DB + sPZ	MP2
[BMIm]Cl	−385.4	−408.1	−398.6	−379.3	−368.4	−378.2
[BMIm]I	−351.0	−379.5	−368.7	−340.8	−332.7	−335.8
[BMIm]SCN	−335.9	−365.9	−363.1	−353.7	−351.4	−348.5
[BMIm][BF4]	−332.8	−360.9	−357.0	−361.0	−355.1	−354.6
[BMIm][N(CN)2]	−315.1	−355.9	−352.4	−346.2	−348.2	−355.1
[BMIm][PF6]	−305.9	−341.3	−339.5	−339.8	−337.0	−340.7
[BMIm][TFSI]	−273.1	−340.2	−335.7	−337.9	−327.8	−336.8
[BMIm][FEP]	−253.1	−304.1	−300.6	−336.1	−305.3	−331.8
[BPy]Cl	−396.4	−416.9	−401.0	−365.4	−362.1	−371.8
[BPy]I	−358.1	−383.7	−367.0	−328.2	−324.5	−329.1
[BPy]SCN	−333.8	−368.2	−364.8	−332.4	−352.1	−348.7
[BPy][BF4]	−317.9	−350.0	−346.0	−350.2	−344.3	−349.7
[BPy][N(CN)2]	−319.1	−359.6	−355.3	−341.0	−349.2	−343.4
[BPy][PF6]	−290.8	−326.2	−322.1	−323.9	−318.4	−325.6
[BPy][TFSI]	−281.5	−335.2	−332.0	−331.4	−339.7	−330.9
[BPy][FEP]	−252.8	−304.1	−300.5	−330.1	−304.7	−326.8
[BMPyr]Cl	−374.6	−397.8	−383.9	−375.7	−353.7	−376.0
[BMPyr]I	−339.0	−366.4	−349.5	−335.9	−321.5	−334.4
[BMPyr]SCN	−326.1	−358.9	−355.8	−346.1	−351.7	−353.0
[BMPyr][BF4]	−326.1	−358.3	−354.9	−353.9	−342.5	−350.2
[BMPyr][N(CN)2]	−307.3	−351.2	−347.9	−339.7	−342.9	−347.5
[BMPyr][PF6]	−294.9	−330.6	−328.9	−326.6	−324.7	−321.8
[BMPyr][TFSI]	−269.2	−330.9	−314.4	−328.4	−315.8	−310.4
[BMPyr][FEP]	−224.9	−272.7	−269.0	−292.6	−267.9	−284.1

---

Fig. 4 Correlation plot for 24 ionic pairs showing revPBE/TZ2P vs. MP2/6-311+G** interaction energy values. Triangles denote ionic pairs from SET1, squares – SET2, and circles – SET3. The applied dispersion, BSSE, scaled PZ SIE corrections, and range-separated HF exchange addition are denoted D, B, sPZ and LCY, respectively.

Table 2 shows the mean absolute deviation (MAD) of various revPBE/TZ2P calculations (including the BSSE, and dispersion corrections) from the BSSE corrected MP2 level for the interaction energies. As can be seen, application of the PZ correction scaled by ⅕ results in a reduction of the MAD. A comparison between calculations with full PZ and scaled PZ corrections is given in Table S6 in the ESI.† A similar decrease of the MAD was obtained for the whole set of ionic pairs in LCY-revPBE calculations. The inclusion of diffuse functions into the basis set only slightly reduces the MAD for SETS 1 and 2 while markedly increasing it for the SET3. Qualitatively these results indicate the crucial effect of the SIE on the energetic characteristics of the ionic associates and indicate a minor role of diffuse functions in the case of Slater-type basis sets. Similarly, a clear impact of the SIE is seen for the electronic characteristics such as the dipole moment of ionic pairs.

Table 2 MAD (kJ mol⁻¹) of revPBE+DB/TZ2P interaction energy values of the MP2 results. In addition to BSSE and dispersion corrections, the calculations include diffuse functions (A), scaled PZ correction (sPZ) and range-separated HF exchange addition (LCY)

	SET1	SET2	SET3
revPBE+DB	24	26	3
revPBE+DB+A	19	20	9
revPBE+DB+sPZ	21	9	5
LCY-revPBE+DB	6	8	5

---

Fig. 5 plots the dipole moment values for all studied ionic pairs using different variations of the revPBE functional (pure GGA, with addition of 38% of HF exchange and range-separated) versus the values obtained at the MP2 level of theory. It can be seen that for the SET3 (circles) and SET1 (triangles) the three methods provide similar results that are in good agreement with the MP2 results. However, for ionic pairs containing Cl⁻, I⁻ and SCN⁻ anions (SET2, squares) the use of range-separated functionals (LCY-revPBE, green marks) or the global hybrid functional (revPBE38, blue marks) is required to obtain similar results to those of MP2.

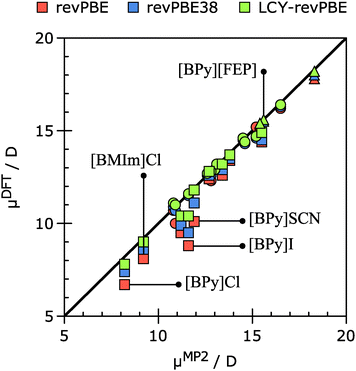Fig. 5 Correlation plot for 24 ionic pairs showing DFT/TZ2P vs. MP2/6-311+G(3df) dipole moment values. Triangles denote ionic pairs from SET1, squares – SET2, and circles – SET3.

3.3 Case study of 48 ionic associates

Fig. 6 illustrates the lower unoccupied molecular orbital (LUMO) of the [BMIm]Cl ionic associate obtained with revPBE and LCY-revPBE density functionals. In the revPBE LUMO (Fig. 6A) there is a mixing of the cation and anion orbitals. If the LCY-revPBE functional is used no mixing is observed (Fig. 6B). This mixing can be interpreted as an artificial charge-transfer between ions, so it can be stated that the inclusion of range-separated functionals almost suppresses the effect of SIE.

Fig. 6 Contour plot of the LUMO of the [BMIm]Cl ionic associate at the revPBE/DZP (A) and LCY-revPBE/DZP (B) levels. Red arrow points at the mixture of the cation and Cl⁻ orbitals. Green arrow indicates the absence of such mixture. Contour isosurface values are ±0.02 a.u.

It can be shown that the established relationship between the chemical structure of ionic pairs and the magnitude of the SIE holds true also for larger associates by comparing interaction energies in 48 associates calculated using revPBE and LCY-revPBE functionals. As can be seen in Fig. 7, there is a clear deviation between the revPBE and LCY-revPBE results of ionic associates from SET1 and SET2. For ionic associates from SET3 the deviation is small (<2%), therefore in calculations of similar systems there is no need using hybrid functionals unless a higher precision is required.

Fig. 7 Correlation plot for 48 ionic associates showing revPBE/DZP vs. LCY-revPBE/DZP interaction energy values. Triangles denote ionic pairs from SET1, squares – SET2, and circles – SET3. Blue diamonds indicate results obtained using revPBE/DZP calcualtions with scaled PZ correction.

As expected, application of the PZ correction scaled by ⅕ results in a reduction of the deviation from the LCY-revPBE/DZP results. However, the utilization of the PZ correction in calculations of larger associates is obstructed by particular implementation of this correction in a given code, e.g. by availability of specific basis sets and parallelization. In Fig. 7 we show the improvement for selected associates. Note that, as has been recently marked by Perdew and co-workers,⁷³ the success of the scaling approach and the failure of the full PZ SIE correction is probably related to the imperfection of commonly used density functionals. Perdew et al.⁷³ suggested that novel strongly constrained density functionals could be compatible with the PZ correction and thus would open a straightforward way to more efficient and more accurate SIE-free DFT calculations. As the studied ionic pairs and larger associates demonstrate a clear dependence of the SIE effect on the chemical structure, such associates could be used in order to verify novel methods for the SIE corrections in future.

4 Conclusions

The implication of the self-interaction error (SIE) on calculations involving ionic liquids has been systematically investigated. Due to this error common density functionals artificially favour the partial charge transfer between anions and cations, and hence, overestimate the interaction energy and underestimate the dipole moment values. Our investigation of 24 ionic pairs and 48 larger ionic associates demonstrates that range-separated density functionals effectively suppress the SIE and provide the dipole moment, ionic charge and interaction energy values that are comparable to those obtained at the MP2 level of theory. The magnitude of the SIE is negligible for SET3 but it is large for SETS 1 and 2; from 24 kJ mol⁻¹ on average up to 40 kJ mol⁻¹ for [BPy]I. For comparison, the magnitude of the basis set superposition error is less than 5 kJ mol⁻¹ for the triple-ζ Slater-type basis, and the Grimme's dispersion correction is on average 37 kJ mol⁻¹.

Therefore, we suggest to be cautious in the analysis of the previous and future DFT calculations of ionic liquids with (pseudo)halide or [FEP]⁻ anions. Besides, we recommend the presented set of ionic associates for testing the Perdew–Zunger correction with novel strongly constrained density functionals.

Acknowledgements

We acknowledge the ARCHIE-WeSt High Performance Computer Centre (http://www.archie-west.ac.uk, EPSRC grant no. EP/K000586/1) and CCC-UAM for providing computational resources and significant assistance, “Ministerio de Ciencia e Innovación” (Project: CTQ2010-19232) and “Comunidad de Madrid” (Project: LIQUORGAS-CM S2013_MAE-2800) for the financial support. This study was also partially funded by the Estonian Energy Technology Program project SLOKT10209T, Project of European Structure Funds SLOKT12026T, Estonian Basic Research project SF0180002s08 and Estonian Center of Excellence in Science project: High-technology Materials for Sustainable Development TK117. We are thankful to the SCM company (Amsterdam, Netherlands) for providing us a version of the ADF software package.

References

1. H.-P. Steinrück and P. Wasserscheid, Catal. Lett., 2014, 145, 1–18.
2. M. V. Fedorov and A. A. Kornyshev, Chem. Rev., 2014, 114, 2978–3036.
3. M. Salanne, Phys. Chem. Chem. Phys., 2015, 17, 14270–14279.
4. E. I. Izgorodina, Phys. Chem. Chem. Phys., 2011, 13, 4189–4207.
5. F. Dommert, K. Wendler, R. Berger, L. Delle Site and C. Holm, ChemPhysChem, 2012, 13, 1625–1637.
6. L. del Olmo, R. López and J. M. García de la Vega, Int. J. Quantum Chem., 2013, 113, 852–858.
7. D. Weingarth, I. Czekaj, Z. Fei, A. Foelske-Schmitz, P. J. Dyson, A. Wokaun and R. Kotz, J. Electrochem. Soc., 2012, 159, H611–H615.
8. S. P. Ong, O. Andreussi, Y. Wu, N. Marzari and G. Ceder, Chem. Mater., 2011, 23, 2979–2986.
9. T. P. C. Klaver, M. Luppi, M. H. F. Sluiter, M. C. Kroon and B. J. Thijsse, J. Phys. Chem. C, 2011, 115, 14718–14730.
10. M. H. Ghatee and F. Moosavi, J. Phys. Chem. C, 2011, 115, 5626–5636.
11. H. Sun, B. Qiao, D. Zhang and C. Liu, J. Phys. Chem. A, 2010, 114, 3990–3996.
12. A. H. Pakiari, S. Siahrostami and T. Ziegler, THEOCHEM, 2010, 955, 47–52.
13. D. Wagle, G. Kamath and G. A. Baker, J. Phys. Chem. C, 2013, 117, 4521–4532.
14. L. Siinor, C. Siimenson, V. Ivaništšev, K. Lust and E. Lust, J. Electroanal. Chem., 2012, 668, 30–36.
15. L. del Olmo, I. Lage-Estebanez, R. López and J. M. García de la Vega, J. Mol. Model., 2014, 20, 2392.
16. L. del Olmo, I. Lage-Estebanez, R. López and J. M. García de la Vega, RSC Adv., 2015, 5, 72709–72715.
17. S. Zahn and B. Kirchner, J. Phys. Chem. A, 2008, 112, 8430–8435.
18. E. I. Izgorodina, U. L. Bernard and D. R. MacFarlane, J. Phys. Chem. A, 2009, 113, 7064–7072.
19. S. Zahn, D. MacFarlane and E. I. Izgorodina, Phys. Chem. Chem. Phys., 2013, 15, 13664–13675.
20. S. Grimme, W. Hujo and B. Kirchner, Phys. Chem. Chem. Phys., 2012, 14, 4875–4883.
21. P. A. Hunt and I. R. Gould, J. Phys. Chem. A, 2006, 110, 2269–2282.
22. S. Tsuzuki, H. Tokuda, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2005, 109, 16474–16481.
23. K. Wendler, M. Brehm, F. Malberg, B. Kirchner and L. Delle Site, J. Chem. Theory Comput., 2012, 8, 1570–1579.
24. V. V. Chaban, I. V. Voroshylova and O. N. Kalugin, Phys. Chem. Chem. Phys., 2011, 13, 7910–7920.
25. Y. Zhang and E. J. Maginn, J. Phys. Chem. B, 2012, 116, 10036–10048.
26. J. Rigby and E. I. Izgorodina, Phys. Chem. Chem. Phys., 2013, 15, 1632–1646.
27. C. Schröder, Phys. Chem. Chem. Phys., 2012, 14, 3089–3102.
28. C. J. Margulis, H. V. R. Annapureddy, P. M. De Biase, D. Coker, J. Kohanoff and M. G. Del Pópolo, J. Am. Chem. Soc., 2011, 133, 20186–20193.
29. I. Skarmoutsos, D. Dellis, R. P. Matthews, T. Welton and P. A. Hunt, J. Phys. Chem. B, 2012, 116, 4921–4933.
30. O. Hollóczki, F. Malberg, T. Welton and B. Kirchner, Phys. Chem. Chem. Phys., 2014, 16, 16880–16890.
31. M. Kohagen, M. Brehm, J. Thar, W. Zhao, F. Müller-Plathe and B. Kirchner, J. Phys. Chem. B, 2011, 115, 693–702.
32. A. Mondal and S. Balasubramanian, J. Phys. Chem. B, 2014, 118, 3409–3422.
33. F. Dommert and C. Holm, Phys. Chem. Chem. Phys., 2013, 15, 2037–2049.
34. M. Shukla and S. Saha, Comput. Theor. Chem., 2013, 1015, 27–33.
35. K. Dong, Y. Song, X. Liu, W. Cheng, X. Yao and S. Zhang, J. Phys. Chem. B, 2012, 116, 1007–1017.
36. L. del Olmo, C. Morera-Boado, R. López and J. M. García de la Vega, J. Mol. Model., 2014, 20, 2175.
37. J.-L. Calais, Int. J. Quantum Chem., 1993, 47, 101.
38. H. Weber, T. Bredow and B. Kirchner, J. Phys. Chem. C, 2015, 119, 15137–15149.
39. T. Tsuneda and K. Hirao, J. Chem. Phys., 2014, 140, 18A513.
40. P. A. Hunt, B. Kirchner and T. Welton, Chem. – Eur. J., 2006, 12, 6762–6775.
41. J. Schmidt, C. Krekeler, F. Dommert, Y. Zhao, R. Berger, L. D. Site and C. Holm, J. Phys. Chem. B, 2010, 114, 6150–6155.
42. F. Dommert, J. Schmidt, C. Krekeler, Y. Y. Zhao, R. Berger, L. Delle Site and C. Holm, J. Mol. Liq., 2010, 152, 2–8.
43. S. Kossmann, J. Thar, B. Kirchner, P. A. Hunt and T. Welton, J. Chem. Phys., 2006, 124, 174506.
44. B. L. Bhargava and S. Balasubramanian, J. Chem. Phys., 2005, 123, 144505.
45. C. G. Hanke, S. L. Price and R. M. Lynden-Bell, Mol. Phys., 2001, 99, 801–809.
46. X. Zhong, Z. Liu and D. Cao, J. Phys. Chem. B, 2011, 115, 10027–10040.
47. J. B. Krieger, Y. Li and G. J. Iafrate, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 101–126.
48. J. B. Krieger, Y. Li and G. J. Iafrate, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 5453–5458.
49. Y. Li, J. B. Krieger and G. J. Iafrate, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 47, 165–181.
50. S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
51. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079.
52. S. Patchkovskii, J. Autschbach and T. Ziegler, J. Chem. Phys., 2001, 115, 26–42.
53. S. Patchkovskii and T. Ziegler, J. Chem. Phys., 2002, 116, 7806–7813.
54. S. Patchkovskii and T. Ziegler, J. Phys. Chem. A, 2002, 106, 1088–1099.
55. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
56. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
57. C. F. Guerra, J. G. Snijders, G. t. Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403.
58. ADF2013, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2012.
59. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
60. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
61. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
62. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
63. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
64. Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890.
65. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
66. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
67. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
68. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
69. M. Seth and T. Ziegler, J. Chem. Theory Comput., 2012, 8, 901–907.
70. V. Ivaništšev, K. Kirchner, K. Karu, I. Lage-Estebanez and M. V. Fedorov, NaRIBaS: A scripting framework for computational modelling of Nanomaterials and Room Temperature Ionic Liquids in Bulk and Slab, http://www.github.com/vladislavivanistsev/NaRIBaS, 2015.
71. L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164.
72. O. A. Vydrov, G. E. Scuseria, J. P. Perdew, A. Ruzsinszky and G. I. Csonka, J. Chem. Phys., 2006, 124, 094108.
73. J. P. Perdew, A. Ruzsinszky, J. Sun and M. R. Pederson, Adv. At., Mol., Opt. Phys., 2015, 64, 1–14.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp05922d

‡ Below referred to as a pseudohalide anion.

---