Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solvent-shared pairs of densely charged ions induce intense but short-range supra-additive slowdown of water rotation†
Ana
Vila Verde
 *,
Mark
Santer
and
Reinhard
Lipowsky
*,
Mark
Santer
and
Reinhard
Lipowsky
Max Planck Institute of Colloids and Interfaces, Theory and Bio-Systems Department, Wissenschaftspark Golm, 14424 Potsdam, Germany. E-mail: ana.vilaverde@mpikg.mpg.de; Fax: +49 (0)331 567 9602; Tel: +49 (0)331 567 9608
First published on 25th November 2015
Abstract
The question “Can ions exert supra-additive effects on water dynamics?” has had several opposing answers from both simulation and experiment. We address this ongoing controversy by investigating water reorientation in aqueous solutions of two salts with large (magnesium sulfate) and small (cesium chloride) effects on water dynamics using molecular dynamics simulations and classical, polarizable models. The salt models are reparameterized to reproduce properties of both dilute and concentrated solutions. We demonstrate that water rotation in concentrated MgSO4 solutions is unexpectedly slow, in agreement with experiment, and that the slowdown is supra-additive: the observed slowdown is larger than that predicted by assuming that the resultant of the extra forces induced by the ions on the rotating water molecules tilts the free energy landscape associated with water rotation. Supra-additive slow down is very intense but short-range, and is strongly ion-specific: in contrast to the long-range picture initially proposed based on experiment, we find that intense supra-additivity is limited to water molecules directly bridging two ions in solvent-shared ion pair configuration; in contrast to a non-ion-specific origin to supra-additive effects proposed from simulations, we find that the magnitude of supra-additive slowdown strongly depends on the identity of the cations and anions. Supra-additive slowdown of water dynamics requires long-lived solvent-shared ion pairs; long-lived ion pairs should be typical for salts of multivalent ions. We discuss the origin of the apparent disagreement between the various studies on this topic and show that the short-range cooperative slowdown scenario proposed here resolves the existing controversy.
1 Introduction
Most biological, geological and atmospheric processes take place in aqueous solutions containing various inorganic salts. These salts are known to significantly alter the properties of aqueous solutions – e.g., their viscosity – or the properties of other solutes in those solutions – e.g., the solubility of molecular oxygen – relative to pure water.1 Because solution properties strongly influence the kinetics and thermodynamics of any chemical or physical processes occurring in solution, a large number of studies have addressed the molecular scale details of the interactions of ions with water, with their counterions and with other solutes in solution.The effect of salts on any given solution property strongly depends on the identity of both ions but, for a given counterion, it is possible to create a series of anions or cations ranked by their impact on any given property. These ionic series are commonly known as Hofmeister series. Notably, these series are remarkably similar for widely different properties, suggesting that ion–ion or ion–water interactions are at least partly at their origin.2–7 In this context, multiple experimental and simulation studies investigating the effect of ions on the structure and dynamics of water molecules have been reported.8–21 These studies indicate that most ions affect water structure and/or dynamics only within their first hydration shell. Only those ions with an unusually large charge density, such as Li+ or Mg2+, appear to perturb water up to their second hydration shell.
While most studies indicate that the magnitude of the effect of a given ion on a particular solution property depends on the identity of the counterion, it is commonly believed that the effects of anions and cations are simply additive. The possibility of supra-additive effects, however, was raised a few years ago. Femtosecond infrared spectroscopy (fs-IR) and dielectric relaxation (DR) studies done in the groups of Bakker and Bonn suggest that pairs of multivalent and/or densely charged ions may supra-additively slow down the rotational dynamics of water molecules much beyond the first hydration shell of the ions.22,23 This possibility is still controversial, though, because other studies on similar salt solutions came to different conclusions. Some studies found no evidence of ion-specific, supra-additive slowdown of water dynamics;20,24–26 another study found that supra-additive effects are restricted to the first hydration layer of the ions;27 still another found that supra-additive effects are not ion-specific.26
Here we examine the issue of supra-additive effects of ions on the rotational dynamics of water by using molecular simulations to investigate aqueous solutions of MgSO4, the salt for which the largest cooperative slowdown effect was proposed based on experimental data. For comparison, we also examine water dynamics in solutions of CsCl, for which experiments suggest only minimal slowdown of water dynamics.22,23 We use polarizable water and ion models because densely charged ions polarize neighboring water molecules,28,29 an effect which may influence water dynamics.30 Because our prior work31 indicates that the anion–cation distance dictates the magnitude of slowdown of water rotation induced by an ion pair, we reparameterize the anion–cation interactions to reproduce the activity derivative of CsCl or MgSO4 solutions at a concentration of 2.5 m, where m denotes “molal” (mol solute per kg solvent) without affecting their ion–water interactions, which were previously parameterized to reproduce the free energy of hydration at infinite dilution. The optimized ion models used here thus adequately capture ion–ion and ion–water interactions, which is indispensable for the proposed study. We relate the dynamics of water molecules in solutions of CsCl and MgSO4 at 0.5, 1.5 and 2.5 m to the contributions of isolated ions, ion pairs, and small ion clusters forming cubes, and identify (i) the extent to which water dynamics near an ion depends on the counterions; (ii) the spatial range and magnitude of additive and supra-additive effects; (iii) the correlation between solution structure as given by its anion–cation radial distribution function and water rotational dynamics; (iv) the correlation between the local electric field experienced by water molecules and their rotational dynamics.
2 Methods
2.1 Models
The “simple water model with four sites and negative Drude polarizability” (SWM4–NDP) together with compatible models for the Mg2+, Cs+, Cl− and SO42− ions are used.31–33 In these models, polarizability is explicitly included using classical Drude oscillators. The water model reproduces reasonably well several experimentally determined properties of water at room temperature such as the change in internal energy upon liquefaction, molar volume, diffusion coefficient, relaxation time from nuclear magnetic resonance measurements, dielectric constant, free energy of hydration and surface tension.32 The model's ability to reproduce both static and dynamic properties of water makes it a suitable choice for this study. The ion models reproduce static properties that reflect both ion–water and ion–ion interactions at room temperature: hydration free energies, the minimum energy and ion–water distance of a monohydrate (1 water + 1 ion) system, the residence time of water molecules in the first hydration layer of magnesium (of order 1 μs),34 the density and the activity derivative of concentrated solutions of the salts studied here, as shown in a prior publication31 and in the ESI.† Adequately reproducing ion–water and ion–ion interactions is indispensable for the study of water dynamics in salt solutions because our prior work indicates that the dynamics of water in the vicinity of an ion pair greatly depends not only on the ion–water interactions, but also on the anion–cation distance.31 Since the published models for the ions adequately capture ion-SWM4–NDP water properties only,31,33 we reparameterize them (ESI†) and obtain new ion models that reproduce properties of concentrated salt solutions – specifically, the activity derivatives of CsCl or MgSO4 solutions with concentration 2.5 m – while leaving the ion–water interactions unchanged. We note that, since we aim to study water dynamics in salt solutions, it would have been desirable to parameterize ion–water and ion–ion interactions to reproduce dynamic solution properties. We did not do so because of the larger uncertainty associated with the measured values of these properties in comparison with the static target properties we selected.2.2 Simulation details
We perform simulations on three different types of systems for each salt: isolated ions, individual ion pairs of freely rotating ions at several fixed anion–cation distances, and solutions of concentration 0.5, 1.5 and 2.5 m; for MgSO4 we perform also simulations of clusters of eight freely rotating ions in cube configurations. Examples of the simulation boxes for some of the systems are shown in Fig. 1. In all simulations of freely rotating ions at fixed ion–ion distances, the negative Drude charges associated with the ions remain free so that the dipole moment of the ions responds to the local electric field; in the case of SO42−, only the sulfur atom is fixed in space.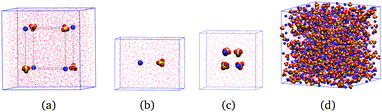 | ||
| Fig. 1 Example geometries of the simulated systems after equilibration, shown here for magnesium sulfate. (a) Isolated ions. (b) Isolated ion pairs. (c) Isolated ion clusters. (d) 2.5 m solution. | ||
The molecular dynamics package NAMD is used for all simulations.35 Visualization and analysis of trajectories is done using the package VMD – Visual Molecular Dynamics.36 Electrostatic interactions are calculated directly up to inter particle distances of 12 Å and via the Particle Mesh Ewald method with 1 Å grid-spacing for larger distances. The van der Waals (vdW) interactions are switched to zero between 10 and 12 Å, and correction terms are applied to the energy and pressure to minimize artifacts introduced by the use of a cutoff. The Brünger–Brooks–Karplus algorithm with multiple time stepping is used for integration, with bonded forces calculated at every time step, and Lennard-Jones and electrostatic forces every two time steps.‡ Unless otherwise noted, 0.5 fs time steps are used. Simulations at constant pressure use a Langevin barostat with a target pressure 1 atm, oscillation period 100 fs and damping timescale 50 fs. Integration is done using an extended Lagrangian dynamics formalism, which yields classical dynamic trajectories near the self-consistent field limit.37 This formalism encompasses two thermostats, one for the Drude particles and a Langevin thermostat for all other particles in the system. The target temperature for the Drude thermostat is 1 K in all cases, and for the Langevin thermostat it is 298.15 K unless otherwise noted. The geometry of the water molecule is kept fix using the SETTLE algorithm.38 Periodic boundary conditions are used.
The initial configurations for the simulations with isolated ions are obtained by placing four pairs of anions and cations (Cs+ and Cl− or Mg2+ and SO42−) in alternating vertices of a cube of edge length 24 Å. Initial configurations for the simulations of isolated ion pairs are generated by placing the ions at the desired anion–cation distance. For CsCl, isolated ion-pairs at two anion–cation distances (D = 3.6, 5.4 Å), corresponding to contact and solvent-shared ion pairs as shown in the Results section, are simulated. For MgSO4, solvent-separated (D = 7.4 Å) and two types of solvent-shared (D = 5.0, 5.6 Å) ion pairs are simulated. The MgSO4 cubic clusters are characterized by these anion–cation distances as well. The ion configurations are subsequently solvated with SWM4–NDP water using tcl scripts implemented through VMD; between each ion in the main simulation box and the ions in the periodic copies of the box there is a minimum of 24 Å of water. The initial configurations for the simulations of CsCl and MgSO4 solutions are generated by randomly placing the desired number of ions in the simulation box and solvating the system with SWM4–NDP water so that the target concentrations of 0.5, 1.5 and 2.5 m are obtained. The large simulation boxes (see Table 1) used here are necessary because the ion–ion radial distribution functions of concentrated salt solutions may exhibit correlations up to tens of angstroms (ESI†). Further details of the systems are given in Table 1.
| System | Box size (Å3) | n pairs | n w |
|---|---|---|---|
| Isol. ions | 47 × 47 × 47 | 4 | 3448 |
| Ion pairs | 29 × 29 × 36 | 1 | 1040 |
| Ion clusters | 31 × 31 × 31 | 4 | 987 |
| CsCl, 0.5 m | 60.4 × 60.4 × 60.4 | 64 | 7087 |
| CsCl, 1.5 m | 60.5 × 60.5 × 60.5 | 185 | 6845 |
| CsCl, 2.5 m | 60.6 × 60.6 × 60.6 | 298 | 6619 |
| MgSO4, 0.5 m | 80.9 × 80.9 × 80.9 | 156 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327 327 |
| MgSO4, 1.5 m | 80.2 × 80.2 × 80.2 | 453 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733 733 |
| MgSO4, 2.5 m | 79.8 × 79.8 × 79.8 | 727 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 185 185 |
The solvated configurations are minimized for 10 to 100 steps and then equilibrated for 2 ps in the canonical (NVT) ensemble at 298.15 K using 0.1 fs time steps. Individual ions, ion pairs and ion clusters are further equilibrated in the NPT ensemble at 298.15 K for 2 ns, sufficient time to ensure that the average volume of the simulation box stabilizes. The starting configurations for the production runs of simulations with isolated ions, ion pairs and ion clusters are extracted from the equilibration simulations by selecting a configuration with box size close to the average box size during the equilibration. Simulations of salt solutions are equilibrated in the NPT ensemble at 298.15 K for 5 ns. From the equilibration simulation of each salt solution, a configuration for which the box size is close to the mean is selected as the starting point for a simulation at constant volume and T = 400 K lasting 9 ns. The starting configurations for the production runs of salt solutions are extracted from this high temperature simulation at equally spaced intervals. This protocol for producing initial configurations for concentrated salt solutions is necessary for MgSO4 because these solutions have very slow dynamics at 298.15 K. To ensure adequate sampling of configuration space at this temperature one must thus perform multiple production runs starting from substantially different initial configurations, which are obtained from the high temperature run. We confirm that the high temperature indeed allows the sampling of substantially different system configurations by calculating the average root mean square displacement (RMSD) of sulfate ions. For the solution with slowest dynamics – MgSO4 at 2.5 m – the RMSD between the start and end times of the high temperature simulation is 30 Å, indicating that substantially different system configurations are sampled during this simulation. For consistency, the same protocol is used to prepare the initial configurations for the simulations of CsCl solutions even though they have much faster dynamics than MgSO4 solutions. During equilibration, both the Langevin and the Drude thermostats use a damping coefficient of 5 ps−1.
Production runs are performed in the NVT ensemble. For the systems with isolated ions, a single production run of duration 5 ns is carried out. For the systems with single ion pairs or ion clusters, 20 production runs each 5 ns long are performed for each anion–cation separation, for a total simulation time of 100 ns for each type of ion pair or ion cluster. This long simulation time is indispensable for the statistically accurate analysis of the reorientation dynamics of small water subpopulations near the ion pairs performed in this study. For the systems with salt solutions, 10 production runs each 5 ns long are performed for each salt concentration. The average temperature during the production runs is T = 298 ± 5 K. The damping coefficient is 0.1 ps−1 for the Drude pairs and 0.05 ps−1 for the Langevin thermostat. Very low values of these damping constants are used here because they only minimally perturb the system dynamics: a prior study shows that these values lead to diffusive behavior very similar to that observed in simulations in the microcanonical (NVE) ensemble.37 Unless otherwise indicated, the statistical uncertainty of reported quantities is estimated by calculating the standard deviation using block averages.39,40
3 Results and discussion
3.1 Water dynamics in MgSO4 and CsCl solutions
We characterize the rotational dynamics of water through the second order rotational autocorrelation function,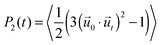 | (1) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) 0 and
0 and ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) t are unit vectors defining the orientation of a OH group at time 0 and t, respectively, and the average is over all time origins and all OH groups considered in the water population being investigated. This function typically decays from its maximum, P2 = 1, to zero as the system achieves full, isotropic 3D decorrelation, but could assume values − 0.5 ≤ P2 < 0 when decorrelation is not isotropic. The minimum P2 = −0.5 occurs if all OH groups simultaneously form a 90° angle relative to their initial orientation. This function is particularly useful because it approximates the observable in pump–probe spectroscopy experiments – the anisotropy decay of OH groups41 – allowing for comparisons with experiment.
t are unit vectors defining the orientation of a OH group at time 0 and t, respectively, and the average is over all time origins and all OH groups considered in the water population being investigated. This function typically decays from its maximum, P2 = 1, to zero as the system achieves full, isotropic 3D decorrelation, but could assume values − 0.5 ≤ P2 < 0 when decorrelation is not isotropic. The minimum P2 = −0.5 occurs if all OH groups simultaneously form a 90° angle relative to their initial orientation. This function is particularly useful because it approximates the observable in pump–probe spectroscopy experiments – the anisotropy decay of OH groups41 – allowing for comparisons with experiment.
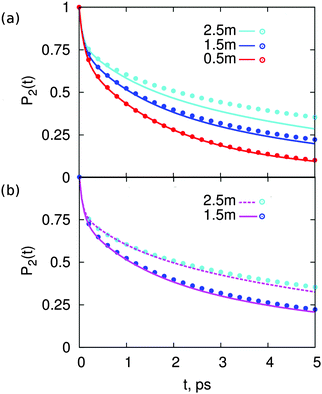
Fig. 2 shows P2(t) for solutions of MgSO4 or CsCl at three concentrations: 0.5, 1.5 and 2.5 m. The P2(t) for pure water is also shown. These functions are calculated over a 5 ps interval only because we aim to compare results with femtosecond infra red experiments and longer times are not accessible to that technique. All P2(t) curves have the typical27,31,41–44 fast, non-exponential decay for t < 200 fs. For larger time scales, the observed decay is well-described by a bi-exponential. The short-time decay is a result of librational motion, whereas the long-time decay arises from structural changes.41,42,44,45 Various prior studies27,31 indicate that structural change for water in the bulk is the result of two main processes: hydrogen bond exchange (i.e., breaking and reformation) and slow reorientation of the intact O–H⋯O atom triad; it is reasonable to expect that the same processes lead to water reorientation in salt solutions and give origin to the decay observed here beyond t > 200 fs.
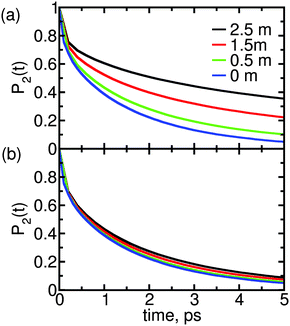 | ||
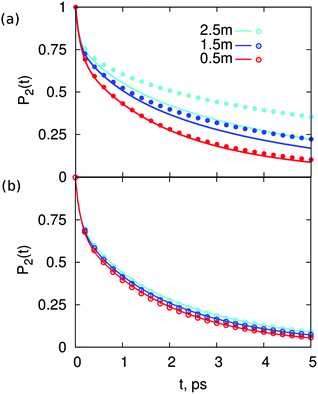
| Fig. 2 Reorientation decay, P2(t), of water in solutions of (a) MgSO4 and (b) CsCl, at the indicated concentrations. For reference, the reorientation decay of pure water is also shown. | ||
The two salts have markedly different effects on water dynamics. MgSO4 visibly slows down the reorientation of water, even at the relatively low concentration of 0.5 m where only 30% of all water molecules§ belong to the first and second hydration layers of Mg2+ or the first hydration layer of SO42−, i.e., the water subpopulations slowed down by isolated ions (ESI†). In contrast, CsCl has only a rather weak influence on the reorientation dynamics of water, even at a concentration of 2.5 m where 75% of all water molecules belong to the first hydration layers of the ions. These results qualitatively agree with experimental ones from pump–probe spectroscopy and terahertz dielectric relaxation experiments, lending confidence to our choice of parameterization scheme.22,46 We avoid making quantitative comparisons with experiment here because the experimental anisotropy includes contributions from non-Condon effects, excited-state absorption and spectral diffusion,47 which are not included in eqn (1). These contributions are of second order but are not negligible, so only qualitative comparisons between experiment and simulation are appropriate.
3.2 Contribution of isolated ions to water slowdown in salt solutions
We next ask what fraction of the large differences in water dynamics between MgSO4 and CsCl solutions arises from differences in the contributions of isolated Mg2+ and SO42− or Cs+ and Cl− to the rotational dynamics of water. To investigate this issue, we first characterize the rotational dynamics of water hydroxyl groups in the first and second hydration layers of each isolated ion. We do so by calculating the autocorrelation function given by eqn (1) for all water hydroxyl groups that, at t = 0, have oxygens belonging to either the first or the second hydration shells of each ion. The boundaries of the hydration shells are the minima of the ion–water oxygen radial distribution function. The reorientation decay curves calculated in this way are shown in the ESI.† Magnesium markedly slows down the rotation of water in its first hydration shell and also slows down, to a lower extent, rotation of waters in its second hydration shell. In contrast, chloride and sulfate slow down the rotation of water in their first hydration shell only, and cesium has virtually no effect on water rotation. We then make the simplifying assumption that all ions in CsCl or MgSO4 solutions are isolated, and estimate the average water reorientation dynamics in CsCl or MgSO4 solutions, P2,solution(t), as the sum of the contributions of water near isolated ions and from water in the bulk, according to the expression: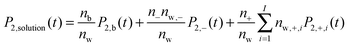 | (2) |
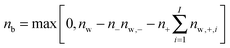 . The results of this model are presented in Fig. 3. For CsCl, the water reorientation dynamics at all concentrations predicted by the model closely matches that directly calculated from simulations of salt solutions at the three concentrations examined here. This result indicates that the average water reorientation in CsCl solutions can indeed be understood as the additive contribution of ions that, from the point of view of water reorientation dynamics, behave as isolated. The model predicts water dynamics equally well at the lowest CsCl concentration tested here, 0.5 m, where 85% of water molecules are considered in the bulk, and at the highest CsCl concentration, 2.5 m, where only 25% of the water molecules are in the bulk. These results suggest that water dynamics in CsCl solutions of concentrations higher than 2.5 m but low enough that each ion still retains an intact first hydration layer may still be understandable as the sum of contributions from isolated ions.
. The results of this model are presented in Fig. 3. For CsCl, the water reorientation dynamics at all concentrations predicted by the model closely matches that directly calculated from simulations of salt solutions at the three concentrations examined here. This result indicates that the average water reorientation in CsCl solutions can indeed be understood as the additive contribution of ions that, from the point of view of water reorientation dynamics, behave as isolated. The model predicts water dynamics equally well at the lowest CsCl concentration tested here, 0.5 m, where 85% of water molecules are considered in the bulk, and at the highest CsCl concentration, 2.5 m, where only 25% of the water molecules are in the bulk. These results suggest that water dynamics in CsCl solutions of concentrations higher than 2.5 m but low enough that each ion still retains an intact first hydration layer may still be understandable as the sum of contributions from isolated ions.
 | ||
| Fig. 3 Estimated average reorientation autocorrelation function, P2(t), of water in solutions of (a) MgSO4 and (b) CsCl, calculated from the contributions of water near isolated ions and water in the bulk according to eqn (2) (lines) or directly calculated from simulations of salt solutions (symbols). | ||
In contrast, for MgSO4 the water dynamics predicted by the model only closely matches that calculated directly from simulations for salt solutions at the lowest concentration, 0.5 m, where only 30% of all water molecules belong to either the first hydration layer of sulfate or the first and second hydration layers of magnesium, i.e., 70% of water molecules are in a bulk-like environment. The model fails visibly already at the intermediate concentration, 1.5 m, where only 8% of water molecules lie in a bulk-like environment, and fails quite dramatically at the highest concentration, 2.5 m, for which 90% of water molecules belong to the first hydration layers of the ions, and the remaining 10% are assigned to the second hydration layer of magnesium. These results show that, although the marked slowdown of water rotation in MgSO4 can partly be assigned to the effect of individual ions on the dynamics of water around them, this effect is insufficient to explain the observed water dynamics at intermediate and high salt concentrations. Our prior work suggests that another effect may be at play in MgSO4 solutions: we have shown that isolated pairs of magnesium and sulfate ions with 5, 6 or 7 Å inter ionic distance may supra-additively slow-down water rotational dynamics.31 In the next section we assess whether ion pairs with inter ionic distances between 5 and 7 Å indeed form in MgSO4 solutions. For comparison, an analogous study is done for the CsCl solutions.
3.3 Ion pairs in MgSO4 and CsCl solutions
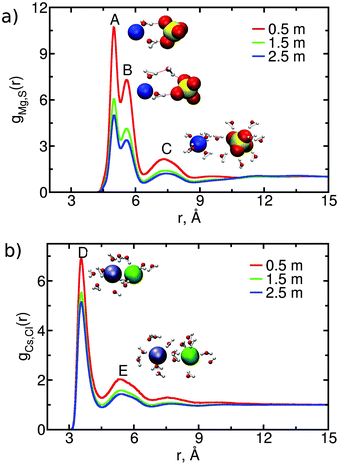
We investigate the association of anions and cations in CsCl or MgSO4 solutions by calculating their anion–cation radial distribution function; for MgSO4, the magnesium–sulfur radial distribution function is calculated. These functions are shown in Fig. 4 for the three concentrations simulated; the position and intensity of the extrema is given in the ESI.†The anion–cation radial distribution functions for each of the MgSO4 solutions have three peaks. The first and second peaks (A and B in Fig. 4(a)) are both solvent-shared ion pairs (SIPs): in both cases the ions share one water layer. The difference between the configurations associated with these two peaks is illustrated in the insets: in peak A, called an inner SIP (SIPi), the two water molecules directly bridging Mg2+ and SO42− often donate a hydrogen bond to the sulfate whereas in peak B, called an outer SIP (SIPo) the sulfate orientation relative to magnesium allows one of the water molecules belonging to the first hydration shell of magnesium to often donate a hydrogen bond to a second water molecule, which then donates a hydrogen bond to sulfate. Peak C corresponds to solvent-separated ion pairs (2SIP), i.e., each ion retains its intact first hydration shell. In contrast to MgSO4, the anion–cation radial distribution functions for CsCl solutions have only two strong peaks, the first one corresponding to contact ion pair and the second to solvent-shared configurations (see peaks D and E in Fig. 4(b)). Configurations corresponding to solvent-separated CsCl ion pairs show only a low probability of occurrence, as indicated by the small height of the third peak in Fig. 4(b). These findings are consistent with experimental data (ESI†).
The contribution of ion pairs to the average water dynamics in solution necessarily depends on their number and lifetime. In Table 2 we show the average number of CIP, SIP and 2SIP ion pairs (nCIP, nSIP or n2SIP) formed per ion, for each concentration. These numbers are obtained by integrating the anion–cation radial distribution functions (shown in Fig. 4) between consecutive minima. Both MgSO4 and CsCl form large numbers of ion pairs, even at the relatively low concentration of 0.5 m. Such large number of ion pairs may at first sight appear somewhat high if one considers that the average distance between ions, estimated from the number of ions and the volume of the simulation box, is approximately 9 Å at 2.5 m and 15 Å at 0.5 m. We note, however, that the concentration of ion pairs that can be expected from a simple random mixing model48 with physically reasonable parameters for ions is already of the same magnitude as, albeit lower than, the numbers shown in Table 2 (calculations not shown), so large numbers of ion pairs are, in fact, to be expected even at low concentrations. In the ESI† we also show the probability that each ion is involved in 0, 1, 2,…, ion pairs. These distributions show that at the highest concentration, the probability that each ion in a MgSO4 solution is involved in three or more ion pairs is high, i.e., ion clusters should be abundant in solution.
| Salt | Conc. (m) | Type | n |
|---|---|---|---|
| MgSO4 | 0.5 | SIPi | 0.5 |
| SIPo | 0.6 | ||
| 2SIP | 0.8 | ||
| 1.5 | SIPi | 0.8 | |
| SIPo | 1.0 | ||
| 2SIP | 1.6 | ||
| 2.5 | SIPi | 1.1 | |
| SIPo | 1.3 | ||
| 2SIP | 2.3 | ||
| CsCl | 0.5 | CIP | 0.2 |
| SIP | 0.5 | ||
| 1.5 | CIP | 0.5 | |
| SIP | 1.1 | ||
| 2.5 | CIP | 0.8 | |
| SIP | 1.5 | ||
The ion pair lifetimes are given in Table 3; note that here the inner and outer SIPs seen in MgSO4 solutions are considered a single state. The lifetimes are calculated using the stable states picture of Northrup and Hynes,49 as implemented by Joung and Cheatham.50 In this framework, only transitions between stable ion pair configurations are considered in the calculation of the lifetime; transient events where the ion pairs breakup and quickly reform are disregarded (ESI†).
| Salt | Conc. (m) | Type | τ IP (ps) |
|---|---|---|---|
| MgSO4 | 0.5 | SIP | 118 |
| 2SIP | 24 | ||
| 1.5 | SIP | 156 | |
| 2SIP | 34 | ||
| 2.5 | SIP | 227 | |
| 2SIP | 53 | ||
| CsCl | 0.5 | CIP | 6.7 |
| SIP | 4.6 | ||
| 1.5 | CIP | 7.0 | |
| SIP | 4.7 | ||
| 2.5 | CIP | 7.5 | |
| SIP | 4.9 | ||
The differences between the ion pair lifetimes of the two salts are striking: ion pairs in MgSO4 solutions are much longer lived than ion pairs in CsCl solutions. Whereas both CIPs and SIPs in CsCl solutions have lifetimes of a few picoseconds – i.e., larger than, but still of the same magnitude of the average reorientation decay times of water in the bulk – MgSO4 solutions have 2SIP lifetimes of 20–50 ps and SIP lifetimes of 100–200 ps. The lifetime of each ion pair increases at higher concentrations for both salts, but the magnitude of this increase is much larger for MgSO4 (τSIP,0.5m = 118 ps, τSIP,2.5m = 227 ps) than for CsCl (τCIP,0.5m = 6.7 ps, τCIP,2.5m = 7.5 ps). The short lifetime of CsCl ion pairs is consistent with the notion that this salt forms only weak ion pairs, as discussed in the ESI.† The long lifetime of MgSO4 ion pairs compared to typical water reorientation times means that their inter ionic distance is essentially unchanged during water rotation. CsCl ion pair lifetimes are governed by diffusion, and the same occurs for the MgSO4 2SIPs; the large differences between these two sets of data arise from the large differences in the solution viscosity. The very large lifetimes of MgSO4 SIPs arise from both the large solution viscosity and the strong electrostatic interactions between the two ions at this short distance, as demonstrated in the ESI.†
These results confirm that ion pairs with inter ionic distances between 5 and 7 Å – shown previously to have the largest effect on water dynamics for all types of ion pairs31 – are indeed abundant in both MgSO4 and CsCl solutions. Since in both salt solutions the ion pair lifetimes are larger than the characteristic reorientation time of water in the bulk, it is natural to ask: (i) what is the effect of isolated versions of the most frequent types of CsCl and MgSO4 ion pairs on the dynamics of water around them; and (ii) why the contributions from isolated Cs+ and Cl− are sufficient to understand the overall water dynamics in CsCl solutions despite the abundance of ion pairs in those solutions. The large number of long-lived ion pairs in MgSO4 solutions also suggests that it might be reasonable to think of ions in these solutions as forming clusters rather than pairs. In this context, we ask: (iii) what is the effect of isolated ion clusters on the dynamics of water around them; and, finally: (iv) whether water dynamics in MgSO4 solutions can be understood in terms of the effect of isolated ion pairs or clusters. These questions are addressed in the following section.
3.4 Water dynamics near isolated ion pairs and clusters
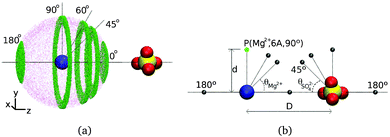
We characterize water reorientation near isolated, ion pairs or octameric clusters with fixed anion–cation distances by calculating the P2(t) function shown in eqn (1) for each hydroxyl group in a given water subpopulation. The inter ionic separations considered correspond to the maxima of the radial distribution functions shown in Fig. 4, i.e., the most abundant ion pair configurations in CsCl and MgSO4 solutions. Each water subpopulation is defined as illustrated in Fig. 5(a): at t = 0, the water oxygens of each subpopulation must simultaneously belong to a spherical layer of mid-radius d and thickness 1 Å centered at one of the ions, and to a slab of thickness 0.5 Å perpendicular to the cation–anion direction and at a given position along that direction. Each position of the slab is associated to an angle θion, with vertex at the ion indicated in subscript, as shown in Fig. 5. Water subpopulations are thus identified by the triad (ion,d,θion), and can be graphically represented as shown in Fig. 5(b).The P2(t) function is calculated for a 5 ps interval, similarly to what was described above for the isolated ions. During this time, the water molecules will diffuse away from their initial positions and some of them will no longer belong to the spatial region defined at time 0. Despite their movement, these water molecules are still included in the calculation of P2(t). Within the 5 ps interval for which P2(t) is calculated, waters typically diffuse no further than the immediately neighboring subpopulations, so each P2(t) retains a strong local character and gives insight into local water dynamics.
Our prior work31 indicates that the P2(t) curves of water subpopulations near ions are well-fitted by a sum of three exponentials. We thus fit a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ1) + b
exp(−t/τ1) + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ2) + c
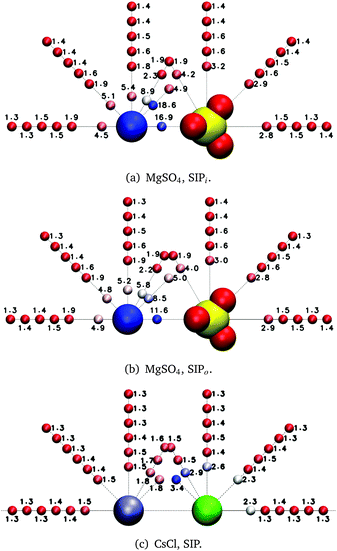
exp(−t/τ2) + c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ3) to the P2(t) curves of all water subpopulations near MgSO4 and CsCl ion pairs. The parameters of the fitted curves are then used to estimate the average OH reorientation decay time of each water subpopulation, τrot: τrot = (aτ1 + bτ2 + cτ3)/(a + b + c). This time constant can be interpreted as that of a single exponential function with the same value at t = 0 and with the same area under the curve as the fitted function. The reorientation decay times obtained in this manner for water subpopulations near MgSO4 and CsCl SIPs are shown in Fig. 6; similar figures for other ion pair configurations are shown in the ESI.†
exp(−t/τ3) to the P2(t) curves of all water subpopulations near MgSO4 and CsCl ion pairs. The parameters of the fitted curves are then used to estimate the average OH reorientation decay time of each water subpopulation, τrot: τrot = (aτ1 + bτ2 + cτ3)/(a + b + c). This time constant can be interpreted as that of a single exponential function with the same value at t = 0 and with the same area under the curve as the fitted function. The reorientation decay times obtained in this manner for water subpopulations near MgSO4 and CsCl SIPs are shown in Fig. 6; similar figures for other ion pair configurations are shown in the ESI.†
The results shown in Fig. 6(c) for the CsCl SIP share some qualitative similarities to those found for the MgSO4 SIPs: water slowdown is no longer spherically symmetric around each of the ions as it was for the isolated ions, but instead the water subpopulations directly between the ions show the slowest water dynamics. Similar trends are observed for the CsCl CIP, but the magnitude of the water slowdown in the water subpopulations between the ions is much smaller than that observed for CsCl in solvent-shared ion pair configuration. Our results on MgSO4 and CsCl ion pairs indicate that, irrespective of the identity of the ions, solvent-shared ion pairs induce the largest slowdown of rotational dynamics of water. The effect of CsCl ion pairs on the dynamics of nearby water molecules is small enough that the overall solution dynamics can still be understood as the sum of the effect of isolated ions. See the ESI† for a deeper discussion of the effects of low charge density ions on the dynamics of water around anions.
In Fig. 7 we look at water dynamics near cubic ion clusters of MgSO4. We consider three types of clusters, with edge distance equal to the location of the first, second or third peak in the MgSO4 radial distribution function; we refer to these clusters as the SIPi, SIPo or 2SIP cluster. Perfect cubic clusters do not exist in solution, but these ideal cases give insight into the dynamics of water near multiple ions. Comparing Fig. 6(a) and 7(a) it is apparent that, for equivalent subpopulations, in most cases the reorientation times increase markedly as one transitions from ion pairs to clusters with identical distance between first-neighbor cations and anions. For example, the (Mg2+, 2 Å, 45°) subpopulation is always the slowest to reorient for the SIPi ion pairs or clusters; its reorientation time goes from 18.6 ps in the ion pair configuration, to 60.6 ps in the cubic cluster. Furthermore, the length scale up to which marked slowdown is observed is also larger for clusters. Whereas reorientation times larger than 2 ps, i.e., 1.5 times larger than the reorientation time of bulk water, are limited to the second hydration layer for ion pairs, they can be found up to the third hydration layer for ion clusters (ESI†). Recent simulations of MgCl2 solutions using a non-polarizable force-field also support the existence of slowly rotating water molecules beyond the ions' first hydration shell.51
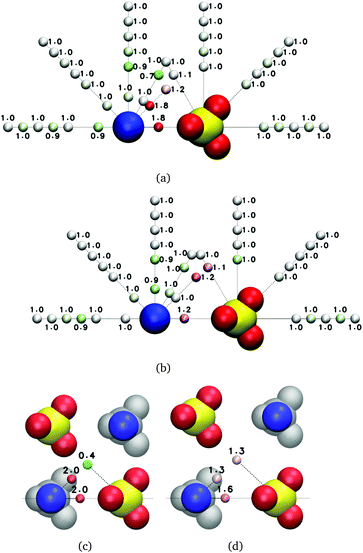
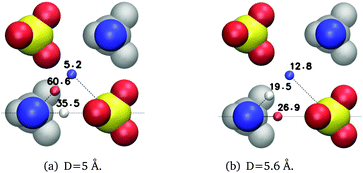 | ||
| Fig. 7 Average reorientation decay times (ps) of water subpopulations near isolated MgSO4 clusters with the indicated minimum anion–cation distance, D. The water subpopulations are defined as illustrated in Fig. 5. The color of the small spheres conveys the magnitude of the average reorientation time shown next to them. | ||
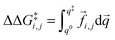 | (3) |
![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) i,j is the sum of the extra forces acting on the rotating water molecule because of the presence of the ion,
i,j is the sum of the extra forces acting on the rotating water molecule because of the presence of the ion, ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) denotes a generic reaction coordinate along which water rotation proceeds, q0 is the starting point for water rotation and q‡ is the location of the maximum of the free energy barrier. The free energy barrier to rotation of waters in subpopulation i near an ion j, ΔG‡i,j, is then given by ΔG‡bulk + ΔΔG‡i,j and the reorientation time for that water subpopulation by
denotes a generic reaction coordinate along which water rotation proceeds, q0 is the starting point for water rotation and q‡ is the location of the maximum of the free energy barrier. The free energy barrier to rotation of waters in subpopulation i near an ion j, ΔG‡i,j, is then given by ΔG‡bulk + ΔΔG‡i,j and the reorientation time for that water subpopulation by 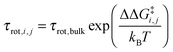 where kB is Boltzmann's constant. For the reference additive model, ion–ion polarizability is neglected, so the extra force acting on a water molecule rotating in the presence of M ions is equal to the sum of the extra forces acting on the equivalent water molecule near each ion in the absence of other ions:
where kB is Boltzmann's constant. For the reference additive model, ion–ion polarizability is neglected, so the extra force acting on a water molecule rotating in the presence of M ions is equal to the sum of the extra forces acting on the equivalent water molecule near each ion in the absence of other ions: 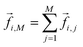 . The expected additive water reorientation times, τrot,i,add, of water subpopulation i near isolated ion pairs or clusters with M ions can then be estimated as
. The expected additive water reorientation times, τrot,i,add, of water subpopulation i near isolated ion pairs or clusters with M ions can then be estimated as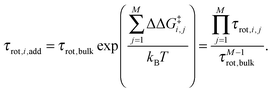 | (4) |
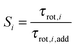 | (5) |
In Fig. 8(a) and (b) we show the cooperative factor, S, for the inner and outer solvent-shared ion pairs formed by MgSO4. This factor is only much larger than one for the two water subpopulations directly between the ions in the SIPi ion pair, i.e., (Mg2+, 2 Å, 45°) and (Mg2+, 2 Å, 0°), the two water subpopulations that have the slowest rotational dynamics, as discussed above. These subpopulations undoubtedly experience supra-additive slowdown. The majority of the remaining water subpopulations around this ion pair, as well as all the water subpopulations in the SIPo, have 0.7 ≤ S ≤ 1.2. Small deviations such as these from S = 1 indicate that water dynamics for these subpopulations is dominated by additive effects.
The supra-additive slowdown seen in the ion pairs becomes, in general, larger for the clusters. For example, the supra-additive factor for subpopulation (Mg2+, 2 Å, 45°) in the SIPi series is S = 1.8 for the ion pair, but S = 2.0 for the cluster; also, whereas the SIPo ion pairs do not induce any marked supra-additive slowdown of water rotation, visible supra-additive effects are at play in the SIPo cluster for the waters shared between the first hydration layers of magnesium and of sulfate, see (Mg2+, 2 Å, 0°) in Fig. 8(d). We note that supra-additive effects are limited to the SIP clusters; the 2SIP ion cluster does not show noteworthy supra-additive slowdown of water rotation (ESI†). We also point out that there are exceptions to the general trend of increasing supra-additive slowdown of water rotation with increasing number of nearby ions: e.g., the subpopulation (SO42−, 3.5 Å, 45°) in the SIPi ion pair has S = 1.4, but has S = 0.4 in the corresponding ion cluster. The level of supra-additivity thus appears to strongly depend on the molecular scale details of the water and ion configurations.
We first ask whether water reorientation in solutions of MgSO4 can be reconstructed from the sum of contributions of water dynamics near isolated ion pairs and pure water. We develop an analytical model (ESI†) similar in concept to that already described above to estimate the water dynamics in solutions from the contributions of isolated ions (see eqn (2)). In Fig. 9(a) we compare predictions from this model against the orientation dynamics directly measured in the simulation. This model predicts water dynamics in MgSO4 solutions of 0.5 and 1.5 m very well, but still fails at the 2.5 m concentration. Comparison of Fig. 9(a) with the results of the isolated ion model predictions shown in Fig. 3(a), however, shows that the predictions of the ion pair model are substantially better than those of the isolated ion model. This result indicates that the isolated ion scenario only holds at concentrations of 0.5 m or lower. At concentrations near 1.5 m, water dynamics can only be understood by accounting for the presence of ion pairs and explicitly considering their cooperative slowdown of water rotation. While the sizable number of ion pairs formed at this concentration indicates that small ion clusters also exist in solutions, these clusters appear to be unnecessary to satisfactorily explain water dynamics. The marked effect of ion pairs on water dynamics is also clearly present at even higher concentrations, near the solubility limit, but in this case it appears to be insufficient to explain the large slowdown of water dynamics seen at such high concentrations. To do so, we must consider the enhanced slowdown of water rotation induced by the presence of large numbers of ion clusters. Similarly to what was done above for the ion pairs, we predict the water dynamics in MgSO4 solutions at 1.5 and 2.5 m from the contributions of water near ion clusters and any remaining water in a bulk-like environment (ESI†). The results from this model are shown in Fig. 9(b). The water dynamics at the 2.5 m concentration can be predicted from the contributions of water near isolated ion clusters, supporting the notion that the very slow water rotation observed at such high concentrations indeed arises from the strong supra-additive slowdown of water rotation induced by such clusters.
3.5 Origin of additive and supra-additive slowdown
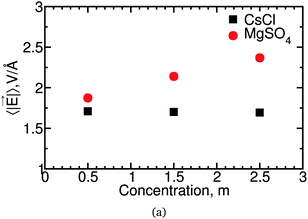
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) , between these salt solutions. In Fig. 10 we show the average magnitude, 〈|
, between these salt solutions. In Fig. 10 we show the average magnitude, 〈|![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) |〉, of the electric field experienced at the negative Drude charge of water molecules. These results indicate that slower water dynamics correlates with higher 〈|
|〉, of the electric field experienced at the negative Drude charge of water molecules. These results indicate that slower water dynamics correlates with higher 〈|![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) |〉 for MgSO4 but not for CsCl solutions. A similar correlation between 〈|
|〉 for MgSO4 but not for CsCl solutions. A similar correlation between 〈|![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) |〉 and water reorientation has been found for Na2SO4, but not for NaClO4.26 Water slowdown in solutions is known to have multiple origins. Two slowdown mechanisms that are well understood are the reduction in the number of transition states associated with hydrogen-bond exchange near solutes, and the stronger hydrogen bonds between water and some anions.58 The correlation between 〈|
|〉 and water reorientation has been found for Na2SO4, but not for NaClO4.26 Water slowdown in solutions is known to have multiple origins. Two slowdown mechanisms that are well understood are the reduction in the number of transition states associated with hydrogen-bond exchange near solutes, and the stronger hydrogen bonds between water and some anions.58 The correlation between 〈|![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) |〉 and water slowdown observed for MgSO4 and for Na2SO4 suggests that simple electrostatic effects will slow down some mechanisms of water rotation, but that this contribution is of importance only for some salts.
|〉 and water slowdown observed for MgSO4 and for Na2SO4 suggests that simple electrostatic effects will slow down some mechanisms of water rotation, but that this contribution is of importance only for some salts.
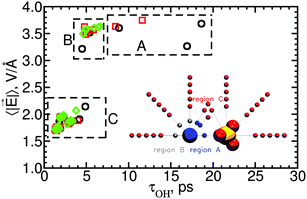
Water subpopulations in Mg2+'s first hydration layer, corresponding to regions A and B in the inset of Fig. 11, have reorientation times that are independent of the field's magnitude: water reorientation times vary by a factor of 3 while the magnitude of the electric field varies by ±10%. Region A includes those water subpopulations that show supra-additive slowdown in SIPi ion pairs; these results thus suggest that supra-additive slowdown is unrelated to the local electric field.
The absence of correlation between supra-additive slowdown and the magnitude of the local electric field for water molecules in region A is surprising because intuitively one would expect that these water subpopulations should reflect the influence of ion–ion polarization, which is one possible cause for supra-additive slowdown. The extra forces acting on water molecules near two polarizable ions relative to the forces acting on water molecules in the absence of those ions can be written as
![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) = = ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) 1 + 1 + ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) 2 + 2 + ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) p12 p12 | (6) |
![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) 1 and
1 and ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) 2 are the extra forces acting on water molecules near a single, isolated, ion of type 1 or 2, and
2 are the extra forces acting on water molecules near a single, isolated, ion of type 1 or 2, and ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) p12 is the extra force acting on the water molecules because of the different polarization state of ions with nearby counterions relative to the situation where the ions are isolated. The
p12 is the extra force acting on the water molecules because of the different polarization state of ions with nearby counterions relative to the situation where the ions are isolated. The ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) p12 term is not included in our reference additive model so, if
p12 term is not included in our reference additive model so, if ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) p12 were large, the cooperativity factor S given by eqn (5) should differ from 1. The absence of correlation between the water reorientation times in region A and the electric field magnitude indicates that
p12 were large, the cooperativity factor S given by eqn (5) should differ from 1. The absence of correlation between the water reorientation times in region A and the electric field magnitude indicates that ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) p12 is small, even for water molecules in between the two ions in SIPi configuration; it follows that ion–ion polarization is not at the origin of supra-additive slowdown of water rotation. See the ESI† for results of extra simulations of SIPi ion pairs with fixed orientation, which further support this conclusion. Because supra-additive slowdown cannot be explained by ion–ion polarization, it should arise from the remaining possible source of non-additive effects: changes in the length and/or shape of the pathway associated with water rotation. Such a detailed study of rotation pathways is outside the scope of the present work and will be the subject of a future paper.
p12 is small, even for water molecules in between the two ions in SIPi configuration; it follows that ion–ion polarization is not at the origin of supra-additive slowdown of water rotation. See the ESI† for results of extra simulations of SIPi ion pairs with fixed orientation, which further support this conclusion. Because supra-additive slowdown cannot be explained by ion–ion polarization, it should arise from the remaining possible source of non-additive effects: changes in the length and/or shape of the pathway associated with water rotation. Such a detailed study of rotation pathways is outside the scope of the present work and will be the subject of a future paper.
4 Concluding remarks
Our present and prior results31 demonstrate that intense supra-additive slowdown of water rotation by ions occurs in MgSO4 solutions. Supra-additive slowdown occurs via an intense decrease in the rotation rate of the small water subpopulation that directly bridges anions and cations in solvent-shared configuration. The model initially proposed by Tielrooij, Garcia-Araez, Bonn, and Bakker22 to explain supra-additive slowdown of water rotation – long-range changes in the number of slow water molecules – is not supported by our calculations. Supra-additive effects are associated with ions in solvent-shared ion pair configurations only: intense supra-additive slowdown already occurs for single ion pairs, and increases in magnitude for water molecules belonging to ion clusters because of the influence of multiple nearby ions. Clusters of MgSO4 ions may also induce marked slowdown of water rotation up to the third hydration layer of the ions, but these long-range effects are additive, not supra-additive.Bakker et al.'s notion of a long range supra-additive slowdown effect stems from fitting their experimental data using a simple two-population model:22,23 the global water dynamics in all salt solutions investigated by them was modeled as the sum of contributions of only two types of water subpopulations – with bulk-like or slow dynamics – the latter with a reorientation time four times that of the bulk-like subpopulation for all salts. Their model thus assumes that all slow water molecules are identical: the magnitude of the water reorientation times of the slow water subpopulation is independent of the identity of the salt, its concentration, and the position of the water molecule relative to nearby ions; only the number of slow water molecules changes with salt identity and concentration. Our results show that such a model is overly simplistic, because the dynamics of water molecules in salt solutions is highly heterogeneous: it strongly depends on the identity of the salt and on the number and lifetime of nearby ion pairs and clusters: e.g., near CsCl ion pairs the slowest reorienting water is only 2.5 times slower than pure water, whereas near MgSO4 ion pairs it is 14 times slower than pure water. Furthermore, the magnitude of water slowdown by an isolated ion pair is strongly spatially inhomogeneous, as illustrated in Fig. 6. Our simulation work shows that the assumptions underlying the two-population model used by Bakker et al. to interpret their results are not met, which suggests that the spatial range for supra-additive effects inferred from that model is incorrect. Their observation of supra-additive slowdown of water rotation, however, is independent of the two-population model they used for analysis. The existence of supra-additive slowdown of water rotation is supported by both their experiments and our simulations.
Our results suggest that supra-additive slowdown of water rotation will be strongest in solutions of salts that preferentially form solvent-shared ion pairs and have high viscosity, i.e., where these ion pairs are expected to have lifetimes longer than the typical water reorientation times. Sodium sulfate, for example, forms solvent-shared ion pairs59 and has reasonably high viscosity at high concentration,60 so cooperative slowdown of water rotation should occur in solutions of this salt. Bakker et al.22 in fact detect large cooperative slowdown of water rotation in Na2SO4 solutions. Recent simulations of Na2SO4 solutions using polarizable models done by Stirnemann, Laage et al.,26 however, state that ion-specific cooperative effects do not occur there, which apparently contradicts the experimental results and the extrapolations we make from the present work on MgSO4. Careful reading of that work, however, indicates that it is in fact largely consistent with our own: both works do not support the increase in the number of slowly rotating water molecules by ions proposed by Bakker et al., but instead indicate that cooperative effects consist of increases in the magnitude of the slowdown and are short-range, arising largely from the overlap of the first hydration layers of two ions. In Fig. 2B of ref. 26, the authors show that adding the contributions of water reorientation near isolated cations, anions and bulk-like water is insufficient to predict the water reorientation dynamics for Na2SO4 solutions with concentration larger than 1 m. In Fig. 3B of the same reference, the authors show that water subpopulations bridging Na2SO4 ion pairs in concentrated solutions rotate much more slowly than an additive picture would predict. These findings are entirely consistent with our own on MgSO4, as mentioned above. The authors clearly state that ions have a short-range effect on water, and that deviations from additivity arise from overlapping hydration shells of the ions, with which we agree. Stirnemann, Laage et al. indicate that deviations from additivity are connected to increases in solution viscosity with increasing salt concentration, as our work also suggests, but claim that this effect is not ion specific, with which we disagree. The viscosity at the same high concentration may vary greatly between different salts, making such an effect undoubtedly ion-specific.
Our results show that intense supra-additive slowdown of water dynamics by ions occurs in concentrated solutions of particular salts, but does not extend beyond the ions' first hydration shell. Long-range, supra-additive effects of ions on water thus appear not to be important to understand the Hofmeister series, even for densely charged ions. The present work also provides clear guidelines for the development of coarse-grained or analytical models of ion solvation. These models should include supra-additive effects for salts of divalent or densely charged ions only up to the first hydration layer. For high concentrations of MgSO4 and possibly other salts these models should, however, reproduce the ability of these ions to additively slow down water dynamics up to the ions' third hydration shell, and may need to include long-range ion–ion structural correlations arising from additive effects. Even in the case of salts like MgSO4, models based on the Generalized Langevin Equation, which are often used to investigate ion dynamics at long time scales,61–63 need only include distance-dependent memory kernels to simulate concentrations beyond 0.5 m.
References
- K. D. Collins and M. W. Washabaugh, Q. Rev. Biophys., 1985, 18, 323–422 CrossRef CAS.
- M. G. Cacace, E. M. Landau and J. J. Ramsden, Q. Rev. Biophys., 1997, 30, 241–277 CrossRef CAS PubMed.
- L. M. Pegram, J. Record and M. Thomas, J. Phys. Chem. B, 2007, 111, 5411–5417 CrossRef CAS.
- R. Zangi, J. Phys. Chem. B, 2009, 114, 643–650 CrossRef.
- Y. He, Q. Shao, S. Chen and S. Jiang, J. Phys. Chem. C, 2011, 115, 15525–15531 CAS.
- C. L. D. Gibb and B. C. Gibb, J. Am. Chem. Soc., 2011, 133, 7344–7347 CrossRef CAS.
- D. E. Otten, P. R. Shaffer, P. L. Geissler and R. J. Saykally, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 701–705 CrossRef CAS.
- S. Koneshan, J. C. Rasaiah, R. M. Lynden-Bell and S. H. Lee, J. Phys. Chem. B, 1998, 102, 4193–4204 CrossRef CAS.
- C. D. Cappa, J. D. Smith, K. R. Wilson, B. M. Messer, M. K. Gilles, R. C. Cohen and R. J. Saykally, J. Phys. Chem. B, 2005, 109, 7046–7052 CrossRef CAS PubMed.
- Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621 CrossRef CAS.
- A. Tanwar, B. Bagchi and S. Pal, J. Chem. Phys., 2006, 125, 214304 CrossRef PubMed.
- K. D. Collins, Biophys. Chem., 2006, 119, 271–281 CrossRef CAS.
- W. Wachter, S. Fernandez, R. Buchner and G. Hefter, J. Phys. Chem. B, 2007, 111, 9010–9017 CrossRef CAS.
- H. J. Bakker, Chem. Rev., 2008, 108, 1456–1473 CrossRef CAS.
- J. D. Smith, R. J. Saykally and P. L. Geissler, J. Am. Chem. Soc., 2007, 129, 13847–13856 CrossRef CAS.
- Y. Marcus, Chem. Rev., 2009, 109, 1346–1370 CrossRef CAS PubMed.
- Y. S. Lin, B. M. Auer and J. L. Skinner, J. Chem. Phys., 2009, 131, 144511 CrossRef.
- J. T. O'Brien, J. S. Prell, M. F. Bush and E. R. Williams, J. Am. Chem. Soc., 2010, 132, 8248–8249 CrossRef PubMed.
- J. S. Prell, J. T. O'Brien and E. R. Williams, J. Am. Chem. Soc., 2011, 133, 4810–4818 CrossRef CAS.
- S. Funkner, G. Niehues, D. A. Schmidt, M. Heyden, G. Schwaab, K. M. Callahan, D. J. Tobias and M. Havenith, J. Am. Chem. Soc., 2012, 134, 1030–1035 CrossRef CAS.
- S. J. Irudayam and R. H. Henchman, J. Chem. Phys., 2012, 137, 034508 CrossRef.
- K. J. Tielrooij, N. Garcia-Araez, M. Bonn and H. J. Bakker, Science, 2010, 328, 1006–1009 CrossRef CAS.
- S. T. van der Post and H. J. Bakker, Phys. Chem. Chem. Phys., 2012, 14, 6280–6288 RSC.
- A. W. Omta, M. F. Kropman, S. Woutersen and H. J. Bakker, Science, 2003, 301, 347–349 CrossRef CAS PubMed.
- C. H. Giammanco, D. B. Wong and M. D. Fayer, J. Phys. Chem. B, 2012, 116, 13781–13792 CrossRef CAS.
- G. Stirnemann, E. Wernersson, P. Jungwirth and D. Laage, J. Am. Chem. Soc., 2013, 135, 11824–11831 CrossRef CAS PubMed.
- L. Yang, Y. Fan and Y. Q. Gao, J. Phys. Chem. B, 2011, 115, 12456–12465 CrossRef CAS.
- D. Jiao, C. King, A. Grossfield, T. A. Darden and P. Ren, J. Phys. Chem. B, 2006, 110, 18553–18559 CrossRef CAS.
- E. Wernersson and P. Jungwirth, J. Chem. Theory Comput., 2010, 6, 3233–3240 CrossRef CAS.
- J. Yoo and A. Aksimentiev, J. Phys. Chem. Lett., 2012, 3, 45–50 CrossRef CAS.
- A. Vila Verde and R. Lipowsky, J. Phys. Chem. B, 2013, 117, 10556–10566 CrossRef CAS.
- G. Lamoureux, E. Harder, I. V. Vorobyov, B. Roux and A. D. MacKerell Jr., Chem. Phys. Lett., 2006, 418, 245–249 CrossRef CAS.
- H. Yu, T. W. Whitfield, E. Harder, G. Lamoureux, I. Vorobyov, V. M. Anisimov, J. MacKerell, D. Alexander and B. Roux, J. Chem. Theory Comput., 2010, 6, 774–786 CrossRef CAS.
- A. Bleuzen, P.-A. Pittet, L. Helm and A. E. Merbach, Magn. Reson. Chem., 1997, 35, 765–773 CrossRef CAS.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- W. Jiang, D. J. Hardy, J. C. Phillips, A. D. MacKerell, K. Schulten and B. Roux, J. Phys. Chem. Lett., 2010, 2, 87–92 CrossRef PubMed.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- W. W. Wood, in Physics of simple Liquids, ed. H. N. V. Temperley, J. S. Rowlinson and G. S. Rushbrooke, North-Holland publishing company – Amsterdam, 1968, ch. 5, pp. 151–155 Search PubMed.
- R. Chitra and S. Yashonath, J. Phys. Chem. B, 1997, 101, 5437–5445 CrossRef CAS.
- Y. S. Lin, P. A. Pieniazek, M. Yang and J. L. Skinner, J. Chem. Phys., 2010, 132, 174505 CrossRef.
- D. Laage and J. T. Hynes, Chem. Phys. Lett., 2006, 433, 80–85 CrossRef CAS.
- A. Vila Verde and R. K. Campen, J. Phys. Chem. B, 2011, 115, 7069–7084 CrossRef CAS PubMed.
- A. Vila Verde, P. G. Bolhuis and R. K. Campen, J. Phys. Chem. B, 2012, 116, 9467–9481 CrossRef CAS.
- D. E. Moilanen, E. E. Fenn, Y.-S. Lin, J. L. Skinner, B. Bagchi and M. D. Fayer, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 5295–5300 CrossRef CAS PubMed.
- S. T. van der Post, K.-J. Tielrooij, J. Hunger, E. H. G. Backus and H. J. Bakker, Faraday Discuss., 2013, 160, 171–189 RSC.
- J. R. Schmidt, S. T. Roberts, J. J. Loparo, A. Tokmakoff, M. D. Fayer and J. L. Skinner, Chem. Phys., 2007, 341, 143–157 CrossRef CAS.
- D. S. Wilcox, B. M. Rankin and D. Ben-Amotz, Faraday Discuss., 2013, 167, 177–190 RSC.
- S. H. Northrup and J. T. Hynes, J. Chem. Phys., 1980, 73, 2700–2714 CrossRef CAS.
- I. S. Joung, I. Cheatham and E. Thomas, J. Phys. Chem. B, 2009, 113, 13279–13290 CrossRef CAS.
- U. Baul and S. Vemparala, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 012114 CrossRef.
- G. Stirnemann, S. R.-V. Castrillon, J. T. Hynes, P. J. Rossky, P. G. Debenedetti and D. Laage, Phys. Chem. Chem. Phys., 2011, 13, 19911–19917 RSC.
- F. Sterpone, G. Stirnemann, J. T. Hynes and D. Laage, J. Phys. Chem. B, 2010, 114, 2083–2089 CrossRef CAS.
- G. Stirnemann, P. J. Rossky, J. T. Hynes and D. Laage, Faraday Discuss., 2010, 146, 263–281 RSC.
- D. Laage and J. T. Hynes, J. Phys. Chem. B, 2008, 112, 14230–14242 CrossRef CAS PubMed.
- D. Laage and J. T. Hynes, Science, 2006, 311, 832–835 CrossRef CAS.
- D. Laage and J. T. Hynes, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 11167–11172 CrossRef CAS.
- D. Laage, G. Stirnemann and J. T. Hynes, J. Phys. Chem. B, 2009, 113, 2428–2435 CrossRef CAS.
- R. Buchner, S. G. Capewell, G. Hefter and P. M. May, J. Phys. Chem. B, 1999, 103, 1185–1192 CrossRef CAS.
- Concentrative properties of aqueous solutions: density, refractive index, freezing point depression, and viscosity, in CRC handbook of chemistry and physics, ed. W. M. Haynes, Taylor & Francis, 2011, pp. 5-123–5-148 Search PubMed.
- Z. Cao, J. F. Dama, L. Lu and G. A. Voth, J. Chem. Theory Comput., 2013, 9, 172–178 CrossRef CAS PubMed.
- S. Roy, I. Mitra and R. Llinas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 041920 CrossRef PubMed.
- D. Gordon, V. Krishnamurthy and S.-H. Chung, J. Chem. Phys., 2009, 131, 134102 CrossRef.
Footnotes |
† Electronic supplementary information (ESI) available: Full details of the parameterization of anion–cation interactions, density of the CsCl and MgSO4 solutions, dipole moment of sulfate as a function of the magnitude of the electric field from quantum mechanics calculations, fitting parameters and average reorientation times associated to the reorientation decay of water in CsCl or MgSO4 solutions, long-range convergence of the anion–cation radial distribution functions, P2(t) for each hydration layer around isolated ions and corresponding average reorientation decay times, position and intensity of the extrema in anion–cation radial distribution functions, discussion of the types of ion pairs formed in CsCl and MgSO4 solutions with respect to experimental information, probability per ion of forming n ion pairs, calculation of ion pair lifetimes, origin of ion pair lifetimes, reorientation decay times and cooperativity factors for ion pairs and ion clusters, deeper discussion of the effects of low charge density ions on the dynamics of water around anions, analytical model to calculate the average solution P2(t) from contributions of water near ion pairs or clusters, reorientation times of the local electric field near MgSO4 SIPis with fixed SO42− orientation, correlation between average OH reorientation times, 〈|![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) |〉 for MgSO4 SIPis with fixed SO42− orientation. See DOI: 10.1039/c5cp05726d |〉 for MgSO4 SIPis with fixed SO42− orientation. See DOI: 10.1039/c5cp05726d |
| ‡ The rotational decay times depend on the choice of multiple time stepping parameters31 but ratios of rotational decay times do not; our conclusions are independent of the multiple time stepping parameters used. |
| § Percentage estimated from the hydration numbers of isolated ions. |
| This journal is © the Owner Societies 2016 |