Understanding the electromagnetic interaction of metal organic framework reactants in aqueous solution at microwave frequencies

Abstract

Preparation of metal organic frameworks (MOFs) via microwave heating is becoming increasingly popular due to reduced reaction times and enhanced control of MOF particle size. However, there is little understanding about the detailed interaction of the electric field portion of the wave with reactants during the synthesis of MOFs. In order to overcome this lack of fundamental understanding, information about the dielectric properties of the reactants is required. In this work the dielectric constants (ε′) and loss factors (ε′′) of benzene-1,4-dicarboxylic acid (H₂BDC; also known as terephthalic acid) and a number of M(III) (M = metal) salts dissolved in deionized water were measured as a function of frequency, temperature and concentration and with varying anions and cations. Dielectric data confirm the aqueous M(III) salts to be strong microwave absorbers, particularly at 915 MHz. M(III) salts with mono-anionic ligands (for example chlorides and nitrates) exhibit higher losses than di-anionic salts (sulfates) demonstrating that the former are heated more effectively in an applied microwave field. Of the M(III) salts containing either singly- or doubly-charged anions, those containing Fe(III) have the highest loss indicating that they will heat more efficiently than other M(III) salts such as Cr(III) and Al(III). Interestingly, H₂BDC exhibits little interaction with the electric field at microwave frequencies.

---

Introduction

Metal organic frameworks (MOFs) have been the subject of significant research and commercial interest due to their high surface areas^1,2 tunability and functionalities.^3,4 Owing to their exceptional porosity, MOFs are ideal candidates for a wide range of applications such as gas storage and separation,^5,6 catalysis,^6,7 supercapacitors,⁸ sensors^9,10 and as electrolytes in fuel cells.^6,8 MOFs are crystalline materials constructed from metal ions or clusters¹¹ and organic linkers,¹² and the variability and availability of different metal centres and clusters and organic linkers has led to the preparation of many structural variants with a variety of materials properties. A major hurdle for the development of MOFs is the long time typically required for their synthesis and inability to scale-up routes to manufacture. Although synthesis by slow evaporation methods can require up to 7 months,¹³ the current predominant synthetic route involves solvothermal reactions (hydrothermal when water is the solvent) in sealed vessels. In these reactions, the reactants are heated above the boiling point of the solvent and retained under autogeneous pressure for up to one week.¹³ A variety of other methods have been investigated including electrochemical,¹⁴ mechanochemical,¹⁵ and sonochemical¹⁶ approaches. However, the most rapid route to date involves microwave irradiation.¹⁷ For example, IRMOF1, IRMOF2 and IRMOF3 have been prepared by Ni and Masel in as little as 25 seconds via microwave-assisted solvothermal reactions (150 W, microwave synthesizer model 520A from Resonance Instrument Inc.).¹⁷ Importantly they noted that the materials prepared using microwave methods were of the same quality as those prepared using conventional solvothermal routes.

In addition to reducing reaction times, work on the synthesis of MOFs using microwaves has focused on investigating phase-selectivity,¹⁸ crystal nucleation rates¹⁹ and controlling particle size.¹⁷ For example, Khan and Jhung demonstrated phase-selective microwave synthesis of MIL-53 and MIL-101 (MIL = Materials Institute Lavoisier), with the latter isolated after reaction times of ca. 1–4 h and the former requiring longer times.¹⁸ This was ascribed to the conversion between the kinetically (MIL-101) and thermodynamically (MIL-53) favourable phases of these Cr(III) materials.¹⁹ Furthermore, phase-selective synthesis of MOFs using microwave irradiation has demonstrated the possibility of producing alternative MOF structures that may not be accessible through conventional solvothermal routes.^18,20

A wide number of frameworks have been synthesised using microwaves.¹³ Despite this activity there is a paucity of information regarding the interaction between microwave irradiation and MOF reactants and intermediates. Current examples of microwave-assisted synthesis of MOFs are all carried out without any analysis of the interaction(s) of reactants with the microwave field; this paper aims to overcome this lack of fundamental understanding.

In order to understand the effects of microwave irradiation during the synthesis of MOFs, information about the dielectric properties (specifically the dielectric constant, ε′, and dielectric loss, ε′′) of the reactants is required. Such information is essential for the optimum design and safe scaling-up of microwave processes as these values quantify how effectively a material will be heated in an electric field. The bulk dielectric permittivity, ε*, is a measure of the extent to which a material can be polarised by an external electric field, and can be expressed in its complex form:

ε* = ε′ − jε′′

where ε′ is the dielectric constant, ε′′ is the dielectric loss and j is the imaginary number where j² = −1.²¹ The dielectric constant reflects the ability of a material to store energy through a form of polarisation, while dielectric loss is the ability of a material to convert the stored energy to heat.²¹ Generally, materials that heat well in an electric field have high values of ε′′ and materials that heat poorly have low ε′′; as such they are often referred to as ‘high loss’ or ‘low loss’ materials, respectively. To place this in context, examples of ε′ and ε′′ for some common industrial materials are given in Table 1. Although there are no precise guidelines for identifying whether a material will be heated well or poorly in an electric field, Krupka has defined low loss materials as those with ε′′ smaller than 1.²² Additionally, Metaxas et al.²³ and the National Physical Laboratory (NPL)²⁴ categorise materials based on tan δ, where tan δ = ε′′/ε′. Low loss materials are those with tan δ < 3 × 10⁻⁴, medium loss materials have tan δ values in the range 3 × 10⁻⁴ ≤ tan δ < 3 × 10⁻² and high loss materials have tan δ ≥ 3 × 10⁻².²⁴

Table 1 Dielectric properties of some common industrial materials at 25 °C and 3.0 GHz

Materials that heat well in the presence of an electric field			Materials that heat poorly in the presence of an electric field
Example	ε′	ε′′	Example	ε′	ε′′
^a23, ^b20, ^c27, ^d22, ^e23 °C. All data from ref. 23 except b^63 and e.^64
Raw potato	53.7	15.7	Plexiglass, perspex^c	2.25	0.0007
Distilled water	76.7	12.0	Polytetrafluoro-ethylene (Teflon)^d	2.1	0.0003
Distilled water + 0.5 M NaCl	67.0	41.48	Fused silica glass	3.78	0.0002
Rapeseed, frost resistant^a	40.0	11.0	Ruby mica, muscovite	5.4	0.0016
Ethanol 99.8% purity^b (containing <0.2% water)	5.99	5.48	Titanium dioxide (Ticon T)^e	100	0.04

---

As well as providing insight into whether a material will heat in an electric field, ε′ and ε′′ also provide information about the mechanisms by which a material interacts with an electric field. For molecules in solution, ε* reflects the frequency dependent polarisation processes that occur as a result of the interaction of charges with the oscillating external electric field. In the frequency range of our study (0.5 to 10.0 GHz, which is in the range of domestic and commercially available microwave heating systems) two processes take place, namely ionic and dipolar polarisation mechanisms. Ionic mechanisms occur in ionic solutions, whereby comparative displacement of cations and anions by the electric field leads to net polarisation of the solution.^21,25 Below 2.0 GHz, the dielectric permittivity of ionic solutions is greatly affected by the ion mobility as it moves with the oscillating electric field.²⁶ The mobility of ions in solution is retarded by surrounding solvation spheres with a concentration-dependent reduction in ε′, i.e. the more ions (and therefore solvation spheres) present in solution, the lower the value of ε′. For example, at 1.0 GHz NiSO₄ dissolved in distilled water at 25 °C exhibits ε′ values of ca. 80 and 70 for the total solution at concentrations of 0.15 and 1.40 M, respectively.²⁷ Additionally, the retarding force exerted on the ion causes a significant lag that arises as a result of the ion being out of phase with the electric field.²⁵ This lag results in high dielectric losses (ε′′) and leads to heating of the solution. For example, a 500 mM solution of NaCl heats well in an electric field since it has an extremely high dielectric loss, ε′′, of 269.0 at 1.0 GHz.²³

Dipolar mechanisms occur for molecules that possess a permanent dipole, such as water.²⁶ Dipolar molecules experience a torque causing them to re-orient in the direction of the applied electric field,²⁵ and as the dipoles re-orient they experience frictional forces from neighbouring molecules.²⁵ The kinetic energy causing friction is lost as heat giving rise to moderate values of ε′′ (e.g. at 3 GHz distilled water has a dielectric loss, ε′′, of 12.00).²³

In this study we examine the dielectric constant (ε′) and loss (ε′′) of reactants commonly used to prepare the MIL-53 and MIL-47 series of MOFs.^28,29 These targets were chosen for two reasons. Firstly, variation of starting metal salt enables MOFs containing different metal nodes to be synthesised using the same organic linker, in this case benzene-1,4-dicarboxylate (BDC²⁻). Secondly, the reaction kinetics^30,31 and both the structure²⁸ and properties²⁹ of these MOFs have been established and are well understood. While it is perhaps unsurprising that the dielectric properties of H₂BDC have not been studied in solution, we were surprised to find that values of ε′ and ε′′ for simple metal salts dissolved in aqueous solution have not been widely reported previously. Such data are fundamental to understanding the interaction of electromagnetic waves with such chemistries. Dielectric analysis of inorganic electrolytes, specifically metal salts dissolved in water, is of course a long-standing area of research.^21,32

The dielectric properties of salt-water solutions depend greatly upon water–water interactions,³³ the nature of hydrogen bonding networks,^26,33,34 solute and solvent concentrations,³⁵ ionic charge,³⁶ ion-pairs,³⁷ and the size effects of the ions^36,38 and their hydration spheres.³⁶ By considering the effect of frequency, concentration, temperature, the choice of cation and anion on the dielectric constant (ε′) and dielectric loss (ε′′) of metal salts and H₂BDC, we have assessed directly the contributions of the above factors on the synthesis of MIL-53 and MIL-47 in an electric field. In this way, we aimed to identify the precise interactions of the electric field taking place in a typical reaction leading to the formation of MOF product(s).

Experimental methods

Chemicals

Al(NO₃)₃·9H₂O, Cr₂(SO₄)₃·H₂O and Fe(NO₃)₃·9H₂O were purchased from Sigma-Aldrich. FeCl₃ was obtained from Merck. Al₂(SO₄)₃·8H₂O, CrCl₃·6H₂O, Cr(NO₃)₃·9H₂O, Fe₂(SO₄)₃·5H₂O and VCl₃ were purchased from Acros Organics. Terephthalic acid was acquired from Alfa Aesar. All chemicals had a purity of 97% or greater and were used as received.

Dielectric analyses

The values of ε′ and ε′′ were measured using an Agilent 85070E Dielectric Probe Kit. The experimental set-up consisted of a performance coaxial probe (2.4 mm male connector and 1.6 mm tip) equipped with an electronic calibration (ECal) module. The coaxial probe was connected to an Agilent N5232A PNA-L (Purpose Network Analyser) operating at 300 kHz–20 GHz via a high quality coaxial cable. The probe was made of T316L stainless steel and had a nickel plated tungsten central conductor with a borosilicate glass seal at the tip. The probe is operational over a temperature range of −40 °C to +200 °C, and a typical measurement involved immersing the probe tip into the test solution and a swept frequency signal (500 MHz–10 GHz) was transmitted from the PNA into the solution via the coaxial line. Measurements were carried out over a temperature range of 20–60 °C. The dielectric constant (ε′) and dielectric loss (ε′′) were recorded using Agilent Technologies 85070 software and processed in Origin 8.0. Values of ε′ and ε′′ were measured for three separate test solutions of the same concentration at temperatures of 20, 40 and 60 °C. The value of ε′ and ε′′ at each point was also measured three times such that each data point represents an average value of 9 measurements. Error bars are plotted ± one standard deviation. The resultant data points (Fig. 1–3 and 5) are so close together that they impact upon the visual output of each data line such that the error bars appear as a continuous line; therefore, the thickness of the line is indicative of the error.

Fig. 1 Plots of average dielectric constant (ε′) vs. frequency for CrCl₃ (A), FeCl₃ (B), Cr₂(SO₄)₃ (C) and Fe₂(SO₄)₃ (D) in deionized water at three concentrations. The value of ε′ was measured at three different temperatures (see legend) for each M(III) salt at a given concentration. Errors are represented by the thickness of each line (see Experimental section for further details).

Fig. 2 Plots of average loss factor (ε′′) vs. frequency for CrCl₃ (A), FeCl₃ (B), Cr₂(SO₄)₃ (C) and Fe₂(SO₄)₃ (D) in deionized water at three concentrations. The value of ε′′ was measured at three different temperatures (see legend) for each M(III) salt at a given concentration. Errors are represented by the thickness of each line (see Experimental section for further details).

Fig. 3 Plots of average dielectric constant (ε′, left axis) and average loss factor (ε′′, right axis) vs. frequency for CrCl₃ (a) and FeCl₃ (b) at three concentrations; 5.0 mM (ε′ brown, ε′′ red), 50.0 mM (ε′ blue, ε′′ pink) and 500 mM (ε′ green, ε′′ black). Plots of dielectric constant (ε′) and loss (ε′′) vs. frequency for Cr₂(SO₄)₃ (c) and Fe₂(SO₄)₃ (d) at three concentrations; 2.5 mM (ε′ brown, ε′′ red), 25.0 mM (ε′ blue, ε′′ pink) and 250 mM (ε′ green, ε′′ black). All data were collected at 20 °C. Errors are represented by the thickness of each line (see Experimental section for further details).

Test solutions were prepared by dissolving the required amount of analyte (metal salt or organic linker) in deionized water to the desired concentration for a 200 mL volume. This volume was used as it was experimentally determined as being sufficiently large enough to ensure that the signal from the probe tip was being transmitted through the test solution only and not the surroundings, i.e. the sample is assumed to be of an infinite volume with respect to the transmitted signal. Concentrations were based upon a 1 : 0.5 : 80 ratio of metal cation : BDC²⁻ : H₂O, commonly used in the synthesis of MIL-53.²⁸ This ratio represents a concentration of BDC²⁻ of 25.0 mM. For the M(III) chlorides and nitrates, a concentration of 50.0 mM was required. As the M(III) sulfates contain two metal cations per molecule, only half the number of moles were required for each test solution such that the corresponding concentration remains 25.0 mM. In order to facilitate complete dissolution of BDC²⁻ in water either sodium hydroxide or ammonium hydroxide were added in a ratio of 1 : 2 of acid : base. Additional concentrations at factors of ×0.1 and ×10 with respect to the ratio of water were also prepared so that concentrations above and below that required for the synthesis of MIL-53 could be analysed. All test solutions were left for a minimum of 24 h before dielectric measurements to allow complete equilibration to their hydrolysed species in solution (as confirmed by UV-visible absorption spectroscopy, see ESI†).

UV-visible absorption spectroscopy

UV-visible absorption spectra were measured using an Ocean Optics USB2000+ UV-VIS-ES spectrometer with a DT-MINI-2GS light source. A typical experiment involved pipetting the analyte into a quartz cuvette and placing the cuvette in a 1 cm holder equipped with a P200-2 transmission fibre optic. Spectra were collected at time intervals of 0, 2 and 24 hours for each analyte. Spectra were recorded using Ocean Optics SpectraSuite 2.0 software and processed in Origin 8.0. Each spectrum was baseline corrected and intensities were normalized with respect to the highest peak. Peak maxima and shoulder positions are accurate to ±5.0 nm.

Results and discussion

In this work the dielectric constants (ε′) and dielectric loss factors (ε′′) of BDC²⁻ and a number of M(III) salts dissolved in deionized water were measured as a function of frequency, temperature and concentration in the presence of various anions. To our knowledge, there are no reports of the dielectric properties of aqueous Fe, Cr and V salts in the literature. Solutions of Al₂(SO₄)₃ have been investigated at concentrations of 0.012–0.65 M³⁹ and 0.1 M⁴⁰ at 25 °C only. Also, Al(NO₃)₃·H₂O at concentrations of 0.5 M to saturation have been examined at 25 °C.⁴¹

The dielectric properties of M(III) salts

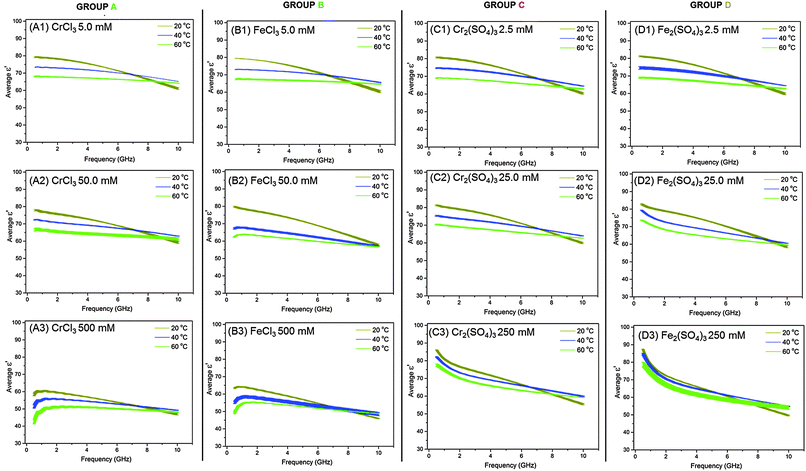
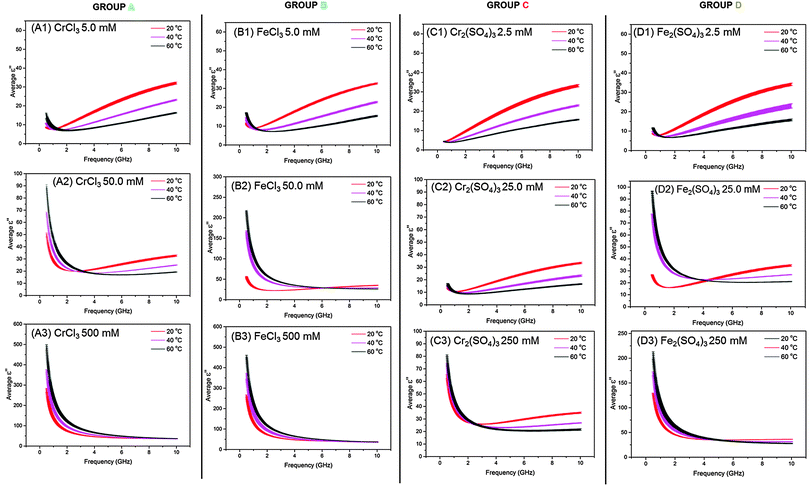
We discuss first the dielectric properties (ε′ and ε′′) of simple M(III) salts, which we can group into four types. The salts studied fall into those containing either mono- or di-charged anions, and based upon their dielectric properties we can divide both types into two separate sub-groups giving 4 categories (A, B, C and D) as shown in Table 2. Group A consists of CrCl₃, Cr(NO₃)₃ and Al(NO₃)₃ all of which contain singly-charged anions and have the same trends in dielectric behaviour. Group B consists of FeCl₃, Fe(NO₃)₃ and VCl₃ which all similarly contain singly-charged anions and are categorized by their trends in dielectric behaviour. Group C comprises Al₂(SO₄)₃ and Cr₂(SO₄)₃, both of which contain doubly-charged anions and exhibit the same trends in dielectric properties. Finally, Group D contains Fe₂(SO₄)₃ which displays unique dielectric behaviour compared to the other metal salts in this study. We describe here the dielectric data (ε′ and ε′′) for one illustrative M(III) salt from each group (Table 2). For Groups A, B and C and D, Fig. 1 and 2 show plots of dielectric constant (ε′) vs. frequency and of dielectric loss (ε′′) vs. frequency, respectively. Dielectric data for all other M(III) salts (i.e. those that are not italicized in Table 2) are given in ESI.†

Table 2 Division of the metal salts investigated in this work

Group A	Group B	Group C	Group D
Italics denotes species explicitly discussed in the main text.
CrCl 3	FeCl 3	Al2(SO4)3	Fe 2 (SO 4 ) 3
Cr(NO3)3	VCl3	Cr 2 (SO 4 ) 3
Al(NO3)3	Fe(NO3)3

---

Effect of frequency. By considering data at a fixed concentration and temperature we are able to observe the effect of frequency upon the dielectric constant (ε′) and dielectric loss (ε′′). For example, a 50.0 mM solution of CrCl₃ (Group A) at 20 °C (Fig. 1: A2 brown line) exhibits a small non-linear decrease in ε′ with frequency from 77.9 ± 0.49 at 0.5 GHz to 59.2 ± 0.63 at 10.0 GHz.

At the same concentration and temperature the dielectric loss, ε′′, (Fig. 2: A2 red line) displays slightly more complex behaviour than ε′. Within the frequency range 0.5–1.0 GHz ε′′ decreases rapidly as frequency increases, from 49.9 ± 1.55 to 28.4 ± 0.63 (Fig. 2: A2 red line). Above 1.0 GHz a non-linear increase in ε′′ up to 32.7 ± 0.65 at 10 GHz is observed with increasing frequency (Fig. 2: A2 red line). These trends in ε′ and ε′′ with frequency are consistent with those observed for all of the M(III) salt solutions in Groups A, B, C and D in this work and those described in the literature for aqueous electrolytic solutions and water.^{21,32,34,39,40,42} Such trends are governed by the polarisability of ions and water molecules in solution in response to the electric field.^21,42c As mentioned in the introduction, ionic polarizations are dominant in the frequency range 0.5–2.0 GHz and dipolar mechanisms dominate in the range 2.0–10.0 GHz. However, perhaps the most interesting observation from these data is that the dielectric loss (ε′′) is significantly higher at low frequency (<1.0 GHz) than at frequencies above 1.0 GHz, suggesting that the metal salts from Groups A, B, C and D will heat more if the electric field applied is at a lower frequency (below 1.0 GHz).

Next we discuss the effect of temperature and concentration on the dielectric constant (ε′) and loss (ε′′) of the M(III) salts. Variation of these parameters indirectly probes water–water interactions,³³ influence of the hydrogen bonding network,^26,33,34 solute and solvent concentrations.³⁵ A solution may have a stronger or weaker interaction with the electric field at different temperatures; for example, distilled water exhibits a reduction in dielectric constant (ε′) and loss (ε′′) with increasing temperature at 3.0 GHz, as shown in Table 3.²¹

Table 3 Dielectric data for liquid water at varying temperature at industrial, scientific and medical (ISM) frequencies⁶³

Temperature (°C)	915 MHz		2.45 GHz		5.6 GHz
	ε′	ε′′	ε′	ε′′	ε′	ε′′
20	80.00	3.98	78.68	10.61	72.91	22.17
30	76.44	2.97	75.66	7.96	72.17	17.15
40	73.1	2.3	72.62	6.21	70.39	13.62
50	69.84	1.79	69.53	4.83	68.1	10.71

---

Effect of temperature. Data in Table 3 confirm that at 0.9 and 2.45 GHz water is heated more effectively in an electric field at lower temperatures than at higher temperatures (ε′′ is lower at 50 °C compared to 20 °C). In addition to the observed decrease in water loss factor with increasing temperatures, the dielectric constant also decreases. This latter effect produces an increment of the electric field magnitude due to the lower reflection at the sample–air interface.⁴³ Therefore, this dielectric constant decrease will balance the decrease of the loss factor. Overall more power is thus required to heat water by the same amount at low compared to high temperatures. Conversely, if a material exhibits an increase in dielectric loss (ε′′) with increasing temperature, less power will be required at higher temperatures to heat the material. For this reason, information on the effect of temperature on the dielectric properties (ε′ and ε′′) of a material is particularly important for scaling up chemical reactions using microwave processing. For example, varying the applied power as the temperature of a reaction changes may allow better control over the bulk temperature during microwave heating and may prevent overheating. In addition, ε′ determines the effective guide wavelength of the electric field propagating through the sample, and therefore information about ε′ is important for numerical modelling simulations used in optimizing microwave furnace designs and choke filters.

Fig. 1(A1) and 2(A1) show the effect of temperature upon ε′ and ε′′, respectively, for a 5.0 mM solution of CrCl₃ in water, and is representative of the M(III) salts in Group A of this study. At this concentration of M(III) salt the dielectric properties of the solution are dominated by those of the bulk water.^42c At frequencies above 9.0 GHz ε′ increases with increasing temperature in the order 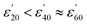(Fig. 1: A1, brown < blue ≈ green line). At frequencies lower than 6.0 GHz the opposite effect is observed, i.e. ε′ decreases with increasing temperature in the order 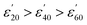(Fig. 1: A1 brown, blue and green lines). For example, at 915 MHz ε′ decreases from 78.96 ± 0.43 at 20 °C to 73.25 ± 0.25 at 40 °C and 67.92 ± 0.23 at 60 °C (Fig. 1: A1 brown, blue and green lines). This behaviour has previously been reported for distilled water and is due to a decrease in the extent of water–water hydrogen bonding with increasing temperature as a result of a shift in the Boltzmann distribution of the water molecules, i.e. more water molecules have the energy required to overcome hydrogen bonding with increasing temperature.^42c,44 The detrimental effect of increasing temperature on the extent of hydrogen bonding is further evidenced by a reduction in ε′′ with increasing temperature for frequencies above 1.4 GHz. For example, at 5.6 GHz ε′′ decreases from 22.02 ± 0.60 at 20 °C to 14.63 ± 0.21 at 40 °C and 10.32 ± 0.21 at 60 °C (Fig. 2: A1 red > pink > black line). A decrease in hydrogen bonding with increasing temperature enables the water molecules to move more freely in solution, thus lowering the rotational drag and ultimately the friction between water molecules.^42c,44 By decreasing the amount of friction between water molecules, less kinetic energy is lost as heat and thus a reduction the value of ε′′ is observed.^42c,44 The trends in ε′ and ε′′ with temperature exhibited by 5.0 mM solutions of Group A salts are also observed for M(III) salt solutions from Groups B, C and D at concentrations of 5.0 (Group B) and 2.5 mM (Group C and D) (see Fig. 1 and 2: B1, C1 and D1). A key feature of the decrease in ε′′ with temperature is that at frequencies above 1.4 GHz, all of the 2.5 and 5.0 mM M(III) salt solutions absorb less microwave power as the solution gets hotter.

While the major component of the dielectric properties (ε′ and ε′′) for 5.0 mM and 2.5 mM solutions of M(III) salts from Groups A, B, C and D arises from bulk water, at frequencies below 1.0 GHz there is some evidence in the ε′′ data of ionic polarisation mechanisms (see Fig. 2: A1 and B1 and D1; red, pink and black lines). In this frequency range a slight increase in dielectric loss (ε′′) is observed with increasing temperature in the order; 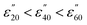(Fig. 2: A1, B1 and D1; red, pink and black lines). For example, a 5.0 mM solution of CrCl₃ (Group A) at 915 MHz shows an increase in ε′′ from 7.49 ± 0.10 at 20 °C to 7.60 ± 0.04 at 40 °C and 9.35 ± 0.80 at 60 °C. We attribute this increase in ε′′ with temperature to two factors; a shift in the ratios of ion-pairs owing to temperature-dependent perturbation of ion-pair association–dissociation equilibrium^45,46 and a rise in frictional heat as a result of augmented ion mobility.^42c,44a The effect of temperature on ε′′ is different for pure water and aqueous ionic solutions as the water molecules in the hydration sphere do not experience the same rotational restrictions as bulk/free water.⁴⁷ Most importantly, below 1.0 GHz, solutions of M(III) salt from Groups A, B and D at concentrations of 5.0 mM (A and B) and 2.5 mM (D) absorb more microwave power as the solution gets hotter.

Significantly, the frequency range in which the metal salt solutions absorb more or less microwave power with temperature varies with concentration. These changes can be observed as points of inflexion in the plot of ε′′ vs. concentration (Fig. 2). At concentrations of 5.0, 50.0 mM (Group A and B) and 2.5, 25.0 and 250 mM (Groups C and D), the frequency at which the points of inflexion occur are unique for each individual M(III) salt. However, the frequency at which the inflexion point is observed increases with increasing concentration. At 500 mM solutions of salts containing singly-charged anions (Group A and B) show no points of inflexion in the ε′′ data, rather the values of ε′′ at each temperature converge with increasing frequency. This result confirms that the amount of ions in solution is sufficient under these conditions for the dielectric properties to be dominated by the interaction of ionic species with the electric field. Importantly, at 500 mM, the M(III) salt solutions of Group A and B absorb more microwave power as the solution gets hotter at frequencies of 0.5–10.0 GHz. The frequency range in which solutions of Group C and D absorb more or less microwave energy can be determined from the inflexion points. At frequencies below the inflexion point (low frequency) solutions of Group C and D absorb more microwave power as the solution heats. Above the inflexion point (high frequency) solutions of Group C and D absorb less microwave power as the solution heats.

Effect of concentration. Comparison of data collected at a fixed temperature of 20 °C for three different concentrations of M(III) salt solution allows investigation into the effect of concentration upon the dielectric properties (Fig. 3). As mentioned previously, the dielectric properties (ε′ and ε′′) of Groups A and B M(III) salts were measured at concentrations of 5.0, 50.0 and 500 mM, while the dielectric properties (ε′ and ε′′) of Groups C and D salts were measured at concentrations of 2.5, 25.0 and 250 mM. These particular concentrations were chosen so that the number of moles of positive and negative charge are equal for each M(III) salt solution. Additionally, these concentrations allow the effect of the electric field on M(III) salts to be compared directly from the point of view of MOF synthesis using microwaves.²⁸

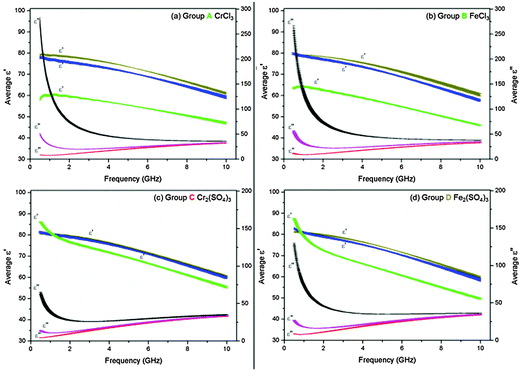
At concentrations of 5.0 and 2.5 mM bulk water dominates the dielectric properties (ε′ and ε′′) of the M(III) salt solutions.^44b All M(III) salt solutions exhibit a decrease in ε′ with increasing concentration over a frequency range of 1.5–10 GHz (Fig. 3(a)–(d) brown > blue > green lines). A reduction in ε′ for solutions with increasing concentration is commonly known as “dielectric decrement”,^21,42c which arises from the mutual dependence of the mobilities of ions and their corresponding hydration spheres. The ions dictate the orientation of surrounding water molecules thereby reducing the ability of the water molecules to orient in the electric field. This in turn causes the hydration spheres to exert a retarding force on the ion as the sphere is less mobile than the ion.^21,47

Indeed, dielectric decrement has been observed for many other electrolytic solutions such as KF, NaCl, NaCl, Al(NO₃)₃ (at 25 °C only),³² MgCl₂⁴⁸ and MgSO₄.⁴⁹ While dielectric decrement does not affect the heating of a material within an electric field, it is important to be aware of changes in ε′ with increasing concentration as this has an impact on the propagation of the electric field through a material and is essential for microwave cell design.

Below 1.5 GHz differences in the trends in ε′ are observed for Groups A and B compared with Groups C and D. These differences are most obvious at the highest concentration. For example a 500 mM solution of CrCl₃ (Group A) displays an increase in ε′ from 58.58 ± 0.68 at 0.5 GHz to 60.44 ± 0.39 at 1.3 GHz at 20 °C (Fig. 3(a)). A 250 mM solution of Cr₂(SO₄)₃ (Group C) exhibits a decrease in ε′ from 85.90 ± 0.11 at 0.5 GHz to 79.41 ± 0.21 at 1.3 GHz at 20 °C (Fig. 3(c)). A possible explanation for this observation is the poor solubility of the salts at concentrations >250 mM. However, further investigations are required to confirm the validity of measurements in this frequency range.

All M(III) salt solutions exhibit the same behaviour in ε′′ with concentration over the 0.5–10.0 GHz frequency range. Below 2.0 GHz a large rise in ε′′ with concentration is observed as a result of increasing ionic polarisation mechanisms (Fig. 3(a)–(d) black > pink > red lines). For example, 5.0, 50.0 and 500 mM solutions of CrCl₃ (Group A) exhibit a rise in ε′′ from 7.49 ± 0.0091 to 30.20 ± 0.68 to 150.24 ± 4.93, respectively, at 915 MHz and 20 °C (Fig. 3(a)). We attribute the increase in ε′′ with molarity to the greater concentration of ions and their corresponding hydration spheres in solution; therefore, more viscous lag is taking place. These observations are consistent with experimental data reported for other electrolytic solutions^35,50 and theoretical dielectric models.^51,52 These results suggest that below 2.0 GHz the most concentrated salt solutions from Groups A, B and D absorb more microwave power than less concentrated solutions owing to selective heating of the ions in solution.

From 2.0–10.0 GHz a smaller increase in ε′′ is exhibited by all M(III) salts compared with that observed below 2.0 GHz (Fig. 3(a)–(d)). For example, 5.0, 50.0 and 500 mM solutions of CrCl₃ (Group A) exhibit a rise in ε′′ from 22.02 ± 0.60 to 24.83 ± 0.62 to 39.83 ± 0.34, respectively, at 5.6 GHz and 20 °C (Fig. 3(a)). These results suggest that at 5.6 GHz, the most concentrated salt solutions from Groups A, B and D absorb more microwave power than less concentrated solutions; however, they will not absorb as much power as that observed below 2.0 GHz.

At 10.0 GHz the ε′′ values for each concentration of M(III) salt begin to diverge (Fig. 3(a)–(d)), suggesting that unrestricted water molecules are able to interact with the electric field despite the increased presence of ions and their hydration spheres in solution, i.e. each concentration still contains un-associated ‘bulk’ water molecules.⁵⁰ At this frequency range it would, therefore, be possible to selectively heat the bulk water molecules only. These results are in agreement with theoretical models used to interpret and/or predict the dielectric properties (ε′ and ε′′) of dilute electrolytic solutions of concentration less than 1000 mM.⁵⁰

Mechanisms. In order to assess the cationic and anionic contributions to the bulk dielectric properties (ε′ and ε′′) of a solution, it is important to identify the ions and ion-pair species in solution. To this end, the M(III) salts in this study were analysed by UV-visible absorption spectroscopy over a period of 24 hours following addition of the metal salt to water. By tracking changes in position of spectral bands in the UV-vis absorption spectra (Fig. 4 and ESI†) it has been possible to monitor the dissociation of contact ion complexes of the M(III) salts investigated in this work. For example, at t = 0, UV-vis absorption spectra of CrCl₃ in deionized water (Group A, Fig. 4(i)) exhibit bands at 448 and 639 nm corresponding to the complex [Cr(H₂O)₅Cl₂]⁺. After 2 h the bands shift to 424 and 600 nm owing to formation of [Cr(H₂O)₅Cl]²⁺. After 24 h bands at 409 and 578 nm correspond to the fully hydrolysed [Cr(H₂O)₆]³⁺ ions (Fig. 4(i) blue line).⁵³ Shifts in spectral peak positions from 430 and 600 nm to 410 and 585 nm respectively in the UV-vis absorption spectra of aqueous Cr₂(SO₄)₃ (Group C, Fig. 4(ii)) confirms dissociation of a contact ion complex [Cr(H₂O)₅SO₄]⁺ to [Cr(H₂O)₆]³⁺ over a period of 24 h. 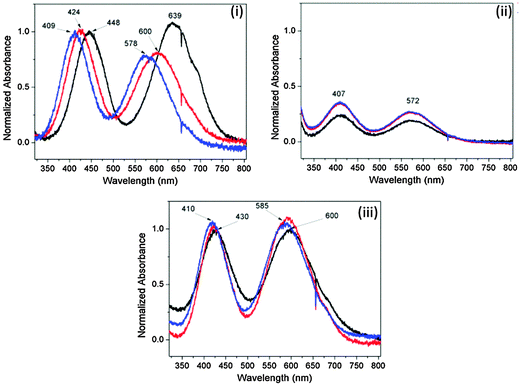Finally, bands at 407 and 572 nm corresponding to [Cr(H₂O)₆]^3+ 53 are observed in the absorption spectra of Cr(NO₃)₃ in deionized water (Group A) at all times owing to the much faster dissociation of the NO₃⁻ anion compared with Cl⁻ and SO₄²⁻.⁵⁴ A thorough assessment of the dielectric properties of the species formed during the initial equilibration phase is beyond the scope of this study and will be addressed in future work. We can reasonably consider the fully equilibrated/hydrated species to be representative of the reactants in a typical MOF synthesis, but it is worth noting that the time taken for full equilibration is significant in the first two examples.

Fig. 4 UV-visible absorption spectra of aqueous (i) CrCl₃·6H₂O (approx. 1.4 mM), (ii) Cr(NO₃)₃·9H₂O (approx. 1.4 mM) and (iii) Cr₂(SO₄)₃·H₂O (approx. 0.7 mM). Spectra were collected at 25 °C and at time intervals of 0 minutes (black line), 2 and 24 hours (red and blue lines, respectively).

Fig. 5 Plots of average dielectric constant (ε′, left axis) and average loss factor (ε′′, right axis) vs. frequency for H₂BDC and ammonium hydroxide (E) and sodium hydroxide (F) in deionized water at three concentrations; (1) 2.5 mM, (2) 25.0 mM and (3) 250 mM. Concentrations are in respect to H₂BDC. ε′ and ε′′ were measured at three different temperatures for each BDC²⁻ solution at each fixed concentration; 20 (ε′ brown, ε′′ red), 40 (ε′ blue, ε′′ pink) and 60 °C (ε′ green, ε′′ black). Each solution contained a stoichiometric ratio of 1 : 2 H₂BDC : base, respectively. Errors are represented by the thickness of each line (see Experimental section for further details).

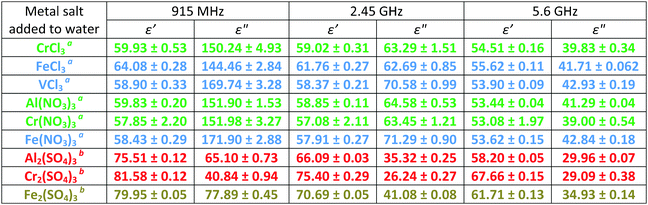
Analyses of the absolute magnitudes of ε′ and ε′′ at three ISM (industrial, scientific and medical) frequencies for the most concentrated solutions allows assessment of the cationic and anionic contributions to the dielectric properties (ε′ and ε′′) of each at a specific temperature (Table 4). The most concentrated solutions are likely to contain a mixture of ion pair types (see below). For example, at 20 °C and a given concentration of 500 mM, all of the Group A M(III) salts [CrCl₃, Cr(NO₃)₃ and Al(NO₃)₃] exhibit the same values of ε′ and ε′′ at 915 MHz and 2.45 GHz, within experimental error (Table 4). This observation suggests that changing either the cation or anion for these particular M(III) salts has a minor effect on the bulk dielectric properties (ε′ and ε′′) at these frequencies. This result is unsurprising as there is little difference between the cationic radii of Al(III) and Cr(III) (0.50⁵⁵ and 0.62 Å,⁵⁶ respectively) and the anionic radii of NO₃⁻ and Cl⁻ (approx. 3.45 and 3.18 Å, respectively).⁵⁴ Additionally, all of these cations adopt the same octahedral hexa-aquo complexes in water⁵³ as confirmed by UV-visible absorption spectroscopy (ESI†). Differences in dielectric properties (ε′ and ε′′) as a result of changing the cation have only been observed for cations with large differences in their radii, for example between alkali earth cations.^42a,d Separate reports have shown that the anionic contribution towards the bulk dielectric properties (ε′ and ε′′) of an aqueous electrolyte is much smaller than that of the cation.^57–60 These results were ascribed to a difference in hydrogen bonding of water–cation complexes compared to water–anion complexes. For water–cation complexes, the water molecule interacts via the oxygen atom, thus preventing the water molecule from undergoing electric dipole rotation.^42d However, in the case of water–anion complexes interaction occurs through one of the water hydrogen atoms such that electric dipole rotation, although restricted, is still possible.^42d Ultimately, data in Table 4 suggest that each M(III) salt from Group A is likely to absorb the same amount of microwave power at 915 MHz and 2.45 GHz, indicating that that the individual effects of both the anion and cation on ε′ and ε′′ for the bulk solution for these M(III) salts are small, in agreement with the literature. Unlike Group A, M(III) salts from Group B exhibit small variations in their absolute values of ε′ and ε′′ at frequencies of 915 MHz and 2.45 GHz (Table 4). Out of the M(III) salts in Group B, and indeed all of the M(III) salts in Group A, FeCl₃ exhibits the largest ε′ at 915 MHz and 2.45 GHz for a concentration of 500 mM. This observation, coupled with the UV-visible absorption spectra (ESI†), is indicative of the formation of ion pairs as solutions containing ion pairs exhibit higher values of ε′.⁵⁰ Three types of ion pairs have been identified for electrolytic solutions: solvent sharing ionic-pairs (SSIPs); two solvent sharing ionic pairs (2SIPs); and contact ion pairs (CIPs).³⁵ The presence of CIPs, particularly [FeCl₄]⁻, is not uncommon for solutions of FeCl₃ at pH < 2.⁵³ Many solutions containing ion pairs have been reported, including for Al₂(SO₄)₃,³⁹ CuSO₄,⁴⁶ ZnCl₂,³⁵ and MSO₄ (M = Mg, Ni, Co).²⁷

Table 4 Summary of ε′ and ε′′ for M(III) salts at industrial, scientific and medical (ISM) frequencies at 20 °C

a Data collected at 20 °C with set concentration of 500 mM. b Data collected at 20 °C with set concentration of 250 mM. Group A, green; Group B, blue; Group C, red; Group D, brown. Values and errors of ε′ and ε′′ written to two decimal figures.

---

The largest values of ε′′ are observed for the Group B salts VCl₃ and Fe(NO₃)₃ at 915 MHz indicating that these M(III) salts will absorb more power than all of the M(III) salts in this study at this particular frequency at a given concentration/temperature. High values of ε′′ (Table 4) may be a consequence of the formation of hydroxy species of Fe and V. Solutions of [M(H₂O)₆]³⁺ (M = Fe, V) are known to react with water to form hydroxyl complexes such as [M(H₂O)₅(OH)]²⁺.⁵³ These data may also arise as a result of the formation of CIPs. Solutions of VCl₃ contain CIPs at high concentration;⁵³ however, solutions of Fe(NO₃)₃ are less likely to contain CIPs as NO₃⁻ ions are more weakly associative than Cl⁻ ions.

At 2.45 GHz any variation in ε′ and ε′′ for M(III) salt solutions in Group A and B of the same concentration is less pronounced than at 915 MHz, i.e. the values are converging (Table 4). At 5.6 GHz values of ε′ and ε′′ are the same for each M(III) salt solution for Groups A and B (Table 4). If the values of ε′ and ε′′ are the same for each metal salt, then they should absorb the same amount of microwave power. Therefore, at 2.45 GHz and 5.6 GHz there should be no difference between the heating for each M(III) salt. However, the large differences in ε′′ at 915 MHz indicate that it may be possible to selectively heat the ions in metal salt solutions at low frequency.

M(III) salt solutions from Groups C and D exhibit a large variation in ε′ and ε′′ with M(III) salt and frequency (Table 4). Again, the Fe(III) salt exhibits the highest value of ε′′ in these two groups and will be heated better in a microwave field than Cr(III) and Al(III) salts. This result is likely a consequence of the formation of CIPs and/or hydroxy species in water, as discussed earlier.⁵³ Differences between the values of ε′ and ε′′ of Groups C and D compared with Groups A and B are due to the variance in concentration.

Dielectric properties of the terephthalate ligand (BDC²⁻)

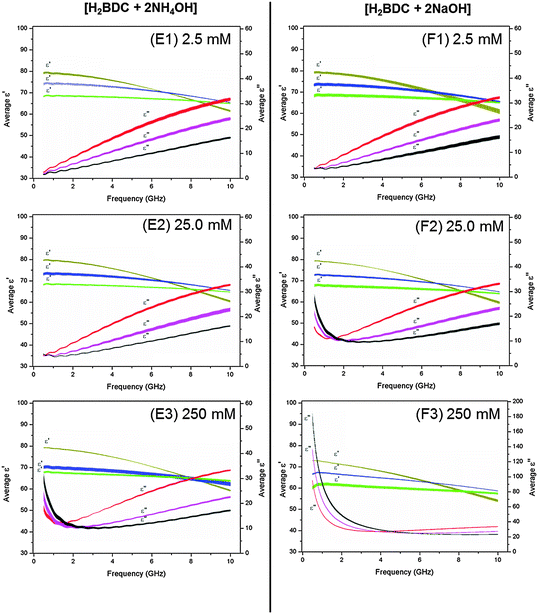
Dissolution of H₂BDC in water was facilitated by addition of two equivalents of base (see Experimental). In order to assess the relative contributions of the base and terephthalate (deprotonated anion of BDC²⁻) to the overall dielectric properties (ε′ and ε′′) of the solution, two bases, NaOH and NH₄OH were investigated. Na⁺ and NH₄⁺ cations have been shown to exhibit very different dielectric behaviour from each other, which therefore facilitates identification of their contribution to the observed dielectric properties.^42a,d,61,62 Moreover, comparison of dielectric data of BDC²⁻ with cations and of the cations in the absence of BDC²⁻ allows extraction of the constant contribution of BDC²⁻ to the overall dielectric properties (Fig. 5: E1–3 and F1–3). Plots of dielectric constant (ε′) and loss (ε′′) versus frequency for bases in the absence of H₂BDC are given in the ESI.† All data at three ISM frequencies are summarized in Table 5.

Table 5 Summary of ε′ and ε′′ for H₂BDC and solubilising base solutions and H₂BDC powder sample at industrial, scientific and medical (ISM) frequencies at 20 °C

Entry no.	Test solution	915 MHz		2.45 GHz		5.6 GHz
		ε′	ε′′	ε′	ε′′	ε′	ε′′
a Data collected at 20 °C with concentrations of 250 mM. b Data collected at 20 °C with concentrations of 500 mM. Solutions containing mixtures of acid and base have a ratio of 1 : 2 BDC : base, respectively. c Data collected at 20 °C on a solid sample using the cavity perturbation method.^66 Values and errors of ε′ and ε′′ written to two decimal figures.
1	[H2BDC + 2NH4OH]^a	78.95 ± 0.15	13.27 ± 0.57	77.49 ± 0.14	14.24 ± 0.08	71.45 ± 0.01	23.81 ± 0.23
2	[H2BDC + 2NaOH]^a	72.66 ± 0.10	55.19 ± 0.24	70.53 ± 0.11	29.33 ± 0.21	64.74 ± 0.27	28.57 ± 0.29
3	NH4OH^b	79.13 ± 0.05	5.70 ± 0.05	77.80 ± 0.04	11.46 ± 0.02	71.66 ± 0.04	22.84 ± 0.02
4	NaOH^b	67.62 ± 0.49	173.76 ± 5.29	67.89 ± 0.36	73.06 ± 1.91	62.84 ± 0.29	47.48 ± 0.77
5	H2BDC^c	2.50 ± 0.14	0.02 ± 0.00	2.53 ± 0.16	0.03 ± 0.00	—	—

---

Contributions of NH₄⁺ and Na⁺. As with the M(III) salt solutions, at concentrations of 2.5 mM (BDC²⁻-containing solutions) and 5.0 mM (NH₄OH and NaOH solutions) the dielectric behaviour (ε′ and ε′′) of each solution is again unsurprisingly dominated by bulk water (Fig. 5: E1, F1 and ESI†).^42a–c Additionally, no ionic polarisation mechanisms are exhibited by any of the solutions at 2.5 or 5.0 mM concentration (see Fig. 5: E1, F1 and ESI†). The absence of ionic polarisation mechanisms are typified by values of ε′′ < 10 below 2.0 GHz and indicate that little microwave power is absorbed by these solutions below this frequency.

At concentrations of 25.0 and 250 mM, stark differences between the dielectric properties of solutions containing NH₄⁺ and Na⁺ cations can be seen in the ε′′ data (Fig. 5: E2 and 3, F2 and 3 for BDC²⁻ with cations; ESI† for cations in the absence of BDC²). For these concentrations at frequencies of 915 MHz a significant increase in ε′′ with increasing temperature is observed for BDC²⁻ solutions containing Na⁺ cations (Fig. 5: F2 and F3, black line > pink line > red line). For example, a 250 mM solution of [H₂BDC + 2NaOH] at 915 MHz shows an increase in ε′′ from 55.17 ± 0.24 at 20 °C to 76.04 ± 0.74 at 40 °C and 99.52 ± 2.07 at 60 °C. This trend of increasing ε′′ with temperature at frequencies below 2.0 GHz is consistent with that observed for the M(III) salts from Groups A, B, C and D and shows that the [H₂BDC + 2NaOH] solution will absorb more microwave power as it is heated. However, this trend is not observed for the BDC²⁻ solutions containing NH₄⁺ cations. Only at a concentration of 250 mM does a solution of BDC²⁻ containing NH₄⁺ cations exhibit values of ε′′ below 2.0 GHz consistent with ionic polarisation mechanisms (Fig. 5: E3 red line > pink line > black line). For example, a 250 mM solution of [H₂BDC + 2NH₄OH] at 915 MHz exhibits ε′′ values of 13.27 ± 0.57 at 20 °C, 14.61 ± 0.98 at 40 °C and 18.10 ± 1.07 at 60 °C. Differences between the dielectric behaviour of Na⁺ and NH₄⁺ cations arise from differences in their ionic radii,^57,60 the tetrahedral geometry of NH₄⁺, and the ability of NH₄⁺ to act as a hydrogen bonding partner with water.^59,61 In contrast, Na⁺ cations, like the M(III) salts in Group A, B, C and D, disrupt the hydrogen bonding in bulk water due to the restricted mobility and preferential orientation of water molecules in the hydration sphere of the cation.^47,42d Importantly, these results confirm that solutions containing Na⁺ cations will absorb more power and therefore will be heated more effectively than solutions containing NH₄⁺ cations at frequencies below 2.0 GHz.

Further differences between NH₄⁺ and Na⁺ are evident in the ε′ data (Fig. 5 E1–3, F1–3 for BDC²⁻ with cations; ESI† for cations in the absence of BDC²⁻). For example, as for the M(III) salts in Groups A, B, C and D, an increase in concentration of metal cations at fixed temperature leads to a reduction in ε′, i.e. dielectric decrement.^21,42c The dielectric decrement displayed by Na⁺ cations is less than for M(III) salts owing to the smaller ionic charge and differences in size of hydration spheres. Solutions containing NH₄⁺ ions do not display dielectric decrement with increasing concentration (Fig. 5: E1–3, brown lines). A larger reduction in ε′ with increasing temperature is observed for NH₄⁺ than for solutions containing NaOH (Fig. 5: E1–3 compared to F1–3, respectively). For example, a 250 mM solution of [H₂BDC + 2NH₄OH] exhibits a reduction in ε′ at 915 MHz from 78.95 ± 0.15 at 20 °C to 69.94 ± 0.65 at 40 °C, whereas a 250 mM solution of [H₂BDC + 2NaOH] at 915 MHz shows a smaller reduction of 72.66 ± 0.10 at 20 °C to 67.26 ± 0.19 at 40 °C. A reduction in ε′ with increasing temperature is due to a decrease in the extent of water–water hydrogen bonding as a result of a shift in the Boltzmann distribution of the water molecules with increasing temperature (as described above).^42c,44a,b

Contributions of BDC²⁻. Over the whole range of ISM microwave frequencies the two solutions containing NH₄⁺ cations ([H₂BDC + 2NH₄OH] and NH₄OH; Table 5, entries 1 and 3) both display the same values of ε′ (ca. 79 at 915 MHz and 2.45 GHz and 71 at 5.6 GHz, Table 5) and ε′′ (13 ± 6 at 915 MHz and 2.45 GHz and 24 at 5.6 GHz, Table 5). These data suggest that there is little contribution from terephthalate towards the dielectric properties (ε′ and ε′′) of the [H₂BDC + NH₄OH] solution. However, large differences in ε′′ values between [H₂BDC + 2NaOH] and NaOH solutions (ε′′ of 55 cf. 174 at 915 MHz, respectively, Table 5 entry 2 vs. 4) are observed. The lower value of ε′′ for the [H₂BDC + 2NaOH] solution may arise if there is incomplete dissociation of the Na⁺ from BDC²⁻ or if the formation of ion pairs (CIPs, SSIPs and/or 2SIPs) based upon Na⁺ in solution is inhibited. Hydrogen bonding may occur between water molecules and the carboxylate groups or even with the aromatic groups of the terephthalate. This type of hydrogen bonding has previously been reported to reduce the dielectric loss (ε′′) of solutions containing aromatic solutes.⁶⁵ As the value of ε′′ for [H₂BDC + 2NaOH] is actually lower than that exhibited by NaOH solution, it can be inferred that BDC²⁻ has little influence on the dielectric properties of the [H₂BDC + 2NaOH] solution, and that the lower value of ε′′ for [H₂BDC + 2NaOH] compared with NaOH is based upon differences in association and solvation of Na⁺. Overall, the dielectric properties of BDC²⁻ with cations and cations in the absence of BDC²⁻ show that BDC²⁻ absorbs very little, if any microwave power.

Conclusions

Variation of metal salts enables the synthesis of MIL-53 and MIL-47 analogues containing different metal nodes with the same organic linker, BDC²⁻.^28,29 In this work the dielectric constants (ε′) and loss factors (ε′′) of a number of M(III) salts and salts of terephthalic acid (H₂BDC) dissolved in deionized water were measured as a function of frequency, temperature, concentration and with several anion and cations. In the frequency range of this study, test solutions have been shown to interact with the electric field via ionic and dipolar polarisation mechanisms.

All solutions exhibit dielectric behaviour (values of ε′ and ε′′) consistent with bulk deionized water at concentrations of 5.0 mM (Group A and B M(III) salts) and 2.5 mM (Group C and D M(III) salts and BDC²⁻ solutions). Above these concentrations the M(III) salts (Group A, B, C and D) show higher dielectric losses (ε′′) and smaller dielectric constants (ε′) than the BDC²⁻ solutions at 915 MHz and 2.45 GHz as a result of ionic polarisation mechanisms. These data indicate that the M(III) salts will absorb more power and therefore be heated more effectively than the ligand. Owing to stoichiometry-driven differences in concentration required for MOF synthesis, M(III) salts with mono-anions (for example with Cl⁻ and NO₃⁻) exhibit higher ε′′ than di-anionic salts (SO₄²⁻) indicating that they will be heated better in an electric field. Of the M(III) salts studied, those containing Fe(III) have the highest ε′′ indicating that they will be heated better in an electric field than M(III) salts containing other metal cations, such as Cr(III) and Al(III).

This work has shown that [H₂BDC + 2NaOH] exhibits much higher dielectric losses (ε′′) than [H₂BDC + 2NH₄OH] and H₂BDC (solid) owing to interaction of Na⁺ with the electric field. Therefore solutions containing [2Na⁺ + BDC²⁻] are likely to heat better than those containing H₂BDC. Also, M(III) salts in Group A, B, C and D show higher dielectric losses (ε′′) at a frequency of 915 MHz than at 2.45 GHz. Thus, heating may be achieved more effectively at 915 MHz than at 2.45 GHz. Information on the dielectric properties (ε′ and ε′′) is essential for the optimum design and safe scaling-up of microwave processes and also in understanding why microwave heated processes are far more rapid than those heated conventionally.

Acknowledgements

We thank the EPSRC for support. MS gratefully acknowledges support from the ERC for an Advanced Grant. NRC gratefully acknowledges a Royal Society Wolfson Merit Award.

References

1. J. L. C. Rowsell and O. M. Yaghi, Microporous Mesoporous Mater., 2004, 73, 3–14; Y. Yan, X. Lin, S. Yang, A. J. Blake, A. Dailly, N. R. Champness, P. Hubberstey and M. Schröder, Chem. Commun., 2009, 1025–1027.
2. O. K. Farha, I. Eryazici, N. C. Jeong, B. G. Hauser, C. E. Wilmer, A. A. Sarjeant, R. Q. Snurr, S. T. Nguyen, A. Ö. Yazaydın and J. T. Hupp, J. Am. Chem. Soc., 2012, 134, 15016–15021; Y. Yan, S. Yang, A. J. Blake and M. Schröder, Acc. Chem. Res., 2014, 47, 296–307; X. Lin, I. Telepeni, A. J. Blake, A. Dailly, C. M. Brown, J. M. Simmons, M. Zoppi, G. S. Walker, K. M. Thomas, T. J. Mays, P. Hubberstey, N. R. Champness and M. Schröder, J. Am. Chem. Soc., 2009, 131, 2159–2171.
3. V. Guillerm, D. Kim, J. F. Eubank, R. Luebke, X. Liu, K. Adil, M. S. Lah and M. Eddaoudl, Chem. Soc. Rev., 2014, 43, 6141–6172.
4. W. Lu, Z. Wei, Z.-Y. Gu, T.-F. Liu, J. Park, J. Park, J. Tian, M. Zhang, Q. Zhang, T. Gentle III, M. Bosch and H.-C. Zhou, Chem. Soc. Rev., 2014, 43, 5561–5593.
5. J.-R. Li, R. J. Kuppler and H.-C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504; S. Yang, A. J. Ramirez-Cuesta, R. Newby, V. Garcia-Sakai, P. Manuel, S. K. Callear, S. I. Campbell, C. C. Tang and M. Schröder, Nat. Chem., 2015, 7, 121–129; W. Yang, A. J. Davies, X. Lin, M. Suyetin, R. Matsuda, A. J. Blake, C. Wilson, W. Lewis, J. E. Parker, C. C. Tang, M. W. George, P. Hubberstey, S. Kitagawa, H. Sakamoto, E. Bichoutskaia, N. R. Champness, S. Yang and M. Schröder, Chem. Sci., 2012, 3, 2993–2999.
6. D. Farrusseng, Metal-Organic Frameworks Applications from Catalysis to Gas Storage, Wiley-VCH, Weinheim Germany, 2011.
7. D. Farrusseng, S. Aguado and C. Pinel, Angew. Chem., Int. Ed., 2009, 48, 7502–7513.
8. A. Morozan and F. Jaouen, Energy Environ. Sci., 2012, 5, 9269–9290.
9. Y.-W. Li, J.-R. Li, L.-F. Wang, B.-Y. Zhou, Q. Chen and X.-H. Bu, J. Mater. Chem. A, 2013, 1, 495–499.
10. M. Dan-Hardi, C. Serre, T. Frot, L. Rozes, G. Maurin, C. Sanchez and G. Férey, J. Am. Chem. Soc., 2009, 131, 10857–10859.
11. M. Eddaoudi, D. B. Moler, H. L. Li, B. L. Chen, T. M. Reineke, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2001, 34, 319–330.
12. G. Ferey, Chem. Soc. Rev., 2008, 37, 191–214.
13. N. Stock and S. Biswas, Chem. Rev., 2012, 112, 933–969.
14. A. M. Joaristi, J. Juan-Alcaniz, P. Serra-Crespo, F. Kapteijn and J. Gascon, Cryst. Growth Des., 2012, 12, 3489–3498.
15. M. Klimakow, P. Klobes, A. F. Thuenemann, K. Rademann and F. Emmerling, Chem. Mater., 2010, 22, 5216–5221.
16. N. A. Khan and S. H. Jhung, Coord. Chem. Rev., 2015, 285, 11–23.
17. Z. Ni and R. I. Masel, J. Am. Chem. Soc., 2006, 128, 12394–12395.
18. N. A. Khan and S. H. Jhung, Cryst. Growth Des., 2010, 10, 1860–1865.
19. E. Haque and S. H. Jhung, Chem. Eng. J., 2011, 173, 866–872.
20. S. H. Jhung, J.-H. Lee, P. M. Forster, G. Férey, A. K. Cheetham and J.-S. Chang, Chem. – Eur. J., 2006, 12, 7899–7905.
21. J. B. Hasted, Aqueous Dielectrics, Chapman and Hall Ltd., London, 1973.
22. J. Krupka, Meas. Sci. Technol., 2006, 17, R55–R70.
23. A. C. Metaxas and R. J. Meredith, Industrial Microwave Heating, The Institution of Engineering and Technology, 2008.
24. R. N. Clarke, A. P. Gregory, D. Cannell, M. Patrick, S. Wylie, I. Youngs and G. Hill, A guide to the characterisation of dielectric materials at RF and microwave frequencies, Institute of Measurement and Control/National Physical Laboratory, 2003.
25. G. B. Dudley, R. Richert and A. E. Stiegman, Chem. Sci., 2015, 6, 2144–2152.
26. U. Kaatze and R. Behrends, Tech. Mess., 2002, 69, 5–11.
27. T. Chen, G. Hefter and R. Buchner, J. Solution Chem., 2005, 34, 1045–1066.
28. C. Serre, F. Millange, C. Thouvenot, M. Nogues, G. Marsolier, D. Louer and G. Férey, J. Am. Chem. Soc., 2002, 124, 13519–13526; T. Loiseau, C. Serre, C. Huguenard, G. Fink, F. Taulelle, M. Henry, T. Bataille and G. Férey, Chem. – Eur. J., 2004, 10, 1373–1382.
29. S. Bourrelly, P. L. Llewellyn, C. Serre, F. Millange, T. Loiseau and G. Férey, J. Am. Chem. Soc., 2005, 127, 13519–13521; K. Barthelet, J. Marrot, D. Riou and G. Férey, Angew. Chem., Int. Ed., 2002, 41, 281–284.
30. E. Haque, J. H. Jeong and S. H. Jhung, CrystEngComm, 2010, 12, 2749–2754.
31. E. Haque, N. A. Khan, J. H. Park and S. H. Jhung, Chem. – Eur. J., 2010, 16, 1046–1052.
32. Y. Marcus, J. Solution Chem., 2013, 42, 2354–2363.
33. U. Kaatze, J. Solution Chem., 1997, 26, 1049–1112; A. K. Lyashchenko and A. Lileev, J. Chem. Eng. Data, 2010, 55, 2008–2016.
34. A. K. Lyashchenko and I. M. Karataeva, Russ. J. Phys. Chem. A, 2010, 84, 320–328.
35. U. Kaatze, V. Lonnecke and R. Pottel, J. Mol. Liq., 1987, 34, 241–255.
36. H. Falkenhagen, Rev. Mod. Phys., 1931, 3, 412–426.
37. J. Barthel, H. Hetzenauer and R. Buchner, Ber. Bunsen-Ges., 1992, 96, 1424–1432.
38. U. Kaatze, Z. Phys. Chem. Neue Fol., 1983, 135, 51–75.
39. S. Schrodle, W. W. Rudolph, G. Hefter and R. Buchner, Geochim. Cosmochim. Acta, 2007, 71, 5287–5300.
40. U. Kaatze and K. Giese, J. Mol. Liq., 1987, 36, 15–35.
41. F. E. Harris and C. T. Okonski, J. Phys. Chem., 1957, 61, 310–319.
42. (a) A. S. Lileev, Z. A. Filimonova and A. K. Lyashchenko, J. Mol. Liq., 2003, 103, 299–308; (b) U. Kaatze and R. Pottel, Z. Phys. Chem. Neue Fol., 1984, 141, 1–13; (c) J. B. Hasted, Liquid water: dielectric properties, Water A comprehensive treatise, Plenum Press, New York, 1972; (d) K. Giese, U. Kaatze and R. Pottel, J. Phys. Chem., 1970, 74, 3718.
43. J. Monzó-Cabrera, J. M. Catala-Civera, A. Díaz-Morcillo, D. Sánchez-Hernández, P. J. Plaza-González and E. de los Reyes, Microwave Opt. Technol. Lett., 2002, 32(6), 465–469; P. J. Plaza-González, J. Monzó-Cabrera, J. M. Catalá-Civera and D. Sánchez-Hernández, IEEE Trans. Microwave Theory Tech., 2005, 53(5), 1699–1706.
44. (a) R. Buchner, J. Barthel and J. Stauber, Chem. Phys. Lett., 1999, 306, 57–63; (b) U. Kaatze, J. Chem. Eng. Data, 1989, 34, 371–374.
45. C. Akilan, N. Rohman, G. Hefter and R. Buchner, ChemPhysChem, 2006, 7, 2319–2330.
46. C. Akilan, G. Hefter, N. Rohman and R. Buchner, J. Phys. Chem. B, 2006, 110, 14961–14970.
47. U. Kaatze R. Behrends and R. Pottel, J. Non-Cryst. Solids, 2002, 305, 19–28.
48. E. Glueckauf, Trans. Faraday Soc., 1964, 60, 1637.
49. R. Buchner, T. Chen and G. Hefter, J. Phys. Chem. B, 2004, 108, 2365–2375.
50. N. Gavish and K. Promislow, Chem. Phys., 2012 , arXiv:1208.5169.
51. A. Levy, D. Andelman and H. Orland, Phys. Rev. Lett., 2012, 108(22), 227801.
52. A. Chandra and B. Bagchi, J. Chem. Phys., 2000, 112, 1876–1886.
53. D. Nicholls, Complexes and first-row transition elements, Macmillan Education Ltd, Basingstoke and London, 1974.
54. P. J. Elving and B. Zemel, J. Am. Chem. Soc., 1957, 79, 1281–1285.
55. Y. Marcus, Chem. Rev., 1988, 88, 1475–1498.
56. R. D. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751–767.
57. J. B. Hubbard, P. Colonomos and P. G. Wolynes, J. Chem. Phys., 1979, 71, 2652.
58. P. G. Kusalik and G. N. Patey, J. Chem. Phys., 1983, 79, 4468.
59. U. Kaatze, J. Solution Chem., 1997, 26, 1049–1112.
60. J. B. Hubbard and R. F. Kayser, J. Chem. Phys., 1981, 74, 3535.
61. U. Kaatze, J. Phys. Chem. B, 2013, 117, 12252–12260.
62. U. Kaatze, Radiat. Phys. Chem., 1995, 45, 549–566.
63. A. P. Gregory and R. N. Clarke, Tables of the Complex Permittivity of Dielectric Reference Liquids at Frequencies up to 5 GHz, 2012, Report ISSN 1754-2979.
64. A. von Hippel, R. G. Breckenridge, F. G. Chesley and L. Tisza, Ind. Eng. Chem., 1946, 38, 1097–1109.
65. U. Kaatze, J. Solution Chem., 1997, 26, 1049–1112.
66. A. von Hippel, Dielectrics and waves, Wiley, Massachusetts, 3rd edn, 1954.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp05426e

---