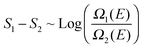Competitive lithium solvation of linear and cyclic carbonates from quantum chemistry†
Oleg
Borodin
*a,
Marco
Olguin
a,
P.
Ganesh
b,
Paul R. C.
Kent
bc,
Joshua L.
Allen
a and
Wesley A.
Henderson
d
aElectrochemistry Branch, RDRL-SED-C, US Army Research Laboratory, 2800 Powder Mill Rd., Adelphi, MD, 20783-1138, USA. E-mail: oleg.a.borodin.civ@mail.mil
bCenter for Nanophase Materials Sciences, Oak Ridge National Laboratory, 1 Bethel Valley Road, Oak Ridge, TN 37831, USA. E-mail: ganeshp@ornl.gov
cComputer Science and Mathematics Division, Oak Ridge National Laboratory, 1 Bethel Valley Road, Oak Ridge, TN 37831, USA
dElectrochemical Materials & Systems Group, Energy & Environment Directorate, Pacific Northwest National Laboratory (PNNL), Richland, WA 99352, USA
First published on 17th November 2015
Abstract
The composition of the lithium cation (Li+) solvation shell in mixed linear and cyclic carbonate-based electrolytes has been re-examined using Born–Oppenheimer molecular dynamics (BOMD) as a function of salt concentration and cluster calculations with ethylene carbonate:dimethyl carbonate (EC:DMC)–LiPF6 as a model system. A coordination preference for EC over DMC to a Li+ was found at low salt concentrations, while a slightly higher preference for DMC over EC was found at high salt concentrations. Analysis of the relative binding energies of the (EC)n(DMC)m–Li+ and (EC)n(DMC)m–LiPF6 solvates in the gas-phase and for an implicit solvent (as a function of the solvent dielectric constant) indicated that the DMC-containing Li+ solvates were stabilized relative to (EC4)–Li+ and (EC)3–LiPF6 by immersing them in the implicit solvent. Such stabilization was more pronounced in the implicit solvents with a high dielectric constant. Results from previous Raman and IR experiments were reanalyzed and reconciled by correcting them for changes of the Raman activities, IR intensities and band shifts for the solvents which occur upon Li+ coordination. After these correction factors were applied to the results of BOMD simulations, the composition of the Li+ solvation shell from the BOMD simulations was found to agree well with the solvation numbers extracted from Raman experiments. Finally, the mechanism of the Li+ diffusion in the dilute (EC:DMC)LiPF6 mixed solvent electrolyte was studied using the BOMD simulations.
Introduction
Further progress for improving electrolytes for lithium batteries could be facilitated by an improved understanding of electrolyte chemistry and electrochemical–structural–transport properties. Conventional lithium battery electrolytes are often comprised of a mixture of linear and cyclic carbonate solvents doped with the LiPF6 salt. Cyclic carbonates such as ethylene carbonate (EC) usually result in high salt dissociation and form a stable solid electrolyte interphase (SEI) on the surface of commonly employed graphite anodes after decomposition as a result of reduction reactions.1,2 Linear carbonates such as dimethyl carbonate (DMC) or ethyl methyl carbonate (EMC) typically possess a low viscosity, but also do not dissociate lithium salts as well as cyclic carbonates. Thus, linear carbonates are often added to the cyclic carbonates in order to improve ion transport, especially at low temperature. When solvent molecules are coordinated to lithium cations (Li+), they are strongly polarized resulting in a higher propensity to accept an electron and undergo a reduction reaction, as compared to solvents that are uncoordinated to Li+ cations. Therefore, when an SEI forms as the electrode potential is gradually lowered during the first formation cycle, solvents with a higher reduction potential and solvents bound to a Li+ tend to undergo reduction first and, thus, preferentially determine the SEI's composition and properties.In 2007 Xu et al. suggested that the eventual interphasial chemistry on graphitic anodes is dictated by the solvation shell composition of the Li+ in typical nonaqueous electrolytes, bringing attention to the importance of understanding the Li+ solvation shell dynamics.3,4 For example, a slight preference for PC over EC to be in the first coordination shell despite a similarity in their reduction potential resulted in a slight preferential reduction of PC in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PC(1
PC(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1)–LiPF6 electrolytes.5 Moreover, the structure of the Li+ solvation shell was suggested to be intimately connected with the cation desolvation process at the SEI–electrolyte interface, affecting interfacial resistance for the graphite–electrolyte, Li4Ti5O12–electrolyte and ceramic–electrolyte (with Li0.35La0.55TiO3 (LLT) and Li4Ti5O12 (LTO)) interfaces.3,6–15 Interestingly, molecular dynamics (MD) simulations showed that the relative populations of EC and DMC in the Li+ solvation shell were found to be dependent on the desolvation stage of the Li+ with a preference for DMC to be desolvated first, while EC desolvated at the later stages.14 The close proximity of negatively or positively charged graphite also influenced the Li+ first solvation shell composition.16
1)–LiPF6 electrolytes.5 Moreover, the structure of the Li+ solvation shell was suggested to be intimately connected with the cation desolvation process at the SEI–electrolyte interface, affecting interfacial resistance for the graphite–electrolyte, Li4Ti5O12–electrolyte and ceramic–electrolyte (with Li0.35La0.55TiO3 (LLT) and Li4Ti5O12 (LTO)) interfaces.3,6–15 Interestingly, molecular dynamics (MD) simulations showed that the relative populations of EC and DMC in the Li+ solvation shell were found to be dependent on the desolvation stage of the Li+ with a preference for DMC to be desolvated first, while EC desolvated at the later stages.14 The close proximity of negatively or positively charged graphite also influenced the Li+ first solvation shell composition.16
A strong preference for EC over DMC or EMC to coordinate Li+ in the gas-phase has been reported from quantum chemistry (QC) calculations17–19 and electro-spray ionization (ESI) mass spectroscopy.20,21 Such a preference was attributed to the difference in the dielectric constants (90 for EC vs. 3 for DMC).22 A strong preference for EC over DMC to directly coordinate a Li+ was also inferred from NMR experiments, while the DMC solvent's contribution to the Li+ solvation shell was determined to be non-negligible.23,24 Such a preference was consistent with EC-reduction compounds dominating the SEI on graphite.23,25 While interpreting NMR data, however, one has to keep in mind that the chemical shift of a related linear carbonate (EMC or ethyl methyl carbonate) in EMC/MP (methyl propionate) mixtures was very small despite EMC being concluded to participate in the Li+ solvation, thus leaving a possibility that the chemical shift of EMC and DMC is not very sensitive to the Li+ coordination as suggested in a previous publication.17
Raman26 and infrared18 (IR) spectroscopy studies indicated a somewhat quantitatively different picture of the Li+ solvation shell composition from NMR measurements. Specifically, a substantial contribution from both EC or PC and DMC to the Li+ solvation shell was found in Raman and IR experiments.18,26 Moreover, at high LiPF6 salt concentration interpretation of IR spectra indicated that PC and DMC contributed equally to the Li+ solvation shell.18 Beguilingly, analysis of Raman data26 indicated a noticeably larger preference for EC vs. DMC than the interpretation of IR experiments raising questions regarding the accuracy of both techniques and the source of discrepancy.18
The goal of this contribution is to provide additional evidence from QC and ab initio MD simulations to the picture of the Li+ solvation for the mixed solvent EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC(1
DMC(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mol ratio)–LiPF6 technologically important electrolytes. In our study, we build upon a large number of experimental,3,22,27–45 QC46–53 and simulation47,54–65 studies of Li+ solvation. While most of the previous QC studies focused on obtaining an understanding of the relative stability of (EC)n(DMC)m–Li+ and (EC)n(DMC)m–LiPF6 clusters in the gas-phase, this study instead focuses on the solvation effects by immersing these clusters in an implicit solvent and performing ab initio MD simulations of liquid EC:DMC–LiPF6 electrolytes with various salt concentrations that explicitly treat both the solvent and salt. Changes in the Raman activities and IR intensities have also been examined in order to gain insight into the reasons behind the different solvation numbers obtained by these techniques.
1 mol ratio)–LiPF6 technologically important electrolytes. In our study, we build upon a large number of experimental,3,22,27–45 QC46–53 and simulation47,54–65 studies of Li+ solvation. While most of the previous QC studies focused on obtaining an understanding of the relative stability of (EC)n(DMC)m–Li+ and (EC)n(DMC)m–LiPF6 clusters in the gas-phase, this study instead focuses on the solvation effects by immersing these clusters in an implicit solvent and performing ab initio MD simulations of liquid EC:DMC–LiPF6 electrolytes with various salt concentrations that explicitly treat both the solvent and salt. Changes in the Raman activities and IR intensities have also been examined in order to gain insight into the reasons behind the different solvation numbers obtained by these techniques.
Simulations methodologies
A. Li+–solvent cluster studies
Binding energies of the (EC)n(DMC)m–Li+ and (EC)n(DMC)m–LiPF6 clusters were calculated using the Gaussian g09 package.66 Integral = ultrafine was used in calculations using the M06-L functional and for the Raman activity calculations using all functionals. Default convergence criteria were used in all of the geometry optimizations.The binding energies of the EC–Li+ and DMC–Li+ complexes from selected DFT functionals are compared in Table 1 with the predictions from the more reliable (but also more computationally expensive) composite G4 method, intermediate G4MP2 method and second order Møller–Plesset perturbation theory (MP2) calculations for the solvent–Li+ geometries shown in Fig. 1. Two DMC cis–cis and cis–trans conformers were examined, denoted in Fig. 1 as DMCcc and DMCct, respectively. Binding energies for all of the DMC-containing complexes were calculated relative to the DMCcc conformer, which is 3.08 kcal mol−1 lower in energy than the DMCct conformer from the G4 level of theory.
| Method | EC–Li+ | DMCcc–Li+ (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ⋯Li) ⋯Li) |
DMCct–Li+ (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ⋯Li) ⋯Li) |
DMCcc–Li+ (b, EO⋯Li) |
|---|---|---|---|---|
| a Tz denotes aug-cc-pvTz basis set. | ||||
| G4 | −48.1 | −41.9 | −45.7 | −39.8 |
| G4MP2 | −47.5 | −41.2 | −45.0 | −39.0 |
| MP2/Tza | −47.8 | −41.3 | −45.3 | −39.6 |
| MP2/6-31+G(d,p) | −47.7 | −40.8 | −45.8 | −41.5 |
| PBE/6-31+G(d,p) | −48.6 | −42.6 | −46.9 | −40.1 |
| PBE/Tza | −50.0 | −44.5 | −48.0 | −40.5 |
| M06-L/6-31+G(d,p) | −47.3 | −40.8 | −45.1 | −37.4 |
| M06-L/Tza | −48.6 | −42.8 | −46.3 | −38.3 |
| B3LYP/6-31+G(d,p) | −50.7 | −44.2 | −48.6 | −41.4 |
| B3LYP/Tza | −52.0 | −46.0 | −49.6 | −41.8 |
| M05-2X/6-31+G(d,p) | −50.8 | −43.6 | −48.3 | −41.6 |
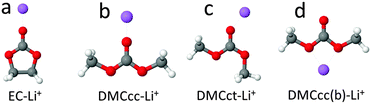 | ||
| Fig. 1 Optimized geometries of EC–Li+ and DMC–Li+ complexes at MP2/Tz level. Element colours: H – white, Li – purple, C – grey, O – red. | ||
Amongst the several DFT functionals investigated, M06-L with larger augmented correlation consistent triple theta aug-cc-pvTz basis set (denoted as Tz) and Perdew–Burke–Ernzerhof (PBE) with 6-31+G(d,p) smaller basis set showed the best agreement with the G4 results which are considered to be the most reliable. M06-L/6-31+G(d,p) calculations slightly underestimated the (EC)–Li+ and (DMC)–Li+ binding energies, while hybrid functionals such as B3LYP and M05-2X predicted binding energies systematically higher than G4, G4MP2 and MP2. Based upon the results from Table 1, a relatively computationally inexpensive PBE/6-31+G(d,p) functional/basis set combination was chosen for further studies of the relative stability of the Li+ coordinated by four solvent molecules and LiPF6 coordinated by three solvent molecules with and without a polarized continuum surrounding the solvate clusters. Select calculations were also performed using MP2/6-31+G(d,p) and M05-2X/6-31+G(d,p) because dispersion interactions between the solvent molecules are often adequately represented by these methods, while the PBE functional often does not adequately describe dispersion interactions. The influence of dispersion interactions on the stability of selected (solvent)4–Li+ clusters was further investigated by including empirical dispersion parameters via the D2 and D3 versions of Grimme's dispersion damping function.67
B. BOMD simulations of liquid electrolytes
In a set of separate simulations using the Vienna ab initio Simulation Package (VASP), Born Oppenheimer molecular dynamics (BOMD) simulations of fixed density, via the NVT ensemble, were run to gain insight into the solvation structure of a Li+ cation in the EC:DMC mixture. We performed BOMD simulations of bulk EC:DMC mixtures with LiPF6 using VASP. The PBE-GGA exchange–correlation functional was used with PAWs following the methodology of a previous study of single solvent electrolytes.68 Simulations were performed at a temperature of 400 K for 26 molecules of EC:DMC corresponding to a density of 1.24 g ml−1, close to the experimental density (∼1.3 g ml−1). A single dissociated LiPF6 was used within the solvent mixture. BOMD simulations were carried out for 35 ps, starting from five different types of Li+ cation coordination configurations, i.e., (EC)(4−n)(DMC)n for n = 0–4. A single k-point (the gamma point) and a plane-wave cutoff of 300 eV were used. A Nose-thermostat was used for the NVT simulation. A histogram of PBE-DFT total energies was constructed from 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 snapshots of a 15 ns long trajectory generated using the APPLE&P force-field17 at 400 K for an EC
000 snapshots of a 15 ns long trajectory generated using the APPLE&P force-field17 at 400 K for an EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC (1
DMC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) mixture with a single Li+ cation in solution. Local Li+ cation coordination shell structures were identified by counting the closest four solvent molecules to the Li+ cation in the solvent mixture. The partial radial distribution function was computed using standard definitions, smoothed with a normalized Gaussian of 0.05 Å width.
1) mixture with a single Li+ cation in solution. Local Li+ cation coordination shell structures were identified by counting the closest four solvent molecules to the Li+ cation in the solvent mixture. The partial radial distribution function was computed using standard definitions, smoothed with a normalized Gaussian of 0.05 Å width.
BOMD simulations were also performed for EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC(1
DMC(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1)–LiPF6 electrolytes using CP2K/QUICKSTEP program at two additional salt concentrations: low salt concentration (LC) (EC)15(DMC)15–(LiPF6)3 with molality m = 1.12 and high salt concentration (HC) (EC)16(DMC)16–(LiPF6)9m = 3.16 at 393 K. BOMD simulations were performed using a hybrid Gaussian and Plane Wave (GPW) density functional scheme. It has a dual representation combining a basis of atom centred Gaussian orbitals to describe the system wavefunction and an auxiliary plane wave basis set to describe the electronic density.
1)–LiPF6 electrolytes using CP2K/QUICKSTEP program at two additional salt concentrations: low salt concentration (LC) (EC)15(DMC)15–(LiPF6)3 with molality m = 1.12 and high salt concentration (HC) (EC)16(DMC)16–(LiPF6)9m = 3.16 at 393 K. BOMD simulations were performed using a hybrid Gaussian and Plane Wave (GPW) density functional scheme. It has a dual representation combining a basis of atom centred Gaussian orbitals to describe the system wavefunction and an auxiliary plane wave basis set to describe the electronic density.
Initial electrolyte configurations for the BOMD simulations were taken from MD simulations using the APPLE&P polarizable force field.17 Both LC and HC salt concentrations were simulated using the PBE functional in the isobaric–isothermal ensemble (NPT) at 1 bar with periodic boundary conditions applied to all three dimensions. We employed a 500 Ry density grid for all NPT simulations. The Nose–Hoover thermostat was applied to all degrees of freedom using a time constant of 1 ps in conjunction with a barostat time constant of 1 ps. The nuclear equations of motion have been integrated using Tuckerman approach based on the Martyna–Tobias–Klein (MTK) algorithm69 with a 1.0 fs time step and hydrogen masses.
A total of 20 ps of NPT simulation time was obtained for the LC system and 38 ps for the HC mixture. Since the energy (energy vs. time) exhibited changes over the first 4 ps of the NPT simulation run, the first 4 ps of the simulation trajectory were discarded with the remaining trajectory used for analysis unless otherwise noted. The differences between the radial distribution functions (RDFs) from the first and second parts of MD trajectories are shown in ESI.† In order to examine the influence of adding an empirical dispersion (D3 without C9 term) to the PBE functional on the Li+ solvation shell composition, a separate set of BOMD simulations were performed for LC electrolyte in the NVT ensemble for 27 ps using the electrolyte density obtained from classical MD simulations using the APPLE&P polarizable force field. Additional details of BOMD simulations are given in ESI.†
Results and discussion
A. Quantum chemistry studies of clusters
A comparison of the EC–Li+ and DMC–Li+ binding energies from the DFT calculations with the most computationally expensive and most reliable (among the methods used in this work) G4 calculations is shown in Table 1. This indicates that commonly used hybrid density functionals such as B3LYP or M05-2X tend to overestimate the solvent–Li+ binding energies, especially if a large aug-cc-pvTz (denoted as Tz) basis set is used. Previous studies of binding energies for the LiFSI, LiTFSI and LiBF4 salts using B3LYP in conjunction with a smaller 6-31+G(d,p) basis set also reported better agreement with complete basis set extrapolated MP2 results than for predictions from B3LYP using a larger basis set aug-cc-pvTz.70 The best agreement observed in this study is between the G4 and the MP2 or M06-L predictions using a large basis set aug-cc-pvTz in accord with conclusions from previous studies of solvent–Li+ and anion–Li+ binding energies.17,70,71 It is also important that the solvent–Li+ binding energies are adequately predicted using the PBE functional, as this functional was chosen in this study for the examination of the relative stability of the Li+ solvates, as well as in the BOMD simulations of the liquid electrolytes.An examination of the EC–Li+ and DMC–Li+ binding energies shows that the DMCct–Li+ complex with DMC having the cis–trans conformation is the most stable amongst the DMC–Li+ complexes, i.e., it has only a 2.4 kcal mol−1 lower binding energy than the EC–Li+ complex from the G4 calculations. The DMCcc–Li+ complex is less stable than the DMCct–Li+ complex due to the much smaller dipole moment of the former. Interestingly, the Li+ binding to both of the noncarbonyl ether-like oxygens denoted as EO of DMCcc (i.e., DMCcc(b)–Li+ in Fig. 1d) is only 2.2 kcal mol−1 less stable than the DMCcc–Li+ complex where the Li+ is bound to the carbonyl oxygen.
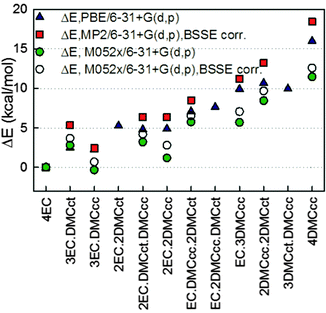
The total binding energy of the (EC)n(DMC)m–Li+ (n + m = 4) complexes relative to EC4–Li+ is shown in Fig. 2. A comparison of the solvates with EC vs. DMC indicates that in the four solvent-coordinated clusters, substitution of EC with DMCcc has an energetic penalty less than 5 kcal mol−1 per solvent molecule with the penalty being substantially less for a few complexes such as (EC)3(DMCcc)–Li+ and (EC)2(DMCcc)2–Li+. This indicates that the EC and DMC interactions with the neighbouring molecules in the four solvent-coordinated Li+ complexes stabilize the (EC)3(DMCcc)–Li+ binding vs. (EC)4–Li+ largely due to a smaller dipole–dipole repulsion between the relatively non-polar DMCcc with EC vs. the highly polar EC with EC. Despite the higher binding energy of DMCct–Li+ as compared to DMCcc–Li+, the (EC)n(DMC)m–Li+ (n + m = 4, n = 1–3), complexes with DMCcc tend to be more stable than the analogous complexes with DMCct. Again, we attribute this to a smaller dipole–dipole repulsion between the relatively non-polar DMCcc vs. the highly polar DMCct conformer with EC solvent molecules in the first solvation shell of the Li+.
A further examination of the binding energies shown in Fig. 2 obtained from different calculations indicates that the M05-2X results predict a larger stabilization of the DMCcc containing complexes relative to the MP2 and PBE predictions. Based upon the better agreement between the PBE and MP2 calculations with the G4 results for EC–Li+ and DMC–Li+ (Table 1), we have a higher confidence in the PBE and MP2 results (as compared to M05-2X) for the relative cluster stabilities. A comparison of the relative binding energies with basis set superposition correction (BSSE) and without it indicates that inclusion of the BSSE correction has a minor effect on the relative binding energies and results in slightly more positive binding energies relative to (EC)4–Li+.
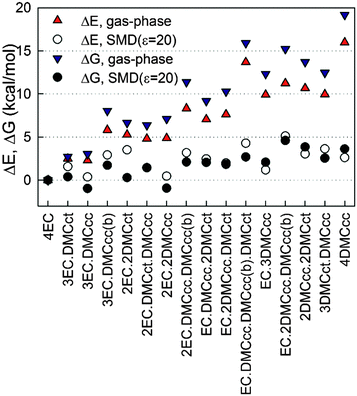
Next, the influence of solvent from the Li+ second solvation shell (and beyond) on the relative stability of the solvates was investigated by utilizing the implicit solvent model SMD as implemented in the g09 package. The relative cluster binding energies in the gas-phase and when immersed in implicit solvent are shown in Fig. 3. A dielectric constant of ε = 20 was chosen for this investigation, as it is representative of the environment in common mixed carbonate electrolytes. Inclusion of the implicit solvent beyond the cation's first solvation shell significantly changes the relative solvate binding energies, thus stabilizing the DMC-containing solvates vs. (EC)4–Li+. In particular, the (EC)2(DMCcc)2–Li+ and (EC)3(DMCcc)1–Li+ solvates become as stable or even slightly more stable (for ΔG) than the (EC)4–Li+ solvate as a result of immersing the solvates in the implicit solvent. Interestingly, the (EC)n(DMC)m–Li+ (n + m = 4) solvates containing a DMCcc conformer tend to have a lower or similar relative total binding energy as compared to the solvates containing a DMCct conformer. This trend is the opposite of what was observed for the binding energy of the gas-phase DMCct–Li+ and DMCcc–Li+ complexes (Table 1), indicating that the DMCcc and DMCct interactions with the other solvents in the first solvation shell and beyond are important for determining cluster relative stability. This is unfortunate from the prospective of high throughput prediction of the Li+ solvate compositions because it indicates that the binding energies between the Li+ and one solvent in the gas-phase are likely to be unreliable predictors of the populations of this solvent in the Li+ first solvation shell in bulk electrolytes. Due to a very low population of the DMCct conformer in liquid DMC19 without a lithium salt (a few percent), the fraction of DMCct vs. DMCcc in the first Li+ solvation shell is expected to be higher when compared to the pure DMC liquid (without salt), in agreement with conclusions from the Raman study of DMC–LiAsF6 electrolytes.19,72
An estimate of the population of EC and DMC in the Li+ solvation shell at room temperature by weighting the Li+ solvates shown in Fig. 3 by Boltzmann factors yielded a ratio of 1.9 to 1 for EC to DMC. Inclusion of empirical dispersion via the Grimme D2 and D3 method67,73 resulted in a slight stabilization of most of the (EC)n(DMC)m–Li+ solvates relative to (EC)4–Li+, as shown in Fig. S4 and Table S1 in the ESI.† The (EC)n(DMC)m–Li+ solvates with the higher DMC fraction tend to be stabilized more than solvates with 1 or 2 DMC. Interestingly, application of the D3 empirical dispersion correction that considers triplets of atoms to account for three-body effects tends to result in the larger stabilization of (EC)n(DMC)m–Li+ solvates relative to (EC)4–Li+ than application of the D2 empirical dispersion that considers only pairs of atoms. Thus, one would expect that its inclusion in the explicit solvent simulations would lead to higher population of DMC vs. EC in the Li+ first solvation shell.
A careful examination of Fig. 3 indicates that while solvates with a Li+ bound to EO (non-carbonyl oxygens), denoted as DMCcc(b) in Fig. 3, are higher in energy than the corresponding solvates with a Li+ bound to a carbonyl oxygen, the energy difference tends to be around 2–4 kcal mol−1, as summarized in Table 2. Inclusion of SMD implicit solvent around the clusters also tends to decrease the energy difference between the solvates with a Li+ coordinated by a DMC via EO as compared to the solvates where a Li+ is coordinated by a DMCcc via the carbonyl oxygen, thereby increasing the population of the former in the condensed phase. If one assumes an average energy difference between EO and carbonyl oxygen binding to be around 2 kcal mol−1, populations of DMCcc(b, EO⋯Li+) bound to a Li+ would be on the order of 4% of the total complexed DMCcc solvent molecules.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ⋯Li)
⋯Li)
| Initial cluster | ε = 1 | ε = 20 | ||
|---|---|---|---|---|
| ΔE | ΔG | ΔE | ΔG | |
| (EC)3(DMCcc)–Li+ | 3.5 | 5.0 | 2.5 | 2.7 |
| (EC)2(DMCcc)2–Li+ | 3.4 | 4.3 | 3.2 | 2.1 |
| (EC)(DMCcc)2(DMCct)–Li+ | 3.8 | 3.6 | 3.1 | 0.6 |
| (EC)(DMCcc)3–Li+ | 3.6 | 4.9 | 3.9 | 2.5 |
The influence of the magnitude of the dielectric constant of the implicit solvent surrounding the solvates was also investigated (Fig. 4) in order to understand how solvate stabilization changes as the relative amounts of the cyclic and linear carbonate solvents vary in the system. Solvate geometry optimized at ε = 20 was used for the single point energy calculations for SMD models with ε = 3.0473 (dibutyl ether), ε = 8.1781 (tributyl phosphate) and ε = 78 (water) using default g09 parameters. An increase of the dielectric constant stabilizes all solvates relative to (EC)4–Li+ resulting in an increase in the DMC population in the solvates with increasing dielectric constant relative to what would be expected from a random contribution that is proportional to solvent composition. This effect largely saturates for ε > 20. While all of the curves monotonically decay with increasing ε in Fig. 4, a larger decay was observed for the solvates containing DMCcc than for the solvates containing DMCct.
 | ||
| Fig. 4 Relative energy vs. (EC)4–Li+ cluster as a function of the dielectric constant of the surrounding solvent. | ||
Due to significant ion pairing in the mixed solvent electrolytes, especially those with a high DMC content, it is important to also examine how the presence of the PF6− anion near a Li+ influences the relative stability of the (EC)n(DMC)m–LiPF6 solvates. Fig. 5 compares the relative binding free energies of solvates with and without a PF6− bound to a Li+ as a function of EC mole fraction (xEC). Only solvates containing the DMCcc conformer were examined as they tend to have a lower energy, with the exception of (DMC)4–Li+. For the contact ion pair solvates, the (EC)2(DMCcc)–LiPF6 complex appears to be the most energetically stable at xEC = 0.66, followed by (EC)3–LiPF6 and (EC)(DMCcc)2–LiPF6. Due to the small energy differences between these three solvates relative to the thermal energy at room temperature (kBT ∼ 0.6 kcal mol−1), all of these are expected to have significant populations present within an electrolyte. Overall, the (EC)n(DMCcc)m–LiPF6 solvates have similar or slightly lower relative energies vs. (EC)3–LiPF6 for similar xEC values, when compared to the relative stabilities of (EC)n(DMCcc)m–Li+vs. (EC)4–Li+, indicating that a similar or even a slightly higher fraction of DMC vs. EC is to be expected for electrolytes in the regime where ion pairing is significant.
 | ||
| Fig. 5 Free energies (ΔG) relative to the (EC)4–Li+ cluster and (EC)3LiPF6 from PBE/6-31+G(d,p), SMD(ε = 20) calculations. | ||
B. Analysis of solvate vibrational bands
The following considerations were undertaken in an effort to reconcile the apparent discrepancies in the relative populations of EC and DMC in the Li+ first solvation shell in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC (1
DMC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 vol/vol) doped with the LiPF6 salt as determined by infrared (IR) and Raman spectroscopic studies.18,26 Specifically, the previous analysis of the EC and DMC Raman vibrational bands near 900 and 920 cm−1 for the uncoordinated solvent and solvent coordinated to a Li+ resulted in the conclusion that there is a rather strong preference for EC vs. DMC coordination, i.e., for a 1 M LiPF6 salt concentration, 3 EC and 1.1 DMC were reported to coordinate a Li+ on average. In contrast, the analysis of IR vibrational bands for the C
1 vol/vol) doped with the LiPF6 salt as determined by infrared (IR) and Raman spectroscopic studies.18,26 Specifically, the previous analysis of the EC and DMC Raman vibrational bands near 900 and 920 cm−1 for the uncoordinated solvent and solvent coordinated to a Li+ resulted in the conclusion that there is a rather strong preference for EC vs. DMC coordination, i.e., for a 1 M LiPF6 salt concentration, 3 EC and 1.1 DMC were reported to coordinate a Li+ on average. In contrast, the analysis of IR vibrational bands for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch mode in PC
O stretch mode in PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC (1
DMC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 vol/vol) doped with LiPF6 indicated a much more similar contribution from PC and DMC to the Li+ solvation shell. As PC prefers to coordinate Li+ to a similar extent18 or even to a slightly greater extent5 than EC, the IR results do not quantitatively agree with the analysis of the Raman data.
1 vol/vol) doped with LiPF6 indicated a much more similar contribution from PC and DMC to the Li+ solvation shell. As PC prefers to coordinate Li+ to a similar extent18 or even to a slightly greater extent5 than EC, the IR results do not quantitatively agree with the analysis of the Raman data.
An analysis of the vibrational band changes due to solvent–Li+ coordination in the gas-phase was shown to significantly exaggerate the shifts of the vibrational bands.55 Increasing the representative cluster size55 or immersing the cluster in an implicit solvent74 in order to better mimic condensed phase effects resulted in an improved prediction of vibrational spectra changes. Changes in the EC and DMC bands around 900 and 1800 cm−1 upon Li+ coordination are given in the ESI† and Table 3 for a single solvent molecule bound to a Li+, as well as for the Li+ coordinated by four solvent molecules surrounded by implicit solvent. The data for the (EC)n(DMC)m–Li+ (n + m = 4) clusters were averaged over 11 low energy clusters from Fig. 3, with inclusion of four clusters with (DMCcc(b))–Li+ where the Li+ is coordinating by EO. Reported frequencies were scaled uniformly by a factor of 1.02 from DFT results, which is very close to the commonly used values for PBE functional of 1.025–1.028.75 The shift upon coordination of the EC Raman active band at 894 cm−1 for both EC–Li+ and (EC)n(DMC)m–Li+ is quite similar, 11 cm−1, and is in excellent agreement with experiments for EC:DMC–LiPF6 electrolyte26 and EC doped with numerous other salts.74 All of the DMC band shifts due to Li+ coordination, however, were significantly larger for the DMC–Li+ complexes as compared to the four solvent-coordinated clusters, indicating that solvent–solvent interactions within the cluster influence the vibrational band positions. Similarly, changes in the Raman activity and IR intensity were also different for the single solvent and the four solvent-coordinated solvates. Nevertheless, the trend indicating that the Raman activity of EC increases by ∼20% relative to that for DMCcc upon Li+ coordination is consistent for both the (solvent)–Li+ and (solvent)4–Li+ complexes.
| ν 0 | Raman | ν 0 | IR | |||
|---|---|---|---|---|---|---|
| Δν | a c/a0 | Δν | I c/I0 | |||
| EC–Li+ and DMC–Li+ | ||||||
| EC | 894 | 11 | 1.01 | 1818 | −49 | 1.16 |
DMCcc (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ⋯Li) ⋯Li) |
918 | 29 | 0.81 | 1760 | −44 | 1.21 |
| DMCcc(b)(EO⋯Li) | −10 | 0.84 | 78 | 1.03 | ||
| DMCct | 860 | 20 | 0.85 | 1766 | −49 | 1.13 |
| (EC)n(DMC)m–Li+ for n + m = 4 | ||||||
| EC | 894 | 11 | 1.18 | 1818 | −28 | 1.04 |
DMCcc (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ⋯Li) ⋯Li) |
918 | 14 | 1.01 | 1760 | −26 | 1.37 |
| DMCcc(b)(EO⋯Li) | −4 | 1.01 | 27 | 0.94 | ||
| DMCct | 860 | 15 | 1.19 | 1766 | −27 | 1.42 |
The shifts of the EC, DMCct and DMCcc bands upon Li+ coordination via the carbonyl oxygen from the analysis of the (solvent)4–Li+ solvates were found to be in excellent agreement with results from Infrared (IR)18 and Raman19,26 spectroscopy studies, indicating that inclusion of the complete first solvation shell surrounded by implicit solvent yields a sufficiently accurate model for the analysis of vibrational frequency shifts. Interestingly, the (DMCct)–Li+ Raman band is located at lower frequencies and close to uncomplexed EC, whereas the coordinated and uncoordinated DMCcc bands have higher frequencies than the coordinated EC. Therefore, the coordinated DMCct conformers were not taken into account in the previous analysis of the Raman spectra of the EC:DMC–LiPF6 mixed electrolytes,26 indicating that the experimentally reported DMC–Li+ coordination number is due only to the DMCcc contribution and additional errors may contribute to the EC–Li+ coordination number. Analysis of the changes in the EC Raman activity ratio upon Li+ coordination indicates that it increases by 17% relative to the increase of the Raman activity for the coordinated DMCcc, suggesting that the EC coordination numbers extracted from the Raman measurements using this vibrational band need to scaled by 17% in order to obtain the correct ratio of EC to DMC in the Li+ first solvation shell. Even scaling the data by 17%, however, will not account for DMCct–Li+ coordination and solvates where DMCcc is bound to the Li+via EO because the latter coordination has a band situated essentially under the dominant uncomplexed DMCcc band.
A similar analysis of the IR active C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibrational band indicated that DMCct and DMCcc conformers bound to the Li+via the carbonyl oxygen have very similar shifts due to Li+ coordination, thus the IR analysis included both DMCcc and DMCct in the number of DMC coordinating the Li+ cations with the exception of DMCcc bound to a Li+via EO. The latter complex has a positive (blue) shift due to Li+ coordination unlike the negative (red) shift observed for the DMCcc bound to a Li+via the carbonyl oxygen. In fact, the experimentally observed IR spectrum shown in Fig. 1c in Seo et al.18 for DMC–LiPF6 electrolytes clearly showed a peak increasing with increasing salt concentration (up to 1.2–1.8 M of LiPF6) in the location of the peak due to DMCcc(b, EO⋯Li+)–Li+ coordination. A further increase in the salt concentration, however, resulted in the disappearance of this peak. This is expected as, at high salt concentration, most of the DMC molecules will be coordinated to Li+via all of the available binding cites and DMC bound to Li+via EO are much more likely to be also be bound to another neighboring Li+via the carbonyl oxygen similar to the coordination shown in Fig. 6 in which the DMC simultaneously binds to two Li+ cations via EO and carbonyl oxygens in highly concentrated DMC/lithium difluoro(oxalato)borate (LiDFOB) electrolytes.76 Similar coordination was also observed in the (DMC)1/4:LiBF4 solvate indicating that it might be a common feature of the highly concentrated DMC-based electrolytes.77
O vibrational band indicated that DMCct and DMCcc conformers bound to the Li+via the carbonyl oxygen have very similar shifts due to Li+ coordination, thus the IR analysis included both DMCcc and DMCct in the number of DMC coordinating the Li+ cations with the exception of DMCcc bound to a Li+via EO. The latter complex has a positive (blue) shift due to Li+ coordination unlike the negative (red) shift observed for the DMCcc bound to a Li+via the carbonyl oxygen. In fact, the experimentally observed IR spectrum shown in Fig. 1c in Seo et al.18 for DMC–LiPF6 electrolytes clearly showed a peak increasing with increasing salt concentration (up to 1.2–1.8 M of LiPF6) in the location of the peak due to DMCcc(b, EO⋯Li+)–Li+ coordination. A further increase in the salt concentration, however, resulted in the disappearance of this peak. This is expected as, at high salt concentration, most of the DMC molecules will be coordinated to Li+via all of the available binding cites and DMC bound to Li+via EO are much more likely to be also be bound to another neighboring Li+via the carbonyl oxygen similar to the coordination shown in Fig. 6 in which the DMC simultaneously binds to two Li+ cations via EO and carbonyl oxygens in highly concentrated DMC/lithium difluoro(oxalato)borate (LiDFOB) electrolytes.76 Similar coordination was also observed in the (DMC)1/4:LiBF4 solvate indicating that it might be a common feature of the highly concentrated DMC-based electrolytes.77
Analysis of the IR scattering intensities indicated that the DMC scattering intensity increases more than the EC intensity upon coordination. This fact, together with the opposite trend for the Raman intensities for the bands around 900 cm−1 and the observation that the previous Raman analysis did not include the coordinated DMCct contribution to the solvation number—while the IR analysis did, provides an explanation for the discrepancies noted between the EC and DMC contributions to the cation coordination extracted from the Raman and IR experiments.
C. Li+ solvation at infinite dilution from BOMD simulations
The energy histograms for the most probable Li+ solvates in EC:DMC–LiPF6 electrolytes are shown in Fig. 7. The energies were computed at the PBE-DFT level for geometries generated using the APPLE&P force field.17 The histograms are strongly overlapping for all of the different configurations, especially for those with 1–3 EC molecules in the first solvation shell. The total energy histograms are proportional to the energy density-of-states (∼Ω(E)). Because one can relate the entropy difference between two different types of solvation shell configurations to the ratio of these histograms:strongly overlapping histograms suggest that the different configurations have very similar entropy at the simulation temperature. But configurations with lower energy tails in the energy histogram exhibit a larger residence time because they are energetically favorable:
F(T) ∼ −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Log Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ω(E) + E Ω(E) + E |
 | ||
| Fig. 7 PBE-DFT computed energy histograms for configurations with different Li-ion solvation shell structure generated using polarizable force-field based MD at 400 K. | ||
From Fig. 7, for the EC:DMC mixture, configurations with high density of states at lower energies are those with (EC)3(DMC)–Li+ indicating that this is expected to be the most stable solvate at low temperatures. At higher temperatures, the (EC)2(DMC)2–Li+ and (EC)4–Li+ solvates are expected to be significantly populated.
We also performed BOMD simulations starting with the Li+ in different types of solvation shell structures. As expected from the histogram analysis and classical simulations, the solvation shell was highly dynamic and varied over time. For a particular simulation where the Li+ solvation shell was dominated by the (EC)3(DMC)–Li+ or (EC)2(DMC)2–Li+ solvates, multiple conversions between these two solvates were observed during the MD simulation run. A Li+ diffusion coefficient was extracted from a 35 ps long NVT simulation at 400 K and the mean squared displacement (MSD) shown in the ESI.† The almost linear behavior of the MSD suggests that the Li+ is in a diffusive state throughout the run time and did not recombine with the PF6− counter anion in solution. The diffusion coefficient was calculated to be 30.0 × 10−10 m2 s−1 at 400 K, which is slightly higher than the extrapolated value of the Li+ diffusion coefficient (9.4 × 10−10 m2 s−1) for an EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC(1
DMC(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 vol/vol) 1 M LiPF6 electrolyte extracted from NMR measurements.78 The average Li+–carbonyl oxygen radial distribution function showed a first peak at 1.92 Å in accord with CP2K BOMD simulations for other concentrations as discussed below and in agreement with previous BOMD results for EC–LiPF6 electrolytes.68,79 Those BOMD simulations starting from the less favorable (EC)(DMC)3–Li+ configuration for the Li+ solvation shell resulted in the Li+ recombining with PF6− to form a solvated LiPF6 contact ion pair, which remained stable for most of the simulation run. This suggests that the first solvation shell structure is important for screening the Li+ from the counter anion and any recombination would be more likely to be followed by an initial dynamical change to the first solvation shell structure with an increased DMC composition that would reduce the local dielectric constant, thereby reducing the electrostatic screening. It also suggests that contact ion pairs may have a higher number of coordinated DMC molecules than for fully solvated Li+ cations.
1 vol/vol) 1 M LiPF6 electrolyte extracted from NMR measurements.78 The average Li+–carbonyl oxygen radial distribution function showed a first peak at 1.92 Å in accord with CP2K BOMD simulations for other concentrations as discussed below and in agreement with previous BOMD results for EC–LiPF6 electrolytes.68,79 Those BOMD simulations starting from the less favorable (EC)(DMC)3–Li+ configuration for the Li+ solvation shell resulted in the Li+ recombining with PF6− to form a solvated LiPF6 contact ion pair, which remained stable for most of the simulation run. This suggests that the first solvation shell structure is important for screening the Li+ from the counter anion and any recombination would be more likely to be followed by an initial dynamical change to the first solvation shell structure with an increased DMC composition that would reduce the local dielectric constant, thereby reducing the electrostatic screening. It also suggests that contact ion pairs may have a higher number of coordinated DMC molecules than for fully solvated Li+ cations.
For the BOMD simulations that started with (EC)4–Li+, the solvation shell quickly rearranged to form the more stable (EC)2(DMC)2–Li+ and (EC)3(DMC)–Li+ dynamically over the remaining part of the trajectory. The MSD from all of these independent BOMD simulation runs that did not show the formation of LiPF6 contact ion pairs are very similar, suggesting that the MD runs are sufficiently long for the near-Li+ structure of the electrolyte to fully equilibrate in this infinite dilution limit. These simulations also suggest that the overall Li+ diffusion in this mixture is dominated by (EC)3(DMC)–Li+ and (EC)2(DMC)2–Li+ solvates.
An inspection of the Li+ motion shown in Fig. 8a suggests that while the Li+ motion was Gaussian-like in pure solvents such as EC, in solvent mixtures there are intermittent flights of long diffusive jumps from one solvation cage to the other between such Gaussian rattling motions. The jumps are accompanied most times by a change in the solvation shell composition. As such, in solvent mixtures there are two types of motion that dominate Li+ diffusion: (1) a carrier-based diffusion (i.e., Li+ trapped in a solvation shell) and (2) a jump diffusion (i.e., jumping from one solvation shell configuration to another).61,80 Such a two-component diffusion could be expected to lead to faster diffusion compared to a purely carrier-based diffusion as was previously observed in pure solvents such as EC.68
 | ||
| Fig. 8 The overlapped trajectories of Li-ion from our 35 ps long EC:DMC/LiPF6 simulation with those in EC/LiPF6,68 (a) and the distribution of Li displacement in a δt = 1 fs time interval (b). A heavy tail in this distribution is seen for mixtures, corresponding to the long intermittent flights (b). | ||
To identify the distribution associated with the diffusion process, we looked at the distribution of displacements by the Li+ in a fixed time interval δt. The distribution is compared between the pure EC and the EC:DMC mixture for an interval of δt = 1 fs in Fig. 8b. It shows a heavy tail in the case of the mixtures, not seen in the pure EC simulation. A similar distribution is seen for any choice of δt (not shown). This is suggestive of a Lévy flight motion.81 Indeed, Lévy flights include long intermittent jumps. While such motions are usually seen to be due to cooperative motion, in our case such intermittent flights are due to the large anisotropy in the local dielectric constant, expected in a mixture of EC and DMC, where EC has a large dielectric constant of ∼90, whereas DMC has a dielectric constant of ∼3. In fact, systems with very high anisotropy have shown such Lévy type paths, e.g., ionically conducting alkali-metal silicate glasses82 and ionic-liquids.83,84
D. Li+ solvation as a function of concentration
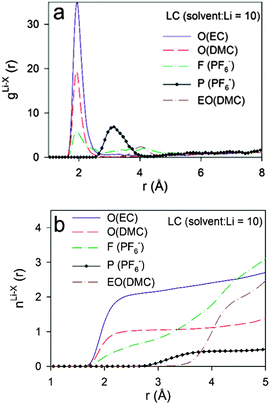
The Li+ solvation shell compositions in the low (LC, solvent:Li = 10) and high (HC, solvent:Li = 3.56) LiPF6 salt concentrations from the BOMD simulations using the PBE functional were examined via RDFs and running coordination numbers (CDN), as shown in Fig. 9 and 10, respectively. We initially focused on the Li+ coordination by the carbonyl oxygens of EC and DMC, noncarbonyl oxygens of DMC and fluorine atoms from the PF6− anion.At LC, the RDFs indicate a significantly higher probability to find carbonyl oxygens from EC rather than from DMC in the Li+ first coordination shell due to the higher magnitude of the first RDF peak located at 1.90–1.95 Å. The first Li–F RDF peak is also located at 1.95 Å, but this is much smaller in magnitude than both of the Li–O peaks indicating that the probability of finding a F(PF6−) atom coordinating a Li+ is approximately 6 and 3 times lower than the carbonyl oxygens from EC and DMC, respectively. Slightly larger intermolecular distances of 2.03–2.08 Å were reported from neutron diffraction with isotopic substitution (NDIS) experiments for Li–O and Li–F in a DMC–LiPF6 electrolyte and Li–O in a PC–LiPF6 electrolyte.45,85 The position of the first Li–P peak is at 3.10 Å. This distance lies between the distances of 2.68 Å and 3.45 Å that correspond to optimized LiPF6 geometries with C2V point group symmetry (bidentate binding) and C4V point group symmetry (monodentate binding, Li⋯F–P angle of 180°).80
The running Li+ solvation numbers shown in Fig. 9b indicate that there are twice as many oxygens from EC relative to DMC in the Li+ first solvation shell. Based upon the RDF and CDN plots, we define the first solvation shell radius as 2.80 Å. Solvation numbers for this cutoff are summarized in Table 4. There is essentially no (<0.07) contribution from EO of DMC to the Li+ first solvation shell. There are 0.72 fluorine atoms from PF6− anions in the solvation shell indicating that at least 28% of the Li+ are “free” cations that do not have coordinated anions. Scrutiny of the RDFs for the HC electrolyte indicates a higher contribution from DMC than from EC to the Li+ first solvation shell. This is a surprising result. However, it is similar to the trend obtained from IR measurements which indicated that the ratio of solvated DMC to solvated cyclic carbonate solvent increases with increasing LiPF6 salt concentration, albeit less dramatically than the BOMD simulations predict. This trend is rationalized by the observation that, for salt concentrations containing less than four solvent molecules per Li+, most of the solvent is participating in the cation solvation. At high concentrations, a small fraction of the DMC becomes coordinated to more than one Li+, similar to the coordination shown in Fig. 6. Such structures provide two Li+ coordination sites per solvent instead of the single coordination site from EC and this may lead to more extensive Li+ solvation for the ultra-high concentration.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC(1
DMC(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mol%)–LiPF6, (solvent:Li = 10) intensity and composition corrected data compared with the interpolated Raman experimental data26
1 mol%)–LiPF6, (solvent:Li = 10) intensity and composition corrected data compared with the interpolated Raman experimental data26
EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC(1 DMC(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mol%)–LiPF6 1 mol%)–LiPF6 |
EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC(1 DMC(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 vol%)–LiPF6 1 vol%)–LiPF6 |
||||
|---|---|---|---|---|---|
| Raw data | Intensity corrected | Raman | |||
| PBE + D3 | PBE | PBE + D3 | PBE | ||
| EC | 1.79 | 2.13 | 2.88 | 3.43 | 2.8 |
| DMC | 1.12 | 1.05 | 0.83 | 0.78 | 1.2 |
Analysis of the PF6−Li+ binding within the HC simulation shows that 2.10 F and 1.65 P (within 4.75 Å) participate in the first solvation of the Li+ cations, indicating that 75% of the anions exhibit monodentate binding to the Li+ and 25% exhibit bidentate binding in accord with the previous comparison of Li–P distance vs. LiPF6 binding patterns.86 The influence on the composition of the Li+ solvation shell of the empirical dispersion addition to the PBE functional was examined by comparing the RDFs and CDNs from the simulations using the PBE + D3 method (Fig. 11) with the results for simulation runs employing the PBE functional shown in Fig. 9. Addition of the D3 dispersion correction leads to a slightly smaller contribution from EC and a slightly larger contribution from DMC to the Li+ first solvation shell. This behaviour is consistent with the observations for the (EC)n(DMC)m–Li+ clusters immersed in an implicit solvent noted above, which showed a slight stabilization of the complexes containing DMC molecules relative to the (EC)4–Li+ complex. We also observe a slightly larger Li–F coordination number resulting in a higher LiPF6 contact ion pairing as a result of the inclusion of the empirical dispersion correction. These trends are also in accord with the reduction of the first Li⋯O(EC) RDF peak after including the empirical dispersion (D2) in previous BOMD simulations of EC–LiPF6.68
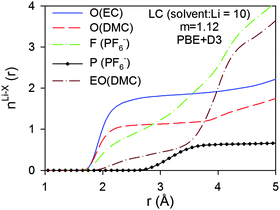 | ||
| Fig. 11 Coordination numbers (n(r)) for LC electrolytes from BOMD simulations using PBE functional. O denotes carbonyl oxygens, EO denotes noncarbonyl oxygens. | ||
It is instructive to compare the Li+ solvation shell compositions obtained from our BOMD simulations with the numbers extracted from Raman experiments using the information about the interpretation of the Raman spectra presented above. In order to perform a head to head comparison, we applied the Raman activity scaling factors from Table 3 to the BOMD simulation results together with the correction for the slight difference in the solvent composition. The Li+ solvation values before and after the corrections are shown in Table 4. Corrected values for the EC solvation number from the PBE + D3 simulations were found to be in excellent agreement with the Raman-derived data. The DMC contribution to the Li+ solvation shell of 0.83 from the PBE + D3 simulations is slightly lower than the experimental value of 1.20. The difference could be due partly to the higher temperature used in the BOMD simulations (393 K) vs. the experiments (298 K) as salt aggregation was previously found to increase and the DMC contribution to the solvation shell to decrease with increasing temperature. We conclude that the PBE + D3 predictions slightly overestimate the ratio of EC to DMC in the Li+ solvation shell, but overall the agreement is quite satisfactory. BOMD simulations without the empirical dispersion correction showed an even higher preference for EC vs. DMC, which is consistent with the stabilization of the (EC)n(DMC)m–Li+ clusters from PBE + D3 vs. PBE calculations as discussed above (see ESI†). We consider predictions from the BOMD simulations using the PBE functional to have a less satisfactory agreement with the Raman data as compared to predictions from the BOMD runs using the PBE + D3 method and thus recommend using the latter for simulation studies of electrolytes for lithium batteries.
Conclusions
Analysis of (EC)n(DMC)m–Li+ (n + m = 1, 4) and (EC)n(DMC)m–LiPF6 (n + m = 3) solvates in the gas-phase and immersed in the implicit solvent modelled via the SMD model in the g09 package have demonstrated a dramatic stabilization of the DMC-containing solvates with the inclusion of the implicit solvent beyond the first solvation shell. In fact, the most stable solvates were (EC)3(DMC)–Li+, (EC)2(DMC)2–Li+ and (EC)4–Li+ after the implicit solvent was included. Increasing the dielectric constant of the implicit solvent resulted in a more pronounced stabilization of the DMC-containing solvates. Detailed analyses of the Li+ binding to DMC uncovered a number of interesting results. Specifically, despite a higher binding energy for (DMCct)–Li+ relative to (DMCcc)–Li+ in the gas-phase (by 3.8 kcal mol−1), the reverse behaviour was observed for (EC)n(DMCcc)m–Li+ solvates surrounded by implicit solvent, where the solvates containing the DMCcc conformer were found to be more stable than the solvates containing the DMCct conformer. A similar conclusion was obtained from the BOMD simulations, where all of the solvent was treated explicitly. Unfortunately, this points to a limitation in extrapolating the solvent–Li+ binding energy correlations from the gas-phase to liquid environments. This result, however, underscores the importance of the solvent–solvent interactions for solvation and solvent packing effects.Changes in the vibrational band positions, Raman activity and IR intensity upon Li+ coordination were examined in the DFT calculations performed on the (EC)n(DMC)m–Li+ (n + m = 1, 4) complexes immersed in implicit solvent. The calculations focused on the Raman bands near 900 cm−1 and the IR band near 1800 cm−1 that are commonly used in the analysis of solvates. The DFT results indicate that the Raman DMCct–Li+ band is located at lower frequencies relative to the pure band of EC and DMC, while the band for the implicitly solvated DMCcc–Li+ complex coordinated via the carbonyl oxygen is located at higher frequencies. The location of the Raman band for the configuration consisting of DMCcc coordinated to a Li+via the noncarbonyl oxygens was essentially the same as the location of the pure band for DMCcc. The Raman activity ratio of EC complexed to Li+ (relative to that of uncoordinated EC) increased by approximately 20%, while the Raman activity for DMC remained essentially unchanged after Li+ coordination. These observations indicate that a previous Raman experimental analysis did not include in the DMC coordination number calculations the coordination for DMCct–Li+ and a portion of DMCcc bound to Li+via EO and, thus, overestimated the EC contribution by more than 20%. A DFT analysis of the changes of the IR spectrum for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibrational band (near 1800 cm−1) indicated that both DMCcc and DMCct bound via the carbonyl oxygen were included in the experimentally determined Li+ solvation numbers, while the contribution to the DMCcc bound to Li+via EO was omitted. An analysis of the IR intensity changes of solvents upon Li+ coordination therefore indicated that IR experiments would tend to slightly overestimate the DMC contribution to the Li+ solvation shell from DMC bound via the carbonyl oxygen. These observations allow us to reconcile the disagreement between the Li+ solvation numbers extracted from the analyses of the previously reported Raman and IR experiments.
O vibrational band (near 1800 cm−1) indicated that both DMCcc and DMCct bound via the carbonyl oxygen were included in the experimentally determined Li+ solvation numbers, while the contribution to the DMCcc bound to Li+via EO was omitted. An analysis of the IR intensity changes of solvents upon Li+ coordination therefore indicated that IR experiments would tend to slightly overestimate the DMC contribution to the Li+ solvation shell from DMC bound via the carbonyl oxygen. These observations allow us to reconcile the disagreement between the Li+ solvation numbers extracted from the analyses of the previously reported Raman and IR experiments.
The BOMD simulations also indicated that both EC and DMC contribute to the Li+ solvation shell with a preference for EC in the dilute electrolyte and a slight preference for DMC in the highly concentrated electrolyte. The application of the correction factors for the Raman activity derived from the DFT studies of the (EC)n(DMC)m–Li+ (n + m = 1, 4) clusters to the BOMD simulations of the EC:DMC–LiPF6 (solvent:Li = 10) electrolyte yielded an EC solvation number in excellent agreement with the Raman data if empirical dispersion was added to the PBE functional. The Li+ solvation number for DMC, however, was found to be slightly lower than the Raman-based solvation number for PBE simulations without empirical dispersion. The preference for EC over DMC to solvate a Li+ cation, in addition to the higher reduction potential of EC–Li+vs. DMCcc–Li+ obtained from the QC calculations,87 strongly suggested preferential reduction of EC vs. DMC during the SEI formation cycle.
In summary, a DFT analysis of solvates using a composite explicit–implicit solvent approach provides a rationalization for the differences in conclusions about Li+ solvation obtained from Raman and IR-based data, while the BOMD simulations using explicit solvent showed promise for predicting competitive solvation of the Li+ by linear and cyclic carbonates.
Notes
This manuscript has been co-authored by UT-Battelle, LLC under Contract No. DE-AC05-00OR22725 with the U.S. Department of Energy. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).Acknowledgements
We thank Kang Xu and Arthur von Cresce for very stimulating discussions. QC calculations of solvates in implicit solvent and BOMD simulations of electrolytes were supported by the ARL Enterprise for Multiscale Research. M. O. was supported by an Oak Ridge Associated Universities (ORAU) Postdoctoral Fellowship. This research used resources of the Oak Ridge Leadership Computing Facility at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725. Plane wave calculations using VASP were supported as part of the Fluid Interface Reactions, Structures and Transport (FIRST) Center, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences.References
- K. Xu, Chem. Rev., 2014, 114, 11503–11618 CrossRef CAS PubMed.
- M. Ue, Y. Sasaki, Y. Tanaka and M. Morita, in Electrolytes for Lithium and Lithium-Ion Batteries, ed. T. R. Jow, K. Xu, O. Borodin and M. Ue, Springer, New York, 2014, ch. 2, vol. 58, pp. 93–165 Search PubMed.
- K. Xu, Y. F. Lam, S. S. Zhang, T. R. Jow and T. B. Curtis, J. Phys. Chem. C, 2007, 111, 7411–7421 CAS.
- K. Xu, J. Electrochem. Soc., 2007, 154, A162–A167 CrossRef CAS.
- A. von Wald Cresce, O. Borodin and K. Xu, J. Phys. Chem. C, 2012, 116, 26111–26117 CAS.
- I. Yamada, Y. Iriyama, T. Abe and Z. Ogumi, Sci. Technol. Adv. Mater., 2006, 7, 519–523 CrossRef CAS.
- Y. Yamada, Y. Iriyama, T. Abe and Z. Ogumi, Langmuir, 2009, 25, 12766–12770 CrossRef CAS PubMed.
- Y. Yamada, F. Sagane, Y. Iriyama, T. Abe and Z. Ogumi, J. Phys. Chem. C, 2009, 113, 14528–14532 CAS.
- Z. Ogumi, Electrochemistry, 2010, 78, 319–324 CrossRef CAS.
- T. R. Jow, S. S. Zhang, K. Xu and J. L. Allen, ECS Trans., 2007, 3, 51–58 CAS.
- K. Xu, Energies, 2010, 3, 135–154 CrossRef CAS.
- K. Xu, A. von Cresce and U. Lee, Langmuir, 2010, 26, 11538–11543 CrossRef CAS PubMed.
- K. Xu and A. von Cresce, J. Mater. Chem., 2011, 21, 9849–9864 RSC.
- O. Borodin and D. Bedrov, J. Phys. Chem. C, 2014, 118, 18362–18371 CAS.
- O. Borodin, in Electrolytes for Lithium and Lithium-Ion Batteries, ed. T. R. Jow, K. Xu, O. Borodin and M. Ue, Springer, New York, 2014, ch. 8, vol. 58, pp. 371–401 Search PubMed.
- J. Vatamanu, O. Borodin and G. D. Smith, J. Phys. Chem. C, 2012, 116, 1114–1121 CAS.
- O. Borodin and G. D. Smith, J. Phys. Chem. B, 2009, 113, 1763–1776 CrossRef CAS PubMed.
- D. M. Seo, S. Reininger, M. Kutcher, K. Redmond, W. B. Euler and B. L. Lucht, J. Phys. Chem. C, 2015, 119, 14038–14046 CAS.
- Y. Kameda, S. Saito, Y. Umebayashi, K. Fujii, Y. Amo and T. Usuki, J. Mol. Liq. DOI:10.1016/j.molliq.2015.07.004.
- A. von Cresce and K. Xu, Electrochem. Solid-State Lett., 2011, 14, A154–A156 CrossRef CAS.
- Y. Matsuda, T. Fukushima, H. Hashimoto and R. Arakawa, J. Electrochem. Soc., 2002, 149, A1045–A1048 CrossRef CAS.
- K. Xu, Chem. Rev., 2004, 104, 4303–4417 CrossRef CAS PubMed.
- L. Yang, A. Xiao and B. L. Lucht, J. Mol. Liq., 2010, 154, 131–133 CrossRef CAS.
- X. Bogle, R. Vazquez, S. Greenbaum, A. v. W. Cresce and K. Xu, J. Phys. Chem. Lett., 2013, 4, 1664–1668 CrossRef CAS PubMed.
- M. Y. Nie, D. Chalasani, D. P. Abraham, Y. J. Chen, A. Bose and B. L. Lucht, J. Phys. Chem. C, 2013, 117, 1257–1267 CAS.
- M. Morita, Y. Asai, N. Yoshimoto and M. Ishikawa, J. Chem. Soc., Faraday Trans., 1998, 94, 3451–3456 RSC.
- J. Arai, K. Nishimura, Y. Muranaka and Y. Ito, J. Power Sources, 1997, 68, 304–306 CrossRef CAS.
- L. O. Valoen and J. N. Reimers, J. Electrochem. Soc., 2005, 152, A882–A891 CrossRef CAS.
- D. Brouillette, G. Perron and J. E. Desnoyers, J. Solution Chem., 1998, 27, 151–182 CrossRef CAS.
- K. Matsubara, R. Kaneuchi and N. Maekita, J. Chem. Soc., Faraday Trans., 1998, 94, 3601–3605 RSC.
- G. E. Blomgren, J. Power Sources, 1999, 82, 112–118 CrossRef.
- K. Hayamizu, Y. Aihara, S. Arai and C. G. Martinez, J. Phys. Chem. B, 1999, 103, 519–524 CrossRef CAS PubMed.
- H. Katayama, J. Arai and H. Akahoshi, J. Power Sources, 1999, 82, 705–708 CrossRef.
- S. S. Zhang, K. Xu and T. R. Jow, J. Power Sources, 2006, 154, 276–280 CrossRef CAS.
- S. S. Zhang, K. Xu and T. R. Jow, J. Power Sources, 2006, 159, 702–707 CrossRef CAS.
- M. S. Ding and T. R. Jow, J. Electrochem. Soc., 2005, 152, A1199–A1207 CrossRef CAS.
- M. S. Ding, K. Xu, S. S. Zhang, K. Amine, G. L. Henriksen and T. R. Jow, J. Electrochem. Soc., 2001, 148, A1196–A1204 CrossRef CAS.
- S. S. Zhang, T. R. Jow, K. Amine and G. L. Henriksen, J. Power Sources, 2002, 107, 18–23 CrossRef CAS.
- M. S. Ding and T. R. Jow, J. Electrochem. Soc., 2004, 151, A2007–A2015 CrossRef CAS.
- M. S. Ding and T. R. Jow, J. Electrochem. Soc., 2003, 150, A620–A628 CrossRef CAS.
- S. S. Zhang, K. Xu and T. R. Jow, J. Solid State Electrochem., 2003, 7, 147–151 CrossRef CAS.
- V. P. Reddy, M. C. Smart, K. B. Chin, B. V. Ratnakumar, S. Surampudi, J. B. Hu, P. Yan and G. K. S. Prakash, Electrochem. Solid-State Lett., 2005, 8, A294–A298 CrossRef CAS.
- M. S. Ding, K. Xu and T. R. Jow, J. Electrochem. Soc., 2000, 147, 1688–1694 CrossRef CAS.
- M. S. Ding, K. Xu, S. S. Zhang and T. R. Jow, J. Electrochem. Soc., 2001, 148, A299–A304 CrossRef CAS.
- Y. Kameda, Y. Umebayashi, M. Takeuchi, M. A. Wahab, S. Fukuda, S. I. Ishiguro, M. Sasaki, Y. Amo and T. Usuki, J. Phys. Chem. B, 2007, 111, 6104–6109 CrossRef CAS PubMed.
- Y. X. Wang and P. B. Balbuena, Int. J. Quantum Chem., 2005, 102, 724–733 CrossRef CAS.
- T. Li and P. B. Balbuena, J. Electrochem. Soc., 1999, 146, 3613–3622 CrossRef CAS.
- Y. X. Wang, S. Nakamura, M. Ue and P. B. Balbuena, J. Am. Chem. Soc., 2001, 123, 11708–11718 CrossRef CAS PubMed.
- Y. X. Wang and P. B. Balbuena, J. Phys. Chem. A, 2001, 105, 9972–9982 CrossRef CAS.
- P. Johansson, Phys. Chem. Chem. Phys., 2007, 9, 1493–1498 RSC.
- J. M. Vollmer, L. A. Curtiss, D. R. Vissers and K. Amine, J. Electrochem. Soc., 2004, 151, A178–A183 CrossRef CAS.
- H. Tachikawa, ChemPhysChem, 2014, 15, 1604–1610 CrossRef CAS PubMed.
- I. Skarmoutsos, V. Ponnuchamy, V. Vetere and S. Mossa, J. Phys. Chem. C, 2015, 119, 4502–4515 CAS.
- M. Masia and R. Rey, J. Phys. Chem. B, 2004, 108, 17992–18002 CrossRef CAS.
- M. Masia, M. Probst and R. Rey, J. Phys. Chem. B, 2004, 108, 2016–2027 CrossRef CAS.
- J. C. Soetens, C. Millot and B. Maigret, J. Phys. Chem. A, 1998, 102, 1055–1061 CrossRef CAS.
- L. B. Silva and L. C. G. Freitas, THEOCHEM, 2007, 806, 23–34 CrossRef CAS.
- O. Borodin and G. D. Smith, J. Phys. Chem. B, 2006, 110, 4971–4977 CrossRef CAS PubMed.
- O. Borodin and G. D. Smith, J. Phys. Chem. B, 2006, 110, 6279–6292 CrossRef CAS PubMed.
- O. Borodin and G. D. Smith, J. Phys. Chem. B, 2006, 110, 6293–6299 CrossRef CAS PubMed.
- O. Borodin and G. D. Smith, J. Solution Chem., 2007, 36, 803–813 CrossRef CAS.
- K. Tasaki and S. Nakamura, J. Electrochem. Soc., 2001, 148, A984–a988 CrossRef CAS.
- J. Newman, K. E. Thomas, H. Hafezi and D. R. Wheeler, J. Power Sources, 2003, 119, 838–843 CrossRef.
- D. W. McOwen, D. M. Seo, O. Borodin, J. Vatamanu, P. D. Boyle and W. A. Henderson, Energy Environ. Sci., 2014, 7, 416–426 CAS.
- S. D. Han, S. H. Yun, O. Borodin, D. M. Seo, R. D. Sommer, V. G. Young and W. A. Henderson, J. Phys. Chem. C, 2015, 119, 8492–8500 CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian. Inc., Wallingford CT, 2013 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- P. Ganesh, D.-e. Jiang and P. R. C. Kent, J. Phys. Chem. B, 2011, 115, 3085–3090 CrossRef CAS PubMed.
- G. J. Martyna, M. E. Tuckerman, D. J. Tobias and M. L. Klein, Mol. Phys., 1996, 87, 1117–1157 CrossRef CAS.
- C. W. Bauschlicher, J. B. Haskins, E. W. Bucholz, J. W. Lawson and O. Borodin, J. Phys. Chem. B, 2014, 118, 10785–10794 CrossRef CAS PubMed.
- V. Bryantsev, Theor. Chem. Acc., 2012, 131, 1–11 CrossRef CAS.
- L. Doucey, M. Revault, A. Lautié, A. Chaussé and R. Messina, Electrochim. Acta, 1999, 44, 2371–2377 CrossRef CAS.
- W. Hujo and S. Grimme, J. Chem. Theory Comput., 2012, 9, 308–315 CrossRef PubMed.
- J. L. Allen, O. Borodin, D. M. Seo and W. A. Henderson, J. Power Sources, 2014, 267, 821–830 CrossRef CAS.
- J. Zheng, I. M. Alecu, B. J. Lynch, Y. Zhao and D. G. Truhlar, Database of Frequency Scale Factors for Electronic Model Chemistries Determined After Finalizing Version 2, http://comp.chem.umn.edu/freqscale/version3b2.htm, accessed 8/20/2015.
- S. D. Han, J. L. Allen, E. Jonsson, P. Johansson, D. W. McOwen, P. D. Boyle and W. A. Henderson, J. Phys. Chem. C, 2013, 117, 5521–5531 CAS.
- T. Afroz, D. M. Seo, S. D. Han, P. D. Boyle and W. A. Henderson, J. Phys. Chem. C, 2015, 119, 7022–7027 CAS.
- P. Porion, Y. R. Dougassa, C. Tessier, L. El Ouatani, J. Jacquemin and M. Anouti, Electrochim. Acta, 2013, 114, 95–104 CrossRef CAS.
- R. Jorn, R. Kumar, D. P. Abraham and G. A. Voth, J. Phys. Chem. C, 2013, 117, 3747–3761 CAS.
- D. M. Seo, O. Borodin, D. Balogh, M. O'Connell, Q. Ly, S.-D. Han, S. Passerini and W. A. Henderson, J. Electrochem. Soc., 2013, 160, A1061–A1070 CrossRef CAS.
- G. M. Viswanathan, V. Afanasyev, S. V. Buldyrev, E. J. Murphy, P. A. Prince and H. E. Stanley, Nature, 1996, 381, 413–415 CrossRef CAS.
- J. Habasaki, I. Okada and Y. Hiwatari, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 6309–6315 CrossRef CAS.
- J. Habasaki and K. L. Ngai, J. Chem. Phys., 2010, 133, 124505 CrossRef CAS PubMed.
- J. Habasaki and K. L. Ngai, J. Chem. Phys., 2008, 129, 194501 CrossRef CAS PubMed.
- K. Kanamura, T. Umegaki, M. Ohashi, S. Toriyama, S. Shiraishi and Z. Takehara, Electrochim. Acta, 2001, 47, 433–439 CrossRef CAS.
- O. Borodin, G. D. Smith and R. L. Jaffe, J. Comput. Chem., 2001, 22, 641–654 CrossRef CAS.
- O. Borodin, M. Olguin, C. E. Spear, K. Leiter and J. Knap, Nanotechnology, 2015, 26, 354003 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp05121e |
| This journal is © the Owner Societies 2016 |