Intramolecular charge transfer in aminobenzonitriles and tetrafluoro counterparts: fluorescence explained by competition between low-lying excited states and radiationless deactivation. Part I: A mechanistic overview of the parent system ABN

Abstract

Recent theoretical and experimental studies on the Intramolecular Charge Transfer (ICT) reaction of some members of the aminobezonitrile family (ABN) suggest the involvement of a (π–σ*) excited state (called ICT(CN) in this work) in the ICT process and the existence of a partially twisted ICT species that could be responsible for the anomalous fluorescence observed. These suggestions made us to revise our previous study on the photophysics of ABN and dimethyl-ABN (DMABN), based on the analysis of the potential energy surfaces of the low-lying excited states by means of ab initio calculations, using the CASSCF/CASPT2 protocol. We have first focused our attention to ABN. We have found that the (π–σ*) excited state can be in fact an intermediary state in the path to populate the ICT bright state, although its involvement in the process is not very probable. Our results suggest that the ICT most stable species is the twisted ICT(TICT) and that the partially twisted ICT minimum found in previous studies could be an artefact of the computational method. We have also found that radiationless deactivation is a competitive reaction that must be taken into account to explain the fluorescence patterns of these systems. To confirm our theories, we have also studied other systems with a similar architecture but with a very different luminescence behaviour: dimethyl-ABN, and the 2,3,4,5-tetrafluoro derivatives of ABN and DMABN (ABN-4F and DMABN-4F). The extension of the work and the different approaches in the study of the parent system and of the derivatives make the division of the work in two parts advisable. Part I collects the characterization of the minima and reaction paths connecting the critical points of the potential energy surfaces of the states involved in the ICT reaction of ABN. We have obtained, for the first time, the pathways of radiationless deactivation for this compound. We have also computed transition energies from the excited minima, to interpret the excited state absorption (ESA) spectra obtained experimentally. This information helps in the elucidation of the mechanism of ICT. In Part II we show an analoguous study for DMABN and ABN-4F and DMABN-4F and analyse and compare these results and those of Part I to explain different luminescence behaviours of the four systems studied.

---

1 Introduction

The family of aminobenzonitriles is one of the most investigated classes of electron donor acceptor (EDA) compounds (Fig. 1), which are considered as the prototype of these kinds of systems.¹ Under UV excitation, the members of this family can show different luminescence patterns, i.e., a normal fluorescence band, an anomalous band (anomalously red shifted) or dual fluorescence.^1,2

Fig. 1 Donor and acceptor moieties in ABN compounds. Derivatives studied in this work: R = H, R′ = H: ABN; R = CH₃, R′ = H: DMABN; R = H, R′ = F: ABN-4F; R = CH₃, R′ = F: DMABN-4F.

The fact that the emission properties of these compounds can be controlled by structural changes in the molecule or external parameters such as solvent polarity or temperature is important for applications in the field of organic materials, for example, as fluorescent markers^3–5 or electrooptical switches.^6–8 The interest focused on the excited states of these systems is therefore cognitive and applied. The original hypothesis of dual fluorescence was proposed by Lippert in 1959.⁹ He suggested that solvent polarity induces the reversal of the two lowest excited states S₁ and S₂ states that were directly populated after initial excitation. Since then, a large number of experimental and theoretical studies have been devoted to the aminobenzonitrile family to determine the nature of emitting species and explain the photochemistry of these compounds (to avoid a long list of publications we just mentioned here the review of ref. 1).

Initially, the involvement of excimers¹⁰ in the mechanism of dual fluorescence was proposed, but subsequent experiments showed that for a broad range of concentration of a luminescent solute, the intensity ratio between the normal and anomalous bands was independent of the concentration,^11,12 so the hypothesis of excimers as being responsible for the red shifted emission was discarded. Another proposal considered was the formation of exciplets by specific interactions with solvent molecules,¹³ but the fact that the anomalous emission is often shown also in the gas phase made this hypothesis implausible.¹⁴

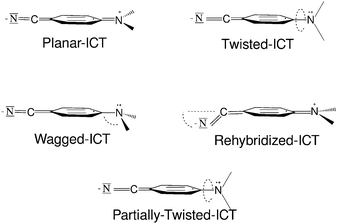
It is now generally accepted that the normal fluorescence band is generated by a locally excited (LE) state while the anomalous band corresponds to emission from an intramolecular charge transfer (ICT) state. Anyway, there still exists a lively debate about some points of the dual fluorescence phenomenon regarding the structure of the emitting species and the detailed mechanism of the ICT reaction. Concerning the geometrical configuration of the ICT species of aminobenzonitriles, four different types of molecular structures have been proposed (Fig. 2).

Fig. 2 Different types of structures proposed for the ICT minima.

The wagged ICT (WICT) suggested by Zachariase et al.^15,16 involves a rehybridization of the amino nitrogen from planar sp² to pyramidal sp³. This model is the least supported. In the planar ICT (PICT) model suggested by Zachariasse,^17–19 the amino group lies in the benzene plane. This model is supported mainly by the fact that ICT emission is also observed in rigidized systems that can hardly abandon the planar conformation. The twisted ICT model (TICT), where the amino group is in a perpendicular or almost perpendicular plane relative to the benzene ring, was proposed by Grabowski and co-workers,²⁰ and is supported by theoretical results. The rehybridized ICT (RICT) model^21,22 involves a rehybridization of the cyano carbon atom from sp to sp² entailing a bend cyano group. This species has been lately discarded for being responsible for the emission, but the excited state (called (π–σ*) in other studies) that leads to the RICT species has been proposed to be involved in the path that populates the luminescent ICT state. Recently, a fifth model has been proposed, with the amino group only partially twisted, and the partially twisted ICT (pTICT).^23,24 This model is based on computational results obtained trying to explain the observations of transient absorption spectrum experiments,²³ but some other contradictory computational results raise some doubts about the actual existence of a stable pTICT species.²⁵

Another question regarding the geometrical structure of the luminescent ICT species is the quinoid (Q) or antiquinoid (AQ) nature of the benzene ring. Although minima on the potential energy surface of the ICT state corresponding to the AQ-ICT species have been located in computational studies for different systems, the Q-ICT analogue has almost always been more stable and consequently a stronger candidate to be the luminescent species.

The reaction mechanism of the charge transfer also leads to a debate that continues to be very lively. In the last decade three different types of mechanisms have been proposed (Fig. 3):

Fig. 3 Different mechanisms proposed for the ICT reaction.

Mechanism 1^26–28. After excitation to the S₂ (ICT) state, the system relaxes through a nearby conical intersection where S₂/S₁ internal conversion takes place. Both CT and LE states show minima on S₁ that are connected also adiabatically. Thus, the S₁ LE-ICT population and dual fluorescence are determined by these adiabatic and non-adiabatic paths connecting both minima.
Mechanism 2^29,30. After population of the ICT state at the Franck–Condon geometry, ICT^FC, a fast switch leads to a bifurcation between the LE and the (π–σ*) states, the last one being a dark state³¹ that leads to a subsequent population of the luminescent TICT state. The primary energetic requirement for the population of the luminescent ICT state is then the presence of a (π–σ*) state between the LE and ICT ones. The absence of the ICT reaction is attributed to the higher energy of TICT relative to the (π–σ*) minimum.
Mechanism 3. This mechanism has been proposed based on the results for DMABN in ref. 23 and 32. After the first excitation the system splits into two excited states, a dark TICT state populated by the dark (π–σ*) state and a fluorescent pTICT state formed from the LE state. That is, the authors suggest the existence of two ICT states and point out that these bright ICT and dark TICT states are non-communicating.

Taking into account that structural changes in the donor or acceptor moieties can modify the interplay between the LE and ICT surfaces, it is not strange that the studies of different systems led to different hypotheses about the ICT mechanism. On top of this diversity, theoretical and experimental studies not always lead to the same conclusions, so the debate about the photochemistry of the ABN family is still open.

Among the aminobenzonitrile compounds, the most studied ones have been 4-(dimethylamino)-benzonitrile (DMABN) and 4-aminobenzonitrile (ABN) because they have similar architecture but show different photophysics. In the fluorescence spectra of DMABN in non-polar solvents, the emission from the ICT state just starts to become observable on the red edge of the fluorescence band of the locally excited LE state.^1,9 Upon increasing the solvent polarity, the efficiency of the ICT reaction becomes progressively larger and DMABN exhibits dual fluorescence in polar solvents.^33,34 Opposite, ABN only shows a normal band in the gas phase as well as in polar solvents.^33,34

Our group developed a computational study on these two members of the aminobezonitrile family some years ago, and set the main milestones to explain the photochemistry of these compounds.²⁷ We found the minima of several ICT species, but focused our attention only on the states in which minima where located on the first excited Potential Energy Surface (PES), which were the minima corresponding to the LE and Q-TICT species. Since then, we have developed some other studies in dual-fluorescent systems,^35,36 but the recent experimental findings suggesting the involvement of a (π–σ*) excited state in the ICT mechanism or the role of the TICT state as a dark state made advisable a revision of the study on aminobenzonitriles. We present here a more exhaustive study where we revise all the proposed luminescent and dark species, the possible paths of population of the ICT states and, for the first time, the radiationless deactivation paths that compete with luminescence.

We have first focused our attention on ABN. With the computational results obtained, we propose a mechanism for the charge transfer reaction and the identification of the dark and luminescent species. We support our hypothesis with quantitative comparison of our data with experimental measurements and qualitative explanation of the experimental observations. To confirm our theories, we have also studied other systems focusing our attention on the points that have been shown to be crucial for the ICT mechanism in ABN. We have chosen systems with a similar architecture but with a very different luminescence behaviour: DMABN, and the 2,3,4,5-tetrafluoro derivatives of ABN and DMABN (ABN-4F and DMABN-4F). The extension of the work and different approaches in the study of the parent system and the derivatives make advisable the division of the work in two parts. Part I collects the characterization of the minima and reaction paths connecting the critical points of the potential energy surfaces (PES) of the states involved in the ICT reaction of ABN. In Part II we show an analoguous study for DMABN, ABN-4F and DMABN-4F and analyse these results comparing them with those of Part I to explain different luminescence behaviours of the four systems studied.

We have performed this study using the CASSCF/CASPT2 methodology, whose applicability and reliability have been extensively demonstrated in a large number of previous cases. We have found that although this is not the most probable path the (π–σ*) excited state can be an intermediary state in the path to populate the ICT bright state, that is the TICT one. Our results suggest that although the pTICT species could exist in some systems, it would be an intermediate in the path of the population of the TICT species.³⁷ On the other hand the AQ-TICT species can play a crucial role in the fluorescence of some systems, but not in the cases studied here. We have also found that radiationless deactivation is a competitive reaction that must be taken into account to explain the fluorescence patterns of these systems.

2 Computational information

The ground state and the low-lying singlet excited states of ABN have been studied using the MS-CASPT2/CASSCF strategy. The active space used in all calculations includes 12 electrons and 11 orbitals: the benzene π and π* orbitals, the amino nitrogen lone pair, and the four π and π* orbitals of the cyano group (more details in ESI†). Full geometry optimizations were performed without any symmetry constraint using the Dunning correlation consistent polarized valence double basis set [9s4p1d/3s2p1d] for carbon and nitrogen atoms, and [4s1p/2s1p] for hydrogen atoms, designated as cc-pVDZ.³⁸

Exceptions to these general lines (larger active space or geometry optimization at CASPT2 level) made in some specific cases are commented explicitly along the text when occurring.

Numerical frequency calculations were run to determine the nature of the stationary points.

Conical intersections (CI) were optimized at the CASSCF level using the algorithm described in ref. 39. State averaged orbitals were used, and the orbital rotation derivative correction to the gradient (which is usually small) was not computed. This gives the lowest energy point on the crossing, but it must not be forgotten that decay can take place away from this point depending on the kinetic energy of the system.

The second order exchange density matrix P_ij has also been calculated, elements P_ij are related to the spin coupling between the electrons localized in the orbitals residing on the atoms i and j.⁴⁰

To incorporate the effect of the dynamic valence electron correlation on the relative energies of the lower excited states, we performed second order multiconfigurational perturbation theory calculations (CASPT2) based on the SA3-CASSCF(12,11) reference function⁴¹ (at the FC region also SA13-CASSCF(12,11) were used as reference functions). CASPT2/cc-pVDZ single point energies of the critical points were calculated at the CASSCF/cc-pVDZ geometries. Energy profiles were calculated at the CASPT2/6-31G* level instead. All valence electrons were correlated. All CASPT2 computations have been performed using the complete Fock matrix in the definition of the zero order Hamiltonian, together with an imaginary level shift of 0.2 in order to avoid the incorporation of intruder states.⁴² The interaction of CASSCF states via dynamic correlation is taken into account by multistate (MS) CASPT2 treatment.⁴³

At the MS-CASPT2 level, the CASSCF states involved in a CI will be mixed in the perturbed modified CAS configuration interaction functions (PM-CAS-CI), splitting the energy of the two states like in an avoided crossing. For this reason, the MS-CASPT2 energies of the minimum energy points of the conical intersections reported in the text and tables will be the average of the energies of the states involved in the corresponding CI.

The CAS state interaction (CASSI) protocol⁴⁴ and the PM-CAS-CI were used to compute transition dipole moments and oscillator strengths to compare transition probabilities in both absorption and radiative emissions.

Minimum energy paths (MEPs),⁴⁵ intrinsic reaction coordinate (IRC)⁴⁶ paths and linearly interpolated internal reaction coordinate (LIIRC) paths were calculated between critical points of interest (stationary points and conical intersections) on several surfaces to ascertain the viability of the proposed reaction mechanisms.

In the LIIRC paths, all the internal coordinates of the geometry of the starting point are changed simultaneously in the intermediate geometries, step by step, to reach the values of the final geometry. It means that the path corresponds to a straight line between the geometries of interest in the space of the internal coordinates. This is not necessarily the path of minimum energy, but the barrier of the path found in this way, which constitutes an upper limit for the barrier of the process.

The CASSCF calculations were carried out using the Gaussian 09 system of programs,⁴⁷ while the CASPT2 computations were performed using the MOLCAS 7.0 program package.⁴⁸

3 Results

3.1 Franck–Condon (FC) region

3.1.1 Ground state geometry. The minimum energy geometry obtained for the ground state (GS) of ABN belongs to the Cs point group with a kekulé nature of the phenyl ring. The molecule is planar, with the exception of the NNH₂ group which shows a pyramidalization of the amino group that can be quantified by the pyramidalization angle ϕ defined in Fig. 4.

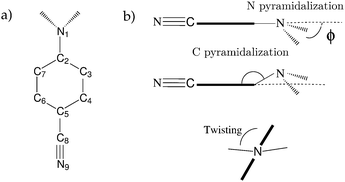Fig. 4 (a) Atom labelling in ABN. (b) Definition of the wagging, pyramidalization and twisting angles.

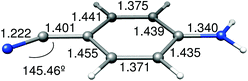
The geometry obtained, shown in Fig. 5, is in good agreement with the X-ray crystal structure reported in ref. 49 as well as with the results from previous calculations.^50,51 Our value of ϕ, 43.0° is slightly larger than the experimental value of 34.84°. The computed bond lengths are also slightly larger than the X-ray data,⁴⁹ with a standard error of 0.015 Å. In the ring, the C₃–C₄ bond is the shortest (together with the C₆–C₇ bond by symmetry), what agrees qualitatively with experimental findings, but the computed C₃–C₄ distance is larger in comparison. Serrano et al. suggested that the reported bond lengths could be too small as it is observed that in the solid phase this type of bond length is often underestimated.⁵²

Fig. 5 Optimized ground state geometry of ABN. In parenthesis experimental geometric parameters of ref. 49.

3.1.2 Nature of excited states and the absorption spectrum. To understand the mechanism of the ICT reaction it is necessary to have identified, at the FC geometry, the low energy excited states of ABN. In principle, we need to consider only the excited states between the ground state and the state that is initially excited. Some of the higher excited states, though, can be stabilized along the reaction path and get involved in the reaction mechanism, so they must also be characterized at the FC zone. On top of this, high excited states can interact with low energy states via dynamic correlation at the MS-CASPT2 level, so it is convenient to include, in the CASSCF step, more excited states than the strictly necessary. For these reasons we included 13 states in the state average procedure at the CASSCF step (SA13-CASSCF) in the initial calculations at the FC zone. An analysis of the influence on the results of the number of states averaged can be found in the ESI.† The excitations that lead to the low lying excited states of ABN are represented in Fig. 6 and the labels assigned to the different states are collected in Table 1. Characterization was made by analysing the contribution of the configuration state functions (CSF) in each PM-CAS-CI function, the difference of electron densities between the excited states and the ground state (schematic plots shown in ESI†), and the occupation numbers of the natural orbitals of each state.

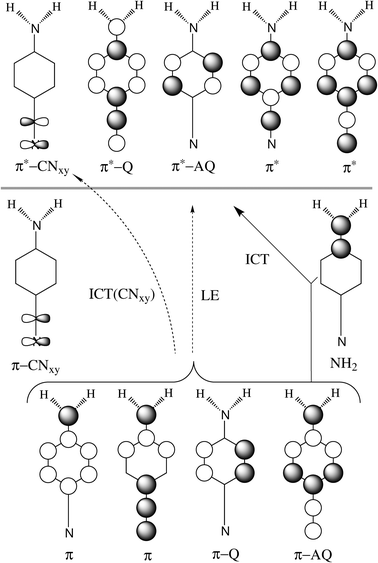Fig. 6 Scheme of excitations. Orbitals below the horizontal line are doubly occupied in the ground state, while orbitals above the line are empty.

Table 1 Nomenclature adopted for the excited states derived from the different types of monoexcitations represented in Fig. 6

States	Label	Excitations
Locally excited	LE	π–Q + π–AQ → π*–Q + π*–AQ
ICT : amino → ring	ICT(Q)	π–AQ → π*–Q
ICT : amino → ring	ICT(AQ)	π + π–AQ + π–Q → π*–AQ
Cyano → ring	CNxy	CNxy; → π*–Q
ICT : cyano → cyano*	ICT(CN)	CNxy + π–AQ → CNxy*
Amino, cyano → ring	D + A → R	(a) π–AQ + π–Q → π*–AQ
		(b) π → π*–Q

---

Table 2 shows the relative energies, dipole moments and oscillator strengths obtained at different levels of calculation for these thirteen states.

Table 2 Vertical energies (in kcal mol⁻¹) and dipole moments (μ in Debyes) of the 13¹³ lowest states of ABN, obtained with a SA13-CASSCF wave function at several levels of calculation

SCF-state	CASSCF	SS-CASPT2	μ	PM-state	MS-CASPT2	μ
S0	0	0	5.33	S0	0	6.77
LE	108.41	108.68	5.13	LE	106.25	6.3
ICT(Q)	155.1	124.19	10.07	ICT(Q)	121.21	9.76
D + A → R(b)	174.3	167.23	4.57	ICT(AQ)′	144.99	8.32
ICT(AQ)	175.38	160.35	6.83	ICT(AQ)	160.33	6.97
CNxy	190.78	177.91	2.22	D + A → R(b)	171.06	4.99
ICT(AQ)	201.23	162.63	6.31	CNxy	179.28	2.74
D + A → R(a)	203.77	165.18	5.03	D + A → R(a)	183.77	3.31
D + A → R(b)	205.9	193.12	4.16	ICT(CN)	186.23	6.26
ICT(CN)	211.68	184.49	6.51	ICT(Q)	191.99	5.43
S11	225.8	197.29	5.91	S 11	209.18	4.36
S12	231.17	211.56	3.12	S 12	211.09	1.69
S13	234.86	209.54	1.40	S 13	216.96	3.18

---

At all levels of calculation the first excited state is of the LE character with a dipole moment of around 6.30 D. This state is composed by two monoexcited CSF, with excitations π–Q → π*–Q and π–Q → π*–AQ. Its characterization as a locally excited state is confirmed by its difference of electronic density with the ground state (see plot in ESI†) and by the occupation numbers of the localized orbitals reported in Fig. 7, which shows that the reduction of the occupation of the amino nitrogen is only 0.025.

Fig. 7 Occupation numbers of the localized orbitals of S₀, LE and ICT states in the FC zone.

The second excited state is ICT(Q). This state is mainly characterized by a charge transfer from the amino group to the carbon of the ring bonded to the cyano group, according with the occupation numbers of the localized orbitals depicted in Fig. 7. The transfer, though, does not correspond to a full electron given that the occupation of the amino nitrogen is reduced only from 1.878 to 1.543. Accordingly, it shows a dipole moment of 9.76 D.

The third and fourth excited PM-CAS-CI states are of the ICT(AQ) character. Both are derived basically from excitations of the type π + π–AQ + π–Q → π*–AQ.

The fifth and seventh excited states involve a transfer of electron density from the π orbitals of the amino group and from the cyano group to the ring, so they are labelled as D + A → R.

The sixth MS-CASPT2 excited state, labelled as CN_xy, is characterized mainly by the monoexcitation CN_xy → π*–Q. Therefore there is a transfer of electronic density from the cyano π in a plane orbital to the benzene ring with a reduction of the dipole moment to 2.74 D (to be compared with the ground state dipole moment of 6.77 D).

The eight MS-CASPT2 excited state is named as ICT(CN). It is of special importance in the study of the deactivation mechanism analyzed here. This state is the one called (π–σ*) in previous studies, and to elucidate its role in the ICT mechanism has been one of the reasons to study again the photochemistry of ABN. It is characterized by a charge transfer from the aminobenzene ring to the cyano group. This state is composed mostly by two CSF: one is a promotion of an electron from the π–AQ to π*–CN_xy orbitals and the other is from π–CN_xy to π*–CN_xy orbitals. The computed dipole moment is 6.26 D, indicating a transfer of charge. The reason to rename this state in this work is that the orbital where the excitation take place is in fact mostly composed by the antibonding π* orbital in the molecular plane orbital of the cyano group, instead of by a σ* orbital.

In principle, all the states involved in the reactivity of interest are included in the set of states described up to here. Nevertheless, given that in the MS-CASPT2 step higher states can get coupled with these ones and modify their description and energies, three additional states were included on an average at the CASSCF level. The detailed description of these states is not essential in this study, although more detailed information can be found in the ESI.†

SA3-CASSCF/CASPT2 results show that, although at Franck–Condon geometry the LE state is more stable than the CT states, the energy gap between them is small, which can have important consequences in the ICT reaction. The effect of the dynamic electron correlation is significantly different in the calculation of the energy of the LE and ICT states. For both, the MS-CASPT2 excitation energies are smaller than the CASSCF ones, but while the stabilization of LE is only of 2.16 kcal mol⁻¹, the CT state is stabilized by 33.89 kcal mol⁻¹. SS-CASPT2 and MS-CASPT2 energy differences are small, given that in the PM-CAS-CI that describes these states, there is no mixing of CASSCF states via dynamic correlation. The oscillator strength from the ground state has been computed to be 0.071 for the LE and 0.623 for the ICT(Q) state. It indicates that the ICT is the state initially populated due to the allowed character of transition. The oscillator strengths are in good agreement with experiments, predicting a weak S₀ → S₁ band and a stronger S₀ → S₂ absorption band (a more detailed study of the transition dipole moment is provided in the ESI†). The energetics is also in fair agreement with the experimental data in non-polar solvents, which is assigned to an energy of 109.4 kcal mol⁻¹ for the absorption band in hexane.^18,53–55

The computed dipole moments in the gas phase for ABN change with the inclusion of interaction of states via dynamic correlation. For the ground state, the dipole is 5.40 D at the CASSCF level, while at the MS-CASPT2 level it is increased to 6.77 D, in good agreement with the estimated experimental value of 6.60 D in non-polar solvents.^15,53 This increase can be attributed to a larger contribution of the charge transfer CSF in the ground state in the PM-CAS-CI wave function, reflected in an increase of the weight of ionic states.

The coupling between the amino group and the benzene ring was also analysed in a previous work. We calculated the coupling between the non bonding pair of the nitrogen of the amino group and the π system of the benzene ring by the values of the second order exchange density matrix (P_ij) between the p orbitals of C₂ and N₁ (see Fig. 4 for labelling). Surprisingly, this value is larger in the ICT state (0.280) than in the ground (0.057) and LE (0.045) states, in agreement with Zachariasse claims that the amino group is strongly coupled to the benzonitrile fragment in the ICT state.⁵⁶

3.2 Minima of the excited states

We explored the PES of the lowest excited states of ABN, considering all those that have an energy similar or lower than the initial excitation of 121 kcal mol⁻¹. The minima of the ICT(AQ) and CN_xy excited states were not found at low energies. In the case of the ICT(AQ) state, the minimum is found on the S₃ surface with a very high energy of 136.0 kcal mol⁻¹. Hence we concluded that the population of the ICT(AQ) state is not probable. This result will be important when compared with other systems (see Part II). In the case of the CN_xy state, its relaxation coordinate stabilizes the ICT(CN) state more, leading to a crossing of these two surfaces. It indicates that the ICT(CN) state can become a low excited state at geometries different from the Franck–Condon one. In fact, we located a minimum of this state on the S₁ PES (RICT structure), but the minima for the LE and ICT(Q) excited states (LE and TICT structures) were also located on this surface and were less energetic. A planar ICT(Q) minimum (PICT structure) was also located, but it was a minimum energy point of the S₂ surface. The geometries of all these minima are depicted in Fig. 8 and the energies are shown in Table 3.

Fig. 8 Optimized structures of excited state minima of ABN. Bond lenghts in angstroms.

Table 3 CASSCF, SS-CASPT2 and MS-CASPT2 energies relative to the S₀ minimum (in kcal mol⁻¹), dipole moments (in Debye) and state nature at the characterized ABN minima. The number of states averaged in the CASSCF reference wave-function corresponds to the number of states shown in each minimum. Data in bold correspond to the optimized root

Minimum	Nature	CASSCF	SS-CASPT2	Dipole	Nature	MS-CASPT2
a Geometry optimized at CASSCF(12,11) level. b Geometry optimized at MS-CASPT2(12,11) level. c Energy calculated at MS-CASPT2(14,13) level at MS-CASPT2(12,11) optimized geometry.
LE	S0	4.13	2.01	5.37	S0	2.01
	LE	104.22	102.73	5.1	LE	102.40
RICT	S0	40.86	31.02	4.86	S0	31.02
	LE	147.04	134.62	4.55	ICT	122.14
	ICT	152.77	122.15	10.45	LE	134.64
TICT(Q)^a	S0	39.14	33.26	3.82	S0	33.26
	LE	133.85	125.86	4.56	ICT	112.94
	ICT	160.93	125.87	10.76	LE	138.80
TICT(Q)^b	S0	49.03	41.05	3.85	S0	41.04
	LE	134.99	122.78	5.13	ICT	110.16
	ICT	164.69	129.59	10.46	LE	142.21
TICT(Q)^c	S0	24.04	33.00	4.31	S0	33.00
	LE	117.92	122.38	5.97	ICT	116.64
	ICT	137.38	132.96	9.59	LE	138.70
PICT	S0	13.26	4.94	6.71	S0	3.74
	LE	116.22	105.74	5.93	LE	105.74
	ICT	146.15	115.79	11.23	ICT	116.99
TICT(AQ)	S0	30.48	18.08	3.80	S0	18.08
	LE	136.97	126.84	3.42	ICT	126.84
	ICT(Q)	163.65	133.58	14.18	LE	133.58
	ICT(AQ)	166.61	136.00	13.79	ICT	136.00

---

But the analysis of the wavefunction at the TICT(Q) minimum shows a peculiar fact: the LE and ICT functions are strongly mixed in the MS-CASPT2 description as reflected in the composition of the PM-CAS-CI wavefunction, with almost equal weights of the two CASSCF functions (see the effective Hamiltonian matrix diagonalization in the ESI†). Mixing of states is only expected near conical intersections, which is not the case at this geometry, so this result highlights two considerations, regarding the geometry and the zero-order wavefunction. First, the ICT state is not well described at this geometry by the CASSCF approximation, so geometry optimization performed at that level could be a bad approximation of the results that would be obtained when including dynamic electron correlation. For this reason a reoptimization of this minimum at the MS-CASPT2 level was performed. The geometry obtained, included in the ESI,† is quite similar to the one obtained previously. The LE and ICT states, though, are still mixed at the PM-CAS-CI wavefunction, so the problem is not yet resolved. It leads to the second consideration: the mixing indicates that the zero order wavefunction of the preturbative treatment is not good enough and consequently the MS-CASPT2 results are not completely reliable. It is known that this problem can be resolved by increasing the active space. By the analysis of the largest contributions to the second order energy, we enlarged the active space of the reference function including the N₁–C₂ σ and σ* orbitals in the first step.

With the new CASSCF(14,13) reference wavefunction the PM-CAS-CI function obtained showed a smaller LE/TICT mixing. It shows that the problem could be completely solved by further increasing the active space, but the small energy change in the TICT energy between the CASPT2(12,11) and CASPT2(14,13) results and the high cost of the calculations discouraged us from continuing along this line.

It has to be pointed out that the mixture of states at the MS-CASPT2 level is not present at the other excited state minima (LE, RICT, ICT(AQ) and PICT), as demonstrated by the composition of the PM-CAS-CI eigenfunctions shown in the ESI,† so the enlargement of the active space is not considered necessary in these other points.

We also looked for a partially twisted ICT minimum (pTICT). We used the twisting angle given in ref. 24 for DMABN to start the search for this minimum. All the different trials performed (freezing the dihedral angle and removing the constrain in a second step, using symmetry constrains in a first step, performing a scan) lead the system towards the TICT species, convincing us that such a minimum definitely did not exist for ABN. It must be pointed out that in the reference cited this species was located for DMABN instead for ABN, so this result is not very surprising, but as it will be explained in Part II of this work, more exhaustive calculations were performed for DMABN with the same result: no pTICT minimum was located.

As a whole, we located three minima on the S₁ PES corresponding to the LE, TICT(Q) and RICT species. The energies (102.40, 116.64 and 122.14 kcal mol⁻¹ respectively) show that the most stable excited structure corresponds to the LE state, so the population of this species is favoured thermodynamically. The PICT structure, low in energy (116.99 kcal mol⁻¹), can be involved in the ICT mechanism, but it is discarded as a possible luminescent species, given that it is located on the S₂ PES. On the other hand, the involvement of the TICT(AQ) structure, high in energy (136.00 kcal mol⁻¹) and located on the S₃ PES, can be discarded for ABN.

To analyse the dynamic factors of the photophysics of ABN we have to study the possible mechanisms of population of several minima located on the S₁ surface and the paths connecting them. This is the subject of the next section.

3.3 Pathways of population of the excited state minima

3.3.1 Relaxation on the S₂ surface. The minimum energy path (MEP) from the FC geometry on the S₂ surface, the one corresponding to the state populated by the initial excitation leads directly to the PICT shallow minimum. From there several pathways are accessible.
Pathway ICT(Q) → LE. A S₂/S₁ conical intersection between the CT and LE states was located, as already reported in the previous work of our group.²⁷ The lowest energy point on this conical intersection seam (Fig. 9) corresponds to a pyramidalised structure where the amino group is untwisted; however, the branching space of the CI is dominated by skeletal deformations of the phenyl ring coupled with the C–N stretch. Thus branching does not involve either the amino group twist or the pyramidalization coordinates and the S₂/S₁ degeneracy will be preserved along the torsional coordinate. The minimum energy of the CI subspace is 114.79 kcal mol⁻¹ (see Table 4), 11.4 kcal mol⁻¹ below the FC excitation energy and 2.20 kcal mol⁻¹ below the PICT minimum, so the CI seam seems to be very accessible. To corroborate it, a linearly interpolated internal reaction coordinate (LIIRC) path between the FC and the ICT(Q)/LE CI geometries was calculated. Fig. 10 shows that there is no barrier to access the CI so this first step in the deactivation process can be very efficient. This figure also shows that the inclusion of dynamic correlation in the calculation locates the crossing at a geometry (near point 7 of the LIIRC) different from the one predicted at the CASSCF level (point 10 of the LIIRC). Due to the preferential stabilization at the CASPT2 level of the CT state, higher in energy, at step 1 the CT-LE energy gap decreases, and the geometry of the new crossing point (shown in Fig. 10 as an inset) is less pyrimidalized. The LE → TICT model explains the appearance or absence of dual fluorescence not only on the basis of the energy of the CI, but also of the location (geometry) of its minimum and of the dynamic evolution of the system. The inclusion of the dynamic correlation in this calculation, although tends to stabilize the ICT state, favours in this path the population of the LE minimum given that the geometry of the crossing gets nearer to the LE minimum.

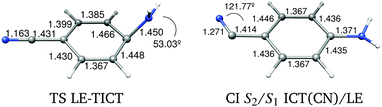
Fig. 9 Geometrical parameters of the S₂/S₁ ICT(Q)/LE CI (bond lengths in angstroms) and branching space.

Table 4 Average energies (relative to the S₀ minimum, in kcal mol⁻¹) of the critical points connecting potential energy surfaces of different states. Energies calculated at MS-CASPT2/cc-pVDZ with

Geom	E MS-CASPT2
a SA2-CASSCF reference function. b SA9-CASSCF reference function.
CT-Q/ICT(CN) CI S3/S2	128.07^a
CT-Q/CT-AQ CI S3/S2	138.86^b
CT-Q/LE CI S2/S1	114.79^a
TS ICT(Q) → LE S1	111.66^a
ICT(CN)/LE CI S2/S1	128.48^a

---

Fig. 10 Profiles of the S₁ and S₂ excited states (LE and ICT) along the LIIRC path from the FC region to the geometry of the S₂/S₁ CI. Energies in kcal mol⁻¹. The structures shown correspond to the CI geometries localized at CASSCF and CASPT2 levels.

But the actual evolution of the system when it reaches the CI also depends on the topology of the surfaces involved in the crossing in the neighbourhood of the CI, so we have performed a more detailed analysis of this area in search for extra information. We have studied the shape of the LE and ICT PES in the branching space (formed by the coordinates that remove the degeneracy at any CI) by means of a Taylor expansion as a function of the gradient difference and derivative coupling vectors. The results (see ESI†) show that the change of energies along the derivative coupling coordinate is negligible compared with the change along the gradient difference one. For this reason we computed two MEPs on the S₁ surface starting at the CI geometry slightly modified along the positive and negative direction of the gradient difference vector to predict the evolution of the system once it has crossed the CI and reached the lower PES. One of the MEPs relaxes to the LE minimum while the other one relaxes to a S₁/S₀ conical intersection, which will be analysed later.

All these results suggest that following the ICT(Q) → LE path, the system preferentially populates the LE minimum, in competition with the radiationless deactivation via S₁/S₀ internal conversion. A polar solvent environment would stabilize preferentially the more polar state, in this case the ICT state. Like the effect of the inclusion of dynamic correlation, the further decrease of the ICT-LE gap will favour even more the population of the LE minimum in the first events of the photochemistry of ABN.

In fact, it has been shown in a recent work²⁵ that the LE and ICT are degenerated also at planar geometries very near to the FC zone. This planar ICT/LE pathway could be faster than the pathway that evolves via ring piramidalization, a slower motion. However, in the gas phase, the energy of the planar ICT/LE CI is higher than the FC energy, making this path efficient and accessible only in polar solvents. In this case the S₂ → S₁ deactivation will occur through this funnel in an ultrafast process.

Pathway mediated by the ICT(CN) PES. Another possible path from the S₂ (ICT) surface leads to a crossing to the ICT(CN) state through a S₃/S₂ CI (Fig. 11) that is located only 1.88 kcal mol⁻¹ above the FC excitation energy (Table 4). The ICT(CN) state involves a change of hybridation of the cyano group that when relaxing leads to a bent geometry that corresponds to the RICT minimum. At the crossing of this state with the ICT the CN group is partially bent with an angle of 145.46°.

Fig. 11 Geometrical parameters of the S₃/S₂ ICT(CN)/ICT(Q) CI. Bond lengths in angstroms.

A LIIRC path between FC and the RICT minimum has also been computed (Fig. 12). In this case the process along the LIIRC on S₂ is not barrierless, but the energy of the CI (1.88 kcal mol⁻¹) can be considered as an upper limit of the activation energy barrier, so this path is easily accessible. After reaching this ICT(Q)/ICT(CN) conical intersection, the ICT(CN) state is populated and the system relaxes to the RICT minimum, where the ICT(CN) is the first excited state (minimum on S₁).

Fig. 12 Profiles of the PES of LE, ICT(Q) and ICT(CN) excited states along the LIIRC path from the FC region to the RICT minimum. Energies in kcal mol⁻¹.

Neverthless, given the existence of a less energetic S₂ → S₁ relaxation route, the probability of population of the ICT(CN) state can be considered low. It is not expected that a polar solvent will modify this path, given that the dipole moment of the ICT(Q) and ICT(CN) states are similar, so their relative energies will not hardly change.

Pathway ICT(Q) → ICT(AQ). In order to determine the possible involvement of the ICT(AQ) state in the deactivation mechanism, a conical intersection S₃/S₂ between the ICT(AQ) and ICT(Q) states was looked for. The energy of its minimum energy point calculated at the SA9-CASSCF/MS-CASPT2 level locates this crossing 17.65 kcal mol⁻¹ higher than the FC excitation. It means that it is 24.07 kcal mol⁻¹ and 10.79 kcal mol⁻¹ above the ICT/LE and ICT(Q)/ICT(CN) conical intersections, so this ICT(AQ)/ICT(Q) is the least favourable route, which has a negligible probability of being followed. Polar solvents will not substantially modify this picture, given that the stabilization of both ICT(Q) and ICT(AQ) states will be similar in this environment.

3.3.2 Topology of the S₁ potential energy surface. Given that all the LE, TICT and RICT minima are located on the S₁ surface, it is convenient to determine the adiabatic and non-adiabatic paths that connect these minima.
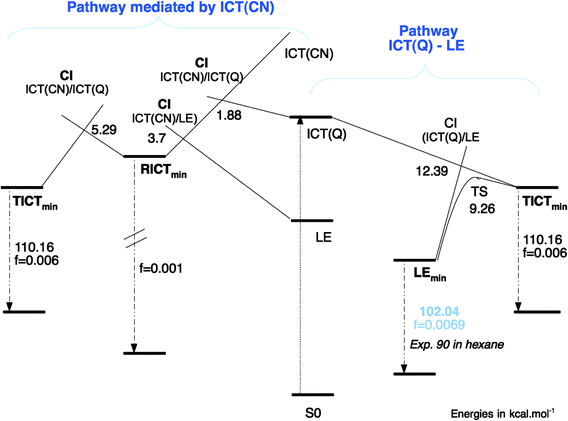
Equilibrium LE-TICT. We have already described the CI where the LE and TICT PES cross, but its energy is only an upper limit of the barrier of the path that must connect the LE and ICT(Q) minima adiabatically along the S₁ PES. We located the transition state of this path (TS_LE-TICT). The geometry shows a pyramidalized untwisted geometry (Fig. 5), with an energy of 111.66 kcal mol⁻¹ (Table 4). The PM-CAS-CI wave-functions for the second and third roots obtained at the MS-CASPT2 level at the TS geometry show a strong mixing of the LE and ICT CASSCF wavefunctions as expected (eigenvectors in ESI†). Globally, the ICT(Q) → LE process is exoergic by 7.76 kcal mol⁻¹ with forward and backward activation barriers of 1.45 and 9.26 kcal mol⁻¹ respectively (Fig. 14).

Therefore as a whole in ABN the population of the LE minimum is the most favoured process: from the thermodynamic point of view this structure is more stable than the TICT one. From the kinetic point of view, two factors control the relative population of the LE and TICT minima. The first one is the location of the geometry where the S₂ → S₁ decay takes place, that in ABN favours the population of the LE minimum. The second factor is the height of the barrier of the adiabatic path that connects the TICT and LE minima, which also favours the TICT → LE process. These characteristics explain why it is difficult to detect the TICT species in ABN. Although polar solvents will stabilize preferentially the TICT species, it has been shown that even in highly polar solvents the effect is not large enough to make the TICT species more stable than the LE one.³⁷

RICT-LE equilibrium. A CI between the LE and ICT(CN) states was found (Fig. 13) with an energy of 127.48 kcal mol⁻¹ relative to the ground state minimum and 5.35 kcal mol⁻¹ above the RICT minimum. Due to the different effects of dynamic correlation in both states, to characterize better the path connecting the RICT and LE minima, an interpolated path between them was calculated at the MS-CASPT2 level (Fig. 15). The barrier found in this way from RICT to LE is very low, of about 3.7 kcal mol⁻¹. Given that the LE minimum is favoured on energetic grounds, it is expected that, if the RICT minimum is populated, it will be quickly depopulated in favour of the LE minimum.

Fig. 13 Geometrical parameters of some critical points on the S₁ PES of ABN.

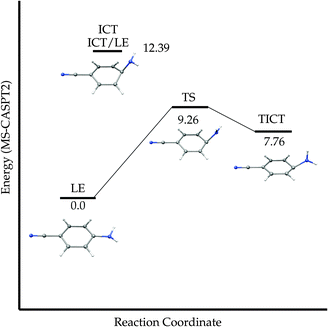Fig. 14 Schematic potential energy profile of the adiabatic path between the LE and TICT minima for ABN. Energies in kcal mol⁻¹.

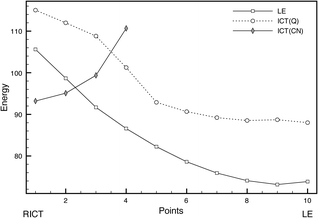Fig. 15 Profiles of the LE, ICT(Q) and ICT(CN) excited states along the LIIRC path from the RICT to the LE minima geometries. Energies in kcal mol⁻¹.

In solution, polar solvents will stabilize preferentially the ICT(CN) state, which has a larger dipole moment. But the energy difference between the LE and RICT minima is so large, that the LE species will be more stable even in highly polar solvents, so the equilibrium will be displaced, like in gas phase, towards the LE species.

RICT-TICT equilibrium. No RICT/TICT conical intersection could be located. Instead, we calculated the LIIRC connecting the TICT and RICT minima. The profiles obtained are shown in Fig. 16. The RICT → TICT process shows a low barrier of about 5.29 kcal mol⁻¹, so the TICT minimum could be populated from the RICT one. As commented before, in this case a polar solvent environment would stabilize both states more or less equally, hardly modifying this equilibrium.

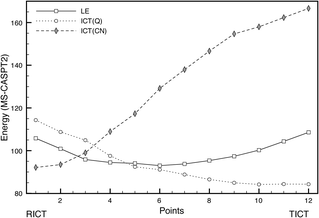Fig. 16 Profiles of the LE, ICT(Q) and ICT(CN) excited states along the LIIRC path between the RICT and TICT minima. Energies in kcal mol⁻¹.

These results show that the minima on the S₁ surface corresponding to the TICT, LE and RICT structures are connected, but the population of the LE minimum is strongly favoured, even in a polar solvent environment.

3.4 Transient absorption

From the experimental point of view, the population of the excited state minima can be checked by means of excited state absorption (ESA) spectra. The results and interpretation of these experiments, though, are not free from disagreement and controversy.

Most of the ESA experiments have been done for DMABN, which shows a different luminescence behaviour from ABN, but for this reason comparing the results of both systems can provide interesting information. The complete set of computational results for transient absorption (TA) calculations in ABN are collected in Table 5. The experimental results and the tentative assignment of experimental bands based in our results are collected in Table 6.

Table 5 Most intense (f > 0.01) MS-CASPT2/cc-pVDZ transient absorption energies and oscillator strengths from different ABN minima. The reference function in the perturbation treatment is SA15-CASSCF

Minimum	PM states	TA (kcal mol^−1)	TA (nm)	f
LE	2 → 4	41.35	691	0.034
	2 → 7	66.66	429	0.075
	2 → 12	100.72	284	0.147
	2 → 14	111.98	255	0.008
RICT	2 → 5	50.32	568	0.178
	2 → 13	98.78	289	0.214
TICT	2 → 3	24.83	1191	0.0496
	2 → 9	86.32	331	0.0148
	2 → 15	133.00	215	0.0269
PICT	2 → 4	46.55	614	0.047
	2 → 9	76.17	375	0.027
	2 → 13	110.65	258	0.019
	2 → 15	116.11	246	0.013

---

Table 6 Experimental maximum band frequencies of ESA spectra of ABN and DMABN and assigned nature of the bands compared with theoretical results obtained for ABN in this work and our assignment of bands

DMABN λ (nm) state	ABN λ (nm) state	Theoretical results (nm) state f
300 LE	295 LE	284 LE 0.147
		289 RICT 0.214
320 TICT	320 LE	330 TICT 0.015
349 LE
420 TICT only in polar solvent
450 LE	450 LE	429 LE 0.075
535 LE
		568 RICT 0.178
>660 LE	>650 RICT
>680 RICT	>650 LE
		691 LE 0.034

---

Table 6 shows that the band observed in ABN at 295 nm and attributed to a LE transition^26,34 should be assigned (based on the results of Table 5) to a transition from the LE species or from the RICT one. The band at 320 nm, which appears both in the ESA spectra of DMABN and ABN, is attributed in the first case to a transition from the TICT intermediate³² and in the second system to one from the LE species.²⁶ Our results support the first assignment, a transition from the TICT intermediate.

The band at 450 nm attributed to both DMABN and ABN to a LE transition,²⁶ is obtained computationally at 429 nm. The agreement, not as good as in previous cases, is nevertheless quite satisfactory, given that the energy difference correspond to only 3 kcal mol⁻¹ approximately and the nature of the transition agrees with the experimental assignment.

The most controversial band and the one obtained theoretically with the largest error is the band above 650 nm (680 nm for DMABN), which is assigned to a LE transition by some authors but to a RICT transition by others. One of the evidences that support the assignment to a LE band is that the decay time of this band is the same as that of the 450 nm band (also assigned to a LE transition).^26,34 Moreover Zachariasse has found similar bands in DMABN analogues without the cyano group,⁵⁷ ruling out the possibility of assignment to the RICT transition and supporting again the assignment to a LE transition. On the other hand, this band blue shifts as the polarity of the solvent increases, the fact related to solutes with a large dipole moment, which supports the assignment made by some experimentalist to a RICT transition.³² In fact, the band at 450 nm, assigned to a LE transition, does not shift with solvent polarity, argument that is used to support the hypothesis that the 450 and 650 nm bands cannot be assigned to the same transient species,³² so the 650 nm band must not originate at the LE minimum. On top of this, the 650 nm band also blue shifts with increasing pump prove delay times, which is consistent with the stabilization of the highly polar RICT species by reorientation of solvent molecules. Another observation is that the decay time of this band is very short for DMABN in acetonitrile but very long for ABN and DMABN in n-hexane, where the ICT reaction does not take place.²⁹ This fact also supports the assignment to a transition from the RICT species.

From the theoretical point of view, previous TDDFT results for ABN²⁹ assign this band to a transition from the RICT species, calculated at 571 nm, because only a (π–σ*) → (π–σ*) transition was obtained above 500 nm.

In this work we obtain two transitions that could be assigned to the 650 nm band; one at 568 nm that corresponds to a ICT(CN) → ICT(CN) transition from the RICT intermediate and the other at 691 nm that corresponds to a LE → ICT(Q) transition from the LE intermediate. The first band is coincident with the one obtained at the TDDFT level. It is possible that the second one was not found at the TDDFT level due to difficulties of this method to describe charge transfer states. Comparing our results with the experimental maximum of the band in n-hexane (approx. 650 nm), we cannot assign the experimental band to one specific transition on energetic grounds, given that the energy differences are similar (both of the order of 5 kcal mol⁻¹). The relationship between the polarity of the species and the shift of the bands could help.

We have to take into account that the shift of a transition with changing solvent polarity is related not only to the character of the initial state, but it depends on the dipole moments of the two states involved in the transition.

The band from the RICT species (calculated at 568 nm) corresponds to an excitation from state 2 (μ = 13.76 D) to state 5 (μ = 9.2 D). State 2 will be more stabilized by polar solvents than state 5 leading to an increase of the energy difference between both states, and to a shortening of the wavelength with a blue-shift of the spectra. This predicted behaviour with solvent polarity is the one observed experimentally (a blue shift of the band when the polarity of the solvent is increased), what supports the assignment of the band at 650 nm to a RICT transition, despite the poorer fit of the calculated transition energy.

On the other hand, the other LE transition calculated at 691 nm is characterized by a promotion from state 2 (μ = 6.78 D) to state 4 (μ = 8.38 D). In the polar solvent the upper state will be stabilized preferentially, decreasing the energy difference and consequently shifting the band to the red. This behaviour is opposite to the one observed experimentally, so the assignment of the band observed at 650 nm to this transition is ruled out, despite the fact that the calculated energy of transition is in better agreement with the experimental measurement.

The assignment of the 650 nm band to a transition from the RICT transient support the mechanism that proposes the ICT(CN) state as intermediate of the ICT reaction. Nevertheless the wideness of the experimental band does not allow ruling out completely the contribution of a transition from the LE species to this band.

As a whole, our results support the hypothesis of the involvement of the ICT(CN) state and the population of the RICT species in the photochemistry of ABN, playing the role of an alternative path of population of the LE minimum.

3.5 Thermally activated radiationless deactivation

Since the fluorescence intensity of ABN strongly decreases when the increase in temperature (ϕ_f = 0.021 and 0.009, at 25 °C and 284 °C in n-hexane respectively),⁵⁵ we also investigated the possible non-radiative decay channels competing with the path of luminiscence from S₁. We will restrict our study to the singlet manifold, so to the possible paths for internal conversion from S₁ to the ground state.

We have found four different channels for S₁–S₀ internal conversion in ABN through conical intersections. Fig. 17 summarizes schematically the profiles of different pathways found. It also displays the structures of the minimum energy points of the S₀/S₁ conical intersections located. In all the cases, the geometrical distortions correspond mainly to the puckering carbon atoms of the ring (geometrical parameters in ESI†). CI-1, CI-3 and CI-4 are LE/S₀ crossings whereas CI-2 corresponds to a CT/S₀ crossing. Fig. 17 also collects the energies of the transition states that we located of the paths leading from the S₁-LE minimum to CI-1 and CI-3.

Fig. 17 Schematic potential energy profiles regarding the S₀/S₁ internal conversion for ABN. MS-CASPT2 energies in kcal mol⁻¹.

We confirmed the absence of TS in the paths to CI-1 and CI-4 calculating the profile of the S₀ and S₁ surfaces along the LIIRC path between the S₁-LE minimum and the corresponding S₀/S₁-CI, which show that the highest energy point in both cases corresponds to the CI. These interpolations, together with a study of the shape (peaked or sloped) of the S₀/S₁ CIs can be found in the ESI.†

As pointed out in ref. 55, the internal conversion activation energy measured experimentally corresponds to the barrier that has to be overcome to bring the system to the S₀/S₁ CI. The lowest activation barrier is 8.69 kcal mol⁻¹, corresponding to the path to CI-4, in surprisingly good agreement with the value of 8.3 kcal mol⁻¹ estimated in n-hexane.⁵⁵ The value of this activation barrier explains that in ABN the decay channel through internal conversion only becomes important above room temperature.

4 Conclusions

In view of the results obtained, we propose the following mechanism to explain the photophysics of ABN. This is resumed in a cartoon like scheme in Fig. 18.

Fig. 18 Schematic excited state reaction profiles of ABN.

The initial excitation populates the second excited state, of the ICT(Q) character, although a small absorption to the first excited state of the LE character is also possible. This prediction is in agreement with the experimental absorption spectra that show an intense S₀ → S₂ band and a weaker S₀ → S₁ band. On the S₂ PES, the most probable process is relaxation to the PICT minimum, but the system immediately decays through a conical intersection to the S₁ surface. Here, the system has two possibilities: to continue in the S₁-ICT(Q) state, or more probably, to undergo internal conversion to the S₁-LE state. If the system moves to the LE surface, there also are two possibilities: to populate the LE minimum or to undergo internal conversion through a S₁/S₀ conical intersection. In the first case the system will decay radiatively leading to the normal emission. To follow the second path, certain activation energy is necessary that the system will only get at high temperatures. In this case we will observe radiationless deactivation, at the expense of fluorescence. These results explain the experimental observation of the decrease of the fluorescence quantum yield when the temperature increases.

If, in the first CI, the system continues on the S₁-ICT(Q) surface, it will relax on this surface and populate the TICT minimum. This species, nevertheless, is less favoured thermodynamically and kinetically than the LE one.

Another possible but less probable event after the initial excitation is a crossing (with a barrier of 1.9 kcal mol⁻¹) from the ICT(Q) state to the ICT(CN). If this state is reached, the system will relax on this surface and populate the RICT minimum. This is adiabatically connected with the LE minimum so, given that the last one is thermodynamically and kinetically favoured, the system will evolve quickly from the RICT minimum to the LE one.

According to our results then, we predict that in the initial steps the LE minimum will be populated preferentially. A smaller proportion of excited molecules will relax along the ICT(Q) PES to reach the TICT minimum, and an even smaller proportion will cross to the ICT(CN) PES to reach the RICT minimum. The life of the RICT and TICT species, though, will be very short, given that the LE species is strongly favoured in ABN, both kinetically and thermodynamically. This hypothesis is supported by the transient absorption experimental and theoretical results: absorption bands from the LE, TICT and RICT minima are predicted in both cases.

This landscape will not change significantly in polar solvents: in spite of the larger stabilization of the ICT(Q) and ICT(CN) states in this environment, the LE minimum will continue corresponding to the most stable species, which explains that the photochemistry of ABN does not change appreciably from the gas phase to the solution.

The photophysics of ABN is explained by the entangled interplay between the potential energy surfaces of the lowest excited states of LE, ICT(Q) and ICT(CN) character. The ICT(AQ) state does not seem to be involved at any stage in the photochemistry of this system. To understand the sequence of events that take place, it is necessary not only to locate and calculate accurately the energy of the excited species, but also to find the possible channels connecting them and to determine the barriers of this paths (given by the energy of conical intersections or transition states) to finally establish the most probable processes. Nevertheless, the study of the photochemistry of ABN should be completed by dynamic calculations, which are out of the scope of this work.

Acknowledgements

Financial support has been provided by the Spanish Administration (CTQ2011-23140 and CTQ2014-51938), the Generalitat de Catalunya (2014SGR199 and Xarxa d'R + D + I en Química Teórica i Computacional, XRQTC).

References

1. Z. R. Grabowski, K. Rotkiewicz and W. Rettig, Chem. Rev., 2003, 103, 3899–4030.
2. V. Rettig, Angew. Chem., Int. Ed. Engl., 1986, 25, 971–988.
3. C. Bosshard, K. Sutter, P. Pretre, J. Hulliger, M. Florsheimer, P. Kaatz and P. Gunter, Organic Nonlinear Optical Materials, Advances in Nonlinear Optics, Gordon and Breach Publishers, New York, 1995.
4. B. Kippelen, H. S. Lackritz and R. O. Claus, Organic Nonlinear Optical Materials and devices, Materials Research Society, Warrendale, 1999.
5. J. P. Lakowicz, Principles of Fluorescence Spectroscopy, Kluwer Academic, Hongham, 1999.
6. J. J. La Chair, Angew. Chem., Int. Ed., 1999, 38, 3047–3050.
7. J. J. La Chair, Angew. Chem., Int. Ed., 1998, 37, 325–329.
8. J. J. La Chair, Angew. Chem., Int. Ed., 1998, 110, 339.
9. E. Lippert, W. W. Lüder, F. Moll, W. Nägele, H. Boos, H. Prigge and I. Seybold-Blankestein, Angew. Chem., 1961, 73, 695.
10. O. Khalil, R. Hofeldt and S. McGlynn, Chem. Phys. Lett., 1972, 17, 479–481.
11. N. Nakashima, H. Inoue, N. Mataga and C. Yamanaka, Bull. Chem. Soc. Jpn., 1973, 46, 2288–2290.
12. E. Chandross and H. Thomas, Chem. Phys. Lett., 1971, 9, 397–400.
13. R. Visser and C. Varma, J. Chem. Soc., Faraday Trans. 2, 1980, 76, 453–471.
14. W. Rettig and G. Wermuth, J. Photochem., 1985, 28, 351–366.
15. W. Schuddeboom, S. A. Jonker, J. H. Warman, U. Leinhos, W. Künhle and K. A. Zachariasse, J. Phys. Chem., 1992, 96, 10809.
16. K. A. Zachariasse, T. Von Der Haar, A. Hebecker, U. Leinhos and W. Künhle, Pure Appl. Chem., 1993, 65, 1745.
17. K. A. Zachariasse, M. Grobys, T. Vonderhaar, A. Hebecker, Y. Ilichev, Y. Jiang, O. Morawski and W. Künhle, J. Photochem. Photobiol., A, 1996, 102, 59–70.
18. K. A. Zachariasse, J. Photochem. Photobiol., A, 1997, 105, 373–383.
19. S. I. Druzhinin, N. P. Ernsting, S. A. Kovalenko, L. P. Lustres, T. A. Senyushkina and K. A. Zachariasse, J. Phys. Chem. A, 2006, 110, 2955–2969.
20. Z. R. Grabowski, K. Rotkiewicz and K. H. Grellman, Chem. Phys. Lett., 1973, 19, 315–318.
21. A. Sobolewski, Chem. Phys. Lett., 1996, 259, 119–127.
22. A. Sobolewski, Chem. Phys. Lett., 1996, 250, 428–436.
23. T. Gustavsson, P. B. Coto, L. Serrano-Andrés, T. Fujiwara and E. C. Lim, J. Chem. Phys., 2009, 131, 031101.
24. P. B. Coto, L. Serrano-Andrés, T. Gustavsson and T. Fujiwara, Phys. Chem. Chem. Phys., 2011, 12, 15182–15188.
25. A. Perveaux, P. J. Castro, D. Lauvergnat, M. Reguero and B. Lasorne, J. Phys. Chem. Lett., 2015, 6, 1316–1320.
26. S. I. Druzhinin, N. P. Enrsting, S. A. Kovalenko, L. Pérez Lustres, T. A. Senyushkina and K. A. Zachariasse, J. Phys. Chem. A, 2006, 110, 2955–2969.
27. I. Gómez, M. Reguero, M. Boggio-Pasqua and M. A. Robb, J. Am. Chem. Soc., 2005, 127, 7119–7129.
28. I. Georgieva, A. J. A. Aquino, F. Plasser, N. Trendafilova, A. Kohn and H. Lischka, J. Phys. Chem. A, 2015, 119, 6232–6243.
29. J.-K. Lee, T. Fujiwara, W. G. Kofron, M. Z. Zgierski and E. C. Lim, J. Chem. Phys., 2008, 128, 164512.
30. R. Ramos, T. Fujiwara, M. Z. Zgierski and E. C. Lim, J. Phys. Chem. A, 2005, 109, 7121–7126.
31. A. L. Sobolewski, W. Sudholt and W. Domcke, J. Phys. Chem. A, 1998, 102, 2716–2722.
32. T. Fujiwara, M. Z. Zgierski and E. C. Lim, Phys. Chem. Chem. Phys., 2011, 13, 6779–6783.
33. W. W. Schuddeboom, S. A. Jonker, J. M. Warman, U. Leinhos, W. Kühnle and K. A. Zachariasse, J. Phys. Chem., 1992, 96, 10809–10819.
34. W. M. Kwok, C. Ma, D. Phillips, P. Matousek, A. W. Parker and M. Towrie, J. Phys. Chem. A, 2000, 104, 4188–4197.
35. I. Gómez, Y. Mercier and M. Reguero, J. Phys. Chem. A, 2006, 110, 11455–11461.
36. M. Segado, M. A. Carvajal, I. Gómez and M. Reguero, Theor. Chem. Acc., 2011, 128, 713–725.
37. I. Gómez, P. J. Castro and M. Reguero, J. Phys. Chem. A, 2015, 119, 1983–1995.
38. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
39. I. N. Ragazos and M. A. Robb, Chem. Phys. Lett., 1992, 197, 217–221.
40. L. Blancafort, P. Celani, M. J. Bearpark and M. A. Robb, Theor. Chem. Acc. Theor. Comput. Model. Theor. Chim. Acta, 2003, 110, 92–99.
41. P. Malmqvist, A. Rendell and B. O. Roos, J. Phys. Chem., 1990, 94, 5477–5482.
42. N. Forsberg and M.-A. Malqvist, Chem. Phys. Lett., 1997, 274, 196–204.
43. J. Finley, P. A. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306.
44. P. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240.
45. L. Serrano-Andrès, M. Merchán and A. C. Borin, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 8691–8696.
46. C. Gonzalez and B. J. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
47. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford, CT, 2004.
48. G. Karlstrom, Comput. Mater. Sci., 2003, 28, 222–239.
49. A. Heine, R. Herbst-Irmer, D. Stalke, W. Kühnle and K. A. Zachariasse, Acta Crystallogr., 1994, B50, 363–373.
50. J. Dreyer and A. J. Kumrow, J. Am. Chem. Soc., 2000, 122, 2577–2585.
51. U. Lommatzsch and B. Brutschy, Chem. Phys., 1998, 234, 35–57.
52. L. Serrano-Andrés, M. Merchan, B. O. Roos and R. Lindh, J. Am. Chem. Soc., 1995, 117, 3189–3204.
53. V. A. Galievsky, S. I. Druzhinin, A. Demeter, Y. Jiang, S. A. Kovalenko, L. P. Lustres, K. Venugopal, N. P. Ernsting, X. Allonas, M. Noltemeyer, R. Machinek and K. A. Zachariasse, ChemPhysChem, 2005, 6, 2307–2323.
54. S. I. Druzhinin, Y. Jiang, A. Demeter and K. A. Zachariasse, Phys. Chem. Chem. Phys., 2001, 3, 5213–5221.
55. S. I. Druzhinin, A. Demeter, V. A. Galievsky, T. Yoshihara and K. A. Zachariasse, J. Phys. Chem. A, 2003, 107, 8075–8085.
56. Y. V. Il'ichev, W. Kühnle and K. A. Zachariasse, J. Phys. Chem., 1998, 102, 5670–5680.
57. K. A. Zachariasse, S. I. Druzhinin, S. A. Kovalenko and T. Senyushkina, J. Chem. Phys., 2009, 131, 224313.

---

Footnote

† Electronic supplementary information (ESI) available: Details on the active space; influence of the number of states averaged on the description of the excited states at GS geometry in ABN; energies and geometries of critical points of secondary importance; and radiationless deactivation in ABN. See DOI: 10.1039/c5cp04690d

---