 Open Access Article
Open Access ArticlePrediction of the Chapman–Jouguet chemical equilibrium state in a detonation wave from first principles based reactive molecular dynamics†
Dezhou
Guo
ab,
Sergey V.
Zybin
b,
Qi
An
b,
William A.
Goddard III
*b and
Fenglei
Huang
a
aState Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, People’s Republic of China
bMaterials and Process Simulation Center, 139-74, California Institute of Technology, Pasadena, California 91125, USA. E-mail: wag@wag.caltech.edu
First published on 17th November 2015
Abstract
The combustion or detonation of reacting materials at high temperature and pressure can be characterized by the Chapman–Jouguet (CJ) state that describes the chemical equilibrium of the products at the end of the reaction zone of the detonation wave for sustained detonation. This provides the critical properties and product kinetics for input to macroscale continuum simulations of energetic materials. We propose the ReaxFF Reactive Dynamics to CJ point protocol (Rx2CJ) for predicting the CJ state parameters, providing the means to predict the performance of new materials prior to synthesis and characterization, allowing the simulation based design to be done in silico. Our Rx2CJ method is based on atomistic reactive molecular dynamics (RMD) using the QM-derived ReaxFF force field. We validate this method here by predicting the CJ point and detonation products for three typical energetic materials. We find good agreement between the predicted and experimental detonation velocities, indicating that this method can reliably predict the CJ state using modest levels of computation.
1 Introduction
Environment and energy needs demand development of maximally efficient propulsion combustion systems and energetic materials that minimize products detrimental to the environment. Moreover, the behaviour of materials under extreme conditions of high temperature and pressure is of critical importance in many fields of physics, astrophysics, planetary science, and hydrodynamics,1,2 where the difficulty in extracting atomistic understanding of reaction mechanisms in hot compressed materials from experiments makes it particularly important to predict the processes from the computational modelling and simulation. The complexity of the combustion and detonation processes might seem to preclude applications of first principles to predict the performance and reaction kinetics for new materials in advance of their synthesis and characterization. However, we propose a practical simulation approach based on first principles theory for predicting the performance of energetic materials, which we validate for three well-known materials.A critical characteristic of energetic materials is the Chapman–Jouguet (CJ) state, which describes the chemical equilibrium of the products at the end of the reaction zone of the detonation wave before the isentropic expansion. In the classical Zel'dovich–Neumann–Döring (ZND) detonation model, the detonation wave propagates at the constant velocity for which the CJ point characterizes the state of reaction products in which the local sound speed decreases to the detonation velocity as the product gases expand. Although a simple concept, the time and length scale of CJ state have thwarted experimental characterization.3 These laboratory challenges have stimulated theoretical developments, such as variational perturbation theory4 and integral equation theory,5,6 to provide numerical models. Unfortunately, these approaches have been hampered by a lack of knowledge about the atomistic chemical and physical processes and by inaccuracy in the assumed equations of state (EOS).
Thus, we need new simulation tools that are capable of establishing the CJ state parameters for proposed materials directly from first principles. These simulation tools must provide an accurate description of the various reaction processes that convert materials to detonation products and they must be capable of making predictions in advance of experiment. Quantum mechanics (QM) can in principle describe reaction processes for new materials but the time and length scales required are many orders of magnitude beyond the capability of current QM methods.
We demonstrate in this paper a practical approach to use reactive molecular dynamics (RMD) to predict the CJ state in which the QM-derived ReaxFF reactive force field is used to provide the detailed description of the atomistic processes occurring in a detonation wave. This allows a practical determination of the CJ parameters for new materials prior to experiment.3,7–12
Here, for the first time the Crussard curve and the CJ point are predicted from first-principles based reactive molecular dynamics (RMD) simulations without the need for ad hoc definitions of reaction products. We demonstrate this approach by applying it to three energetic materials that are currently widely used in industry:
• Cyclotrimethylene-trinitramine (RDX),
• Cyclotetramethylene tetranitramine (HMX), and
• Pentaerythritol-tetranitrate (PETN).
2. Methodology
The ReaxFF reactive force field combines• charge equilibration method (EEM or QEq13) to predict the changes in the partial charges on atoms at every time step of the reaction dynamics. Here the parameters were determined to fit QM charges of isolated molecules. In this method the charges of bonded atoms are allowed to interact, but they decreased by shielding based on atomic sizes
• a bond order versus bond distance sigmoid-like relationship and a bond energy versus bond order relationship adjusted to fit the results of QM calculations as function of bond distance for numerous systems
• van der Waals type nonbond interactions adjusted to describe long range London attraction, intermediate range steric effects, and short range Pauli repulsion between all atoms (including bonded atoms)
• various other valence interactions (bond angle and torsion) that all go to zero as bonds are broken with parameters fitted to a large data set of QM calculations.
ReaxFF has now been established to provide nearly the accuracy of QM calculations14–16 with computational costs nearly that of molecular dynamics (MD) with ordinary force fields (FFs).17,18 This has enabled the simulation of complex sequence of reactions and multiple intermediates during shock transformation and thermal decomposition of energetic materials, with application to 3.7 million atoms for ∼100 nanoseconds.19–26 Thus, ReaxFF enables the atomistic description of the chemical reactions and products in detonation wave defining the CJ state. Moreover, the reactive molecular dynamics (RMD) using ReaxFF provide the means for obtaining the equation of state (EOS) of reacting materials at the atomistic level without the necessity of ad hoc assumptions about reaction products and their properties. Indeed we obtain a detailed description of all chemical reactions during the decomposition processes, including the formation of carbonaceous clusters generally ignored in previous models. This allows a direct comparison of the theory with experiment through the CJ state parameters while providing atomistic information about the chemical reaction processes and products on each dynamics step inaccessible from experiments. Moreover it allows the prediction of these detonation properties prior to experimental synthesis and characterization, to enable in silico design of new energetic materials.
According to the classical ZND model, the thermodynamic quantities of a material in the initial unshocked state and the final shocked state are related by the conservation equations of mass, momentum, and energy across the shock front as
| ρ0D = ρ(D − u), | (1) |
| p − p0 = ρ0uD, | (2) |
| e + pv + ½(D − u)2 = e0 + p0v0 + ½D2, | (3) |
| H = e − e0 − ½(p + p0)(v0 − v). | (4) |
The Hugoniot function relates the energy of two thermodynamic states: the initial unshocked state and the shocked state, so that H = 0 simply expresses the energy conservation in the shock or detonation wave. The set of (p,v,T) parameters for which H = 0 determines the Hugoniot curve of shocked states in the inert (unreacted) material as well as the states along the Rayleigh line in the reacting material. According to the ZND model, the explosive material remains inert during the shock compression at the detonation front, which is considered as a sudden step-like increase in the temperature and pressure. Then the chemical reactions start, followed by further increase in the temperature due to the exothermic energy release and decrease in the pressure due to the expansion of the reaction products. As a result, the states in the reacting material follow the expansion pathway along the Rayleigh line down to the CJ state on the Crussard curve, which is an expansion isentrope of the detonation products. In fact, there are many expansion isentropes corresponding to different product compositions, but only one has a tangent point to the Rayleigh line, which satisfies CJ condition and is called the CJ state.
Our first test of this ReaxFF Reactive Dynamics to CJ point protocol (Rx2CJ) is on RDX. Here we start with equilibration of the RDX supercell containing 96 molecules (or 2016 atoms) at constant temperature T0 = 300 K and pressure p0 = 1 atm, obtaining an initial state equilibrium volume v0 = 0.568 cm3 g−1 and density ρ0 = 1.76 g cm−3 (in a good agreement with the 1.806 g cm−3 experimental density of neat RDX).
Then we use ReaxFF to predict the final state in which complete reaction products are calculated from a long cook-off holding the system at a prescribed temperature that leads to stable products (H2O, CO2, N2, CO etc.). We find that this requires ∼250 ps for the energetic materials being considered here.
Fig. 1 illustrates one example for RDX at T = 2700 K and V = 0.85 V0. We observe the gradual approach to equilibrium for the potential energy, as well as the stable compositions of the final products (inset of figure), indicating that steady state convergence is reached after 200 ps. Consequently, we average the properties of the trajectories over the last 100 of the 350 ps total trajectory. In the earlier energy releasing period within the first 250 ps, the Hugoniot and potential energy curve trend downward, indicating the dominance of exothermic chemical reactions.
 | ||
| Fig. 1 Time evolution of the potential energy per unit mass and reaction products (inset for the last 100 ps of NVT simulation) for RDX at T = 2700 K and V/V0 = 0.85. The solid horizontal line shows an average over the final 100 ps of simulation while the dashed lines mark the standard deviation above and below the average values from five independent simulations. The corresponding plots for PETN and HMX are included in the ESI.† | ||
To validate that 350 ps was sufficient to reach equilibrium, we extended one case for RDX decomposition up to 550 ps and calculated the averages of thermal properties and the main reaction products from 200 ps to 550 ps. The potential energy of −1.127 ± 0.014 kcal g−1 for the last 100 ps of the 550 ps simulation agrees with the previous value of −1.130 ± 0.014 kcal g−1 averaged between 200 and 300 ps. The product distributions were also the same as shown in Fig. S2 of the ESI.†
For each specific temperature we obtain a family of Hugoniot function values by changing the density (volume) of the material. From these curves we find the Hg = 0 points that determine the Crussard curve. We determine five Hg = 0 points to describe the Crussard curve accurately. Each Hg = 0 point corresponds to a specific temperature. For each temperature, we do at least three different compression ratios to bracket the Hg = 0 case, as shown in Fig. 2. The compression volume ratios at the intersection between Hugoniot function for a fixed temperature and the Hg = 0 axis provides the location of one point in the Crussard curve of Fig. 3a.
 | ||
| Fig. 2 The family of isotherms (spline fitted) for RDX at compression ratios from 0.60 to 0.85 for five different temperatures. For each temperature we did five independent calculations to estimate the standard deviation error bars. The intersection of these curves with the H = 0 line provides five points along the Crussard isentrope that are plotted in Fig. 3: V/V0 = 0.660 at 3000 K, 0.685 at 2900 K, 0.715 at 2800 K, 0.760 at 2700 K, and 0.830 at 2600 K. The corresponding plots for PETN and HMX are included in the ESI.† | ||
 | ||
| Fig. 3 Calculation of the CJ state parameters by fitting the Crussard curve to a series of equilibrium states simulated by the ReaxFF RMD method (Rx2CJ). (a) The CJ point is the tangent point of the Rayleigh line to the Crussard curve fitted with a quadratic polynomial. This fitting provides the CJ point with compression ratio V/V0 = 0.76 and pressure PCJ = 28.62 GPa for RDX. (b) Equilibrium temperatures for the various points along the Crussard curve, fitted to a quadratic polynomial. The predicted CJ temperature for RDX30,31 is 2700 K, as indicated by the circle. The corresponding plots for PETN and HMX are included in the ESI.† | ||
We examined the points obtained from Fig. 2 at each temperature and found that their Hugoniot values remain quite close to 0. Thus these points provide an accurate description of the Crussard curve. Then, as shown in Fig. 3a, we fit the pressure versus V/V0 to a quadratic polynomial that expresses the evolution of pressure as a function of the volume compression. The temperature is expressed in the same way, as shown in Fig. 3b.
Once we have determined the Crussard curve as in Fig. 3, we can determine the CJ point. The CJ point is the tangent point between the Rayleigh line and the Crussard curve, as illustrated in Fig. 3. Thus, at the CJ point, the derivative of the pressure along the Crussard curve with respect to the volume is given by the slope of the Rayleigh line. We represent the Crussard curve and Rayleigh line as:
| P = a0 + a1n + a2n2 | (5) |
| P = an + b | (6) |
Here, as the shock wave starts from the undisturbed material, the Rayleigh line starts from the point at (1, 0). As a result, the Rayleigh line can be expressed as:
| P = an − a. | (7) |
For the Rayleigh line that is a tangent line to the Crussard curve, we obtain:
| a = a1 + 2a2n. | (8) |
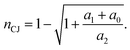 | (9) |
From here, we obtain the CJ temperature by substituting nCJ into the temperature-compression ratio curve.
We denote this method as the ReaxFF RMD to CJ point method (Rx2CJ). From the calculated PCJ and nCJ, we calculate the detonation velocity DCJ, using the following equation derived from the Hugoniot relations:
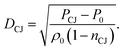 | (10) |
This predicted detonation velocity is important because it can be measured directly from experiments, providing an overall validation of the entire computational process of predicting the CJ state parameters from atomistic simulations.
3. Results and discussions
We applied the Rx2CJ protocol to predict the Crussard curve and CJ state parameters for 4 systems:• An RDX supercell containing 96 molecules (or 2016 atoms) at constant temperature T0 = 300 K and pressure p0 = 1 atm, obtaining an initial state equilibrium volume v0 = 0.568 cm3 g−1 and density ρ0 = 1.76 g cm−3, (in good agreement with the 1.806 g cm−3 experimental density of neat RDX). This leads to D = 8266 ± 198 m s−1 for RDX, which is 4.7% below the experimental values of 8639 ± 41 m s−1 and 8700 m s−1.
• A β-HMX supercell containing 96 molecules (or 2688 atoms) at constant temperature T0 = 300 K and pressure p0 = 1 atm, obtaining an initial state equilibrium volume v0 = 0.538 cm3 g−1 and density ρ0 = 1.86 g cm−3, (in good agreement with the 1.90 g cm−3 experimental density of neat β-HMX). This leads to D = 8401 ± 217 m s−1 for β-HMX which is 4.5% below the experimental values of 8740 m s−1 and 8880 m s−1.
• A PETN supercell containing 72 molecules (or 2088 atoms) at constant temperature T0 = 300 K and pressure p0 = 1 atm, obtaining an initial state equilibrium volume v0 = 0.581 cm3 g−1 and density ρ0 = 1.72 g cm−3, (in good agreement with the 1.77 g cm−3 experimental density of neat PETN). This leads to D = 7440 ± 209 m s−1 for PETN, which is 7.1% below with the experimental values of 7975 m s−1 and 8260 m s−1.
• The decomposition of a model mixture of 27 H2 and 27 O2 molecules using the same ReaxFF parameters started an initial density of 0.09 g cm−3 at an initial temperature of 123 K. This leads to a CJ temperature of 2600 K and a detonation velocity of 2538 ± 377 m s−1, which is 9.3% below the experimental values32, which range from 2800 to 3000 m s−1 (see more details in ESI†).
The predicted CJ parameters are in reasonable agreement with experiment data, but they are slightly below the experimental values. We believe that this is because the products evolution shown in Fig. 1 on the timescale up to 350 ps still contains carbonaceous products (0.47 mol/mol for RDX, 0.52 mol/mol for PETN 0.48 mol/mol for β-HMX). Under experimental conditions in which the reaction zone persists for microseconds, much of these carbonaceous materials may burn off to form additional gases and hence a higher velocity. We consider that these results validate the Rx2CJ method for first principles based predictions of performance properties for new propellants and explosive materials, where the systematic underestimate of the experimental velocity will still provide a valid measure of performance.
Sewell and co-workers33,34 suggested that quantum nuclear vibrational effects ignored in classical MD, lead to an underestimate of the temperature along the Hugoniot curve for weak to medium shocks (<1 km s−1). Moreover, Goldman et al.35 suggest that such problems with classical MD could explain the discrepancy of their QM simulations with experiments. The quantum nuclear vibrational effects might slightly affect the calculated pressure and temperature at the CJ conditions.36 The quantum effects will enhance the chemical reactivity of the system, allowing it to approach chemical equilibrium more rapidly.36
The predicted properties at CJ state for the three materials are collected in Table 1.
| RDX | PETN | HMX | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ReaxFF | Exp138 | Exp239 | ReaxFF | Exp140 | Exp239 | ReaxFF | Exp141 | Exp241 | |
| Density (g cm−3) | 1.76 | 1.767 | 1.77 | 1.72 | 1.67 | 1.76 | 1.86 | 1.832 | 1.875 |
| P CJ (GPa) | 28.62 ± 4.77 | 22.47 ± 3.09 | 32.68 ± 3.43 | ||||||
| T CJ (K) | 2700 ± 56 | 2460 ± 40 | 2680 ± 58 | ||||||
| V CJ (cm3 g−1) | 0.433 ± 0.019 | 0.445 ± 0.013 | 0.404 ± 0.021 | ||||||
| D CJ (m s−1) | 8266 ± 198 | 8639 ± 41 | 8700 | 7440 ± 209 | 7975 | 8260 | 8401 ± 223 | 8740 | 8880 |
Along with these detonation parameters, we can extract from our simulations detailed distribution of chemical products at the CJ states. We do this using a bond order based molecular fragment analysis on the RMD simulation trajectory (tabulated in ESI†), leading to the results shown in Table 2. These results are averaged over 3 independent trajectories and over the last 100 ps of the 350 ps simulation.
| RDX | PETN | HMX | |||||
|---|---|---|---|---|---|---|---|
| Experiment confined (gas phase) | ReaxFF (condensed) | Experiment confined (gas phase) | ReaxFF (condensed) | Experiment confined (gas phase) | ReaxFF (condensed) | ||
| a Number of atoms (% of system total) included in the above products. b Some small aggregates still exist at such high temperature and pressure conditions in the CJ state. | |||||||
| Density (g cm−3) | 1.76 | 1.76 | 1.73 − 1.74 | 1.72 | 1.89 | 1.86 | |
| ΔH (cal g−1) | 1452 ± 15 | 1458 ± 12 | 1370 | 1331 ± 15 | 1479 ± 12 | 1520 ± 19 | |
| Products | N2 | 2.80 | 2.38 ± 0.04 | 2.00 | 1.81 ± 0.02 | 3.68 | 3.13 ± 0.03 |
| (mol/mol) | H2O | 2.34 | 1.50 ± 0.05 | 3.50 | 3.00 ± 0.03 | 3.18 | 2.45 ± 0.04 |
| HO | 0.24 ± 0.05 | 0.20 ± 0.06 | 0.25 ± 0.05 | ||||
| CO2 | 1.39 | 1.14 ± 0.03 | 3.39 | 2.37 ± 0.06 | 1.92 | 1.29 ± 0.03 | |
| CO | 1.10 | 0.23 ± 0.02 | 1.69 | 0.18 ± 0.01 | 1.06 | 0.24 ± 0.02 | |
| C(S) | 0.44 | 0.97 | |||||
| H2 | 0.34 | 0.43 ± 0.01 | 0.45 | 0.27 ± 0.01 | 0.30 | 0.41 ± 0.01 | |
| NH3 | 0.028 | 0.46 ± 0.03 | 0.038 | 0.20 ± 0.02 | 0.39 | 0.43 ± 0.02 | |
| HCN | 0.029 | 0.008 | |||||
| CH4 | 0.041 | 0.003 | 0.039 | ||||
| Material recovery (%)a | |||||||
| C | 85.5 | 45.67 | 101.5 | 51.00 | 75.6 | 42.5 | |
| H | 94 | 91.33 | 100.1 | 91.75 | 104 | 90.75 | |
| N | 94.2 | 87.00 | 100.8 | 95.50 | 97.1 | 83.63 | |
| O | 104 | 66.50 | 99.7 | 67.67 | 101 | 72.38 | |
| (mol/mol) | Carbon clusters b | 0.47 | 0.52 | 0.48 | |||
| Cluster composition | C2.3H0.7N1.0O2.5 | C3.3H0.6N0.3O2.6 | C2.3H0.7N1.3O2.2 | ||||
| Total molecules | 96 | 72 | 96 | ||||
For example, for each mole of the PETN explosive we find that the main products at the CJ state are
• 1.81 moles of N2 (2.00 experimental),
• 3.00 moles of H2O (3.50 experimental),
• 2.37 moles of CO2 (3.39 experimental),
• 0.18 moles of CO (1.69 experimental) and
• carbonaceous clusters with an overall composition of C3.3H0.6N0.3O2.6 containing approximately 49% of the original C, 32% of the original O and 8% of the original H atoms (these clusters are not characterized experimentally at the CJ state).
We also found small amounts of other molecules, such as 0.20 moles of NH3, 0.20 moles of OH and 0.27 moles of H2.
The total number of N2, H2 and H2O molecules agrees well with calorimeter bomb experiment;37 but the prediction for CO2 from PETN is 30% lower than observed experimentally, while that of CO is 89% lower. This is because the products in calorimetric experiments are formed over a timescale of seconds, allowing further expansion along the Crussard isentrope and cooling down into the gas phase at normal conditions. However our constant-volume simulations measure the product composition at the CJ state for thermodynamic conditions in the hot compressed material. Thus we end up in a state with temperature of 2000–4000 K and pressure of 20–50 GPa. As a result, our simulations show an additional number of carbon and oxygen atoms remaining agglomerated in small carbon containing clusters. Although this may affect slightly the resulting product distribution and the total energy release over the 350 ps timescale of our simulations it should allow accurate comparisons in performance of various materials.
We estimated the mass percentage of carbon clusters, final products, and other small isolated molecules at the CJ state conditions for RDX, as shown in Fig. 4(a). About 29% mass of the system is in the form of clusters containing C, O, N, and H.
To determine the stability and evolution of these clusters in expanding gases, we applied the “linear volume expansion” procedure24 using variable-volume RMD simulations: here the system volume V0 is increased very slowly at a linear rate within 100 ps until it expands to 8 V0. The evolution of carbon clusters, CO2 and CO molecules during the expansion are shown in Fig. 4(b). As expected, many agglomerates continue to decompose, producing additional CO2 and CO products. Indeed we saw exactly the same result in our previous expanded-volume RMD simulations of RDX16 as well as for HMX and TATB.24 We expect that this after-burning of carbonaceous clusters would affect the predicted product compositions in expanded gases, bringing it closer to experiment.
To estimate the additional energy release from carbonaceous cluster decomposition induced by the expansion simulation of 100 ps, we recompressed the expanded system back to the CJ volume and temperature over an additional 50 ps (see Fig. 5). We found that the potential energy release increased about 2.4% and the pressure increased about 2.1%, leading to a detonation velocity of 8314 m s−1, which is ∼0.6% higher than the previous results (8266 m s−1).
Some of the minor discrepancies between Rx2CJ prediction and experiment may reflect inaccuracy in the ReaxFF description and some may arise from imperfections in the experiments (e.g. nonuniform detonation front conditions and difficulties in precise measurements of detonation temperature and pressure).
Previous studies aimed at predicting the CJ state parameters were based on the simple nonreactive potentials for intermolecular interactions3,9 and involved Monte Carlo estimates of statistical ensembles with a predefined set of the reactions over a small set of molecules (RxMC).27–29 Thus these previous approaches depend strongly on defining an ad hoc set of the final products and their reactions for an assumed chemical equilibrium of their mixture. In contrast, our Rx2CJ approach predicts the detonation products at the CJ state without any assumption about their composition. It does this directly from the ReaxFF RMD simulation of the complex chemical reactions, starting from the initial neat reactant to obtain the CJ state thermodynamic conditions. A similar approach employing MD simulations with the generic reactive AB-potential10 was recently applied to calculate the CJ state properties as well as complex cellular structure of the detonation front for an AB-model of a diatomic explosive.42
4. Summary and conclusions
We propose the first-principles based ReaxFF Reactive Dynamics to CJ state protocol (Rx2CJ) to predict the thermochemical parameters at the CJ state characterizing a self-sustaining detonation wave in energetic materials. We applied Rx2CJ to three well-studied explosives (RDX, PETN and HMX) and to a H2/O2 mixture.The predicted CJ detonation velocities are in good agreement with available experimental data: for RDX, HMX, and PETN, but systematically low by 4% to 7%. We consider that part of this modest error may arise because even after ∼250 ps of the system evolution in the NVT simulation, a significant number of carbon and oxygen atoms remains agglomerated in small carbonaceous clusters (0.47 mol/mol for RDX, 0.52 mol/mol for PETN, 0.48 mol/mol for β-HMX), while the typical reaction zone in detonation experiment is thought to be considerably longer (from nano- to microseconds). Thus, the carbon clusters may continue to burn off to form additional gases, leading to additional energy release hence a higher velocity.
Indeed, allowing the RDX system volume to expand isoentropically by a factor of 8 over an additional 100 ps, we observed the formation of additional CO and CO2 gases.
We consider that these results validate the Rx2CJ method for first principles based predictions of performance properties for new propellants and explosive materials.
This Rx2CJ first principle based protocol for predicting the CJ point provides the matching point between first principles based atomistic reaction dynamics simulations and the macroscopic properties of detonation. Thus Rx2CJ can now be used for in silico predictions of the CJ state parameters as a measure of performance for in silico design of new materials, using it to assess proposed new high energy materials prior to the difficult task of their synthesis and characterization. This can be used to discover new higher performance energetic materials that might optimize energy release, sensitivity, and environmental impact.
Our Rx2CJ calculations also provide the detailed properties and products at the CJ point that could be used as input into for macroscale continuum simulations of explosives and propellants.
Acknowledgements
This work was supported by the U.S. ONR (N00014-12-1-0538, Dr Cliff Bedford). It was also supported by the National Natural Science Foundation of China (Grant No. 11172044 and 11221202).Notes and references
- P. J. Kortbeek, C. A. Ten Seldam and J. A. Schouten, Mol. Phys., 1990, 69, 1001–1009 CrossRef CAS.
- Z. Duan, N. Møller and J. H. Weare, Geochim. Cosmochim. Acta, 1996, 60, 1209–1216 CrossRef CAS.
- B. M. Rice, W. Mattson, J. Grosh and S. F. Trevino, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 611–622 CrossRef CAS.
- M. Ross, J. Chem. Phys., 1979, 71, 1567–1571 CrossRef CAS.
- G. Zerah and J. P. Hansen, J. Chem. Phys., 1986, 84, 2336–2343 CrossRef CAS.
- L. E. Fried and W. M. Howard, J. Chem. Phys., 1998, 109, 7338–7348 CrossRef CAS.
- J. H. Batteh and J. D. Powell, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 1398–1409 CrossRef CAS.
- B. L. Holian, W. G. Hoover, B. Moran and G. K. Straub, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 22, 2798–2808 CrossRef CAS.
- J. J. Erpenbeck, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 6406–6416 CrossRef CAS.
- D. W. Brenner, D. H. Robertson, M. L. Elert and C. T. White, Phys. Rev. Lett., 1993, 70, 2174–2177 CrossRef CAS PubMed.
- J. B. Maillet, M. Mareschal, L. Soulard, R. Ravelo, P. S. Lomdahl, T. C. Germann and B. L. Holian, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 63, 016121 CrossRef PubMed.
- J. D. Kress, S. Mazevet, L. A. Collins and W. W. Wood, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 63, 024203 CrossRef.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- W. Liu, S. V. Zybin, S. Dasgupta, T. M. Klapötke and W. A. Goddard III, J. Am. Chem. Soc., 2009, 131, 7490–7491 CrossRef CAS PubMed.
- Q. An, W. A. Goddard III and T. Cheng, Phys. Rev. Lett., 2014, 113, 095501 CrossRef PubMed.
- A. Strachan, E. M. Kober, A. C. T. van Duin, J. Oxgaard and W. A. Goddard III, J. Chem. Phys., 2005, 122, 054502 CrossRef PubMed.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard III, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- L. Liu, Y. Liu, S. V. Zybin, H. Sun and W. A. Goddard III, J. Phys. Chem. A, 2011, 115, 11016–11022 CrossRef CAS PubMed.
- Q. An, S. V. Zybin, W. A. Goddard III, A. Jaramillo-Botero, M. Blanco and S. Luo, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 220101 CrossRef.
- Q. An, W. A. Goddard III, S. V. Zybin, A. Jaramillo-Botero and T. Zhou, J. Phys. Chem. C, 2013, 117, 26551–26561 CAS.
- D. Guo, Q. An, W. A. Goddard III, S. V. Zybin and F. Huang, J. Phys. Chem. C, 2014, 118, 30202–30208 CAS.
- D. Guo, Q. An, S. V. Zybin, W. A. Goddard III, F. Huang and B. Tang, J. Mater. Chem., 2015, 3, 5409–5419 RSC.
- A. Strachan, A. C. T. van Duin, D. Chakraborty, S. Dasgupta and W. A. Goddard III, Phys. Rev. Lett., 2003, 91, 098301 CrossRef PubMed.
- L. Zhang, S. V. Zybin, A. C. T. van Duin, S. Dasgupta, W. A. Goddard III and E. M. Kober, J. Phys. Chem. A, 2009, 113, 10619–10640 CrossRef CAS PubMed.
- T. Zhou, H. Song, Y. Liu and F. Huang, Phys. Chem. Chem. Phys., 2014, 16, 13914–13931 RSC.
- T. Zhou, L. Liu, W. A. Goddard III, S. V. Zybin and F. Huang, Phys. Chem. Chem. Phys., 2014, 16, 23779–23791 RSC.
- J. K. Brennan and B. M. Rice, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 021105 CrossRef PubMed.
- E. Bourasseau, V. Dubois, N. Desbiens and J. B. Maillet, J. Chem. Phys., 2007, 127, 084513 CrossRef PubMed.
- E. Bourasseau, J. B. Maillet, N. Desbiens and G. Stoltz, J. Phys. Chem. A, 2011, 115, 10729–10737 CrossRef CAS PubMed.
- L. E. Finger M, Helm FH, Hayes B, Hornig H, McGuire R, Kahara M, Guidry M presented in part at the 6th Syrup (International) on Detonation, Washington, DC 710, 1980.
- LASL Explosive Property Data, ed. C. L. Madar, Los Alamos Data Center, University of California Press, Berkeley, Los Angeles, London, 1980 Search PubMed.
- R. Zitoun, D. Desbordes, C. Guerraud and B. Deshaies, Shock Waves Chem., 1995, 4, 331–337 CrossRef.
- A. Piryatinski, S. Tretiak, T. Sewell and S. McGrane, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 214306 CrossRef.
- R. Dawes, A. Haghighi, T. Sewell and D. Thompson, J. Chem. Phys., 2009, 131, 224513 CrossRef PubMed.
- N. Goldman, E. Reed and L. Fried, J. Chem. Phys., 2009, 131, 204103 CrossRef PubMed.
- T. Qi and E. Reed, J. Phys. Chem. A, 2012, 116, 10451–10459 CrossRef CAS PubMed.
- D. L. Ornellas, Calorimetric Determinations of the Heat and Products of Detonation for Explosives: October 1961 to April 1982, Lawrence Livermore Laboratory, University of California, Livermore, CA, 1982 Search PubMed.
- W. E. Deal, J. Chem. Phys., 1957, 27, 796–800 CrossRef CAS.
- W. M. Evans, Proc. R. Soc. London, 1951, 204A, 12–17 Search PubMed.
- W. C. Davis, B. G. Craig and J. B. Ramsay, Phys. Fluids, 1965, 8, 2169–2182 CrossRef.
- J. Kurrle, HMX Detonation vs. Density, Report OSAO No. 4148, SANL No. 901-003, 1971.
- V. V. Zhakhovsky, M. M. Budzevich, A. C. Landerville, I. I. Oleynik and C. T. White, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 03331234 CrossRef PubMed.
- B. M. Dobratz and P. C. Crawford, LLNL Handbook: Properties of Chemical Explosives and Explosive Simulants, Lawrence Livermore National Laboratory, Livermore, CA, 1985 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp04516a |
| This journal is © the Owner Societies 2016 |


