Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Initial stages of water solvation of stepped platinum surfaces†
Manuel J.
Kolb
,
Jasper
Wermink
,
Federico
Calle-Vallejo
,
Ludo B. F.
Juurlink
and
Marc T. M.
Koper
*
Leiden Institute of Chemistry, Leiden University, Einsteinweg 55, 2333CC Leiden, The Netherlands. E-mail: m.koper@lic.leidenuniv.nl
First published on 21st August 2015
Abstract
Platinum is an active catalyst for a large number of (electro)chemical reactions in aqueous solution. The observed catalytic activities result from an interplay between the intrinsic adsorption properties of platinum surfaces and their interaction with the aqueous environment. Although water networks have been extensively studied on close-packed surfaces, little is known about high-coverage solvation environments around defects. Here, we report DFT calculations on medium- to high-coverage water adsorption structures near the (100) step edge on Pt(533). We find that isolated ring structures adjacent to step edges form hexagons or pentagons. For higher coverages, 6 possible adsorption structures with varying ring sizes along the step edge and almost identical adsorption energies are observed. From our results we conclude that the favorable interaction of the H-down oriented water molecules, adjacent to the step edge, with the step dipole plays an important role in the formation of these structures. Furthermore, our results explain why water networks on stepped surfaces originate at the step edges, and extend towards the adjacent terraces, in agreement with previous experiments. These results show how step edges act as anchoring points for water adsorption and suggest that solvation of defects might dominate water structures on real platinum surfaces.
1 Introduction
Platinum is a prominent catalyst for a wide variety of chemical reactions1–3 in liquid environments. In those environments, the effect of the solvent on the adsorption of reactants, intermediates and products plays a major role in the overall catalytic performance of platinum surfaces.4,5 As water is the most frequently used solvent in chemistry, a significant effort has been devoted to water adsorption on Pt(111) surfaces,6–8 leading to several models of catalytic reactions in solvated environments that can be quantitatively compared to experiments.7,9However, in order to model realistic catalytic systems based on nanoparticles with multiple facets, edges and corners, the flat, pristine Pt(111) surface may not provide a comprehensive representation of the entire catalytic system. Defects are known to play a large role in either promoting10,11 or hindering12 (electro)chemical reactions. Moreover, Pt(111) does not always provide the active site for a given catalytic reaction, as, for instance, certain reactions prefer pristine (100) facets.12,13 Therefore, it is important to understand how the solvation environment at defects influences the stability of adsorbed intermediates of (electro)catalytic reactions and the associated impact on reactivity. For instance, it is still a matter of debate14,15 whether water thermodynamically favors the generation of OH at step edges and why stepped Pt(111) surfaces in acidic media are more active for the oxygen reduction reaction than the Pt(111) itself.16 Shedding light on these important matters is, however, rather challenging from a computational perspective, in view of the large unit cells needed to describe the surfaces in question and the large number of possible configurations for the adsorbed solvent molecules. This is why, to date, most studies have focused on the treatment of the low-coverage limit of a filled step edge, combined with a clean terrace,17–19 with exception of the recent work of Jinnouchi et al.5 on Pt. Additionally, extended water structures on stepped gold surfaces were studied by Groß et al.20,21 Since in most experiments the coverages are always above the low-coverage limit, high-coverage computational studies are required to close the “coverage gap”.
In this study we approach the real catalytic system from the standpoint of regularly stepped surfaces, particularly the Pt(533) surface, which has a 4-atom-wide (111) terrace and a (100)-type step (see Fig. S1 in the ESI†). Our group has previously carried out experimental work on this model surface in ultra-high-vacuum (UHV)14 using temperature programmed desorption (TPD) measurements. It was found that at the highest coverage water exhibits a desorption spectrum with three features: at 188 K there is a distinct peak, attributed to water desorbing from the (100) step edge which, with increasing coverage, grows a shoulder at 171 K, assumed to be related to water desorbing from a terrace structure. At very high coverages a “multi-layer” peak appears at 146 K, namely the desorption pattern of multiple water layers above the first adsorbed layer. A more recent publication22 focused on the Pt(755) and Pt(977) surfaces, which have the same step type but an increased terrace width. The wider terraces of these surfaces lead to the presence of a (111)-like desorption peak, which indicates the formation of well-ordered (111)-like water networks. However, on all of the stepped surfaces, the prominence of the step-related desorption peak is higher than expected based on the ratio between step to terrace atoms. This striking observation suggests that the influence of the step edge on the water adsorption structure extends beyond the immediate vicinity of the step itself and hinders the formation of the (111)-like peak observed on pristine surfaces.
Recently, we carried out density functional theory (DFT) calculations on the adsorption of a single water molecule on Pt(533)23 that showed good qualitative agreement with the trends in the experimental desorption temperatures. However, we were not able to achieve an explanation for the absence of a fully developed (111)-terrace peak on Pt(533). This is a clear indication of the fact that the complexity of water solvation at stepped surfaces cannot be fully captured without accounting for cooperative water–water interaction. Here, we investigate the effect of higher water coverage near the step edge of Pt(533) to observe trends in the adsorption energy of more complex water structures and will attempt to link these trends to the findings previously obtained by TPD experiments.
2 Computational methods
The computations were performed using the ab initio density functional code VASP,24–27 the PBE functional28 and PAW projectors.29,30 The PBE functional was chosen in order to obtain reasonable adsorption energies of water, as well as to adequately describe hydrogen bonding among the water molecules.31 These appropriate features of PBE, combined with the fact that we focus mainly on the trends in adsorption energies, not the absolute values which are important for e.g. wetting behavior, which are described correctly by PBE,17,32 ensure that no higher levels of DFT, such as vdW corrected functionals, are required for our purposes.The reciprocal space was sampled with the Monkhorst–Pack scheme33 using 3 × 9 × 1 grids for the Pt(533) surface with two atoms per unit cell along the step edge. Larger unit cells were sampled with correspondingly smaller grids, a full list of which can be found in the ESI.† For all calculations first-order Methfessel–Paxton smearing34 with a sigma of 0.2 eV was applied and all energies were extrapolated to 0 K. A plane-wave basis set with a cut-off energy of 550 eV was chosen. Fig. S1 in the ESI† shows a side view of the Pt(533) surface, which, as described above, consists of a 4-atom-wide (111)-terrace and a (100)-type step. More information about the surface model used can be found in ref. 23.
The average Gibbs energies per molecule for the adsorption of a structure of nH2O molecules were calculated as follows:
 | (1) |
| Gtot,nH2Oads = EDFT,H2O + ZPEnH2Oads − T·S(nH2O),vib | (2) |
| Gtot,H2O(g) = EDFT,H2O + ZPEH2O − T·SH2O,tot | (3) |
All adsorption energies reported below are Gibbs energies, corrected for zero-point energy (ZPE) and vibrational entropy at 100 K, following the methods described by Loffreda.36 A reference temperature of 100 K was chosen to facilitate comparison with experimental STM and TPD data. A full set of DFT adsorption energies can also be found in the ESI.† It should be noted that the ZPE and entropy does not change significantly between different configurations with the same number of adsorbed molecules.
3 Results and discussion
In presenting our results, the coverage of water will be gradually increased to allow for a more detailed understanding of the consequences of the preferred adsorption structures near the step edge at higher coverages.3.1 Low coverage limit
It is well known that on platinum surfaces water adsorbs in a configuration with oxygen on-top of a Pt atom and both hydrogen atoms oriented parallel to the surface plane.23,37,38 Increasing the coverage on Pt(111) leads to interconnected structures, forming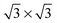 ,39,40
,39,40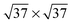
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41 or
41 or 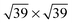
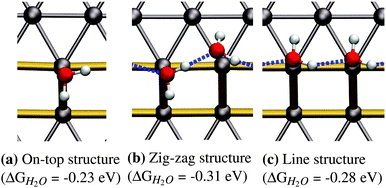
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41 superstructures, depending on environmental conditions, such as the total coverage of water. On the stepped Pt(533) surface, H2O still prefers to adsorb flat on-top of the Pt atoms with a noticeably increased adsorption energy17–19,23 on the Pt step-edge atoms as compared to the terrace atoms. Fig. 1a shows one of the possible orientations of water on the step edge of Pt(533). Rotation around the oxygen has a low energy cost, as long as both hydrogen atoms are still oriented parallel to the terrace plane.
41 superstructures, depending on environmental conditions, such as the total coverage of water. On the stepped Pt(533) surface, H2O still prefers to adsorb flat on-top of the Pt atoms with a noticeably increased adsorption energy17–19,23 on the Pt step-edge atoms as compared to the terrace atoms. Fig. 1a shows one of the possible orientations of water on the step edge of Pt(533). Rotation around the oxygen has a low energy cost, as long as both hydrogen atoms are still oriented parallel to the terrace plane.
3.2 One dimensional chains along the step edge
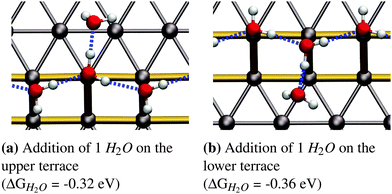
As reported in earlier publications17–19 water will form 1-D chain networks on the step edge of Pt(533) and other stepped surfaces due to the higher adsorption energy on the step edge. It is generally accepted that water will assume a “zig-zag” configuration with one water molecule oriented towards the lower terrace and the other one pointing towards the upper terrace, as illustrated in Fig. 1b. It should be noted that both water molecules are not oriented parallel to the terrace plane of the stepped surface, but are slightly tilted. Alternatively, a configuration with all free hydrogen atoms pointing in one direction, as shown in Fig. 1c, was observed, but found to be energetically less favorable by 0.03 eV per H2O molecule.Increasing the coverage by adding another water molecule to the lower edge, as shown in Fig. 2b, or the upper step edge, as shown in Fig. 2a, yields a slight improvement of the mean adsorption energy. Since the water next to the step edge always binds in an H-down configuration, which has an unfavorable adsorption energy on the terrace, this would suggest that the hydrogen bond to the step-edge water molecules is significantly stronger than those on the flat Pt(111) terrace. Additionally, we will argue below that this water molecule interacts with the step dipole, enhancing the stability of this adsorption structure. Furthermore, it was observed that the line structure converts back to the zig-zag configuration, after the addition of the water molecule adjacent to the step edge.
3.3 Isolated ring structures on the step edge
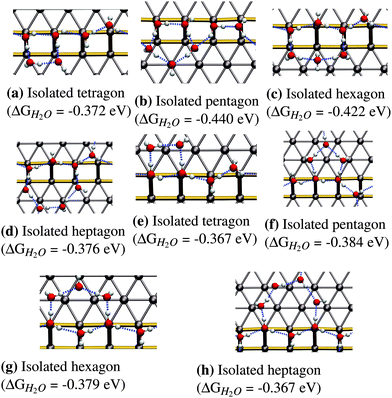
The next logical step for increasing the coverage is to assume that water will form closed ring structures, since this will maximize the number of hydrogen bonds per water molecule in the structure. We tested adsorption structures for ring sizes from 4 (tetragon) to 7 (heptagon) to understand the influence of the ring size on the mean adsorption energy. Smaller rings with 3 molecules are not stable due to the large distortion of the hydrogen-bonding angle needed to form a triangle. Structures larger than the heptagon have not been considered due to the limitation in terrace width imposed by the Pt(533) surface. Such a situation would lead to a significant interaction of the structure with the next step edge, resulting in the rupture of the polygons into smaller parts located on both the upper and the lower step edge.In the following we will only discuss the most favorable structures, which are the isolated hexagon (see Fig. 3c) and the isolated pentagon (see Fig. 3b). The term isolated in this case refers to a water framework in which the polygons do not share adjacent edges. Adsorption energies for the most favorable configurations of the other two ring-sizes (tetragon and heptagon) can be found in Fig. 3a and d.
The pentagonal structure prefers adsorbing on the lower step edge as can be seen from the adsorption energy of −0.440 eV in Fig. 3b compared to −0.384 eV in Fig. 3f. The most stable configuration (Fig. 3b) shows a peculiar structure that breaks the zig-zag arrangement on the step edge completely and replaces it with a hydrogen bonding chain that points down the step edge twice. Given the relatively high stability of the most favorable pentagonal structure on the upper step edge, we conclude that the pentagon itself is quite stable on the (100) step edge, although it is not easily incorporated into the favorable 1D zig-zag arrangement on the step edge, shown in Fig. 1b.
The next larger ring structure is the hexagon. Again, we find the extension of the water structure to the lower step edge to be more stable with an adsorption energy of −0.422 eV per H2O molecule leading to a structure with an H2O molecule that symmetrically accepts two hydrogen bonds, as shown in Fig. 3c. The two sides of the predicted hexagonal structure fit readily into the favorable zig-zag configuration along the step edge that was discussed earlier.
In summary, pentagonal and hexagonal structures adjacent to the step edge are the most favorable isolated ring structures. Furthermore, we observe enhanced binding for adsorption on the lower step edge for pentagons and hexagons compared to the upper step edge configuration. On the other hand, tetragons (see Fig. 3a and e) and heptagons (see Fig. 3d and h) show similar energies for both the lower and upper terrace configuration.
3.4 Fully covered step edge
In this section we will discuss our findings on fully covered steps, namely configurations that consist of a 1D chain and a fully covered lower or upper step edge. It should be clear that the structures presented in the previous section do not directly translate over to this higher coverage regime. This is mainly because the most stable low-coverage regime structures cannot be repeated so as to generate fully covered step edges (see Fig. 3). In this section we will only discuss the most favorable adsorption structures, while a full list of all performed calculations can be found in the ESI.†Fig. 4 shows the most favorable adsorption structures for the studied coverage. We found that there are several different ring sizes with nearly identical binding energies, all extending towards to lower step edge:
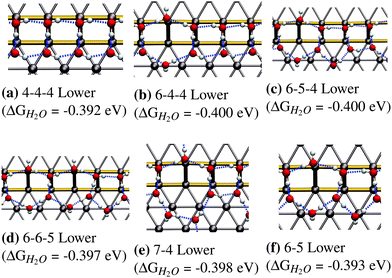 | ||
| Fig. 4 Most favorable adsorption structures for fully H2O-covered step edges on Pt(533). All of these structures have comparable adsorption energetics. | ||
• The 4-4-4 structure with an adsorption energy of −0.392 eV consisting of a periodic arrangement of tetragons (see Fig. 4a).
• The 6-4-4 structure with an adsorption energy of −0.400 eV consisting of a hexagon and two tetragons (see Fig. 4b).
• The 6-5-4 structure with an adsorption energy of −0.400 eV which consists of a hexagon followed by a pentagon and a tetragon (see Fig. 4c).
• The 6-6-5 structure shows an adsorption energy with −0.397 eV and consists of two hexagons followed by a pentagon (see Fig. 4d).
• The 7-4 structure, which consists of a heptagon followed by a tetragon, and shows an adsorption energy of −0.398 eV (see Fig. 4e).
• The 6-5 structure, which consists of a hexagon followed by a pentagon, and shows an adsorption energy of −0.393 eV (see Fig. 4f).
The fact that adsorption geometries extending towards the lower terrace are more favorable, as observed in for the structures in Fig. 3, is also found for these extended structures, is in accordance to the experimental STM findings of Morgenstern et al.42 They found that water on defective Pt(111) surfaces, prefers to form clusters located at the bottom of (100) step edges.
The differences in the adsorption energies of all the structures in Fig. 4 are within the intrinsic error associated with the calculated adsorption energies at the DFT-GGA level. This means that we cannot make a clear distinction as to which of these structures, if any, is the most stable. It should be noted that the presence of all observed structures is to be expected in a real system to varying degrees, due to configurational entropy, which is not included in our estimation of the free energies.
The most favorable structures observed for isolated adsorption, namely the hexagon and the pentagon, are not found to be most stable in the high-coverage regime, for two different reasons. Firstly, the most favorable hexagonal structure in the low-coverage regime, as can be seen in Fig. 3c, does not lead to a framework of polygons with adjacent edges, covering the entire step edge. This structure showed a significantly increased adsorption energy compared to those alternatives that were able to fully cover the edge, which makes a full coverage of hexagons energetically less favorable than other possibilities. On the other hand, the pentagon (see Fig. 3b) occupies significantly more space along the lower step edge than along the upper edge, so it experiences compressive strain when forming a structure that is fully occupying the step edge. This compressive strain adversely affects the stability of the entire water framework, making it bind weaker compared to other structures.
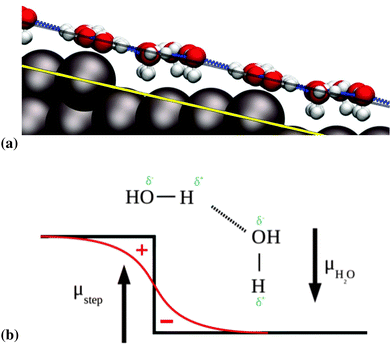
We observe that the water molecules adjacent to the step edge prefer to bind in an H-down orientation, as can be seen in Fig. 5a. A similar tendency was observed on the stepped gold surfaces studied by Groß et al.,20 however this tendency was not absolute, as upper step edge water could still point H-up, in contrast to our findings here. We ascribe this tendency to the Smoluchowski effect at the step edge.43 This effect consists of a lack of charge at the top of step edges, which is compensated by an excess charge at the bottom of the step edge. This leads to the generation of a net dipole moment. The component perpendicular to the terrace of this dipole moment interacts favorably with the natural dipole moment of the water molecules that are oriented in an H-down configuration. This situation is illustrated in Fig. 5b, in which we represent the vectors of the dipole moments with the tips pointing from negative to positive charges.
The adsorption height of the step-edge water molecules (for example we observe Pt–O distances of 2.01–2.39 Å for the zig-zag part of the 6-5-4 structure in Fig. 4c) is found to be slightly shorter than the ones encountered for water monomer adsorption on Pt(111) where a Pt–O distance of 2.46 Å for a single water molecule sitting on-top on Pt(111) was found. Note that this is in agreement with the trends in adsorption energies. The height of the adsorbates bordering the lower step edge, with a Pt–O distance of 3.23–3.49 Å for the 6-5-4, are comparable to the adsorption heights measured for the 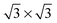 adsorption layer on Pt(111), which shows Pt–O distances of 3.24–3.50 Å.
adsorption layer on Pt(111), which shows Pt–O distances of 3.24–3.50 Å.
For larger structures that extend further onto the terrace we observe that the oxygen atoms of the terrace water molecules arrange themselves almost perfectly along the surface plane of the stepped surface, as can be seen in Fig. 5a, where the solid yellow line corresponding to the surface plane is parallel to the dashed black line, on which most of the adsorbates lie. This suggests that the water bilayer in contact with the Pt(533) surface aligns itself as a flat “carpet” regardless of the presence of the (100) defect.
3.5 1D water structures at surface defects and implications for water networks at terraces
When small amounts of water are dosed onto a stepped platinum surface, the preferred binding site is the on-top site at the step edge,17–19,23 rather than the (111)-like terraces. This preference is due to the decreased coordination number of the step-edge Pt atom.38 The low diffusion barrier for water on flat Pt(111) surfaces,44 combined with this enhanced binding energy at the step edge, leads to a marked tendency to form dimers and larger structures on the step edges.Intuitively, the water chain on the step edge can be viewed as an extended one-dimensional defect when comparing it to the regular hexagonal arrangement of water on the (111) terrace. However, we find that the step edge water framework is actually the nucleation point for further water adsorption on terraces. This means that the actual influence area of the step edge extends to at least one or two rows of platinum atoms onto the terrace (see Fig. 5a). The effect that the step edge will have on the adsorption geometry is expected to diminish with the distance from the step edge. Hence, the adsorption characteristics of water on a stepped surface with a rather “short” terrace will be dominated by the influence area of the step edge. This explains the absence of a fully developed (111)-like desorption feature observed in TPD experiments for the Pt(533) surface and the appearance of such a peak on the larger Pt(755) and (977) surfaces.22 This explanation cannot be drawn from a single-molecule or even low-coverage adsorption approach.
It is worth noting that the term “short terrace” depends strongly on the adsorbate in question, its coverage, the step-edge geometry and of course the substrate. For instance, for hydrogen adsorption the Pt(533) surface can be considered to have a “wide” terrace with clear Pt(111)-like features, while for water adsorption the (111) features are absent.22,45 Our results indicate that these differences arise due to the existence of long-range cooperative effects in water structures extending beyond the step edge.
4 Conclusions
In this study we have performed DFT calculations on the adsorption geometries and energetics of water on and near the step edge of the Pt(533) surface. The coverages that were studied were increased beyond the one-dimensional chain that was previously discussed in the literature. The first stage, beyond the 1D chain studied before, was the appearance of isolated water ring structures at the step edges. It was found that the (100) step edge prefers to form isolated hexagonal or pentagonal rings in this case. Furthermore, it was observed that the isolated rings preferentially form in the direction towards the lower terrace on the stepped surface. Additionally, water molecules that are not bound to the step edge prefer to adsorb in an H-down configuration.At higher coverage a full arrangement of periodically ringed structures is formed along the step edge. Multiple structures with similar energies are possible at this coverage. Besides, the observation regarding H-down adsorption and the preference to adsorb towards the lower terrace was also made at these coverages. Our results suggest that the formation of water frameworks on Pt(533) will start at step edges, and extend towards the lower terrace, adjacent to the step edge, in accordance with the observations by Morgenstern et al.42
Furthermore, the observed structures tend to occupy a large portion of the terrace, as for example the 7-4 structure in Fig. 4e, from which we conclude that the area in which the step edge influences the adsorption geometry extends beyond its immediate vicinity, due to long-range cooperative water–water interactions. This explains the absence of a (111)-like peak in the recorded TPD spectrum of the Pt(533) surface, and suggests a lack of ordered hexagonal water adsorption structures on the terrace of Pt(533). In contrast, stepped surfaces with larger terraces and the same kind of step, such as the Pt(755) and Pt(977) surfaces, allow for an area of hexagonal adsorption structures on them, leading to a (111)-like desorption peak, as observed in TPD.22 Still, this (111)-like desorption feature is smaller than expected based on the width of the terraces, and we can now ascribe this to the formation of more extended ring-like structures on and near the step edge.
While for (111) surfaces approaches exist to estimate the influence of solvation on adsorption energies9 by making use of hexagonal water frameworks, very little is known about higher coverage solvation effects at step edges. The periodic structures reported here provide an accurate starting point for such studies. This will ultimately lead to a comprehensive treatment of solvation in aqueous environments that will contribute to a more realistic representations of catalytic processes at electrified solid–liquid interfaces.
Acknowledgements
We gratefully acknowledge financial support from the Netherlands Organization for Scientific Research (NWO) as a TOP grant awarded to LBFJ and MTMK. This work was sponsored also by the NWO Exacte Wetenschappen, EW (NWO Physical Sciences Division) for the use of supercomputer facilities, with financial support from the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (Netherlands Organisation for Scientific Research, NWO). We furthermore acknowledge that the results of this research have been achieved using the PRACE-2IP project (FP7 RI-283493) resource SISU based in Finland at CSC Finland. FCV acknowledges funding by the Netherlands Organisation for Scientific Research (NWO), Veni project number 722.014.009.References
- V. Climent and J. Feliu, J. Solid State Electrochem., 2011, 15, 1297–1315 CrossRef CAS.
- H. A. Gasteiger, S. S. Kocha, B. Sompalli and F. T. Wagner, Appl. Catal., B, 2005, 56, 9–35 CrossRef CAS.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Norskov, Nat. Mater., 2006, 5, 909–913 CrossRef CAS PubMed.
- A. Fortunelli, W. A. Goddard III, L. Sementa and G. Barcaro, Nanoscale, 2015, 7, 4514–4521 RSC.
- R. Jinnouchi, K. Kodama and Y. Morimoto, J. Electroanal. Chem., 2014, 716, 31–44 CrossRef CAS.
- P. J. Feibelman, N. C. Bartelt, S. Nie and K. Thürmer, J. Chem. Phys., 2010, 133, 154703 CrossRef PubMed.
- E. Skúlason, V. Tripković, M. E. Björketun, S. Gudmundsdöttir, G. Karlberg, J. Rossmeisl, T. Bligaard, H. Jónsson and J. K. Nørskov, J. Phys. Chem. C, 2010, 114, 18182–18197 Search PubMed.
- M. T. M. Koper, Electrochim. Acta, 2011, 56, 10645–10651 CrossRef CAS.
- V. Tripković, E. Skúlason, S. Siahrostami, J. K. Nørskov and J. Rossmeisl, Electrochim. Acta, 2010, 55, 7975–7981 CrossRef.
- M. T. M. Koper, Nanoscale, 2011, 3, 2054–2073 RSC.
- A. P. O'Mullane, Nanoscale, 2014, 6, 4012–4026 RSC.
- H. Li, F. Calle-Vallejo, M. J. Kolb, Y. Kwon, Y. Li and M. T. M. Koper, J. Am. Chem. Soc., 2013, 135, 14329–14338 CrossRef CAS PubMed.
- H. Li, Y. Li, M. T. M. Koper and F. Calle-Vallejo, J. Am. Chem. Soc., 2014, 136, 15694–15701 CrossRef CAS PubMed.
- M. J. T. C. van der Niet, A. den Dunnen, L. B. F. Juurlink and M. T. M. Koper, J. Chem. Phys., 2010, 132, 174705 CrossRef PubMed.
- D. Donadio, L. M. Ghiringhelli and L. Delle Site, J. Am. Chem. Soc., 2012, 134, 19217–19222 CrossRef CAS PubMed.
- A. S. Bandarenka, H. A. Hansen, J. Rossmeisl and I. E. L. Stephens, Phys. Chem. Chem. Phys., 2014, 16, 13625–13629 RSC.
- R. Peköz, S. Wörner, L. M. Ghiringhelli and D. Donadio, J. Phys. Chem. C, 2014, 118, 29990–29998 Search PubMed.
- L. Arnadottir, E. M. Stuve and H. Jonsson, Surf. Sci., 2010, 604, 1978–1986 CrossRef CAS.
- S. Meng, E. G. Wang and S. Gao, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 195404 CrossRef.
- X. Lin and A. Groß, Surf. Sci., 2012, 606, 886–891 CrossRef CAS.
- A. Groß, F. Gossenberger, X. Lin, M. Naderian, S. Sakong and T. Roman, J. Electrochem. Soc., 2014, 161, E3015 CrossRef.
- A. den Dunnen, M. J. T. C. van der Niet, C. Badan, M. T. M. Koper and L. B. F. Juurlink, Phys. Chem. Chem. Phys., 2015, 17, 8530–8537 RSC.
- M. J. Kolb, F. Calle-Vallejo, L. B. F. Juurlink and M. T. M. Koper, J. Chem. Phys., 2014, 140, 134708 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, R10157–R10160 CrossRef CAS.
- J. Carrasco, J. Klimeš and A. Michaelides, J. Chem. Phys., 2013, 138, 024708 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS.
- NIST-JANAF Thermochemical Tables, ed. M. W. Chase, C. A. Davies, J. R. Downey, D. J. Frurip, R. A. MacDonald and A. N. Syverud, Suppl. 1 to Vol. 14 of J. Phys. Chem. Ref. Data, American Institute of Physics, 1985 Search PubMed.
- D. Loffreda, Surf. Sci., 2006, 600, 2103–2112 CrossRef CAS.
- A. Michaelides, Appl. Phys. A: Mater. Sci. Process., 2006, 85, 415–425 CrossRef CAS.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, P. Sautet and D. Loffreda, Angew. Chem., Int. Ed., 2014, 53, 8316–8319 CrossRef CAS PubMed.
- T. Roman and A. Groß, Catal. Today, 2013, 202, 183–190 CrossRef CAS.
- S. Schnur and A. Groß, New J. Phys., 2009, 11, 125003 CrossRef.
- G. Zimbitas, S. Haq and A. Hodgson, J. Chem. Phys., 2005, 123, 174701 CrossRef CAS PubMed.
- M. Morgenstern, T. Michely and G. Comsa, Phys. Rev. Lett., 1996, 77, 703–706 CrossRef CAS PubMed.
- H. Ibach, Physics of Surfaces and Interfaces, Wiley, 2006 Search PubMed.
- L. Arnadottir, E. M. Stuve and H. Jonsson, Surf. Sci., 2012, 606, 233–238 CrossRef CAS.
- C. Badan, M. T. M. Koper and L. B. F. Juurlink, J. Phys. Chem. C, 2015, 119, 13551–13560 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp04468e |
| This journal is © the Owner Societies 2016 |