Open Access Article
Open Access ArticleBombardment induced ion transport – part IV: ionic conductivity of ultra-thin polyelectrolyte multilayer films
Veronika
Wesp
a,
Matthias
Hermann
a,
Martin
Schäfer
a,
Jonas
Hühn
b,
Wolfgang J.
Parak
*b and
Karl-Michael
Weitzel
*a
aFachbereich Chemie, Philipps-Universität Marburg, Germany. E-mail: weitzel@chemie.uni-marburg.de
bFachbereich Physik, Philipps-Universität Marburg, Germany. E-mail: wolfgang.parak@physik.uni-marburg.de
First published on 21st September 2015
Abstract
The dependence of the ionic conductance of ultra-thin polyelectrolyte multilayer (PEM) films on the temperature and the number of bilayers has been investigated by the recently developed low energy bombardment induced ion transport (BIIT) method. To this end multilayers of alternating poly(sodium 4-styrene sulfonate) (PSS) and poly(allylamine hydrochloride) (PAH) layers were deposited on a metal electrode and subsequently bombarded by a low energy potassium ion beam. Ions are transported through the film according to the laws of electro-diffusion towards a grounded backside electrode. They are neutralized at the interface between the polymer film and the metal electrode. The detected neutralization current scales linearly with the acceleration potential of the ion beam indicating Ohmic behavior for the (PAH/PSS)x multilayer, where x denotes the number of bilayers. The conductance exhibits a non-monotonic dependence on the number of bilayers, x. For 2 ≤ x ≤ 8 the conductance increases non-linearly with the number of bilayers. For x ≥ 8 the conductance decreases with increasing number of bilayers. The variation of the conductance is rationalized by a model accounting for the structure dependence of the conductivity. The thinnest sample for which the conductance has been measured is the single bilayer reflecting properties dominated by the interface. The activation energy for the ion transport is 0.49 eV.
Introduction
Polyelectrolyte multilayers (PEM) synthesized by the layer by layer (LbL) assembly are tailor-made materials with specific transport properties.1 The variation of preparation parameters like pH-value, salt concentration and temperature can tune the physical and chemical properties of PEMs.2,3 The LbL technique intrinsically allows precise adjustment of the thickness of the film.Polyelectrolyte multilayers consisting of poly(allylamine hydrochloride) (PAH) and poly(sodium 4-styrene sulfonate) (PSS) are promising materials in applications such as catalysis,4 organic thin-film transistors,5 vehicles for drug delivery6 and sensors. Sensors have been for example demonstrated which consist of PEM shells which act as a semi-permeable membrane and contain encapsulated analyte-sensitive fluorophores for determination of the analyte concentration using fluorescence response measurements. This method is applicable for small molecules like urea, CO2, ions like sodium, potassium and chlorine7 and for pH value determination,8i.e. for analytes that are small enough for being able to diffuse through the PEM shell. The basis of the sensor function is the transport of the ions through the PEM shells to the ion-sensitive fluorophores, i.e. the ion conductivity of the PEM shell. A limited number of conductivity measurements – mainly based on impedance spectroscopy – have been reported to date. The nature of the charge carrier is not automatically clear.
First results investigating the parameters affecting the ion transport through such PEM shells and films were published recently.9 Objectives of the investigation were the diffusion time of ions into the PEM capsules detected by fluorescence response measurements and the temperature dependent ionic conductivity of (PAH/PSS)16 and (PAH/PSS)(PAH/AuNPs/PSS)15 measured by the low energy bombardment induced ion transport (BIIT) technique. BIIT is an ideal technique for determining the ionic conductivity of ultra-thin sensitive films as (PAH/PSS)x since only one electrode at the backside is necessary for conduction measurements.10–12 A second electrode that would cause the risk of damaging the fragile sample is not required. As reported in recent work,11,13 BIIT-measurements yield the same results for the conductance as obtained by impedance spectroscopy. BIIT measurements have been carried out on PEM films with and without integrated Au nanoparticles.9 The BIIT results showed no significant difference in the overall conductance for PEM films with or without gold nanoparticles (NP), the conductance values being on the order of 1.0 × 10−9 S.9 However, details of the recorded current–voltage relation were different. While the multilayer without gold nanoparticles exhibited a linear current–voltage relation with Ohmic behavior over the complete temperature range, the sample with gold nanoparticles incorporated showed more complex, non-linear current–voltage characteristics.
In the current work we investigate the variation of the conduction properties as a function of the number of bilayers in a PEM and the temperature. To this end the conductance of (PAH/PSS)x multilayers ranging from 1 bilayer to 18 bilayers have been studied. In this work the outermost layer is always a PSS layer. The investigation sheds new light on the mechanism of ion conduction in PEM's. For reasons of completeness we mention that studies also have been performed on half-numbered bilayers such that the top most layer can be switched from PSS to PAH.14
Experimental setup
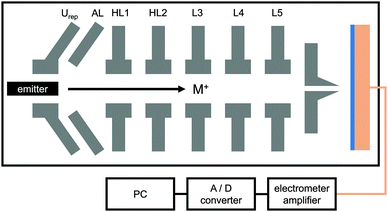
The (PAH/PSS)x multilayer were synthesized using the layer by layer (LbL) deposition technique (Fig. 1). Therefore, a copper backside electrode was rinsed with Milli-Q water and sonicated in acetone for 30 min at room temperature. The rinsed copper plate was dipped in a hydrogen peroxide solution (Roth) at 373 K for 15 min and then in 7 M HNO3 for 1 min in order to remove the oxide layer. Further rinsing with Milli-Q water, EtOH and drying under nitrogen stream followed. For functionalization of the copper surface, the copper disc was immersed in an aqueous solution of 3-mercaptopropionic acid (Sigma-Aldrich) over night and rinsed again with Milli-Q water. The negatively charged surface was then dipped into a 0.0317 M poly(allylamine hydrochloride) solution (PAH, Sigma Aldrich) with 0.5 M NaCl and a pH = 6.5 for 30 min. The free PAH was then removed by washing with Milli-Q water. The attached PAH causes an inversion of the surface charge. The copper disc was subsequently dipped into a 0.0589 M poly(sodium 4-styrenesulfonate) solution (PSS, Sigma-Aldrich) with 0.5 M NaCl and a pH = 6.5 for another 30 min and rinsed afterwards with Milli-Q water to remove the free PSS. For generation of more multilayers, the dipping processes with PAH and PSS solution and the rinsing with Milli-Q water were repeated until the final architecture had been reached. The immersion time was reduced to 10 min for these additional layers. The increased immersion time for the first layer has been chosen in order to improve the sticking characteristics.The experimental setup for the bombardment induced ion transport experiments is shown schematically in Fig. 2. All experiments were performed under reduced pressure around 10−7 mbar. The spectrometer comprises a rod system on which the essential components are mounted. These components contain the ion source (thermionic emitter) and the ion optics for guiding the ion beam. A conducting metal electrode at the end of the rod system is used either pure for reference experiments or with the sample of interest deposited on the metal surface. The temperature control of the electrode is realized by a PID-controller (Eurotherm 3216), a Pt-100 and a heating foil (MINCO) at the backside of the sample. Precise temperature dependent measurements were carried out in the range of 333–343 K with a deviation of ±0.1 K.
The ion source is a home-made thermionic synthetic leucite K[AlSi2O6] emitter. The properties of this thermionic ion source are described elsewhere.13,15 The emitter was synthesized by mixing K2CO3, Al2O3 and SiO2 in a ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. The reactants were ball milled and then transferred into a corundum tube and heated to 1273 K. Milling and heating at 1473 K were repeated for homogenization over a period of 12 h. To guarantee homogeneous electronic and thermal distribution in the emitter material molybdenum powder was added in a ratio of 1
4. The reactants were ball milled and then transferred into a corundum tube and heated to 1273 K. Milling and heating at 1473 K were repeated for homogenization over a period of 12 h. To guarantee homogeneous electronic and thermal distribution in the emitter material molybdenum powder was added in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 and pressed in a stainless steel husk and sintered (under high vacuum) at 1473 K for another 12 h. Mounting the hull on a glow plug allows heating during the experiment using heating currents of up to 4.5 A.
4 and pressed in a stainless steel husk and sintered (under high vacuum) at 1473 K for another 12 h. Mounting the hull on a glow plug allows heating during the experiment using heating currents of up to 4.5 A.
The potassium ions leaving the emitter surface are repelled by a conical repeller lens Urep. The voltages applied to this lens ultimately define the initial kinetic energy of the ions. In the current case, we applied voltages between 0.5 V and 5 V with respect to ground. The ions are accelerated towards the abstraction lens AL which is kept at a constant voltage of −469 V. The ion beam is then focused and guided through a set of five lenses as indicated in Fig. 2. A funnel L6 placed 1 mm in front of the sample serves both, as focusing device of the ion beam and as geometrical restriction for the bombarded area due to the small diameter of the funnel opening (2 mm). Eventually, the ions hit the surface of the sample and land softly.
The soft landing of the potassium ions and hence the attachment of them to the sample surface create a finite surface potential. Once the surface potential reaches the potential applied at the repeller lens, excess carriers are deflected such that eventually a homogeneous surface potential is reached. Due to the grounded backside electrode a potential gradient arises across the sample. Additionally, the deposition of potassium ions to the front side of the sample also induces a gradient of the potassium ion density. Both gradients contribute to the total ion flux, where the prevailing effect originates from the potential gradient. In other words, the electro-diffusive flux is dominated by migration rather than diffusion. The ion transport is detected as a neutralization current Idet at the backside electrode of the film. The detection of the current is carried out with a home-made electrometer amplifier directly at the heated copper electrode. In general, the detected ion current exhibits a time dependence which is not in the focus of this manuscript. Here, we focus on the steady-state situations that occurs after several hours. Such a steady-state situation is reached when the deposited ionic charge per unit time Iinput at the surface becomes equal with the detect current at the backside electrode, Idet. The detected current is A/D converted and processed in a personal computer. The value of the surface potential depends on the potential Urep applied to the ion source. Further details have been described elsewhere.16
In the following sections the backside current is investigated as a function of the initial ion kinetic energy, i.e. of the applied repeller voltage Urep for (PAH/PSS)x multilayers with different numbers of bilayers x (x from 1 bilayer to 18 bilayers) at 333 K. In addition, temperature dependent measurements of the PEM consisting of 12 bilayers (PAH/PSS)12 has been carried out. From the temperature dependence of the conductivity, the activation energy was derived.
Experimental results and discussion
In order to determine the conductance of (PAH/PSS)x as a function of the number of bilayers, samples from 1 bilayer to 18 bilayers have been bombarded with a spatially homogeneous potassium ion beam at a constant temperature of 333 K.The ion current has been detected at the backside electrode as a function of the repeller voltage where voltages between 0.5 V and 5 V are applied. The ion current arriving at the sample position has been detected in a reference experiment where the sample has been replaced by a copper plate. The reference current has been chosen >140 pA during the entire experiments, sufficiently large to guarantee that the surface potential reaches the repeller potential everywhere, thus ensuring a homogeneous surface potential. For the temperature dependent measurement, a (PAH/PSS)12 film has been investigated in a temperature range from 333 K up to 342 K in order to determine the activation energy for the ion transport process.
In order to quantify the conductance as a function of the number of the multilayers we present in Fig. 3 the results of current–voltage measurements for (PAH/PSS)x multilayers with x = 1, 2, 4, 6, 8, 10, 12, 14, 16, 18 bilayers. The measurements were performed at a constant temperature of 333 K. Conduction characteristics obeying Ohm's law are observed for each multilayer. The conductance G of each sample can be determined directly from the slope of the current–voltage curves using eqn (1)
 | (1) |
Physically the current–voltage data all have finite offsets in current and voltage. The current offset is −15 pA ± 5 pA due to the electrometer amplifier. Taking into account this current offset the relevant voltage offset is approximately 1.5 V. This offset is connected to the electrical contact between the PEM, the layer of neutralized charge carrier at the backside electrode and the metal electrode itself. However, it may also contain contributions from the ion source. In the current work, we focus on the slope of the current–voltage data, i.e. the conductance, which is not affected by these offsets. The offset will be discussed in a forthcoming paper. The data presented in Fig. 3 show that the current–voltage traces depend characteristically on the number of bilayers x.
The corresponding conductance G is shown in Fig. 4a as a function of x. Two regimes with different trends are observed. While the conductance increases non-linearly between 2 and 8 bilayers, a pronounced decrease of the conductance with the number of bilayers is observed for more than 8 bilayers. All detected conductance values lie between G = 9.22 × 10−13 S (for 2 bilayers) and G = 2.97 × 10−11 S (8 bilayers). In the frame of the BIIT theory, a purely Ohmic conductor with homogenous charge carrier density and homogenous diffusion coefficient would exhibit a neutralization current according to the relation10
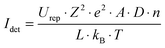 | (2) |
 | ||
| Fig. 4 Representation of conductance G (a) and the bilayer conductivity (b) vs. number of bilayer x. The solid line is the result of a model calculation. For further details see the text. | ||
In order to normalize the conductance with respect to the number of bilayers x, one may define a bilayer conductivity as given by
 | (3) |
The entire dependence of the bilayer conductivity on the number of the bilayers may be described in terms of a sigmoid law
 | (4) |
Ultimately, we find good agreement between the experimental results and the model for a = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, b = 1.5, σ1 = 1.11 × 10−6 S m−2, σ2 = 8.59 × 10−5 S m−2. The conductance and the bilayer conductivity predicted by these parameters is given as red lines in Fig. 4. The mere fact of a constant conductivity implies that the conductance must decrease from x = 1 to x = 2, as shown in Fig. 4a.
000, b = 1.5, σ1 = 1.11 × 10−6 S m−2, σ2 = 8.59 × 10−5 S m−2. The conductance and the bilayer conductivity predicted by these parameters is given as red lines in Fig. 4. The mere fact of a constant conductivity implies that the conductance must decrease from x = 1 to x = 2, as shown in Fig. 4a.
Most strikingly, the dependence of the conductance on the number of bilayers is non-monotonous. Hence, we may state that we find a fundamental change in the conduction behavior between 6 and 8 bilayers. Obviously, samples with more than 8 bilayers behave as expected from a normal bulk material, i.e. the conductance is compatible with a reciprocal variation with the number of bilayers. Hence, we have to address the question what is different for a smaller number of bilayers.
According to the literature, (PAH/PSS)x-films often show a variation in their fundamental conduction behavior between 6 and 8 bilayers, even though the preparation conditions as well as the humidity and hence the exact thickness of the films in these investigations may vary. For example Tarek et al. reported a clear inhibition of the ferrocyanite transport for more than 8 bilayers.20 Han et al. reported that cyclic voltammograms become irreversible for more than 7 or 8 bilayers.21 There have been different attempts to explain the change of properties for a certain number of bilayers. Ladam et al. introduced a three zone model,22 where an approximately 6 bilayers thick zone I is determined by the vicinity of the substrate. There, the substrate influences the PEM properties. Zone II represents the bulk of the sample while the sample in zone III is influenced by the solution environment. Another model, the so called capillary membrane model, has been introduced by Silva et al.23,24 where it is assumed that the coverage of the layers is not complete at the early stage of the multilayer growth process. Uncovered spots remain through which the transport is favored. The more layers are added, the less important the spots become. Beyond about 10 layers, the membranes behave like a homogeneous material. Beside these two models, it is known that the growth of PEM multilayers occurs non-homogeneously, i.e. the first layers are thinner than the layers deposited consecutively.18,25–27 Tarek et al. reported that the first layers contain more small ions, which in turn probably exhibit a stronger hydration.20 As a consequence, the permeability of the sample becomes larger.
In contrast to most reports in the literature, the samples presented here are investigated under reduced pressure conditions in a high vacuum setup (p < 10−6 mbar). We assume that under these conditions water is evaporated from the film such that the film moisture is reduced. It is known that the humidity of the environment and hence the moisture of the film has a strong influence on the conductivity of (PAH/PSS)x-films.28 A reduction of the humidity from 90% to 10% may decrease the conductivity by 5 orders of magnitude.29 For the measurements presented here, we assume that an inhomogeneous growth occurs for the first few deposited layers of PAH/PSS, which may be triggered by the relatively rough substrate surface (polished copper). Under these conditions, we expect that water may very efficiently gas out of the film into the vacuum chamber. Hence, the corresponding films are in general dry and consequently show a very low conductance.
For 4 to 8 bilayers, we observe an exponential increase of the conductance. In this regime the openings or channels become closed and consequently the loss of water is reduced. The exponential increase of the conductance in this regime matches nicely the exponential increase of the conductivity with increasing moisture.29 For more than 8 monolayers, the samples are homogeneous and open channels do not exist anymore such that the water loss from the films is minimized. Hence, for 8 or more layers, the sample conditions do not change dramatically anymore and the conductance follows the expected 1/x behavior.
If one compares the experimental data with the model given by the red line, we find a very good agreement for all but the single bilayer. The model calculation predict a minimum in the conductance at x = 2 in line with the experimental observation. Yet, the experimentally found conductance for the single bilayer is higher than predicted. The conductance of the single bilayer may well be strongly influenced by the close neighborhood to the substrate. Most likely the structural characteristics of the single bilayer differ from the multi layers. In this case, the fraction of open channels may be very large such that the conductance is increased.
Fig. 5 shows the temperature dependent measurement of a bulk dominated sample comprising 12 bilayers, (PAH/PSS)12, in the range of 333–341 K. One observes that with increasing temperature, the conductance increases as well. Increasing the temperature by 9 K correlates with rising the conductance by a factor 1.5 from 2.24 × 10−11 S to 3.34 × 10−11 S. The temperature dependent measurement for (PAH/PSS)12 result in bilayer conductivities ranging from 8.55 × 10−7 S cm−2 to 1.276 × 10−6 S cm−2 within a temperature increase of 9 K.
The temperature dependence of the ionic conductance is depicted in Fig. 6 as an Arrhenius plot of ln(GT) versus 1/T, where the slope of the linear regression is given by −EA/kB. The activation energy is derived as EA = 0.49 eV ± 0.04 eV. Silva et al. reported IS measurements for a (PSS/PAH)3 multilayer on gold electrodes leading to a slightly higher activation energy of EA = 0.61 eV.24
Previously published data for (PAH/PSS)16 showed an activation energy EA = 1.77 eV for potassium ion transport through PEM. The reason for the difference is most likely connected to the preparation method. In the current work as well as in the work by Silva et al. the PEMs were synthesized by a layer-by-layer dipping process. In ref. 9 the 16 bilayers were prepared by dripping the PAH respectively the PSS solution onto the copper electrode. It appears conceivable that structural and electronic differences may cause the difference in the activation energies. The conductivities reported in the literature have all been obtained by IS. In previous work we demonstrated that BIIT and IS yield identical conductivity for native ion bombardment. At this point we cannot completely rule out a possible difference between BIIT and IS experiments in the case where an ion species not contained in the ion beam contributes to the conductivity.
The PEMs investigated in this manuscript exhibit a linear current–voltage characteristic in close accordance to the temperature dependent measurements on a 16 bilayer thick (PAH/PSS)16 film, which was dripped on the copper backside electrode.9 Linear current–voltage curves are also observed in ion conduction glasses11 or in polymers when non-intermitted ion paths are present that reach through the entire sample.30 In both cases, the concentration of charge carriers inside the sample is in first approximation space independent. The fact, that we observe Ohmic behavior for the PEMs suggests that the number of charge carriers introduced by the BIIT must be small compared to the number of carriers that are already contained in the sample prior to the bombardment.10 Possible mobile charge carriers within the PEMs include protons as well as ions from the salt solution which may have remained in spite of thorough rinsing in the LbL process. In the current experiment the most relevant cation from the preparation step is the sodium ion. The primary effect of the ion attachment in the BIIT is the establishment of a homogeneous surface potential. However, it should be noted that even the movement of Na+ ions away from the front electrode towards the backside electrode requires a K+ entering into that place.31 Further studies are required to unambiguously identify the charge carriers.
As demonstrated by Akgöl et al. the conductivity of PAH/PSS multilayers strongly depends on preparation conditions, as temperature, pH and salt concentration.17 Values reported in the literature span a range of 7 orders of magnitude. Assuming an average thickness of about 4 nm per bilayer18 and an irradiated area of A = 0.0314 cm2, our bilayer conductivities correspond to specific conductivities between σDC = 2.4 × 10−17 S cm−1 and σDC = 3.4 × 10−15 S cm−1. Akgöl et al. discuss a humidity dependent conductivity which may be extrapolated to a value of about σDC = 10−12 S cm−1 at zero humidity.17 This value has been recorded at 295 K, the activation energy has not been reported. Durstock and Rubner reported a specific conductivity of σDC = 2 × 10−11 S cm−1 at 160 °C and an activation energy of 1.2 eV, which leads to an extrapolated value of σDC = 1.3 × 10−13 S cm−1 at 333 K.3 The quantification of specific conductivities requires knowledge of the thickness of the multilayers. The thickness, however, may depend on many external parameters, first of all the relative humidity.19 In fact, the uncertainty in the thickness is the reason why we prefer to report the bilayer normalized conductance. The conductivities measured in the current work are still smaller than the values cited above. Given the sensitivity of conductivities to subtle details of the preparation process the values do not seem unreasonable. Most likely the values reported here correspond to very dry samples and thus to a limiting intrinsic property of the PEMs.
Summary and outlook
The BIIT technique gives access to the investigation of ultra-thin, low-conductive PEM membranes in the range below 100 nm film-thickness. Layer and temperature dependent current–voltage curves have been recorded exhibiting Ohm's law like behavior. Analysis of the slope of the current–voltage plots provides access to the conductance of each sample. The conductance varies non-monotonically with the number of bilayers. A maximum of the conductance is observed for x = 8. The film consisting of a single bilayer exhibits a conductance deviating from the other trends in bulk films reflecting possibly influence from the substrate or an artificial overestimation of the conductivity by a non-complete deposition procedure.Between 2 and 8 bilayers, the conductance is observed to increase exponentially with the number of bilayers. This situation may be explained by a non-homogenous deposition of the bilayers which leads to open spots that may trigger water to leave the membrane under high vacuum conditions. The drier the film, the lower the conductivity. As a consequence, very low conductivity values are observed. For 8 or more bilayers, the samples become homogeneous which minimizes the water loss. Hence, the conductivity remains nearly the same for all sample sizes such that the conductance decreases with a 1/x function. In order to describe the full conduction behavior, we introduce a specific bilayer conductivity which follows a sigmoid law.
The change in characteristics of PEMs at about 8 bilayers reported here is compatible with experimental findings in several other reports. In fact the number of bilayers appears to be the origin of the variation in conductivity characteristics rather than the thickness. The thickness of the PEMs depends on a number of external parameters including the preparation of the film and the humidity of the film. As mentioned before the thickness of the PEMs does not necessarily scale linear with the number of bilayers, since the bilayers may structurally interweave. Several publications report on parameters influencing dielectric properties of (PAH/PSS)x films, e.g. temperature, moisture content and general deposition conditions (salt content and pH-value etc.).3,17 Yet, none of them addresses the role of these parameters in water free environment. The chemical identity of the mobile charge carrier remains difficult to resolve. Additional information could in principle arrive from a systematic variation of the type of the salt and the salt content. A long term BIIT investigation followed by an ex situ ToF-SIMS concentration profiling could in principle contribute to a better understanding of the charge carrier. However this would require a considerably thicker multilayer than the ones investigated in this work. These aspects are beyond the scope of this manuscript but will be the subject of future investigation.
Performing the BIIT measurements at various temperatures allows to derive the activation energy for the ion transport through the film. The BIIT technique applied in the current work presents an alternative to CV or IS for measuring conductivity properties of ultra-thin PEMs, especially if water free environment is desired or the conductivity is very low.
Acknowledgements
Parts of this project were supported by the German Research Foundation (DFG grant PA794/15-1 to WJP). V.W. acknowledges a Kekulé fellowship from the Fonds of the Chemical Industry (FCI). We gratefully acknowledge contributions by Susanne Schulze in the early stage of this project.References
- S. Yılmaztürk, H. Deligöz, M. Yılmazoğlu, H. Damyan, F. Öksüzömer, S. N. Koç, A. Durmuş and M. A. Gürkaynak, J. Membr. Sci., 2009, 343, 137–146 CrossRef.
- N. Parveen and M. Schönhoff, Macromolecules, 2013, 46, 7880–7888 CrossRef CAS.
- M. F. Durstock and M. F. Rubner, Langmuir, 2001, 17, 7865–7872 CrossRef CAS.
- L. Zhang, N. Zhou, B. Wang, C. Liu and G. Zhu, J. Colloid Interface Sci., 2014, 421, 1–5 CrossRef CAS PubMed.
- J. T. Stricker, A. D. Gudmundsdottir, A. P. Smith, B. E. Taylor and M. F. Durstock, J. Phys. Chem. B, 2007, 111, 6322–6326 CrossRef CAS PubMed.
- M. Ochs, S. Carregal-Romero, J. Rejman, K. Braeckmans, S. C. De Smedt and W. J. Parak, Angew. Chem., Int. Ed., 2013, 52, 695–699 CrossRef CAS PubMed.
- L. L. del Mercato, A. Z. Abbasi and W. J. Parak, Small, 2011, 7, 351–363 CrossRef CAS PubMed.
- O. Kreft, A. M. Javier, G. B. Sukhorukov and W. J. Parak, J. Mater. Chem., 2007, 17, 4471–4476 RSC.
- S. Carregal-Romero, P. Rinklin, S. Schulze, M. Schäfer, A. Ott, D. Hühn, X. Yu, B. Wolfrum, K.-M. Weitzel and W. J. Parak, Macromol. Rapid Commun., 2013, 34, 1820–1826 CrossRef CAS PubMed.
- M. Schäfer and K.-M. Weitzel, Phys. Chem. Chem. Phys., 2011, 13, 20112–20122 RSC.
- P. V. Menezes, J. Martin, M. Schäfer, H. Staesche, B. Roling and K.-M. Weitzel, Phys. Chem. Chem. Phys., 2011, 13, 20123–20128 RSC.
- S. Schulze, M. Schäfer, A. Greiner and K.-M. Weitzel, Phys. Chem. Chem. Phys., 2013, 15, 1481–1487 RSC.
- B. David, Z. Julia, M. Johannes, M. Pramod, S. Martin and W. Karl-Michael, Z. Phys. Chem., 2014, 228, 609–627 Search PubMed.
- V. García-Morales, T. H. Silva, C. Moura, J. A. Manzanares and F. Silva, J. Electroanal. Chem., 2004, 569, 111–119 CrossRef.
- T. Kolling, A. Schlemmer, C. Pietzonka, B. Harbrecht and K.-M. Weitzel, J. Appl. Phys., 2010, 107, 014105 CrossRef.
- S. Schulze, J. Zakel, M. Schäfer and K.-M. Weitzel, IEEE Trans. Dielectr. Electr. Insul., 2012, 19, 1167–1174 CrossRef CAS.
- Y. Akgöl, C. Cramer, C. Hofmann, Y. Karatas, H.-D. Wiemhöfer and M. Schönhoff, Macromolecules, 2010, 43, 7282–7287 CrossRef.
- F. Caruso, K. Niikura, D. N. Furlong and Y. Okahata, Langmuir, 1997, 13, 3422–3426 CrossRef CAS.
- R. Koehler, R. Steitz and R. von Klitzing, Adv. Colloid Interface Sci., 2014, 207, 325–331 CrossRef CAS PubMed.
- T. R. Farhat and J. B. Schlenoff, Langmuir, 2001, 17, 1184–1192 CrossRef CAS.
- S. Han and B. Lindholm-Sethson, Electrochim. Acta, 1999, 45, 845–853 CrossRef CAS.
- G. Ladam, P. Schaad, J. C. Voegel, P. Schaaf, G. Decher and F. Cuisinier, Langmuir, 2000, 16, 1249–1255 CrossRef CAS.
- S. V. P. Barreira, V. García-Morales, C. M. Pereira, J. A. Manzanares and F. Silva, J. Phys. Chem. B, 2004, 108, 17973–17982 CrossRef CAS.
- T. H. Silva, V. Garcia-Morales, C. Moura, J. A. Manzanares and F. Silva, Langmuir, 2005, 21, 7461–7467 CrossRef CAS PubMed.
- J. J. Ramsden, Y. Lvov and G. Decher, Thin Solid Films, 1995, 254, 246–251 CrossRef CAS.
- P. Lavalle, C. Gergely, F. J. G. Cuisinier, G. Decher, P. Schaaf, J. C. Voegel and C. Picart, Macromolecules, 2002, 35, 4458–4465 CrossRef CAS.
- C. Picart, G. Ladam, B. Senger, J.-C. Voegel, P. Schaaf, F. J. G. Cuisinier and C. Gergely, J. Chem. Phys., 2001, 115, 1086 CrossRef CAS.
- M. Schönhoff, A. W. Imre, A. Bhide and C. Cramer, Z. Phys. Chem., 2010, 224, 1555–1589 CrossRef.
- Y. Akgöl, C. Hofmann, Y. Karatas, C. Cramer, H.-D. Wiemhöfer and M. Schönhoff, J. Phys. Chem. B, 2007, 111, 8532–8539 CrossRef PubMed.
- V. Wesp, J. Zakel, M. Schäfer, I. Paulus, A. Greiner and K.-M. Weitzel, Electrochim. Acta, 2015, 170, 122–130 CrossRef CAS.
- L. Rossrucker, P. V. Menezes, J. Zakel, M. Schaefer, B. Roling and K.-M. Weitzel, Z. Phys. Chem., 2012, 226, 341–353 CrossRef CAS.
| This journal is © the Owner Societies 2016 |