Experimental and theoretical study of weak intermolecular interactions in crystalline tertiary squaramides

Abstract

We report the X-ray solid state structures of two tertiary squaramides, i.e. 3-(diethylamino)-4-ethoxy-cyclobutene-1,2-dione (1) and bis-3,4-(diethylamino)-cyclobutene-1,2-dione (2). Compound 1 forms electrostatically compressed dimers in the solid state. Moreover, compound 2 exhibits a remarkable solid state architecture resembling a lipid bilayer. This supramolecular assembly has been analyzed using high level DFT calculations and Bader's theory of “atoms-in-molecules”. The antiparallel CO⋯CO interactions of the cyclobutenedione rings and hydrophobic interactions involving the ethyl chains are crucial for the formation of the bilayer assembly in the solid state.

---

1. Introduction

Squaric acid amides are interesting four-membered ring systems with a strong ability to form H-bonds both as donors and acceptors. This high capacity for hydrogen bonding has been rationalized taking into consideration an increase in aromaticity of the ring upon the formation of H-bonds.¹ Remarkably, they are easy to synthesize and have recently attracted attention in several fields such as catalysis,² supramolecular chemistry³ and transmembrane transport.⁴ Basically due to their rigidity and H-bonding flexibility, they are ideal supramolecular synthons for generating interesting assemblies in the solid state.⁵ In fact, the use of squarate and hydrogen squarate salts is frequent in crystal engineering⁶ and organic material research.⁷ A topic of continuous interest by some of us is the electrostatic compression phenomenon⁸ that we have used to explain the face-to-face π-stacked assemblies exhibited by a series of zwitterionic squaric acid/squaramide compounds.⁹ However, the application of this phenomenon has been scarcely exploited in the crystal engineering field to date. Thus, in this paper we intend to combine the π-stacking interactions of tertiary squaramides with hydrophobic interactions with the aim of exploring new crystal architectures based on a design resembling lipid bilayers. Since tertiary squaramides are a family of compounds poorly studied in the solid state with only 10 structures deposited at the CCDC (Refcodes: AKOFIQ, AKOFOW, AKOGAJ, AKOGEN, DICQIQ, FATSUP, GAHMEH, NANQUO, NANQUO02, QORQIY), we have designed two new tertiary squaramides with the additional objective of extending the knowledge about the forces that govern some supramolecular assemblies in the solid state by combining crystal structure and computational analysis of these two model compounds (see Scheme 1). In particular, we focus our attention on analysis of the arrangement of the ethyl chains in compound 2 that provokes the formation of several layers (resembling lipid bilayers, vide infra) dominated by both hydrophobic forces and unconventional π-stacking interactions. That is, instead of conventional π-stacking interactions involving the π-system of the four membered rings, as observed before in these compounds,⁹ the stacking in 2 is governed by antiparallel CO⋯CO interactions. Concerning latter interactions, Allen et al. have proposed that they can be competitive with hydrogen bonds.¹⁰ There are three possible motifs for the carbonyl–carbonyl interactions: slightly sheared antiparallel, perpendicular and sheared parallel. We have used the Cambridge Structural Database to further analyze this interaction in squaric acid derivatives. A similar lipid bilayer architecture has been previously described and somewhat generalized studying the solid state of pyrimidine bases substituted with long aliphatic chains that leads to very interesting architectures.¹¹ The hydrogen bond donor/acceptor capability of the nucleobase is responsible for the formation of a 2D-hydrogen bonding network that nicely stacks with another 2D layer by means of π–π interactions forming the bilayer (see Scheme 1, right).

Scheme 1 Compounds 1 and 2 studied in this work.

2. Experimental and theoretical methods

2.1 Materials and measurements

All chemicals used were of reagent grade and used as received from Sigma-Aldrich.

2.2 Synthesis

Synthesis of 1 and 2 was carried out following a reported methodology.¹² Suitable crystals of 1 for SXRD analysis were obtained in ethanol while crystals of 2 were obtained in diethyl ether.

2.3 X-ray crystallographic analysis

Single crystal X-ray diffraction intensity data of compound 1 were collected using a D8 Venture system equipped with a multilayer monochromator and a Mo microfocus source (λ = 0.71073 Å). Frames were integrated with the Bruker SAINT software package using a SAINT algorithm. Data were corrected for absorption effects using the multi-scan method (SADABS).¹³ The structure was solved and refined using the Bruker SHELXTL Software Package, a computer program for automatic solution of crystal structures, and refined by the full-matrix least-squares method with ShelXle Version 4.8.0, a Qt graphical user interface for the SHELXL computer program.¹⁴

Powder X-ray diffraction patterns of compound 2 were obtained on a PANalytical X'Pert PRO MPD diffractometer in transmission configuration using Cu Kα₁₊₂ radiation (λ = 1.5406 Å) with a focalizing elliptic mirror and a PIXcel detector working at a maximum detector's active length of 3.347°. Capillary geometry has been used with samples placed in glass capillaries (Lindemman) of 0.5 millimetre diameter measuring from 2 to 70° in 2θ, with a step size of 0.013° and a total measuring time of 18 hours. The powder diffractogram data was perfectly indexed to a primitive monoclinic cell of about 2139 ų by means of Dicvol04,¹⁵ and the space group was determined to be P2₁/c from systematic absences. With the asymmetric unit containing two independent molecules of 2 (Z = 8), the crystal structure was determined by direct space methodologies starting from a molecular model optimized with the commercial software SPARTAN by means of the program FOX¹⁶ with the parallel tempering algorithm. Some constraints were introduced to FOX, considering aromatic rings as rigid groups. Several trials of 20 million runs were performed. The best structure solution (i.e., the trial structure with the lowest R_wp obtained in the calculations) was used as the initial structural model for Rietveld refinement using FullProf.¹⁷ The final Rietveld refinement was carried out using the data set recorded over the 2θ range 2–70°. Only the atomic coordinates and isotropic displacement parameters of non-hydrogen atoms were refined and finally the hydrogen positions were calculated with the software SPARTAN. Fig. 1 depicts the final Rietveld plot.

Fig. 1 Final Rietveld plot for the crystal structure refinement of compound 2. Agreement factors: R_wp = 16.02%, χ² = 35.9. The upper plot shows the experimental powder XRD profile (red + marks), the calculated powder XRD profile (black solid line), and the difference profile (blue, lower line) in the 2θ range 5–35°. Tick marks indicate peak positions. The lower plot shows the experimental powder XRD profile (red + marks) and the calculated powder XRD profile (black solid line) in the 2θ range 35–70° magnified by a factor of 10 for better visualization.

A summary of crystal data and relevant refinement parameters is given in Table 1.

Table 1 Crystal data and structure refinement parameters

Structure	1	2
Empirical formula	C12H20N2O2	C10H15NO3
Formula weight	224.30	197.23
Temperature (K)	293(2)	293
Wavelength (Å)	0.71073	1.54060
Crystal system	Orthorhombic	Monoclinic
Space group	Pbcn	P21/c
a, b, c (Å)	11.6214(17), 12.966(2), 7.8494(13)	18.38627(19), 8.63088(11), 13.6582(2)
α, β, γ (°)	90, 90, 90	90, 99.1227(8), 90
Volume (Å^3)	1182.8(3)	2139.99(5)
Z, Density (calc.) (Mg m^−3)	4, 1.260	8, 1.224
Absorption coefficient (mm^−1)	0.086	—
F(000)	488	—
Crystal size (mm^3)	0.25 × 0.15 × 0.14	—
θ range for data collection (°)	2.353 to 25.114	1.009 to 34.991
Limiting indices	−13 ≤ h ≤ 13, −15 ≤ k ≤ 12, −8 ≤ l ≤ 9	—
Reflections collected/unique	3316	—
Completeness to θ (%)	95.1	—
Absorption correction	Multi-scan	—
Max. and min. transmission	0.7452 and 0.3477	—
Refinement method	Full-matrix least-squares on F^2	Rietveld
Data/parameters	1021/0/75	2145/97/162
Goodness-of-fit on F^2	1.023	χ = 7.20
Final R indices [I > 2σ(I)]	R 1 = 0.0581, wR2 = 0.1281	—
R indices (all data)	R 1 = 0.1164, wR2 = 0.1585	R wp = 16.02, χ^2 = 35.99
Largest diff. peak and hole (e Å^−3)	0.250 and −0.279 e Å^−3	—
CCDC	1476790	1476791

---

2.4 Theoretical methods

The geometries of the complexes included in this study were computed at the BP86-D3/def2-TZVP level of theory using the crystallographic coordinates within the TURBOMOLE program.¹⁸ This level of theory that includes the latest available dispersion correction (D3) is adequate for studying noncovalent interactions dominated by dispersion effects like π-stacking. The basis set superposition error for the calculation of interaction energies has been corrected using the counterpoise method.¹⁹ The “atoms-in-molecules” (AIM)²⁰ analysis of the electron density has been performed at the same level of theory using the AIMAll program.²¹

The supramolecular cluster approach is an appropriate strategy to estimate interaction energies in the solid state.²² In this approach, the supramolecular cluster of a crystal is formed by a given central molecule (M₁) that is in contact with other M_n molecules and forms the first coordination sphere. In this manner, the molecular coordination number (MCN) is determined. This methodology has been successfully used to predict/rationalize crystal growth in a given compound.²² However, in this manuscript we have used a more simple approach to estimate the strength of the noncovalent interactions that play important roles in the crystal packing of compound 2. That is, we have selected several dimers and trimers from the solid state crystal structures and evaluated the binding energies as a difference between the energy of the supermolecule and the sum of the monomers.

3. Results and discussion

3.1 Description of squaric acid derivatives 1 and 2

X-ray crystallographic characterization revealed that 1 crystallizes in the orthorhombic system with the space group Pbcn and half a molecule of 1 in the asymmetric unit. Electrostatically compressed columns of disquaramides in a zigzag fashion are parallel packed (Fig. 2a), creating hydrophobic channels formed by the ethyl residues (Fig. 2b).

Fig. 2 (a) Electrostatically compressed columns and (b) hydrophobic channels formed in the crystal structure of 1.

On the other hand, 2 crystallizes in the monoclinic space group P2₁/c with two non-equivalent molecules in the asymmetric unit which differ in the conformation of the diethylamido group (Fig. 3). The most remarkable difference between both structures is that while the hydrophobic regions in 1 are organized in channels running along the stacked columns of squaramides, they form lipidic bilayers in 2. The later organization has been studied more deeply by performing specific computational calculations.

Fig. 3 The two non-equivalent molecules in the asymmetric unit of 2 showing the anti and cis conformations of the N,N-dimethylamido group.

3.2 Theoretical study

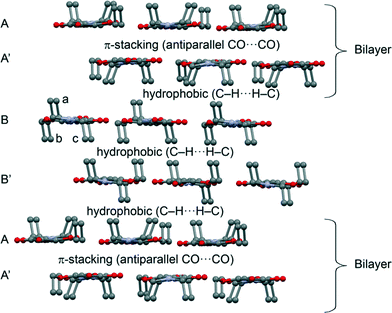
The theoretical study is devoted to the analysis of the noncovalent forces that govern the crystal packing in 2. It presents a fascinating solid state architecture where different 2D layers are interconnected by means of hydrophobic interactions or π-stacking. The 2D layers are dominated by weak C–H⋯N/O interactions. In Fig. 4 we represent the 3D architecture of 2 where the different layers are represented. The molecules that have all ethyl groups pointing to the same direction form the bilayers as shown in Scheme 1 (constituted by A and A′ 2D monolayers). These bilayers are interconnected by means of two additional layers (B and B′) formed by molecules of 2 where two ethyl groups point to one direction (denoted as b and c, in Fig. 4) and one ethyl group (denoted as a) to the opposite direction. Interestingly, the hydrophobic interactions are compensated in such a way that the face of layer B that has only one ethyl group (a) from each molecule interacts with the face of the bilayer that has three ethyl groups pointing to that region. Moreover the opposite face of layer B (two ethyl groups b and c from each molecule pointing to the same direction) interacts with the symmetrically related B′ layer in the same face (also two ethyl groups from each molecule). Therefore, the A′⋯B and B⋯B′ interlayer interactions are equivalent in terms of the number of ethyl groups pointing to the same region.

Fig. 4 Partial view of the crystal packing of compound 2. Hydrogen atoms omitted for clarity.

We have further analyzed the noncovalent forces that are responsible for the interaction of the different 2D layers shown in Fig. 5. As aforementioned, the π-stacking (A⋯A′ interlayer interaction) that facilitates the formation of the bilayer is basically controlled by antiparallel CO⋯CO and weak C–H⋯N H-bonding interactions. We have computed the interaction energy of the CO⋯CO interaction using a dimer retrieved from the crystallographic coordinates of 2 (see Fig. 5), which is significant (ΔE₁ = −7.7 kcal mol⁻¹). We have used Bader's theory of “atoms in molecules”, which provides an unambiguous definition of chemical bonding, to further describe the noncovalent interactions studied herein. The CO⋯CO interaction is characterized by the presence of two bond critical points (red spheres) connecting both CO groups (see Fig. 5). Moreover, the distribution also shows two additional H-bonding interactions characterized by two symmetrically related bond critical points connecting the O atoms of the COs (that do not participate in the CO⋯CO interaction) with the H atoms of the ethyl groups. This H-bond interaction is expected to be very weak since the O⋯H distance is longer than 3 Å (see Fig. 5). In order to evaluate the contribution of these H-bonds to the total interaction energy we have computed an additional model where we have replaced the ethyl groups that participate in the H-bonds with hydrogen atoms (see small arrows in Fig. 5). As a result, the interaction energy is reduced to ΔE₂ = −6.0 kcal mol⁻¹ that corresponds to the antiparallel CO⋯CO and the difference (ΔE₁ − ΔE₂ = −1.7 kcal mol⁻¹) is the contribution of both long H-bonds. The other interaction that also contributes to the formation of the A⋯A′ layer is represented in Fig. 5. The interaction energy of this dimer is ΔE₃ = −4.2 kcal mol⁻¹, weaker than the CO⋯CO interaction. AIM analysis shows a bond CP that connects the H atom with the N atom thus confirming the C–H⋯N bond. Moreover, it also shows the presence of a C–H⋯H–C interaction involving the ethyl groups (Fig. 5F).

Fig. 5 (A–C) X-ray dimers used to evaluate the interlayer A⋯A′ noncovalent interactions. (D–F) AIM analyses of the X-ray dimers of compound 2. Bond and ring critical points are represented by red and yellow spheres, respectively. The bond paths connecting bond critical points are also represented by dashed lines. Distances are in Å.

The models used to evaluate the interactions that control the formation of A⋯B and B⋯B′ bilayers are shown in Fig. 6 along with their AIM analyses. For the A⋯B interaction we have used a trimer where two molecules belong to the A layer and one molecule to the B layer. The interaction energy due to the hydrophobic interactions is ΔE₄ = −6.3 kcal mol⁻¹ and corresponds to an intricate combination of interactions as evidenced by the AIM analysis (see Fig. 6). Apart from the C–H⋯H–C interactions between the ethyl groups, there are two very long CO⋯HC interactions. The dimer that is used to evaluate the C–H⋯H–C interactions in the B⋯B′ interlayer is shown in Fig. 6. It is stabilized by three C–H⋯H–C interactions and two symmetrically related C–H⋯π interactions (see Fig. 6). The π-system of latter interactions is the C=C double bond of the cyclobutenedione ring. The resulting interaction energy is ΔE₅ = −5.6 kcal mol⁻¹ which is similar to ΔE₄, in agreement with the number of ethyl groups pointing to the interlayer region (vide supra).

Fig. 6 (A and B) X-ray dimer used to evaluate the interlayer A⋯B and B⋯B′ noncovalent interactions. (C and D) AIM analyses of the X-ray dimers. Bond and ring critical points are represented by red and yellow spheres, respectively. The bond paths connecting bond critical points are also represented by dashed lines. Distances are in Å.

3.3 CSD analysis

From the latter theoretical study, it has been evidenced that the CO⋯CO interaction is important and energetically relevant for the formation of the 3D structure of compound 2 in the solid state. We have analyzed the CSD, which is a convenient reservoir of geometry information, in order to investigate if other X-ray solid state structures of squaric acid derivatives also present this interaction in the solid state. Remarkably, we have found 20 solid state X-ray structures (see Table 2), including squarate salts, where the antiparallel CO⋯CO interaction is present. In case the search is restricted to neutral squaric acid derivatives (amides/esters), the number of X-ray structures is reduced to only three (entries 1, 15 and 24), which correspond to CSD codes WECCOY,²³ OMEXOT²⁴ and XOPWEF03,²⁵ which are shown Fig. 7 along with their CO⋯CO interaction energies that range from −11.8 to −17.7 kcal mol⁻¹. The WECCOY structure is very similar to compound 2 (amide–ester) and the other two are squaramides. It is interesting to highlight that the intermolecular C⋯O distance in compound 2 is significantly shorter than those exhibited by the X-ray structures retrieved from the CSD search (see Table 2, D₁ and D₂ parameters). In fact compound 2 exhibits a C⋯O distance (2.879 Å) that is considerably shorter than the sum of O and C van der Waals radii (3.22 Å). This short distance can be related to crystal packing forces and the compression phenomenon of the solid state structure. In fact, we have further analyzed the effect of the compression on the CO⋯CO interaction by comparing the AIM analyses of compound 2 to those obtained for WECCOY and OMEXOT structures. The results are shown in Fig. 8, and the distribution of critical points that characterizes the CO⋯CO interaction is different. In WECCOY and OMEXOT structures two symmetrically related bond critical points and bond paths connect the O atom with the C atom and vice versa. In sharp contrast, the bond critical points in 2 connect both O atoms. This counterintuitive result is due to the short CO⋯CO stacking distance due to the crystal compression that provokes the approximation of both O atoms to a distance that is shorter than the sum of the van der Waals radii (3.04 Å). In fact, all structures gathered in Table 2 present O⋯O distances longer than the sum of van der Waals radii (denoted as D₃). Therefore the short O⋯O distance observed in 2 is unprecedented in squaric acid derivatives. According to Bader's definition,²⁶ the bond path is the line of maximum density linking neighboring nuclei in a system in stable electrostatic equilibrium regardless of the nature of the interaction. Due to the strong electronegativity of the O atom and the polarization of the C=O bond, the bond path that characterizes the CO⋯CO interaction in 2 initially heads to the carbon and, unexpectedly, changes the trajectory and finishes at the O atom because it is the path of maximum electron charge density. In the other two compounds the O atoms are more separated and the bond path starts in the O atom and ends in the C atom. This differentiating behavior in 2 is a clear consequence of the compression phenomenon.

Table 2 CSD reference codes of the squaric acid derivatives that present antiparallel CO⋯CO interactions. The intermolecular C⋯O and O⋯O distances in Å are also included

Entry	CSD code	C⋯O distances^a		O⋯O distance (D3)
		D 1	D 2
a See Fig. 7 for the definition of D1 and D2.
1	XOPWEF03	3.094	3.103	3.461
2	AGEQIO	3.092	3.213	3.340
3	AWOVEO	3.174	3.174	3.225
4	BUBWUR	3.185	3.185	3.422
5	COZSIU	3.145	3.145	3.405
6	EZEPAA	3.077	3.077	3.120
7	FEFLEI	3.041	3.041	3.313
8	HERDOX	3.080	3.080	3.286
9	HSQCRA	3.135	3.135	3.168
10	IJOPIH	3.217	3.217	3.113
11	KECYBU16	3.194	3.194	3.198
12	OMEXOT	3.034	3.034	3.250
13	QIHPUS	3.157	3.193	3.305
14	SOCLEC	3.150	3.150	3.263
15	TURQAY	3.166	3.166	3.286
16	TURQOM	3.132	3.132	3.211
17	TURRAZ	3.198	3.198	3.387
18	VASQUC	3.066	3.066	3.204
19	WECCOY	3.075	3.075	3.320
20	ZOSWEK	3.179	3.179	3.457
21	Compound 2	2.879	2.879	3.019

---

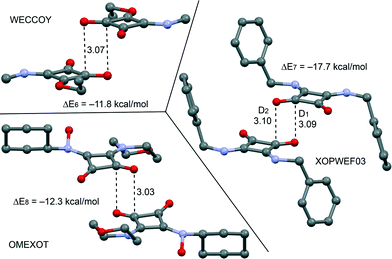Fig. 7 X-ray solid state structures of compounds WECCOY, OMEXOT and XOPWEF03 exhibiting CO⋯CO interactions. Distances are in Å.

Fig. 8 AIM analyses of several X-ray dimers. Bond and ring critical points are represented by red and yellow spheres, respectively. The bond paths connecting bond critical points are also represented by dashed lines.

Conclusions

Two squaric acid derivatives have been synthesized and characterized by single crystal and powder X-ray diffraction. One of the two presents an interesting solid state architecture, where several 2D layers interacts by means of different noncovalent interactions, which has been analyzed by means of DFT calculations and the AIM method. Antiparallel CO⋯CO interactions play a prominent role in the formation of assemblies that resemble lipid bilayers. We have also analyzed the Cambridge Structural Database and found other X-ray structures than exhibit similar interactions. However, compound 2 presents a very short CO⋯CO distance, which is unprecedented. This is likely due to the compression of the structure and it clearly affects the distribution of critical points that characterize the interaction due to the short O⋯O distance. In contrast, compound 1 does not present CO⋯CO interactions in the solid state. The crystal packing and compression are due to H-bonding interactions.

Acknowledgements

AB and AF thank DGICYT of Spain (projects CTQ2014-57393-C2-1-P and CONSOLIDER INGENIO CSD2010–00065, FEDER funds) for funding and the CTI (UIB) for free allocation of computer time.

Notes and references

1. A. Frontera, P. M. Deyà, D. Quiñonero, C. Garau, P. Ballester and A. Costa, Chem. – Eur. J., 2002, 8, 433–438.
2. (a) D. Enders, U. Kaya, P. Chauhan, D. Hack, K. Deckers, R. Puttreddy and K. Rissanen, Chem. Commun., 2016, 52, 1669–1672; (b) A. S. Kumar, T. P. Reddy, R. Madhavachary and D. B. Ramachary, Org. Biomol. Chem., 2016, 14, 5494–5499; (c) D. Zhou, Z. Huang, X. Yu, X. Y. Wang, J. Li, W. Wang and H. Xie, Org. Lett., 2015, 17, 5554–5557; (d) L. Chen, Z.-J. Wu, M.-L. Zhang, D.-F. Yue, X.-M. Zhang, X.-Y. Xu and W.-C. Yuan, J. Org. Chem., 2015, 80(24), 12668–12675; (e) B. Shan, Y. Liu, R. Shi, S. Jin, L. Li, S. Chen and Q. Shu, RSC Adv., 2015, 5, 96665–96669; (f) M.-X. Zhao, H.-K. Zhu, T.-L. Dai and M. Shi, J. Org. Chem., 2015, 80, 11330–11338; (g) J. Peng, B.-L. Zhao and D.-M. Du, Adv. Synth. Catal., 2015, 357, 3639–3647; (h) W. Sun, L. Hong, G. Zhu, Z. Wang, X. Wei, J. Ni and R. Wang, Org. Lett., 2014, 16, 544; (i) X.-B. Wang, T.-Z. Li, F. Sha and X.-Y. Wu, Eur. J. Org. Chem., 2014, 739; (j) V. Kumar and S. Mukherjee, Chem. Commun., 2013, 49, 11203–11205; (k) K. S. Yang, A. E. Nibbs, Y. E. Turkmen and V. H. Rawal, J. Am. Chem. Soc., 2013, 135, 16050–16053; (l) P. Kasaplar, C. Rodriguez-Escrich and M. A. Pericas, Org. Lett., 2013, 15, 3498–3501; (m) P. Kasaplar, P. Riente, C. Hartmann and M. A. Pericas, Adv. Synth. Catal., 2012, 354, 2905–2910.
3. (a) R. B. P. Elmes, P. Turner and K. A. Jolliffe, Org. Lett., 2013, 15, 5638–5641; (b) K. Bera and I. N. N. Namboothiri, Chem. Commun., 2013, 49, 10632–10634; (c) C. Jin, M. Zhang, L. Wu, Y. Guan, Y. Pan, J. Jiang, C. Lin and L. Wang, Chem. Commun., 2013, 49, 2025–2027; (d) C. Lopez, E. Sanna, L. Carreras, M. Vega, C. Rotger and A. Costa, Chem. – Eur. J., 2013, 8, 84–87; (e) B. Soberats, L. Martinez, E. Sanna, A. Sampedro, C. Rotger and A. Costa, Chem. – Eur. J., 2012, 18, 7533–7542; (f) V. Amendola, L. Fabbrizzi, L. Mosca and F.-P. Schmidtchen, Chem. – Eur. J., 2011, 17, 5972; (g) S. Tomas, R. Prohens, G. Deslongchamps, P. Ballester and A. Costa, Angew. Chem., Int. Ed., 1999, 38, 2208–2211.
4. N. Busschaert, I. L. Kirby, S. Young, S. J. Coles, P. N. Horton, M. E. Light and P. A. Gale, Angew. Chem., Int. Ed., 2012, 51, 4426–4430.
5. (a) A. Portell and R. Prohens, Cryst. Growth Des., 2014, 14, 397–400; (b) A. Portell, X. Alcobe, L. M. Lawson Daku, R. Cerny and R. Prohens, Powder Diffr., 2013, 28, S470–S480; (c) R. Prohens, A. Portell and X. Alcobe, Cryst. Growth Des., 2012, 12, 4548–4553.
6. (a) T. Kolev, R. W. Seidel, H. Mayer-Figge, M. Spiteller, W. S. Sheldrick and B. B. Koleva, Spectrochim. Acta, Part A, 2009, 72, 502–509; (b) T. Kolev, H. Mayer-Figge, R. W. Seidel, W. S. Sheldrick, M. Spiteller and B. B. Koleva, J. Mol. Struct., 2009, 919, 246–254; (c) B. Ivanova and M. Spiteller, Spectrochim. Acta, Part A, 2010, 77, 849–855; (d) S. L. Georgopoulos, H. G. M. Edwards and L. F. C. De Oliveira, Spectrochim. Acta, Part A, 2013, 111, 54–61.
7. (a) C. Qin, Y. Numata, S. Zhang, X. Yang, A. Islam, K. Zhang, H. Chen and L. Han, Adv. Funct. Mater., 2014, 24, 3059–3066; (b) Z. Dega-Szafran, G. Dutkiewicz and Z. Kosturkiewicz, J. Mol. Struct., 2012, 1029, 28–34; (c) P. Barczyński, Z. Dega-Szafran, A. Katrusiak and M. Szafran, J. Mol. Struct., 2012, 1018, 28–34.
8. A. Portell, M. Font-Bardia and R. Prohens, Cryst. Growth Des., 2013, 13, 4200–4203.
9. R. Prohens, A. Portell, M. Font-Bardia, A. Bauzá and A. Frontera, Cryst. Growth Des., 2014, 14, 2578–2587.
10. F. H. Allen, C. A. Baalham, J. P. M. Lommerse and P. R. Raithby, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 320–329.
11. (a) M. Barceló-Oliver, C. Estarellas, A. Garcia-Raso, A. Terrón, A. Frontera, D. Quiñonero, E. Molins and P. M. Deyà, CrystEngComm, 2010, 12, 362–365; (b) M. Barceló-Oliver, C. Estarellas, A. Garcia-Raso, A. Terrón, A. Frontera, D. Quiñonero, I. Mata, E. Molins and P. M. Deyà, CrystEngComm, 2010, 12, 3758–3767.
12. R. Prohens, S. Tomas, J. Morey, P. M. Deya, P. Ballester and A. Costa, Tetrahedron Lett., 1998, 39, 1063–1066.
13. SADABS Bruker AXS, Madison, Wisconsin, USA, 2004; SAINT, Software Users Guide, Version 6.0, Bruker Analytical X–ray Systems, Madison, WI, 1999; G. M. Sheldrick, SADABS v2.03: Area–Detector Absorption Correction, University of Göttingen, Germany, 1999; Saint Version 7.60A, Bruker AXS, 2008; SADABS V. 2008–1, 2008.
14. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
15. A. Boultif and D. Loue, J. Appl. Crystallogr., 1991, 24, 987–993.
16. V. Favre-Nicolin and R. Cerny, J. Appl. Crystallogr., 2002, 35, 734–743.
17. J. Rodriguez-Carvajal, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 192, 55–69.
18. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
19. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
20. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
21. T. A. Keith, AIMAll (Version 13.05.06), TK Gristmill Software, Overland Park KS, USA, 2013.
22. M. A. P. Martins, C. P. Frizzo, A. C. L. Martins, A. Z. Tier, I. M. Gindri, A. R. Meyer, H. G. Bonacorso and N. Zanatta, RSC Adv., 2014, 4, 44337–44349; M. A. P. Martins, A. R. Meyer, A. Z. Tier, K. Longhi, L. C. Ducati, H. G. Bonacorso, N. Zanatta and C. P. Frizzo, CrystEngComm, 2015, 17, 7381–7391; C. P. Frizzo, A. Z. Tier, I. M. Gindri, A. R. Meyer, G. Black, A. L. Belladonaa and M. A. P. Martins, CrystEngComm, 2015, 17, 4325–4333.
23. R. Prohens, A. Portell, C. Puigjaner, R. Barbas, X. Alcobe, M. Font-Bardia and S. Tomas, CrystEngComm, 2012, 14, 5745–5748.
24. N. C. Lim, M. D. Morton, H. A. Jenkins and C. J. Bruckner, Organomet. Chem., 2003, 68, 9233–9241.
25. A. Portell, X. Alcobe, M. Latevi, R. Cerny and R. Prohens, Powder Diffr., 2013, 28, S470–S480.
26. R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323.

---

Footnote

† CCDC 1476790 and 1476791. For crystallographic data in CIF or other electronic format see DOI: 10.1039/c6ce01299j

---