Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enormous lattice distortion through an isomorphous phase transition in an organic–inorganic hybrid based on haloantimonate(III)†
Martyna
Wojciechowska
a,
Przemysław
Szklarz
a,
Agata
Białońska
a,
Jan
Baran
b,
Rafał
Janicki
a,
Wojciech
Medycki
c,
Piotr
Durlak
a,
Anna
Piecha-Bisiorek
*a and
Ryszard
Jakubas
a
aFaculty of Chemistry, University of Wrocław, Joliot-Curie 14, 50-383 Wrocław, Poland. E-mail: anna.piecha@chem.uni.wroc.pl
bInstitute of Low Temperature and Structure Research, Polish Academy of Science, Okólna 2, PO Box 937, 50-950 Wrocław 2, Poland
cInstitute of Molecular Physics, Polish Academy of Science, M. Smoluchowskiego 17, 60-179 Poznań, Poland
First published on 27th June 2016
Abstract
Bis(diisobutylammonium) octabromodiantimonate(III), [(i-C4H9)2NH2]2Sb2Br8, has been synthesized. The differential scanning calorimetric measurements indicate a reversible, first-order phase transition at 222/229 K (cooling/heating). The single crystal X-ray diffraction studies reveal that the phase transition is isomorphous and is accompanied by a huge distortion of the crystal lattice. By comparison of the crystal structures of [(i-C4H9)2NH2]2Sb2Br8 and [(i-C4H9)2NH2]2Sb2Cl8, an analogous mechanism of the phase transition of the former is proposed. The change of the electronic structure of the complex during the phase transition was analyzed by UV-vis spectroscopy. A low-frequency dielectric relaxation process appears over phase I (below the room temperature) and corresponds to the dynamics of dipolar diisobutylammonium cations. The detailed analysis of the molecular motions of the organic cations studied by means of proton magnetic resonance (1H NMR) in a wide temperature range indicates a leading role of the methyl groups in the relaxation mechanism. A variable-temperature investigation of the infrared spectra of [(i-C4H9)2NH2]2Sb2Br8 confirms, in turn, the influence of the diisobutylammonium cation dynamics on the molecular mechanism of the structural transformation at 229 K.
Introduction
The compounds of haloantimonates(III) and halobismuthates(III) with amines have been known for over a century. Current interest in these compounds stems from their possible applications as nonlinear optical (NLO) and nonlinear dielectric (polar) materials.1–12 During the past 25 years, in the family of crystals described by the formula RaMbX(3b+a) (X = Cl, Br, I; M = Sb(III), Bi(III) and R is an organic cation), a dozen of novel ferroelectrics have been obtained. In spite of the fact that haloantimonates(III) and halobismuthates(III) are characterized by a rich diversity of the anionic networks in the crystal lattices, the ferroelectric properties are limited only to several chemical stoichiometries namely: R5M2X11,13–17 R3M2X9,18–21 R2MX5 (ref. 22 and 23) and RMX4,24,25 where the cations are usually small alkylammonium ones or five and six-membered heteroaromatic rings. In general, most of the paraelectric–ferroelectric phase transitions (PTs) are characterized by an ‘order–disorder’ mechanism connected with the dynamics of the organic counterions.In our search for new acentric and switchable dielectric PT materials, we have extended our studies on derivatives containing bulky secondary aliphatic amines. It should be emphasized that simple (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) ionic compounds built from expanded secondary aliphatic amines, for example diisopropylammonium chloride26 and diisopropylammonium bromide,27,28 are very promising room temperature ferroelectric materials with spontaneous polarization comparable with those of well known perovskite-like ferroelectrics (BaTiO3). Diisobutylamine molecules are characterized by a significant dipole moment, which makes them good candidates as components in inorganic–organic hybrid compounds. A change in the dynamics/reorientation of such dipolar units in the crystal lattice may lead to interesting dielectric properties (a tunable and switchable dielectric constant) and PTs.29
1) ionic compounds built from expanded secondary aliphatic amines, for example diisopropylammonium chloride26 and diisopropylammonium bromide,27,28 are very promising room temperature ferroelectric materials with spontaneous polarization comparable with those of well known perovskite-like ferroelectrics (BaTiO3). Diisobutylamine molecules are characterized by a significant dipole moment, which makes them good candidates as components in inorganic–organic hybrid compounds. A change in the dynamics/reorientation of such dipolar units in the crystal lattice may lead to interesting dielectric properties (a tunable and switchable dielectric constant) and PTs.29
Here we present two novel organic–inorganic hybrid materials, diisobutylammonium analogs based on haloantimonates(III); [(i-C4H9)2NH2]2Sb2Cl8 and [(i-C4H9)2NH2]2Sb2Br8. As it turned out only the latter compound was found to undergo isomorphous structural PT of the first-order at 222 K (cooling). The proposed mechanism of the PT was based on the thermal, vibrational (IR) and dielectric studies, while the molecular motions of diisobutylammonium cations in [(i-C4H9)2NH2]2Sb2Br8 were studied by means of proton magnetic resonance (1H NMR) spectroscopy. The comparison of the crystal structures between the bromide (two phases) and the chloride compounds allowed us to explain/propose the origin of the PT in [(i-C4H9)2NH2]2Sb2Br8.
Results and discussion
DSC measurements, presented in Fig. 1(a), indicate the presence of a perfectly reversible first-order structural PT which is characterized by a strong heat anomaly at about 222/229 K (cooling–heating) and thermal hysteresis (ΔT = 7 K). The entropy change (ΔStr) was estimated to be ca. 26 J mol−1 K−1. It should be also added that a study of the phase situation based on dilatometric measurement (see Fig. S1 – ESI†) confirms the sequence and the nature of the low-temperature PT. The observation of the single crystal sample under a polarized microscope in the ac plane disclosed a characteristic phase front which shifts along the a-axis as it can be seen in Fig. S2.† It confirms the first-order character of the PT at 222 K. The optical observations disclose also an additional feature of the title compound which is related to the mechanical instability around Tc. Attached films (F1) show that the discontinuous PT, which is related to the huge distortion of the inorganic substructure (see Table 1), affects the characteristic bending of the crystal sample. No reversible PT was detected in [(i-C4H9)2NH2]2Sb2Cl8 below room temperature (RT). | ||
| Fig. 1 (a) DSC traces upon cooling and heating (5 K min−1) for [i-(C4H9)2NH2]2Sb2Br8 (m = 9.822 mg); (b) simultaneous thermogravimetric and differential thermal analyses scan (ramp rate: 2 K min−1). | ||
| Phase I (250 K)exp. | Phase II (100 K)calc. | Phase II (100 K)exp. | |
|---|---|---|---|
| Symmetry codes: i 1 − x, 1 − y, −z; ii 1 + x, y, z; exp. – X-ray diffraction; calc. – calculations. | |||
| Sb–Br(1) | 2.5253(13) | 2.6689 | 2.5261(9) |
| Sb–Br(2) | 3.1196(14) | 3.2718 | 3.0280(6) |
| Sb–Br(2)i | 3.174(2) | 3.2864 | 3.3163(8) |
| Sb–Br(3) | 2.5656(14) | 2.5934 | 2.6170(5) |
| Sb–Br(4) | 2.5476(18) | 2.5659 | 2.5393(7) |
| Sb–Br(1)ii | 3.4918(16) | 3.7214 | 3.6698(12) |
| Br(1)–Sb–Br(3) | 93.33(4) | 91.85 | 92.254(16) |
| Br(1)–Sb–Br(4) | 95.55(7) | 100.87 | 95.02(2) |
| Br(3)–Sb–Br(4) | 93.48(4) | 93.19 | 91.057(12) |
| Br(1)–Sb–Br(2) | 86.80(3) | 79.86 | 86.831(14) |
| Br(3)–Sb–Br(2) | 176.66(4) | 165.36 | 178.305(13) |
| Br(4)–Sb–Br(2) | 89.83(3) | 90.21 | 87.603(11) |
Above RT, the compound shows complex thermal properties because the visible heat anomalies are only partially reversible and connected with a simultaneously weak decomposition of the sample (see Fig. S3†). Fig. 1(b) shows the TGA–DTA scan of the [(i-C4H9)2NH2]2Sb2Br8 crystal between 300 and 700 K. The first two endothermic peaks at ca. 370 and 387 K correspond to the irreversible PTs detected by DSC (see also Fig. S3†). The next heat anomaly at 408 K is due to the melting of the sample and onset of the decomposition of the compound.
Single-crystal X-ray diffraction and theoretical structure analysis
The single crystal X-ray diffraction experiment revealed that both phases of [(i-C4H9)2NH2]2Sb2Br8 adopt the monoclinic P21/c space group (no. 14). The independent portion of the unit cell at 250 K, together with the atom numbering scheme, is presented in Fig. 2(a). It consists of one diisobutylammonium cation and half of the [Sb2Br82−] anion. In both phases all atoms occupy the general positions; however, the centre of gravity of the [Sb2Br82−] anions is placed at the symmetry centre. | ||
| Fig. 2 The atom numbering scheme of [(i-C4H9)2NH2]2Sb2Br8 at (a) 250 K and (b) 100 K (symmetry codes: i 1 − x, 1 − y, −z; ii 1 + x, y, z). | ||
The centrosymmetric [Sb2Br82−] ions consist of two distorted square pyramids sharing a basal edge (Fig. 2(a)). At 250 K, the diisobutylammonium cations reveal disorder, in which each isobutyl group is distributed between two sites (Fig. 2(a) and 3(b)). At 100 K (phase II), the disorder disappears and diisobutylammonium cations are fully ordered (Fig. 2(b) and 3(c)).
The components of the anionic network ([Sb2Br82−] moieties) are stacked along the [100] direction (a-axis). The shortest Sb⋯Br distance between neighboring [Sb2Br82−] units along the [100] direction, which is equal to 3.67 Å, suggests a possible halogen–metal interaction and leads to formation of anionic supramolecular ribbons (see Fig. 3(a), 4 and Table 1). The diisobutylammonium cations are located in grooves of the supramolecular anionic ribbons, formed between neighboring [Sb2Br82−] units. The diisobutylammonium cations interact via N–H⋯Br hydrogen bonds with neighboring [Sb2Br82−] units additionally stabilizing the anionic supramolecular structure (Table 2). The relatively high thermal vibration factors of the terminal Br atoms in the high temperature phase indicate significant librational motions of the whole [Sb2Br82−] anions with respect to their symmetry centre. In the low-temperature phase II, the [Sb2Br82−] anions reduce significantly their librational motion. The PT is not accompanied by a change in the space group, thus this transition is classified as an isomorphous one.
| D–H⋯A | d(D–H) | d(H⋯A) | d(D⋯A) | ∠(DHA) |
|---|---|---|---|---|
| Symmetry code: ix − 1, y, z. | ||||
| N–H(2)⋯Br(2) calculated | 0.99/0.91 | 2.54/2.60 | 3.386(7)/3.398(3) | 143/147 |
| —/1.02 | —/2.69 | —/3.621 | —/150 | |
| N–H(1)⋯Br(2)i calculated | 0.89/0.91 | 2.62/2.70 | 3.355(7)/3.540(3) | 140/154 |
| —/1.01 | —/2.72 | —/3.684 | —/152 | |
The PT is accompanied by a huge distortion of the crystal lattice. After the transition, the dimensions of a and c of the unit cell increase by about 0.09 and 0.45 Å, respectively, whereas the dimension of b is significantly reduced by about 1.91 Å (above 9%). Also the β angle changes during the PT (decreases about 2.93°). The huge distortion of the crystal lattice during the PT does not lead to the breaking of the symmetry (see Table S1 – ESI†). Such an effect, rarely encountered, is a result of the fact that all the atoms of the ions are placed in general positions and anions are additionally situated at the symmetry centre. In consequence, even the huge distortion of the crystal lattice due to the PT retains the same symmetry (space group) of the phases II and I.
For better understanding of the mechanism of the PT and especially of the huge distortion of the crystal lattice observed for [(i-C4H9)2NH2]2Sb2Br8 during the PT, we additionally synthesized and structurally characterized the [(i-C4H9)2NH2]2Sb2Cl8 analog. The crystal structure of [(i-C4H9)2NH2]2Sb2Cl8 is quite similar to [(i-C4H9)2NH2]2Sb2Br8. However, the diisobutylammonium cations in [(i-C4H9)2NH2]2Sb2Cl8 are ordered in the temperature range 100–250 K and the geometry as well as the mutual orientation of the [Sb2Cl82−] units remains without more significant changes (ESI†). The [(i-C4H9)2NH2]2Sb2Cl8 does not reveal any PT in the temperature range of 100–250 K. The average Sb–Br distance in [(i-C4H9)2NH2]2Sb2Br8 is about 0.13 Å greater than the average Sb–Cl distance in [(i-C4H9)2NH2]2Sb2Cl8. This causes a weak fitting of the diisobutylammonium cations to the grooves of the anionic ribbons and leads to the disorder of the cations in [(i-C4H9)2NH2]2Sb2Br8 at 250 K. However, at 100 K, some Sb–Br distances of [Sb2Br82−] units are even greater (even about 0.14 Å) than at 250 K, and diisobutylammonium cations are ordered. Simultaneously, after the PT in the cooling mode, the Br–Sb–Br angles of [SbBr4−] reveal a noticeable tendency to be closer to 90 or 180°, which is not observed in the [(i-C4H9)2NH2]2Sb2Cl8 analog. Taking into account the changes of the Br–Sb–Br angles, the PT in the cooling mode is related to a smoothing of the anion distortion. The bridging Br2–Sb–Br2(1 − x, 1 − y, −z) angle does not follow this trend and the PT in the cooling mode leads to further deepening of the distortion of the Br2–Sb–Br2(1 − x, 1 − y, −z) angle. The PT in the cooling mode leads to differentiation of the Sb–Br bonds. The greatest changes of the Sb–Br distances are observed for the bridging Sb–Br2 and Sb–Br2(1 − x, 1 − y, −z) bonds. One is shortened about 0.09 Å and the other is elongated about 0.14 Å. Moreover, the [Sb2Br82−] units of the supramolecular ribbons are shifted with respect to each other. These changes make the grooves shallow, lead to better fitting of the cation and allow neighboring anionic ribbons to be closer to each other along the [011] and [0−11] directions. The PT is also accompanied by rotation of the [Sb2Br82−] units with respect to each other. At 250 K, the angle between basal planes of the [Sb2Br82−] units of neighboring ribbons is equal to 5.79° (Fig. 4(a)). At 100 K, the angle is equal to 25.47° (Fig. 4(b)). The reorientation of the [Sb2Br82−] units related to the change of the angle leads to additional shortening of the lattice constant b.
Full geometry and cell parameter optimisation for the solid state has been carried out to obtain the minimum structure of the [(i-C4H9)2NH2]2Sb2Br8 crystal. The computational details are contained in the General section of this manuscript. The selected calculated results presented in Tables 1 and 2 show a good agreement with the X-ray diffraction data. Referring to Tables 1 and 2, it may be noticed that structural differences in the calculated and experimental parameters are small and do not exceed ca. 5%. The largest errors (ca. 6.4–8.0%) have been found for the calculated structural angles.
Moreover, the optimized parameters of the unit cell (a = 6.1949 Å, b = 17.0841 Å, c = 14.2261 Å, β = 95.77°) are in reasonable agreement with the experimental values (a = 6.046 Å, b = 18.1863 Å, c = 14.839 Å, β = 96.322°). For full comparison please see also Table S1.† This confirms the need to use dispersion corrections to the full energy for calculations on the DFT method level. The optimised structure of the investigated crystal was applied to calculate the frequencies in the IR and Raman spectra in the harmonic approximation. The calculation of the frequencies allows one to verify that the optimised structure is in the global minimum on the potential energy surface (PES).
UV-vis electronic spectroscopy
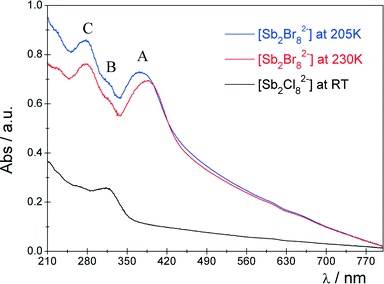
The structural changes of the [Sb2Br82−] complex modify the electronic structure of the complex. This should be reflected in the UV-vis electronic spectra. The spectra of the powdered compound under study are shown in Fig. 5. The RT spectrum of the isostructural [(i-C4H9)2NH2]2Sb2Cl8 compound is also included in this figure for the purpose of comparison.The spectra of the Sb3+ ion may be generally analyzed in terms of either the s → p transitions in the free Sb3+ ([Kr]4d10s2) ion30 or the transitions between molecular orbitals of the [Sb2Br82−] complex.31 The excited 5s5p configuration generates 3P and 1P levels which then branch into levels in sequence of increasing energy (3P0, 3P1, 3P2, 1P1) due to the spin–orbit coupling (Fig. 6(a)).30
 | ||
| Fig. 6 (a) Representation of the energy-level scheme of the Sb3+ ion; (b) qualitative MO scheme of the AL5 complex (square pyramid with Cs symmetry). | ||
For the case of the [Sb2Br82−] complex, which possesses Cs symmetry, all these transitions are symmetry allowed; however, due to the selection rules ΔS = 0 and ΔJ ≠ 0 and 2, the 1S0 ↔ 3P0 and 1S0 ↔ 3P2 transitions are forbidden.
Three well separated broad bands attributed to the 1S0 → 3P1 (A), 1S0 → 3P2 (B) and 1S0 → 1P1 (C) transitions30 are observed in the spectral range of 200–400 nm. A bathochromic shift of the band maxima is observed for [Sb2Br82−] compared to the relevant bands in the spectrum of [Sb2Cl82−]. This may suggest some increase of the covalent contribution to the Sb–Br bonding. Moreover, the baseline in the spectra of the [Sb2Br82−] complex gradually rises compared to the spectrum of [Sb2Cl82−]. This is probably caused by a strong ligand-to-metal charge-transfer (LMCT) band, which is strongly delocalized and appears usually as a broad, intense band.30,32 Due to the lower optical electronegativity32 as well as the higher oxidation potential of Br− ions than Cl−, the energy of the LMCT transition decreases significantly in the case of the bromide complex. The PT at 222/229 K, related to the structural rearrangement of the [Sb2Br82−] anion, is reflected in the UV-vis spectrum. There is a distinct shift of the A band, while the energy of the remaining B and C bands remains essentially unchanged. The qualitative MO scheme for the AL5 type complex with Cs symmetry (Fig. 6) may be helpful to elucidate such a spectral feature.
Within this simple MO approach, the observed A, B and C bands may be assigned to the 1A′ → 3A′, 1A′ → 3A′ and 1A′ → 1A′′ transitions, respectively.
As it was shown in the Single-crystal X-ray diffraction and theoretical structure analysis section, the PT results in certain elongation of two equatorial Sb–Br(2)i and Sb–Br(3) bond lengths and shortening of the Sb–Br(2) bond on decrease of the temperature. The distance between the sixth Br− anion and Sb3+ cation (Sb–Br(1)ii 3.49 Å) in phase I may suggest a weak interaction between these ions and the formation of a quasi 6-coordinate surrounding of Sb3+. In phase II, the latter interaction is reduced due to significant elongation of the Sb–Br(1)ii distance (3.67 Å). Taking into account these structural changes, one may conclude that the more rigid structure of the anionic complex in phase I becomes less tight in phase II. As a result of the I → II PT, the energy of the antibonding 1a′*, 3a′*, 1a′′* orbitals should decrease, while the energy of the 2a′* orbital should be only slightly affected. Within this simple, qualitative model, a certain increase of the energy of the 1A′ → 3A′ transition should be expected. Indeed, the energy of the A transition increases by ∼900 cm−1 on decrease of the temperature, while the energy of A and B bands is practically unchanged.
We have also recorded the luminescence spectra of the compound under study. Interestingly, a red emission was observed at 77 K when the sample was excited with 360 nm light, while it was practically quenched at RT. This raises questions whether the appearance of luminescence at low-temperature is connected with the PT or is it brought about by another reason? Trying to explain this we have measured the luminescence spectra of the [Sb2Br82−] complex at different temperatures (Fig. 7).
As it can be seen from Fig. 7, the red emission centered at 650 nm and attributed to the 1S0 → 3P1,0 transitions appears at 175 K. Below 175 K, the intensity of the 1S0 → 3P1,0 band gradually increases with decrease of the temperature. At 220 K the luminescence is definitely quenched and therefore cannot provide any information about the PT. The large Stokes shift, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120 cm−1, may indicate that the structure of the [Sb2Br82−] complex in the excited state is strongly affected compared to that in the ground state.30,31 This implies a high value of the electron-lattice coupling parameter S and the absence of the vibrational structure. Indeed, the estimated value of the Huang–Rhys33 coupling constant S ≈ 21 and the effective phonon energy ℏω = 286 cm−1 using eqn (1) and (2) suggest strong vibronic coupling of electronic states with Sb–Br oscillations.
120 cm−1, may indicate that the structure of the [Sb2Br82−] complex in the excited state is strongly affected compared to that in the ground state.30,31 This implies a high value of the electron-lattice coupling parameter S and the absence of the vibrational structure. Indeed, the estimated value of the Huang–Rhys33 coupling constant S ≈ 21 and the effective phonon energy ℏω = 286 cm−1 using eqn (1) and (2) suggest strong vibronic coupling of electronic states with Sb–Br oscillations.
| ΔES = (2S − 1)·ℏω | (1) |
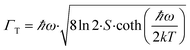 | (2) |
ΔES is the Stokes shift/cm−1;
Γ T is the half width of the emission band/cm−1;
S is the Huang–Rhys electron-lattice coupling constant;
ℏω is the effective phonon energy/cm−1;
k is the Boltzmann constant (0.695 cm−1 K−1); and
T is the temperature/K.
As it was shown by Blasse et al., for the case of Bi3+ complexes, there is a strong negative correlation (R = −0.97) between the energy difference of the excited 3P1, 3P0 states and the Stokes shift of the emission band.30b It may suggest that the energy of the 3P1 state is close to the 3P0 one in our case. These results, namely strong vibronic coupling, close energies of the emission 3P1, 3P0 states as well as a relatively low energy of the LMCT, seem to be reasons for the effective luminescence quenching of the compound under study at room temperature. A more detailed study on the luminescence properties of the compound is outside the scope of this paper.
Dielectric properties
The dielectric response of [(i-C4H9)2NH2]2Sb2Br8 in the radio-frequency region below RT is illustrated in Fig. 8(a) and (b).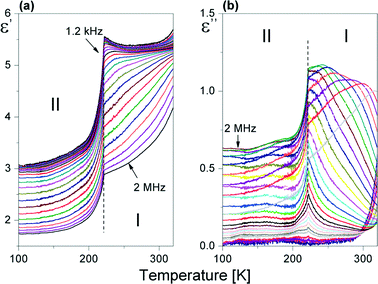 | ||
| Fig. 8 Temperature dependence of the (a) real (ε′) and (b) imaginary (ε′′) parts of the complex dielectric constant (ε*) measured for the powder sample of [(i-C4H9)2NH2]2Sb2Br8 upon cooling. | ||
The real part of the dielectric constant, ε′, in the vicinity of 222 K falls abruptly, which confirms the first-order character of I → II PT. Over phase I, the imaginary part of the dielectric constant (ε′′) shows the characteristic shift of ε′′max with frequency towards higher temperatures, which confirms the low-frequency relaxation process. This process may be well described by the Cole–Cole relation:34
 | (3) |
The Cole–Cole diagrams at selected temperatures (between 230 and 300 K) are presented in Fig. S4.† The Cole–Cole plots deviate from the semi-circles over the analyzed temperature region, (α ranges between 0.05 and 0.20), which means that we deal with a polydispersive relaxation process approaching 222 K. We have fitted the experimental Cole–Cole plots at selected temperatures with eqn (3) and determined the fitting parameters ε0, ε∞ and τ. Since we deal with weak dipole–dipole interactions (the lack of long-range order), we can assume that the macroscopic relaxation time is close to a microscopic one. Thus, the energy barrier Ea can be estimated from the Arrhenius relation:
 | (4) |
Proton magnetic resonance studies (1H NMR)
The temperature relations of the proton nuclear relaxation time T1 for 15 MHz and 25 MHz are shown in Fig. 9(a). There are two different temperature ranges above and below the PT temperature at 229 K. The low-temperature range of the spin–lattice relaxation time function reveals two weakly separated minima characterized by nearly the same depth, which are better separated at the frequency of 15 MHz. | ||
| Fig. 9 (a) Temperature dependence of 1H T1 observed for [(i-C4H9)2NH2]2Sb2Br8 at 15 MHz and 25 MHz. The solid lines were calculated by using the best-fit parameters given in Table S4.† (b) Temperature dependence of 1H NMR second moment of [(i-C4H9)2NH2]2Sb2Br8. | ||
When considering different mechanisms of the proton relaxation occurring in [(i-C4H9)2NH2]2Sb2Br8, one can distinguish the following possibilities of motions:
(a) Molecular motions of the four methyl groups and otherwise motion of the [(i-C4H9)2NH2+] cation (axial motion of the (i-C4H9) side chain attached to the nitrogen atom);
(b) Reorientations of the four methyl groups of two different and structurally inequivalent [(i-C4H9)2NH2+] cations; and
(c) The inequivalent two pairs of methyl groups of (i-C4H9) side chains of the same organic cation (see Fig. S6†).
The first possibility, (a), should be rejected because of almost the same values of T1min and the similar dynamical parameters of both fitted minima which lead to the conclusion that we have the same origin of both component minima. The second possibility, (b), should be also rejected because the X-ray data exclude the presence of structurally inequivalent cations. Therefore, it seems that the third possibility (c) is realized in [(i-C4H9)2NH2]2Sb2Br8. Both T1 relaxation time minima originate from a pair methyl groups of the side chain bonded to the N atom in the same cation. Both pairs of CH3 groups have different molecular dynamics resulting in different temperature dependence trends.
This fact confirms that above 229 K (phase I), the relaxation mechanism of indistinguishable methyl groups dominates. It may also indicate the unification of two previously independent side chain parts of the [(i-C4H9)2NH2+] cation via spin diffusion. In the T1 measurements, any other possible reorientation such as the expected axial movement of the side chains is still not visible (more in ESI†).35–45 The temperature dependence of the second moment M2 of the 1H NMR line (Fig. 9(b)) has been measured between 99 K and 293 K. With the increase of temperature from 99 K to the PT point at 229 K, the value of 1H M2 is nearly constant, experiencing only a slight reduction from ca. 14.5 G2 to 13 G2. At the PT, the M2 value drops to ca. 7 and then continuously decreases down to 6.5 G2 at 293 K. The calculations of M2 of the 1H NMR line for a rigid lattice were made using the van Vleck formula taking into account the homo-nuclear H–H and hetero-nuclear H–N intramolecular interactions.46 For the H–H interaction, we found MHHrigid to be 25.1 G2 and for the H–N interaction MHNrigid was estimated to be ca. 3.8 G2, whereas the inter-cation contribution is about 1 G2. It should be noticed that even at the lowest temperature (99 K), the expected high value of M2 is not reached. In turn, the experimental reduced M2 value of the order of 7 G2 close to Tc suggests the expected axial motion of [(i-C4H9)2NH2+] cations. The value of M2 (ca. 14 G2) found below Tc, originates, most probably, from the axial movement of one of both cation side chains (i-butylammonium) or only any partial motion inside side chains of the cation.
Vibrational spectroscopy
In both phases i.e. at room temperature (phase I) and at 100 K (phase II), the title crystal is monoclinic and belongs to the P21/c (= C2h5) space group, Z = 4. Thus, in the unit cell of the title crystal there are two symmetry equivalent centrosymmetric anions [Sb2Br82−] and four symmetry equivalent diisobutylammonium cations, which occupy the general C1 sites. The low-temperature phase II is strictly ordered, i.e. both anions (octabromodiantimonate(III)) and cations (diisobutylammonium) are ordered. However, in phase I, the diisobutylammonium cations ((C4H9)2NH2(1+)) exhibit disorder, in which both isobutyl groups of each diisobutylammonium cation are distributed between two sites. Simultaneously, the anions remain ordered and preserve the Ci site symmetry.The numbers of normal modes of the isolated cation of C1 symmetry (its normal modes can be divided into 3 A-type librational modes, 3 A-type translational modes and 81 A-type internal modes) and those of the isolated anion of Ci symmetry (its 30 normal modes can be divided into: 3 librational modes (3 Ag), 3 translational modes (3 Au) and 24 (12 Ag + 12 Au) internal modes) are identical in both phases, respectively. However, for the low-temperature ordered phase II, one may expect an additional splitting of each normal mode due to the Davydov type coupling. Thus, each mode of A-type may split into four (Ag + Bg + Au + Bu) unit cell modes, the Ag-type modes into two (Ag + Bg) and the Au-type modes into two other (Au + Bu) unit cell modes. The results of the fundamental mode analysis for phase II of the title crystal is given in Table S5.† The Davydov type splitting should not appear for the normal modes of cations in the high temperature phase I, due to their disorder therein. A problem then exists – if whether the Davydov type splitting may appear or not for the ordered part (anions) of the crystal in this high temperature phase.
Generally, the positions/wavenumbers of the majority of the bands assigned to the internal vibrations of cations in [(i-C4H9)2NH2]2Sb2Br8 do not experience any noticeable changes in their positions due to the PT (Fig. S7†). Nevertheless, some bands show a significant continuous and discontinuous change of their positions, intensities and FWHM (full width at half maximum) in the vicinity of Tc (see also Fig. S8–S10†).
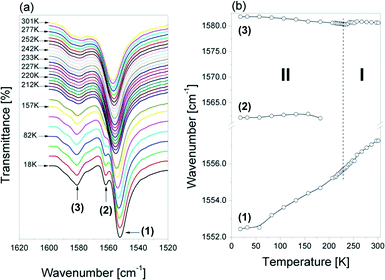
Fig. 10(a) shows an evolution of the IR spectra in the range between 1040 and 960 cm−1 as a function of temperature. The bands in this wavenumber range arise from the νa(CNC), νs(CCC) and νs(CNC) vibrations. Distinct changes in the position of these bands are observed at ca. 230 K (see Fig. 10(b)). For two of these bands, a step-wise change in their position occurs, i.e. the band at 963 cm−1 (marked as (1)) shifts towards higher wavenumbers, while the one at 974 cm−1 (described as (2)) shifts towards lower ones on increasing temperature. The positions of the remaining components are not sensitive to the PT.
The temperature behavior of the bands assigned to the δ(NH2+) vibrations appearing between 1605 and 1530 cm−1 (Fig. 11 (a) and (b)) differs clearly from that presented earlier. The higher frequency component (marked as (3)) experiences only a slight anomaly around the Tc, while the lower one (denoted as (1)) shifted towards higher wavenumbers in a continuous way (without visible changes around Tc) on heating. The shoulder (2) at about 1562 cm−1 disappears on heating in the low-temperature phase (at about 200 K).
The lowest frequency band observed at 1557 cm−1 in this region at room temperature shifts to 1552 cm−1 in the spectrum measured at 18 K, however, without any drop of the PT temperature. This can be related to the observed decrease of the N–H⋯O hydrogen bond strength on cooling down, which is clearly indicated by the N⋯Br distances determined for the structure at 250 K (3.355(7), 3.386 Å) and at 100 K (3.540(3) and 3.398(3) Å), respectively (see Table 2). As this band arises from the δNH2 vibration, therefore its wavenumber may be very sensitive to the strength of the hydrogen bonds in which the protons of this group are involved. With decrease of the strength (i.e. increase of the N⋯Br distance), this mode should shift to lower wavenumbers.
Experimental section
Synthesis of the complexes
All reagents used for the syntheses of [(i-C4H9)2NH2]2Sb2Br8 and [(i-C4H9)2NH2]2Sb2Cl8 were purchased from commercial sources (Sigma-Aldrich) and used without further purification: diisobutylamine (99%,), Sb2O3 (99%), Bi2O3 (99.999%), HBr (48%) and HCl (37%).General
Conclusion
In this paper we have reported the physicochemical properties of the [(i-C4H9)2NH2]2Sb2Br8 crystal, which was found to undergo isomorphous PT of the first-order type at 222/229 K (cooling–heating). The molecular mechanism of this transition is rather complex because two contributions should be considered. The calorimetric studies allow us to estimate the transition entropy value (ΔStr = 26 J mol−1 K−1) which clearly indicates an “order–disorder” contribution to the PT. The structure of [(i-C4H9)2NH2]2Sb2Br8 consists of [Sb2Br82−] anions with a geometry of two square pyramids sharing a basal edge and diisobutylammonium cations which are highly disordered in phase I and fully ordered in phase II. The PT in the cooling mode is additionally related to the smoothing of the Br–Sb–Br angle distortion of the [SbBr4−] units. In turn, deepening of distortion in the bridging part of the [Sb2Br82−] unit and shifting as well as rotation of the [Sb2Br82−] units in relation to each other, leading to the enormous crystal lattice distortion compared with phase I, cause a better fit of diisobutylammonium cations to the anionic moiety. These changes within the anionic moieties are treated as a “displacive” contribution to the mechanism of PT.The dielectric dispersion measurements confirmed the dynamical disorder of the cationic dipolar units in phase I which is reflected in the presence of the low frequency relaxation process. It should be added that librational motions of the whole [Sb2Br82−] anions with respect to their symmetry centre in phase I may also contribute to the dielectric relaxation. The contribution of the cation motion to the molecular mechanism of PT is evidently reflected in the drastic reduction of the second moment value of the 1H NMR line at 229 K. These studies lead to the following conclusions:
(a) In the temperature range of 50–229 K (phase II), only the C3-type motion of CH3 groups contributes to the relaxation time T1. Dynamical inequality of both side chains of the [(i-C4H9)2NH2+] cation in this phase is postulated.
(b) The methyl group relaxation still prevails over phase I (above 229 K). On the other hand, two different axial reorientations on the opposite side of the chain of the [(i-C4H9)2NH2+] cation have been observed in the second moment studies.
The anomalies found in the temperature dependent infrared spectra around Tc are generally quite subtle. Most of the modes exhibit different temperature coefficients describing the temperature dependence of their wavenumbers. The discontinuous changes of the band positions are observed for some modes around 229 K, but they are very small. This may be explained by the fact that the space group of the neighboring phases and the environment of the cations in the crystal lattice do not change throughout the PT.
Infrared and Raman spectra have also been recorded for the studied [(i-C4H9)2NH2]2Sb2Br8 crystal and comparative vibrational analysis has been performed. Vibrational analysis is very important since it proves that the results of the static structure optimisation are correct. The comparison between experimental and calculated vibrational frequencies for the studied crystal has been presented in Table S6.† Due to the fact that the calculation of vibrational frequencies was performed at the gamma-point and also in the harmonic approximation, the calculated wavenumbers presented in Table S6† are shifted towards higher wavenumbers by about 200 cm−1 or less. The shift values of the frequency of vibration caused by harmonic approximation seem to decrease with decrease of the wavenumbers of oscillations. The stretching vibrations of the Sb–Br bonds appear in the range from 220 to 100 cm−1 and their bands are relatively intense. This is a typical position of the stretching bands for molecular [Sb–Br] systems and may be an important contribution to the stability of the crystal structure. The occurrence of these stretching bands in the region of low frequencies indicates that the [Sb–Br] crystal is held by very weak interactions. Consequently, we have observed appearance of easy reorganisations of the chemical bonds in the molecular complex, which favours the phase transition possibility.
Acknowledgements
This work was supported by the National Science Centre; grant no. 2013/11/D/ST8/03297 (A. Piecha-Bisiorek). One of the authors (Piotr Durlak, Ph.D.) would like to gratefully acknowledge the Wroclaw Centre for Networking and Supercomputing (WCSS) for allocation of computer time on the BEM Cluster.References
- J. F. Scott, Ferroelectric Memories, Springer, Berlin, 2000 Search PubMed.
- R. Waser, Nanoelectronics and information technology, Wiley-VCH, Weinheim, Germany, 2003 Search PubMed.
- Z. G. Ye, Handbook of advanced dielectric, piezoelectric and ferroelectric materials: Synthesis, properties and applications, Woodhead Publishing, Cambridge, UK, 2008 Search PubMed.
- J. F. Scott, Science, 2007, 315, 954 CrossRef CAS PubMed.
- M. Owczarek, P. Szklarz, R. Jakubas and A. Miniewicz, Dalton Trans., 2012, 41, 7285 RSC.
- X. H. Zhao, X. C. Huang, S. L. Zhang, D. Shao, H. Y. Wei and X. Y. Wang, J. Am. Chem. Soc., 2013, 135, 16006 CrossRef CAS PubMed.
- J. Burschka, N. Pellet, S.-J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Grätzel, Nature, 2013, 499, 316 CrossRef CAS PubMed.
- M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643 CrossRef CAS PubMed.
- W. Zhang, H. Y. Ye, R. Graf, H. W. Spiess, Y. F. Yao, R. Q. Zhu and R.-G. Xiong, J. Am. Chem. Soc., 2013, 135, 5230 CrossRef CAS PubMed.
- S. H. Park, I. H. Oh, S. Park, Y. Park, J. H. Kim and Y. D. Huh, Dalton Trans., 2012, 41, 1237 RSC.
- H. Xu, R. Chen, Q. Sun, W. Lai, Q. Su, W. Huang and X. Liu, Chem. Soc. Rev., 2014, 43, 3259 RSC.
- Y. Zhang, H.-Y. Ye, H. L. Cai, D. W. Fu, Q. Ye, W. Zhang, Q. H. Zhou, J. L. Wang, G. L. Yuan and R.-G. Xiong, Adv. Mater., 2014, 26, 4515 CrossRef CAS PubMed.
- L. Sobczyk, R. Jakubas and J. Zaleski, Pol. J. Chem., 1997, 71, 265 CAS (and references cited therein).
- J. Jóźków, R. Jakubas, G. Bator and A. Pietraszko, J. Chem. Phys., 2001, 114, 7239 CrossRef.
- R. Jakubas, A. Piecha, A. Pietraszko and G. Bator, Phys. Rev. B, 2005, 72, 104107 CrossRef.
- A. Piecha, A. Pietraszko, G. Bator and R. Jakubas, J. Solid State Chem., 2008, 118, 1155 CrossRef.
- A. Piecha, A. Białońska and R. Jakubas, J. Phys.: Condens. Matter, 2008, 20, 325224 CrossRef.
- R. Jakubas, U. Krzewska, G. Bator and L. Sobczyk, Ferroelectrics, 1988, 77, 129 CrossRef CAS.
- R. Jakubas, Solid State Commun., 1989, 69, 267 CrossRef CAS.
- R. Jakubas, Z. Czapla, Z. Galewski and L. Sobczyk, Ferroelectr., Lett. Sect., 1986, 5, 143 CrossRef CAS.
- J. Zaleski and A. Pietraszko, Acta Crystallogr., Sect. B: Struct. Sci., 1996, 52, 287 Search PubMed.
- W. Bi, N. Leblanc, N. Mercier, P. Auban-Senzier and C. Pasquier, Chem. Mater., 2009, 21, 4099 CrossRef CAS.
- A. Piecha, A. Białońska and R. Jakubas, J. Mater. Chem., 2012, 22, 333 RSC.
- G. Xu, Y. Li, W.-W. Zhou, G.-J. Wang, X.-F. Long, L.-Z. Cai, M.-S. Wang, G.-C. Guo, J.-S. Huang, G. Bator and R. Jakubas, J. Mater. Chem., 2009, 19, 2179 RSC.
- R. Jakubas, Z. Ciunik and G. Bator, Phys. Rev. B, 2003, 67, 024103 CrossRef.
- D.-W. Fu, W. Zhang, H.-L. Cai, J.-Z. Ge, Y. Zhang and R.-G. Xiong, Adv. Mater., 2011, 23, 5658 CrossRef CAS PubMed.
- A. Piecha, A. Gągor, R. Jakubas and P. Szklarz, CrystEngComm, 2013, 15, 940 RSC.
- D.-W. Fu, H.-L. Cai, Y. Liu, Q. Ye, W. Zhang, Y. Zhang and X.-Y. Chen, Science, 2013, 25, 425 CrossRef PubMed.
- A. Piecha-Bisiorek, A. Białońska, R. Jakubas, P. Zieliński, M. Wojciechowska and M. Gałązka, Adv. Mater., 2015, 27, 5023 CrossRef CAS PubMed.
- (a) A. Vogler, A. Paukner and H. Kunkely, Coord. Chem. Rev., 1990, 97, 285 CrossRef CAS; (b) G. Blasse, Electronic and Vibronic Spectra of Transition Metal Complexes I in Topics in Current Chemistry, ed. H. Yersin, 1994, vol. 171, p. 1 Search PubMed.
- (a) A. Vogler and H. Nikol, Comments Inorg. Chem., 1993, 4, 245 CrossRef; (b) T. A. Albright, J. K. Burdett and M.-H. Whangbo, Orbital Interactions in Chemistry, Willey, 2013 Search PubMed.
- C. K. Jørgensen, Absorption Spectra and Chemical Bonding in Complexes, Oxford, 1964 Search PubMed.
- K. Huang and A. Rhys, Proc. R. Soc. London, Ser. A, 1950, 204, 406 CrossRef CAS.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341 CrossRef CAS.
- D. E. Woessner, J. Chem. Phys., 1962, 36, 1 CrossRef CAS.
- W. Medycki, Z. Zimpel, N. Piślewski and R. Jakubas, Solid State Commun., 1990, 76, 869 CrossRef.
- W. Medycki, N. Piślewski and R. Jakubas, Solid State Nucl. Magn. Reson., 1993, 2, 197 CrossRef CAS PubMed.
- W. Medycki, R. Jakubas, N. Piślewski and J. Lefebvre, Z. Naturforsch., A: Phys. Sci., 1993, 48, 748 CrossRef.
- J. Zaleski, W. Medycki, N. Piślewski and R. Jakubas, Phys. Status Solidi A, 1994, 144, 81 CrossRef CAS.
- J. Zaleski, W. Medycki, N. Piślewski and R. Jakubas, Phys. Status Solidi B, 1995, 190, 199 CrossRef CAS.
- W. Medycki, Solid State Nucl. Magn. Reson., 1999, 13(4), 213 CrossRef CAS PubMed.
- W. Medycki, Solid State Nucl. Magn. Reson., 1999, 14, 137 CrossRef CAS PubMed.
- W. Medycki and R. Jakubas, Solid State Nucl. Magn. Reson., 1999, 15(2), 73 CrossRef CAS PubMed.
- M. Wojtaś, R. Jakubas, Z. Ciunik and W. Medycki, J. Solid State Chem., 2004, 177, 1575 CrossRef.
- B. Kulicka, R. Jakubas, Z. Ciunik, G. Bator, W. Medycki, J. Świergiel and J. Baran, J. Phys. Chem. Solids, 2004, 65, 871 CrossRef CAS.
- V. Vleck, Phys. Rev., 1948, 74, 1168 CrossRef.
- CrysAlis RED, ver. 1.171, Oxford Diffraction Poland, 1995–2003 Search PubMed.
- R. C. Clark and J. S. Reid, Acta Crystallogr., Sect. A: Found. Crystallogr., 1995, 51, 887 CrossRef.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- D. Zeroka, J. O. Jensen and A. C. Samuels, Int. J. Quantum Chem., 1999, 72, 109 CrossRef CAS.
- J. R. Durig, J. J. Klaassen, I. D. Darkhalil, W. A. Herrebout, J. J. Dom and B. J. van der Veken, J. Mol. Struct., 2012, 1009, 30 CrossRef CAS.
- Y. Hamada, M. Tsuboi, M. Nakata and M. Tasumi, Chem. Phys., 1988, 125, 55 CrossRef CAS.
- J. Jóźków, G. Bator, R. Jakubas and J. Baran, J. Mol. Struct., 1998, 450, 247 CrossRef.
- B. Staśkiewicz, J. Baran and Z. Czapla, J. Phys. Chem. Solids, 2013, 74, 1848 CrossRef.
- N. Alpert, W. Keiser and H. Szymanski, IR: Theory and Practice of Infrared Spectroscopy, Plenum Press, New York, 1964 and 1970 Search PubMed.
- S. J. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, Ph. D'Arco and M. Llunell, CRYSTAL09 User's Manual, University of Torino, Torino, 2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- K. Kim and K. D. Jordan, J. Phys. Chem., 1994, 98, 10089 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- M. F. Peintinger, D. Vilela Oliveira and T. Bredow, J. Comput. Chem., 2013, 34, 451 CrossRef CAS PubMed.
- P. Durand and J. C. Barthelat, Theor. Chim. Acta, 1975, 38, 283 CrossRef CAS.
- M. Causà, R. Dovesi and C. Roetti, Phys. Rev. B: Solid State, 1991, 43, 11937 CrossRef.
- R. Dovesi, R. Orlando, B. Civalleri, C. Roetti, V. R. Saunders and C. M. Zicovich-Wilson, Z. Kristallogr., 2005, 220, 571 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Crystal structure, thermal, optical and dielectric properties as well as proton magnetic resonance (1H NMR) and IR studies. CCDC 1475468–1475471. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6ce01008c |
| This journal is © The Royal Society of Chemistry 2016 |