Open Access Article
Open Access ArticleMetal–organic and supramolecular lead(II) networks assembled from isomeric nicotinoylhydrazone blocks: the effects of ligand geometry and counter-ion on topology and supramolecular assembly†
Ghodrat
Mahmoudi
*a,
Antonio
Bauzá
b,
Antonio
Frontera
 b,
Piotr
Garczarek
c,
Vladimir
Stilinović
*d,
Alexander M.
Kirillov
*e,
Alan
Kennedy
f and
Catalina
Ruiz-Pérez
g
b,
Piotr
Garczarek
c,
Vladimir
Stilinović
*d,
Alexander M.
Kirillov
*e,
Alan
Kennedy
f and
Catalina
Ruiz-Pérez
g
aDepartment of Chemistry, Faculty of Science, University of Maragheh, P.O. Box 55181-83111, Maragheh, Iran. E-mail: mahmoudi_ghodrat@yahoo.co.uk
bDepartment of Chemistry, Universitat de les Illes Balears, Crta. de Valldemossa Km 7,5, 07122 Palma de Mallorca (Baleares), Spain. E-mail: toni.frontera@uib.es
cFaculty of Chemistry, Wrocław University of Technology, 27 Wybrzeze Wyspiańskiego Street, 50-370 Wrocław, Poland
dDepartment of Chemistry, Faculty of Science, University of Zagreb, Horvatovac 102a, HR-10000 Zagreb, Croatia
eCentro de Química Estrutural, Complexo I, Instituto Superior Técnico, Universidade de Lisboa, Av. Rovisco Pais, 1049-001, Lisbon, Portugal. E-mail: kirillov@tecnico.ulisboa.pt
fDepartment of Pure & Applied Chemistry, University of Strathclyde, 295 Cathedral Street, Glasgow G1 1XL, Scotland, UK
gLaboratorio de Rayos X y Materiales Moleculares, Dpto. Física Fundamental II. Facultad de Física, Universidad de La Laguna, E-38204 La Laguna, Tenerife, Spain
First published on 25th May 2016
Abstract
A new series of six structurally diverse lead(II) coordination compounds was assembled from two isomeric nicotinoylhydrazones as neutral ligands and three Pb(II) salts with different monoanions (chloride, nitrate and thiocyanate) as starting materials. The products were isolated in good yields and were fully characterized, including by single-crystal X-ray diffraction and theoretical methods. Within the six compounds, three feature 2D metal–organic networks, two are 1D coordination polymers, and another one comprises discrete 0D dimeric units. The structures of the latter low dimensional compounds are extendable into 2D supramolecular networks. The topology of the coordination or supramolecular networks is primarily dictated by the geometry of the nicotinoylhydrazone used as a main building block. In contrast, supramolecular interactions are greatly influenced by the choice of the anion in the starting lead(II) salt, which is demonstrated by Hirshfeld surface analysis. In fact, the topological analysis and classification of metal–organic or supramolecular underlying networks in the obtained compounds was performed, disclosed the hcb, 2C1, gek1, SP 1-periodic net (4,4)(0,2) and 3,4L83 topological types; the latter topology was documented for three compounds, including both coordination and supramolecular networks. In the two compounds containing thiocyanate moieties, there are supramolecular contacts between the thiocyanate anions and lead centres. These were shown by DFT calculations to be strong tetrel bonds (−15.3 and −16.7 kcal mol−1) between the σ-hole of the lead atom and the π-system of the thiocyanate S–C bond.
1. Introduction
Research on metal–organic frameworks (MOFs) or coordination polymers (CPs) is nowadays among the most attractive areas in modern chemistry.1–11 This is largely due to promising and already recognized applications of such compounds as functional materials in gas storage and separation,12–17 catalysis,18–21 chemical sensing22–24 and many other areas. Therefore, substantial effort has been put into the design and synthesis of novel MOFs or CPs with a multitude of different structural and topological types, since the combination of metal nodes and organic spacers or linkers provides unlimited possibilities for the fabrication of materials with various structures and functions.The structures and properties of CPs depend on a number of factors such as, for example, (1) the coordination geometries of metal centres, (2) the geometries and connectivity of ligands, (3) the supramolecular interactions between the CPs' components and (4) the presence of neighbouring/interpenetrating nets or interstitial guest molecules. If the organic ligands are neutral molecules, CPs would typically include inorganic ions which will either occupy interstices in the structures or act as additional ligands.25–31 Because of this, the choice of counter-ions can play a significant role in guiding the structures of MOFs or CPs that are driven by organic building blocks.32–37
The metal–organic networks or coordination polymers based on lead(II) remain less explored, mostly due to the toxicity of this metal, as well as its somewhat unpredictable coordination behaviour. In fact, the electronic configuration of Pb(II) allows the Pb2+ cation to exhibit a large variety of coordination numbers (from 2 to 10) and geometries. However, interest in CPs of lead has recently substantially increased. This is presumably related to the diversity of coordination modes of this metal and the unique supramolecular architectures and physical properties of such compounds.38–46 Hence, Pb-based CPs find potential applications as luminescent materials,47–52 ion exchangers53 and nonlinear optical materials.54 As Pb(II) cations have an affinity towards organic ligands containing O, N and S donor atoms,55–59 hydrazone containing building blocks are often employed in the construction of Pb(II) coordination compounds, also due to their excellent coordinating ability, versatile coordination modes, and possible supramolecular interactions.
Additional interest in the chemistry of Pb(II) arises from our recent work and concerns the unique ability of lead(II) to participate in the formation of tetrel bonds.60 This newly (re)discovered supramolecular interaction61–66 is formed between a positively charged region on a group 14 atom in continuation of a covalent bond (a σ-hole) and an electron donor, analogously to a more common halogen bond. Lead(II) is particularly prone to the formation of tetrel bonds because of its size and polarizability, as well as its specific hemidirectional coordination67,68 which leaves a gap in the coordination sphere of the Pb(II) cation, thus enabling the approach of the electron-donor. This makes lead(II) metal–organic networks particularly sensitive to the choice of ligands and counter-ions to form supramolecular interactions not only between each other, but also with the metal ion itself.
Herein we describe a study of the effect of counter-ion on the topology, geometry, and supramolecular structure of metal–organic frameworks in two series of coordination compounds having a general formula [PbLX2], where X is a singly charged anion (Cl−, NO3−, or SCN−), and L is a nicotinoylhydrazone ligand. The effect of the counter-ion was tested against two isomeric ligands L1 and L2, differing only in the position of the pyridyl nitrogen atom within one of the pyridine rings (Scheme 1). This difference renders their potential for assembling rather distinct metal–organic frameworks, as L1 is expected to act as a bridging block between two metal centres (chelating mode and binding via a pyridine nitrogen atom), while L2 can bridge three metal centres (binding via the central hydrazone group and two interactions involving two terminal pyridine nitrogen atoms). On the other hand, the counter-ions widely differ in their coordination ability, as well as in the possibility for the formation of supramolecular interactions, in particular, hydrogen and tetrel bonds. These factors can thus exert a decisive control over the structure of the resulting solids.
2. Experimental
2.1. Materials and measurements
The nicotinoylhydrazone derivatives (L1 and L2) were prepared following the reported method40 and used without further purification. All other reagents and solvents used for the synthesis and analysis were commercially available and were used as received. FT-IR spectra were recorded on a Bruker Tensor 27 spectrometer. Microanalyses were performed using a Heraeus CHN-O-Rapid analyser. Syntheses were carried out using a branched tube apparatus.2.2. Syntheses of lead(II) compounds (1–6)
2.3. X-ray crystallography
Single crystals of 1–6 suitable for X-ray analyses were selected and crystallographic data were collected on Enraf Nonius FR590 or Oxford Diffraction Xcalibur E68 or Bruker-AXS Kappa APEX II CCD69,70 diffractometers with Mo Kα radiation (λ = 0.71073 Å). Each data set was treated with SADABS absorption corrections based on redundant multi-scan data.71 All the structures were solved by direct methods and refined by full matrix least-squares procedures.72 All non-hydrogen atoms were refined with anisotropic displacement parameters whereas hydrogen atoms not involved in hydrogen bonding were placed in calculated positions and given isotropic U values 1.2 times that of the atom to which they are bonded.2.4. Topological analysis
Topological analysis of coordination (or supramolecular) networks in 1–6 was performed using Topos software and following the concept of the simplified underlying net.73,74 Such nets were generated by contracting organic ligands (for analysis of coordination polymers) or discrete metal–complex units (for analysis of supramolecular networks), maintaining their connectivity via coordination bonds (including some rather long bonds/interactions) or hydrogen bonds. For the analysis of networks involving H-bonding interactions, only strong D–H⋯A hydrogen bonds were considered, wherein the H⋯A < 2.50 Å, D⋯A < 3.50 Å, and ∠(D–H⋯A) > 120°; D and A stand for donor and acceptor atoms.732.5. Theoretical methods
The geometries of the compounds included in this study were computed at the BP86-D3/def2-TZVP level of theory using the crystallographic coordinates within the TURBOMOLE program.75 This level of theory that includes the latest available dispersion correction (D3) is adequate for studying noncovalent interactions dominated by dispersion effects like π-stacking. The basis set superposition error for the calculation of interaction energies has been corrected using the counterpoise method.76 The “atoms-in-molecules” (AIM)77 analysis of the electron density has been performed at the same level of theory using the AIMAll program.782.6. Hirshfeld surface analysis
Hirshfeld surfaces79–81 and fingerprint plot (devs. di) calculations were performed using the Crystal Explorer package ver. 3.1.82 Crystal structures were imported from CIF files. Hirshfeld surfaces were generated for complex molecules using high resolution and mapped with the dnorm or shape index functions.3. Results and discussion
3.1. Synthesis and spectroscopic results
The reactions of L1 or L2 with PbX2 (X = Cl, NO3 and SCN), in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio in methanol, resulted in the formation of compounds 1–6. In the IR spectra of 1–6, the ν(C
1 molar ratio in methanol, resulted in the formation of compounds 1–6. In the IR spectra of 1–6, the ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) + ν(C
N) + ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) stretching vibrations31 are in the 1650–1560 cm−1 range, characteristic for hydrazones bound to a metal ion. The bands at 1317, 1031 and 849 cm−1 are assignable to νas(NO3), νs(NO3) and δ(NO3) vibrations of nitrate ligands in 2, but in 5 these bands appear at 1312, 1027 and 813 cm−1. The separation between the νas and νs bands corroborates the symmetric coordination of the nitrate ion.22 In 4, the νas(NCS) and ν(CS) stretches of S-coordinated thiocyanate21 appear as strong bands at 2111 and 765 cm−1, respectively. Additionally, a δ(NCS) band is found at 452 cm−1. All other less characteristic vibrations of organic ligands are seen in the 1600–600 cm−1 range (Fig. S19–S22†).
C) stretching vibrations31 are in the 1650–1560 cm−1 range, characteristic for hydrazones bound to a metal ion. The bands at 1317, 1031 and 849 cm−1 are assignable to νas(NO3), νs(NO3) and δ(NO3) vibrations of nitrate ligands in 2, but in 5 these bands appear at 1312, 1027 and 813 cm−1. The separation between the νas and νs bands corroborates the symmetric coordination of the nitrate ion.22 In 4, the νas(NCS) and ν(CS) stretches of S-coordinated thiocyanate21 appear as strong bands at 2111 and 765 cm−1, respectively. Additionally, a δ(NCS) band is found at 452 cm−1. All other less characteristic vibrations of organic ligands are seen in the 1600–600 cm−1 range (Fig. S19–S22†).
3.2. Crystal structures of 1–6
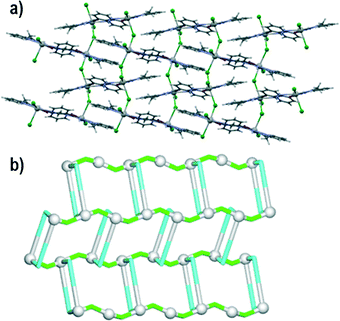
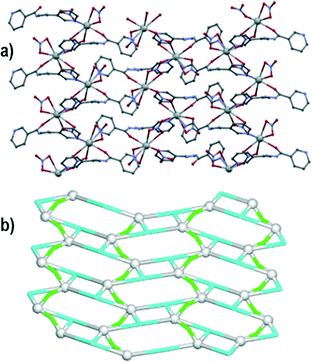
Compound 1 crystallizes in the P21/c space group. The asymmetric unit consists of one lead(II) atom, one μ2-L1 tetradentate ligand and two chloride moieties (one terminal and μ2-bridging). The Pb1 centres adopt a distorted pentagonal bipyramid geometry with three chelating atoms from one L1 moiety, pyridyl nitrogen from a second L1 molecule and a terminal chloride ligand in the equatorial positions. The axial sites are taken by two symmetry equivalent μ2-Cl ligands. The Pb–N and Pb–Cl bond distances are in the 2.640(2)–2.841(2) and 2.7027(8)–3.1048(8) Å range, respectively. The Pb–O bond has a length of 2.586(2) Å. The 3-pyridyl groups of the L1 ligands bind adjacent Pb1 atoms forming centrosymmetric dimeric units, whereas the μ2-Cl linkers bridge these dimeric units generating a 2D metal–organic network perpendicular to the crystallographic axis a (Fig. 1a). For the sake of topological analysis, this network was simplified73,74 resulting in a uninodal 3-connected underlying net (Fig. 1b). It is composed of the 3-connected Pb1 nodes and the 2-connected μ2-L1 and μ2-Cl linkers, and displays the hcb [Shubnikov hexagonal plane net/(6,3)] topology with the point symbol of (63). Besides, the terminal chloride ligand acts as an acceptor in N–H⋯Cl (N3–H3⋯Cl1 of 3.285 Å) hydrogen bonds and weak C–H⋯Cl contacts (C7–H7C⋯Cl1 and C11–H11⋯Cl2), thus resulting in the extension of 2D metal–organic layers into a 3D supramolecular structure.Compound 2 crystallizes in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group with one lead(II) atom, one L1 moiety and two nitrate ligands (one terminal and one μ2-bridging) in the asymmetric unit. The Pb1 atom is bound by a tridentate chelating L1 moiety, as well as one terminal bidentate and two bridging μ2-nitrate ligands. The latter bind adjacent Pb1 centres to form centrosymmetric dimers. The Pb–O bond distances fall in the 2.511(2)–2.867(2) Å range, whereas the Pb–N distances vary from 2.531(2) to 2.638(2) Å. The eighth coordination position is occupied by a pyridyl nitrogen from a second L1 molecule, with an elongated Pb–N bond (2.923(2) Å). The resulting structure can be considered as a zigzag 1D metal–organic chain (Fig. 2a). Topological analysis of this chain discloses a 2-connected underlying 1D network with the 2C1 topology (Fig. 2b). The adjacent chains are interconnected by hydrogen bonds between the N–H groups of L1 moieties and terminal nitrate ligands (N3–H3⋯O2 of 2.971 Å forming a centrosymmetric R22(12) motif) into 2D H-bonded layers perpendicular to the a axis. There is also π–π stacking between the L1 ligands in adjacent chains (closest contact, C3⋯C11 of 3.318 Å, is between 2-pyridyl and 3-pyridyl carbon atoms).
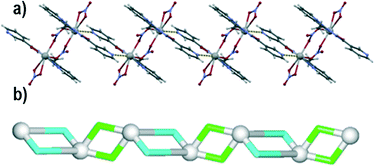
space group with one lead(II) atom, one L1 moiety and two nitrate ligands (one terminal and one μ2-bridging) in the asymmetric unit. The Pb1 atom is bound by a tridentate chelating L1 moiety, as well as one terminal bidentate and two bridging μ2-nitrate ligands. The latter bind adjacent Pb1 centres to form centrosymmetric dimers. The Pb–O bond distances fall in the 2.511(2)–2.867(2) Å range, whereas the Pb–N distances vary from 2.531(2) to 2.638(2) Å. The eighth coordination position is occupied by a pyridyl nitrogen from a second L1 molecule, with an elongated Pb–N bond (2.923(2) Å). The resulting structure can be considered as a zigzag 1D metal–organic chain (Fig. 2a). Topological analysis of this chain discloses a 2-connected underlying 1D network with the 2C1 topology (Fig. 2b). The adjacent chains are interconnected by hydrogen bonds between the N–H groups of L1 moieties and terminal nitrate ligands (N3–H3⋯O2 of 2.971 Å forming a centrosymmetric R22(12) motif) into 2D H-bonded layers perpendicular to the a axis. There is also π–π stacking between the L1 ligands in adjacent chains (closest contact, C3⋯C11 of 3.318 Å, is between 2-pyridyl and 3-pyridyl carbon atoms).
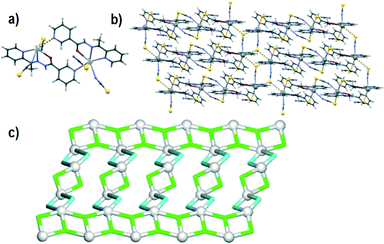
Although compound 3 also crystallizes in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group, its asymmetric unit consists of a non-centrosymmetric dimer comprising two crystallographically nonequivalent lead(II) atoms, two μ2-L1 moieties and four thiocyanate ligands (Fig. 3a). Both six-coordinate lead(II) atoms are surrounded by the tridentate μ2-L1 ligands, pyridyl nitrogen of the other L1 moiety and two terminal N- and S-bound thiocyanates. However, relative disposition of donor atoms around the two lead centres is markedly different. The Pb1 atom is coordinated in an extremely disordered octahedral fashion with the chelating and monodentate L1 moieties lying in one plane and the two thiocyanate ligands in trans position. The Pb2 centre adopts a distorted pentagonal pyramidal coordination environment with one oxygen and four nitrogen atoms (from two L1 moieties as well as one thiocyanate ligand) in the basal sites, whereas a thiocyanate S atom takes the apical position. The thiocyanate ligands bonded to Pb2 are thus at an angle of ca. 72°, as opposed to Pb1 where they are in a trans configuration (ca. 152°). Another significant difference is in the Pb–N bond lengths between the lead(II) centres and the pyridyl N atoms; it is normal for Pb2 (2.76 Å), but extremely long for Pb1 (3.20 Å). Other than this, the Pb–O, Pb–N, and Pb–S bond lengths are within normal ranges of 2.518(3)–2.525(3), 2.506(3)–2.763(3), and 2.8335(9)–3.0019(10) Å, respectively.
space group, its asymmetric unit consists of a non-centrosymmetric dimer comprising two crystallographically nonequivalent lead(II) atoms, two μ2-L1 moieties and four thiocyanate ligands (Fig. 3a). Both six-coordinate lead(II) atoms are surrounded by the tridentate μ2-L1 ligands, pyridyl nitrogen of the other L1 moiety and two terminal N- and S-bound thiocyanates. However, relative disposition of donor atoms around the two lead centres is markedly different. The Pb1 atom is coordinated in an extremely disordered octahedral fashion with the chelating and monodentate L1 moieties lying in one plane and the two thiocyanate ligands in trans position. The Pb2 centre adopts a distorted pentagonal pyramidal coordination environment with one oxygen and four nitrogen atoms (from two L1 moieties as well as one thiocyanate ligand) in the basal sites, whereas a thiocyanate S atom takes the apical position. The thiocyanate ligands bonded to Pb2 are thus at an angle of ca. 72°, as opposed to Pb1 where they are in a trans configuration (ca. 152°). Another significant difference is in the Pb–N bond lengths between the lead(II) centres and the pyridyl N atoms; it is normal for Pb2 (2.76 Å), but extremely long for Pb1 (3.20 Å). Other than this, the Pb–O, Pb–N, and Pb–S bond lengths are within normal ranges of 2.518(3)–2.525(3), 2.506(3)–2.763(3), and 2.8335(9)–3.0019(10) Å, respectively.
Interestingly, in spite of the differences in the coordination environment, both lead atoms are hemidirectionally coordinated and are involved in supramolecular tetrel bonding with the sulphur atoms of the N-bound thiocyanate ligands of the neighbouring dimers. The Pb1 centre thus binds to two S4 atoms from two dimers, while the Pb2 centre binds to the S2 atom from a third dimer moiety. This leads to the formation of a supramolecular layer perpendicular to the [011] direction (Fig. 3b). From a topological perspective,73,74 this supramolecular 2D layer can be classified as a binodal 3,4-connected underlying net with the 3,4L83 topology (Fig. 3c). It is described by the point symbol of (42·63·8)(42·6), wherein the (42·63·8) and (42·6) notations are those of the 4-connected Pb1 and the 3-connected thiocyanate nodes, respectively. There are also Pb2, L1 and other thiocyanate moieties that participate in the formation of the net and which are considered as linkers.
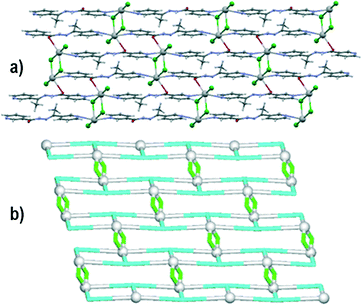
Compound 4 crystallizes in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group and has a lead(II) atom, a μ3-L2 block, one μ2-bridging and one terminal chloride ligand in the asymmetric unit. The lead(II) centre is octahedrally coordinated by three Cl ligands as well as two pyridyl nitrogen atoms and a carbonyl oxygen atom from three L2 moieties. These in turn act as tridentate bridging ligands and coordinate three different Pb ions. The μ2-Cl and μ3-L2 moieties act as linkers and spacers and interconnect the adjacent Pb1 atoms to give a 2D metal–organic network (Fig. 4a). The adjacent 2D sheets in 4 are further interconnected along the a axis by the N3–H3⋯Cl2 hydrogen bonds, involving the amide N–H group of L2 and the terminal chloride ligand. Topological classification of such 2D sheets discloses a binodal 3,4-connected underlying network with the 3,4L83 topology (Fig. 4b). Although this topology is similar to that of the supramolecular net of 3, it however corresponds to the metal–organic net in 4.
space group and has a lead(II) atom, a μ3-L2 block, one μ2-bridging and one terminal chloride ligand in the asymmetric unit. The lead(II) centre is octahedrally coordinated by three Cl ligands as well as two pyridyl nitrogen atoms and a carbonyl oxygen atom from three L2 moieties. These in turn act as tridentate bridging ligands and coordinate three different Pb ions. The μ2-Cl and μ3-L2 moieties act as linkers and spacers and interconnect the adjacent Pb1 atoms to give a 2D metal–organic network (Fig. 4a). The adjacent 2D sheets in 4 are further interconnected along the a axis by the N3–H3⋯Cl2 hydrogen bonds, involving the amide N–H group of L2 and the terminal chloride ligand. Topological classification of such 2D sheets discloses a binodal 3,4-connected underlying network with the 3,4L83 topology (Fig. 4b). Although this topology is similar to that of the supramolecular net of 3, it however corresponds to the metal–organic net in 4.
Compound 5 crystallizes in the P21/c space group and possesses one lead(II) centre, one μ3-L2 block, and two nitrate ligands (one μ2-bridging and one terminal) in the asymmetric unit. The lead(II) centre is eight-coordinated by six oxygen atoms, coming from one L2 moiety and three nitrate ligands, and two nitrogen atoms from two different L2 blocks. The bond distances lie in the range of 2.551(2)–2.874(2) Å for Pb–O bonds and 2.722(3)–2.776(3) Å for Pb–N bonds. Similarly to 4, each μ3-L2 moiety bridges three lead(II) atoms, whereas a μ2-nitrate ligand acts as an additional linker (Fig. 5a). As a result, an intricate 2D metal–organic network is generated (Fig. 5a). To get further insight into this rather complex network, we carried out its topological analysis by generating a simplified underlying net. It is composed of the 5-connected Pb1 and the 3-connected μ3-L2 nodes, as well as the 2-connected μ2-nitrate linkers (Fig. 5b). This net can be classified as a binodal 3,5-connected layer with a rare gek1 topology. It is defined by the point symbol of (3·4·5)(32·4·5·62·74), wherein the (3·4·5) and (32·4·5·62·74) notations correspond to the μ3-L2 and Pb1 nodes, respectively. Besides, the adjacent metal–organic layers in 5 are extended into a 3D supramolecular network through weak C–H⋯O hydrogen bonds (C2–H2⋯O5, C10–H10⋯O4).
Compound 6 crystallizes in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group and has one lead(II) atom, one μ3-L2 block, and two thiocyanate moieties (one terminal ligand and one anion) in the asymmetric unit (Fig. 6). The lead(II) centre is four-coordinated showing a disphenoidal geometry that is filled by three μ3-L2 moieties (two via pyridine nitrogen and one via the oxygen atom), and a nitrogen atom from a thiocyanate ligand. Although the other thiocyanate is not coordinated to the Pb1 atom, it is hydrogen bonded to the amide N–H of L2 (N2–H2n⋯N6 of 2.939 Å). Each L2 bridges three lead(II) atoms, thus interconnecting them into ladder-like cationic [PbL2(SCN)]nn+ 1D chains along the [011] direction (Fig. 6a). From a topological viewpoint,73 these chains are driven by the 3-connected and topologically equivalent Pb1 and μ3-L2 nodes (Fig. 6c). These chains can be classified as a uninodal 3-connected underlying net with the SP 1-periodic net (4,4)(0,2) topology and a point symbol of (42·6). The low coordination number of Pb1 allows an easy approach of two thiocyanate ions to the lead(II) centres, forming close Pb⋯S tetrel bonding contacts. These contacts interconnect the metal–organic chains into supramolecular sheets perpendicular to the [101] direction (Fig. 6b). Topological classification of such supramolecular sheets reveals the 3,4L83 topology, which is analogous to the coordination network in 4.
space group and has one lead(II) atom, one μ3-L2 block, and two thiocyanate moieties (one terminal ligand and one anion) in the asymmetric unit (Fig. 6). The lead(II) centre is four-coordinated showing a disphenoidal geometry that is filled by three μ3-L2 moieties (two via pyridine nitrogen and one via the oxygen atom), and a nitrogen atom from a thiocyanate ligand. Although the other thiocyanate is not coordinated to the Pb1 atom, it is hydrogen bonded to the amide N–H of L2 (N2–H2n⋯N6 of 2.939 Å). Each L2 bridges three lead(II) atoms, thus interconnecting them into ladder-like cationic [PbL2(SCN)]nn+ 1D chains along the [011] direction (Fig. 6a). From a topological viewpoint,73 these chains are driven by the 3-connected and topologically equivalent Pb1 and μ3-L2 nodes (Fig. 6c). These chains can be classified as a uninodal 3-connected underlying net with the SP 1-periodic net (4,4)(0,2) topology and a point symbol of (42·6). The low coordination number of Pb1 allows an easy approach of two thiocyanate ions to the lead(II) centres, forming close Pb⋯S tetrel bonding contacts. These contacts interconnect the metal–organic chains into supramolecular sheets perpendicular to the [101] direction (Fig. 6b). Topological classification of such supramolecular sheets reveals the 3,4L83 topology, which is analogous to the coordination network in 4.
3.3. Hirshfeld surface analysis
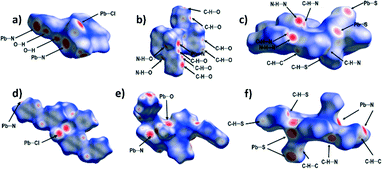
To analyse the intermolecular interactions in the crystal structures of 1–6, Hirshfeld surfaces have been calculated for all the structures. For the polymeric structures (1, 2, 4, 5 and 6), the Hirshfeld surfaces have been calculated around monomeric units. This leads to areas of the Hirshfeld surfaces with large dnorm values corresponding to coordination bonds (Fig. 7).The analyses of the Hirshfeld surfaces reveal that the dominant supramolecular interactions are primarily defined by the choice of the anionic co-ligand. Thus, in both 1 and 4 the dominant supramolecular interactions are hydrogen bonds involving the chloride ligands (24.6% of the Hirshfeld surface in 1 and 27.0% in 4), and dispersive H⋯H contacts (24.0% of the Hirshfeld surface in 1 and 26.1% in 4). Of these, the most notable are numerous C–H⋯Cl and N–H⋯Cl hydrogen bonding contacts corresponding to areas of large values of dnorm (Fig. 7a and d). The most significant difference between 1 and 4 is in the importance of C–H⋯π interactions (H⋯C contacts comprising 21.0% of the HS in 1 but only 7.0% in 4). This difference is readily observed when the shape index function is mapped onto the Hirshfeld surfaces, as this clearly shows large red ‘hollows’ indicating the presence of C–H⋯π interactions (marked with plain arrows on Fig. 8a) on the HS of 1 – a feature absent on the Hirshfeld surface of 4 (Fig. 8d).
In 2 and 5 by far the most dominant feature is the O⋯H contacts (corresponding to 47.6% of the Hirshfeld surface in 2 and 41.1% in 5) indicative of the numerous hydrogen bonds with nitrate oxygen atoms as acceptors. In both cases there is an area of large dnorm corresponding to the N–H⋯O hydrogen bond, and many others, corresponding to C–H⋯O contacts. In addition, there are significant contributions of C–H⋯π interactions (11.2% in 2 and 11.4% in 5) and dispersive H⋯H contacts (11.2% of the Hirshfeld surface in 2 and 18.7% in 5). When the shape index function is used to map the surface, bow-tie motifs can be noticed which indicate the presence of aromatic ring stacking contacts (Fig. 8b and f).
The dominant supramolecular interactions in 3 and 6 are hydrogen bonding contacts, in particular, multiple strong N–H⋯N and weaker C–H⋯N, C–H⋯S, and C–H⋯π hydrogen bonds. –N–H⋯N and C–H⋯N contacts constitute 18.0% of the Hirshfeld surface in 3 and 13.2% in 6, C–H⋯S hydrogen bonds 19.1% and 20.0%, and H⋯C contacts 19.7% and 19.9% respectively. Short N–H⋯N hydrogen bonds are noticeable as long, sharp ‘spikes’ on the 2D plot (Fig. 9).
 | ||
| Fig. 9 Decomposed fingerprint plots showing the main types of intermolecular contacts in the structures of 1–6. | ||
A particularly interesting feature of structures 3 and 6 is the presence of Pb⋯S tetrel bonds. In order to observe them by Hirshfeld surface analysis it was necessary to define the unit of the polymeric 6 for which the Hirshfeld surface had to be expanded to include the two additional L2 ligands covalently bonded to the Pb centre, and contacts between the Pb centre within the surface and atoms outside were studied. In both 3 and 6 there are areas of high dnorm (Fig. 10) corresponding to tetrel bonds between the Pb centre and thiocyanate ions. Interestingly, not only the thiocyanate sulphur, but also the carbon atom, appears to be in contact with the lead(II) ions. This is apparent from the Hirshfeld surface mapped with dnorm as pairs of fused red circles, corresponding to pairs of Pb⋯S and Pb⋯C contacts. The corresponding traces in the decomposed fingerprint plots (Fig. 11) are considerably different, with the trace corresponding to the Pb⋯S contact markedly sharper and Pb⋯C more diffuse. There is also in both structures a minute contribution of the Pb⋯N contact.
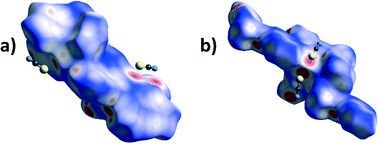 | ||
| Fig. 10 Hirshfeld surfaces mapped with dnorm for a) a molecule of 3 and b) an extended monomer of 6 showing the tetrel bonding between the Pb atoms (within the surface) and thiocyanate anions. | ||
3.4. DFT study
We have focused our study to the analysis of the noncovalent tetrel bonding interactions involving the Pb and several electron rich atoms. These interactions are very important factors governing the crystal packing, as has been explained above. Obviously in all structures reported herein, hydrogen bonding interactions are very relevant in the solid state, as demonstrated by the examination of the forces that govern the crystal packing and the Hirshfeld analysis (vide supra). However, in some structures (compounds 3 and 6), the existence of noncovalent S⋯Pb noncovalent interactions is worth of investigation. Moreover, in compound 3 antiparallel stacking interactions between the pyridine rings of the organic ligands have been also investigated. We have first examined the molecular electrostatic potential surface (MEPS) of the asymmetric unit of compound 3 and a model of compound 6, since it is polymeric. From the inspection of the surfaces, some considerations arise. First, small regions of positive potential (σ-holes) are clearly observed in the Pb atoms (+45 kcal mol−1 for 1 and +54 kcal mol−1 for 6, see Fig. 12) that anticipate their ability to interact with concentrations of negative charge. Second, the SCN co-ligands show an ambidentate behaviour. That is, one is coordinated through the N atom and the other through the S atom. The electrostatic potential at the end of the ligand is very different depending on the type of coordination. The N-coordinated ligand presents a modest potential in the S end (−16 kcal mol−1) and, conversely, the S-coordinated ligand shows a strong electrostatic potential at the N end (−58 kcal mol−1). This very different electrostatic characteristic of the SCN ligand is important in the crystal packing since the N-end of the Pb-SCN ligand in 3 interacts with the N–H group forming a strong H-bond as demonstrated in its Hirshfeld analysis (Fig. 7 and 9).At this point, it should be emphasized that the simultaneous ambidentate SCN coordination in Pb complexes is quite unusual. A search in the Cambridge Structural Database of complexes containing the Pb(SCN)2 fragment reveals that only three structures have been structurally characterized exhibiting both binding modes in the same complex (μ1,3-bridging ligands have not been considered in the search). Therefore, the complexes reported herein are exceptional in this sense. Interestingly, the CSD search also reveals that only 5 structures present both SCN co-ligands coordinated via the S atoms and that the usual behaviour is the coordination via the N atom (17 structures).
In compound 3 we have studied energetically the formation of a self-assembled dimer in the solid state that is characterized by a double tetrel bond interaction where the Pb atoms act as acceptors and the π-system of the SCN ligands as donors (Fig. 13). The Pb is almost equidistant to the S and C atoms and the interaction energy is ΔE1 = −30.6 kcal mol−1, indicating that each tetrel bond is approximately −15.3 kcal mol−1 (similar to a strong H-bond interaction). Pb interacts preferably with the π-system rather than the sulfur atom, because the electrostatic potential around S atom is anisotropic with larger negative values perpendicular to the S–C bond than in its direction. We have also computed the interaction energy of the antiparallel stacking between the pyridine rings observed in the solid state. This interaction is responsible for the formation of an infinite 1D chain in the crystal structure. The interaction energy is larger than expected (ΔE2 = −22.9 kcal mol−1) for a stacking interaction due to the strong influence of the metal coordination to the N atom of pyridine, which reinforces the π-stacking (by increasing the dipole–dipole contribution to the interaction).
 | ||
| Fig. 13 Theoretical models used to analyse (a) tetrel bonding and (b) stacking interactions in compound 3. Distances in Å. | ||
In compound 6, S⋯Pb noncovalent interactions are also observed in the solid state. These interactions connect the polymeric chains that are observed in the crystal packing (see Fig. 6 and 14). We have used a discrete model of the polymeric chain in order to evaluate the tetrel bonding interactions. The interaction energy of the model is ΔE3 = −33.4 kcal mol−1, indicating that each tetrel bond is approximately −16.7 kcal mol−1. This energy is slightly higher than the one observed for compound 3, in good agreement with the MEP value observed in the σ-hole, which is greater in compound 6 (see Fig. 12).
 | ||
| Fig. 14 Left: Partial view of the X-ray structure of compound 6. Right: Theoretical model used to analyse the tetrel bonding interactions in compound 6. Distances in Å. | ||
Finally, we have used Bader's theory of “atoms in molecules” (AIM) to analyse the noncovalent interactions described above. The presence of a bond critical point and a bond path connecting two atoms is a clear indication of bonding. The AIM analysis obtained for compounds 3 and 6 is shown in Fig. 15. Both tetrel bonding interactions are characterized by the presence of a bond critical point (red sphere) that connects the S atom to the Pb metal centre. In compound 6, the S atom also interacts with a hydrogen atom of the pyridine ring since a bond critical point and a bond path connecting both atoms are observed in the AIM analysis. This C–H⋯S hydrogen bond also contributes to the interaction between the infinite polymeric chains of the crystal structure. The values of the Laplacian of the charge density measured at the bond critical points that characterize the tetrel bonding interactions are positive, as is common in closed-shell interactions (Fig. 15).
 | ||
| Fig. 15 AIM distribution of bond and ring critical points (red and yellow spheres, respectively) in compounds 3 and 6. The bond paths connecting the bond critical points are also shown. | ||
Conclusions
In the present study, we synthesized and fully characterised a new series of lead(II) coordination compounds assembled from the neutral nicotinoylhydrazone blocks L1 or L2 and different inorganic anions (chloride, nitrate, or thiocyanate) as auxiliary ligands. The obtained compounds range from a discrete 0D lead(II) dimer 3 and infinite 1D coordination polymers 2 and 6 to 2D metal–organic networks 1, 4, and 5. Their structures are further extended via different supramolecular interactions.In the crystal structures of 1–3, the L1 block acts as a neutral ligand in the expected 3 + 1 manner, with three atoms (hydrazone oxygen and nitrogen and the 2-pyridyl nitrogen) chelating to one lead(II) cation, and one atom, the 3-pyridyl nitrogen, bridging to a neighbouring one. Unlike L1, L2 does not act as a chelating ligand, but rather behaves as a spacer between three lead(II) centres. Consequently, compounds 4–6 are all coordination polymers.
Topological classification of the metal–organic (in 1, 2, 4, 5 and 6) and supramolecular (in 3) underlying networks was performed, disclosing a uninodal 4-connected layer with the hcb topology in 1, a uninodal 2-connected chain with the 2C1 topology in 2, binodal 3,4-connected nets with the 3,4L83 topology in 3 and 4, a 3,5-connected layer with the gek1 topology in 5, as well as a uninodal 3-connected chain with the SP 1-periodic net (4,4)(0,2) topology in 6. Unlike the geometry and the topology of the coordination networks, the supramolecular bonding was found to be primarily defined not by the choice of the organic ligand but rather the anionic co-ligand. Interesting similarities within the pairs 1 and 4 (chloride derivatives), 2 and 5 (nitrate derivatives), and 3 and 6 (thiocyanate derivatives) were observed. The supramolecular structures of the latter compounds were found to be greatly affected by the tetrel bonding between the lead(II) containing cations and the thiocyanate moieties. These noncovalent interactions were energetically evaluated and confirmed by means of the AIM analysis.
Acknowledgements
We are grateful to the University of Maragheh for financial support of this research. A. B. and A. F. thank DGICYT of Spain (projects CTQ2014-57393-C2-1-P and CONSOLIDER INGENIO CSD2010–00065, FEDER funds) for funding. We thank the CTI (UIB) for free allocation of computer time. AMK acknowledges the FCT (UID/QUI/00100/2013).Notes and references
- J. C. Bailar Jr., Prep. Inorg. React., 1964, 1, 1 Search PubMed.
- B. F. Hoskins and R. Robson, J. Am. Chem. Soc., 1989, 111, 5962 CrossRef CAS.
- B. F. Hoskins and R. Robson, J. Am. Chem. Soc., 1990, 112, 1546 CrossRef CAS.
- B. Moulton and M. J. Zaworotko, Chem. Rev., 2001, 101, 1629 CrossRef CAS PubMed.
- A. Y. Robin and K. M. Fromm, Coord. Chem. Rev., 2006, 250, 2127 CrossRef CAS.
- N. Stock and S. Biswas, Chem. Rev., 2012, 112, 933 CrossRef CAS PubMed.
- K. Otsubo, Y. Wakabayashi, J. Ohara, S. Yamamoto, H. Matsuzaki, H. Okamoto, K. Nitta, T. Uruga and H. Kitagawa, Nat. Mater., 2011, 10, 291 CrossRef CAS PubMed.
- S. Kitagawa, R. Kitaura and S. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334 CrossRef CAS PubMed.
- G. Ferey, C. Mellot-Draznieks, C. Serre, F. Millange, J. Dutour, S. Surble and I. Margiolaki, Science, 2005, 309, 2040 CrossRef CAS PubMed.
- J. R. Long and O. M. Yaghi, Chem. Soc. Rev., 2009, 38, 1213 RSC.
- (a) H.-C. Zhou, J. R. Long and O. M. Yaghi, Chem. Rev., 2012, 112, 673 CrossRef CAS PubMed; (b) Y.-K. Deng, H.-F. Su, J.-H. Xu, W.-G. Wang, M. Kurmoo, S.-C. Lin, Y.-Z. Tan, J. Jia, D. Sun and L.-S. Zheng, J. Am. Chem. Soc., 2016, 138, 1328 CrossRef CAS PubMed; (c) S. Yuan, Y.-K. Deng and D. Sun, Chem. – Eur. J., 2014, 20, 10093 CrossRef CAS PubMed; (d) F.-L. Liu, B. Kozlevčar, P. Strauch, G.-L. Zhuang, L.-Y. Guo, Z. Wang and D. Sun, Chem. – Eur. J., 2015, 21, 18847 CrossRef CAS PubMed; (e) D. Sun, S. Yuan, H. Wang, H.-F. Lu, S.-Y. Feng and D.-F. Sun, Chem. Commun., 2013, 49, 6152 RSC; (f) X.-Y. Li, H.-F. Su, R.-Q. Zhou, S. Feng, Y.-Z. Tan, X.-P. Wang, J. Jia, M. Kurmoo, D. Sun and L.-S. Zheng, Chem. – Eur. J., 2016, 22, 3019 CrossRef CAS PubMed.
- Y. E. Cheon and M. P. Suh, Angew. Chem., Int. Ed., 2009, 48, 2899 CrossRef CAS PubMed.
- R. Poloni, B. Smit and J. B. Neaton, J. Am. Chem. Soc., 2012, 134, 6714 CrossRef CAS PubMed.
- L. J. Murray, M. Dincă and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294 RSC.
- J.-R. Li, J. Sculley and H.-C. Zhou, Chem. Rev., 2012, 112, 869 CrossRef CAS PubMed.
- S. Ma and H.-C. Zhou, Chem. Commun., 2010, 46, 44 RSC.
- S. Yang, X. Lin, A. J. Blake, G. S. Walker, P. Hubberstey, N. R. Champness and M. Schröder, Nat. Chem., 2009, 1, 487 CrossRef CAS PubMed.
- J. S. Seo, D. Whang, H. Lee, S. I. Jun, J. Oh, Y. J. Jeon and K. Kim, Nature, 2000, 404, 982 CrossRef CAS PubMed.
- J. Y. Lee, O. K. Farha, J. Roberts, K. A. Scheidt, S. T. Nguyenand and J. T. Hupp, Chem. Soc. Rev., 2009, 38, 1450 RSC.
- L. Ma, C. Abney and W. Lin, Chem. Soc. Rev., 2009, 38, 1248 RSC.
- D. Farrusseng, S. Aguado and C. Pinel, Angew. Chem., Int. Ed., 2009, 48, 7502 CrossRef CAS PubMed.
- B. Chen, S. Xiang and G. Qian, Acc. Chem. Res., 2010, 43, 1115 CrossRef CAS PubMed.
- L. E. Kreno, K. Leong, O. K. Farha, M. Allendorf, R. P. Van Duyne and J. T. Hupp, Chem. Rev., 2012, 112, 1105 CrossRef CAS PubMed.
- J. S. Qin, D. Y. Du, W. L. Li, J. P. Zhang, S. L. Li, Z. M. Su, X. L. Wang, Q. Xu, K. Z. Shao and Y. Q. Lan, Chem. Sci., 2012, 3, 2114 RSC.
- L. N. Dawe, T. S. M. Abedin and L. K. Thompson, Dalton Trans., 2008, 1661 RSC.
- L. N. Dawe, K. V. Shuvaev and L. K. Thompson, Inorg. Chem., 2009, 48, 3323 CrossRef CAS PubMed.
- L. N. Dawe, K. V. Shuvaev and L. K. Thompson, Chem. Soc. Rev., 2009, 38, 2334 RSC.
- M. Ruben, J. Rojo, F. J. Romero-Salguero, L. H. Uppadine and J.-M. Lehn, Angew. Chem., Int. Ed., 2004, 43, 3644 CrossRef CAS PubMed.
- M. Ruben, J.-M. Lehn and P. Müller, Chem. Soc. Rev., 2006, 35, 1056 RSC.
- V. A. Milway, S. M. T. Abedin, V. Niel, T. L. Kelly, L. N. Dawe, S. K. Dey, D. W. Thompson, D. O. Miller, M. S. Alam, P. Müller and L. K. Thompson, Dalton Trans., 2006, 2835 RSC.
- G. Mahmoudi, V. Stilinović, M. Servati Gargari, A. Bauzá, G. Zaragoza, W. Kaminsky, V. Lynch, D. Choquesillo-Lazarte, K. Sivakumar, A. Akbar Khandar and A. Frontera, CrystEngComm, 2015, 17, 3493 RSC.
- X.-P. Li, J.-Y. Zhang, M. Pan, S.-R. Zheng, Y. Liu and C.-Y. Su, Inorg. Chem., 2007, 46, 4617 CrossRef CAS PubMed.
- M. Yaghi, H. Li and T. L. Groy, Inorg. Chem., 1997, 36, 4292 CrossRef PubMed.
- C.-L. Chen, B.-S. Kang and C.-Y. Su, Aust. J. Chem., 2006, 59, 3 CrossRef CAS.
- B. D. Wagner, G. J. McManus, B. Moulton and M. J. Zaworotko, Chem. Commun., 2002, 2176 RSC.
- M. Beatty, Coord. Chem. Rev., 2003, 246, 131 CrossRef.
- M. Servati-Gargari, G. Mahmoudi, S. R. Batten, V. Stilinović, D. Butler, L. Beauvais, W. S. Kassel, W. G. Dougherty and D. VanDerveer, Cryst. Growth Des., 2015, 15, 1336 CAS.
- D. S. Li, Y. P. Wu, P. Zhang, M. Du, J. Zhao, C. P. Li and Y. Y. Wang, Cryst. Growth Des., 2010, 10, 2037 CAS.
- X. L. Wang, Y. Q. Chen, Q. Gao, H. Y. Lin, G. C. Liu, J. X. Zhang and A. X. Tian, Cryst. Growth Des., 2010, 10, 2174 CAS.
- G. P. Yang, L. Hou, Y. Y. Wang, Y. N. Zhang, Q. Z. Shi and S. R. Batten, Cryst. Growth Des., 2011, 11, 936 CAS.
- Z. Y. Du, H. B. Xu, X. L. Li and J. G. Mao, Eur. J. Inorg. Chem., 2007, 4520 CrossRef CAS.
- B. Ding, Y. Y. Liu, X. X. Wu, X. J. Zhao, G. X. Du, E. C. Yang and X. G. Wang, Cryst. Growth Des., 2009, 9, 4176 CAS.
- J. Yang, J. F. Ma, Y. Y. Liu, J. C. Ma and S. R. Batten, Cryst. Growth Des., 2009, 9, 1894 CAS.
- S. H. Li, S. K. Gao, S. X. Liu and Y. N. Guo, Cryst. Growth Des., 2010, 10, 495 CAS.
- T. F. Liu, J. Lu, C. B. Tian, M. N. Cao, Z. J. Lin and R. Cao, Inorg. Chem., 2011, 50, 2264 CrossRef CAS PubMed.
- A. Thirumurugan, R. A. Sanguramath and C. N. R. Rao, Inorg. Chem., 2008, 47, 823 CrossRef CAS PubMed.
- L. Zhang, Z. J. Li, Q. P. Lin, Y. Y. Qin, J. Zhang, P. X. Yin, J. K. Cheng and Y. G. Yao, Inorg. Chem., 2009, 48, 6517 CrossRef CAS PubMed.
- J. D. Lin, S. T. Wu, Z. H. Li and S. W. Du, CrystEngComm, 2010, 12, 4252 RSC.
- E. C. Yang, J. Li, B. Ding, Q. Q. Liang, X. G. Wang and X. J. Zhao, CrystEngComm, 2008, 10(158), 11 Search PubMed.
- J. Yang, G. D. Li, J. J. Cao, Q. Yue, G. H. Li and J. S. Chen, Chem. – Eur. J., 2007, 13, 3248 CrossRef CAS PubMed.
- K. L. Huang, X. Liu, J. K. Li, Y. W. Ding, X. Chen, M. X. Zhang, X. B. Xu and X. J. Song, Cryst. Growth Des., 2010, 10, 1508 CAS.
- Y. H. Zhao, H. B. Xu, Y. M. Fu, K. Z. Shao, S. Y. Yang, Z. M. Su, X. R. Hao, D. X. Zhu and E. B. Wang, Cryst. Growth Des., 2008, 8, 3566 CAS.
- K. Kavallieratos, J. M. Rosenberg and J. C. Bryan, Inorg. Chem., 2005, 44, 2573 CrossRef CAS PubMed.
- X. R. Meng, Y. L. Song, H. W. Hou, Y. T. Fan, G. Li and Y. Zhu, Inorg. Chem., 2003, 42, 1306 CrossRef CAS PubMed.
- R. L. Davidovicha, V. Stavilab, D. V. Marinina, E. I. Voita and K. H. Whitmire, Coord. Chem. Rev., 2009, 253, 1316 CrossRef.
- K. L. Zhang, Y. Chang, C. T. Hou, G. W. Diao, R. T. Wu and S. W. Ng, CrystEngComm, 2010, 12, 1194 RSC.
- J. Yang, J. F. Ma, Y. Y. Liu, J. C. Ma and S. R. Batten, Inorg. Chem., 2007, 46, 6542 CrossRef CAS PubMed.
- C. Gabriel, C. P. Raptopoulou, V. Psycharis, A. Terzis, M. Zevou, C. Mateescu and A. Salifoglou, Cryst. Growth Des., 2011, 11, 382 CAS.
- R. L. Davidovicha, V. Stavilab and K. H. Whitmire, Coord. Chem. Rev., 2010, 254, 2193 CrossRef.
- M. Servati Gargari, V. Stilinović, A. Bauzá, A. Frontera, P. McArdle, D. Van Derveer, S. W. Ng and G. Mahmoudi, Chem. – Eur. J., 2015, 17951 CrossRef CAS PubMed.
- A. Bauzá, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2013, 52, 12317 CrossRef PubMed.
- S. J. Grabowski, Phys. Chem. Chem. Phys., 2014, 16, 1824 RSC.
- (a) A. Bauzá, T. J. Mooibroek and A. Frontera, Chem. – Eur. J., 2014, 20, 10245 CrossRef PubMed; (b) A. Bauzá, T. J. Mooibroek and A. Frontera, Chem. Commun., 2014, 50, 12626 RSC.
- J. S. Murray, P. Lane and P. Politzer, J. Mol. Model., 2009, 15, 723 CrossRef CAS PubMed.
- A. Bundhun, P. Ramasami, J. S. Murray and P. Politzer, J. Mol. Model., 2013, 19, 2739 CrossRef CAS PubMed.
- L. Shimoni-Livny, J. P. Glusker and C. W. Bock, Inorg. Chem., 1998, 37, 1853 CrossRef CAS.
- R. L. Davidovich, V. Stavila, D. V. Marinin, E. I. Voit and K. H. Whitmire, Coord. Chem. Rev., 2009, 253, 1316 CrossRef CAS.
- Oxford Diffraction (2003), CrysAlis CCD and CrysAlis RED. Version 1.170., Oxford Diffraction Ltd, Wroclaw, Poland.
- APEX II, v. 2011.4, Bruker AXS, Madison, WI, 2009.
- SAINT+, v. 7.68A, Data Reduction and Correction Program, Bruker AXS, Madison, WI, 2009.
- SADABS, v. 2008/1: An Empirical Absorption Correction Program, Bruker AXS Inc., Madison, WI, 2008.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- (a) V. A. Blatov, IUCr CompComm Newsletter, 2006, vol. 7, p. 4 Search PubMed; (b) V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576 CrossRef CAS.
- (a) M. O'Keeffe and O. M. Yaghi, Chem. Rev., 2012, 112, 675 CrossRef PubMed; (b) M. Li, D. Li, M. O'Keeffe and O. M. Yaghi, Chem. Rev., 2014, 114, 1343 CrossRef CAS PubMed.
- R. Ahlrichs, M. Bär, M. Haser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893 CrossRef CAS.
- T. A. Keith, AIMAll (Version 13.11.04), TK Gristmill Software, Overland Park KS, USA, 2013 Search PubMed.
- M. J. Białek, J. K. Zaręba, J. Janczak and J. Zoń, Cryst. Growth Des., 2013, 13, 4039 Search PubMed.
- J. K. Zaręba, M. J. Białek, J. Janczak, J. Zon and A. Dobosz, Cryst. Growth Des., 2014, 14, 6143 Search PubMed.
- J. J. McKinnon, M. A. Spackman and A. S. Mitchell, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 627 CrossRef PubMed.
- S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, Crystal Explorer ver. 3.1, University of Western Australia, Perth, Australia, 2013 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: CCDC 1474988–1474993 contain the supplementary crystallographic data for 1–6. CCDC 1474988–1474993. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6ce00900j |
| This journal is © The Royal Society of Chemistry 2016 |