Open Access Article
Open Access ArticleA zeolitic imidazolate framework with conformational variety: conformational polymorphs versus frameworks with static conformational disorder†
Sergej
Springer
a,
Igor A.
Baburin
b,
Thea
Heinemeyer
a,
Jan Gerrit
Schiffmann
c,
Leo
van Wüllen
c,
Stefano
Leoni
d and
Michael
Wiebcke
*a
aInstitut für Anorganische Chemie, Leibniz Universität Hannover, Callinstraße 9, 30167 Hannover, Germany. E-mail: Michael.Wiebcke@acb.uni-hannover.de; Fax: +49 511 7623006; Tel: +49 511 7623698
bInstitut für Physikalische Chemie und Elektrochemie, Technische Universität Dresden, Mommsenstraße 13, 01062 Dresden, Germany
cInstitut für Physik, Universität Augsburg, Universitätsstraße 1, 86159 Augsburg, Germany
dSchool of Chemistry, Cardiff University, Main Building, Park Place, Cardiff, CF10 3AT, UK
First published on 3rd March 2016
Abstract
We show via structural considerations and DFT calculations that for a zeolitic imidazolate framework (ZIF) with sodalite (SOD) topology, [Zn(dcim)2]-SOD (dcim = 4,5-dichloroimidazolate), structural models of an infinite number of hypothetical conformational polymorphs with distinct linker orientations can be generated, which can be interconverted most likely only via reconstructive structural transitions. The relative total energies suggest that some of those polymorphs might be synthetically accessible. Efforts in that direction led to the synthesis of new trigonal 1 and previously known cubic 2 with improved crystallinity. According to structural analyses based on powder X-ray diffraction (PXRD) methods supported by NMR spectroscopy, 1 is the most stable of the theoretically predicted SOD-type framework conformers (isostructural to ZIF-7), whereas 2, at variance with a recent proposal, is a SOD-type material with a high degree of orientational disorder of the dcim linker units. The statistics of the linker orientations in 2 is close to that in 1, indicating that the disorder in 2 is not random. Rather, crystals of 2 are likely twins consisting of nanoscopic domains of trigonal 1 that are deformed to a cubic metric, with linker disorder located in the domain interfaces. As structural differences appear to be more related to characteristics of real as opposed to ideal crystal structures, we propose to not consider 1 and 2 as true conformational polymorphs. Systematic investigations of solvent mixtures led to the discovery of intermediate materials of 1 and 2. The PXRD patterns and SEM images indicate that they belong to a complete series of structural intermediates. Differences in the Ar adsorption/desorption behaviours reveal that 1, in contrast to 2, is a flexible ZIF framework.
Introduction
Crystalline zeolitic imidazolate frameworks (ZIFs) are a distinctive subclass of porous metal organic framework (MOF) materials.1 They are assembled from divalent metal cations and linking imidazolate and/or substituted imidazolate anions and possess framework structures with zeolite-related topologies.2 Current tremendous interest in these porous materials has arisen because ZIFs are more easily tunable towards specific applications than pure inorganic zeolites due to the modifiable imidazolate-based linkers. In addition some ZIFs combine permanent porosity with high thermal, chemical and, in particular, water stability,3 a combination of properties that is rare among MOF materials but desirable for many potential applications.4 Framework flexibility in response to guest adsorption/desorption, temperature or external pressure is an additional interesting property of some ZIFs.5We are currently exploring the zinc 4,5-dichloroimidazolate, [Zn(dcim)2], system as a ZIF model system. Our primary concern is to gain deeper understanding of the polymorphism and phase formation mechanisms.6 The [Zn(dcim)2] system was previously included in a broad exploratory high-throughput synthetic screening study, which resulted in the discovery of two topological polymorphs, porous RHO-type ZIF-71 and dense lcs-type ZIF-72.7 We reported more recently in addition the preparation and characterisation of [Zn(dcim)2] materials with SOD topology.6a The SOD-type materials exhibited apparently some structural variety as indicated by slight differences in the powder X-ray diffraction (PXRD) patterns that were recorded from different products. In the first approach to structural analysis two structural models with cubic symmetry but distinct orientation of the linker, representing hypothetical conformational SOD-type polymorphs, were generated and optimised using density functional theory (DFT) calculations. Subsequent Rietveld refinements against PXRD data recorded from samples with a cubic metric were in favour of the energetically less stable structure. The refinements were however not completely satisfactory and indicated that the structural model did not mirror all aspects of the real crystal structure.
In this contribution we first address the potential existence of conformational polymorphs in the [Zn(dcim)2] system more deeply by theoretically predicting further SOD-type framework conformers, in addition to the two above mentioned cubic SOD-type structures, and considering their relative energies as estimated by DFT calculations. Second, we report on a synthetic work that resulted in the successful experimental realisation of a new, so far only predicted trigonal SOD-type compound and on an improved synthesis for the recently reported cubic SOD-type material. Third, we discuss the results of structural analyses performed on PXRD data, which confirmed the trigonal structure and yielded a satisfactory structural model of the cubic material, which is at variance with the recently reported structural model. Fourth, we report on a systematic synthetic work performed to gain insight into how the choice of solvent crucially influences the crystallisation of the trigonal and cubic compounds, and which resulted in the discovery of a series of intermediate materials. Fifth, gas sorption properties of the trigonal and cubic materials are compared.
To our knowledge this is the first contribution that reports in a single paper the successful experimental realisation of two guest-free forms of a ZIF, [Zn(dcim)2]-SOD, with identical framework topology but different orientations of the linker, which in turn gives rise to differences in the gas sorption properties. It is discussed below that in the present case the different trigonal and cubic materials are better not considered as true conformational polymorphs, because structural differences are more related to characteristics of real as opposed to ideal crystal structures. Conformational polymorphism and real crystal structures are important aspects in ZIFs that have rarely been addressed so far in the literature.8,9
In the following we use Arabic numerals to distinguish experimentally realised [Zn(dcim)2]-SOD materials, 1 (trigonal) and 2 (cubic). Different ideal structural models of predicted and DFT-optimised conformational SOD-type polymorphs are denoted by Roman numerals I–IV.
Experimental section
DFT calculations
Hypothetical conformational [Zn(dcim)2]-SOD polymorphs were theoretically derived and some of them were optimised by periodic DFT calculations. Details of structure derivation are reported in the Results and discussion section. For the DFT studies, the rVV10 DFT functional10 which takes van der Waals interactions into account was used, as implemented in the PWscf/Quantum ESPRESSO package.11 The Kohn–Sham equations were solved using the plane-wave pseudo-potential approach applying ultrasoft pseudo-potentials without spin polarisation. A kinetic energy cutoff of 80 Ry and a density cutoff of 460 Ry were used to achieve fully converged results. During structure relaxation the atomic positions and unit cell constants were optimised. The final residual forces were <0.02 eV A−1 and the pressure converged within 0.1 kbar.Materials
Chemicals were purchased from commercial suppliers and used as received: zinc nitrate hexahydrate (Zn(NO3)2·6H2O, Sigma-Aldrich, ≥99.0%), zinc acetate dihydrate (Zn(OAc)2·2H2O, Sigma-Aldrich, ≥95.0%), aqueous ammonia (NH4OH, Sigma-Aldrich, 28–30% NH3), ethanol (EtOH, Carl Roth, ≥99.8%), 1-propanol (1-PrOH, Sigma-Aldrich, ≥99.5%), 2-propanol (2-PrOH, Sigma-Aldrich, 99.5%), 1-butanol (1-BuOH, Sigma-Aldrich, ≥99.4%), formamide (FA, Sigma-Aldrich, ≥99.5%), N,N-dimethylformamide (DMF, Sigma-Aldrich, ≥99.8%), N,N-diethylformamide (DEF, Sigma-Aldrich, 99.0%), dimethyl sulfoxide (DMSO, Carl Roth, ≥99.5%), tetrahydrofuran (THF, AppliChem, 99.0%), 4,5-dichloroimidazole (Hdcim, abcr, 98.0%), and 1-methylimidazole (1-mim, Sigma-Aldrich, 99.0%).Synthesis of 1
Synthesis of 1 was carried out solvothermally in 25 mL glass vials with screw lids employing a reactant ratio of Zn(OAc)2·2H2O/Hdcim/1-mim/DMF = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500. Typically, 113.4 mg (0.517 mmol) of Zn(OAc)2·2H2O was dissolved in 10 mL (129.138 mmol) of DMF. A second solution was prepared by dissolving 424.5 mg (3.099 mmol) of Hdcim and 0.205 mL (2.583 mmol) of 1-mim in 10 mL of DMF. The latter clear solution was poured rapidly in the former clear solution. The resultant clear solution was gently shaken and then heated unstirred at 120 °C for 24 h. After cooling to room temperature the solid was recovered by centrifugation and washing with DMF. Three cycles of redispersion and washing were performed. After drying at room temperature under reduced pressure, the yield of 1 was 44% (based on Zn). For activation the product was subjected to Soxhlet extraction with EtOH for 24 h and afterwards dried under reduced pressure at 70 °C. After digestion of a sample in a liquid DCl/D2O mixture,6a the almost complete absence of solvent was confirmed by 1H NMR spectroscopy.
500. Typically, 113.4 mg (0.517 mmol) of Zn(OAc)2·2H2O was dissolved in 10 mL (129.138 mmol) of DMF. A second solution was prepared by dissolving 424.5 mg (3.099 mmol) of Hdcim and 0.205 mL (2.583 mmol) of 1-mim in 10 mL of DMF. The latter clear solution was poured rapidly in the former clear solution. The resultant clear solution was gently shaken and then heated unstirred at 120 °C for 24 h. After cooling to room temperature the solid was recovered by centrifugation and washing with DMF. Three cycles of redispersion and washing were performed. After drying at room temperature under reduced pressure, the yield of 1 was 44% (based on Zn). For activation the product was subjected to Soxhlet extraction with EtOH for 24 h and afterwards dried under reduced pressure at 70 °C. After digestion of a sample in a liquid DCl/D2O mixture,6a the almost complete absence of solvent was confirmed by 1H NMR spectroscopy.
Synthesis of 2
Synthesis of 2 was carried out solvothermally in 25 mL glass vials with screw lids employing a reactant ratio of Zn(OAc)2·2H2O/Hdcim/1-mim/THF = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2000. Typically, 27.1 mg (0.123 mmol) of Zn(OAc)2·2H2O was dissolved in 10 mL (123.423 mmol) of THF. A second solution was prepared by dissolving 101.4 mg (0.741 mmol) of Hdcim and 0.177 mL (2.222 mmol) of 1-mim in 10 mL of THF. The latter clear solution was poured rapidly in the former clear solution which became turbid immediately. The mixture was gently shaken and heated unstirred at 120 °C for 24 h. After cooling to room temperature the solid was recovered by centrifugation and washing with THF. Three cycles of redispersion and washing were performed. After drying at room temperature under reduced pressure the yield of 2 was 57% (based on Zn). For activation the product was subjected to Soxhlet extraction with EtOH for 24 h and afterwards dried under reduced pressure at 70 °C. After digestion of a sample in a liquid DCl/D2O mixture,6a the almost complete absence of solvent was confirmed by 1H NMR spectroscopy.
2000. Typically, 27.1 mg (0.123 mmol) of Zn(OAc)2·2H2O was dissolved in 10 mL (123.423 mmol) of THF. A second solution was prepared by dissolving 101.4 mg (0.741 mmol) of Hdcim and 0.177 mL (2.222 mmol) of 1-mim in 10 mL of THF. The latter clear solution was poured rapidly in the former clear solution which became turbid immediately. The mixture was gently shaken and heated unstirred at 120 °C for 24 h. After cooling to room temperature the solid was recovered by centrifugation and washing with THF. Three cycles of redispersion and washing were performed. After drying at room temperature under reduced pressure the yield of 2 was 57% (based on Zn). For activation the product was subjected to Soxhlet extraction with EtOH for 24 h and afterwards dried under reduced pressure at 70 °C. After digestion of a sample in a liquid DCl/D2O mixture,6a the almost complete absence of solvent was confirmed by 1H NMR spectroscopy.
Additional synthetic work to study the influence of solvents
To investigate the influence of solvents on phase formation, various solvents (FA, DMF, DEF, 1-PrOH, 2-PrOH, 1-BuOH, THF, DMSO) were used employing a total molar ratio of reactants of Zn(OAc)2·2H2O/Hdcim/1-mim/solvent = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500. In addition, various DMF/THF solvent mixtures with a reactant ratio of Zn(OAc)2·2H2O/Hdcim/1-mim/DMF/THF = 1
500. In addition, various DMF/THF solvent mixtures with a reactant ratio of Zn(OAc)2·2H2O/Hdcim/1-mim/DMF/THF = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x
x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y with x + y = 500 were studied. All syntheses followed the same procedure as exemplified in the following for the experiment with a DMF/THF ratio of 250
y with x + y = 500 were studied. All syntheses followed the same procedure as exemplified in the following for the experiment with a DMF/THF ratio of 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250. 113.4 mg (0.517 mmol) of Zn(OAc)2·2H2O was dissolved in a mixture of 5 mL (64.569 mmol) of DMF and 5.23 mL (64.569 mmol) of THF. A second solution was prepared by dissolving 424.5 mg (3.099 mmol) of Hdcim and 0.206 mL (2.583 mmol) of 1-mim in a mixture of 5 mL of DMF and 5.23 mL of THF. The latter solution was poured rapidly in the former solution. The mixture was gently shaken and then heated under static conditions at 120 °C for 24 h. After cooling to room temperature the solid was recovered by centrifugation and washing with EtOH. Three cycles of redispersion and washing were performed. The product was dried at room temperature under reduced pressure.
250. 113.4 mg (0.517 mmol) of Zn(OAc)2·2H2O was dissolved in a mixture of 5 mL (64.569 mmol) of DMF and 5.23 mL (64.569 mmol) of THF. A second solution was prepared by dissolving 424.5 mg (3.099 mmol) of Hdcim and 0.206 mL (2.583 mmol) of 1-mim in a mixture of 5 mL of DMF and 5.23 mL of THF. The latter solution was poured rapidly in the former solution. The mixture was gently shaken and then heated under static conditions at 120 °C for 24 h. After cooling to room temperature the solid was recovered by centrifugation and washing with EtOH. Three cycles of redispersion and washing were performed. The product was dried at room temperature under reduced pressure.
Methods of characterisation
PXRD patterns were recorded using Stoe STADI-P transmission diffractometers equipped with sealed Cu X-ray tubes, curved Ge(111) monochromators delivering CuKα1 radiation (λ = 1.540594 Å) and linear position-sensitive detectors (PSDs). The samples were contained either between X-ray amorphous foils for measurements in ω–2θ geometry or in thin-walled glass capillaries for measurements in Debye–Scherrer geometry.SEM images were taken using a Jeol JSM-6700F instrument with a field emitter as the electron source using a low accelerating voltage of 2 kV. A Jeol JSM-6610LV instrument with a tungsten hairpin cathode as the electron source was used to take images of low magnification.
A Bruker Avance III 300 spectrometer operating at 300 MHz was used for recording 1H MAS NMR and 13C{1H} CP/MAS NMR spectra from solid samples. Samples were contained in 1.3 mm (1H) and 4.0 mm (13C) zirconia rotors and spun under the magic angle (MAS) at frequencies of 30.0 kHz (1H) and 8.9 kHz (13C). The contact time for 13C{1H} cross polarization (CP) was 3 ms.
Thermogravimetric (TG) analysis was performed simultaneously with differential thermal analysis (DTA) using a Netzsch 429 thermoanalyser. Samples were filled in alumina crucibles and heated in a flow of air with a ramp of 5 °C min−1 up to 1000 °C. For argon physisorption measurements at −186 °C a Quantachrome Autosorb-1-MP apparatus was used. Samples were outgassed in dynamic vacuum at 70 °C for 48 h before start of the sorption measurements. Surface areas were estimated applying the Brunauer–Emmett–Teller (BET) equation. The Micropore BET Assistant implemented in the ASiQwin 2.0 software from Quantachrome was used to determine the relative pressure range for the BET plot in accordance with the criteria of Rouquerol.12 Mesopore size distributions were estimated by the Barrett–Joyner–Halenda (BJH) method. The same apparatus was used to measure CO2 adsorption/desorption isotherms at 0 °C.
Structural analyses
The PXRD measurements were performed at room-temperature on a Stoe STADI-P diffractometer (see above) in Debye–Scherrer geometry with the samples contained in borosilicate glass capillaries with outer diameters of 0.5 mm. The internal PSD resolution was 0.01° 2θ. PXRD patterns were recorded from the following materials: activated (solvent-free) 1, as-synthesised (DMF-containing) 1 (1-DMF), activated (solvent-free) 2 and as-synthesised (THF-containing) 2 (2-THF). The patterns of 1 and 1-DMF could be indexed on the basis of the rhombohedron-centered hexagonal Bravais lattice; those of 2 and 2-THF were indexed on the basis of the body-centred cubic Bravais lattice. The TOPAS program system13 was used for Rietveld refinements. The PXRD profiles were modeled using Thompson–Cox–Hastings pseudo-Voigt peak-shape and Chebychev polynomial background functions. A simple axial model was used to treat peak asymmetry. The dcim linker units were generally treated as rigid bodies during all refinements. Initially applied soft restraints on Zn–N bond lengths were completely released in the final cycles of refinement. Two isotropic displacement parameters were refined, one common to Zn2+ ions and one common to the linker atoms.The starting point for refinement of solvent-free 1 was the DFT-optimised model of the new trigonal framework conformer III (Table S1, ESI†). To derive a starting model of the DMF solvent structure in the void system of 1, molecular dynamics (MD) simulations in space group P1 were first performed applying the UFF force field, as implemented in Materials Studio software.14 The derived model was then used to construct a model of disordered DMF molecules in R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) for subsequent refinement. The MD-derived positions of the DMF molecules were essentially in line with difference Fourier syntheses performed after refinement of the framework which revealed residual electron densities in particular in the small secondary cavities formed by the six-membered ring windows. During refinement of 1-DMF the positions of the solvent molecules were fixed; the occupancy factors of the solvent molecules were varied in alteration with fixation of the displacement parameters.
for subsequent refinement. The MD-derived positions of the DMF molecules were essentially in line with difference Fourier syntheses performed after refinement of the framework which revealed residual electron densities in particular in the small secondary cavities formed by the six-membered ring windows. During refinement of 1-DMF the positions of the solvent molecules were fixed; the occupancy factors of the solvent molecules were varied in alteration with fixation of the displacement parameters.
In the case of 2 it was particularly advisable to collect PXRD data from both solvent-free and as-synthesised samples because a highly crystalline material could be prepared but subsequent activation resulted in a significant loss of crystallinity. Thus structural analysis was hampered in the latter case by the necessity to model the disordered solvent molecules and in the former case by comparatively poor data quality.
To obtain a satisfactory Rietveld refinement of 2 structural models of different SOD-type framework conformers were theoretically derived and some of them were optimised by DFT. Details of model derivation are presented in the Results and discussion section. The most satisfactory structural model according to Rietveld analysis in Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m exhibits orientational disorder of the dcim linkers. The occupancy factors of the linker atoms were varied in alteration with fixation of the displacement parameters. For refinement of 2-THF a starting model of the solvent structure was derived by MD simulations in P1 using the structural model of framework conformer I (Table S1, ESI†) and subsequent construction of a disorder model in Im
m exhibits orientational disorder of the dcim linkers. The occupancy factors of the linker atoms were varied in alteration with fixation of the displacement parameters. For refinement of 2-THF a starting model of the solvent structure was derived by MD simulations in P1 using the structural model of framework conformer I (Table S1, ESI†) and subsequent construction of a disorder model in Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. Difference Fourier syntheses after framework refinement essentially agreed with the MD-derived solvent structure. In particular they revealed residual electron densities in the small secondary cavities formed by the six-membered ring windows. The occupancy factors of the THF molecules were varied in alteration with fixation of the displacement parameters during refinement.
m. Difference Fourier syntheses after framework refinement essentially agreed with the MD-derived solvent structure. In particular they revealed residual electron densities in the small secondary cavities formed by the six-membered ring windows. The occupancy factors of the THF molecules were varied in alteration with fixation of the displacement parameters during refinement.
Crystal data and details of Rietveld refinement for 1, 1-DMF, 2 and 2-THF are summarised in Table 1. Atomic parameters and selected bond lengths and angles are reported in Tables S2–S6 (ESI†). The VOID routine of the MERCURY program system15 was used for analysis of the internal void systems.
| 1 | 1-DMF | 2 | 2-THF | |
|---|---|---|---|---|
| Chemical formula | C6H2Cl4N4Zn | C8.7H8.2O0.9Cl4N4.9Zn | C5.9H2Cl3.9N3.9Zn | C8.7H7.6O0.7Cl4.2N4.2Zn |
| M/g mol−1 | 337.31 | 402.20 | 333.29 | 394.65 |
| Crystal system | Trigonal | Trigonal | Cubic | Cubic |
| Space group, Z |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , 18 , 18 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , 18 , 18 |
Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, 12 m, 12 |
Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, 12 m, 12 |
| a/Å | 22.7273(3) | 23.0989(4) | 16.7441(7) | 16.8507(3) |
| c/Å | 15.6196(3) | 15.4848(3) | — | — |
| V/Å3 | 6987.1(2) | 7155.2(3) | 4694.4(6) | 4784.7(3) |
| ρ/g cm−3 | 1.443 | 1.680 | 1.415 | 1.643 |
| No. of reflections | 256 | 256 | 55 | 67 |
| R wp/% | 3.61 | 4.53 | 4.39 | 4.08 |
| R Bragg/% | 1.70 | 2.39 | 1.97 | 1.78 |
| GoF | 2.33 | 2.17 | 2.22 | 2.46 |
Results and discussion
Hypothetical SOD-type conformational polymorphs
In our first effort to determine the crystal structure of newly prepared [Zn(dcim)2]-SOD material we have recently generated theoretical structural models of the two cubic conformational polymorphs I and II.6a The structural model of a trigonal conformational polymorph, III, has been obtained in this work by simply modifying the structure of well known [Zn(bim)2]-SOD (ZIF-7)16 by replacing the benzimidazolate (bim) by the dcim linker and subsequent optimisation of the structure using periodic DFT methods, that took van der Waals interactions into account. Pertinent data of the three framework structures is listed in Table S1 (ESI†). The crystallographically unique truncated octahedral [46·68] cavities generated in each framework are displayed in Fig. 1, along with the unique four- (4R) and six-membered rings (6R) existing in each structure. It can be seen that the frameworks differ considerably in their conformations as expressed by the orientations (twists) of the dcim linkers and rotations (tilts) of the ZnN4 tetrahedra. The latter are slightly distorted from ideal geometry to an extent that is not unusual for known ZIFs. The shortest inter-linker Cl⋯Cl and H⋯H distances in each framework are slightly larger than the respective van der Waals distances. The estimated relative total energies at −273 °C follow the order I (39.8 kJ mol−1) > II (28.9 kJ mol−1) > III (15.9 kJ mol−1). Considering previous literature data,5c,17–19 conformers II and III appear to be only moderately destabilised against dense lcs-type ZIF-72 (0 kJ mol−1), as is shown in an energy-density diagram of hypothetical and known topological and conformational [Zn(dcim)2] polymorphs (Fig. 2). The DFT calculations further predict that III is more stable than known RHO-type ZIF-71 (22.3 kJ mol−1).20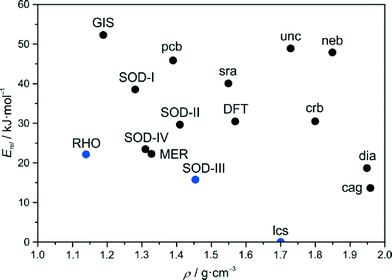 | ||
| Fig. 2 Energy-density diagram of the topological and conformational polymorphs in the [Zn(dcim)2] system. The framework types are given in black and blue colours for hypothetical and experimentally realised polymorphs, respectively. The diagram is a modification of a recently reported diagram.6a,20 | ||
Cubic polymorph I with space group Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m exhibiting maximal symmetry represents the fully expanded conformational state with the lowest framework density (largest cell volume and porosity).21 In its flat 4R all planar dcim linkers are oriented such that their C–H vectors point to the 4R centre (dcim twist angle: 0°). The 6R is characterised by an alternate up and down orientation of the dcim units (±125.3°). This is the framework structure that we proposed recently for cubic 2.6a Cubic polymorph II in I
m exhibiting maximal symmetry represents the fully expanded conformational state with the lowest framework density (largest cell volume and porosity).21 In its flat 4R all planar dcim linkers are oriented such that their C–H vectors point to the 4R centre (dcim twist angle: 0°). The 6R is characterised by an alternate up and down orientation of the dcim units (±125.3°). This is the framework structure that we proposed recently for cubic 2.6a Cubic polymorph II in I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m represents a denser, partially collapsed conformation.21 The dcim units are strongly twisted alternately up and down in the 4R (±116.5°), while their orientations in the 6R are approximately in plane (8.7°) and strongly out of plane (118.2°) in an alternating sequence. This framework conformation is similar to the conformations of SOD-type ZIFs containing 2-substituted imidazolate linkers, e.g. the low-pressure and high-pressure forms of ZIF-8.5a,b,d Trigonal polymorph III in R
3m represents a denser, partially collapsed conformation.21 The dcim units are strongly twisted alternately up and down in the 4R (±116.5°), while their orientations in the 6R are approximately in plane (8.7°) and strongly out of plane (118.2°) in an alternating sequence. This framework conformation is similar to the conformations of SOD-type ZIFs containing 2-substituted imidazolate linkers, e.g. the low-pressure and high-pressure forms of ZIF-8.5a,b,d Trigonal polymorph III in R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) represents another kind of distortion from maximal symmetry. Two opposite dcim units lay approximately in the plane of the 4R (±4.9°) with the remaining two linkers strongly twisted in opposite directions (±112.2°) against the 4R plane. Two unique 6Rs exist in III that occur in a ratio of 1
represents another kind of distortion from maximal symmetry. Two opposite dcim units lay approximately in the plane of the 4R (±4.9°) with the remaining two linkers strongly twisted in opposite directions (±112.2°) against the 4R plane. Two unique 6Rs exist in III that occur in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. The conformation of the 6R perpendicular to the hexagonal c axis, 6R-A (±130.6°), resembles that of I, while the conformation of the 6R slightly inclined against the hexagonal c axis, 6R-B, is less symmetric (±26.4°, ±114.9°, ±131.0°). This framework conformation is similar to the conformations of the guest-containing and guest-free forms of ZIF-7.16,22 Simulated PXRD patterns of the three framework conformers are reported in Fig. S1 (ESI†). It is interesting to note that the analogues of all three framework conformers are known in guest-free/guest-containing silica sodalites.23
3. The conformation of the 6R perpendicular to the hexagonal c axis, 6R-A (±130.6°), resembles that of I, while the conformation of the 6R slightly inclined against the hexagonal c axis, 6R-B, is less symmetric (±26.4°, ±114.9°, ±131.0°). This framework conformation is similar to the conformations of the guest-containing and guest-free forms of ZIF-7.16,22 Simulated PXRD patterns of the three framework conformers are reported in Fig. S1 (ESI†). It is interesting to note that the analogues of all three framework conformers are known in guest-free/guest-containing silica sodalites.23
Despite the considerable different linker orientations in the three framework conformers, the internal void systems are rather similar as shown in Fig. S2 (ESI†). The walls are essentially built by the chlorine substituents that generate slightly distorted [46·68] cavities with small interconnecting channels running through the 6Rs. The centres of the 6Rs are defined with small secondary cavities. The chlorine positions approximately overlap for the three structures.
One aspect of the conformational polymorphs warrants special attention. The considerable differences in the linker orientations suggest that the structures are unlikely to be interconvertible via displacive phase transition pathways with comparatively low energy barriers, as it is the case for reversible transitions in ZIFs that occur in response to external stimuli.5,22 Although we cannot predict any such transition pathway that would be coupled to low-frequency vibrations,24 simplified considerations suggest that the necessary concerted linker movements have to pass through the small 6R windows and should therefore be strongly hindered by close, forbidden Cl⋯Cl contacts. Rather possible interconversions are likely to be reconstructive in nature and along with the consideration of the strong Zn–N bonds in ZIFs,2 it is reasonable to expect that the three structures represent local minima in the energy landscape, which are separated from each other by high energy barriers, comparable to the situation for topological polymorphs.
A simple structural relationship between I and III is shown in Fig. 3. One can formally interconvert I and III by moving half of the linkers in the 4Rs through the planes of the neighbouring 6R-A rings, that is by moving all alternating linkers in each 6R-A ring in opposite directions (neglecting forbidden Cl⋯Cl contacts). It has been found that such a concerted switch of linkers can actually be performed independently for any single 6R-A ring, as after such a switch no forbidden inter-linker atom⋯atom distances or unacceptably distorted ZnN4 tetrahedra result. This means that it is readily possible to construct an infinite number of hypothetical structural intermediates of I and III, ranging from structures with local defects (orientational switch of all six linkers within one 6R-A ring) through structures with local extended planar faults (orientational switch of all linkers in a layer of 6R-A rings perpendicular to a body diagonal in I or chex in III) to periodic or non-periodic intergrowth structures. As an example we provide in Fig. S3 (ESI†) a structural model derived from III by switching all linkers in every third 6R-A layer perpendicular to chex to the conformation as in I. By additional DFT calculations it has been estimated that this structural model in P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1, IV, is destabilised against III by only 7.5 kJ mol−1 (23.4 kJ mol−1 higher than lcs-type ZIF-72) and is more stable than I and II and approximately isoenergetic with RHO-type ZIF-71 (Fig. 2). This example indicates that similar intermediate defective and intergrowth structures should show a tendency towards low relative energies.
m1, IV, is destabilised against III by only 7.5 kJ mol−1 (23.4 kJ mol−1 higher than lcs-type ZIF-72) and is more stable than I and II and approximately isoenergetic with RHO-type ZIF-71 (Fig. 2). This example indicates that similar intermediate defective and intergrowth structures should show a tendency towards low relative energies.
Taken together the above theoretical considerations predict that the [Zn(dcim)2]-SOD framework potentially exhibits a great static conformational variety, which has to be distinguished from stimuli-responsive dynamic conformational changes in flexible ZIF frameworks.5 Due to the estimated moderate energetic differences and expected high energy barriers between different hypothetical structures it might be possible to synthetically access some of the SOD-type conformational polymorphs.
Synthesis of 1 and 2
The first hints for the possible synthetic accessibility of trigonal 1, identical to III, were obtained when inspecting PXRD patterns recorded from solids produced by reacting at room temperature Zn(NO3)2·6H2O and Hdcim in 1-propanolic solutions containing aqueous ammonia. This was a modification of the syntheses reported by Zhu et al.25 The patterns (Fig. S4, ESI†) exhibit clear indications for the splitting of the most intense reflection at about 7.4° 2θ that is typical of trigonal III compared to cubic I and II. Replacing the solvent 1-PrOH by DMF yielded materials with PXRD patterns that matched the pattern of III very well. As in DMF solution solid products could only be obtained after heating to 120 °C but not at room temperature and as volatility of ammonia became an inconvenience, the ammonia modulator was replaced by 1-methylimidazole (1-mim).26 The need of a modulator in DMF solution indicates that under these conditions the modulator functions as a base to deprotonate the Hdcim linker.27 The yield could then be improved when replacing the nitrate by the more basic acetate salt.28 An optimised synthesis of 1 employing a molar ratio of Zn(OAc)2·2H2O/Hdcim/1-mim/DMF = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
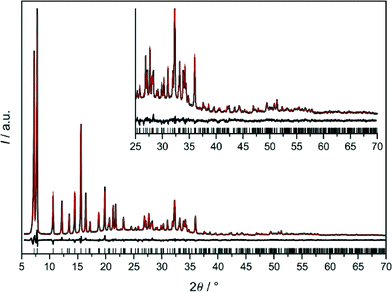
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 is reported in the Experimental section. Phase identity and purity were checked and confirmed by PXRD including Rietveld analysis as reported below. As-synthesised 1 consisted of micrometer-sized, aggregated rhombic dodecahedral crystals (Fig. 4).
500 is reported in the Experimental section. Phase identity and purity were checked and confirmed by PXRD including Rietveld analysis as reported below. As-synthesised 1 consisted of micrometer-sized, aggregated rhombic dodecahedral crystals (Fig. 4).
Our recently reported syntheses of cubic 2, and less-symmetric variants thereof, yielded poorly crystalline products that diffracted X-rays up to only low 2θ angles.6a It has been found during this work that crystallinity could be significantly improved when replacing the solvent 1-PrOH by THF and the nitrate by the acetate salt. An optimised synthesis of 2 employing a molar ratio of Zn(OAc)2·2H2O/Hdcim/1-mim/THF = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2000 is reported in the Experimental section. Phase identity and purity were checked and confirmed by PXRD including Rietveld analysis as reported below. The well shaped rhombic dodecahedral crystals of as-synthesised 2 were about 1.5 μm in size (Fig. 4). As reported in the ESI,† changing the molar ratio of the reactants allowed us to produce a nanocrystalline material of 2 as well (Fig. S5†).
2000 is reported in the Experimental section. Phase identity and purity were checked and confirmed by PXRD including Rietveld analysis as reported below. The well shaped rhombic dodecahedral crystals of as-synthesised 2 were about 1.5 μm in size (Fig. 4). As reported in the ESI,† changing the molar ratio of the reactants allowed us to produce a nanocrystalline material of 2 as well (Fig. S5†).
To this end, we have not been able to produce further [Zn(dcim)2]-SOD materials apart from intermediates of 1 and 2 that are reported below.
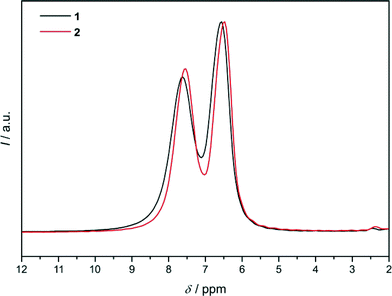
Crystal structures of 1 and 1-DMF
The final Rietveld plot for 1 (Fig. 5) shows very good agreement between experimental and calculated PXRD profiles and thereby confirms the successful experimental realisation of predicted framework conformer III. The 1H MAS NMR spectrum (Fig. 6) exhibits two signals with an intensity ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and chemical shifts at 6.55 and 7.60 ppm. This is in line with the two unique hydrogen atoms (two unique dcim linkers) occurring in the crystallographic asymmetric unit of 1. On the other hand in the 13C{1H} CP/MAS NMR spectrum the signals of the two unique linkers are not resolved (Fig. S6, ESI†). The Rietveld refinement of 1-DMF (Fig. S7, ESI†) yielded the composition [Zn(dcim)2]·0.89DMF, which agrees well with the results from TG analysis, [Zn(dcim)2]·0.91DMF (Fig. S8, ESI†).
1 and chemical shifts at 6.55 and 7.60 ppm. This is in line with the two unique hydrogen atoms (two unique dcim linkers) occurring in the crystallographic asymmetric unit of 1. On the other hand in the 13C{1H} CP/MAS NMR spectrum the signals of the two unique linkers are not resolved (Fig. S6, ESI†). The Rietveld refinement of 1-DMF (Fig. S7, ESI†) yielded the composition [Zn(dcim)2]·0.89DMF, which agrees well with the results from TG analysis, [Zn(dcim)2]·0.91DMF (Fig. S8, ESI†).
For 1 and 1-DMF the experimental unit cell constants (Table 1) as well as bond lengths and angles (Table S2, ESI†) and linker twist angles are in fair agreement with the respective values obtained by DFT (Table S1, ESI†). For example the experimental cell volumes of 1 and 1-DMF deviate from the DFT-estimated values by −0.58 and +1.81%, respectively. As described above the void system in 1 comprises two small unique secondary cavities formed by the two different 6R-A and 6R-B rings and one larger unique primary [46·68] cavity (Fig. S2 and Table S2, ESI†). The DMF molecules in 1-DMF were found to occupy in particular the 6R-B cavities (Fig. S9, ESI†). The structural analyses further revealed that activation of 1-DMF is accompanied by a small decrease of the cell volume (−2.36% at room temperature, air atmosphere) with retention of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry of the framework structure. This is in contrast to the situation found in isostructural ZIF-7. Removal of DMF from as-synthesised ZIF-7 has been reported to result in a reversible distortion of the framework from R
symmetry of the framework structure. This is in contrast to the situation found in isostructural ZIF-7. Removal of DMF from as-synthesised ZIF-7 has been reported to result in a reversible distortion of the framework from R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (ZIF-7-I) to P
(ZIF-7-I) to P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (ZIF-7-II) symmetry and an increase in the cell volume.22a
(ZIF-7-II) symmetry and an increase in the cell volume.22a
Crystal structures of 2 and 2-THF
As Rietveld refinements starting with framework models I or II had not been completely satisfactory,6a we searched for further starting models. The need to do so was also indicated by the 1H MAS NMR spectrum of 2 (Fig. 6), which resembles that of 1 and exhibits two signals with an intensity ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and chemical shifts at 6.47 and 7.53 ppm. This is not compatible with the cubic structural models because in each of them only one unique dcim linker occurs. Due to the similarity of the 1H NMR spectra of 1 and 2 refinements against PXRD data of 2 were started with framework model III in R
1 and chemical shifts at 6.47 and 7.53 ppm. This is not compatible with the cubic structural models because in each of them only one unique dcim linker occurs. Due to the similarity of the 1H NMR spectra of 1 and 2 refinements against PXRD data of 2 were started with framework model III in R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) which was deformed to a cubic metric. It should be noted that the hexagonal (rhombohedral) unit cell of III with a ratio of ahex/chex = 1.455 (αrhom = 107.21°) is close to a body-centered cubic cell with an expected ratio of ahex/chex = 1.633 (αrhom = 109.45°). The obtained Rietveld plot (Fig. 7a) reveals good agreement between the experimental and calculated data. This was a surprising finding, raising the question how the same solvent-free structure could exist with different metrics. The fact that this is not the case became clear by close inspection of the Rietveld plot which revealed that a weak reflection at about 16.7° 2θ is not well modeled. In addition the 13C{1H} CP/MAS NMR spectrum of 2 (Fig. S6, ESI†), albeit it does not indicate the presence of more than one unique linker, nonetheless exhibits noticeable differences to the spectrum of 1 in the width of the signals originating from the chlorine-substituted carbons, therefore suggesting that some difference must exist between the structures of 1 and 2.
which was deformed to a cubic metric. It should be noted that the hexagonal (rhombohedral) unit cell of III with a ratio of ahex/chex = 1.455 (αrhom = 107.21°) is close to a body-centered cubic cell with an expected ratio of ahex/chex = 1.633 (αrhom = 109.45°). The obtained Rietveld plot (Fig. 7a) reveals good agreement between the experimental and calculated data. This was a surprising finding, raising the question how the same solvent-free structure could exist with different metrics. The fact that this is not the case became clear by close inspection of the Rietveld plot which revealed that a weak reflection at about 16.7° 2θ is not well modeled. In addition the 13C{1H} CP/MAS NMR spectrum of 2 (Fig. S6, ESI†), albeit it does not indicate the presence of more than one unique linker, nonetheless exhibits noticeable differences to the spectrum of 1 in the width of the signals originating from the chlorine-substituted carbons, therefore suggesting that some difference must exist between the structures of 1 and 2.
The Rietveld plot in Fig. 7b demonstrates that a satisfactory refinement for 2 was finally obtained in cubic Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m with a structural model containing one unique Zn site and two unique sites for the dcim linker in the crystallographic asymmetric unit. The latter have almost equal statistical occupancy factors (sof) of 0.453 and 0.532, respectively, in total corresponding to a ratio of Zn/linker = 1
m with a structural model containing one unique Zn site and two unique sites for the dcim linker in the crystallographic asymmetric unit. The latter have almost equal statistical occupancy factors (sof) of 0.453 and 0.532, respectively, in total corresponding to a ratio of Zn/linker = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.97. This is in good agreement with the intensity ratio of the two signals in the 1H NMR spectrum. Considering the one unique Zn⋯Zn edge in the crystal structure the linkers are disordered over three different principal orientations as is shown in Fig. 8a. In Fig. 8b it can be seen that in the unique 4R the linkers are either strongly twisted against the 4R plane in one of two opposite directions (±105.9°, sof = 0.266) or lay in the 4R plane (0°, sof = 0.453), while in the unique 6R they are oriented strongly up or down (±125.3°, sof = 0.453; ±128.9°, sof = 0.266) or slightly up or down (±19.4°, sof = 0.266). A satisfactory Rietveld refinement with the same disordered framework model was also obtained with the higher-quality PXRD data recorded from 2-THF (Fig. S10, ESI†). The refinement confirms that the unique linkers occur in an approximately 1
1.97. This is in good agreement with the intensity ratio of the two signals in the 1H NMR spectrum. Considering the one unique Zn⋯Zn edge in the crystal structure the linkers are disordered over three different principal orientations as is shown in Fig. 8a. In Fig. 8b it can be seen that in the unique 4R the linkers are either strongly twisted against the 4R plane in one of two opposite directions (±105.9°, sof = 0.266) or lay in the 4R plane (0°, sof = 0.453), while in the unique 6R they are oriented strongly up or down (±125.3°, sof = 0.453; ±128.9°, sof = 0.266) or slightly up or down (±19.4°, sof = 0.266). A satisfactory Rietveld refinement with the same disordered framework model was also obtained with the higher-quality PXRD data recorded from 2-THF (Fig. S10, ESI†). The refinement confirms that the unique linkers occur in an approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio and yielded a composition, [Zn(dcim)2]·0.69THF, that agrees well with the TG results, [Zn(dcim)2]·0.66THF (Fig. S8, ESI†). Upon activation the unit cell of 2-THF shrinks by −1.89% with retention of framework symmetry (Table 1). The bond lengths and angles in 2 and 2-THF are in reasonable agreement with those in 1 and 1-DMF (Table S2, ESI†).
1 ratio and yielded a composition, [Zn(dcim)2]·0.69THF, that agrees well with the TG results, [Zn(dcim)2]·0.66THF (Fig. S8, ESI†). Upon activation the unit cell of 2-THF shrinks by −1.89% with retention of framework symmetry (Table 1). The bond lengths and angles in 2 and 2-THF are in reasonable agreement with those in 1 and 1-DMF (Table S2, ESI†).
The fact that linker disorder can be inferred from the PXRD data suggests that it must exist on a small length scale. This could be achieved in a crystal with random linker disorder or, more likely, in a domain or twinned crystal. While the magnitudes of the three principal twist angles in 2 resemble those found in I–III (and any intermediate of I and III), the statistics of in-plane and out-of-plane linker orientations in the 4Rs and 6Rs in 2 is only, approximately, compatible with that in III. Thus a twinned crystal (merohedral twin) could consist of nanoscopic domains of III with R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry that are deformed to a cubic metric and aligned with their
symmetry that are deformed to a cubic metric and aligned with their ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) axes along the cubic <111> directions. The energetic cost of deformation from a hexagonal to a cubic metric has been estimated by DFT to be very small (Ecub − Ehex = 2.3 kJ mol−1). Various twin laws could relate individual domains, as the static conformational variety (three principal linker orientations) should enable the formation of corresponding low-energy domain interfaces.29 A structural model of a coherent (ideal) twin boundary with a mirror plane parallel {110} is shown in Fig. S11 (ESI†) as an example. However experimental data suggest that in 2 domain boundaries are unlikely to be structurally that ideal because the PXRD pattern is not completely in line with the R
axes along the cubic <111> directions. The energetic cost of deformation from a hexagonal to a cubic metric has been estimated by DFT to be very small (Ecub − Ehex = 2.3 kJ mol−1). Various twin laws could relate individual domains, as the static conformational variety (three principal linker orientations) should enable the formation of corresponding low-energy domain interfaces.29 A structural model of a coherent (ideal) twin boundary with a mirror plane parallel {110} is shown in Fig. S11 (ESI†) as an example. However experimental data suggest that in 2 domain boundaries are unlikely to be structurally that ideal because the PXRD pattern is not completely in line with the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) structural model (Fig. 7a) and gas sorption measurements have established the existence of mesopores (see below).
structural model (Fig. 7a) and gas sorption measurements have established the existence of mesopores (see below).
The structural analyses above have experimentally revealed the static conformational variety of the [Zn(dcim)2]-SOD framework due to three principal linker orientations in each Zn⋯Zn edge (Fig. 8a). The selection between ordered 1 and disordered 2 must occur during the crystal formation processes. 2 represents an example where static conformational variety causes disorder resulting in a real ZIF structure that differs from the ordered (ideal) structure 1. As the structural differences in this case are more related to characteristics of real as opposed to ideal crystal structures we propose to not consider 1 and 2 as true conformational polymorphs.
Similar considerations with regard to static conformational variety could apply to other 4,5-disubstituted SOD-type ZIFs depending on steric demand of the substituents and inter-linker interactions. Of particular interest here are two recent independent and parallel reports by Diring et al. and Bennett et al. of a trigonal and a cubic [Zn(mnim)2]-SOD (mnim = 4-methyl-5-nitroimidazolate), respectively.30 Single-crystal XRD structural analysis clearly revealed that the trigonal material adopts ordered framework conformation III (when considering the imidazolate rings) but with positional disorder of the methyl and nitro substituents. The structure of the cubic material could however not be clearly determined from single-crystal XRD data as indicated for example by high residual factors. The authors ascribed this to extensive disorder of the substituents and they proposed a structural model that, judged from the drawing presented in their paper, is based on ordered framework conformation I with positional disordered substituents. If correct this would mean that the trigonal and cubic [Zn(mnim)2]-SOD materials represent the first example of conformational polymorphs in ZIFs. However a more convincing structural analysis of the cubic form needs to be presented for final confirmation.
Systematic studies of the influence of solvents on the formation of 1 and 2
Since it is well known that the choice of solvent or structure directing agent may have an impact on phase formation in ZIFs,31 we systematically studied the influence of different solvents on phase formation in the [Zn(dcim)2] system. In the first series of experiments the molar ratio of the reactants (Zn(OAc)2·2H2O/Hdcim/1-mim/solvent = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500) and reaction parameters (120 °C, 24 h) were kept constant while the solvent (FA, DMF, DEF, 1-PrOH, 2-PrOH, 1-BuOH, DMSO, THF) was varied. In the second series the same reactions were quenched 1 h after precipitation was visually observed to follow to some extent the evolution of the reacting systems with time. If precipitation took place immediately after mixing the reactant solutions the system was not heated but the solid recovered after 1 h of aging at room temperature.
500) and reaction parameters (120 °C, 24 h) were kept constant while the solvent (FA, DMF, DEF, 1-PrOH, 2-PrOH, 1-BuOH, DMSO, THF) was varied. In the second series the same reactions were quenched 1 h after precipitation was visually observed to follow to some extent the evolution of the reacting systems with time. If precipitation took place immediately after mixing the reactant solutions the system was not heated but the solid recovered after 1 h of aging at room temperature.
With the exception of DMSO, solid products were obtained with all solvents. The PXRD patterns of the as-synthesised products are displayed in Fig. S12 and S13 (ESI†), while the results are summarised in Table 2. It can be seen that under the conditions considered here the formation of SOD-types 1 and 2 crucially depended on the appropriate choice of solvent. 2 was only obtained in THF, already at room temperature and also after 24 h of heating. For the recovery of 1 in DMF on the other hand heating for 24 h was necessary, while heating for only 1 h yielded a product that can be considered according to its PXRD pattern as an intermediate of 1 and 2 (see below). In contrast to that, choice of solvent was less crucial for the formation of RHO-type ZIF-71, which crystallised within 1 h as pure phase in DEF, 1-PrOH and 2-PrOH and as the major phase in 1-BuOH admixed with a small amount of lcs-type ZIF-72. Furthermore in all alcohols we observed after 24 h of heating the complete or partial transformation of metastable ZIF-71 into stable ZIF-72 (see Fig. 2). In the case of 1-PrOH a weak reflection at about 7.4° 2θ is seen in the PXRD, which can be assigned to the most intense 110 Bragg peak of SOD-type 2. This is principally in line with our previous observations of the transient occurrence of 2 during the ZIF-71-to-ZIF-72 transformation.6a Such transformations to stable ZIF-72 did not take place in DMF, DEF and THF even after prolonged heating for 7 d (PXRD data not shown), suggesting that these solvents are good space fillers to stabilise the void system in 1, ZIF-71 and 2, respectively.
| Solvent | Time/1 h | Time/24 h |
|---|---|---|
| a Intermediate of 1 and 2. | ||
| DMSO | — | — |
| THF | SOD (2)* | SOD (2) |
| FA | lcs (ZIF-72)* | lcs (ZIF-72) |
| DMF | SOD (1–2)a | SOD (1) |
| DEF | RHO (ZIF-71) | RHO (ZIF-71) |
| 1-PrOH | RHO (ZIF-71)* | lcs (ZIF-72)/RHO (ZIF-71)/SOD (1) |
| 2-PrOH | RHO (ZIF-71)* | RHO (ZIF-71)/lcs (ZIF-72) |
| 1-BuOH | RHO (ZIF-71)/lcs (ZIF-72)* | lcs (ZIF-72) |
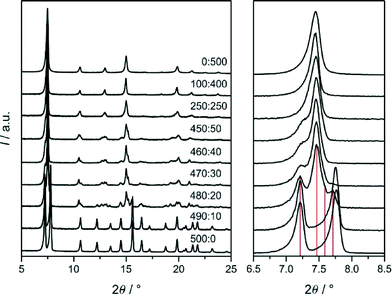
To elucidate more deeply the influence of solvent on the selection of SOD-type 1 and 2 we performed additional syntheses with the same reactant ratios as given above and heating to 120 °C for 24 h in various DMF/THF solvent mixtures. PXRD patterns of the products are displayed in Fig. 9. It can be seen that 1 was obtained in DMF containing only up to very small amounts of THF (DMF/THF ≥ 490![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10). A slightly larger fraction of THF already yielded materials that are characterised by rather complex PXRD patterns demonstrating the great sensitivity of the crystallisation of 1 on the kind of solvent. On the other hand, the formation of 2 was found to be more tolerant to solvent variation, as it was obtained in THF containing larger amounts of DMF (DMF/THF ≤ 250
10). A slightly larger fraction of THF already yielded materials that are characterised by rather complex PXRD patterns demonstrating the great sensitivity of the crystallisation of 1 on the kind of solvent. On the other hand, the formation of 2 was found to be more tolerant to solvent variation, as it was obtained in THF containing larger amounts of DMF (DMF/THF ≤ 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250). The PXRD pattern of the product recovered from the 250
250). The PXRD pattern of the product recovered from the 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 mixture exhibits asymmetric and split reflections identifying this material as a less-symmetric, non-cubic variant of 2 as was already observed recently.6a The PXRD patterns of the 480
250 mixture exhibits asymmetric and split reflections identifying this material as a less-symmetric, non-cubic variant of 2 as was already observed recently.6a The PXRD patterns of the 480![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20- to 450
20- to 450![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50-products might be interpreted as originating from mixtures of trigonal 1 and non-cubic 2. However this idea is not directly confirmed by the SEM images (Fig. 10), which show for each product crystals with rather homogenous size and shape distribution and no indications of any heterogeneity. The crystal sizes increased with increasing DMF content of the synthesis mixture from about 100 nm to 15 μm. Thus there might exist a complete series of structural intermediates of 1 and 2. It was beyond the scope of the present work to elucidate the detailed structures of the intermediate materials that exhibit rather complex PXRD patterns indicative of structures with low symmetry. It is our current hypothesis that the intermediates, as 2, are twinned crystals consisting essentially of domains of III with different degrees of structural deformation and domain sizes and domain interface structures. It should be noted that relative peak intensities and positions in the patterns shown in Fig. 9 may be affected to some extent by the solvent that remained in the pores after the washing and drying procedure, i.e. not fully activated samples were measured.
50-products might be interpreted as originating from mixtures of trigonal 1 and non-cubic 2. However this idea is not directly confirmed by the SEM images (Fig. 10), which show for each product crystals with rather homogenous size and shape distribution and no indications of any heterogeneity. The crystal sizes increased with increasing DMF content of the synthesis mixture from about 100 nm to 15 μm. Thus there might exist a complete series of structural intermediates of 1 and 2. It was beyond the scope of the present work to elucidate the detailed structures of the intermediate materials that exhibit rather complex PXRD patterns indicative of structures with low symmetry. It is our current hypothesis that the intermediates, as 2, are twinned crystals consisting essentially of domains of III with different degrees of structural deformation and domain sizes and domain interface structures. It should be noted that relative peak intensities and positions in the patterns shown in Fig. 9 may be affected to some extent by the solvent that remained in the pores after the washing and drying procedure, i.e. not fully activated samples were measured.
 | ||
| Fig. 10 Typical SEM images of the products obtained in various DMF/THF mixtures with the molar DMF/THF ratios indicated. | ||
The experiments with the DMF/THF mixtures suggest that not only framework topology but also framework conformation, at least to some degree in the case of [Zn(dcim)2]-SOD, are controllable via careful choice of synthesis conditions. The reports by Diring et al. and Bennett et al. are generally in line with our findings as trigonal and cubic [Zn(mnim)2]-SODs were obtained in DMF and 2-PrOH solvents, respectively.30
Gas sorption properties of 1 and 2
Microcrystalline samples of 1 and 2 with typical crystal morphologies as shown by the SEM images in Fig. 4 were subjected to Soxhlet extraction with EtOH and subsequently activated under reduced pressure. The TG traces measured in a flow of air verified the almost complete removal of the solvent (Fig. S14, ESI†). As demonstrated by the Ar adsorption/desorption isotherms displayed in Fig. 11, 1 and 2 exhibit unambiguous differences in their gas sorption properties. The steep uptakes at low relative pressure (p/p0 ≤ 1 × 10−3) seen on the adsorption isotherms confirm the microporosity for both materials, and very similar values for the respective micropore volumes (1: 0.21 cm3 g−1; 2: 0.20 cm3 g−1) and apparent specific BET surface areas (1: 600 m2 g−1; 2: 600 m2 g−1) have been estimated. This is not surprising due to the very similar micropore systems (see structure descriptions above). The experimental micropore volumes are in good agreement with the values (1: 0.19 cm3 g−1; 2: 0.21 cm3 g−1) calculated from estimates of the contact surface (probe radius 1.7 Å) in the crystal structures (1: 27.4%; 2: 30.2%). | ||
| Fig. 11 Ar sorption isotherms of 1 and 2 at −186 °C with adsorption (closed squares) and desorption (open squares) branches. The inset is an expansion of the low pressure region (p/p0 ≤ 0.02). | ||
Importantly, in contrast to 2, the steep uptake in 1 is a two-step process with an inflection point at about three quarters (Vad/STP = 113 cm3 g−1) of the total uptake (Vad/STP = 155 cm3 g−1) at low relative pressure and a small hysteresis between the adsorption and desorption branches above the inflection point. This suggests that small reorientational movements of the linkers occur at the inflection point (p/p0 = 0.014) to enable accommodation of additional Ar atoms, as the two-step isotherm of 1 in this region resembles, for example, the two-step isotherm reported for adsorption of N2 in ZIF-8 that has been unambiguously assigned to a displacive structural transition of the flexible framework.5a,b Our data suggest that a similar Ar-induced transition might occur at cryogenic temperatures, possibly after a prior cooling-induced displacive transition from the well established room-temperature structure of solvent-free 1 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) to a low-temperature form, with or without change of symmetry, as has been recently reported for ZIF-4.5c The sorption behaviour of 1 is expected to differ from that of the extensively investigated isostructural ZIF-7 (ref. 22 and 32) due to its considerably larger pore sizes (smaller dcim linker). On the other hand the different uptake behaviours of 1 and 2 are a clear signature of their different real crystal structures, i.e. ordered versus conformational disordered framework. It is known that real structure phenomena (defects) can have a profound effect on gas sorption behaviour in MOFs.33 This has been demonstrated here for a ZIF material by clearly uncovering the nature of the structural defects (static conformational disorder).9
) to a low-temperature form, with or without change of symmetry, as has been recently reported for ZIF-4.5c The sorption behaviour of 1 is expected to differ from that of the extensively investigated isostructural ZIF-7 (ref. 22 and 32) due to its considerably larger pore sizes (smaller dcim linker). On the other hand the different uptake behaviours of 1 and 2 are a clear signature of their different real crystal structures, i.e. ordered versus conformational disordered framework. It is known that real structure phenomena (defects) can have a profound effect on gas sorption behaviour in MOFs.33 This has been demonstrated here for a ZIF material by clearly uncovering the nature of the structural defects (static conformational disorder).9
At relative pressures above the steep gas uptake, the isotherm of 1 reaches a clear, first plateau while the behaviour of 2 is different. In the latter case a gradual increase of the adsorbed volume up to a total pore volume of 0.27 cm3 g−1 (taken at p/p0 = 0.95) is observed in this case with a broad hysteresis loop seen between 0.4 < p/p0 < 0.8. This suggests the presence of mesopores with a broad size distribution as internal volume defects and is in line with the comparatively poor crystallinity of the disordered material. Interestingly in the adsorption isotherm of 1 at large relative pressure (p/p0 > 0.7), a second, comparatively sharp step is seen with a type H1 or H2 hysteresis loop34 and a clear, second plateau. This step would usually be assigned to the presence of mesopores that have a relatively narrow size distribution being centered, in this case, at about 6 nm as estimated by the BJH method (Fig. S15, ESI†). The total pore volume corresponds to 0.26 cm3 g−1. However, the presence of such mesopores in a material with an apparent high crystallinity and structural order is a somewhat surprising finding and the origin of the second step is not completely understood yet.
Stepped uptakes are not seen in the low-pressure CO2 adsorption/desorption isotherms of 1 and 2 at 0 °C (Fig. S16, ESI†).
Conclusions
By theory and experiment we have demonstrated that Zn-based ZIFs with SOD topology made from 4,5-disubstituted linkers may be prone to static conformational variety enabling different ordered and/or disordered framework structures having distinctly different linker orientations and small energy differences. On the other hand such conformational variety cannot exist in SOD-type ZIFs containing 2-substituted imidazolate linkers. The latter can adopt only one (II) out of three principal framework conformations (I–III) due to steric hindrance between the substituents in the four-membered rings of the frameworks (I, III). Static conformational variety has to be distinguished from dynamic linker reorientations observed in the course of stimuli-responsive displacive structural transitions in flexible ZIF frameworks. We have further demonstrated experimentally that static linker orientations in SOD-type ZIFs are at least to some degree controllable via careful choice of synthesis conditions and that they can affect framework flexibility and gas sorption properties. We propose that the prediction of hypothetical and potentially synthetically accessible ZIF structures should consider in the future not only topology, solvent and temperature, as has already been successfully done,17,18,35 but in addition framework conformation.8,36The three so far experimentally realised topological [Zn(dcim)2] polymorphs with ordered frameworks (RHO, SOD, lcs) are amongst the most stable predicted phases in the [Zn(dcim)2] system.
Acknowledgements
The authors are grateful to Jann Lippke, Alexander Mohmeyer and Nadeschda Schmidt for performing gas sorption experiments, Bastian Hoppe for taking SEM images and to Dr. Jörg Fohrer for collecting liquid-state NMR spectra. We thank ZIH, Dresden, for allocation of computational resources. Financial support by the German Research Foundation (DFG) within the framework of the Priority Program 1415 (Crystalline Non-equilibrium Phases) is gratefully acknowledged.Notes and references
- (a) H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed; (b) G. Férey, Chem. Soc. Rev., 2008, 37, 191 RSC.
- (a) A. Phan, C. J. Doonan, F. J. Uribe-Romo, C. B. Knobler, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2010, 43, 58 CrossRef CAS PubMed; (b) J.-P. Zhang, Y.-B. Zhang, J.-B. Lin and X.-M. Chen, Chem. Rev., 2012, 112, 1001 CrossRef CAS PubMed.
- (a) N. T. T. Nguyen, H. Furukawa, F. Gándara, H. T. Nguyen, K. E. Cordova and O. M. Yaghi, Angew. Chem., Int. Ed., 2014, 53, 10645 CrossRef CAS PubMed; (b) C. Mottillo and T. Friscic, Angew. Chem., Int. Ed., 2014, 53, 7471 CrossRef CAS PubMed; (c) B. P. Biswal, T. Panda and R. Banerjee, Chem. Commun., 2012, 48, 11868 RSC.
- N. C. Burtch, H. Jasuja and K. S. Walton, Chem. Rev., 2014, 114, 10575 CrossRef CAS PubMed.
- (a) D. Fairen-Jimenez, S. A. Moggach, M. T. Wharmby, P. A. Wright, S. Parsons and T. Düren, J. Am. Chem. Soc., 2011, 133, 8900 CrossRef CAS PubMed; (b) J.-P. Zhang, A.-X. Zhu and X.-M. Chen, Chem. Commun., 2012, 48, 11395 RSC; (c) M. T. Wharmby, S. Henke, T. D. Bennett, S. R. Bajpe, I. Schwedler, S. P. Thompson, F. Gozzo, P. Simoncic, C. Mellot-Draznieks, H. Tao, Y. Yue and A. K. Cheetham, Angew. Chem., Int. Ed., 2015, 54, 6447 CrossRef CAS PubMed; (d) S. A. Moggach, T. D. Bennett and A. K. Cheetham, Angew. Chem., Int. Ed., 2009, 48, 7087 CrossRef CAS PubMed.
- (a) M. E. Schweinefuß, S. Springer, I. A. Baburin, T. Hikov, K. Huber, S. Leoni and M. Wiebcke, Dalton Trans., 2014, 43, 3528 RSC; (b) C. A. Schröder, S. Saha, K. Huber, S. Leoni and M. Wiebcke, Z. Kristallogr., 2014, 229, 807 Search PubMed; (c) S. Saha, S. Springer, M. E. Schweinefuß, D. Pontoni, M. Wiebcke and K. Huber, Cryst. Growth Des., 2015 DOI:10.1021/acs.cgd.5b01594.
- R. Banerjee, A. Phan, B. Wang, C. Knobler, H. Furukawa, M. O'Keeffe and O. M. Yaghi, Science, 2008, 319, 939 CrossRef CAS PubMed.
- I. A. Baburin and S. Leoni, CrystEngComm, 2010, 12, 2809 RSC.
- (a) D. S. Sholl and R. P. Lively, J. Phys. Chem. Lett., 2015, 6, 3437 CrossRef CAS PubMed; (b) V. I. Hegde, J.-C. Tan, U. V. Waghmare and A. K. Cheetham, J. Phys. Chem. Lett., 2013, 4, 3377 CrossRef CAS PubMed; (c) C. Zhang, C. Han, D. S. Sholl and J. R. Schmidt, J. Phys. Chem. Lett., 2016, 7, 459 CrossRef CAS PubMed; (d) P. Cheng and Y. H. Hu, J. Phys. Chem. C, 2014, 118, 21866 CrossRef CAS.
- R. Sabatini, T. Gorni and S. de Gironcoli, Phys. Rev. B: Condens. Matter, 2013, 87, 041108 CrossRef.
- http://www.quantum-espresso.org.
- Y.-S. Bae, O. R. Yazaydin and R. Q. Snurr, Langmuir, 2010, 26, 5475 CrossRef CAS PubMed.
- TOPAS, Bruker AXS GmbH, Karlsruhe, Germany, 2009 Search PubMed.
- Materials Studio Forcite 8.0, BIOVIA, San Diego, CA, 2015 Search PubMed.
- C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466 CrossRef CAS.
- (a) X.-C. Huang, J.-P. Zhang and X.-M. Chen, Chin. Sci. Bull., 2003, 48, 1531 CrossRef CAS; (b) K. S. Park, Z. Ni, A. P. Côté, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 27, 10186 CrossRef PubMed.
- (a) I. A. Baburin, S. Leoni and G. Seifert, J. Phys. Chem. B, 2008, 112, 9437 CrossRef CAS PubMed; (b) I. A. Baburin and S. Leoni, J. Mater. Chem., 2012, 22, 10152 RSC.
- (a) R. Galvelis, B. Slater, A. K. Cheetham and C. Mellot-Draznieks, CrystEngComm, 2012, 14, 374 RSC; (b) R. Galvelis, B. Slater, R. Chaudret, B. Creton, C. Nieto-Draghi and C. Mellot-Draznieks, CrystEngComm, 2013, 15, 9603 RSC.
- J. T. Hughes, T. D. Bennett, A. K. Cheetham and A. Navrotsky, J. Am. Chem. Soc., 2013, 135, 598 CrossRef CAS PubMed.
- In Fig. 12 of ref. 6a we unfortunately reported an erroneous relative energy for RHO-type ZIF-71.
- W. Depmeier, Rev. Mineral. Geochem., 2005, 57, 203 CrossRef CAS.
- (a) P. Zhao, G. I. Lampronti, G. O. Lloyd, M. T. Wharmby, S. Facq, A. K. Cheetham and S. Redfern, Chem. Mater., 2014, 26, 1767 CrossRef CAS PubMed; (b) Y. Du, B. Wooler, M. Nines, P. Kortunov, C. S. Pauer, J. Zengel, S. C. Weston and P. I. Ravikovitch, J. Am. Chem. Soc., 2015, 137, 13603 CrossRef CAS PubMed.
- (a) K. Knorr, C. M. Braunbarth, G. van der Goor, P. Behrens, C. Griewatsch and W. Depmeier, Solid State Commun., 2000, 503, 114–117 Search PubMed; (b) R. S. P. King, S. E. Dann, M. R. J. Elsegood, P. F. Kelly and R. J. Mortimer, Chem. – Eur. J., 2009, 15, 5441 CrossRef CAS PubMed.
- M. R. Ryder, B. Civalleri, T. D. Bennett, S. Henke, S. Dudić, G. Cinque, F. Fernandez-Alonso and J.-C. Tan, Phys. Rev. Lett., 2014, 113, 215502 CrossRef PubMed.
- A.-X. Zhu, R.-B. Lin, X.-L. Qi, Y. Liu, Y.-Y. Lin, J.-P. Zhang and X.-M. Chen, Microporous Mesoporous Mater., 2012, 157, 42 CrossRef CAS.
- J. Cravillon, R. Nayuk, S. Springer, A. Feldhoff, K. Huber and M. Wiebcke, Chem. Mater., 2011, 23, 2130 CrossRef CAS.
- J. Cravillon, C. A. Schröder, H. Bux, A. Rothkirch, J. Caro and M. Wiebcke, CrystEngComm, 2012, 14, 492 RSC.
- S. Springer, A. Satalov, J. Lippke and M. Wiebcke, Microporous Mesoporous Mater., 2015, 216, 161 CrossRef CAS.
- Th. Hahn and H. Klapper, International Tables for Crystallogr., Vol. D, 2006, p. 393 Search PubMed.
- (a) S. Diring, D. O. Wang, C. Kim, M. Kondo, Y. Chen, S. Kitagawa, K. Kamei and S. Furukawa, Nat. Commun., 2013, 4, 2684 Search PubMed; (b) T. D. Bennett, P. J. Saines, D. A. Keen, J.-C. Tan and A. K. Cheetham, Chem. – Eur. J., 2013, 19, 7049 CrossRef CAS PubMed.
- (a) Y.-Q. Tian, Y.-M. Zhao, Z.-X. Chen, G.-N. Zhang, L.-H. Weng and D.-Y. Zhao, Chem. – Eur. J., 2007, 13, 4146 CrossRef CAS PubMed; (b) B. P. Biswal, T. Pande and R. Banerjee, Chem. Commun., 2012, 48, 11868 RSC; (c) M. He, J. Yao, Q. Liu, Z. Zhong and H. Wang, Dalton Trans., 2013, 42, 16608 RSC; (d) C.-T. He, L. Jiang, Z.-M. Ye, R. Krishna, Z.-S. Zhong, P.-Q. Liao, J. Xu, G. Ouyang, J.-P. Zhang and X.-M. Chen, J. Am. Chem. Soc., 2015, 137, 7217 CrossRef CAS PubMed.
- (a) S. Aguado, G. Bergeret, M. P. Titus, V. Moizan, C. Nieto-Draghi, N. Bats and D. Farrusseng, New J. Chem., 2011, 35, 546 RSC; (b) J. van den Bergh, C. Gücüyener, E. A. Pidko, E. J. M. Hensen, J. Gascon and F. Kapteijn, Chem. – Eur. J., 2011, 17, 8832 CrossRef CAS PubMed; (c) W. Cai, T. Lee, M. Lee, W. Cho, D.-Y. Han, N. Choi, A. C. K. Yip and J. Choi, J. Am. Chem. Soc., 2014, 136, 7961 CrossRef CAS PubMed; (d) P. Zhao, G. I. Lampronti, G. O. Lloyd, E. Suard and S. A. Redfern, J. Mater. Chem. A, 2014, 2, 620 RSC.
- Z. Fang, B. Bueken, D. E. de Vos and R. A. Fischer, Angew. Chem., Int. Ed., 2015, 54, 7234 CrossRef CAS PubMed.
- K. S. W. Sing, D. H. Everett, R. A. W. Haul, L. Moscou, R. A. Pierotti, J. Rouquerol and T. Siemieniewska, Pure Appl. Chem., 1985, 57, 603 CrossRef CAS.
- (a) J. A. Gee and D. S. Sholl, J. Phys. Chem. C, 2013, 117, 20636 CrossRef CAS; (b) L. B. du Bourg, A. U. Ortiz, A. Boutin and F.-X. Courdert, APL Mater., 2014, 2, 124110 CrossRef.
- (a) S. Amirjalayer and R. Schmid, J. Phys. Chem. C, 2008, 112, 14980 CrossRef CAS; (b) S. Bureekaew, V. Balwani, S. Amirjalayer and R. Schmid, CrystEngComm, 2015, 17, 344 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Tables of crystal and structural data obtained by DFT and X-ray structure analyses, structural drawings, Rietveld plots, PXRD patterns, NMR spectra, TG traces, and gas sorption isotherms. See DOI: 10.1039/c6ce00312e |
| This journal is © The Royal Society of Chemistry 2016 |