A crystal structure prediction enigma solved: the gallic acid monohydrate system – surprises at 10 K

Abstract

The seemingly unpredictable structure of gallic acid monohydrate form IV has been investigated using accurate X-ray diffraction measurements at temperatures of 10 and 123 K. The measurements demonstrate that the structure is commensurately modulated at 10 K and disordered at higher temperatures. Aided by charge-density modeling and periodic DFT calculations we show that the disorder gives a substantial stabilization of the structure.

---

Crystal structure prediction of small organic molecular systems has become very successful over the last decade^1–4 mainly due to advances in the theoretical methods,² such as the use of tailor-made force-fields and periodic DFT calculations.⁵ This success has important implications for understanding and controlling the organic solid state – and thereby the design and production of many materials, such as drugs, foods and explosives.

However, one system has been shown to be unpredictable in the crystal structure prediction blind tests, namely the polymorphs of gallic acid monohydrate (GAM, Fig. 1). A polymorph of GAM^6,7 was the target of structure prediction in the fifth blind test¹ (CSP target XXI, CSD reference codes KONTIQ03⁷ and KONTIQ05⁶), yet it was the only system that could not be predicted within the three most likely structures by any of the fourteen participating research groups.¹ Subsequent thorough experimental screening for polymorphs revealed a fifth polymorph and a wealth of solvates,⁸ yet it did not resolve the enigma: the system consists of rigid molecules of light elements, and therefore normally falls within the range of systems that should be easy to predict by contemporary methods. However, this is a two-component system, which is still considered challenging.

Fig. 1 Gallic acid monohydrate.

Is GAM unpredictable because the crystal energy is not determined with sufficient accuracy, as claimed in a recent work⁹ on benzene polymorphs? Are hydrates and other co-crystals too complicated for contemporary crystal structure prediction methods?¹⁰ Are the structures not the thermodynamically most stable forms, but simply the kinetically most favored?¹¹ To answer such questions we have carefully considered the experimental evidence for the reported polymorphic structures.

One major problem in crystal structure prediction in general – and for GAM in particular – is that the results are compared with room temperature single crystal X-ray diffraction data.¹§ Certainly, the ability to predict crystal forms under ambient conditions is important, yet contemporary methods for crystal structure prediction rely on the assessment of the most thermodynamically stable structure in terms of the structure with the lowest potential energy (a few exceptions exist, see e.g. the fourth³ and sixth¹² blind tests).

This means that little, if any, concern is taken to include thermal effects, such as vibrational enthalpy and entropy, which is necessary to obtain the true thermodynamic stability, given by the Gibbs free energy, G = H-TS.

Moreover, as we demonstrate in the present work, room temperature structures may mask important information regarding alternative molecular conformations in the crystal.

Therefore, because the results of CSP are neglecting thermal motion and disorder, they should be compared with accurate structures from low-temperature measurements.¹³ Subsequently, high temperature structures should be used in comparison with CSP methods that take entropy into account.

To shed light on the enigmatic GAM system, we have investigated the CSP blind-test target GAM XXI using accurate single-crystal X-ray diffraction measurements at temperatures of 10 and 123 K.

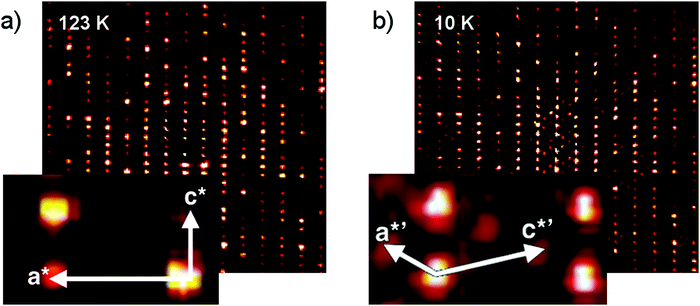
Surprisingly, and in contrast to our measurements at room temperature and 123 K, which confirmed the unit cell dimensions found in previous works,^6–8 a supercell with three formula units in the asymmetric unit (Z′ = 3) was observed at 10 K. Crystallographic and experimental details are presented in Table S1 in the ESI.†

To understand how this structure is related to the high-temperature phase, layers of the reciprocal lattice were reconstructed based on the full data collections. The h1l planes of the 10 K and 123 K data are compared in Fig. 2a and b. Furthermore, additional peaks larger than two standard uncertainties were harvested in the 10 K diffraction images and visualized in a coordinate system corresponding to the Z′ = 1 reciprocal cell. A plot showing these harvested spots is given in the ESI.† Both types of plots clearly indicate that a larger unit cell is present; however, the additional Bragg peaks are weak, indicating that the 10 K structure is a modulation of the high-temperature structure.

Fig. 2 (a and b) Reciprocal layers h1l of GAM form IV at 10 K and at 123 K. The naming of layers corresponds to the Z′ = 1 unit cell. The size and direction of the reciprocal unit cell vectors are shown as an inset.

Indeed, the Z′ = 3 structure can be approximated by the Z′ = 1 structure using the reciprocal space transformation matrix [1/3, 0, 1/3, 0, 1, 0, −2/3, 0, 1/3].¹⁴ The additional peaks can be understood as a commensurate displacive modulation of the high-temperature phase.

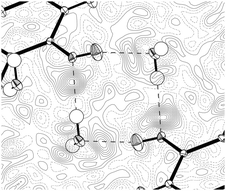
It is possible to refine a Z′ = 1 basic structure against the 10 K data, at the expense of omitting the satellite reflections corresponding to the larger cell. The final agreement with the experimental data is quite similar for the Z′ = 3 and Z′ = 1 models; however, there are larger peaks in the residual density of the Z′ = 1 structure indicating a substantial amount of disorder (see Fig. 3).

The changes in the diffraction signal as a function of temperature indicate a phase transformation. Should the structures observed at 123 K and 10 K be considered different phases? It is evident that the diffraction pattern observed at 10 K indicates a structural correlation – a modulation – that is not present at 123 K. The peak profile of the satellite reflections is similar to the profile of the main reflections. This indicates that the peaks correspond to long-range ordering, and that the structure is a new phase, although closely related to the high-temperature phase.

However, upon close inspection of the residual density after an aspherical atom model refinement against the high-resolution 123 K data, the residual density shows signs of disorder. We tested whether a model including anharmonic motion could describe these features, but this was not possible. Rather, these features correspond to the observed differences in positions and torsional angles between the three symmetry-independent molecules (Fig. 3b, 5 and 6) observed at 10 K. This suggests that the molecules at 123 K are distributed stochastically between the three positions observed at 10 K. As the temperature is reduced, the differences in intermolecular interactions among the molecules become significant compared to the thermal energy, and we observe a packing correlation of molecules in the different positions and conformations.

Fig. 3 The residual density of the Z′ = 1 (a) and Z′ = 3 (b) models for the 10 K data (contour level −0.7 e Å⁻³, green surfaces are positive contours, and brown surfaces are negative).

Apart from this displacive modulation, the low-temperature experiments also reveal new information regarding the positions of hydrogen atoms in the structure.

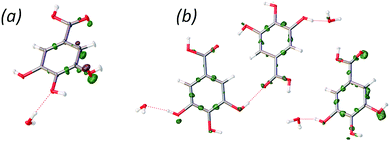
The correct positions of the hydrogen atoms in GAM were difficult to predict in the CSP blind test, because several alternative hydrogen bond patterns could be proposed for the same overall structure: a ring of hydrogen bonds between two gallic acid molecules and two water molecules can be reversed (see Fig. 4). Our single crystal X-ray diffraction measurements at 10 K and 123 K exhibit maxima of residual density between the oxygen atoms from the p-hydroxyl group and the hydrogen atoms from a distance different from what can be expected for lone-pair densities of the oxygen atoms. This indicates the presence of static disorder corresponding to two different orientations of the hydrogen atoms. This alternative orientation appears to be present in roughly 20 percent of the crystal, as indicated by refinement of the occupation of the alternative H positions (see Fig. 4).

Fig. 4 The residual density (10 K data) in the plane of the intermolecular hydrogen bond network involving water. The contour map was drawn using contouring levels of 0.07 e Å⁻³. The peaks between hydroxyl oxygen and water have maxima of 0.42 e Å⁻³, at a distance of 0.732 Å from oxygen.

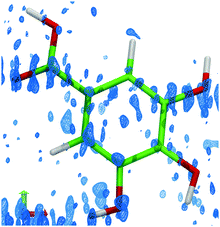Fig. 5 The residual density (isosurface level 0.2 e Å⁻³), showing the differences in electron density based on the observed data and a refined model using aspherical atomic scattering factors.^21,22 Residual density corresponding to the alternative molecular conformations is clearly visible near the carboxyl oxygen atom and on the hydroxyl groups at meta positions.

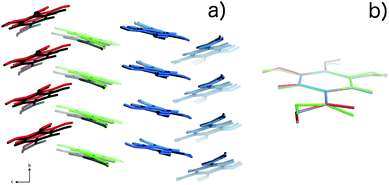Fig. 6 (a) Packing of the three molecules in the Z′ = 3 structure for 10 K data, (colored red, green and blue) compared with the packing in the Z′ = 1 structure (colored black). (b) Overlay of structures¹⁴ corresponding to the three independent molecules in the Z′ = 3 model. The packing similarity is further discussed in the ESI.†

What are the implications of these structural features for the prediction of the GAM system?

To investigate whether the Z′ = 3 structure would change the ranking of structures, we computed the energy difference between the structures with Z′ = 1 and Z′ = 3. Periodic dispersion corrected DFT calculations of the computed total electronic ab initio energy and cohesive energy¹⁵ (electronic energy difference between the crystal and the isolated molecule in the crystal conformation) reveal that the Z′ = 3 structure is more stable in terms of both total electronic and cohesive energies. As expected the differences are very small: the total energy difference is 0.6 kJ mol⁻¹ per molecule, whereas for the cohesive energy it is 0.3 kJ mol⁻¹ per molecule. The stabilization is thus both a consequence of packing and conformational relaxation. Such energy differences can change the ranking of structures after CSP. Additionally, differences in the vibrational entropy may give a contribution to the thermodynamic stabilization.^16–20 To shed further light on the stability of the Z′ = 3 structure, we performed a full geometry-optimization of coordinates and cell parameters, starting from the Z′ = 3 structure as well as from the Z′ = 1 structure in the supercell corresponding to Z′ = 3. In both cases we obtained a structure closely resembling the Z′ = 3 structure. This result confirms the Z′ = 3 structure, and indicates that this structure can be predicted, if present CSP methods were adapted to look for all local energy minima.

However, at high temperatures the structure is not modulated, and it is therefore of relevance in the present context to consider the entropy due to the disorder of the hydrogen bond pattern and to the modulation observed at 10 K, which appears as disorder at 123 K. An estimate of these contributions can be obtained by calculating the entropy of mixing.

Considering the disorder related to the modulation, the 10 K structure suggests three local minima on the potential energy surface, which at higher temperatures can be populated by the gallic acid molecules. We make the assumption of three minima based on the fact that we have three independent molecules in the 10 K structure, and that at higher temperatures, disorder is present at the corresponding positions in the Z′ = 1 structure. Further computational work to test this hypothesis is needed.

Assuming an equal and random distribution among these sites gives an entropic contribution of 9.1 J mol⁻¹ K⁻¹ – a huge difference in entropy, which corresponds to a stabilization of 2.7 kJ mol⁻¹ at room temperature. This must be considered an upper bound of the entropy of mixing: although the residual density indicates disorder, it is hardly corresponding to an equal distribution among the three sites. To obtain an estimate of the distribution, we performed a constrained refinement of three partly overlapping structures stemming from the Z′ = 3 geometry. For each structure an overall occupancy was refined, and contributions of 20, 42 and 38 percent, respectively, were observed. Based on these occupancies, the entropy of mixing is 8.8 J mol⁻¹ K⁻¹, or a stabilizing factor of 2.6 kJ mol⁻¹ at room temperature.

Similar considerations can be applied to the entropy of the disorder associated with the hydrogen bond patterns. A random 20 : 80 percent distribution gives an entropic stabilization of 4 J mol⁻¹ K⁻¹, corresponding to 1.2 kJ mol⁻¹ at room temperature.

In conclusion, by using accurate X-ray diffraction measurements at very low temperatures we have demonstrated that the CSP target structure of GAM is in fact a very complex system. At 10 K, the structure is commensurately modulated with respect to the room temperature one.

Even using this model there is still disorder, which is not described. At higher temperatures, the modulation is no longer present, but the variable molecular positions and molecular geometry are retained to some extent, giving rise to a disorder, as evidenced by the residual density. Of further interest is the clear demonstration that some H atoms are disordered over two sites, giving rise to two different hydrogen bond patterns.

The disorder present at 123 K gives rise to a considerable entropic stabilization of the structure – corresponding to more than 3 kJ mol⁻¹ at room temperature. This large stabilization, which is not considered by current crystal structure prediction methods, is sufficient to alter the energy landscape significantly, and may allude to the difficulties associated with predicting polymorph IV as a stable structure.

We hope that these results will open the eyes of the crystallography community to the – in our opinion – absolute necessity of using very accurate structures, collected at the lowest possible temperature for the understanding of complex phenomena in molecular crystalline solids – such as the development of CSP methods. Such accurate structures provide the best possible platform for the assessment of crystal energies. Only then may the incorporation of thermal effects, such as enthalpies and entropies of vibration – subsequently – provide sufficient information to predict the structures and properties at ambient temperature. It is not worthwhile predicting ghost structures!

We acknowledge the Villum foundation and the Carlsberg foundation for financial support. Calculations were carried out using resources provided by the Wrocław Centre for Networking and Supercomputing (Grant 115).

Notes and references

1. D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. M. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. Della Valle, G. R. Desiraju, B. P. van Eijck, J. C. Facelli, M. B. Ferraro, D. Grillo, M. Habgood, D. W. M. Hofmann, F. Hofmann, K. V. J. Jose, P. G. Karamertzanis, A. V. Kazantsev, J. Kendrick, L. N. Kuleshova, F. J. J. Leusen, A. V. Maleev, A. J. Misquitta, S. Mohamed, R. J. Needs, M. A. Neumann, D. Nikylov, A. M. Orendt, R. Pal, C. C. Pantelides, C. J. Pickard, L. S. Price, S. L. Price, H. A. Scheraga, J. van de Streek, T. S. Thakur, S. Tiwari, E. Venuti and I. K. Zhitkov, Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 535–551.
2. M. A. Neumann, F. J. J. Leusen and J. Kendrick, Angew. Chem., Int. Ed., 2008, 47, 2427–2430.
3. G. M. Day, T. G. Cooper, A. J. Cruz-Cabeza, K. E. Hejczyk, H. L. Ammon, S. X. M. Boerrigter, J. S. Tan, R. G. Della Valle, E. Venuti, J. Jose, S. R. Gadre, G. R. Desiraju, T. S. Thakur, B. P. van Eijck, J. C. Facelli, V. E. Bazterra, M. B. Ferraro, D. W. M. Hofmann, M. A. Neumann, F. J. J. Leusen, J. Kendrick, S. L. Price, A. J. Misquitta, P. G. Karamertzanis, G. W. A. Welch, H. A. Scheraga, Y. A. Arnautova, M. U. Schmidt, J. van de Streek, A. K. Wolf and B. Schweizer, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 107–125.
4. S. L. Price, Phys. Chem. Chem. Phys., 2008, 10, 1996.
5. E. Gibney, Nature, 2015, 527, 20–21.
6. H. D. Clarke, K. K. Arora, Ł. Wojtas and M. J. Zaworotko, Cryst. Growth Des., 2011, 11, 964–966.
7. G. Demirtaş, N. Dege and O. Büyükgüngör, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2011, 67, o1509–o1510.
8. D. E. Braun, R. M. Bhardwaj, A. J. Florence, D. A. Tocher and S. L. Price, Cryst. Growth Des., 2013, 13, 19–23.
9. J. Yang, W. Hu, D. Usvyat, D. Matthews, M. Schütz and G. K.-L. Chan, Science, 2014, 345, 640–643.
10. H. D. Clarke, K. K. Arora, H. Bass, P. Kavuru, T. T. Ong, T. Pujari, L. Wojtas and M. J. Zaworotko, Cryst. Growth Des., 2010, 10, 2152–2167.
11. J. Kendrick, F. J. J. Leusen, M. A. Neumann and J. van de Streek, Chem. – Eur. J., 2011, 17, 10736–10744.
12. A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. DiStasio Jr, A. Dzyabchenko, B. P. van Eijck, D. M. Elking, J. A. van den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C.-A. Gatsiou, T. S. Gee, R. de Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. M. Hofmann, J. Hoja, R. K. Hylton, L. Iuzzolino, W. Jankiewicz, D. T. de Jong, J. Kendrick, N. J. J. de Klerk, H.-Y. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. L. Price, A. Pulido, M. G. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, A. Vazquez-Mayagoitia, L. Vogt, Y. Wang, R. E. Watson, G. A. de Wijs, J. Yang, Q. Zhu and C. R. Groom, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439–459.
13. N. Wahlberg, P. Ciochoń, V. Petriĉek and A. Ø. Madsen, Cryst. Growth Des., 2014, 14, 381–388.
14. A. L. Spek, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, 46, 34.
15. B. Civalleri, C. M. Zicovich-Wilson, L. Valenzano and P. Ugliengo, CrystEngComm, 2008, 10, 405–410.
16. A. Gavezzotti, CrystEngComm, 2002, 4, 343.
17. J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154–5165.
18. A. Ø. Madsen and S. Larsen, Angew. Chem., Int. Ed., 2007, 46, 8609–8613.
19. A. Ø. Madsen, R. Mattson and S. Larsen, J. Phys. Chem. A, 2011, 115, 7794–7804.
20. T. Aree, H.-B. Bürgi, D. Chernyshov and K. W. Törnroos, J. Phys. Chem. A, 2014, 118, 9951–9959.
21. R. F. Stewart, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 565–574.
22. N. K. Hansen and P. Coppens, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1978, 34, 909–921.

---

Footnotes

† Electronic supplementary information (ESI) available: Description of crystallographic experiments, data treatment and modelling, as well as details of the ab initio calculations are provided. CCDC 1454062–1454064. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6cc06799a

‡ A. A. H and I. S. contributed equally to this work.

§ The structure used for the CSP blind test is reported (ref. 1) to be collected at 100 K. We believe this is a typo, since the related submission in the CSD (ref. 6) reports room temperature measurements, and the volume is similar to the other room temperature structure found in the literature (ref. 7).

---