Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Anion size control of the packing in the metallic versus semiconducting chiral radical cation salts (DM-EDT-TTF)2XF6 (X = P, As, Sb)†
Flavia
Pop
a,
Pascale
Auban-Senzier
b,
Enric
Canadell
c and
Narcis
Avarvari
*a
aUniversité d'Angers, CNRS, Laboratoire MOLTECH-Anjou, UMR 6200, UFR Sciences, Bât. K, 2 Bd. Lavoisier, 49045 Angers, France. E-mail: narcis.avarvari@univ-angers.fr
bLaboratoire de Physique des Solides, Université Paris-Sud, UMR 8502, Bât. 510, 91405 Orsay, France
cInstitut de Ciència de Materials de Barcelona (CSIC), Campus de la UAB, E-08193 Bellaterra, Spain
First published on 27th September 2016
Abstract
Control of the structural type in metallic enantiopure and racemic radical cation salts is achieved through hydrogen bonding interactions between the chiral donor DM-EDT-TTF and the XF6 anions (X = P, As, Sb), determined by the anion size and the chiral information.
Chiral tetrathiafulvalenes (TTF) have attracted much attention especially in the last decade,1 as they can provide chiral crystalline molecular conductors which, among other interesting features, should in principle show electrical magneto-chiral anisotropy (eMChA), recently observed for the first time in TTF based materials.2 The corresponding enantiomeric conductors (DM-EDT-TTF)2ClO4 have been obtained by electrocrystallization of either (S,S) and (R,R) dimethyl-ethylenedithio-tetrathiafulvalene (DM-EDT-TTF) (Scheme 1). Here the chirality conferred by the two stereogenic carbon atoms has been transferred at the microscopic scale providing enantiomorphic crystals.
While chirality in TTF precursors has been introduced through various functions such as stereogenic carbon atoms,1,3–6 sulfoxides,7 allenes,8 binapththyls,9 helicenes,10para-cyclophanes,11 and even expressed at supramolecular level in helical aggregates,12 examples of conducting chiral radical cation salts are still rare comparatively. Beside the ones derived from DM-EDT-TTF,2 they include those prepared out of dimethylated (DM-BEDT-TTF)13 and tetramethylated bis(ethylenedithio)-tetrathiafulvalene (TM-BEDT-TTF),14 the last donor representing the first reported enantiopure TTF derivative.15 Besides the manifestation of eMChA, which is a synergistic effect of the chirality on the resistivity of chiral conductors measured in a magnetic field collinear with the current,16 the conductivity of enantiopure conductors can be higher than that of the racemic counterparts when structural disorder is present in the latter despite identical cell parameters and donor anion ratio. Such differences have been observed in enantiomeric and racemic radical cation salts based either on TTF-oxazolines17 or TM-BEDT-TTF.18 However, in the absence of crystalline disorder the conducting properties of the enantiopure and racemic forms were found to be similar.14b,19 Less often is the case where enantiopure and racemic salts prepared from the same donor in the same conditions show completely different packings. In this respect we have recently described the complete series of radical cation salts (DM-EDT-TTF)2PF6 for which the enantiopure compounds crystallized in the monoclinic space group P21 with four independent donor molecules and two anions in the unit cell, while the racemic salt crystallized in the triclinic centrosymmetric space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with one independent donor in the asymmetric unit and the anion located on an inversion centre.20 An interesting feature of these salts concerns the templating role of the PF6− anion through the establishment of C–H⋯F hydrogen bonding, leading to packings where donor layers are interconnected via the anions, all the fluorine atoms being involved in hydrogen bonding with either vinyl C
with one independent donor in the asymmetric unit and the anion located on an inversion centre.20 An interesting feature of these salts concerns the templating role of the PF6− anion through the establishment of C–H⋯F hydrogen bonding, leading to packings where donor layers are interconnected via the anions, all the fluorine atoms being involved in hydrogen bonding with either vinyl C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH, methyne CHMe or methyl protons. The final architectures very likely result from a delicate balance between these anion–donor hydrogen bonding and van der Waals S⋯S and orbital overlap interactions typical for oxidized TTF donors. We hypothesize that the massive difference in packing, and subsequently in transport properties, between the racemic and enantiopure salts finds its origin in this competition of intermolecular interactions. Thus, the use of the bigger congeners AsF6− and SbF6− could possibly influence on the stability of one or the other phase, i.e. monoclinic or triclinic, or maybe lead to completely new packings. Although generally for a given TTF type donor isostructural radical cation salts are observed within the series PF6, AsF6, SbF6,14b,21 there are only few cases,22,23 to the best of our knowledge, where structural differences occur, including the (EDT-TTF)2XF6 (X = P, As) salts, where the one with PF6 crystallized in an orthorhombic phase, while for the AsF6 salt a second triclinic phase was observed.22 We describe herein complete series of chiral radical cation salts of DM-EDT-TTF 1 with AsF6− and SbF6− anions and compare their structural features and conducting properties with the previously reported PF6 counterparts.
CH, methyne CHMe or methyl protons. The final architectures very likely result from a delicate balance between these anion–donor hydrogen bonding and van der Waals S⋯S and orbital overlap interactions typical for oxidized TTF donors. We hypothesize that the massive difference in packing, and subsequently in transport properties, between the racemic and enantiopure salts finds its origin in this competition of intermolecular interactions. Thus, the use of the bigger congeners AsF6− and SbF6− could possibly influence on the stability of one or the other phase, i.e. monoclinic or triclinic, or maybe lead to completely new packings. Although generally for a given TTF type donor isostructural radical cation salts are observed within the series PF6, AsF6, SbF6,14b,21 there are only few cases,22,23 to the best of our knowledge, where structural differences occur, including the (EDT-TTF)2XF6 (X = P, As) salts, where the one with PF6 crystallized in an orthorhombic phase, while for the AsF6 salt a second triclinic phase was observed.22 We describe herein complete series of chiral radical cation salts of DM-EDT-TTF 1 with AsF6− and SbF6− anions and compare their structural features and conducting properties with the previously reported PF6 counterparts.
Enantiopure and racemic donor 1, prepared as previously described,20 have been electrocrystallized in chloroform in the presence of [(n-Bu)4N]XF6 (X = As, Sb), the experimental conditions being identical in all the experiments with those employed for the PF6 series.20 Unexpectedly, while for the SbF6− anion only one crystalline phase has been obtained either for the enantiopure or the racemic donor, in the electrocrystallization cells with the AsF6− anion three types of crystals have been collected for enantiopure 1 and only one type when racemic 1 was used. The racemic AsF6 and SbF6 crystalline compounds are formulated as [(rac)-1]2XF6 (X = As, Sb) and are isostructural with the previous described PF6 metallic salt.20 They crystallize in the triclinic centrosymmetric space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with one independent donor molecule and half of anion, located on an inversion centre, in the asymmetric unit (see ESI† for details on single crystal X-ray measurements and Table S1 for crystal parameters). The central C
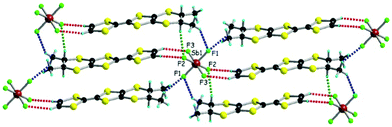
with one independent donor molecule and half of anion, located on an inversion centre, in the asymmetric unit (see ESI† for details on single crystal X-ray measurements and Table S1 for crystal parameters). The central C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths (1.371(6) Å and 1.369(5) Å for As and Sb, respectively) together with the internal C–S bond lengths, with an average value of 1.738 Å for both compounds, are in agreement with a +0.5 oxidation state of the donor and are comparable with the values measured for the PF6 salt (Table S2, ESI†). The paramount role of the anion in the solid state architecture is evidenced through the complex set of hydrogen bonding interactions established between the fluorine atoms and CHvinyl, CH3 and CHMe hydrogen atoms24 leading to a packing where the anions are surrounded by donors, all the F atoms being involved in such short C–H⋯F contacts (Fig. 1 for SbF6, Fig. S1 and S2 for PF6 and AsF6, and Table S3, ESI† for C–H⋯F distances and angles).
C bond lengths (1.371(6) Å and 1.369(5) Å for As and Sb, respectively) together with the internal C–S bond lengths, with an average value of 1.738 Å for both compounds, are in agreement with a +0.5 oxidation state of the donor and are comparable with the values measured for the PF6 salt (Table S2, ESI†). The paramount role of the anion in the solid state architecture is evidenced through the complex set of hydrogen bonding interactions established between the fluorine atoms and CHvinyl, CH3 and CHMe hydrogen atoms24 leading to a packing where the anions are surrounded by donors, all the F atoms being involved in such short C–H⋯F contacts (Fig. 1 for SbF6, Fig. S1 and S2 for PF6 and AsF6, and Table S3, ESI† for C–H⋯F distances and angles).
When comparing the three racemic structures there is a clear increase of the average C–H⋯F distances by changing the anion from PF6 to AsF6, and then to SbF6 (Table S3, ESI†), while the intrastack intermolecular S⋯S distances remain essentially the same, in the range of 3.63–3.69 Å (vide infra), thus ensuring an optimum overlap between open shell species. As the average X–F bond length varies from 1.57 Å for P to 1.69 Å for As, and then to 1.85 Å for Sb, clearly the average C–H⋯F distance has to vary in the opposite way in order to keep the same arrangement of the donors, providing a fine control of the solid state architecture at the nanoscale level. However, this type of packing allows the involvement of the six fluorine atoms in short C–H⋯F contacts for the three anions in spite of their difference in size.
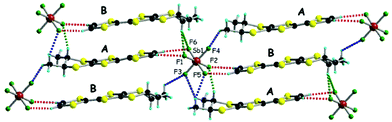
The situation is more complex for the enantiopure donors, since, as mentioned above, three different crystalline phases were obtained with the AsF6 anion, while only one phase was isolated with SbF6 and PF6. As the enantiomeric pairs (S,S) and (R,R) were isostructural according to crystal cell determination, only the former will be detailed for the new phases. The enantiopure radical cation salt with the SbF6 anion formulated as [(S,S)-1]2SbF6 is, interestingly, isostructural with the racemic phase, excepting the space group which is the non-centrosymmetric P1 in this case. The asymmetric unit contains one anion and two independent donor molecules A and B alternating in the stack (Fig. 2). This is in sharp contrast with the previous results in the PF6 system where the monoclinic P21 structure was formed by 4 independent donor molecules and 2 anions.20 Interestingly, the link between the two situations is provided by the AsF6− anion for which both crystalline phases are formed, i.e. triclinic P1 [(S,S)-1]2AsF6 and monoclinic P21 [(S,S)-1]4(AsF6)2, together with a third one, monoclinic P21 [(S,S)-1]2(AsF6)2. The second is thus isostructural with the poorly conducting [(S,S)-1]4(PF6)2 phase20 and will not be further detailed. As for the racemic counterparts, in the enantiopure triclinic phases [(S,S)-1]2XF6 (X = As, Sb) the bond distances indicate donor molecules in mixed valence state (Table S4, ESI†). While the packings of [(rac)-1]2SbF6 (Fig. 1), [(S,S)-1]2SbF6 (Fig. 2) and [(S,S)-1]2AsF6 (Fig. S3, ESI†) present the same general features, some very fine differences in the C–H⋯F contacts can be disclosed, as the disposition of the stereogenic centres is different. Accordingly, the differences concern especially the interactions involving CHMe and CH3 groups. In order to satisfy at maximum the hydrogen bonding demand of the fluorine atoms, the donors slightly shift within the stack in order to optimize the C–H⋯F contacts (Table S5, ESI†).
The C–H⋯F distances are clearly larger in average for the AsF6 salt (3.50 and 3.46 Å for H3C⋯F and MeHC⋯F distances, respectively) than for the SbF6 one (3.45 and 3.40 Å for H3C⋯F and MeHC⋯⋯F distances, respectively) (Table S5, ESI†). Consequently, the fluorine atoms will be less involved in stabilizing hydrogen bonding contacts when going from SbF6 to AsF6 in the triclinic phase, therefore the donors will tend to adopt a different packing with the AsF6 anion in the monoclinic 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 phase in order to maximize the hydrogen bonding interactions. This tendency is even higher for the PF6− anion, smallest of the series, exclusively providing the monoclinic phase in which all the fluorine atoms are involved in short C–H⋯F contacts (Fig. S4–S6, ESI†). Clearly, throughout this series, the chiral centres play the determining role in the fine tuning of the intermolecular interactions in the donors⋯anion aggregates, favouring either the triclinic (SbF6), monoclinic (PF6) or both (AsF6) phases. Worth mentioning is that in the structures discussed thus far the methyl groups adopt equatorial (eq, eq) positions. However, in the third crystalline phase obtained with the AsF6 anion the methyl groups show axial (ax, ax) disposition (Fig. S7 and S8, ESI†).25 This compound, formulated as [(S,S)-1]2(AsF6)2 (its enantiomeric (R,R) counterpart is isostructural), crystallizes in the monoclinic non-centrosymmetric space group P21 with two independent donors and two anions in the asymmetric unit. The anions engage in hydrogen bonding interactions with the donors (Fig. S7, ESI†) which form strong dimers according to the very short intradimer S⋯S distances (Fig. S8, ESI†). The dimers further arrange in step-chains along the a direction. This type of arrangement is reminiscent with the one observed in the isostructural insulating radical cation salt [(rac)-1]ClO4.2
2 phase in order to maximize the hydrogen bonding interactions. This tendency is even higher for the PF6− anion, smallest of the series, exclusively providing the monoclinic phase in which all the fluorine atoms are involved in short C–H⋯F contacts (Fig. S4–S6, ESI†). Clearly, throughout this series, the chiral centres play the determining role in the fine tuning of the intermolecular interactions in the donors⋯anion aggregates, favouring either the triclinic (SbF6), monoclinic (PF6) or both (AsF6) phases. Worth mentioning is that in the structures discussed thus far the methyl groups adopt equatorial (eq, eq) positions. However, in the third crystalline phase obtained with the AsF6 anion the methyl groups show axial (ax, ax) disposition (Fig. S7 and S8, ESI†).25 This compound, formulated as [(S,S)-1]2(AsF6)2 (its enantiomeric (R,R) counterpart is isostructural), crystallizes in the monoclinic non-centrosymmetric space group P21 with two independent donors and two anions in the asymmetric unit. The anions engage in hydrogen bonding interactions with the donors (Fig. S7, ESI†) which form strong dimers according to the very short intradimer S⋯S distances (Fig. S8, ESI†). The dimers further arrange in step-chains along the a direction. This type of arrangement is reminiscent with the one observed in the isostructural insulating radical cation salt [(rac)-1]ClO4.2
Single crystal temperature dependent resistivity measurements on triclinic [1]2XF6 (X = As, Sb) show metallic behaviour in the high temperature range both for racemic (Fig. S9, ESI†) and enantiopure salts (Fig. 3).
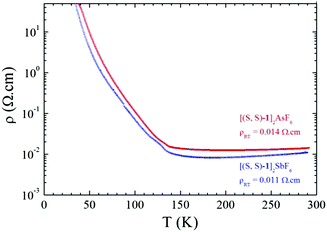 | ||
| Fig. 3 Temperature dependence of the electrical resistivity ρ for a single crystal of [(S,S)-1]2AsF6 (red line) and a single crystal of [(S,S)-1]2SbF6 (blue line). | ||
Room temperature conductivity values are of the same order of magnitude for the enantiopure salts, i.e. 90 S cm−1 for SbF6 and 70 S cm−1 for AsF6, being slightly lower than those for the racemic salts, amounting to 250 S cm−1 for PF6 and 125 S cm−1 for AsF6. Most importantly, the enantiopure phases are metallic with a broad minimum of resistivity around 200 K then a metal to insulator (MI) transition takes place around 130–135 K. This temperature dependence of the resistivity is similar to that of racemic salts with only slightly higher transition temperatures (Fig. S9, ESI†).
The donor layers of triclinic (DM-EDT-TTF)2XF6 (X = P, As, Sb) are very similar. Those of the (S,S) salts contain two symmetry non-equivalent donors and six different donor⋯donor interactions labelled I to VI (Fig. 4). The donor layers of the racemic salts are very similar although with only one symmetry non-equivalent donor and five different interactions (i.e. interactions V and VI are equivalent for these salts). All of these layers are made of a series of parallel donor chains along the (a–b) direction. The strength of the different intermolecular interactions in all these salts can be assessed from the calculated |βHOMO–HOMO| interaction energies.26
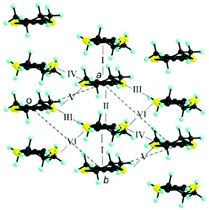 | ||
| Fig. 4 Donor layer of (S,S)- and (rac)-(DM-EDT-TTF)2XF6 triclinic salts discussed in this work where the different intermolecular interactions are labelled. | ||
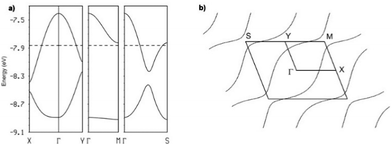
The intrastack interactions (I and II) are considerably stronger than all the interstack ones and, although geometrically very different, their calculated |βHOMO–HOMO| values differ only by around 15% (Table S6 (ESI†) for [(S,S)-1]2SbF6 and Tables S7–S10 (ESI†) for the other salts). Thus, from the viewpoint of the HOMO⋯HOMO interactions, these stacks are quite uniform chains of interacting HOMOs. Since the stacks run along the (a–b)-direction of the crystal structure, the two bands of the system (there are two donors per repeat unit of the donor layer) should exhibit strong dispersion along this direction (not far from Γ → S in reciprocal space) and considerably smaller along the perpendicular direction (not far from Γ → M in reciprocal space).
This is in fact what the calculated band structure (Fig. 5a for [(S,S)-1]2SbF6, see ESI† for the other salts) shows. The inter-stack interactions (III to V/VI) are one order of magnitude smaller but their contributions add to give a quite sizeable dispersion to the upper band along the interstack direction (i.e. approximately along Γ → M) so that the system should be seen as a series of substantially coupled and quite uniform stacks along the (a–b) direction. Because of the stoichiometry, the two HOMO bands (Fig. 5a) should contain one hole so that the upper band is half-filled. Since this band is quite dispersive, these salts are predicted to be metallic, in agreement with our conductivity measurements.
This analysis is confirmed by the calculated Fermi surface (Fig. 5b) which is built from a series of warped open lines perpendicular to the stacks direction. Thus, the present salts should be pseudo-one-dimensional metals at room temperature.
Can this analysis provide any guideline in trying to correlate the structural and transport properties of this family of salts? This is admittedly not an easy task because of the similarity in electronic structures and conductivity measurements (considering a larger number of crystals for every compound may be also important) along the series. Looking at the different interaction energies for all compounds of this series (Tables S6–S10, ESI†) we note that the two types of interstack interactions (III/IV and V/VI) are not only one order of magnitude smaller than the intrastack ones but their variation along the series is also considerably smaller. Thus, the intrastack HOMO⋯HOMO interactions are those dominating the shape of the upper partially filled band, i.e. the transport properties of the salts. For chains like those along (a–b) in Fig. 4, with two different but strong interactions along the chain, the slope of the upper band around the Fermi level should be dominated by the strength of the weaker of the two interactions. Thus the |βHOMO–HOMO| value for interaction II should be an adequate electronic structure parameter allowing classifying the different salts according to their conductivity: larger values of this parameter should be associated with higher conductivities. Using this simple guideline and the calculated |βHOMO–HOMO| values it follows that: (i) the conductivity should decrease along a given type of salt when the size of the anion increases, (ii) for the same anion the (rac)-salts should be more conductive when there is no disorder. When examining the structural origin of the variation in the |βHOMO–HOMO| values it is clear that the main factor lies in the evolution of the intermolecular S⋯S contacts and to a lesser extent the slight sliding motions induced by the different anions. Thus, the chiral information is transmitted to the conductivity carriers through the F(anion)⋯H(donor) interactions which, in turn, together with the anion size, influence the intrastack interactions, and, more specially, the weaker of the two intrastack interactions. This simple approach represents a step further with respect to simple anion size based ideas since suggests differences between the enantiopure and racemic salts. The presently known conductivity results are grossly in agreement with these ideas although more extensive work is in order. In particular the values for the SbF6 salts may require further attention.
Further work in this series will be devoted to the investigation of the conducting properties of the enantiopure salts under magnetic field and the use of variable composition alloys of XF6 anions in order to have a complete picture of these intriguing systems.
This work was supported in France by the ANR (Project 09-BLAN-0045-01), the CNRS and the University of Angers. Work in Spain was supported by the Spanish MINECO through Grant FIS2015-64886-C5-4-P and the Severo Ochoa Centers of Excellence Program under Grant SEV-2015-0496. We warmly thank M. Allain (MOLTECH-Anjou, Angers) for valuable technical help with the X-ray analysis.
Notes and references
- N. Avarvari and J. D. Wallis, J. Mater. Chem., 2009, 19, 4061–4076 RSC.
- F. Pop, P. Auban-Senzier, E. Canadell, G. L. J. A. Rikken and N. Avarvari, Nat. Commun., 2014, 5, 3757 Search PubMed.
- J.-P. Griffiths, H. Nie, R. J. Brown, P. Day and J. D. Wallis, Org. Biomol. Chem., 2005, 3, 2155–2166 CAS.
- S. Yang, A. C. Brooks, L. Martin, P. Day, H. Li, P. Horton, L. Male and J. D. Wallis, CrystEngComm, 2009, 11, 993–996 RSC.
- F. Riobé and N. Avarvari, Chem. Commun., 2009, 3753–3755 RSC.
- I. Awheda, S. J. Krivickas, S. Yang, L. Martin, M. A. Guziak, A. C. Brooks, F. Pelletier, M. Le Kerneau, P. Day, P. N. Horton, H. Akutsu and J. D. Wallis, Tetrahedron, 2013, 69, 8738–8750 CrossRef CAS.
- M. Chas, M. Lemarié, M. Gulea and N. Avarvari, Chem. Commun., 2008, 220–222 RSC.
- M. Hasegawa, Y. Sone, S. Iwata, H. Matsuzawa and Y. Mazaki, Org. Lett., 2011, 13, 4688–4691 CrossRef CAS PubMed.
- (a) R. Gómez, J. L. Segura and N. Martin, J. Org. Chem., 2000, 65, 7566–7574 CrossRef; (b) A. Saad, F. Barrière, E. Levillain, N. Vanthuyne, O. Jeannin and M. Fourmigué, Chem. – Eur. J., 2010, 16, 8020–8028 CrossRef CAS PubMed.
- T. Biet, A. Fihey, T. Cauchy, N. Vanthuyne, C. Roussel, J. Crassous and N. Avarvari, Chem. – Eur. J., 2013, 19, 13160–13167 CrossRef CAS PubMed.
- K. Kobayakawa, M. Hasegawa, H. Sasaki, J. Endo, H. Matsuzawa, K. Sako, J. Yoshida and Y. Mazaki, Chem. – Asian J., 2014, 9, 2751–2754 CrossRef CAS PubMed.
- F. Pop, C. Melan, I. Danila, M. Linares, D. Beljonne, D. B. Amabilino and N. Avarvari, Chem. – Eur. J., 2014, 20, 17443–17453 CrossRef CAS PubMed.
- (a) S. Matsumiya, A. Izuoka, T. Sugawara, T. Taruishi, Y. Kawada and M. Tokumoto, Bull. Chem. Soc. Jpn., 1993, 66, 1949–1954 CrossRef CAS; (b) F. Pop, M. Allain, P. Auban-Senzier, J. Martínez-Lillo, F. Lloret, M. Julve, E. Canadell and N. Avarvari, Eur. J. Inorg. Chem., 2014, 3855–3862 CrossRef CAS.
- (a) J. R. Galán-Mascarós, E. Coronado, P. A. Goddard, J. Singleton, A. I. Coldea, J. D. Wallis, S. J. Coles and A. Alberola, J. Am. Chem. Soc., 2010, 132, 9271–9273 CrossRef PubMed; (b) S. Yang, F. Pop, C. Melan, A. C. Brooks, L. Martin, P. Horton, P. Auban-Senzier, G. L. J. A. Rikken, N. Avarvari and J. D. Wallis, CrystEngComm, 2014, 16, 3906–3916 RSC; (c) M. Atzori, F. Pop, P. Auban-Senzier, R. Clérac, E. Canadell, M. L. Mercuri and N. Avarvari, Inorg. Chem., 2015, 54, 3643–3653 CrossRef CAS PubMed.
- J. D. Dunitz, A. Karrer and J. D. Wallis, Helv. Chim. Acta, 1986, 69, 69–70 CrossRef.
- (a) G. L. J. A. Rikken, J. Fölling and P. Wyder, Phys. Rev. Lett., 2001, 87, 236602 CrossRef CAS PubMed; (b) V. Krstic, S. Roth, M. Burghard, K. Kern and G. L. J. A. Rikken, J. Chem. Phys., 2002, 117, 11315–11319 CrossRef CAS.
- C. Réthoré, N. Avarvari, E. Canadell, P. Auban-Senzier and M. Fourmigué, J. Am. Chem. Soc., 2005, 127, 5748–5749 CrossRef PubMed.
- F. Pop, S. Laroussi, T. Cauchy, C. J. Gómez-García, J. D. Wallis and N. Avarvari, Chirality, 2013, 25, 466–474 CrossRef CAS PubMed.
- A. M. Madalan, C. Réthoré, M. Fourmigué, E. Canadell, E. B. Lopes, M. Almeida, P. Auban-Senzier and N. Avarvari, Chem. – Eur. J., 2010, 16, 528–537 CrossRef CAS PubMed.
- F. Pop, P. Auban-Senzier, A. Frąckowiak, K. Ptaszyński, I. Olejniczak, J. D. Wallis, E. Canadell and N. Avarvari, J. Am. Chem. Soc., 2013, 135, 17176–17186 CrossRef CAS PubMed.
- (a) K. Bechgaard, C. S. Jacobsen, K. Mortensen, H. J. Pedersen and N. Thorup, Solid State Commun., 1980, 33, 1119–1125 CrossRef CAS; (b) J. Tarrés, N. Santaló, M. Mas, E. Molins, J. Veciana, C. Rovira, S. Yang, H. Lee, D. O. Cowan, M.-L. Doublet and E. Canadell, Chem. Mater., 1995, 7, 1558–1567 CrossRef; (c) T. Shirahata, K. Shiratori, S. Kumeta, T. Kawamoto, T. Ishikawa, S. Koshihara, Y. Nakano, H. Yamochi, Y. Misaki and T. Mori, J. Am. Chem. Soc., 2012, 134, 13330–13340 CrossRef CAS PubMed.
- R. Kato, H. Kobayashi and A. Kobayashi, Chem. Lett., 1989, 781–784 CrossRef CAS.
- T. Shirahata, M. Kibune and T. Imakubo, J. Mater. Chem., 2005, 15, 4399–4402 RSC.
- (a) G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond in Structural Chemistry and Biology, OUP, Chichester, 1999 Search PubMed; (b) G. R. Desiraju, Acc. Chem. Res., 2002, 35, 565–573 CrossRef CAS PubMed; (c) G. R. Desiraju, Acc. Chem. Res., 1996, 29, 441–449 CrossRef CAS PubMed.
- F. Pop, P. Batail and N. Avarvari, Crystals, 2016, 6, 8 CrossRef.
- M.-H. Whangbo, J. M. Williams, P. C. W. Leung, M. A. Beno, T. J. Emge and H. H. Wang, Inorg. Chem., 1985, 24, 3500–3502 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1498583–1498588. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6cc06706a |
| This journal is © The Royal Society of Chemistry 2016 |