Determining carbon–carbon connectivities in natural abundance organic powders using dipolar couplings

Abstract

We present a solid-state NMR methodology capable of investigating the carbon skeleton of natural abundance organic powders. The methodology is based on the ¹³C–¹³C dipolar coupling interaction and allows carbon–carbon connectivities to be unambiguously established for a wide range of organic solids. This methodology is particularly suitable for disordered solids, such as natural or synthetic macromolecules, which cannot be studied using conventional diffraction or NMR techniques.

---

Determining the connectivity between carbon atoms is the first and most important step for the structural investigation of organic molecules. In the case of organic powders that cannot be studied by conventional diffraction techniques, solid-state nuclear magnetic resonance (SSNMR) is usually regarded as a key technique.^1–6 Notably, the carbon skeleton of organic powders is usually investigated using two-dimensional correlation experiments based on ¹³C–¹³C scalar (J) couplings to transfer magnetisation between ¹³C nuclei separated by a single covalent bond. Although such J-based experiments have been shown to produce correlations between ¹³C that are not directly bonded (thereby potentially leading to wrong assignments),⁷ these experiments usually lead to the accurate determination of carbon connectivities and are particularly valuable to investigate samples isotopically enriched in ¹³C nuclei.^8–18

In the case of natural-abundance (NA) samples, however, the applicability of J-based experiments is often limited. In fact, because the magnetisation transfer arising from ¹³C–¹³C J-couplings is slow (with respect to the decay of the ¹³C transverse magnetisation), it is typically barely detectable for NA samples. As a result, establishing carbon–carbon connectivities in NA samples using J-based experiments usually requires extensively long experimental times in the case of crystalline or semi-crystalline samples^19–28 (approximately a week) and is seldom practicable in the case of NA disordered solids that display broad ¹³C NMR linewidths arising from fast ¹³C transverse magnetisation decay.^29,30

Herein, we demonstrate that an unambiguous assignment of carbon connectivities in NA organic powders, especially disordered solids, can be obtained from 2D correlation experiments that are based on ¹³C–¹³C dipolar couplings.^30,31 An important feature of dipolar-based experiments is that the magnetisation transfer builds up much faster than in J-based experiments, and hence dipolar-based experiments are suitable for organic solids with fast ¹³C transverse magnetisation decays. Moreover, we show here that a magnetisation transfer time of 0.4 ms leads exclusively to correlation signals between covalently bonded ¹³C–¹³C pairs. In contrast, signals arising from ¹³C–¹³C pairs separated by more than one covalent bond are at least 5 times weaker, and thus would not be detected in 2D ¹³C–¹³C DQ dipolar correlation spectra of NA samples (ESI†).

Fig. 1 shows the pulse sequence for magic-angle spinning (MAS) 2D dipolar-based ¹³C–¹³C correlation experiments. The recoupling of the ¹³C–¹³C dipolar interaction is based on the R20⁹₂ symmetry,^32–34 which generates during the first delay τ_DQ double quantum (DQ) coherences that subsequently evolve during t₁ at the sum of the chemical shift frequencies of pairs of coupled ¹³C–¹³C nuclei, before being reconverted during the second τ_DQ into single quantum coherences for detection during t₂. It should be noted that, for NA samples, DQ coherences are useful not only for straightforward data interpretation but also to suppress intense signals arising from the large number of uncoupled ¹³C nuclei.

Fig. 1 Pulse sequence for 2D ¹³C–¹³C correlation experiments based on dipolar coupling (a). The RN^ν_n symmetry was applied during the delays τ_DQ to excite and reconvert double quantum (DQ) coherences, yielding correlation peaks in the indirect dimension of the 2D spectrum at the sum of the chemical shifts of the 2 coupled ¹³C nuclei. The selected symmetry (N = 20, n = 2 and ν = 9) led to 10 R_ϕ,R_−ϕ′ elements fitting into 2 rotor periods, with ϕ = 81° (b). The basic element is shown in (c) and it consists of a composite 180° pulse.

Interestingly, the R20⁹₂ symmetry is particularly robust with respect to ¹H–¹³C dipolar coupling and ¹³C chemical shift anisotropy (CSA).^32,35–37 Notably, no ¹H decoupling is required during the ¹³C recoupling periods τ_DQ^32–34 and, thus, this experiment is very easy to implement (only the ¹³C 90° pulse needs to be calibrated). It should be noted that the R20⁹₂ symmetry is appropriate for a MAS frequency of 10 kHz. In this case, a 4 mm MAS rotor can be used, providing the best compromise between MAS frequency and sensitivity for NA samples at 9.4 T.

Furthermore, using our instrumentation, the DQ recoupling of the ¹³C–¹³C dipolar interaction using the R20⁹₂ symmetry is 1.7 times more efficient than standard dipolar recoupling symmetries, such as POST-C7³⁸ or SPC5³⁹ (see the ESI†). This enhancement translates in substantial shorter experimental times, i.e. 2.9 times faster, and as a result, 2D ¹³C–¹³C correlation experiments for NA samples can be obtained within practicable experimental durations using standard solid-state NMR hardware at room temperature.

The 2D dipolar-based ¹³C–¹³C correlation spectrum for a powder sample of L-tyrosine ethyl ester is shown in Fig. 2. The 2D spectrum was recorded using a 9.4 T magnet and a MAS frequency of 10 kHz; the experimental time was 3 days. The 1D ¹³C cross-polarisation (CP) MAS spectrum is also shown above the 2D spectrum. Remarkably, the resonances corresponding to aromatic carbons are significantly broader than the other ¹³C signals. This broadening results from the fast ¹³C transverse magnetisation decay arising from molecular motion.^40,41 As a result, correlation signals involving the aromatic carbons are not detectable using J-based correlation experiments.²² In contrast, all the ¹³C–¹³C correlation signals between covalently bonded ¹³C nuclei are observed in the 2D dipolar-based ¹³C–¹³C correlation spectrum with excellent resolution and sensitivity.

Fig. 2 ¹³C–¹³C DQ dipolar correlation spectrum of L-tyrosine ethyl ester powder. The spectrum was recorded using τ_DQ = 0.4 ms, a MAS frequency of 10 kHz, 27 t₁ increments and 1600 repetitions for each t₁ increment. The repetition delay was 3 s. The total experimental time was 3 days. The ¹³C CPMAS spectrum is shown in the top projection. The symbol (*) indicates spinning sidebands.

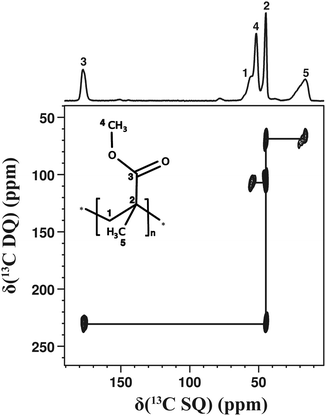
Fig. 3 illustrates the capabilities of 2D dipolar-based ¹³C–¹³C correlation experiments to investigate a disordered solid, here, an amorphous poly(methyl methacrylate) (PMMA) sample. This spectrum has been recorded in less than 2 days. Interestingly, the ¹³C signals of PMMA arise from both mobile and rigid ¹³C sites. For example, the OCH₃ or CO resonances correspond to the mobile part of PMMA while the CH₂ or CH₃ resonances correspond to the more rigid backbone chain.⁴² We notice in Fig. 3 that, notwithstanding significant mobility differences, all the correlation peaks arising from covalently bonded ¹³C–¹³C pairs could be observed in the 2D ¹³C–¹³C DQ dipolar correlation spectrum.‡ We emphasise that 2D dipolar-based ¹³C–¹³C correlation experiments are suitable to samples that give rise to observable signals in ¹³C CPMAS experiments. In the case of samples with high molecular mobility, which are intrinsically unsuitable for ¹³C CPMAS experiments,⁴³ it would be more advantageous to directly excite ¹³C nuclei and to explore ¹³C–¹³C connectivities through J-based experiments.³⁰ Nevertheless, we have shown here (Fig. 2 and 3) that 2D dipolar-based ¹³C–¹³C correlation experiments are useful even for solids subjected to molecular motions.

Fig. 3 ¹³C–¹³C DQ dipolar correlation spectrum of a synthetic polymer, the poly(methyl methacrylate) (PMMA), recorded with τ_DQ = 0.4 ms, a MAS frequency of 10 kHz, 38 t₁ increments and 1024 repetitions for each t₁ increment. The repetition delay was set to 2 s. The total experimental time was 1.8 days. The ¹³C CPMAS spectrum is shown in the top projection.

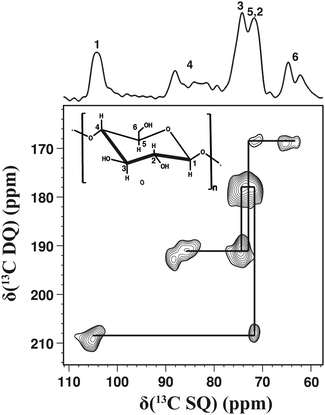
An additional example is shown in Fig. 4 for cellulose, a natural polymer containing both amorphous and crystalline phases. The 1D ¹³C CPMAS spectrum is shown above the 2D ¹³C–¹³C DQ dipolar correlation spectrum. In the 1D ¹³C CPMAS spectrum the apparent line widths range from 400 to 600 Hz and are partly related to the disordered character of the sample. The 2D ¹³C–¹³C DQ dipolar correlation spectrum was recorded within 3 days and all one-bond correlations were observed with very good sensitivity and satisfactory resolution. Notably, the assignment based on dipolar coupling experiments is in agreement with the assignment based on J-coupling experiments.§²⁹ Moreover, correlation peaks corresponding to both amorphous and crystalline signals are observed in the 2D ¹³C–¹³C DQ dipolar correlation spectrum, as exemplified for the signals at 86 ppm and 63 ppm.

Fig. 4 ¹³C–¹³C DQ dipolar correlation spectrum of cellulose, recorded with τ_DQ = 0.4 ms, a MAS frequency of 10 kHz, 20 t₁ increments and 2048 repetitions for each t₁ increment. The repetition delay was 3.2 s. The total experimental time was approximately 3 days. The ¹³C CPMAS spectrum is shown in the top projection.

In summary, we have shown that unambiguous carbon–carbon connectivities in NA organic solids can be determined using dipolar-based ¹³C–¹³C correlation experiments. These experiments can be performed within practicable experimental times and are suitable for different kinds of samples, such as molecular crystals and disordered solids including synthetic or natural polymers. This methodology is complementary to J-based ¹³C–¹³C correlation experiments, especially in the case of NA disordered solids having fast ¹³C transverse magnetisation decay. Finally, the methodology presented here can be carried out at room temperature and is thus complementary to ¹³C–¹³C correlation experiments enhanced with dynamic nuclear polarisation,^44–47 which require samples that can be analysed at cryogenic temperatures and in the presence of paramagnetic dopants.

This work has been carried out thanks to the support from the French National Research Agency (ANR) grant number ANR-13-JS080001.

References

1. D. Massiot, R. J. Messinger, S. Cadars, M. Deschamps, V. Montouillout, N. Pellerin, E. Veron, M. Allix, P. Florian and F. Fayon, Acc. Chem. Res., 2013, 46, 1975–1984.
2. R. J. Messinger, K. Na, Y. Seo, R. Ryoo and B. F. Chmelka, Angew. Chem., Int. Ed., 2015, 54, 927–931.
3. M. R. Hansen, R. Graf and H. W. Spiess, Chem. Rev., 2016, 116, 1272–1308.
4. S. Radhakrishnan, P.-J. Goossens, P. C. M. M. Magusin, S. P. Sree, C. Detavernier, E. Breynaert, C. Martineau, F. Taulelle and J. A. Martens, J. Am. Chem. Soc., 2016, 138, 2802–2808.
5. C. M. Widdifield, H. Robson and P. Hodgkinson, Chem. Commun., 2016, 52, 6685–6688.
6. S. E. Ashbrook and D. McKay, Chem. Commun., 2016, 52, 7186–7204.
7. F. Fayon, D. Massiot, M. H. Levitt, J. J. Titman, D. H. Gregory, L. Duma, L. Emsley and S. P. Brown, J. Chem. Phys., 2005, 122, 194313.
8. G. Grasso, T. M. de Swiet and J. J. Titman, J. Phys. Chem. B, 2002, 106, 8676–8680.
9. G. De Paepe, N. Giraud, A. Lesage, P. Hodgkinson, A. Böckmann and L. Emsley, J. Am. Chem. Soc., 2003, 125, 13938–13939.
10. E. H. Hardy, A. Detken and B. H. Meier, J. Magn. Reson., 2003, 165, 208–218.
11. S. Cadars, A. Lesage and L. Emsley, J. Am. Chem. Soc., 2005, 127, 4466–4476.
12. L. Chen, R. A. Olsen, D. W. Elliott, J. M. Boettcher, D. H. Zhou, C. M. Rienstra and L. J. Mueller, J. Am. Chem. Soc., 2006, 128, 9992–9993.
13. F. Fayon, C. Roiland, L. Emsley and D. Massiot, J. Magn. Reson., 2006, 179, 49–57.
14. R. Witter, U. Sternberg, S. Hesse, T. Kondo, F.-T. Koch and A. S. Ulrich, Macromolecules, 2006, 39, 6125–6132.
15. L. Chen, J. M. Kaiser, T. Polenova, J. Yang, C. M. Rienstra and L. J. Mueller, J. Am. Chem. Soc., 2007, 129, 10650–10651.
16. N. Baccile, G. Laurent, F. Babonneau, F. Fayon, M.-M. Titirici and M. Antonietti, J. Phys. Chem. C, 2009, 113, 9644–9654.
17. D. Lee, J. Struppe, D. W. Elliott, L. J. Mueller and J. J. Titman, Phys. Chem. Chem. Phys., 2009, 11, 3547–3553.
18. X. Liu, W. Chen, Y. lee Hong, S. Yuan, S. Kuroki and T. Miyoshi, Macromolecules, 2015, 48, 5300–5309.
19. A. Lesage, C. Auger, S. Caldarelli and L. Emsley, J. Am. Chem. Soc., 1997, 119, 7867–7868.
20. R. A. Olsen, J. Struppe, D. W. Elliott, R. J. Thomas and L. J. Mueller, J. Am. Chem. Soc., 2003, 125, 11784–11785.
21. H. Kono, T. Erata and M. Takai, Macromolecules, 2003, 36, 5131–5138.
22. G. De Paëpe, A. Lesage, S. Steuernagel and L. Emsley, ChemPhysChem, 2004, 5, 869–875.
23. H. Kono, Biopolymers, 2004, 75, 255–263.
24. J. Brus and A. Jegorov, J. Phys. Chem. A, 2004, 108, 3955–3964.
25. R. K. Harris, S. A. Joyce, C. J. Pickard, S. Cadars and L. Emsley, Phys. Chem. Chem. Phys., 2006, 8, 137–143.
26. R. K. Harris, S. Cadars, L. Emsley, J. R. Yates, C. J. Pickard, R. K. R. Jetti and U. J. Griesser, Phys. Chem. Chem. Phys., 2007, 9, 360–368.
27. M. Deschamps, S. Cadars, E. Gilbert, P. Azas, E. Raymundo-Pinero, F. Béguin and D. Massiot, Solid State Nucl. Magn. Reson., 2012, 42, 81–86.
28. M. Baias, J.-N. Dumez, P. H. Svensson, S. Schantz, G. M. Day and L. Emsley, J. Am. Chem. Soc., 2013, 135, 17501–17507.
29. A. Lesage, M. Bardet and L. Emsley, J. Am. Chem. Soc., 1999, 121, 10987–10993.
30. Y. Su and M. Hong, J. Phys. Chem. B, 2011, 115, 10758–10767.
31. M. Hong, J. Magn. Reson., 1999, 136, 86–91.
32. M. Carravetta, M. Eden, O. G. Johannessen, H. Luthman, P. J. E. Verdegem, J. Lugtenburg, A. Sebald and M. H. Levitt, J. Am. Chem. Soc., 2001, 123, 10628–10638.
33. M. H. Levitt, in Encyclopedia of Nuclear Magnetic Resonance, ed. D. M. Grant and R. Harris, John Wiley & Sons, Ltd, Chichester, 2002, vol. 9, p. 165.
34. M. Eden, eMagRes, John Wiley & Sons, Ltd, 2013, vol. 2, pp. 351–364.
35. C. E. Hughes, S. Luca and M. Baldus, Chem. Phys. Lett., 2004, 385, 435–440.
36. I. Marin-Montesinos, D. H. Brouwer, G. Antonioli, W. C. Lai, A. Brinkmann and M. H. Levitt, J. Magn. Reson., 2005, 177, 307–317.
37. O. Lafon, J. Trebosc, B. Hu, G. De Paepe and J.-P. Amoureux, Chem. Commun., 2011, 47, 6930–6932.
38. M. Hohwy, H. J. Jakobsen, M. Edén, M. H. Levitt and N. C. Nielsen, J. Chem. Phys., 1998, 108, 2686.
39. M. Hohwy, C. M. Rienstra, C. P. Jaroniec and R. G. Griffin, J. Chem. Phys., 1999, 110, 7983.
40. L. Frydman, S. Vallabhaneni, Y. K. Lee and L. Emsley, J. Chem. Phys., 1994, 101, 111–117.
41. X. Helluy and A. Sebald, J. Phys. Chem. B, 2003, 107, 3290–3296.
42. E. R. deAzevedo, W.-G. Hu, T. J. Bonagamba and K. Schmidt-Rohr, J. Am. Chem. Soc., 1999, 121, 8411–8412.
43. R. Zhang, K. H. Mroue and A. Ramamoorthy, J. Magn. Reson., 2016, 266, 59–66.
44. A. J. Rossini, A. Zagdoun, F. Hegner, M. Schwarzwälder, D. Gajan, C. Copéret, A. Lesage and L. Emsley, J. Am. Chem. Soc., 2012, 134, 16899–16908.
45. H. Takahashi, D. Lee, L. Dubois, M. Bardet, S. Hediger and G. De Paepe, Angew. Chem., Int. Ed., 2012, 51, 11766–11769.
46. G. Mollica, M. Dekhil, F. Ziarelli, P. Thureau and S. Viel, Angew. Chem., Int. Ed., 2015, 54, 6028–6031.
47. R. L. Johnson, F. A. Perras, T. Kobayashi, T. J. Schwartz, J. A. Dumesic, B. H. Shanks and M. Pruski, Chem. Commun., 2016, 52, 1859–1862.

---

Footnotes

† Electronic supplementary information (ESI) available: Predicted signal intensities, experimental recoupling efficiencies, experimental details. See DOI: 10.1039/c6cc04202c

‡ Molecular mobility could potentially reduce the DQ correlation intensity as a result of partial averaging of the ¹³C–¹³C DQ dipolar coupling.

§ J-coupling experiments were recorded on a partially ¹³C enriched cellulose sample.

---