Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Combining solid-state NMR spectroscopy with first-principles calculations – a guide to NMR crystallography
Sharon E.
Ashbrook
* and
David
McKay

School of Chemistry, EaStCHEM and Centre of Magnetic Resonance, University of St Andrews, St Andrews, KY16 9ST, UK. E-mail: sema@st-andrews.ac.uk
First published on 21st April 2016
Abstract
Recent advances in the application of first-principles calculations of NMR parameters to periodic systems have resulted in widespread interest in their use to support experimental measurement. Such calculations often play an important role in the emerging field of “NMR crystallography”, where NMR spectroscopy is combined with techniques such as diffraction, to aid structure determination. Here, we discuss the current state-of-the-art for combining experiment and calculation in NMR spectroscopy, considering the basic theory behind the computational approaches and their practical application. We consider the issues associated with geometry optimisation and how the effects of temperature may be included in the calculation. The automated prediction of structural candidates and the treatment of disordered and dynamic solids are discussed. Finally, we consider the areas where further development is needed in this field and its potential future impact.
1. Introduction
Nuclear magnetic resonance (NMR) spectroscopy is one of the most widely-used analytical tools in the chemical sciences.1,2 The sensitivity of this method to the local atomic-scale structure has seen widespread application in academia, medicine and industry. Many of the interactions that affect the nuclear spins (and ultimately provide the wealth of information available from a spectrum) are anisotropic, i.e., orientation dependent, but are averaged in solution by rapid tumbling, enabling element-specific, detailed information on the three-dimensional shape and chemical bonding of molecules to be determined. In contrast, solid-state NMR spectra typically exhibit broadened lineshapes as a result of this anisotropy, hindering the extraction of information and detailed structural characterisation.1,2 There are a number of approaches now available for improving resolution (and, concomitantly, sensitivity), many involving specialist hardware or complex pulse sequences, opening up a range of potential opportunities for the characterisation of solid materials.Even when high-resolution approaches are used, solid-state NMR spectra may still contain complicated or overlapped spectral lineshapes, particularly as the structural complexity of the materials studied increases, and it can remain difficult both to assign signals to chemically- or crystallographically-distinct species and to extract the structural information available.1,2 This problem can be greatest for inorganic materials, where a range of less commonly-studied nuclear species are typically investigated, many of which have inherently low natural abundance or low sensitivity, and there is often relatively little information in the literature to aid spectral acquisition or interpretation. In recent years, these challenges have resulted in growing interest in the experimental solid-state NMR community in the use of first-principles calculations, i.e., the computational prediction of NMR parameters for a specified structural model. The use of quantum-chemical calculations to predict NMR parameters has a long history, but most applications have been restricted to discrete systems.3,4 In these approaches, an extended periodic solid has to be treated as a small molecule, or cluster of atoms, with the termination of bonds, usually by H. Such treatment does not necessarily represent the real solid-state structure; the artificial presence of a surface affects the electronic properties of species in the bulk (though the effect decays exponentially with cluster size), while the electric field (net zero in solids) is non zero in all but extremely large clusters.5 These phenomena can affect the computed NMR parameters and may limit their value.
The application of theoretical calculations for solid materials was revolutionised in 2001 through the introduction, by Pickard and Mauri, of the gauge-including projector augmented wave (GIPAW)6–8 approach, which enabled the calculation of magnetic shielding in a periodic system, using a planewave basis set. Exploiting the inherent periodicity of a solid, i.e., recreating a repeating three-dimensional structure from a small-volume unit, enables accurate calculations for all atoms within a system simultaneously, providing a significant saving in time and cost. For experimentalists, calculations have a number of potential uses, including the assignment of well-resolved spectral resonances for ordered crystalline materials, to support unusual or unexpected values of experimentally-observed NMR parameters, or to provide information about parameters that are challenging to measure experimentally (such as anisotropies or tensor orientations), but that can have a significant effect on the spectra.7–9 Calculations also have the ability to predict spectra and guide experimental acquisition, particularly when sensitivity is limiting or acquisition conditions are challenging. For more complex structures, calculations offer the opportunity to easily evaluate the effect of structural changes, such as atom substitution or bond length/angle changes, upon the NMR parameters, and if there is no confirmed structure for a material, calculated NMR parameters for candidate structures can be compared to those determined by experiment.
Calculations can offer significant insight into the interpretation of the complex NMR spectra exhibited by disordered materials, providing information by which broadened lineshapes can be decomposed into a number of different contributions. For some materials, defining “the structure” using a framework based on inherent periodicity might not be appropriate, producing an average structural picture not relevant to the NMR spectrum observed; however, calculations showing the effect on the NMR parameters of changes to the local environment can still aid spectral interpretation. Although calculations are inherently carried out at 0 K (unless temperature effects are explicitly considered), they can provide insight into the motional processes in the solid state. At a very basic level, significant differences between experiment and calculation can suggest the presence of dynamics, and as the complete interaction tensor (including isotropic, anisotropic and orientational information) is determined, it is then possible to consider how this can be averaged under different motional models and compare these results to variable-temperature experiments.
In recent years, the advances in NMR spectroscopy, and its growing use for determining or refining structural models, have led to the emergence of a new field, termed “NMR Crystallography”.10,11 While more generally defined in terms of the use of NMR spectroscopy (often in combination with diffraction experiments) to determine structural information, in many applications calculation also plays a major role (an approach sometimes referred to as “SMARTER Crystallography”12). In all cases, however, the ultimate goal is for the combination of a number of methods to be able to provide much greater insight than any individual approach. Here, we set out our philosophy for combining state-of-the-art experimental solid-state NMR spectroscopy and theoretical calculations, primarily using the periodic GIPAW approach, to characterise the structures of materials. After briefly discussing the basic principles of both the experimental and computational approaches that are widely used, we describe the initial calculations required to achieve the best computational model for the chemical system of interest, the types of calculation required to determine the full range of NMR parameters and the steps that can be taken to model the effects of temperature and disorder on NMR parameters. Finally, we present our view on the frontiers of the application of periodic calculations to solid-state NMR spectroscopy and comment on the status and future development of this field. By its very nature this overview is not a complete summary of all activity in this area, and readers are referred to the comprehensive reviews in ref. 7 and 8 for more information.
1.1 Experimental solid-state NMR spectroscopy
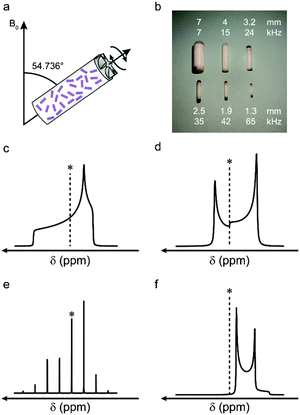
The wide utility of NMR spectroscopy results from the range of interactions that the nuclear spins experience, and their ability to report on the local structural environment in an element- and site-specific manner. For nuclei with spin quantum number I = 1/2, information can be obtained through the chemical shielding interaction (i.e., the modification of the local magnetic field by the surrounding electrons), and internuclear couplings, both through space (dipolar couplings) or through bond (J couplings). The anisotropic nature of these interactions leads to spectral broadening in a powdered solid (where all crystallite orientations are present simultaneously). An example of this can be seen in Fig. 1c, where a powder-pattern lineshape (simulated for a nucleus subject to an anisotropic shielding interaction) is shown. Although the anisotropic broadening can, in principle, provide information on symmetry and bonding, the broadening can hinder spectral interpretation, particularly when more than one distinct species is present in the spectrum.1,2 Over the years, the quest to improve resolution and sensitivity has driven development of both hardware and pulse sequence design, primarily to remove anisotropy (and achieve high resolution spectra) and, subsequently, to selectively reintroduce and accurately measure anisotropic interactions.Many of the interactions that affect NMR spectra have a similar orientational dependence, (proportional to the second-order Legendre polynomial P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) = (3
θ) = (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1)/2), and for a specific orientation (θ = 54.736°) the anisotropic component is zero. Hypothetically, if it were possible to orient all crystallites in a powder at this angle simultaneously, high-resolution spectra would be obtained directly. Although clearly not practical, a similar effect can be achieved using a physical rotation of the sample about an axis inclined at 54.736° to the external magnetic field, B0, in an approach termed magic angle spinning (MAS), shown schematically in Fig. 1a.13 Although a distribution of crystallite orientations is still present, if sample rotation is sufficiently rapid the average orientation for every crystallite is now aligned along the rotor axis. As shown in Fig. 1, for interactions to be effectively removed the rotation rate must be comparable to (or larger than) the magnitude of the interaction. The rotation rate is limited by the diameter of the sample holder (rotor) that is used (see Fig. 1b), with the highest commercially-available rates ∼110 kHz. MAS is able to remove the shielding anisotropy (∼102–105 Hz), the dipolar coupling (∼103–105 Hz) and the anisotropic J coupling (∼1–103 Hz). In most cases, at relatively slow rotation rates, the lineshape is broken up into a manifold of “spinning sidebands” (shown in Fig. 1e for a lineshape subject to a CSA) separated from the isotropic centreband by multiples of the spinning rate. For some interactions, e.g., homonuclear dipolar couplings, fast MAS rates are required before resolved sidebands are observed. For nuclei with poor sensitivity (e.g., low natural abundance) signal intensity can be enhanced by using cross polarisation (CP) – a transfer of magnetisation from high sensitivity, highly-abundant nuclei (typically 1H).1,2,14–16 The transfer is mediated via the dipolar coupling, resulting in spectral editing, with the intensity of the signal dependent on the spatial proximity of the atoms.
θ − 1)/2), and for a specific orientation (θ = 54.736°) the anisotropic component is zero. Hypothetically, if it were possible to orient all crystallites in a powder at this angle simultaneously, high-resolution spectra would be obtained directly. Although clearly not practical, a similar effect can be achieved using a physical rotation of the sample about an axis inclined at 54.736° to the external magnetic field, B0, in an approach termed magic angle spinning (MAS), shown schematically in Fig. 1a.13 Although a distribution of crystallite orientations is still present, if sample rotation is sufficiently rapid the average orientation for every crystallite is now aligned along the rotor axis. As shown in Fig. 1, for interactions to be effectively removed the rotation rate must be comparable to (or larger than) the magnitude of the interaction. The rotation rate is limited by the diameter of the sample holder (rotor) that is used (see Fig. 1b), with the highest commercially-available rates ∼110 kHz. MAS is able to remove the shielding anisotropy (∼102–105 Hz), the dipolar coupling (∼103–105 Hz) and the anisotropic J coupling (∼1–103 Hz). In most cases, at relatively slow rotation rates, the lineshape is broken up into a manifold of “spinning sidebands” (shown in Fig. 1e for a lineshape subject to a CSA) separated from the isotropic centreband by multiples of the spinning rate. For some interactions, e.g., homonuclear dipolar couplings, fast MAS rates are required before resolved sidebands are observed. For nuclei with poor sensitivity (e.g., low natural abundance) signal intensity can be enhanced by using cross polarisation (CP) – a transfer of magnetisation from high sensitivity, highly-abundant nuclei (typically 1H).1,2,14–16 The transfer is mediated via the dipolar coupling, resulting in spectral editing, with the intensity of the signal dependent on the spatial proximity of the atoms.
It is also possible to remove anisotropic couplings between nuclei using decoupling, i.e., the application of radiofrequency pulses during signal acquisition.1,2,17–20 Decoupling can be performed on static samples (thereby removing couplings but not the shielding anisotropy) or in conjunction with MAS, particularly in the presence of strong interactions that would require unfeasibly high sample rotation rates. Decoupling is usually more straightforward for heteronuclear couplings as the S spin can be easily irradiated during acquisition of the I-spin signal. For homonuclear couplings (e.g., between I1 and I2) decoupling is considerably more challenging, requiring simultaneous irradiation and acquisition of the same spin. This is usually performed using “windowed” schemes, where the acquisition of data points takes place during short intervals between the decoupling pulses.17–20
NMR spectra for nuclei with spin quantum number I > 1/2 (which account for ∼75% of all NMR-active nuclei) are additionally broadened by the quadrupolar interaction (an interaction with the electric field gradient (EFG) at the nucleus).21 This can be very large, resulting in spectral broadening of 103–107 Hz. For most practically-relevant cases, the interaction can be treated as a perturbation to the conventional Zeeman energy levels. To a first-order approximation, the effect of the quadrupolar interaction is to perturb the Zeeman levels and lift the degeneracy of the transitions – producing (for half-integer spins) an (unaffected) central transition (CT) and satellite transitions (ST), with frequencies that depend on the magnitude of the interaction. In a powdered sample this results in a sharp CT and broader, powder-pattern lineshapes for the STs (often not considered when acquiring an NMR spectrum). When the quadrupolar interaction is large, a second-order perturbation must also be considered; this affects all transitions (including the CT, as shown in Fig. 1d for a spin I = 3/2 nucleus), but is usually much smaller, resulting in spectral broadening typically over ∼1–10 kHz. Although MAS could, in principle, remove the first-order quadrupolar broadening (if sufficiently fast MAS rates are available), the orientation dependence of the second-order anisotropic interaction is more complex (with terms proportional to P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) and to P4(cos
θ) and to P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)). This results in the retention of the spectral broadening (and an additional isotropic shift) even under sample rotation, as shown in Fig. 1f, for a nucleus with I = 3/2. Although the shape and width of the lineshape can provide information, the presence of more than one component once again limits resolution.
θ)). This results in the retention of the spectral broadening (and an additional isotropic shift) even under sample rotation, as shown in Fig. 1f, for a nucleus with I = 3/2. Although the shape and width of the lineshape can provide information, the presence of more than one component once again limits resolution.
It is possible to remove the second-order quadrupolar broadening completely, but more complex approaches are required. One option is to utilise sample rotation about two angles. This can be achieved simultaneously as in the double rotation, or DOR,21,22 approach, where an inner rotor spins at one angle (30.56°) inside a much larger outer rotor inclined at the magic angle. In the dynamic angle spinning, or DAS,21,23 experiment the sample is rotated about two different angles sequentially in a two-dimensional experiment. Although both approaches have been successfully applied, they have not generated widespread interest owing to their technical complexity, the need for specialist probe hardware and (for DOR) the limited sample rotation rates that are possible.
A more popular approach, using only conventional hardware, is the multiple-quantum (MQ) MAS experiment,21,24 where manipulation of the nuclear spins and sample rotation are combined to remove the second-order quadrupolar broadening. MQMAS is a two-dimensional experiment where different transitions within the multi-level nuclear spin systems are correlated in two different time periods in the pulse sequence. Although very commonly employed, MQMAS does suffer from relatively poor sensitivity – a problem addressed by the conceptually similar satellite-transition (STMAS) experiment,21,25 where the correlation now involves the satellite and central transitions. STMAS exhibits much higher sensitivity but is more technically challenging to implement, requiring very accurate adjustment of the spinning angle, a stable and controlled spinning rate and accurate pulse timings.
If the anisotropic interactions present are very significant sufficiently high MAS rates to average these interactions may not be practically achievable. In such cases, it is possible to acquire a “wideline” spectrum of a non-rotating sample and attempt to measure the broad lineshapes directly. This typically involves the use of spin echo experiments (to avoid lineshape distortions) and, for very broad lines, can involve the acquisition of the spectrum in a number of separate steps, acquired at different frequencies.21,26 Although wideline NMR spectra can provide information on very large interactions, there is typically little site resolution and it is generally only feasible to extract information when the number of species present is low.
Following the acquisition of high-resolution NMR spectra, there are many ways to obtain additional information. In many cases, the aim is to selectively reintroduce (or recouple) interactions that have been removed by MAS, such that they can be accurately measured separately.1,2,27,28 The measurement of additional parameters aids unambiguous spectral assignment and provides more information for comparison to calculated parameters. The interactions between spins can also be exploited for the transfer of magnetisation in two-dimensional experiments,1,2 which are able to probe through-bond connectivities (via the J coupling) or spatial proximities (via the dipolar coupling).
Whatever the type of spectrum acquired, extracting accurate NMR parameters and deciphering the structural information it contains remains a perpetual challenge. Without help from computation it is possible that much of the structural insight afforded by NMR spectroscopy will lie unexploited. Understanding how computation can work alongside experiment and aid spectral interpretation is, therefore, a vital step in the structural characterisation of complex materials.
1.2 Theoretical simulation of solid-state NMR parameters
In order to compute the NMR parameters for a solid, a quantum mechanical (QM) model, whereby the Schrödinger equation is approximated, is required, providing the total energy from which all properties can subsequently be derived. The overwhelming majority of QM calculations applied to the solid state adopt the framework set out by density functional theory (DFT), where the ground state electronic energy, E0, can be described as a functional solely of the electron density, ρ(r).29,30 Within DFT, the electronic energy is given by| E0[ρ(r)] = ENe[ρ(r)] + TS[ρ(r)] + J[ρ(r)] + EXC[ρ(r)], | (1) |
Owing to the periodic nature of most solids, Bloch's theorem,
| V(r + L) = V(r), | (2) |
| ψk(r) = eik·ruk(r), | (3) |
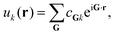 | (4) |
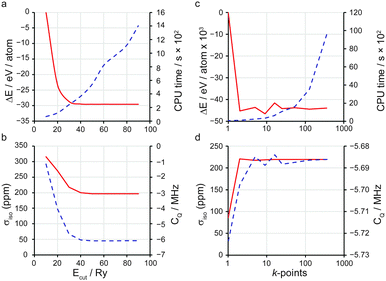
Two key factors contribute to the quality of a planewave DFT calculation: (i) the number of indices k in eqn (3) and (4) (termed k-points) for the sampling of the first Brillouin zone in reciprocal space; and (ii) the number of indices G in eqn (4) (termed G-vectors) for the number of planewave basis functions. The choice of these parameters is typically treated as a convergence problem, where each is improved separately to the point where the desired property is invariant (at an appropriate level of accuracy) to further improvement. The k-points are typically placed on a Monkhorst–Pack (MP) grid,35 where the density is easily controlled by a k-point spacing parameter, which is then transferable between related systems. The number of planewaves is simply controlled via a kinetic energy cut off,
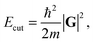 | (5) |
An additional consideration in many planewave DFT codes is the use of pseudopotentials. These allow for two key approximations to be applied to the core regions of atoms, providing enormous efficiency benefits with little loss in accuracy (since the total energy and most chemical properties rely on the valence regions): (i) the frozen core approximation, where the region within a defined atomic core radius, rcut, is determined from an isolated atom and fixed thereafter, thus reducing the number of electrons that need to be explicitly considered; and (ii) the rapid oscillations of wavefunctions close to nuclei are removed and replaced with a “smoothed”, or “pseudised” wavefunction (and associated potential) more easily described by the planewave basis set. The most commonly-adopted pseudopotentials are norm-conserving pseudopotentials (NCP).36 Though widely adopted in condensed matter calculations, these suffer from poor transferability and lack “softness”, requiring large Ecut values, thus reducing computational efficiency. Another approach is that of ultra-soft pseudopotentials (USP),37 in which the norm-conservation rule is relaxed. USPs offer increased softness and transferability, though their increased complexity has slowed their implementation in scientific codes. Their use in the CASTEP code38 for many tasks (including NMR calculations39) has recently been shown to be well converged against the all-electron WIEN2k40 and other solid-state DFT codes.41
For certain solid-state properties, such as NMR chemical shifts, the nature of the all-electron (AE) wavefunction, in particular in the region close to the nucleus, is important. Following a pseudopotential electronic structure calculation, it is desirable to reconstruct the AE wavefunction before calculating such properties. A method for performing this reconstruction through the projector augmented wave (PAW) was set out by van de Walle and Blöchl42 as
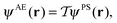 | (6) |
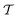 , is generated alongside the pseudopotential. A key extension of this theory that has resulted in the widespread uptake within the solid-state NMR community is the GIPAW method,6 and later its implementation with USPs.39 Therein
, is generated alongside the pseudopotential. A key extension of this theory that has resulted in the widespread uptake within the solid-state NMR community is the GIPAW method,6 and later its implementation with USPs.39 Therein 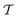 is replaced with a field-dependent transformation operator,
is replaced with a field-dependent transformation operator, 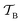 , which resolves the gauge-origin problem introduced by PAW.43 GIPAW allowed magnetic response properties to be computed for the first time in a periodic DFT code.
, which resolves the gauge-origin problem introduced by PAW.43 GIPAW allowed magnetic response properties to be computed for the first time in a periodic DFT code.
A more recent development for solid-state NMR calculations is the consideration of scalar relativistic effects through use of the Zero-Order Relativistic Approximation (ZORA) in the pseudopotential generation.44 Relativity becomes increasingly more relevant with increasing nuclear mass, as the velocities of electrons near the nucleus approach a significant fraction of the speed of light. Relativistic effects can be considered through less accurate Koelling–Harmon calculations, which give absolute shielding values that differ from ZORA values approximately by a constant and, therefore, could be dealt with by referencing (see Section 2.1.2). However, with more recent advances, such as J-coupling calculations (see Section 2.1.5), in which the core–valance interactions become vital, require highly accurate consideration of relativistic effects.
2. The combination of solid-state NMR and planewave DFT
2.1 NMR parameters and conventions
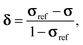 | (7) |
| δ ≈ σref − σ, | (8) |
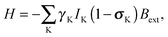 | (9) |
| Bin(RK) = −σKBext, | (10) |
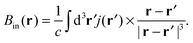 | (11) |
Diagonalisation of the symmetric part of σ gives the three principal components, where, by convention,45 |σ33| ≥ |σ22| ≥ |σ11| (i.e., |δ11| ≥ |δ22| ≥ |δ33|) and the isotropic magnetic shielding, σiso = (σ11 + σ22 + σ33)/3. Common conventions for describing the chemical shift anisotropy (CSA) are due to Herzfeld and Berger, and Haeberlen.46 In the former, the span, Ω = (δ11 − δ33) = σ33 − σ11 (Ω ≥ 0), describes the width of the lineshape and the skew, κ = 3(δ22 − δiso)/Ω = 3(σiso − σ22)/Ω(−1 ≤ κ ≤ 1), describes the asymmetry of the tensor, where κ = ±1 represents axial symmetry. In the latter convention, where |δzz − δiso| ≥ |δyy − δiso| ≥ |δxx − δiso|, the reduced anisotropy, δ = δzz − δiso and asymmetry parameter, η = (δyy − δxx)/δ(0 ≤ η ≤ 1) are used.
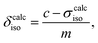 | (12) |
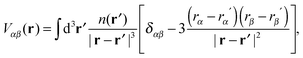 | (13) |
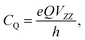 | (14) |
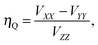 | (15) |
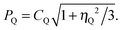 | (16) |
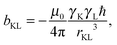 | (17) |
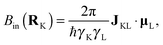 | (18) |
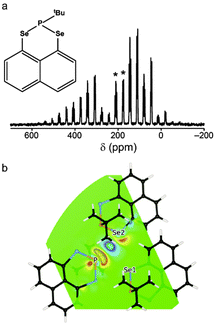 | ||
| Fig. 3 (a) 77Se (9.4 T, 5 kHz MAS) NMR spectrum of 1, with isotropic centreband multiplets denoted *. (b) CDD plot of the 77Se2–31P through-space J coupling in 1 at the PBE/USP (non-relativistic) level. Reprinted with permission from ref. 57 Copyright 2015 American Chemical Society. | ||
2.2 Geometry selection and optimisation
A vital pre-requisite for ab initio prediction of NMR parameters is an accurate structural model. Models can be generated computationally or from experiment, the latter typically using Bragg diffraction. In both cases, it is important to understand the expected accuracy (and limitations) of any experimental approaches, to consider exactly how structures were generated and whether they have been modified in any way. The sensitivity of NMR spectroscopy to the local structural environment can result in significant variation of NMR parameters as a result of only very small changes in the geometry. In many cases, the structural models produced initially do not correspond to a DFT energy minimum. For example, those generated computationally may have been produced using a different level of theory, or may result from a manual modification of an existing structure (i.e., substitution of atom types). Models refined from diffraction measurements will vary in accuracy depending upon whether they have been obtained from single-crystal or powder X-ray diffraction (XRD), using synchrotron radiation or from neutron diffraction. Typically, diffraction experiments are performed between room and cryogenic temperatures, while DFT calculations typically do not include temperature effects, effectively representing the system at absolute zero. As a consequence, the experimental unit cell volumes and atomic positions may differ from those in the lowest-energy DFT structure.Although NMR calculations are valid for all possible atomic arrangements, it is generally recommended to first optimise the atomic positions at the DFT level of theory, minimising the forces acting upon the atoms. Important considerations include the optimisation protocol, the use of symmetry, which allows high computational efficiency but may prevent the location of lower-symmetry minima, and the use of a dispersion correction scheme, particularly for molecular crystals or flexible materials.
Yates et al. demonstrated the importance of geometry optimisation in a combined computational and experimental study of flubiprofen,62 where mean differences between experimental and computed 13C NMR δcalciso values were improved from 5.5 ppm for the XRD structure to 2.7 ppm through strategy (i), and finally to 2.5 ppm by strategy (ii). 1H and 19F NMR parameters were also improved, and structural parameters were shown to more closely match neutron data than those from XRD. Brouwer et al.52 investigated the 13C CSA tensors for two forms of glucose, α-glucose (structure obtained from neutron scattering) and α-glucose·H2O (structure from single-crystal XRD). The former showed good agreement between predicted and experimental NMR parameters, whereas the latter required optimisation of the H positions before agreement could be obtained. Although one might reasonably expect the position of heavier atoms to be more accurately determined using XRD, optimisation of the atomic positions of nearby atoms may still produce better agreement between experimental and calculation and, more generally, may improve on any inherent inaccuracies and refinement biases. The larger shift range often observed for heavier atoms, and the presence of a number of interactions (e.g., quadrupolar couplings) can provide a sensitive probe of specific geometries, particularly for inorganic compounds. For the microporous aluminophosphate, AlPO-14, Ashbrook et al. found significantly-improved agreement between computed and experimental 27Al and 31P NMR parameters upon optimisation.9,63 GIPAW calculations of δcalciso, following optimisation of XRD geometries, gave mean unsigned errors (MUE) against experiment for 27Al and 31P of 4.5 and 3.7 ppm by strategy (i), 2.1 and 2.6 ppm by strategy (ii) and 1.0 and 2.6 ppm by strategy (iii). Indeed, for 31P, geometry optimisation changed the spectral assignment. Predicted 27Al quadrupolar parameters were also significantly improved upon optimisation, reducing the MUE in CQ from 3 to 0.3 MHz.
The aim of NMR crystallography is the production of a structural model that gives a closer match to experimental NMR spectra, with DFT optimisation of the crystallographically-determined structure typically playing a key role. This has led some to remark that the accuracy of neutron scattering may be achieved through the combination of X-ray crystallography and DFT geometry optimisation,62,64,65 with fitting to solid-state NMR spectra providing experimental verification of the optimised structure. As examples, Kibalchenko et al. studied three possible models for the hydrogen-bonding network in α-D-galactose, comparing PBE and semi-empirical KT3 exchange–correlation functionals for geometry optimisation (H positions only) and GIPAW calculations.65 Upon optimisation of the H positions, two of the models were indistinguishable, but 1H GIPAW calculations were able to distinguish between the remaining options. Widdifield and Bryce,66 exploited the sensitivity of the 81Br CQ to the local structure to refine the displacement of Br along the c axis in MgBr2. Best agreement with experiment was obtained when the unit cell parameters were varied in the optimisation. In some cases, the changes produced by geometry optimisation can alter the scientific conclusion, as demonstrated by Johnston et al.67 who had shown in previous work that many bulk powders of NaNbO3, prepared using a variety of synthetic approaches, contained a mixture of different perovskite phases.68 GIPAW calculations by other authors69 had suggested that 93Nb NMR would provide a useful tool for distinguishing between NaNbO3 polymorphs, but high forces on the atoms indicated optimisation may be required. Upon optimization of the structural models, most of the phases exhibited very similar NMR parameters (with some 93Nb CQ values changing by as much as ∼20 MHz) suggesting that 93Nb NMR would not be able to distinguish polymorphs, or to confirm the phase purity of a synthetic sample.67
Although the advantages of geometry optimisation are well established, it should be noted that this is not always required. If initial structural models are accurate (i.e., have low forces on the atoms) satisfactorily good agreement with experiment may be obtained. This can be the case when models are obtained from neutron diffraction52,62 or using more sophisticated diffraction approaches. This was shown in a study of AlPO-15,70 where two structural models were considered, one obtained using charge-density experiments and one using synchrotron single-crystal diffraction. Good agreement with experiment was obtained for both candidate structures, without any optimization. The increased accuracy of the initial models was reflected in the average rms displacement of any atom along either x, y or z upon optimisation (0.015 Å and 0.026 Å), in comparison to the 0.0925 Å observed previously for a structure of templated AlPO-14 obtained from power XRD.63 Avoiding optimization also has the advantage that no errors or inaccuracies in geometry can be introduced from insufficiently high levels of theory, or the neglect of any interactions within the theoretical framework used. This problem was encountered by Martineau et al.,71 who found that agreement between experimental and calculated 19F NMR parameters in α-LaZr2F11 was poorer upon DFT optimization.
The neglect of dispersion interactions in a DFT calculation can have a number of effects on the optimisation of a structural model, commonly including expansion of the unit cell. The magnitude of these changes depends upon the functional used, and might be less of a concern in densely-packed rigid crystal lattices, but can be very significant for molecular crystals (where the absence of dispersion can cause the structure to “fall apart” or the packing of molecules to be significantly altered under DFT optimisation), or for more flexible microporous solids, such as metal–organic frameworks (MOFs). For example, no energy minimum was found for the narrow-pore form of MIL-53(Al) under DFT (PBE) optimisation, with the structure opening up to give the large-pore form.78 However, using the DFT-D2 scheme, an energy minimum was obtained. One solution to prevent unreasonable cell expansion is to constrain the cell parameters to those determined by diffraction. This is a commonly-used approach for molecular crystal structures, and was employed in many of the examples described in the previous section. However, this is not always a useful solution, as it assumes not only that the experimental measurements are accurate, but that the “average” structure produced by diffraction experiments at finite temperature is similar to the 0 K DFT energy minimum. This approach will also cause problems for any cases where there is modification of the model (e.g., atom substitution) prior to optimisation.
In recent years the inclusion of SEDC schemes in many planewave codes has enabled their use in geometry optimisation, and also in modelling adsorption or surface interactions. Dudenko et al.79 exploited SEDC schemes in recent work probing intermolecular hydrogen bonding and π–π interactions in an organic co-crystal. DFT optimisation using PBE gave a unit cell expansion of ∼19%, while the use of DFT-D2 and TS both resulted in a contraction of the unit cell (of ∼6% and ∼3%, respectively). Best agreement with the experimental unit cell parameters was achieved using TS, and this correction also gave the closest agreement with the chemical shifts calculated for a fixed unit cell. A Grimme (D2) dispersion correction scheme was also used by Folliet et al.80 to study the adsorption of glycine into mesoporous silica, with calculated NMR parameters able to differentiate between different binding sites (e.g., vicinal silanols or at silanol nests). The flexibility of MOFs, described above, can result in significant changes in structure and NMR parameters after DFT optimisation. Fig. 4 shows the example of MIL-53(Sc),81 where the diffraction-based structural model of the closed-pore form (green in Fig. 4) shows a “flattened” pore structure resulting from π–π interactions between the terephthalate linkers. However, the predicted NMR parameters, given in Table 1, are in relatively poor agreement with experiment. DFT optimisation using purely PBE gives a more expanded structure (black in Fig. 4), and the NMR parameters are significantly different, and in poor agreement with experiment. Fig. 4 shows that the optimised structures obtained using either PBE with DFT-D2 or TS correction schemes are extremely similar to that from diffraction, and the NMR parameters are much closer to experiment. Sneddon et al.82 considered the effect of SEDC schemes for AlPO frameworks – porous materials which have more structural flexibility than dense solids, but are more rigid than many MOFs. For a series of as-made AlPOs, poor agreement between experimental and calculated NMR parameters was observed when diffraction-based structures were used, demonstrating the need for optimisation. Optimisation using PBE alone resulted in an increase in unit cell volume (of 2.5–4%), while the use of DFT-D2 or TS dispersion corrections with PBE gave a decrease in cell volume (of 0.5–1%). Interestingly, calculated NMR parameters showed much better agreement with experiment after optimisation, but very little difference was observed for structures optimised with or without dispersion, as a result of the similarity of the local structure in the optimised models.
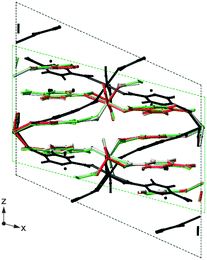 | ||
| Fig. 4 Overlay of the XRD structure of MIL-53(Sc) (green) and those optimised under PBE (black), PBE-D2 (grey) and PBE-TS (red). | ||
2.3 Computational structure generation
In some cases, diffraction-based structural models are not available or are incomplete, and an alternative approach is required. The simplest option is to manually adapt an available model for a related material with a similar structure, making atom substitutions, removing water molecules and modifying the length of alkyl chains or orientation of molecules. This can be very successful, although optimisation of the geometry (and the unit cell dimensions) is now a necessity. It is also possible to obtain partial or approximate structural models from other experimental and theoretical approaches, including solid-state NMR spectroscopy, where measurements that rely on dipolar interactions can provide distance constraints. As an example, elegant work by Brouwer et al. provided structural models for silica zeolites from 29Si–29Si double-quantum experiments.83 An automated model-building algorithm, which searches for the Si coordinates that provide best agreement between calculated and experimental double-quantum signal intensities was employed, along with some basic information (typically the space group) from diffraction. However, although a “structure solution” is obtained using this approach (i.e., the zeolite topology has been determined), the model remains incomplete, as the position of the bridging oxygen atoms is unknown, and there is uncertainty in the exact Si positions. Models can be refined either by DFT optimisation84 or by using NMR parameters (measured experimentally) as constraints.84,85 Perras and Bryce proposed a similar approach for the refinement of materials for which only low quality structural models were available, minimising the differences between experimentally-determined EFG tensors in Na2Al2B2O7 and those predicted by calculation.86 EFG tensor components were also used as constraints in the further refinement of the structure of ZrMgMo3O12.87 In work by Martineau et al.,12 basic powder XRD information (space group and unit cell parameters) was combined with a variety of solid-state NMR measurements (27Al, 19F and 67Zn NMR of the framework, and 1H, 13C and 15N NMR of the linker) to provide constraints for structural models of a Zn3Al2F12·[HAmTAZ]6 MOF. These were used as input for Monte-Carlo-based searches for candidate structures. Optimization of the atomic coordinates of the most likely structure was carried out using DFT, and the calculated NMR parameters shown to be in good agreement with experiment, confirming the accuracy of the model.In 2010, Day, Emsley and co-workers demonstrated the use of 1H solid-state NMR, CSP and GIPAW calculations for the NMR-crystallographic determination of thymol.95 The CSP adopted the general protocol introduced earlier:96 (i) subject the isolated molecule to a conformational search under molecular mechanics (MM); (ii) generate loosely-packed crystal structures of rigid molecules through Monte Carlo simulated annealing in common space groups and (iii) optimise selected stable structures (ca. 104) through a hybrid DFT/MM approach and rank by energy. From these, “physically realistic” structures (<10 kJ mol−1 above the most stable) were subjected to periodic GIPAW DFT calculations. Comparison of computed and experimental 1H chemical shifts, and of 1H spin-diffusion data, led to a predicted structure with a rmsd of 0.29 Å from the single-crystal XRD structure. Interestingly, the best structure was the third lowest in energy, emphasising the advantage of using a combination of methods (as opposed to CSP alone). In a subsequent study,97 this strategy was applied to the structural determination of four pharmaceutically-important molecules, namely cocaine, flutamide, flufenamic acid and theophylline. For the first three, the method was successful in determining the known XRD structures, although it was noted that (partial) assignment of the experimental spectrum adds to the robustness of the method, as the order of δcalciso values can change between predicted structures. In the case of theophylline, failure to discriminate between candidate structures was suggested to be due to the presence of only three peaks in the experimental 1H NMR spectrum, which was insufficient for statistical comparison. Most recently, a pharmaceutical with potential applications in Type 2 diabetes (AZD8329 form 4), with no known crystal structure, was subjected to CSP.98 The conformational space of isomers was explored through rotations about exocyclic single bonds, providing a set of geometries for CSP. In total, 80 conformations were tested in the 32 most common space groups, each with one molecule per unit cell. The NMR parameters were computed for a set of predicted structures (up to 30 kJ mol−1 above the most stable) and compared to pre-assigned 1H and 13C NMR spectra. The structure chosen was that with the smallest rmsd from the comparison of the 1H NMR parameters, and, notably, was not the lowest in energy.
To date, the combination of AIRSS and GIPAW calculations has featured in studies of battery materials101,102 and minerals.103 Morris and co-workers investigated LixE1−x (E = Si, Ge) phases by combining AIRSS and “species swapping” where Li and E were swapped into known structures from the ICSD.104 Convex hull diagrams, which enable a visual representation of relative stability over different compositions, suggested a range of new stoichiometries for both series. Following this work, in a study on germanium anodes in Li-ion batteries that combined AIRSS and in and ex situ solid-state NMR spectroscopy, Jung et al.101 showed that a previously unknown Li7Ge3 phase is the initial product of inclusion of Li into Ge. See et al.102 investigated the structures of LixSy battery systems using the same approach. Structures from AIRSS and species swapping resulted in a convex hull in which Li2S was the only stable structure. However, a range of metastable structures was also predicted, and the variation of 7Li and 33S NMR parameters investigated. More recently, Moran et al., used AIRSS to study the hydration of inner Earth minerals.103 Experimental investigation of these systems is extremely challenging, owing to the low levels of H, the small sample volumes (∼1–3 mg) that result from high-pressure syntheses, and the general problem of locating H crystallographically. Starting from the structure of the anhydrous wadsleyite, β-Mg2SiO4, the AIRSS protocol used was to substitute one Mg2+ cation (from the Mg3 site) with two H+ cations inserted at random positions within 3 Å of the vacancy, as shown in Fig. 5. Structures were then optimised using DFT (at relatively low values of Ecut and k-point spacing). The resulting 819 structures were ranked according to their relative enthalpy, before 103 structures were selected for more accurate DFT optimisation, and in silico NMR study, as shown in Fig. 5c. The calculated 1H, 2H, 29Si and 17O NMR parameters were used to assign the previous experimental spectra.105 The unusual 1H chemical shifts were shown to result from strong hydrogen bonding, with 1H δcalciso and 2H CQ having a linear dependence on the O–H and H⋯O hydrogen bond distances (Fig. 5d).
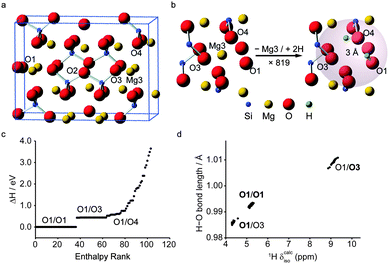 | ||
| Fig. 5 (a) View of the unit cell of β-Mg2SiO4 with (b) the AIRSS protocol used to produce 819 structures. (c) Enthalpy ranking of 103 AIRSS-generated structures chosen for more accurate DFT optimisation and NMR calculations (labels give the two sites of protonation). (d) Plot of H–O bond length against calculated 1H δiso for low-enthalpy structures; bold text signifies the protonation site leading to the labelled data points. Reproduced (in part) from ref. 103 with permission of the PCCP Owner Societies. | ||
2.4 The effect of temperature
Although DFT calculations are carried out on static structures at 0 K, NMR experiments NMR are typically performed at or close to room temperature. It may, therefore, be necessary to consider the effect of temperature and molecular motion on the computed parameters and tensors, both to improve agreement with experiment and to increase accuracy to the point where calculations can be used within an automated structural refinement process. Motion occurs in solids on many different timescales, and results in a variety of effects upon the NMR spectrum. Perhaps of most general interest is the effect of fast motion, such as molecular vibrations and conformational changes, in the prediction of NMR parameters.The effect of vibrational motion on NMR parameters has been investigated using Monte Carlo sampling of the quasi-harmonic vibrational wavefunction106,107 and vibrational configuration interaction techniques.108 Most recently, cheaper, less labour-intensive techniques for approximating temperature effects on NMR parameters have been reported.109,110 Monserrat et al.109 showed that the vibrational phonon modes provided by static DFT, can be coupled to the shielding tensor. Assuming a quadratic coupling, calculations for MgO, L-alanine and β-aspartyl-L-alanine performed well against (increasingly more expensive) harmonic and anharmonic Monte Carlo calculations, and displayed an improvement in agreement with experiment. Fig. 6 shows the change in magnetic shieldings from static DFT GIPAW calculations (with Δσcalciso = 0 ppm). Nemausat et al.110 also involved phonon modes at the equilibrium geometry of MgO, formulating the perturbation of the shielding tensor under the quasi-harmonic approximation, allowing anharmonic thermal-expansion effects to be taken into account in DFT. Such techniques could be applied generally and relatively cheaply (i.e., limited only by the cost of a phonon calculation) and suggest that temperature effects could be systematically and routinely included in NMR calculations in the future.
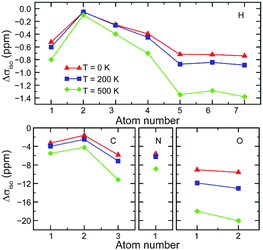 | ||
| Fig. 6 Change from static DFT (Δσcalciso = 0 ppm) in GIPAW isotropic shielding parameters of L-alanine with temperature corrections at 0, 200 and 500 K. Reprinted with permission from ref. 109. Copyright 2014, AIP Publishing LLC. | ||
To consider larger variations in conformation and geometry, or processes that occur on longer (i.e., ps to ns) timescales, more explicit treatment of temperature must be employed. Molecular dynamics (MD) is the most commonly-applied technique in this area.106,111–115 In MD, forces acting upon atoms are propagated over time as classical particles via Newton's equations of motion, where the source of the forces can be a parameterised forcefield (classical MD) or DFT calculations (ab initio MD or BOMD, i.e., applying the Born–Oppenheimer approximation at each instantaneous nuclear configuration). An ensemble of dynamical “snapshots” is generated, over which computed NMR parameters can be averaged. Where parameters are available, classical MD is of lower cost, and longer timescales can be considered. However, ab initio MD is not reliant on parameterisation and can achieve high accuracy, but at relatively high computational cost, necessitating short timescales and potentially precluding the modelling of slower dynamic processes. A combination of these approaches was demonstrated by Robinson and Haynes, where a classical force field was parameterised with quantum-mechanical forces,114 leading to close reproduction of the GIPAW NMR parameters obtained from ab initio MD for L-alanine with marked savings in cost. Fully classical MD simulations were employed by De Gortari et al.,113 along with GIPAW calculations, to compute the time-averaged 13C NMR parameters of a peptide. Ab initio MD has been applied to investigate 2H quadrupolar interactions,106 and dynamics in proton conductors111 and organic solids.112 A key benefit of ab initio MD is the adoption of a methodology consistent with that used to compute the NMR parameters. An additional class of dynamic calculations is path integral MD (PIMD), where the nuclei, as well as the electrons, are modelled as quantum particles; the former modelled as a number of “beads” by linking multiple parallel ab initio MD simulations. As a result, quantum nuclear effects, such as zero-point motion and tunnelling can be considered. Dračínský and Hodgkinson116 showed improved agreement with experiment for NMR parameters averaged over PIMD snapshots, with 1H delocalisation resulting in a deshielding of the alkyl 13C resonances in molecular crystals.
As the timescale and type of motional processes vary, their effects upon the NMR spectrum will also change. If motion is rapid, a time-averaged spectrum is observed. Computationally, it is possible to understand this spectrum by averaging NMR parameters for each relevant static 0 K structure (ensuring for anisotropic interactions that the orientation of the tensor and not just the principal components are considered). A common example is methyl group rotation in organic molecules (where one rather than three distinct 1H shifts are observed experimentally). Griffin et al. showed that isotropic 17O MQMAS spectra of hydrated silicate minerals could only be reproduced computationally if an average of the 17O quadrupolar and shielding tensors for different OH group orientations was considered, demonstrating a fast exchange between the various H positions.117 The averaging effect of motion on NMR parameters was also demonstrated by Bonhomme and co-workers in a series of studies of octameric silsesquioxanes.118–121 For 13C CP MAS NMR spectra, a simple geometrical model was used to rationalise the reduction in CP efficiency,118–120 resulting from the averaging of heteronuclear dipolar interactions by fast reorientation of the alkyl groups around the Si–C bonds. The 13C CSA tensors were also affected by dynamics, and averaging of a series of theoretical tensors determined from GIPAW calculations provided much better agreement with the experimental lineshapes.121
For motion on slower timescales, averaging (particularly of anisotropic interactions) may be incomplete, leading to broadening of spectral resonances and changes in shifts and lineshapes in experimental spectra. Additional information can be extracted by performing variable-temperature NMR experiments, changing the rate of motional processes and their effect upon the NMR spectrum. While it is not always possible to change rates to such a degree that fast averaging is observed (at higher temperatures), or that motion is ceased completely (at lower temperatures), the variation in the experimental spectra provide information on the type and rates of the dynamics present. The complex spectral lineshapes can be difficult to interpret directly, but the interaction tensors provided by static GIPAW calculations provide a vital input for lineshape simulation packages. As an example, recent work by Kim et al. used variable-temperature 17O NMR spectroscopy and GIPAW calculations to investigate dynamics in the proton conductor, CsH2PO4.122 GIPAW calculations were able to prove that H1 is localized in an asymmetric O–H–O hydrogen bond, while H2 proton undergoes rapid exchange between two sites within a hydrogen bond, at rates of >107 Hz.
Variable-temperature 17O MAS NMR spectra could only be reproduced in simulation by considering at least two rate constants for rotations of the phosphate ions, as shown in Fig. 7. GIPAW calculations were also used to understand the linebroadening associated with proton hopping in silicate humite minerals in 17O STMAS and 2H MAS NMR spectra.117,123 Unlike MQMAS, STMAS is sensitive to microsecond-timescale dynamics,124 and the broadening observed depends upon the variation in the quadrupolar coupling and the timescale of this change. GIPAW calculations were able to provide information on the former (from the magnitude, asymmetry and relative orientation of the quadrupolar tensor for each static model structure), enabling the latter to be determined by comparison to experiment. The rate constant extracted (3.2 × 107 s−1)117 was in good agreement with that found independently from 2H MAS experiments, which also enabled an activation energy of 40 ± 4 kJ mol−1 to be determined.123
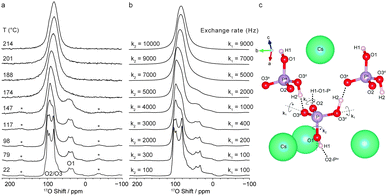 | ||
| Fig. 7 (a) 17O (16.4 T) variable-temperature MAS NMR spectrum of CsH2PO4 and (b) simulated 17O lineshapes assuming exchange rates for rotations of k1 and k2. (c) Structure around a phosphate ion showing bond rotations considered. Reproduced from ref. 122. | ||
2.5 Treatment of disordered systems
A general feature of the solid state is its inherent periodicity or translational symmetry, which facilitates structural characterisation by diffraction, as evidenced by the extensive use of diffraction-based structural models in NMR crystallography. However, variation of one or more aspects of the periodicity can modify the optical, electrical or thermal properties of a material, widening potential applications. Such disordered materials can be challenging to characterise, with diffraction techniques producing information only on the “average” structure. In contrast, the sensitivity of NMR spectroscopy to the local structural environment, without any requirement for long-range order, makes it an ideal probe of disordered solids. The complexity of the lineshapes that result, however, hinders spectral assignment or interpretation and the extraction of detailed structural information. At first sight, this appears to be a perfect opportunity to support experiment with theoretical calculations, but difficulties both in producing relevant structural models, and in understanding their exact relationship to the material studied experimentally, poses a considerable challenge. It may not be possible to generate models that contain all short- and long-range environments present in a material, particularly as the extent of disorder increases, but insight into experimental spectra can be obtained using simpler, systematic structural changes.7,9,125For low levels of substitution, it may be possible to construct relevant structural models by substituting just one atom into the structure of a pure end member. DFT calculations then provide insight into the NMR parameters for the substituted atom itself and typical changes in the NMR parameters of the surrounding atoms. If substitution onto more than one crystallographic site is possible, a series of calculations is required. For very low levels of substitution or smaller unit cells, it may be necessary to construct a supercell to ensure that substituted atoms are sufficiently isolated. This approach was used very successfully by Laurencin et al.126 to study doping of Mg in hydroxyapatite. Calculations carried out on 1 × 2 × 1 supercells with one Ca atom substituted by Mg (corresponding to a substitution level of 5%), showed an energetic preference for Mg to substitute onto the Ca(II) position, specifically at the Ca(IIb) or Ca(IIc) sites, in agreement with 43Ca NMR spectra. Grey and co-workers127 also used supercells (3 × 3 × 3) to consider low-level doping of Y into BaSnO3. Calculations showed that Y preferred to substitute onto the Sn site rather than the Ba site. Griffin et al.47 considered the substitution of F− (for OH−) in clinohumite, 4Mg2SiO4·Mg(OH)2, as the relative F−/OH− ordering could not be determined by diffraction. Calculations showed that the 19F chemical shift was sensitive to the nature of the species on the two closest anion sites, at 2.7 and 3.2 Å, respectively, leading, as shown in Fig. 8a, to four different 19F chemical shifts. This was in good agreement with the four resonances observed in the 19F MAS NMR spectrum, enabling these to be assigned, and their relative intensities provided information on anion disorder. Similar approaches, considering a limited number of possible structural models were used by Cuny et al. for rare earth metal carbides (e.g., YB2C), enabling possible arrangements of B and C to be excluded, owing to poor agreement with the experimental 11B NMR spectra,128 and by Seymour et al. for Mg-substituted AlPO frameworks, confirming preferential substitution of Mg onto the Al1 site.129 When the number of possible atomic arrangements increases to the point where these cannot all be considered, it may be necessary to select a subset of models for computational study. One approach is to create a series of structures where the environment of a species is systematically varied, to consider the effect of changing either neighbouring, next-nearest neighbouring (NNN) or longer-range neighbouring atoms. While this may not provide perfect agreement with experiment (as some structures may not be chemically feasible, or the set may exclude arrangements that are present experimentally), the changes in the predicted NMR parameters may provide sufficient insight to assign the NMR spectrum. This was demonstrated by Ashbrook and co-workers in a series of studies of Y2(Sn,Ti)2O7 pyrochlores,53,54,130,131 where the effect of NNN cation substitution was investigated using 89Y and 119Sn NMR spectroscopy. In order to assign the experimental NMR spectra a series of DFT calculations were performed where the atoms on the six B sites (see Fig. 8b) surrounding Y or Sn were varied, while the remaining B-site cations were all occupied either by Sn or by Ti, resulting in 13 × 4 models. As shown in Fig. 8c, a systematic change in δcalciso was observed for 89Y as Ti was substituted for Sn, while the changes for 119Sn were much smaller, resulting in an overlap of spectral resonances. Although a limited set of calculations, the information obtained was sufficient to assign the 89Y spectral resonances, and analysis proved a random distribution of B-site cations.53,54,130,131
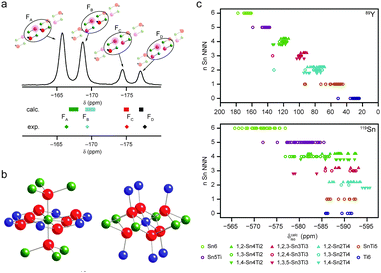 | ||
| Fig. 8 (a) 19F MAS NMR spectra of (54%) fluorinated clinohumite (4Mg2SiO4·Mg(OH,F)2), with calculated chemical shifts for model structures with varying F substitution shown. Reprinted with permission from ref. 47 Copyright 2010 American Chemical Society. (b) Local arrangement of atoms around the A (occupied by Y) and B (occupied by Sn or Ti) sites in a pyrochlore structure. (c) Plots showing the calculated 89Y and 119Sn isotropic chemical shifts as a function of the number of Sn NNN. Reprinted with permission from ref. 53 Copyright 2009 American Chemical Society. Reproduced (in part) from ref. 131 with permission of the PCCP Owner Societies. | ||
A similar approach was taken by Massiot and co-workers for the study of chemical disorder in gehlenite (Ca2Al2SiO7).125,132 The gehlenite structure consists of alternating layers of (Si/Al)O4 tetrahedra, which contain T1 sites fully occupied by Al, and T2 sites occupied by Si or Al. There are seven possible Al environments, which cannot be distinguished in the average structural model from diffraction. The NMR parameters measured experimentally were compared to those from DFT supercell calculations, allowing spectral assignment and confirming that the Si/Al distribution deviated from that predicted by Loewenstein's rule.125,132 Where systematic variation of a structure is not feasible, structural models may be generated by randomly distributing atoms onto crystallographic sites, either in a unit cell or supercell. This approach was used in recent work by Ferrara et al.133 who considered the distribution of La and Sr in six (2 × 2 × 4) supercells of LaSrAl3O7, with cation arrangements obtained using a simple pseudorandom number generator. A linear relationship was observed between the 27Al CQ and the distortion of the AlO4 tetrahedra, while the distortions themselves were shown to result from the distribution of La and Sr. Although clearly not a procedure that considers all possible distributions of atoms, the number of different environments sampled was sufficient to assign the 27Al resonances, and to provide insight into the distributions of quadrupolar and shielding parameters. Looking forward, as the number of potential models that need to be considered for more complex problems increases, more rapid (but less accurate) computational methods, such as Monte Carlo techniques and/or new algorithms to accommodate disorder in supercells, may be required to generate a large number of models, before a subset are selected for detailed analysis.
Recent work by Cadars et al.134 attempted to reproduce the variation in chemical shift that arises from slight structural disorder in an organic molecular solid. Calculation of the low-energy vibrational modes in bisphosphinoamine provided a series of physically reasonable local distortions that were then used as candidate structural models to represent a static distribution of local geometries. Calculated 31P NMR parameters were used to simulate two-dimensional correlation spectra, and comparison to experiment identified the types of structural deformation compatible with the local disorder. In many materials, atoms or groups are disordered over a small number of relatively well-defined sites. When this is the case, and the proportion of atoms with varying position or the number of sites involved is small, a reasonable number of calculations can accurately model the spectrum of the disordered material. For example, this approach has been used successfully in recent work on AlPO frameworks,135 and perovskite-based materials.136 Seymour et al.135 were able to assign the 27Al and 31P NMR spectra of as-made STA-2, where the number and position of OH groups coordinated to the framework was unknown. A combination of solid-state NMR experiments and powder XRD measurements determined that the OH groups bridged between Al1 and Al2, and identified three potential sites within the framework cancrinite cages. NMR parameters calculated for nine models with varying relative OH positions were all in reasonable agreement with the NMR spectra (enabling assignment), but some were shown had much poorer agreement with experimental 27Al/31P correlation spectra. Grey and co-workers136 investigated the a hydrated brownmillerite phase, Ba2In2O4(OH)2. This material contains partially-occupied H sites, and calculations with differing H arrangements were able to assign the experimental 1H and 17O NMR spectra, identifying three possible proton sites and differing hydrogen-bonding arrangements.
The lack of positional periodicity can arise from differences in the packing of individual molecules or of chains/layers. For example, Carnevale et al.137 showed that the linewidths in 13C MAS spectra of boroxophenanthrene anhydrides resulted from disorder in the orientation of the B–O–B bridges in the π-stacked molecules. They were also able to identify the formation of the anhydride (from the corresponding dimer) in a low-temperature solid-state reaction, a transformation that was not detected by XRD. Disorder in the stacking of layers in silicate materials was studied by Cadars et al.138 NMR spectroscopy was able to provide information on the number and multiplicity of Si sites, the Si–O–Si connectivities and constraints on interatomic distances in a new layered silicate [Si5O11H][C9N2H15]·1.9(H2O). Possible space groups were identified by XRD, but the incomplete stacking of the silicate sheets prevented full structure solution. Only one of the possible space groups suggested was in agreement with NMR measurements, providing three similar, but distinct, structure solutions. A set of models, with the organic template inserted between the layers at different positions and with different orientations, was considered using DFT calculations, and the single model that showed the best agreement with the calculated NMR parameters selected. Work by Véron et al.139 considered positional disorder in CaSi1/3B2/3O8/3, where the average diffraction structure contains arrays of TO4 chains, with partial occupancy of the bridging O site, with T = 1/3 Si and 2/3 B, and significant distortion of the tetrahedra. 11B NMR confirmed the presence of BO3 units, each associated with an oxygen vacancy in the chain, confirming B–O–B bonds were not present, and that the structure is made up of different topological arrangements of Ca3B2SiO8 units.
In some materials the position of atoms or groups may not be determined at all by diffraction, e.g., for light atoms in dense solids, or for systems with significant disorder. In this case, simple structural models can be constructed by placing atoms at chemically-reasonable positions, or at positions indicated by NMR experiments (which provide information on the number and type of coordinating atoms, or constraints on internuclear distances). This approach was taken by Griffin et al. in early work on the hydration of wadsleyite,105 where the position of the substituted H had not been determined. Based on information from 1H, 2H, 29Si and 17O NMR, and suggestions from previous work, H were placed in chemically-reasonable positions, generating a series of candidate structures. Comparison of predicted and experimental NMR parameters supported the presence of H in some positions, but demonstrated that substitution at some sites was much less likely. It is clear that when atoms or groups are placed manually, not only are a limited subset of models considered, but there may be bias in the type(s) of positions chosen. In contrast, automated computational approaches can enumerate, simulate or randomise large sets of candidate structures with the reduction of any bias (for the case of wadsleyite, the authors went on to explore the use of AIRSS, as described above).
One very successful combination of NMR, MD and GIPAW has been in understanding the structure of glasses, work pioneered by (among others) Charpentier.140,141 In one approach, using classical MD, the glass structure is represented by an ensemble of particles using empirical forcefields, with initial configurations generated using a random distribution of a specified number of atoms in a cubic box (consistent with the experimental composition and density). To ensure periodicity is not imposed on too small a length scale, large boxes, containing thousands of atoms, are required. Typically, a melt-quench approach is used, with MD simulations carried out at high temperature (to simulate a liquid), before the system is cooled and equilibrated. While successful, the need to derive interatomic potentials poses a challenge for multicomponent glasses, and transferability can be limited. These limitations can, in principle, be overcome using ab initio MD, where empirical parameters are not required. However, to ensure larger systems may still be studied efficient computational algorithms are required, and the increase in computational cost is significant. Typical ab initio MD calculations can be carried out on ∼300 atoms over times of 100 ps, and are probably limited to glasses that contain four or fewer oxides. Once structures have been obtained, GIPAW calculations provide the distribution of NMR parameters expected, and simulated lineshapes can be compared to experiment. Spectral features can be assigned to particular chemical environments, and structural motifs that do not agree with experiment can be discounted. This MD-GIPAW approach has been applied with great success to vitreous oxides, silicate, aluminosilicate and borosilicate glasses (see ref. 141 for a recent review), with good agreement with experiment for MAS and MQMAS lineshapes.142 The flexibility of the glass structure may lead to larger discrepancies to experiment as a result of temperature effects, and thermal and effects may need to be included in future studies. Advances in computational hardware and code development will also enable the consideration of larger and more complex systems in the future.
3. Outlook
The use of NMR crystallography, and more generally of NMR spectroscopy, to determine detailed structural information, has significantly grown in popularity in recent years. This results, in part, from experimental advances, with the availability of higher magnetic field strengths, faster MAS rates and more complex hardware, such as multiple-channel probes, enabling sophisticated multinuclear and multi-dimensional experiments. Considerable recent progress has also been made in the efficiency and accuracy of computational approaches, and the increasing accessibility of computation to experimentalists. However, perhaps what has driven the growth of NMR crystallography most is the increasing realisation among practitioners of many specialist techniques that no one approach can usually “provide it all”. Solid-state structure can, and in fact should, be considered on differing length- and timescales, and combining information on long-range order and symmetry within a solid with more detailed information on the local structural environment, is vital for understanding the properties of materials, and how these can be controlled and directed. It is clear that NMR offers particular advantages for disordered systems that lack some aspect of periodicity, and for materials where dynamics are present. It is also clear that, in many cases, the structural models produced by diffraction are incomplete or not sufficiently accurate, and refinement of atomic positions, particularly of light atoms, is necessary. The exquisite sensitivity of NMR to small changes in local structure provides great complementarity to diffraction and enables a full (and detailed) structural picture to be obtained.It is evident that we are still relatively early in the development of NMR crystallography, and much of the potential of this approach has yet to be exploited. The future promises continued improvements in NMR hardware, probe technology and pulse sequence development. It may be argued that many advances will perhaps be more incremental, although the recent commercialisation of dynamic nuclear polarisation (DNP) techniques143 promises improvements in NMR sensitivity of one or two orders of magnitude, providing the prospect of more routine study of challenging nuclei, the observation of species (and defects) present at low levels in bulk materials, and the availability of greater amounts of structural information owing to the time saving available. If realised as envisaged, this will also force simultaneous improvements in computation and theory – areas where perhaps the most significant gains for NMR crystallography are to be realised. There is an urgent need for improvement in the accuracy (and efficiency) of computation, particularly if the goal of incorporating NMR into automated structure refinement is to be achieved. This may require the inclusion of temperature effects into calculations (to facilitate direct comparison to experiment), and the ability to consider larger numbers of atoms more routinely. There are many possible theoretical improvements to be made, not least in the accuracy and, perhaps more importantly, the transferability, of computational methodologies. The need for more complete inclusion of relativistic effects in periodic codes is becoming clearer for heavier nuclei. A significant advance would be the ability to calculate NMR parameters for paramagnetic systems in commercial periodic codes, as it is not easy to predict the shifts in NMR spectra, hindering spectral assignment significantly even for relatively small systems. This was highlighted in recent work by Dawson et al.144 studying paramagnetic Cu-based MOFs, where 13C shifts between +850 and −100 ppm (typical range 0–200 ppm) were observed. Simple approaches (considering proximities to the paramagnetic centre) were shown (using expensive and difficult 13C isotopic labelling) to produce an incorrect spectral assignment. For disordered solids, the requirement to generate and compute ever-larger numbers of candidate structures places increasing demands on software efficiency of software and hardware availability. While these have improved in recent years, the computational demands posed by systems of increasing chemical and topological complexity ensures these will be constant drivers. Improving protocols and workflow for approaches that require different computational methods (e.g., MM, MD, MC, DFT) to be combined, and enabling the transferability of information, sounds a much more trivial task, but will be able to provide significant and almost instant benefits.
The more philosophical challenge facing practitioners is the need to know what information is actually required in any particular case – whether accuracy levels of fractions of a ppm are vital, or whether a more general understanding of the absolute, or relative, magnitudes of interactions is sufficient. For disordered systems, deciding which structural models are relevant, how many can be considered on realistic timescales and levels of resource, and what information is required for structural insight are ongoing issues. How many models are “enough” to understand a disordered system? Can they provide a realistic description of the materials studied experimentally? Is this even needed to for spectral assignment and structural insight? Perhaps even more generally, chemists need to consider if it is always feasible to define “the structure” for complex materials – whether our apparent need for some form of pictorial representation is determining the methodology applied, restricting the information considered and is imposing undesirable constraints on the models produced, preventing a detailed atomic-scale understanding. Is it conceivable that, one day, an NMR spectrum could be considered a more detailed “picture” of the atomic level structure in a complex solid (assuming the components and contributions to the lineshapes can be interpreted) than an idealised ball-and-stick model of limited dimensions, containing non-chemical species with fractional occupancies and compositions? NMR crystallography is a long way from convincing people this is true, but it is starting to raise these questions and to initiate discussion about what a “structure solution” means for many materials. The current state-of-the-art is providing a significant motivation for the increasing use of simultaneous combinations of experimental (and theoretical) approaches, and demonstrating the unique insight that can then be obtained. It is to be hoped that future development of all aspects both fuels debates on how and why we characterise structure, but more importantly enables the design, control and development of new materials, with increasingly-useful applications of industrial, social and economic benefit.
Acknowledgements
The authors would like to thank the ERC (EU FP7 Consolidator Grant 614290 “EXONMR”) and SEA would like to thank the Royal Society and the Wolfson Foundation for a merit award, and the RSC for the award of the 2015 Corday Morgan Prize.References
- D. Apperley, R. Harris and P. Hodgkinson, Solid state NMR: basic principles & practice, Momentum Press LLC, New York, 2012 Search PubMed.
- S. E. Ashbrook, D. M. Dawson and J. M. Griffin, in Inorg Mat Ser, ed. D. W. Bruce, D. Ohare and R. I. Walton, Blackwell Science Publ, Oxford, 2014, pp. 1–88 Search PubMed.
- W. Koch and M. C. Holthausen, A Chemist's Guide to Density Functional Theory, Wiley-VCH, Weinheim, 2nd edn, 2001 Search PubMed.
- Calculation of NMR and EPR Parameters: Theory and Applications, ed. M. Kaupp, M. Bühl, V. G. Malkin, Wiley-VCH, Weinheim, 2004 Search PubMed.
- C. Pickard and F. Mauri, in Calculation of NMR and EPR Parameters: Theory and Applications, ed. M. Kaupp, M. Bühl and V. G. Malkin, Wiley-VCH, Weinheim, 2004, pp. 265–278 Search PubMed.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef.
- C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azaïs, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 112, 5733–5779 CrossRef CAS PubMed.
- T. Charpentier, Solid State Nucl. Magn. Reson., 2011, 40, 1–20 CrossRef CAS PubMed.
- S. E. Ashbrook and D. M. Dawson, Acc. Chem. Res., 2013, 46, 1964–1974 CrossRef CAS PubMed.
- NMR Crystallography, ed. R. K. Harris, R. E. Wasylishen and M. J. Duer, John Wiley & Sons, Hoboken, 2009 Search PubMed.
- C. Martineau, J. Senker and F. Taulelle, Annu. Rep. NMR Spectrosc., 2014, 82, 1–57 CrossRef.
- C. Martineau, A. Cadiau, B. Bouchevreau, J. Senker, F. Taulelle and K. Adil, Dalton Trans., 2012, 41, 6232–6241 RSC.
- E. R. Andrew, A. Bradbury and R. G. Eades, Nature, 1958, 182, 1659 CrossRef CAS.
- A. Pines, M. G. Gibby and J. S. Waugh, J. Chem. Phys., 1973, 59, 569–590 CrossRef CAS.
- S. R. Hartmann and E. L. Hahn, Phys. Rev., 1962, 128, 2042–2053 CrossRef CAS.
- D. P. Burum, Cross Polarization in Solids, eMagRes, John Wiley & Sons, Ltd, 2007 Search PubMed.
- P. Hodgkinson, Prog. Nucl. Magn. Reson. Spectrosc., 2005, 46, 197–222 CrossRef CAS.
- A. J. Shaka, Decoupling Methods, eMagRes, John Wiley & Sons, Ltd, 2011 Search PubMed.
- B. C. Gerstein, CRAMPS: High-Resolution NMR of High-γ Nuclei in Solids, eMagRes, John Wiley & Sons, Ltd, 2009 Search PubMed.
- P. K. Madhu, Isr. J. Chem., 2014, 54, 25–52 CrossRef CAS.
- R. E. Wasylishen, S. E. Ashbrook and S. Wimperis, NMR of Quadrupolar Nuclei in Solid Materials, John Wiley & Sons, Ltd., Chichester, UK, 2012 Search PubMed.
- R. Dupree, Double Rotation NMR, eMagRes, John Wiley & Sons, Ltd, 2007 Search PubMed.
- P. J. Grandinetti, Dynamic Angle Spinning, eMagRes, John Wiley & Sons, Ltd, 2007 Search PubMed.
- J.-P. Amoureux and M. Pruski, MQMAS NMR: Experimental Strategies and Applications, eMagRes, John Wiley & Sons, Ltd, 2007 Search PubMed.
- S. E. Ashbrook and S. Wimperis, Advances in STMAS, eMagRes, John Wiley & Sons, Ltd, 2007 Search PubMed.
- R. W. Schurko, Acquisition of Wideline Solid-State NMR Spectra of Quadrupolar Nuclei, eMagRes, John Wiley & Sons, Ltd, 2007 Search PubMed.
- M. H. Levitt, Symmetry-Based Pulse Sequences in Magic-Angle Spinning Solid-State NMR, eMagRes, John Wiley & Sons, Ltd, 2007 Search PubMed.
- I. Schnell, Prog. Nucl. Magn. Reson. Spectrosc., 2004, 45, 145–207 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- M. Ernzerhof, J. P. Perdew and K. Burke, Int. J. Quantum Chem., 1997, 64, 285–295 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, Chem. Rev., 2012, 112, 1839–1862 CrossRef CAS PubMed.
- P. J. Hasnip, K. Refson, M. I. J. Probert, J. R. Yates, S. J. Clark and C. J. Pickard, Philos. Trans. R. Soc. London, Ser. A, 2014, 372, 20130270 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- D. R. Hamann, M. Schlüter and C. Chiang, Phys. Rev. Lett., 1979, 43, 1494–1497 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401 CrossRef.
- P. Blaha, K. Schwarz, G. Madsen, D. Kvasnicka and J. Luitz, WIEN2k, Karlheinz Schwarz, Techn. Universität Wien, Austria, 2001, ISBN 3-9501031-1-2 Search PubMed.
- K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. D. Corso, S. d. Gironcoli, T. Deutsch, J. K. Dewhurst, I. D. Marco, C. Draxl, M. Dułak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Grånäs, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. Iuan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Küükbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordström, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G.-M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunström, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. v. Setten, V. V. Speybroeck, J. M. Wills, J. R. Yates, G.-X. Zhang and S. Cottenier, Science, 2016 DOI:10.1126/science.aad3000.
- C. G. Van de Walle and P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 4244–4255 CrossRef.
- J. R. Yates and C. J. Pickard, Computations of Magnetic Resonance Parameters for Crystalline Systems: Principles, eMagRes, John Wiley & Sons, Ltd, 2007 Search PubMed.
- T. F. G. Green and J. R. Yates, J. Chem. Phys., 2014, 140, 234106 CrossRef PubMed.
- J. Mason, Solid State Nucl. Magn. Reson., 1993, 2, 285–288 CrossRef CAS PubMed.
- R. K. Harris, E. D. Becker, S. M. C. de Menezes, P. Granger, R. E. Hoffman and K. Zilm, Pure Appl. Chem., 2008, 80, 59–84 CrossRef CAS.
- J. M. Griffin, J. R. Yates, A. J. Berry, S. Wimperis and S. E. Ashbrook, J. Am. Chem. Soc., 2010, 132, 15651–15660 CrossRef CAS PubMed.
- A. Zheng, S.-B. Liu and F. Deng, J. Phys. Chem. C, 2009, 113, 15018–15023 CAS.
- A. Sadoc, M. Body, C. Legein, M. Biswal, F. Fayon, X. Rocquefelte and F. Boucher, Phys. Chem. Chem. Phys., 2011, 13, 18539–18550 RSC.
- R. K. Harris, S. A. Joyce, C. J. Pickard, S. Cadars and L. Emsley, Phys. Chem. Chem. Phys., 2006, 8, 137–143 RSC.
- J. C. Johnston, R. J. Iuliucci, J. C. Facelli, G. Fitzgerald and K. T. Mueller, J. Chem. Phys., 2009, 131, 144503 CrossRef PubMed.
- D. H. Brouwer, K. P. Langendoen and Q. Ferrant, Can. J. Chem., 2011, 89, 737–744 CrossRef.
- S. W. Reader, M. R. Mitchell, K. E. Johnston, C. J. Pickard, K. R. Whittle and S. E. Ashbrook, J. Phys. Chem. C, 2009, 113, 18874–18883 CAS.
- M. R. Mitchell, D. Carnevale, R. Orr, K. R. Whittle and S. E. Ashbrook, J. Phys. Chem. C, 2012, 116, 4273–4286 CAS.
- M. Profeta, F. Mauri and C. J. Pickard, J. Am. Chem. Soc., 2003, 125, 541–548 CrossRef CAS PubMed.
- S. A. Joyce, J. R. Yates, C. J. Pickard and F. Mauri, J. Chem. Phys., 2007, 127, 204107 CrossRef PubMed.
- P. Sanz Camacho, K. S. Athukorala Arachchige, A. M. Z. Slawin, T. F. G. Green, J. R. Yates, D. M. Dawson, J. D. Woollins and S. E. Ashbrook, J. Am. Chem. Soc., 2015, 137, 6172–6175 CrossRef CAS PubMed.
- T. Wiegand, H. Eckert, J. Ren, G. Brunklaus, R. Fröhlich, C. G. Daniliuc, G. Lübbe, K. Bussmann, G. Kehr, G. Erker and S. Grimme, J. Phys. Chem. A, 2014, 118, 2316–2331 CrossRef CAS PubMed.
- T. Wiegand, H. Eckert, O. Ekkert, R. Fröhlich, G. Kehr, G. Erker and S. Grimme, J. Am. Chem. Soc., 2012, 134, 4236–4249 CrossRef CAS PubMed.
- M. W. Stanford, F. R. Knight, K. S. Athukorala Arachchige, P. Sanz Camacho, S. E. Ashbrook, M. Buhl, A. M. Z. Slawin and J. D. Woollins, Dalton Trans., 2014, 43, 6548–6560 RSC.
- R. K. Harris, P. Hodgkinson, C. J. Pickard, J. R. Yates and V. Zorin, Magn. Reson. Chem., 2007, 45, S174–186 CrossRef CAS PubMed.
- J. R. Yates, S. E. Dobbins, C. J. Pickard, F. Mauri, P. Y. Ghi and R. K. Harris, Phys. Chem. Chem. Phys., 2005, 7, 1402–1407 RSC.
- S. E. Ashbrook, M. Cutajar, C. J. Pickard, R. I. Walton and S. Wimperis, Phys. Chem. Chem. Phys., 2008, 10, 5754–5764 RSC.
- T. Pawlak, M. Jaworska and M. J. Potrzebowski, Phys. Chem. Chem. Phys., 2013, 15, 3137–3145 RSC.
- M. Kibalchenko, D. Lee, L. Shao, M. C. Payne, J. J. Titman and J. R. Yates, Chem. Phys. Lett., 2010, 498, 270–276 CrossRef CAS.
- C. M. Widdifield and D. L. Bryce, Phys. Chem. Chem. Phys., 2009, 11, 7120–7122 RSC.
- K. E. Johnston, J. M. Griffin, R. I. Walton, D. M. Dawson, P. Lightfoot and S. E. Ashbrook, Phys. Chem. Chem. Phys., 2011, 13, 7565–7576 RSC.
- K. E. Johnston, C. C. Tang, J. E. Parker, K. S. Knight, P. Lightfoot and S. E. Ashbrook, J. Am. Chem. Soc., 2010, 132, 8732–8746 CrossRef CAS PubMed.
- J. V. Hanna, K. J. Pike, T. Charpentier, T. F. Kemp, M. E. Smith, B. E. G. Lucier, R. W. Schurko and L. S. Cahill, Chem. – Eur. J., 2010, 16, 3222–3239 CrossRef CAS PubMed.
- P. J. Byrne, J. E. Warren, R. E. Morris and S. E. Ashbrook, Solid State Sci., 2009, 11, 1001–1006 CrossRef CAS.
- C. Martineau, C. Legein, M. Body, O. Peron, B. Boulard and F. Fayon, J. Solid State Chem., 2013, 199, 326–333 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- P. Jurečka, J. Černý, P. Hobza and D. R. Salahub, J. Comput. Chem., 2007, 28, 555–569 CrossRef PubMed.
- F. Ortmann, F. Bechstedt and W. G. Schmidt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205101 CrossRef.
- V. G. Ruiz, W. Liu, E. Zojer, M. Scheffler and A. Tkatchenko, Phys. Rev. Lett., 2012, 108, 146103 CrossRef PubMed.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- A. M. Walker, B. Civalleri, B. Slater, C. Mellot-Draznieks, F. Cora, C. M. Zicovich-Wilson, G. Roman-Perez, J. M. Soler and J. D. Gale, Angew. Chem., Int. Ed., 2010, 49, 7501–7503 CrossRef CAS PubMed.
- D. V. Dudenko, J. R. Yates, K. D. M. Harris and S. P. Brown, CrystEngComm, 2013, 15, 8797–8807 RSC.
- N. Folliet, C. Gervais, D. Costa, G. Laurent, F. Babonneau, L. Stievano, J. F. Lambert and F. Tielens, J. Phys. Chem. C, 2013, 117, 4104–4114 CAS.
- J. P. S. Mowat, V. R. Seymour, J. M. Griffin, S. P. Thompson, A. M. Z. Slawin, D. Fairen-Jimenez, T. Duren, S. E. Ashbrook and P. A. Wright, Dalton Trans., 2012, 41, 3937–3941 RSC.
- S. Sneddon, D. M. Dawson, C. J. Pickard and S. E. Ashbrook, Phys. Chem. Chem. Phys., 2014, 16, 2660–2673 RSC.
- D. H. Brouwer, R. J. Darton, R. E. Morris and M. H. Levitt, J. Am. Chem. Soc., 2005, 127, 10365–10370 CrossRef CAS PubMed.
- D. H. Brouwer, I. L. Moudrakovski, R. J. Darton and R. E. Morris, Magn. Reson. Chem., 2010, 48, S113–S121 CrossRef CAS PubMed.
- D. H. Brouwer, J. Am. Chem. Soc., 2008, 130, 6306–6307 CrossRef CAS PubMed.
- F. A. Perras and D. L. Bryce, J. Phys. Chem. C, 2012, 116, 19472–19482 CAS.
- C. P. Romao, F. A. Perras, U. Werner-Zwanziger, J. A. Lussier, K. J. Miller, C. M. Calahoo, J. W. Zwanziger, M. Bieringer, B. A. Markinovic, D. L. Bryce and M. A. White, Chem. Mater., 2015, 27, 2633–2646 CrossRef CAS.
- D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. M. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. Della Valle, G. R. Desiraju, B. P. van Eijck, J. C. Facelli, M. B. Ferraro, D. Grillo, M. Habgood, D. W. M. Hofmann, F. Hofmann, K. V. J. Jose, P. G. Karamertzanis, A. V. Kazantsev, J. Kendrick, L. N. Kuleshova, F. J. J. Leusen, A. V. Maleev, A. J. Misquitta, S. Mohamed, R. J. Needs, M. A. Neumann, D. Nikylov, A. M. Orendt, R. Pal, C. C. Pantelides, C. J. Pickard, L. S. Price, S. L. Price, H. A. Scheraga, J. van de Streek, T. S. Thakur, S. Tiwari, E. Venuti and I. K. Zhitkov, Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 535–551 CAS.
- G. M. Day, T. G. Cooper, A. J. Cruz-Cabeza, K. E. Hejczyk, H. L. Ammon, S. X. M. Boerrigter, J. S. Tan, R. G. Della Valle, E. Venuti, J. Jose, S. R. Gadre, G. R. Desiraju, T. S. Thakur, B. P. van Eijck, J. C. Facelli, V. E. Bazterra, M. B. Ferraro, D. W. M. Hofmann, M. A. Neumann, F. J. J. Leusen, J. Kendrick, S. L. Price, A. J. Misquitta, P. G. Karamertzanis, G. W. A. Welch, H. A. Scheraga, Y. A. Arnautova, M. U. Schmidt, J. van de Streek, A. K. Wolf and B. Schweizer, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 107–125 CAS.
- G. M. Day, W. D. S. Motherwell, H. L. Ammon, S. X. M. Boerrigter, R. G. Della Valle, E. Venuti, A. Dzyabchenko, J. D. Dunitz, B. Schweizer, B. P. van Eijck, P. Erk, J. C. Facelli, V. E. Bazterra, M. B. Ferraro, D. W. M. Hofmann, F. J. J. Leusen, C. Liang, C. C. Pantelides, P. G. Karamertzanis, S. L. Price, T. C. Lewis, H. Nowell, A. Torrisi, H. A. Scheraga, Y. A. Arnautova, M. U. Schmidt and P. Verwer, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 511–527 CAS.
- J. P. M. Lommerse, W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Gavezzotti, D. W. M. Hofmann, F. J. J. Leusen, W. T. M. Mooij, S. L. Price, B. Schweizer, M. U. Schmidt, B. P. van Eijck, P. Verwer and D. E. Williams, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 697–714 CAS.
- W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Dzyabchenko, P. Erk, A. Gavezzotti, D. W. M. Hofmann, F. J. J. Leusen, J. P. M. Lommerse, W. T. M. Mooij, S. L. Price, H. Scheraga, B. Schweizer, M. U. Schmidt, B. P. van Eijck, P. Verwer and D. E. Williams, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 647–661 Search PubMed.
- G. M. Day, Crystallogr. Rev., 2011, 17, 3–52 CrossRef.
- C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201 CrossRef PubMed.
- E. Salager, G. M. Day, R. S. Stein, C. J. Pickard, B. Elena and L. Emsley, J. Am. Chem. Soc., 2010, 132, 2564–2566 CrossRef CAS PubMed.
- G. M. Day, W. D. S. Motherwell and W. Jones, Phys. Chem. Chem. Phys., 2007, 9, 1693–1704 RSC.
- M. Baias, C. M. Widdifield, J.-N. Dumez, H. P. G. Thompson, T. G. Cooper, E. Salager, S. Bassil, R. S. Stein, A. Lesage, G. M. Day and L. Emsley, Phys. Chem. Chem. Phys., 2013, 15, 8069–8080 RSC.
- M. Baias, J.-N. Dumez, P. H. Svensson, S. Schantz, G. M. Day and L. Emsley, J. Am. Chem. Soc., 2013, 135, 17501–17507 CrossRef CAS PubMed.
- C. J. Pickard and R. J. Needs, Phys. Rev. Lett., 2006, 97, 045504 CrossRef PubMed.
- J. P. K. Doye and C. P. Massen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 016128 CrossRef PubMed.
- H. Jung, P. K. Allan, Y.-Y. Hu, O. J. Borkiewicz, X.-L. Wang, W.-Q. Han, L.-S. Du, C. J. Pickard, P. J. Chupas, K. W. Chapman, A. J. Morris and C. P. Grey, Chem. Mater., 2015, 27, 1031–1041 CrossRef CAS.
- K. A. See, M. Leskes, J. M. Griffin, S. Britto, P. D. Matthews, A. Emly, A. Van der Ven, D. S. Wright, A. J. Morris, C. P. Grey and R. Seshadri, J. Am. Chem. Soc., 2014, 136, 16368–16377 CrossRef CAS PubMed.
- R. F. Moran, D. McKay, J. Pickard Chris, A. J. Berry, J. M. Griffin and S. E. Ashbrook, Phys. Chem. Chem. Phys., 2016, 18, 10173–10181 RSC.
- A. J. Morris, C. P. Grey and C. J. Pickard, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 054111 CrossRef.
- J. M. Griffin, A. J. Berry, D. J. Frost, S. Wimperis and S. E. Ashbrook, Chem. Sci., 2013, 4, 1523–1538 RSC.
- J. Schmidt and D. Sebastiani, J. Chem. Phys., 2005, 123, 074501 CrossRef CAS PubMed.
- E. Salager, R. S. Stein, C. J. Pickard, B. Elena and L. Emsley, Phys. Chem. Chem. Phys., 2009, 11, 2610–2621 RSC.
- M. Dračínský and P. Bouř, J. Comput. Chem., 2012, 33, 1080–1089 CrossRef PubMed.
- B. Monserrat, R. J. Needs and C. J. Pickard, J. Chem. Phys., 2014, 141, 134113 CrossRef PubMed.
- R. Nemausat, D. Cabaret, C. Gervais, C. Brouder, N. Trcera, A. Bordage, I. Errea and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 144310 CrossRef.
- Y. J. Lee, B. Bingöl, T. Murakhtina, D. Sebastiani, W. H. Meyer, G. Wegner and H. W. Spiess, J. Phys. Chem. B, 2007, 111, 9711–9721 CrossRef CAS PubMed.
- J.-N. Dumez and C. J. Pickard, J. Chem. Phys., 2009, 130, 104701 CrossRef PubMed.
- I. D. Gortari, G. Portella, X. Salvatella, V. S. Bajaj, P. C. A. van der Wel, J. R. Yates, M. D. Segall, C. J. Pickard, M. C. Payne and M. Vendruscolo, J. Am. Chem. Soc., 2010, 132, 5993–6000 CrossRef PubMed.
- M. Robinson and P. D. Haynes, J. Chem. Phys., 2010, 133, 084109 CrossRef PubMed.
- M. Dračínský and P. Hodgkinson, CrystEngComm, 2013, 15, 8705–8712 RSC.
- M. Dračínský and P. Hodgkinson, Chem. – Eur. J., 2014, 20, 2201–2207 CrossRef PubMed.
- J. M. Griffin, S. Wimperis, A. J. Berry, C. J. Pickard and S. E. Ashbrook, J. Phys. Chem. C, 2009, 113, 465–471 CAS.
- C. Bonhomme, P. Toledano, J. Maquet, J. Livage and L. Bonhomme-Coury, J. Chem. Soc., Dalton Trans., 1997, 1617–1626 RSC.
- C. Zhang, F. Babonneau, C. Bonhomme, R. M. Laine, C. L. Soles, H. A. Hristov and A. F. Yee, J. Am. Chem. Soc., 1998, 120, 8380–8391 CrossRef CAS.
- F. Mammeri, N. Douja, C. Bonhomme, F. Ribot, F. Babonneau and S. Dirè, Mater. Res. Soc. Symp. Proc., 2004, 847, EE13.26 CrossRef.
- C. Gervais, L. Bonhomme-Coury, F. Mauri, F. Babonneau and C. Bonhomme, Phys. Chem. Chem. Phys., 2009, 11, 6953–6961 RSC.
- G. Kim, J. M. Griffin, F. Blanc, S. M. Haile and C. P. Grey, J. Am. Chem. Soc., 2015, 137, 3867–3876 CrossRef CAS PubMed.
- J. M. Griffin, A. J. Miller, A. J. Berry, S. Wimperis and S. E. Ashbrook, Phys. Chem. Chem. Phys., 2010, 12, 2989–2998 RSC.
- S. Antonijevic, S. E. Ashbrook, S. Biedasek, R. I. Walton, S. Wimperis and H. Yang, J. Am. Chem. Soc., 2006, 128, 8054–8062 CrossRef CAS PubMed.
- D. Massiot, R. J. Messinger, S. Cadars, M. Deschamps, V. Montouillout, N. Pellerin, E. Veron, M. Allix, P. Florian and F. Fayon, Acc. Chem. Res., 2013, 46, 1975–1984 CrossRef CAS PubMed.
- D. Laurencin, N. Almora-Barrios, N. H. de Leeuw, C. Gervais, C. Bonhomme, F. Mauri, W. Chrzanowski, J. C. Knowles, R. J. Newport, A. Wong, Z. Gan and M. E. Smith, Biomaterials, 2011, 32, 1826–1837 CrossRef CAS PubMed.
- L. Buannic, F. Blanc, D. S. Middlemiss and C. P. Grey, J. Am. Chem. Soc., 2012, 134, 14483–14498 CrossRef CAS PubMed.
- J. Cuny, S. Messaoudi, V. Alonzo, E. Furet, J.-F. Halet, E. Le Fur, S. E. Ashbrook, C. J. Pickard, R. Gautier and L. Le Polles, J. Comput. Chem., 2008, 29, 2279–2287 CrossRef CAS PubMed.
- V. R. Seymour, E. C. V. Eschenroeder, P. A. Wright and S. E. Ashbrook, Solid State Nucl. Magn. Reson., 2015, 65, 64–74 CrossRef CAS PubMed.
- M. R. Mitchell, D. Carnevale, R. Orr, K. R. Whittle and S. E. Ashbrook, J. Phys. Chem. C, 2012, 116, 4273–4286 CAS.
- M. R. Mitchell, S. W. Reader, K. E. Johnston, C. J. Pickard, K. R. Whittle and S. E. Ashbrook, Phys. Chem. Chem. Phys., 2011, 13, 488–497 RSC.
- P. Florian, E. Veron, T. F. G. Green, J. R. Yates and D. Massiot, Chem. Mater., 2012, 24, 4068–4079 CrossRef CAS.
- C. Ferrara, C. Tealdi, A. Pedone, M. C. Menziani, A. J. Rossini, G. Pintacuda and P. Mustarelli, J. Phys. Chem. C, 2013, 117, 23451–23458 CAS.
- S. Cadars, A. Lesage, C. J. Pickard, P. Sautet and L. Emsley, J. Phys. Chem. A, 2009, 113, 902–911 CrossRef CAS PubMed.
- V. R. Seymour, E. C. V. Eschenroeder, M. Castro, P. A. Wright and S. E. Ashbrook, CrystEngComm, 2013, 15, 8668–8679 RSC.
- R. Dervioğlu, D. S. Middlemiss, F. Blanc, Y.-L. Lee, D. Morgan and C. P. Grey, Chem. Mater., 2015, 27, 3861–3873 CrossRef PubMed.
- D. Carnevale, V. del Amo, D. Philp and S. E. Ashbrook, Tetrahedron, 2010, 66, 6238–6250 CrossRef CAS.
- S. Cadars, M. Allix, D. H. Brouwer, R. Shayib, M. Suchomel, M. N. Garaga, A. Rakhmatullin, A. W. Burton, S. I. Zones, D. Massiot and B. F. Chmelka, Chem. Mater., 2014, 26, 6994–7008 CrossRef CAS.
- E. Véron, M. N. Garaga, D. Pelloquin, S. Cadars, M. Suchomel, E. Suard, D. Massiot, V. Montouillout, G. Matzen and M. Allix, Inorg. Chem., 2013, 52, 4250–4258 CrossRef PubMed.
- T. Charpentier, S. Ispas, M. Profeta, F. Mauri and C. J. Pickard, J. Phys. Chem. B, 2004, 108, 4147–4161 CrossRef CAS.
- T. Charpentier, M. C. Menziani and A. Pedone, RSC Adv., 2013, 3, 10550–10578 RSC.
- A. Pedone, E. Gambuzzi and M. C. Menziani, J. Phys. Chem. C, 2012, 116, 14599–14609 CAS.
- Q. Z. Ni, E. Daviso, T. V. Can, E. Markhasin, S. K. Jawla, T. M. Swager, R. J. Temkin, J. Herzfeld and R. G. Griffin, Acc. Chem. Res., 2013, 46, 1933–1941 CrossRef CAS PubMed.
- D. M. Dawson, L. E. Jamieson, M. I. H. Mohideen, A. C. McKinlay, I. A. Smellie, R. Cadou, N. S. Keddie, R. E. Morris and S. E. Ashbrook, Phys. Chem. Chem. Phys., 2013, 15, 919–929 RSC.
| This journal is © The Royal Society of Chemistry 2016 |